Measuring of Thermal Conductivities of Soils and Rocks to Be Used in the Calculation of A Geothermal Installation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Suggested Method
2.2. Theoretical Basis
2.3. Heat Flux Analysis
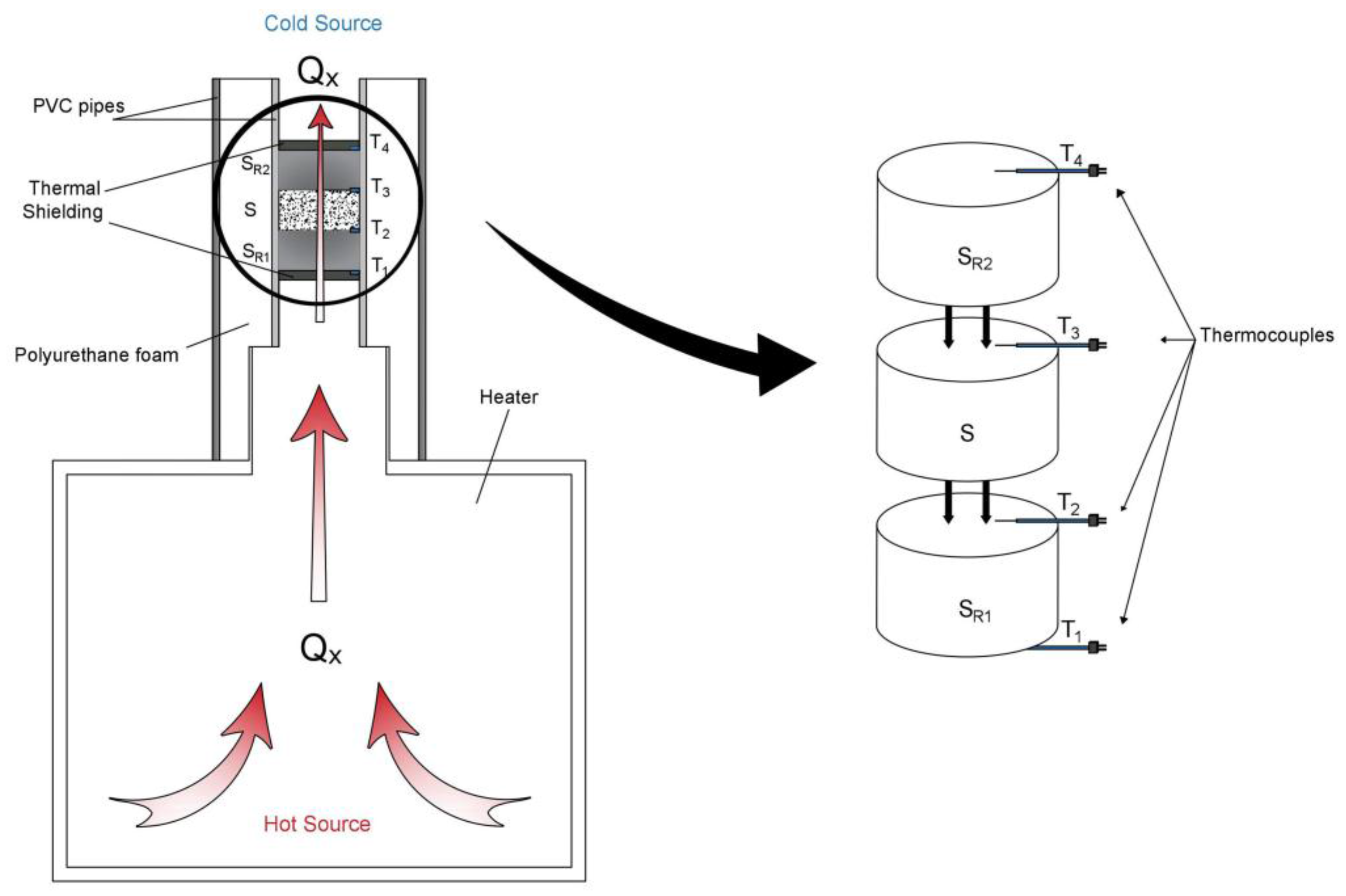
2.4. Equipment Description
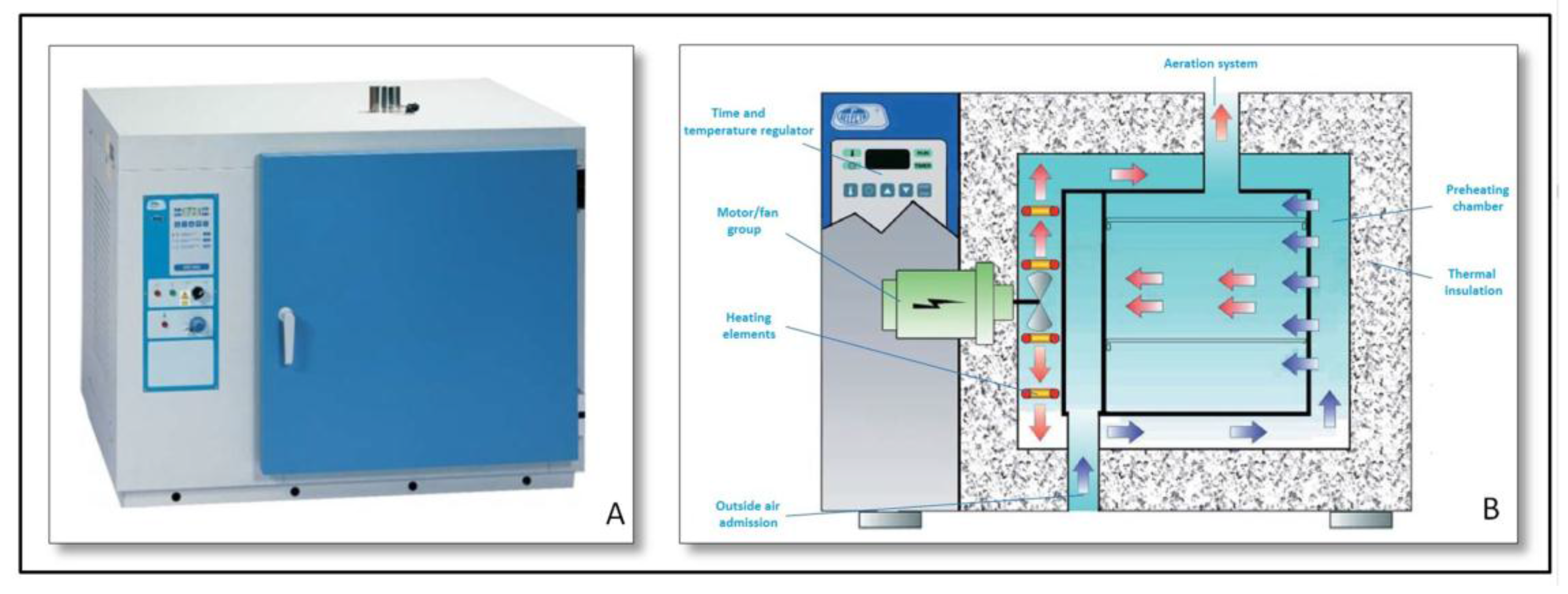
- Sterilization and drying heater “Dry-Big” (Figure 3):Heater with air force circulation mechanism, regulated by a microprocessor and with temperature and time digital reading. It constitutes the heat source used for the calculation of the thermal conductivity parameter.A set of working temperatures was tested to analyze the evolution of the thermal conductivity with the temperature. Thus, heat source was regulated according to the most suitable temperature.
- PVC pipes (Figure 1):Two PVC hollow cylinders were used in the construction of the equipment.
- Hollow cylinder of diameter slightly higher to the air outlet placed on the top of the heater. This PVC pipe of diameter (0.10 m) coupled to the air outlet was adiabatically insulated in the whole contour by polyurethane foam.
- Hollow cylinder 0.052 m of diameter, placed inside the previous pipe. It behaves as fastener of the samples. The space between both pipes was adiabatically insulated by polyurethane foam.
- Polyurethane foam (Figure 1):Polyurethane foam was used to insulate the system from any external influence getting at the same time one-dimensional circulation of the heat flux through the samples.It is a porous plastic material made up of a bubble aggregation. It consists of the chemical reaction of two polyol and isocyanate, although it accepts multiple additives. Its insulation capacity comes from the low thermal conductivity of the gas that its closed cells send.
- Pattern samples (Figure 2):Two reference samples with known thermal conductivity values were used. These samples are made of pure aluminum. Given the high thermal conductivity of this element, it facilitates the heat flux transmission through the system. The dimensions of both patterns are: 0.10 m of thickness and 0.05 m of diameter.
- Thermocouples (Figure 1):Four sounding lines (constituted by chrome and aluminum alloys) connected to a digital thermometer made possible the measurement of temperatures in four areas. Before its use, thermocouples were duly calibrated [28].
3. Methodology of the Thermal Conductivity Test
3.1. Materials Selection
3.2. Samples Preparation
3.2.1. Rocky Samples
3.2.2. Soil Samples
3.3. Placing of Samples in the Measuring Equipment and Determination of Thermal Conductivities
4. Analysis of the Measuring Process
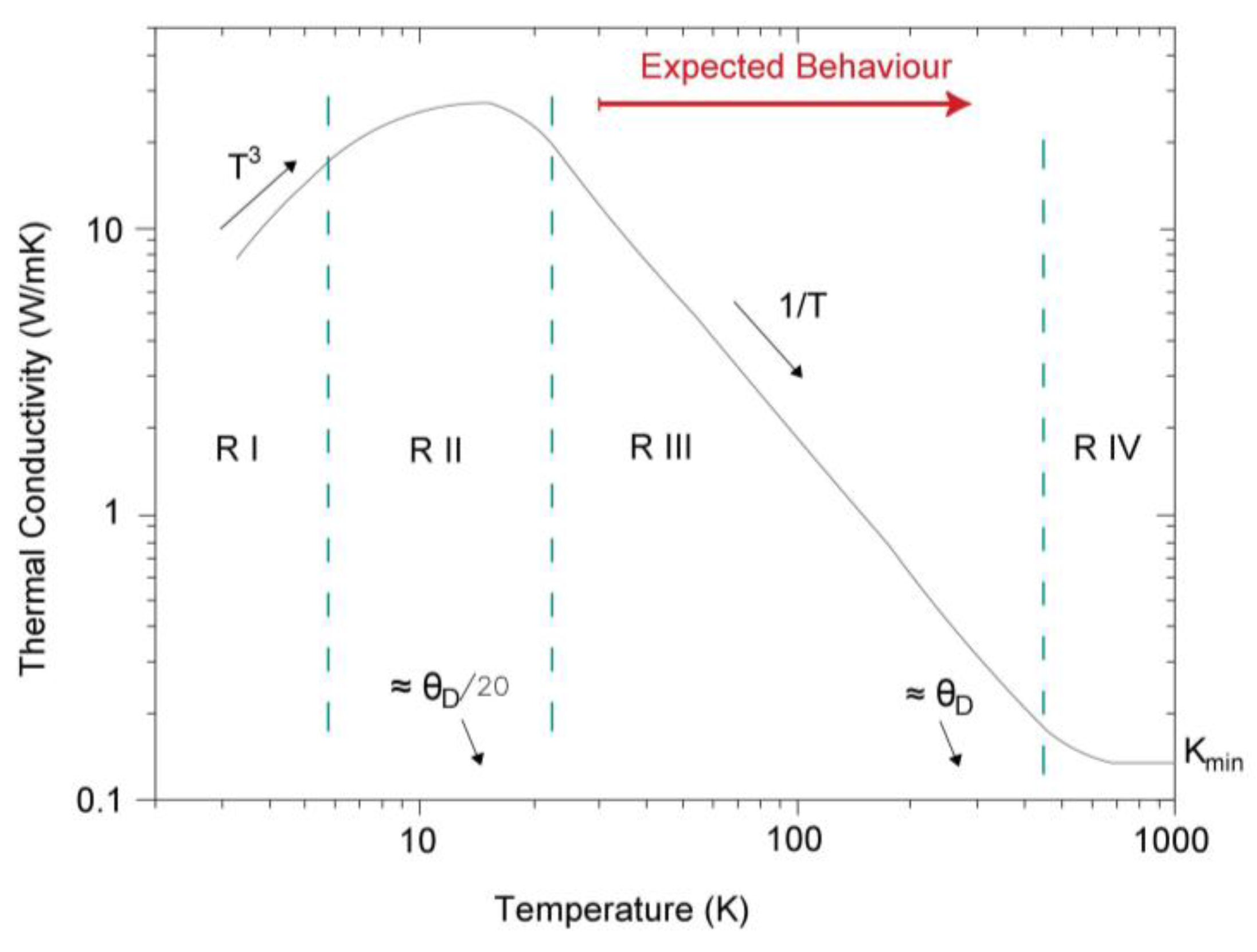
4.1. Evolution of the Thermal Conductivity with Temperature
4.2. Variation of the Thermal Conductivity with the Sample Thickness
- Most of the thermal conductivity values are around 2 W/mK. Increasing the temperature, these values decrease as it was expected for a crystalline solid. However, the reduction of the thermal conductivity parameter is not constant in the different sample thicknesses, and is not the expected 0.0084 W/mK calculated in Section 4.1. Evolution of thermal conductivity with temperature.Therefore, in a crystalline solid, thermal conductivity decreases when temperature grows. However, it was not possible to set a model of behavior of this reduction because it does not follow any constant pattern.
- Regarding the different sample thickness, Table 4 shows the measurements carried out at the laboratory equipment (four different thicknesses for each one of the three work temperatures). The optimal dimensions of the sample S could be established based on the results of these measurements.Thus, analyzing Table 4, it can be observed that, for the three temperatures, the values of thermal conductivity for each of the thickness are around the same value (~2 W/mK). These data agree with the expected thermal conductivity value for a granitic material. However, for the case of the highest thickness, the result of thermal conductivity moves away from the rest of results for lower thickness. All this made it possible to set the sample thicknesses for which the present method works properly.On the basis of these results, with sample thicknesses greater than 0.0131 m, the procedure described in this paper does not provide reliable values. In these cases, results are highly anomalous due to a high dissipation of the heat flux through the sample S.
- The following working conditions were established in the thermal conductivity apparatus:
- −
- Temperature of the heat source was set in 313.15 K. Although results were acceptable in the three temperatures (313.15 K, 338.15 K and 358.15 K), this value is closer to the ground temperature in a very low enthalpy geothermal installation.
- −
- Thickness of the sample S could not exceed in any case the mentioned 0.0131 m for the reasons previously justified.
5. Thermal Conductivity Results
6. Validity of the Method
7. Influence of the Thermal Conductivity Parameter in the Geothermal Measuring
8. Conclusions
- Temperature of the cold source (ambient temperature) was controlled at all times and set in a constant value to avoid external thermal influences on the thermal conductivity device.
- The insulation placed around the system minimized the radial heat flux but did not eliminate it. As a result, corrections of this heat flux were made for each of the temperatures set at the heater.
- A high precision was needed when measuring the sample thickness due to its excessive influence in the calculation of the thermal conductivity parameter.
- Thermocouples were carefully placed to ensure a complete contact with the faces of the samples.
- Long-term measurements to guarantee the stabilization of the heat flux.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Leach, A.G. The thermal conductivity of foams. I: Models for heat conduction. J. Phys. D 1993, 26, 733–739. [Google Scholar] [CrossRef]
- Balbay, A.; Esen, M. Experimental investigation of using ground source heat pump system for snow melting on pavements and bridge decks. Sci. Res. Essays 2010, 5, 3955–3966. [Google Scholar]
- Balbay, A.; Esen, M. Temperature distributions in pavement and bridge slabs heated by using vertical ground-source heat pump systems. Acta Sci. Technol. 2013, 35, 677–685. [Google Scholar] [CrossRef]
- Kabar, M.; Nowak, W.; Sobanski, R. Principles of Exploitation Geothermal Energy Water at Targets of Heating Buildings; Project KBN; Energy Water at Targets of Heating Buildings: Szczecin, Poland, 1999. [Google Scholar]
- Blázquez, C.S.; Martín, A.F.; García, P.C.; Sánchez Pérez, L.S.; del Caso, S.J. Analysis of the process of design of a geothermal installation. Renew. Energy 2016, 89, 188–199. [Google Scholar] [CrossRef]
- Peláez, P.C.; Carnicero, J.M.P.; García, R.L.; Peragon, F.C. Desarrollo de equipo para la realización de test de respuesta térmica del terreno (TRT) en instalaciones geotérmicas. Dyna 2014, 89, 316–324. [Google Scholar] [CrossRef]
- ASTM International. ASTM Standard C 177-10, Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Terzic, M.; Miloševic, N.; Stepanic, N.; Petricevic, S. Development of a single-sided guarded hot plate apparatus for thermal conductivity measurements. Therm. Sci. 2016, 20, S321–S329. [Google Scholar] [CrossRef]
- Ramstad, R.K.; de Beer, H.; Midttømme, K.; Koziel, J.; Wissing, B. Thermal Diffusivity Measurement at NGU—Status and Method Development 2005–2008; Geological Survey of Norway: Trondheim, Norway, 2009. [Google Scholar]
- Lira-Cortés, L.; González Rodríguez, O.J.; Méndez-Lango, E. Sistema de Medición de la Conductividad Térmica de Materiales Sólidos Conductores, Diseño y Construcción; Simposio de Metrología Santiago de Querétaro: Querétaro, Mexico, 2008. [Google Scholar]
- Liou, J.-C.; Tien, N.-C. Estimation of the thermal conductivity of granite using a combination of experiments and numerical simulation. Int. J. Rock Mech. Min. Sci. 2016, 81, 39–46. [Google Scholar] [CrossRef]
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Krishnaiah, S.; Singh, D.N.; Jadhav, G.N. A methodology for determining thermal properties of rocks. Min. Sci. 2004, 41, 877–882. [Google Scholar] [CrossRef]
- Kukkonen, I.; Lindberg, A. Thermal Conductivity of Rocks at the TVO Investigation Sites Olkiluoto, Romuvaara and Kivetty; Report YJT-95-08, 29; Nuclear Waste Commission of Finnish Power Companies: Helsinki, Finland, 1995. [Google Scholar]
- Jorand, R.; Vogt, C.; Marquart, G.; Clauser, C. Effective thermal conductivity of heterogeneous rocks from laboratory experiments and numerical modeling. J. Geophys. Res. 2013, 118, 5225–5235. [Google Scholar] [CrossRef]
- Popov, Y.A. Optical scanning technology for nondestructive contactless measurements of thermal conductivity and diffusivity of solid matters. In Proceedings of the 4th World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Brussels, Belgium, 2–6 June1997; pp. 109–116. [Google Scholar]
- Xiao, B.; Yang, Y.; Chen, L. Developing a novel form of thermal conductivity of nanofluids with Brownian motion effect by means of fractal geometry. Powder Technol. 2013, 239, 409–414. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int. J. Heat Mass Transf. 2017, 105, 623–637. [Google Scholar] [CrossRef]
- Blázquez, C.S.; Martín, A.F.; Nieto, I.M.; García, P.C.; Pérez, L.S.S.; Aguilera, D.G. Thermal conductivity map of the Avila region (Spain) based on thermal conductivity measurements of different rock and soil samples. Geothermics 2017, 65, 60–71. [Google Scholar] [CrossRef]
- Barry-Macaulay, D.; Bouazza, A.; Singh, R.M.; Wang, B.; Ranjith, P.G. Thermal conductivity of soils and rocks from the Melbourne (Australia) region. Eng. Geol. 2013, 164, 131–138. [Google Scholar] [CrossRef]
- ASTM International. ASTM D5334, Standard Test Method for Determination of Thermal Conductivity of Soil and Soft Rock by Thermal Needle Probe Procedure; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ASTM International. ASTM E1225-99, Standard Test Method for Thermal Conductivity of Solids by the Guarded Comparative Longitudinal Heat Flow Technique; ASTM International: West Conshohocken, PA, USA, 1999. [Google Scholar]
- Jean-Baptiste, J.F. Remarques generales sur les temperatures du globe terrestre et des espaces plan etaires. Ann. Chim. Phys. 1824, 27, 136–167. [Google Scholar]
- Jean-Baptiste, J.F. Theorie Analytique de la Chaleur; Firmin Didot: Paris, France, 1822. [Google Scholar]
- Jean-Baptiste, J.F. Memoire sur les temperatures du globe terrestre et des espaces planetaires. Mem. l’Acad. R. Sci. 1827, 7, 569–604. [Google Scholar]
- Bevington, R.P.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 2nd ed.; WCB/McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Pei, W.; Yu, W.; Li, S.; Zhou, J. A new method to model the thermal conductivity of soil–rock media in cold regions: An example from permafrost regions tunnel. Cold Reg. Sci. Technol. 2013, 95, 11–18. [Google Scholar] [CrossRef]
- ASTM International. ASTM E220, Test Method for Calibration of Thermocouples by Comparison Techniques; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- AENOR. UNE 103-300-93. Determinación de la Humedad de un Suelo Mediante Secado en Estufa; AENOR: Marid, Spain, 1993. [Google Scholar]
- AENOR. UNE 103-500-94. Ensayo Proctor de Compactación; AENOR: Marid, Spain, 1994. [Google Scholar]
- Chung, P.W.; Tamma, K.K.; Namburu, R.R. Homogenization of temperature-dependent thermal conductivity in composite materials. J. Thermophys. Heat Transf. 2001, 15, 10–17. [Google Scholar] [CrossRef]
- Fernández, F.; Rondón, E.; Sánchez, F.; Salas, K.; García, V.; Briceño, J. Conductividad térmica en sólidos a altas temperaturas. Rev. Fac. Ing. UCV 2006, 21, 21–27. [Google Scholar]
- Nakshabandi, G.A.I.; Kohnke, H. Thermal conductivity and diffusivity of soils as related to moisture tension and other physical properties. Agric. Meteorol. 1965, 2, 271–279. [Google Scholar] [CrossRef]
- Taylor, R.J. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Herndon, VA, USA, 1997. [Google Scholar]
- Kukkonen, I.; Lindberg, A. Thermal Properties of Rocks at the Investigation Sites: Measured and Calculated Thermal Conductivity. Specific Heat Capacity and Thermal Diffusivity; Geological Survey of Finland: Espoo, Filand, 1998. [Google Scholar]
- Prontuario de Soluciones Constructivas; Código Técnico de la Edificación; Instituto de Ciencias de la Construcción Eduardo Torroja e Instituto de Ciencias de la Construcción de Castilla y León: Castilla y León, Spain, 2007.






| Authors | Contributions | Limitations |
|---|---|---|
| Terzic et al., 2016 | The model offers an estimation of the both separate and total parasitic heat fluxes, improving the accuracy and uncertainty of final results. | The method is limited to solid materials with thermal conductivity values from 0.1 to 2 W/mK, in the temperature range 10–50 °C. |
| Ramstad et al., 2009 | The measurement time is around 200 s. It allows thermal conductivity measurements up to 4.5 W/mK. | The improved version of this method requires a heat source with constant temperature of 300 °C. |
| Lira-Cortés et al., 2008 | The system is suitable to measure the thermal conductivity of conductive materials with a design error of 2% order. | The method cannot be used in poor conductivity materials given the high design errors |
| Liou and Tien, 2016 | The three techniques provide fairly similar values for the same granite sample. TPS method presents high accuracy and simplicity to sample preparation. | For the thermal probe test, it is difficult to ensure that the air in filled holes is completely removed. |
| Krishnaiah et al., 2004 | The method considers the thermal conductivity variations with the samples porosity. | Trends variations of thermal conductivity with porosity were not established and validated in a standard way. |
| Kukkonen and Lindberg, 1995 | Thermal conductivity is calculated from using the arithmetic, harmonic and geometric mean values and compared with the measured one. | The grain size and the textural variation of some samples affect the thermal conductivity measurements. |
| Jorand et al., 2013 | It combines high-accuracy laboratory measurements and numerical petro physics. They use thermal conductivity scanning for obtaining 2-D thermal conductivity maps reflecting the structural heterogeneity in two samples. Measurements are made in two profiles along the core axis and perpendicular to it. Anisotropy of thermal conductivity is also estimated. | Heterogeneous proportions of lateral heat flow within the sample affect both heat transport in general and the determination of effective thermal conductivity. The method might not solve the entire upscaling problem. |
| Proposed method | The method allows both rocks and soils thermal conductivity measurements. It also allows thermal conductivity measurements up to the aluminum thermal conductivity. Thermal conductivity results agree with the common values officially accepted for each material. | Long term measurements. It requires a constant ambient temperature to avoid influencing the measurements. Anisotropy is not considered. |
| Sample | Description |
|---|---|
| 1 | Common Granite Constituted by quartz, feldspar and micas and very varied group of secondary minerals in percentages under 5% like: apatite, esfena, oxides, allanite, zircon, etc. |
| 2 | Adamellite Plutonic igneous rock, with more than 65% of silica and more than 20% of quartz. |
| 3 | Granodiorite Plutonic rock of quartz, plagioclases, potassium feldspar, biotite and amphibole. |
| 4 | Red Granite Igneous rock known as “Bleeding Granite” with a high silica corn (more than 80%). |
| 5 | Common Slate Thin grain metamorphic rock with sericite, muscovite, chlorite and quartz. |
| 6 | Quartzite Hard metamorphic rock composed by quartz (more than 90%), it can also contain muscovite, orthoses or albite. Its structure presents soldered quartz crystals. |
| 7 | Sandstone Sedimentary rock with clasts about the size of the sand. The grains have quartz, feldspars or rock fragments. |
| 8 | Gypsum Mineral of hydrated calcium sulphate givingmono mineral sedimentary rocks. |
| 9 | Pumice Vitreous volcanic igneous rock. It is grey with silica dioxide, aluminum oxide and other oxides. |
| 10 | Orto gneiss Gneiss generated by dynamic metamorphism of eruptive rocks of silica. It is composed by quartz, feldspar and mica. |
| 11 | White marble Metamorphic compact rock with calcium carbonates (more than 90%). It is predominately white. |
| 12 | Basaltic sandstone Sandstones (<15% of matrix) whose content in rock fragments is superior to 25% and higher to the feldspar content. Its origin is basaltic, coming from a volcanic igneous rock characteristic for its dark color and mafic structure. |
| 13 | Tertiary Soils Tertiary materials (clays, sands, sandstones and conglomerates) without compaction among the grains. |
| Substance | Debye Temperature (K) |
|---|---|
| Aluminum | 428 |
| Cadmium | 209 |
| Chromium | 630 |
| Copper | 343.5 |
| Gold | 165 |
| Iron | 470 |
| Lead | 105 |
| Manganese | 410 |
| Nickel | 450 |
| Platinum | 240 |
| Silicon | 645 |
| Silver | 225 |
| Tantalum | 240 |
| Tin | 200 |
| Titanium | 420 |
| Wolfram | 400 |
| Zinc | 327 |
| Carbon | 2230 |
| Ice | 192 |
| Heat Source Temperature (K) | Sample Thickness (m) | Sample Medium Temperature (K) | Heat Flux “Q“ (W) | Thermal Conductivity “k” (W/mK) |
|---|---|---|---|---|
| 313.15 | 0.0061 | 295.95 | 8.13 | 2.11 |
| 0.0090 | 295.92 | 5.42 | 2.16 | |
| 0.0131 | 295.80 | 5.42 | 2.13 | |
| 0.0162 | 299.55 | 8.13 | 5.59 | |
| 338.15 | 0.0061 | 296.20 | 19.22 | 2.06 |
| 0.0090 | 302.30 | 13.31 | 2.10 | |
| 0.0131 | 302.30 | 9.24 | 2.13 | |
| 0.0162 | 305.55 | 18.49 | 4.77 | |
| 358.15 | 0.0061 | 305.90 | 23.58 | 1.98 |
| 0.0090 | 309.90 | 22.43 | 2.09 | |
| 0.0131 | 308.15 | 17.83 | 2.12 | |
| 0.0162 | 306.10 | 21.28 | 4.75 |
| Increase of Temperature from 313.15 K to 338.15 K | |||
|---|---|---|---|
| Thickness (m) | Increase of “T” among Samples (°) | Difference of “k” (W/mK) | Decrease by Grade (W/mK) |
| 0.0061 | 0.25 | 0.05 | 0.2000 |
| 0.0090 | 6.38 | 0.06 | 0.0094 |
| 0.0131 | 6.50 | 0.00 | 0.0000 |
| 0.0162 | 6.00 | 0.82 | 0.1366 |
| Increase of Temperature from 338.15 K to 358.15 K | |||
|---|---|---|---|
| Thickness (m) | Increase of “T” among Samples (K) | Difference of “k” (W/mK) | Decrease by Grade (W/mK) |
| 0.006 | 9.70 | 0.08 | 0.0082 |
| 0.009 | 7.60 | 0.01 | 0.0013 |
| 0.013 | 5.85 | 0.01 | 0.0017 |
| 0.016 | 0.55 | 0.02 | 0.0360 |
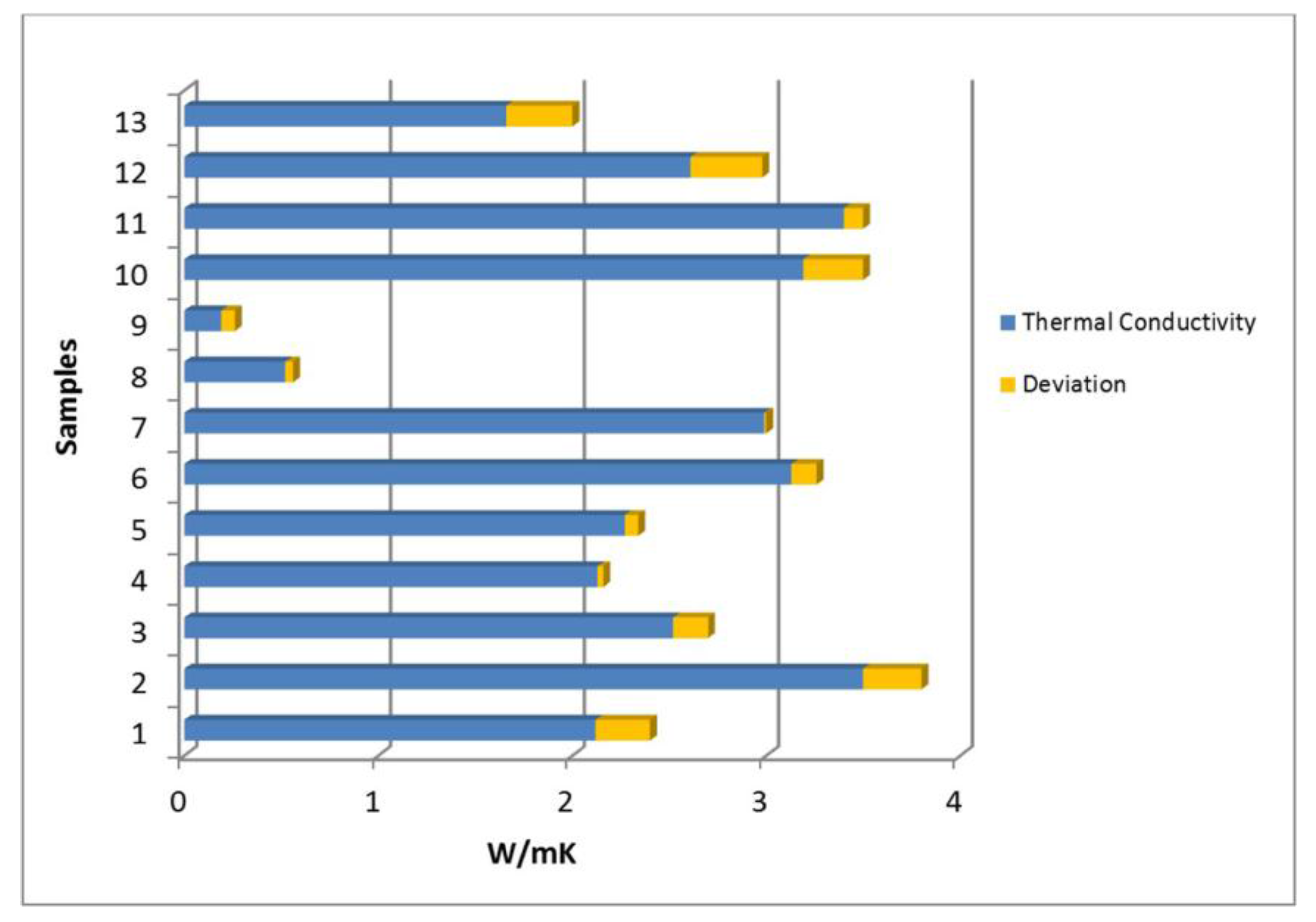
| Sample | Thickness (m) | K1 (W/mK) | K2 (W/mK) | K3 (W/mK) | Medium K <x> (W/mK) | Standard Deviation σx | Derivate Error |
|---|---|---|---|---|---|---|---|
| 1 | 0.0090 | 2.16 | 2.12 | 2.09 | 2.12 | 0.035 | ±0.10 |
| 2 | 0.0102 | 3.58 | 3.42 | 3.51 | 3.50 | 0.080 | ±0.10 |
| 3 | 0.0131 | 2.57 | 2.61 | 2.39 | 2.52 | 0.117 | ±0.10 |
| 4 | 0.0103 | 2.15 | 2.11 | 2.13 | 2.13 | 0.020 | ±0.10 |
| 5 | 0.0130 | 2.24 | 2.31 | 2.25 | 2.27 | 0.038 | ±0.10 |
| 6 | 0.0124 | 3.11 | 3.10 | 3.18 | 3.13 | 0.043 | ±0.10 |
| 7 | 0.0132 | 2.99 | 2.97 | 3.02 | 2.99 | 0.025 | ±0.10 |
| 8 | 0.0085 | 0.53 | 0.53 | 0.51 | 0.52 | 0.012 | ±0.10 |
| 9 | 0.0051 | 0.21 | 0.18 | 0.19 | 0.19 | 0.016 | ±0.10 |
| 10 | 0.0082 | 3.15 | 3.24 | 3.17 | 3.19 | 0.047 | ±0.10 |
| 11 | 0.0091 | 3.39 | 3.38 | 3.44 | 3.40 | 0.032 | ±0.10 |
| 12 | 0.0063 | 2.63 | 2.59 | 2.61 | 2.61 | 0.020 | ±0.10 |
| 13 | 0.0090 | 1.77 | 1.58 | 1.63 | 1.66 | 0.098 | ±0.10 |
| Sample | K Measured (W/mK) | K Reference (W/mK) | Deviation-Reference Value (W/mK) |
|---|---|---|---|
| 1 | 2.12 | 2.4 (15% of quartz) | 0.28 |
| 2 | 3.50 | 3.2 (40% of quartz) | 0.3 |
| 3 | 2.52 | 2.7 (25% of quartz) | 0.18 |
| 4 | 2.13 | 2.1 (5% of quartz) | 0.03 |
| 5 | 2.27 | 2.2 | 0.07 |
| 6 | 3.13 | 3 | 0.13 |
| 7 | 2.99 | 3 | 0.01 |
| 8 | 0.52 | 0.56 | 0.04 |
| 9 | 0.19 | 0.12 | 0.07 |
| 10 | 3.19 | 3.5 | 0.31 |
| 11 | 3.40 | 3.5 | 0.1 |
| 12 | 2.61 | 3 | 0.37 |
| 13 | 1.66 | 2 | 0.34 |
| EED Measuring | |||
|---|---|---|---|
| Sample 1 | |||
| k (W/mK) | 2.12 * | 1.80 ** | 2.44 *** |
| Drilling length (m) | 185 | 194 | 174 |
| Sample 2 | |||
| k (W/mK) | 3.50 * | 2.97 ** | 4.02 *** |
| Drilling length (m) | 153 | 161 | 143 |
| Sample 3 | |||
| k (W/mK) | 2.52 * | 2.14 ** | 2.90 *** |
| Drilling length (m) | 174 | 182 | 163 |
| Sample 4 | |||
| k (W/mK) | 2.13 * | 1.81 ** | 2.45 *** |
| Drilling length (m) | 185 | 193 | 173 |
| Sample 5 | |||
| k (W/mK) | 2.27 * | 1.93 ** | 2.61 *** |
| Drilling length (m) | 181 | 192 | 172 |
| Sample 6 | |||
| k (W/mK) | 3.13 * | 2.66 ** | 3.60 *** |
| Drilling length (m) | 160 | 170 | 151 |
| Sample 7 | |||
| k (W/mK) | 2.99 * | 2.54 ** | 3.44 *** |
| Drilling length (m) | 163 | 174 | 154 |
| Sample 8 | |||
| k (W/mK) | 0.52 * | 0.44 ** | 0.60 *** |
| Drilling length (m) | 324 | 333 | 316 |
| Sample 9 | |||
| k (W/mK) | 0.19 * | 0.16 ** | 0.22 *** |
| Drilling length (m) | 449 | 483 | 422 |
| Sample 10 | |||
| k (W/mK) | 3.19 * | 2.71 ** | 3.67 *** |
| Drilling length (m) | 158 | 169 | 150 |
| Sample 11 | |||
| k (W/mK) | 3.40 * | 2.89 ** | 3.91 *** |
| Drilling length (m) | 155 | 166 | 147 |
| Sample 12 | |||
| k (W/mK) | 2.61 * | 2.22 ** | 3.00 *** |
| Drilling length (m) | 172 | 183 | 163 |
| Sample 13 | |||
| k (W/mK) | 1.66 * | 1.41 ** | 1.91 *** |
| Drilling length (m) | 206 | 216 | 196 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sáez Blázquez, C.; Farfán Martín, A.; Martín Nieto, I.; Gonzalez-Aguilera, D. Measuring of Thermal Conductivities of Soils and Rocks to Be Used in the Calculation of A Geothermal Installation. Energies 2017, 10, 795. https://doi.org/10.3390/en10060795
Sáez Blázquez C, Farfán Martín A, Martín Nieto I, Gonzalez-Aguilera D. Measuring of Thermal Conductivities of Soils and Rocks to Be Used in the Calculation of A Geothermal Installation. Energies. 2017; 10(6):795. https://doi.org/10.3390/en10060795
Chicago/Turabian StyleSáez Blázquez, Cristina, Arturo Farfán Martín, Ignacio Martín Nieto, and Diego Gonzalez-Aguilera. 2017. "Measuring of Thermal Conductivities of Soils and Rocks to Be Used in the Calculation of A Geothermal Installation" Energies 10, no. 6: 795. https://doi.org/10.3390/en10060795
APA StyleSáez Blázquez, C., Farfán Martín, A., Martín Nieto, I., & Gonzalez-Aguilera, D. (2017). Measuring of Thermal Conductivities of Soils and Rocks to Be Used in the Calculation of A Geothermal Installation. Energies, 10(6), 795. https://doi.org/10.3390/en10060795









