Abstract
To strengthen the integration of the primary and secondary systems, a concept of Cyber Physical Systems (CPS) is introduced to construct a CPS in Power Systems (Power CPS). The most basic work of the Power CPS is to build an integration model which combines both a continuous process and a discrete process. The advanced form of smart grid, the Active Distribution Network (ADN) is a typical example of Power CPS. After designing the Power CPS model architecture and its application in ADN, a Hybrid System based model and control method of Power CPS is proposed in this paper. As an application example, ADN flexible load is modeled and controlled with ADN feeder power control by a control strategy which includes the normal condition and the underpowered condition. In this model and strategy, some factors like load power consumption and load functional demand are considered and optimized. In order to make up some of the deficiencies of centralized control, a distributed control method is presented to reduce model complexity and improve calculation speed. The effectiveness of all the models and methods are demonstrated in the case study.
1. Introduction
With the rapid development of network technology, and increasing requirements for accuracy and efficiency of industry control, the industry needs to strengthen information acquisition, application and coordination control with the hierarchy-distributed control system. Hence, a new concept of Cyber Physical Systems (CPS) is proposed to promote the tight integration of control, communication, information, industry process, and reveal the integration mechanism of the real and virtual world [1].
CPS stems from embedded systems. To satisfy the performance requirement of spatial layout and power consumption, the traditional embedded system focuses on the optimal resource utilization of hardware and software [2]. However, the embedded system in CPS concentrates on the interaction with the real physical system (controlled object), and focuses on problems such as concurrent event which cannot be perceived if the controlled object is too complicated [3].
Several research results on CPS have been presented. The purpose of them is to explore principle of interaction between cyber and physical systems, promote the system ability of sensing, analysis, decision and control. For example, when operating cardiac surgery by robot arms, the arms should vibrate with the heart at the same frequency to maintain relative rest [4]. CPS models are built in [5,6] for fuel management and airspace management of aviation systems to optimize flight operation.
A power system meets the basic form of CPS. Especially after the smart grid and micro grid are presented, intellectualization and informatization cover almost all parts of the power system from source side to load side, and then the relationship and coordination among these parts are tighter. So the power system has had basis and actual demand to construct a complete CPS.
There are a few researches of CPS in the power system at present. Most of them focus on the influence brought from the information system (including the secondary system and the communication network) to the primary system. For example, in the aspect of reliability of relay protection, cyber factors like fault rates of logical nodes and logical connections in IEC61850 based substation automation system [7] and the fault rate of a communication link [8] are all considered in a traditional physical device reliability assessment. In the aspect of communication network, information system elements including communication routing [9], network time delay [10] and system observability [11] have been integrated into the primary system to analyze stability margin. There are also some researches about information security in the power system, such as information attack occurring in SCADA [12] and substation automation [13]. To test the interaction between the information and primary system, several simulation platforms have been built such as INSPIRE [14], GECO [15], and TASSCS [16].
Besides the influence of information system, some researches consider that continuity and discrete are the main attributes of Cyber and Physical system respectively. So they try to rebuild power grid model according to Hybrid System theory which describes both the continuous dynamic and discrete state, then the object-oriented hybrid power system model library is developed [17], and sliding mode control based on the hybrid models can be applied to DG integrated shipboard power grid [18].
The main target of the Active Distribution Network (ADN) is to promote Distributed Generation (DG) utilization and reduce energy from the external system [19]. In ADN, the control system coordinate with the primary system, complex energy flow, and information flow coexist when operating. Hence, ADN is suitable to be a study object for Power CPS. But, most of the existing ADN researches is on DGs control, and load control has still not been fully considered. The hierarchical control system in [20] is not only used in DG power control, but also in load control.
The load control is always a hot point for research. For instance, the relationship of refrigerators and the frequency in the micro grid are explored in [21]. A Model Predictive Control (MPC) based method is proposed in [22] to optimize the profit of power demand in the commercial office building. From the point of CPS, literature [23] introduces a method of a Real-Time Physical System to reduce system instantaneous power consumption by adjusting the load coincidence factor.
There are several types of model which can be used in CPS to solve different problems. The Hybrid System is a typical one which can reflect CPS connotations, and can be used in control. This paper builds a Hybrid System based modeling structure for Power CPS which is beneficial for analyzing the interactive mechanism between information and the primary system. Then according to the modeling structure, an integration model method and its application are studied to optimally and predictively control the power system by an example of a flexible load control in ADN.
The rest of the paper is organized as follows: Section 2 describes the composition and characteristics of the Power CPS model, and designs application schemes in ADN. Section 3 presents a Hybrid System based CPS model and the control strategy for an ADN flexible load. Aiming at some shortages in Section 3, a distributed ADN flexible load control method is proposed in Section 4. All the models and methods are applied to simulated examples in Section 3 and Section 4 respectively. Section 5 provides concluding remarks.
2. Power CPS Model and Its Application in ADN
Power CPS technical features and key techniques have been summarized in [24]. Among these key techniques, the Cyber Physical model is the most basic work. Figure 1 shows the relationship between technical features and model in Power CPS.
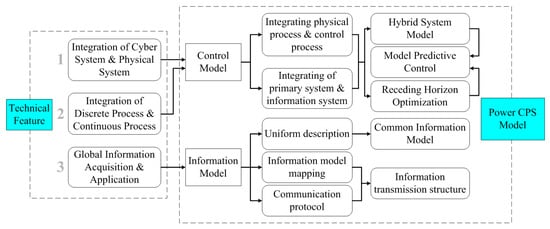
Figure 1.
Relationship of technical features and model in Power Cyber Physical Systems (CPS).
According to the three features in Figure 1, the Power CPS model can be classified into two kinds: “Control Model” and “Information Model”. The “Information Model” corresponds to Feature (3), and this type of model mainly studies a uniform information description mode which can be applied in information exchange after combining with an information transmission structure including the model mapping method and communication protocol.
The “Control Model” reflects Features (1) and (2), and this type of model focuses on promoting the interaction and eliminating the heterogeneity between the primary and the information system in the power grid.
2.1. Control Model Based on Hybrid System
Compared with the Information Model, the ‘Control Model’ undertakes the main tasks of Power CPS control. As is shown in Figure 1, the ‘Control Model’ strengthens the integration of cyber and physical in two aspects.
(1) Integrating physical process and control process
This aspect reflects the interaction between physical characteristic and the control input of primary devices. During the operation, the state variable and output of the primary device change with time continuously, but the control input can be seen as a kind of disturbance which interrupts and changes the current’s continuous dynamic. No matter how the input is transmitted to the primary device, the input affects the device’s physical process in a certain time interval, thus the continuous dynamic switches to new states discretely. Therefore, when the control input is being generated to control a device, continuous process of this device and discrete state switching caused by input should both be considered.
(2) Integrating of primary system and information system
This aspect describes the interaction between the information system, control process and primary system. Where, the information system not only refers to the nodes which may be traversed by information flow, but also the sequence and time of different information flow. So the influence caused by the information system can be represented as topology and sequential logic, and incorporated in the ‘integrating of physical process and control process’ introduced above. Figure 2 illustrates the relationship between two aspects of ‘integrating’ in the ‘Control Model’.
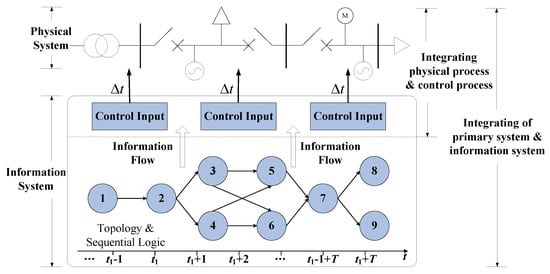
Figure 2.
Relationship between two “Integration” of “Control Model”.
It can be concluded that the controlled primary system contains continuous process and state switching; the information system works discretely and logically. Continuity and discrete are the major attributes of the physical and cyber system respectively. So, Power CPS needs a common model method which is suitable for the physical and the cyber system. Moreover, the common model needs to be used in optimal control.
Several researches have used the mixed continuous and discrete model in power system optimization. The Mixed Integer Quadratic Programming (MIQP) models are built for unit commitment problem in [25,26] and are solved by the cut-and-branch method. A scenario based dynamic economic dispatch model is presented by [27] to optimize the operation cost of uncertain the renewable energy integrated power system. The MIQP model is also used in [28] to diminish power losses in the microgrid laboratory system with several kinds of DGs.
The Hybrid System is such a kind of model that combines the continuous dynamic and discrete state together. It is also able to be transformed to the predictive model and used in receding horizon optimization, and then MPC listed in Figure 1 can be applied based on the Hybrid System model. The Hybrid System based method in Power CPS is not only to optimize the primary system, but also to incorporate the information process into the traditional power system.
2.2. CPS Model and Control in ADN
The ADN control system is shown in Figure 3 which contains three control levels which are the Global Energy Manage System (Global EMS), Area coordination controllers, and Device coordination controllers.
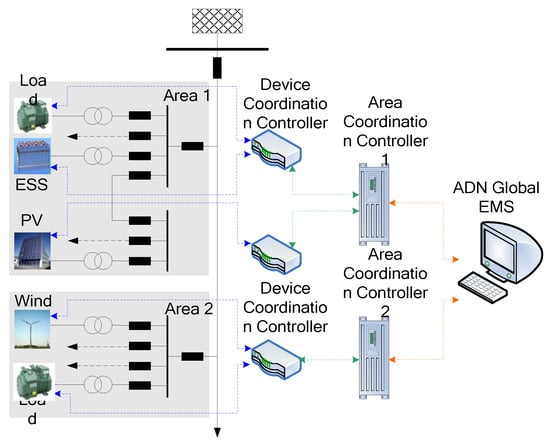
Figure 3.
Control system of Active Distribution Network (ADN).
The Global EMS monitors and gathers information of the ADN, and computes a long-time operation mode according to the electrical constraints. ADN is divided into several coordination control areas, and the Area coordination controllers are allocated to every area and control the area in a short time interval. The Device coordination controllers are connected to each primary device, and control these devices directly. At present, this control system has been applied in ADN feeder power control [29,30], voltage control [31], and feeder automation [32].
The ADN control system meets the features of Power CPS: (1) The cyber system (controllers and communication network) and the physical system (primary devices) are heterogeneous systems; (2) Controllers implement closed-loop control to primary devices, and there are discrete state switching and continuous dynamic in this process; (3) Information flow exists in the information and control system.
However, ADN does not realize the integration of cyber and physical because of the lack of a suitable integration model and control method. Table 1 lists existing problems in the ADN control process, solutions are also given in the table.

Table 1.
The problems of Active Distribution Network and solution based on Cyber Physical Systems (CPS).
Problem (1) is related to the primary system modeling. The ADN primary system model may change if state events disturb continuous operation. Now, ADN computes global target by long time optimization, and the optimal model only describes the dynamic of a certain state, but the optimal switching of the multi-state is not considered.
Being one of the Hybrid System models, Mixed Logical Dynamical (MLD) describes objects by dynamic and logic rules, and puts the objects’ discrete and continuous characteristics into a unified framework [33]. If the ADN primary system is modeled by MLD, all the separated operation states can be optimized together.
Just like Problem (1), Problem (2) is also caused by the model, and can be solved by MLD. According to route and sequence rules, information flow transmits in the control system. If these rules are modeled by logical expression, and transformed to inequality constraints by MLD, then the information flow and also the structure of the control system will be involved in the control strategy.
Problem (3) is associated with the control method. The control period of ADN long time optimization is about 10–15 min. However, the system finds it hard to maintain an optimal target because of so many variable factors. So, it is necessary to predict the state of the controlled object and reduce the control period. Moreover, if some disturbances take place, the control model should be rectified in the next period. Hence, MLD based MPC can be used to solve Problem (3).
Obviously, MLD and the control method based on it are able to diminish the ADN’s existing weakness. As a preliminary study of the Power CPS model, this paper pays attention to the ADN primary device control which corresponds to the “Integrating physical and control processes”, and lays the foundation for future work.
3. ADN Flexible Load Control Based on the Hybrid System Model
3.1. Flexible Load Control Strategy
There are usually some high-power loads in the distribution network such as conditioning, cold storage, and the pump station. These loads need to achieve a function such as controlling temperature or water level. Two features can be concluded from them: (1) Operate segmentally in accordance with a different state; (2) Load functional demand (temperature, water level, etc.) is accumulative during the operation period. Loads meet these two features and are suitable to be modeled by MLD and applied MPC.
The optimal target of flexible load is to reduce power consumption on the premise of satisfying load functional demand. But in the perspective of the system, load consumption needs to be controlled near a stable target.
ADN feeder power control is affected by loads to a great extent. The control purpose of ADN feeder power is to sustain exchange power between control area and feeder (named: Area Power), also the exchange power between the feeder and the external system (named: Feeder Power). Uncontrolled load may switch state optionally in a short time and make exchange power fluctuate frequently and sharply, so the ADN feeder is apt to deviate from the operation target.
If flexible loads are incorporated into ADN control, and feeder power distribution adjusted with DGs, the feeder and loads will both share the benefit.
As shown in Table 2, ADN flexible control is classified into two conditions. When the feeder works normally, in every area, the DGs power satisfies the loads’ demand. Based on global optimal computation, Feeder Power and Area Power should be maintained near the optimal point. Under this condition: (1) Each area coordination controller controls the flexible loads of this area to run at a minimum consumption mode; (2) All the DGs in this area sustain the area’s Area Power.

Table 2.
ADN flexible load control strategy.
When a bigger power shortage occurs in the feeder (for example when some DGs quit because of the weather), Area Power of this feeder severely deviates from the target, so the main purpose at this time is to reduce Feeder Power deviation by flexible load coordination control. Under this condition: (1) The global EMS calculates the operation mode for all the flexible loads in the feeder, and controls the Feeder Power near its target value as well as being more stable; (2) The rest of the DGs are controlled to stabilize Feeder Power fluctuation.
3.2. Hybrid System Model of Flexible Load
The flexible load which meets the two features in 3.1 is modeled by MLD in this section.
(1) State model
The state model describes the load’s functional demand, control input and the relation with outside disturbance. After discretization, n flexible loads can be expressed as a state function as Equation (1).
where x(t) = [x1(t), x2(t) … xn(t)] is the functional index which reflects the loads’ functional demand at time t. u(t) = [u1(t), u2(t) … un(t)]T is the control input, and the element un(t) U = {un1, un2 … uni} denotes that each load contains i kinds of input and can only chose one of these inputs to control the load at time t.
A, B2 are n × n coefficient matrixes of the x(t) and u(t), they are determined by load type. B1(t) = [B11(t), B12(t) … B1n(t)]T is the outside disturbance which will affect the function index at time t + 1.
(2) Power consumption model
This model describes the loads’ power under different control inputs. Equation (2) is the discrete power consumption model.
where y(t) denotes the total power of n flexible loads at time t. D = [p1(t), p2(t) … pn(t)] consists of the power of each load at time t, and pn(t) P = {pn1, pn2 … pni}. The elements of P have a one-to-one correlation with U and denote the power of i-th control inputs of n flexible loads.
(3) MLD model
If the flexible load of Equation (1) contains a finite control input selection, then it can be considered as states switching. By setting logical variables, the separate states can be integrated.
During a time step Δt, n loads work under different states, so there are j = in kinds of operation modes that u(t) = um = [u1(t), u2(t) … un(t)]T and m{1, 2 … j}. According to Equation (3), set a logical variable for each of the j operation modes respectively, and make up a column vector δ(t) = [δ1(t), δ2(t) … δm(t) … δj(t)]T, where δ(t){0, 1}, m{1, 2 … j}. Each element of δ(t) means a state combination of the loads’ operation mode. When the loads work under this state combination, set the corresponding element of δ(t) to 1, that is δ(t) = 1 ⇔ u(t) = um.
Based on Equation (3), the Equation (1) is denoted by δ(t), and then a n × j matrix B2t = {B2t1, B2t2 … B2ti} is deduced. The elements (they are all n-dimension column vectors) of B2t is calculated by B1(t) + B2·um which represents the influence factors brought to a functional index which are caused by load disturbance or load control under the operation mode δm(t).
Replace the control input u(t) of Equation (2) with δ(t), then the meaning of D changes from the description of each load’s power to the description of n loads’ total power under j state combinations. So set a j-dimension row vector D2t = [P1, P2… Pm … Pj] which consists of j possible total powers corresponding to j kinds of state combinations, where Pm = D·um.
At any time t, all the flexible loads can work under only one combination, so there is only one element of δ(t) can be set to 1. This constrain is written as Equation (4), where 1 is the n-dimension vector of only 1.
With Equations (1)–(4), and considering the limit of functional index x(t) [a, b], a MLD based flexible load model Equation (5) is acquired, where 0n is a n-dimension zero matrix and In is a n-dimension identity matrix.
3.3. MPC of Flexible Load
The MPC problem is to obtain a series of control inputs which satisfy optimal function Equation (6) and meet the constraint conditions Equation (5). The Qδ, Qx, Qy in Equation (6) is weight factors of logical variable, functional index, and total power consumption.
ADN load control has been classified into Normal Condition and Underpowered Condition in 3.1, and the conditions are distinguished in accordance with the feeder power shortage ΔP(t) of Equation (7).
where (t|t − t1) means the values of time t are predicted at time t − t1. So represents the predictive sum of q DGs’ maximum power of time t; Pthreshold(t|t − t1) is the total consumption of all the common load in the feeder at time t, and this is predicted at time t − t1 too; Pf-ref denotes target of the Feeder Power which is obtained by global EMS; indicates the maximum consumption of n flexible loads.
Figure 4 shows the control procedure of ADN flexible load. The ΔP(t) will be computed firstly to judge whether its value exceeds a preset threshold Pthreshold. If ΔP(t) ≤ Pthreshold, the feeder is in the Normal Condition. All the flexible loads run independently to reduce power consumption in a control period T, and Equation (5) should set target points as δf = δmin, δmin → (Pmin = 0) or yf = Pmin = 0.
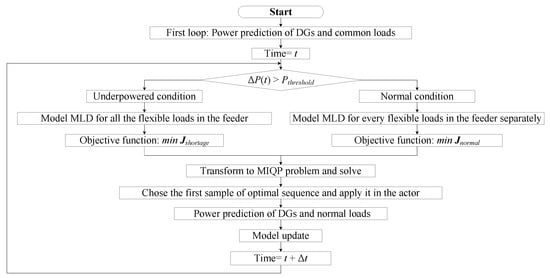
Figure 4.
Block diagram of control of the ADN flexible loads.
If ΔP(t) ≥ Pthreshold, the area coordination control will be closed at once. All the flexible loads, DGs in the feeder are controlled to mitigate fluctuation and diminish deviation of the Feeder Power. Then choose a consumption target Pm from the flexible loads’ achievable power set D2t. The chosen Pm makes to be minimal, and it means that the flexible loads try their best to counteract the power shortage.
After condition judgment and target setting, the optimal control models of Equations (5) and (6) are transformed to a Mixed Integer Quadratic Programming (MIQP) problem. Then the problem is solved and only the first sample of the optimal sequence is applied to the flexible loads by terminal controllers before the next control period arrives.
The flexible load model is able to be updated before the next period. Updating requests may be proposed from feeder side or load side. For instance, the feeder or load both can adjust the limit of the functional index x(t), and this will lead to a negotiation mechanism between the two sides.
3.4. Case Study
The MLD based CPS model of ADN flexible load and its MPC method is tested using the 10 kV feeder system shown in Figure 5.
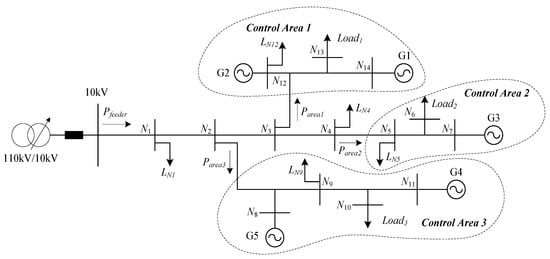
Figure 5.
Topological connection of ADN feeder containing flexible load.
The feeder contains a main line and three branches, and it is divided into three coordination control areas (dashed boxes). There are five DGs (including three green energies and two energy storages) and three flexible loads distributed in the three branches. There are also five common loads locate in Node 1, 4, 5, 9, 12. The global optimization determines the feeder’s operation targets for a long period. Table 3 shows the main parameters and targets of the feeder system.

Table 3.
Main electrical specifications of feeder system and operation target.
The three flexible loads are all middle-type cold storages which keep inner temperatures within the limits by electric refrigeration equipment. The inner temperatures of the three cold storages can be modeled as Equation (1), where x(t) is inner temperature at time t; B1(t) indicates temperature disturbance caused by outside heat, and it is invariant in this example; B2 denotes the refrigeration effect coefficient matrix; the control input u(t) has two states including Stop and Start, the two states represented by 0 and 1 respectively, that is un(t) U = {0, 1}, n {1, 2, 3}; set the control step Δt = 2 s. Table 4 lists the typical parameters of the three types of cold storages.

Table 4.
Parameters of flexible loads in three refrigerators.
Now the three flexible loads’ control model as Equation (5) under the Normal and Underpowered condition can be obtained.
(1) Normal condition control
The control purpose is to minimize the load’s consumption of each area. Set control period T = 10Δt (20 s), and simulation period is 0–200 s, so there are 100 times MPC computations during this period.
From Figure 6, it can be found that the flexible load temperature controlled by the model and method of this paper (flexible group) is better than the loads controlled by the traditional method (traditional group). In Figure 6a, at any time, three temperatures are all restricted in the low and up boundaries and the curves seems more stable. This is because the load models predict the future trend and avoid the possibility of out-of-limit. In addition, Equation (6) contains reduction of the deviation of x(t), and this contributes to the stability.
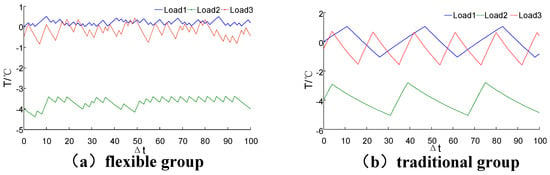
Figure 6.
The function indexes comparison of refrigerator loads under normal condition; (a) flexible group; (b) traditional group.
The traditional group is controlled by simple if-then modes. Because of the lack of prediction, the controllers do not act only when the x(t) exceeds the limit. Moreover, by this mode, x(t) always occupies the whole range of the limit and leads to sharp fluctuation.
In Figure 7, loads of the flexible group act more times than the traditional group. This phenomenon implies that load devices in the flexible group need higher reliability, and it can be adjusted by weight factors for different demand.
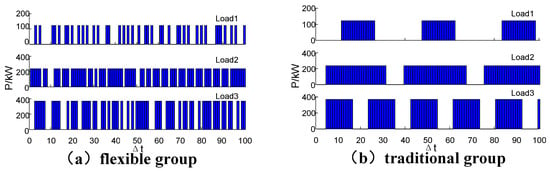
Figure 7.
The power consumption comparison of refrigerator loads under normal condition.
Table 5 indicates the power consumption of two groups. It is obvious that each load’s energy consumption and mean power of flexible group is lower than that of the traditional group. However, because the flexible loads are not optimized together under the normal condition, loads in different control areas do not improve the load coincidence factor.

Table 5.
The comparison of power consumption under normal condition.
Figure 8 reflects the Feeder Power and 3 Area power. Every curve involves power pulse which is due to the loads’ frequent switching. The power pulses also imply that when load disturbance occurs, the ADN feeder power control will change the DGs’ output for the corresponding area and the external input to counteract the disturbance and maintain the optimal target.
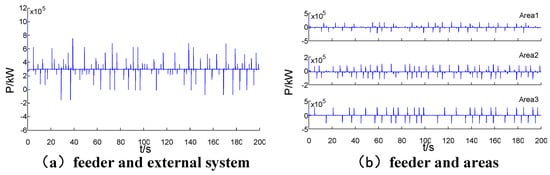
Figure 8.
The exchange power of ADN feeder and control areas under normal condition; (a) feeder and external system; (b) feeder and areas.
(2) Underpowered condition control
If at time t = 1, because of the weather, DG1 reduces its output 215 kW, and DG2 reduce 250 kW, there is a power shortage of ΔP = 365 kW in the feeder according to Equation (7). Under this condition, all the flexible loads are controlled, unified, and undertake some of the power shortage. In this case, the power target of the three loads is 356 kW, set control step Δt = 2 s, control period T = 10Δt, and simulation period is 0–200 s.
The same as the normal condition, because of the strict constraints and prediction in Equation (5), the temperatures of the three cold storages of the flexible group in the underpowered condition are all in the feasible range, and more stable than the traditional group. (Shown in Figure 14a).
Figure 9 and Table 6 compare the total power of the two groups. From Figure 9, the flexible group undertakes the power shortage effectively, and operates very close to the target of 356 kW and the RMS value deviates from 356 kW only about 30% which is lower than the traditional group. Additionally, the flexible group avoids a sharp power change, and the maximal load difference between the two steps is only 370 kW. However, in the traditional group, the power changes sharply and irregularly. Obviously, the phenomenon in the traditional group is negative for ADN feeder power. From the point of view of energy conservation, the flexible group never works at the peak power of 726 kW, and the total energy is 4.5% lower than the traditional group.
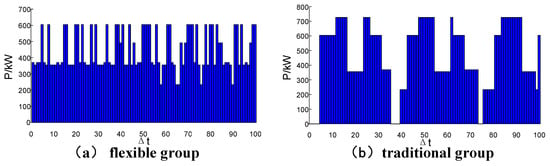
Figure 9.
The total power consumption comparison of ADN flexible loads in the underpowered condition; (a) flexible group; (b) traditional group.

Table 6.
The comparison of power consumption under power shortage condition.
The Feeder Power curve is shown in Figure 10. It is easy to see that the flexible group keeps near the target. However, the traditional group has loss of stability, the frequent and large power change makes the Feeder Power oscillate severely, and the target value cannot be held.
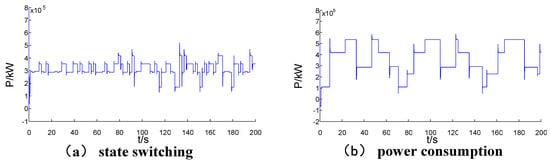
Figure 10.
The comparison of the ADN Feeder Power in underpowered condition; (a) state switching; (b) power consumption.
4. Distributed Load Control in the Underpowered Condition
Section 3 introduces a Hybrid System based CPS model and control method for the flexible load. The model and method promote load participation in ADN control, improve load consumption and ADN operation, and form positive interaction of loads and system.
However, there are also three aspects to the problems in the unified load control of the underpowered condition.
- (1)
- Complex control model of the large scale system. When all loads are controlled together, there are too many possible state switching and combinations, this leads to a huge model for Equation (5). After the model is transformed to MIQP, the scale and complexity of the calculation model expand with the increase of the control period T.
- (2)
- Non-convergence caused by a distinction of model objects. There are always some differences between different kinds of objects like the model parameter and the control period. If these objects are modeled together, the control problem may last too long or even be unsolvable.
- (3)
- The interaction between area coordination controllers is insufficient. The modeling and controlling mostly rely on global EMS, and do not take full advantage of the ability of lower-level controllers.
In this section, the distributed model and the MPC control method for flexible load, based on Section 3, are proposed to help with solving the three problems above.
4.1. Distributed MPC in ADN
The distributed control usually has two types. The first one; the control problem is split into several parts at the boundary point. These sub-problems are solved by alternating iteration. The second one; the control problem is separated into several coupled sub-problems according to the arrangement of controllers and category of the controlled object. These coupled sub-problems are solved by transmitting coupling information [34].
Considering the calculation speed and the existing control system, the second type is more suitable for ADN. Figure 11 shows the differences between distributed control and centralized control in Section 3 of the ADN flexible load when power shortage happens in the feeder. There are three main differences.
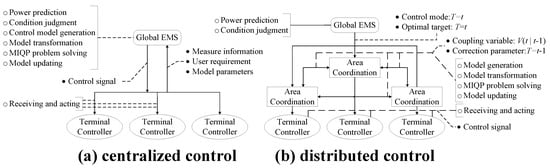
Figure 11.
Comparison of centralized and distributed ADN load control in underpowered condition; (a) centralized control; (b) distributed control.
Difference (1): Control structure. The centralized control only has two control levels, global EMS and terminal controller, and all the information is exchanged between these two levels. The distributed mode contains three levels, and the communication not only appears between levels, but also appears between controllers in the same level.
Difference (2): Control task. The hollow circles in Figure 11 indicate the main tasks of each control level. In centralized mode, the global EMS undertakes almost all the modeling and computation but in distributed mode, some tasks are assigned to the area coordination control level.
Difference (3): Control information. The solid circles in Figure 11 show the main information exchanged in the control process. The distributed model adds coupling information transmission of the same level, and because the coupling information is not generated in real time, there is therefore some information of a different time.
Even though, in distributed control, the optimal performance may be lost and the complexity of communication is increased, the control model is simplified significantly and computation time is reduced, also the flexibility of the control is strengthened.
4.2. Distributed Control Model and Method of Flexible Load
When the centralized control solves the optimal model, the coupling relationship between controlled objects exists naturally during the iteration. Only if all the variables including coupling variables satisfy the constraints and optimal purpose, is then the feasible solution acquired. However, the coupling is impossible to automatically appear in the distributed control process, because the sub-problems are separated; additionally, independent control makes it that every controller cannot obtain accurate and real-time state information of the coupled controllers. These two problems are solved by reconstructing the models of Section 3.
(1) Classifying Load Controlled Object
The Load Controlled Object is a flexible loads set, and all the flexible loads of the set are controlled with the same controller. The classification relates to the load type and area, in general, loads of the same type and with similar parameter or the same time step are placed into a category. Let express the set of n × n matrices which only consists of elements 0 and 1. Introduce an incidence matrix which defines relation of n loads of s classes in ADN. Only when the matrix’s element AI(i,j) = 1, i = 1,…,s, j = 1,…,n, the j-th load belongs to the i-th class LCOi.
(2) Coupling relationship of LCOs
The coupling relationship means that several LCOs affect the optimal target, and this relationship determines if information exchange exists between controllers of the same level. Introduce an incidence vector which defines the relation between the q-th LCOq and other s − 1 LCOs. If the q-th LCOq couples with the p-th LCOp, the vector’s elements AII-q(1,p) = 1, p = 1,…,s, p ≠ q, and AII-q(1,q) = 0.
(3) Coupling variable
In Equation (6), every flexible load contributes to the optimization of total power y(t), and LCOs are the same after the n loads are classified into s LCOs. Hence, the s LCOs has a coupling relation to y(t), that is y(t) = y1(t) + + yq(t) + + ys(t).
However, each LCO is controlled by the corresponding controller, and the q-th controller Ctrlq knows the model of q-th LCOq including the state model (Equation (1)) and the power consumption model (Equation (2)). Moreover, the Ctrlq does not consider the rest of s − 1 LCOs. Because of this, other controllers such as the p-th controller Ctrlp must offer power information at time t to the Ctrlq, that is y(t) = y1|t(t) + + yq|t(t) + + ys|t(t), where yp|t is the knowable coupling variable, p = 1, …, s, and p ≠ q.
Unfortunately, at time t, due to the same reason of lack of coupling information, yp|t is unable to be obtained. As shown in Figure 12, the coupling information can be replaced by the predictive control results of [t1 − 1, t1 − 1 + T] which are calculated at time t = t1 − 1, and T is the control period.

Figure 12.
The relationship of coupling information among controllers.
According to the principle of receding horizon optimization, when Ctrlq operates at time t = t − 1, it predicts the LCOq’s functional index of t = [t1, t1 − 1 + T], that is xq(t1|t1 − 1)~xq(t1 – 1 + T|t1 − 1). Then the control input uq(t1 − 1|t1 − 1)~uq(t1 − 1 + T − 1|t1 − 1) and the power yq(t1 − 1|t1 − 1)~yq(t1 − 1 + T − 1|t1 − 1) also can be obtained. Other controllers like Ctrlp get the power yp(t1 − 1|t1 − 1)~yp (t1 − 1 + T − 1|t1 − 1) too.
With the action of uq (t1|t1 − 1), Ctrlq moves to time t = t1, and a new control loop begins. At this time, set yp|t = yp(t|t1 − 1) for every step of t = [t1, t1 − 1 + T − 1].
However, for time t = t1 + T − 1, there is no yp(t1 + T − 1|t1 − 1) that can be assigned to yp|t1+T-1. Define constants yf-q and yf-p, p = 1, …, s, and p ≠ q. yf-q and yf-p consist of a power combination of all the LCOs. The power combination corresponds to a kind of load operation mode δm and satisfies , where the meaning of δm and Pm can be found in 3.3. Let yp|t1+T-1 = yf-p, in other words, the unknown coupling variable yp|t1+T -1 is set artificially based on Pm. Besides, in the first loop of control, for time t = [0, T − 1], set yp|t = yf-p.
(4) Keep the consistency of coupling variables
No matter how the coupling variable gets its value, the Ctrlp may not follow the yp|t which has been sent to Ctrlq. So, there should be some restrictions in optimal function or constraint to keep the actual trajectory of LCO consistent with the coupling variables of the coupled controllers.
In optimal function, during a control period t = [t1, t1 + T], minimizing the deviation between yq(t) and yq|t, gives Equation (8).
In control model, add inequality constraints, and make the deviation between yq(t) and yq|t of any step during the control period t = [t1, t1 + T] not larger than the maximal deviation in the last control period t = [t1 − 1, t1 − 1 + T]. That is Equation (9).
(5) Optimal function
The optimal function of LCOq includes the functional index deviation Jx, load consumption deviation Jy, and coupling variable deviation Jy.
Like Equation (6), Jx keeps xq(t) tracing the target xf-q in the control period t = [t1, t1 + T], that is Equation (10).
Jy contains coupling relationship of LCOq and LCOp, and reflects the difference of total consumption and its target. Define matrix , is the coupling information set of time t which should have been sent by s controllers to each other. Also the load consumption deviation of LCOq is shown as Equation (11).
Jyq has been presented in Equation (8). So the optimal function is Equation (12).
(6) Control model and method
Model the s LCOs respectively based on 3.2, and MLD models as Equation (5) are acquired. Then add Equations (9) and (12) to each LCO, and the control model is completed.
The optimization problem is that s LCOs are controlled by s controllers on the basis of coupling information to get control inputs. The solution must satisfy Equations (5) and (9), and make Equation (12) optimal.
The control procedure is shown in Figure 13. By the prediction of DGs and common loads, the ADN feeder is in the underpowered condition; every controller accepts the coupling information of the other controllers and the power consumption target from the global EMS; all the controllers generate control models of their own LCO and solve them, then act on the first sample of the optimal sequence; all the controllers send coupling information to other controllers and prepare for the next period of control.
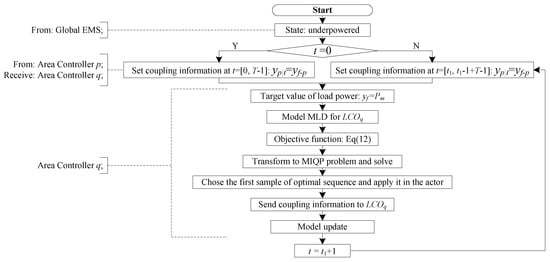
Figure 13.
Block diagram of distributed predictive control of ADN flexible load.
4.3. Case Study
The distribution ADN flexible load control model and method of underpowered condition is tested by the case in 3.4.
According to 4.2, the three flexible loads of Load1, Load2, Load3 are classified to three LOCs of LOC1, LOC2, LOC3. Based on Table 3 and Equations (5) and (9), three MLD models of LOCs are built. Set the total power consumption target Pm = 356 kW, then the three optimal functions can be obtained by Equation (12). The models and optimal function are controlled 100 times according to the procedure in Figure 13.
Area coordination controllers are simulated by three IBM Flex System x240 Compute Nodes, and configure another Compute Node to simulate the physical system of the ADN feeder. Each Compute Node contains two Intel Xeon E5-2600 Core6 2.1 GHz processors and 16G memory. An inbuilt Gigabit Switch is used for communication.
Matlab/Simulink is the simulating and computing tool for every Compute Node, and a Socket interface is used for software to communicate with each other. There is also a synchronous program to prevent possible asynchronous problems occurring between different Compute Nodes. So the simulation of ADN feeder including three loads does not begin, only when the feeder has received all the load control inputs from other Compute Nodes.
Figure 14 shows the temperature of the distributed and centralized mode in the underpowered condition. The curves of the two modes all locate in the feasible range. The three loads of the distributed mode change their states about 56, 48, and 52 times respectively, and the loads in the centralized mode change only 48, 45, 46 times. The more frequent state switching makes the loads of the distributed mode have a lower fluctuation. Especially the Load3, it not only operates steadily, but also works at a lower temperature.
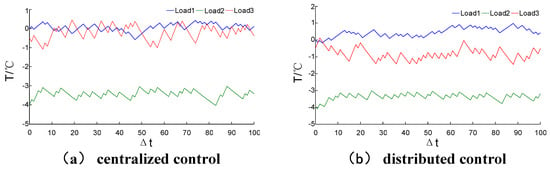
Figure 14.
The function indexes comparison of centralized and distributed control; (a) centralized control; (b) distributed control.
This phenomenon is caused by the method difference of how to balance the optimal target of the two modes. Load3 is the largest load, and the centralized mode considers the optimization from the overall model, so the action of Load3 should be diminished and the lower loads work more to counteract disturbance. However, in the distributed mode, the controller manages only one load, and does not need to consider other problems.
Figure 15 shows the state switching and total power of distributed control. From Figure 15b, the three loads’ total consumption is able to be kept near 356 kW. But compared with Figure 9a, a sharp power change occurs in the distributed mode, and the curve is more unstable. This is caused by inaccurate coupling information between controllers. So, the optimal performance of the distributed mode is worse.
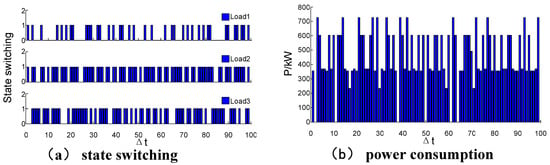
Figure 15.
The state switching and power consumption of distributed control; (a) state switching; (b) power consumption.
The detailed comparison of total consumption and calculation performance between the two modes is listed in Table 7. Though there is a loss of optimal performance, the speed of distributed control is promoted.

Table 7.
The comparison of centralized and distributed control.
5. Conclusions
The characteristics of discrete and logical of the control system determine that in order to realize integrated analyzing and control of Power CPS, the first thing is to build a Hybrid System model which is able to describe the continuous dynamic process and discrete process for the primary system of the power grid.
This paper applies the MLD method to build a Hybrid System based Power CPS control model for ADN flexible load control. Combining with the ADN feeder power control, a flexible load control strategy is designed for normal and underpowered conditions of ADN feeder. To solve the problems of centralized control mode when the feeder is in the underpowered condition, a model and method of distributed control for flexible load is proposed.
From the study case, it can be concluded that compared with the traditional load control, the proposed flexible load control contains two advantages: (1) With the help of the hybrid model the predictability of the control is better, by which the flexible loads’ operation constraints are satisfied strictly when the traditional loads violate the limit; (2) The hybrid model has the ability to combine the discrete process into the optimal control of continuous variables, in that the ADN flexible load state switching can be optimized to meet continuous variables, so that ADN flexible load state switching can be optimized to meet consumption demand. In the case study simulation of this paper, the flexible load power consumption is lower, and the most load’s energy conservation reaches 11% of the traditional load; when the coordinates with DGs in the ADN, flexible load power consumption can be sustained near a target value and the deviation of RMS is 30% which is lower than 46% of the traditional load control.
Simulations of centralized and distributed control models of flexible load show that both of them have their advantages and disadvantages. The centralized control has higher efficiency and the target deviation is 7% lower than the distributed control in the study case. However, the distributed control is suitable for some complex situations, and computes faster (0.794 s in study case) than the centralized mode. Besides, the distributed control makes full use of the ADN control system, and has some practical value.
In conclusion, the Hybrid System based model proposed in this paper combines continuous dynamic, discrete state and even complex logical description in a unified expression, therefore physical process, control process and information flow is able to be described by mathematics directly. According to the model, the control method optimized continuous variables and state switching together in a control step. The ADN flexible load control is an example to illustrate the “integrating physical process and the control process” of the “Control Model”, and the characteristics of the information system will be considered in the future to show the “integration of the primary and information systems”.
Acknowledgments
The authors would like to thank the support of The National Natural Science Foundation of China (with issue number: 51677116).
Author Contributions
Yun Wang and Dong Liu conceived and designed the experiments; Yun Wang performed the experiments; Yun Wang and Dong Liu analyzed the data; Chen Sun contributed analysis tools; Yun Wang wrote the paper.
Conflicts of Interest
The authors declare no conflict of Interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CPS | Cyber Physical Systems |
| Power CPS | CPS in Power Systems |
| ADN | Active Distribution Network |
| DG | Distributed Generation |
| MPC | Model Predictive Control |
| EMS | Energy Management System |
| RHO | Receding Horizon Optimization |
| MLD | Mixed Logical Dynamical |
| MIQP | Mixed Integer Quadratic Programming |
| RMS | Root Mean Square |
| LCO | Load Controlled Object |
| Ctrlq | The q-th Controller |
References
- Kyoung, D.K.; Kumar, P.R. Cyber-physical systems: A perspective at the centennial. Proc. IEEE 2012, 100, 1287–1380. [Google Scholar] [CrossRef]
- Edward, A.L.; Sanjit, A.S. Introduction to Embedded Systems: A Cyber-Physical Systems Approach; China Machine Press: Beijing, China, 2012. [Google Scholar]
- Eidson, J.; Edward, A.L.; Matic, S. Time-Centric Models for Designing Embedded Cyber-Physical Systems; University of California, Berkeley, Technical Memorandum: Berkeley, CA, USA, 2009. [Google Scholar]
- Radha, P. Cyber-Physical Systems: Close encounters between two parallel worlds. Proc. IEEE 2010, 98, 1363–1366. [Google Scholar]
- Derler, P.; Edward, A.L.; Vincentelli, A.S. Modeling cyber-physical systems. Proc. IEEE 2011, 100, 13–28. [Google Scholar] [CrossRef]
- Krishna, S.; Radha, P. Cyber-physical system framework for future aircraft and air traffic control. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–9.
- Du, S.; Wang, X.; Xie, G.; Cai, T.; Zhang, Q. Reliability evaluation of substation automation system based on IEC61850. Power Syst. Prot. Control 2012, 5, 32–41. [Google Scholar]
- Yu, B.; Guo, C.; Wang, Y.; Zhang, L. Research on the reliability of the power system considering impacts of the information system. Power Syst. Prot. Control 2013, 7, 7–13. [Google Scholar]
- Li, H.; Qiu, R.C.; Wu, Z. Routing in cyber physical systems with application for voltage control in microgrids: A hybrid system approach. In Proceedings of the 32nd International Conference on Distributed Computing Systems Workshops, Macau, China, 18–21 June 2012; pp. 254–259.
- Yoshihiko, S.; Koo, T.J.; Hiroaki, E.; Takuya, Y.; Takashi, O.; Takuji, U.; Takashi, H. A hybrid system approach to the analysis and design of power grid dynamic performance. Proc. IEEE 2012, 1, 225–239. [Google Scholar]
- Hiskens, I.A. Power system modeling for inverse problems. IEEE Trans. Circuits Syst. 2004, 3, 539–551. [Google Scholar] [CrossRef]
- Davis, C.M.; Tate, J.E.; Okhravi, H.; Grier, C.; Overbye, T.J.; Nicol, D. SCADA cyber security testbed development. In Proceedings of the 38th North American Power Symposium, Carbondale, IL, USA, 17–19 September 2006; pp. 483–488.
- Sun, C.-C.; Hong, J.; Liu, C.-C. A co-simulation environment for integrated cyber and power systems. In Proceedings of the IEEE International Conference on Smart Grid Communications, Miami, FL, USA, 1–5 November 2015; pp. 133–138.
- Georg, H.; Muller, S.C.; Dorsch, N.; Rehtanz, C.; Wietfeld, C. INSPIRE: Integrated co-simulation of power and ICT systems for real-time evaluation. In Proceedings of the IEEE International Conference on Smart Grid Communications, Vancouver, BC, Canada, 21–24 October 2013; pp. 576–581.
- Lin, H.; Veda, S.S.; Shukla, S.S.; Mili, L.; Thorp, J. GECO: Global event-driven co-simulation framework for interconnected power system and communication network. IEEE Trans. Smart Grid 2012, 3, 1444–1456. [Google Scholar] [CrossRef]
- Mallouhi, M.; Al-Nashif, Y.; Cox, D.; Chadaga, T.; Hariri, S. A testbed for analyzing security of SCADA control systems (TASSCS). In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Anaheim, CA, USA, 17–19 January 2011; pp. 1–7.
- Zhao, H. Hybrid Modeling and Analysis of Power Systems. Ph.D. Thesis, North China Electric Power University, Baoding, China, 2004. [Google Scholar]
- Sayak, B. Cyber-Physical Modeling, Analysis, and Optimization—A Shipboard Smart Grid Reconfiguration Case Study. Ph.D. Thesis, Kansas State University, Manhattan, Kansas, 2004. [Google Scholar]
- You, Y.; Liu, D.; Yu, W.; Chen, F.; Pan, F. Technology and its trends of active distribution network. Autom. Electr. Power Syst. 2012, 18, 10–16. [Google Scholar]
- Yu, W.; Liu, D.; Yu, N. Feeder control error and its application in coordinate control of active distribution network. Proc. CSEE 2013, 33, 108–115. [Google Scholar]
- Jia, H.; Qi, Y.; Mu, Y. Frequency response of autonomous micro grid based on family-friendly controllable loads. Sci. China Technol. Sci. 2013, 56, 693–702. [Google Scholar] [CrossRef]
- Faran, A.; Tomasz, T.; Colin, N. Model predictive control for market-based demand response participation. IFAC Proc. Vol. 2014, 3, 11153–11158. [Google Scholar]
- Tullio, F.; Marco, L.; Della, V. Real-time modeling for direct load control in cyber-physical power systems. IEEE Trans. Ind. Inform. 2011, 4, 689–698. [Google Scholar]
- Liu, D.; Sheng, W.; Wang, Y.; Lu, Y.; Sun, C. Key technologies and trends of cyber physical system for power grid. Proc. CSEE 2015, 14, 3522–3531. [Google Scholar]
- Zheng, H.; Jian, J.; Yang, L.; Quan, R. A deterministic method for the unit commitment problem in power systems. Comput. Oper. Res. 2016, 66, 241–247. [Google Scholar] [CrossRef]
- Marcovecchio, M.G.; Novais, A.Q.; Grossmann, I.E. Deterministic optimization of the thermal Unit Commitment problem: A Branch and Cut search. Comput. Aided Chem. Eng. 2014, 67, 53–68. [Google Scholar] [CrossRef]
- Zaman, F.; Elsayed, S.M.; Ray, T.; Sarker, R.A. Evolutionary algorithms for power generation planning with uncertain renewable energy. Energy 2016, 112, 408–419. [Google Scholar] [CrossRef]
- Khodr, H.; Halabi, N.; García-Gracia, M. Intelligent renewable microgrid scheduling controlled by a virtual power producer: A laboratory experience. Renew. Energy 2012, 48, 269–275. [Google Scholar] [CrossRef]
- Yu, W.; Liu, D.; Huang, Y. Operation optimization based on the power Supply and storage capacity of an active distribution network. Energies 2013, 6, 6423–6438. [Google Scholar] [CrossRef]
- You, Y.; Liu, D.; Zhong, Q.; Yu, N. Multi-time scale coordinated control of distributed generators based on active distribution network. Autom. Electr. Power Syst. 2014, 9, 192–198. [Google Scholar]
- Chen, F.; Liu, D.; Chen, Y. Hierarchically Distributed Voltage Control Strategy for Active Distribution Network. Autom. Electr. Power Syst. 2015, 39, 61–67. [Google Scholar]
- Weng, J.; Liu, D.; Luo, N. Distributed processing based fault location, isolation, and service restoration method for active distribution network. J. Mod. Power Syst. Clean Energy 2015, 3, 494–503. [Google Scholar] [CrossRef]
- Alberto, B.; Manfred, M.; Della, V. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 35, 407–427. [Google Scholar]
- William, B.D. Distributed Receding Horizon Control of Multi-Agent Systems. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2004. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).