Design of Parallel Air-Cooled Battery Thermal Management System through Numerical Study
Abstract
:1. Introduction
2. Models
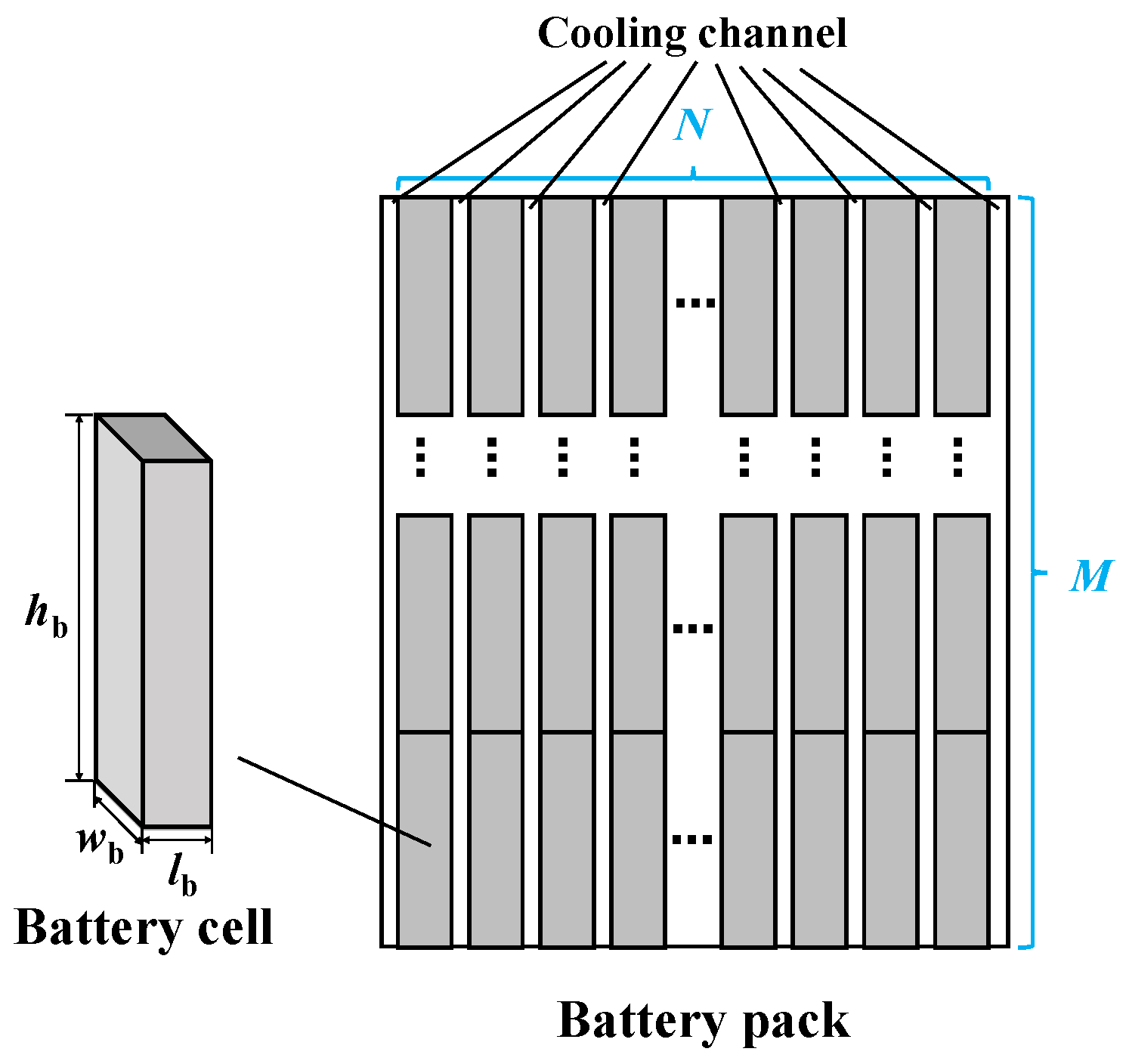
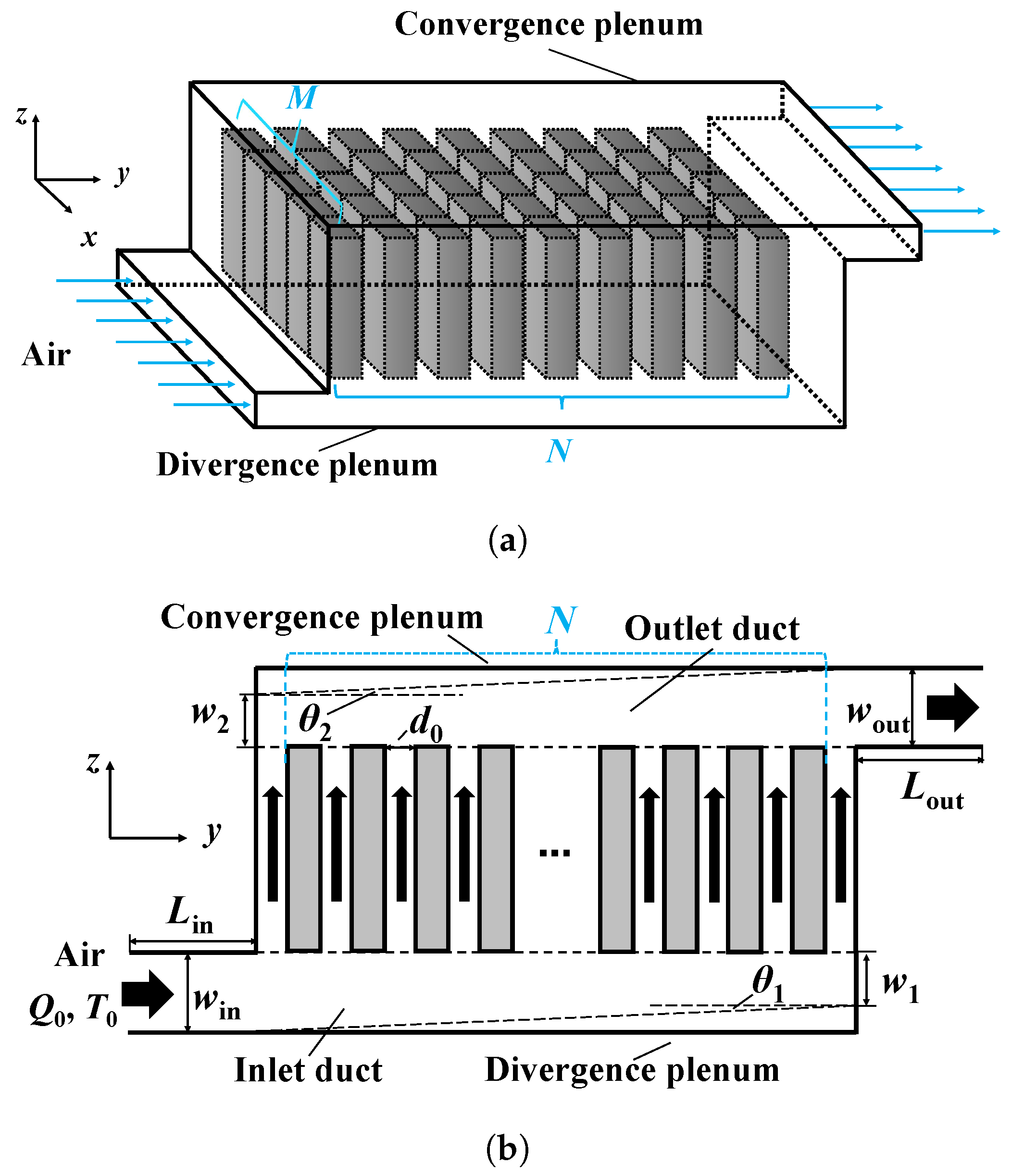
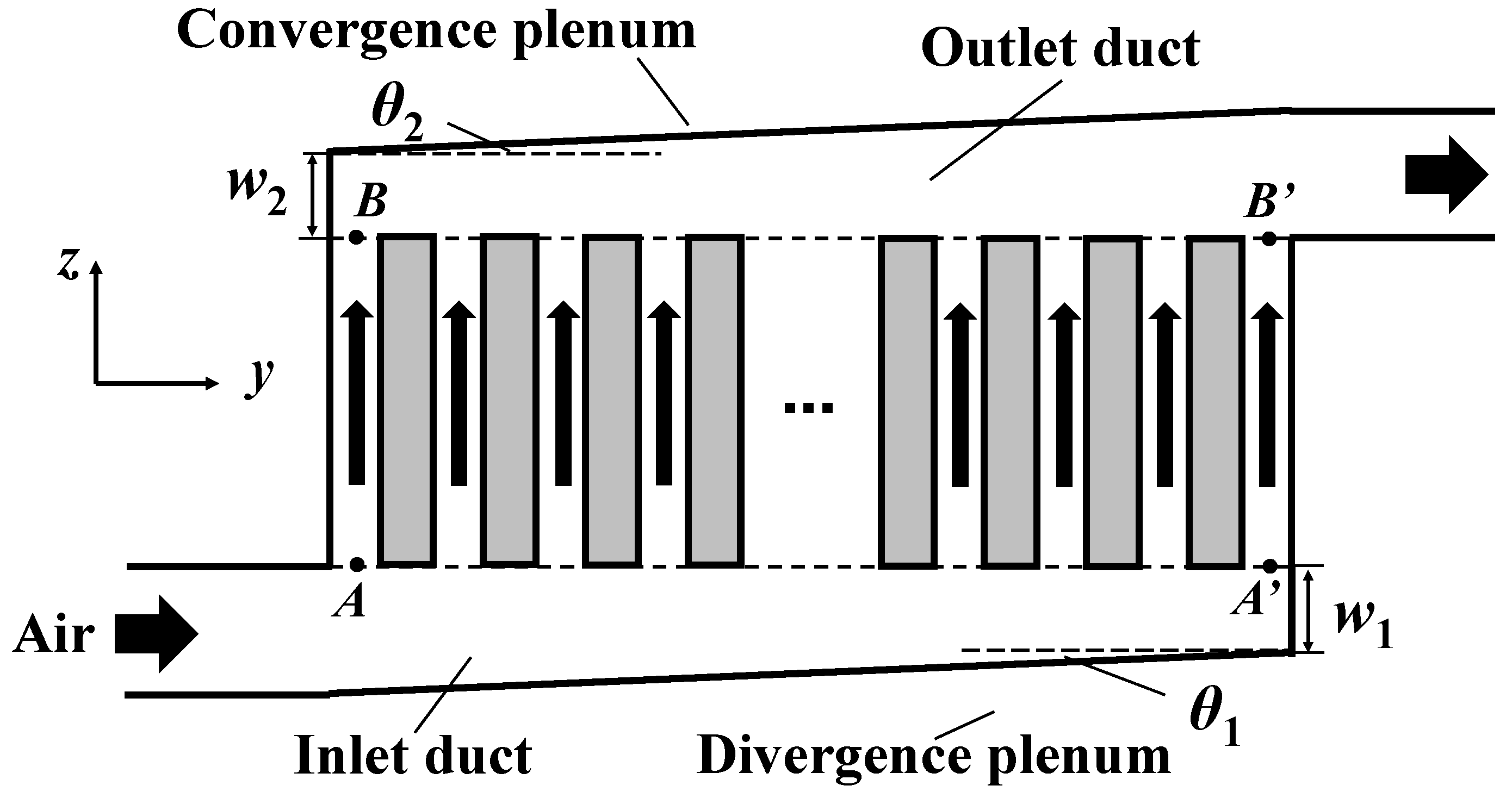
2.1. Illustration of the Parallel Air-Cooled BTMS
2.2. Computational Fluid Dynamics Calculation
3. Numerical Procedure
3.1. Parameters of the Numerical Cases
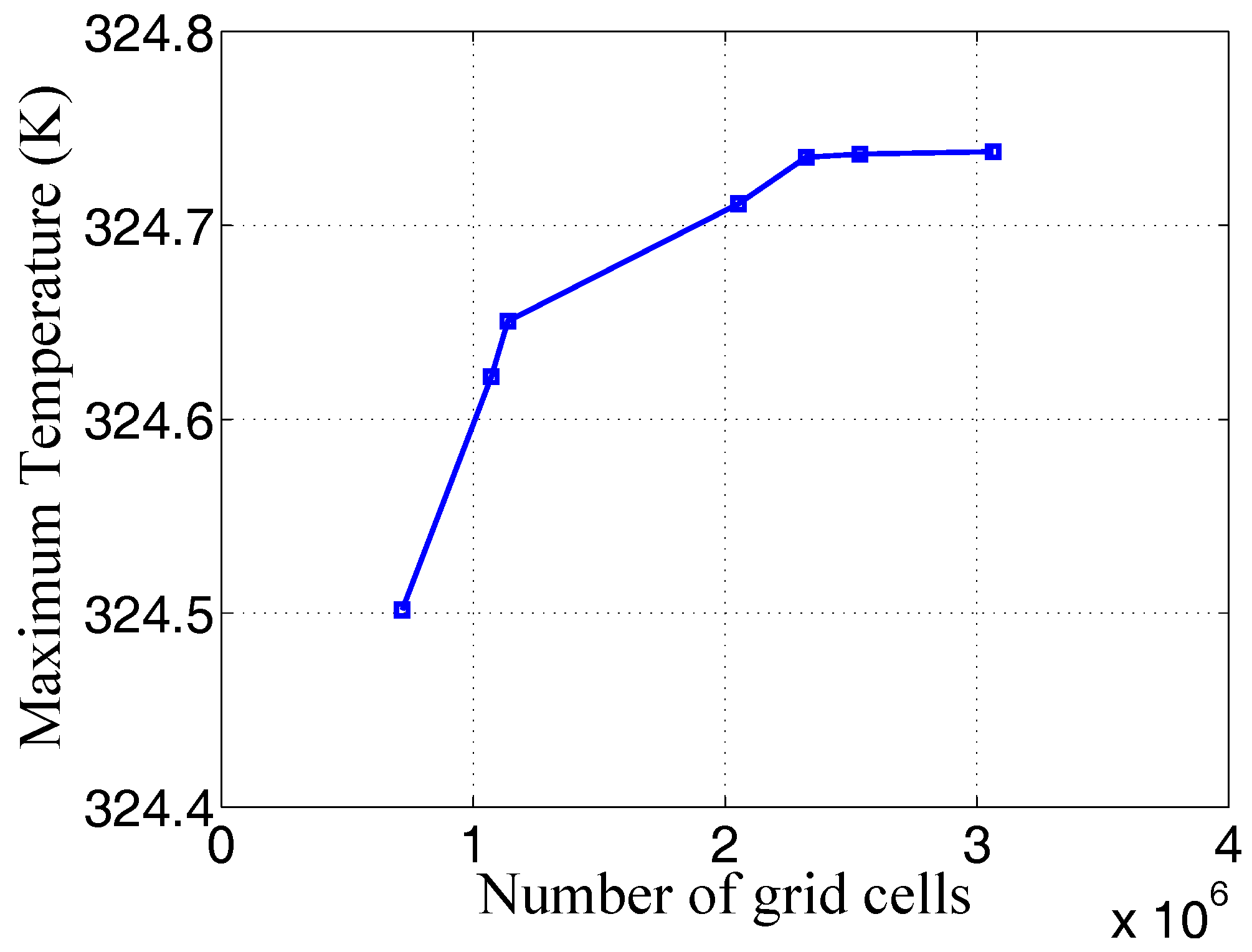
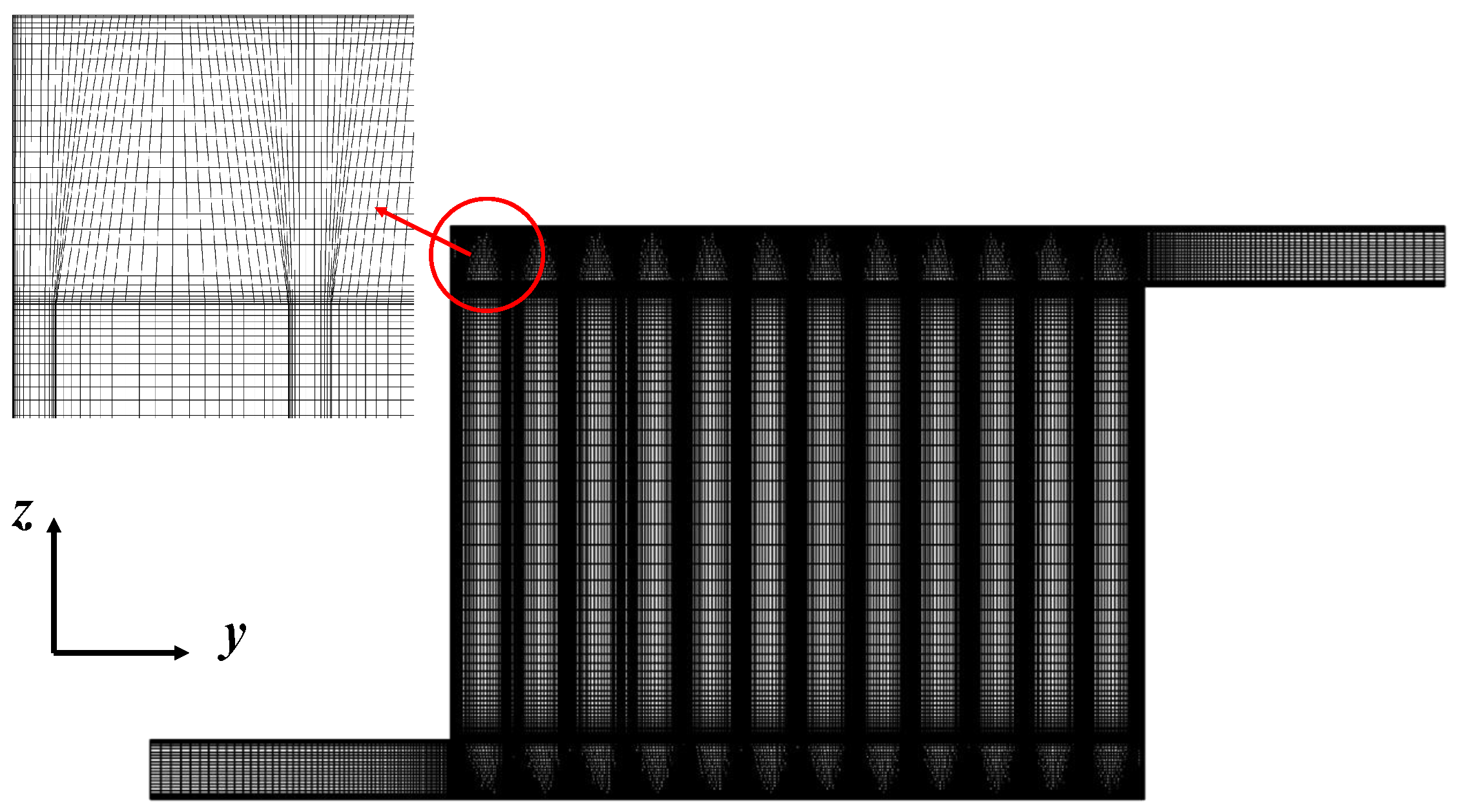
3.2. Grid Dependence Analysis
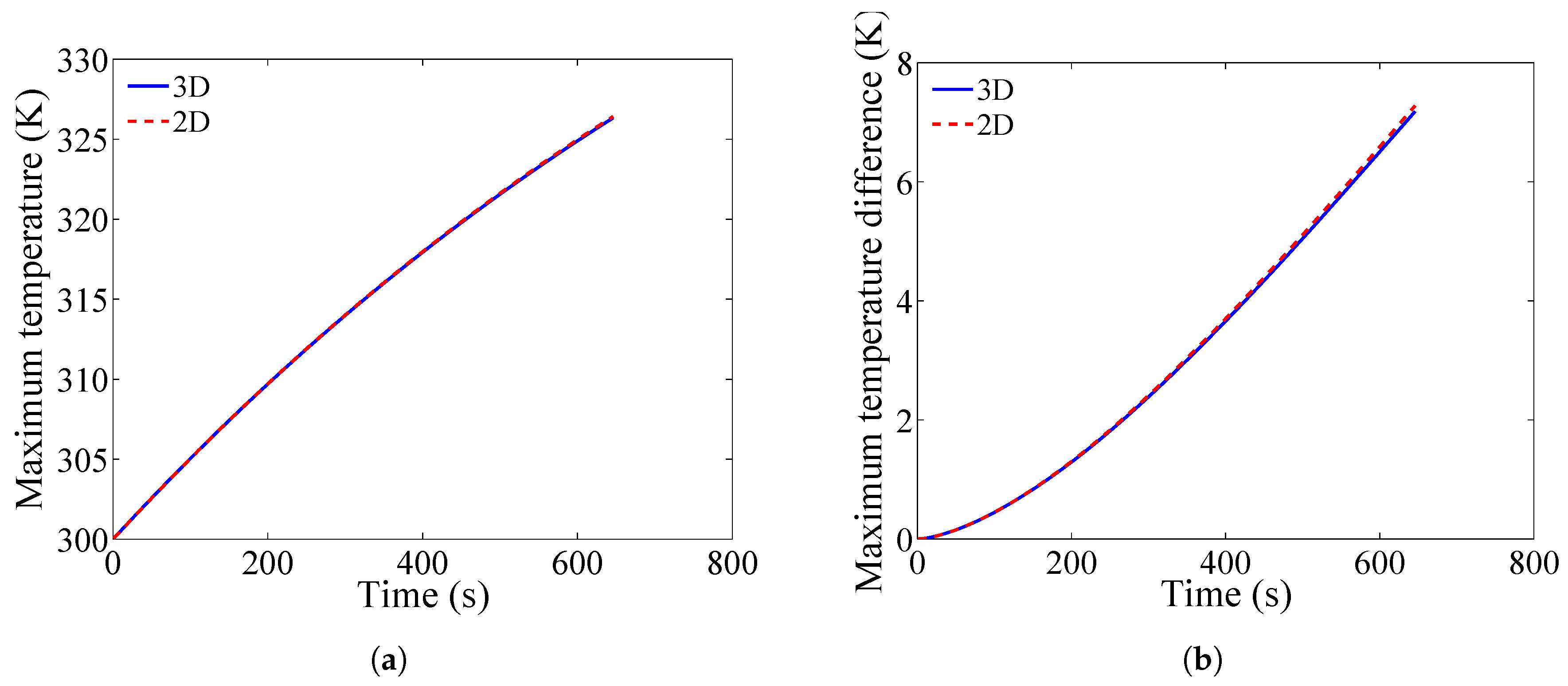
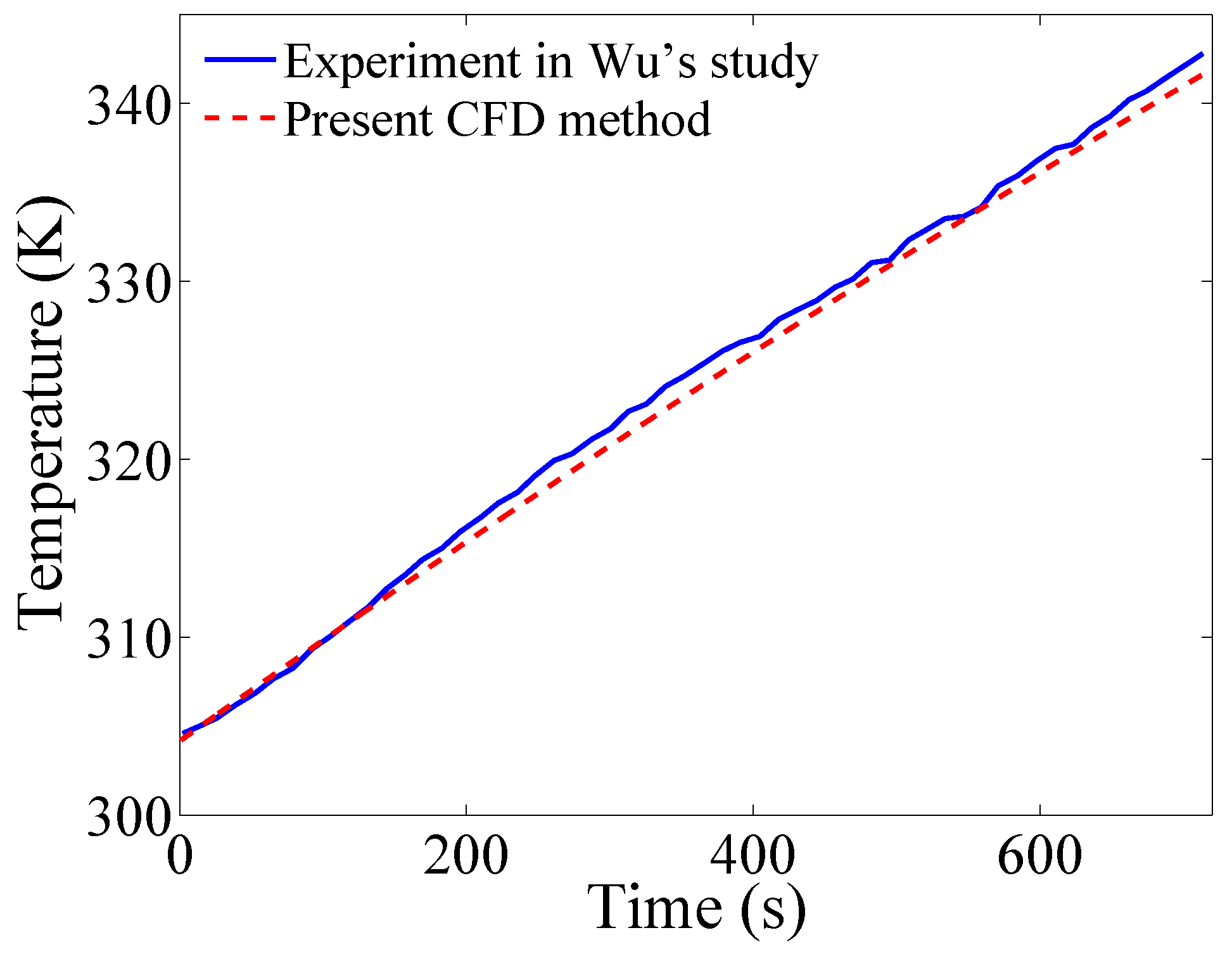
3.3. Validation of the CFD Method
4. Influences of the System Parameters on Performance
4.1. Influence of the Discharge Rate
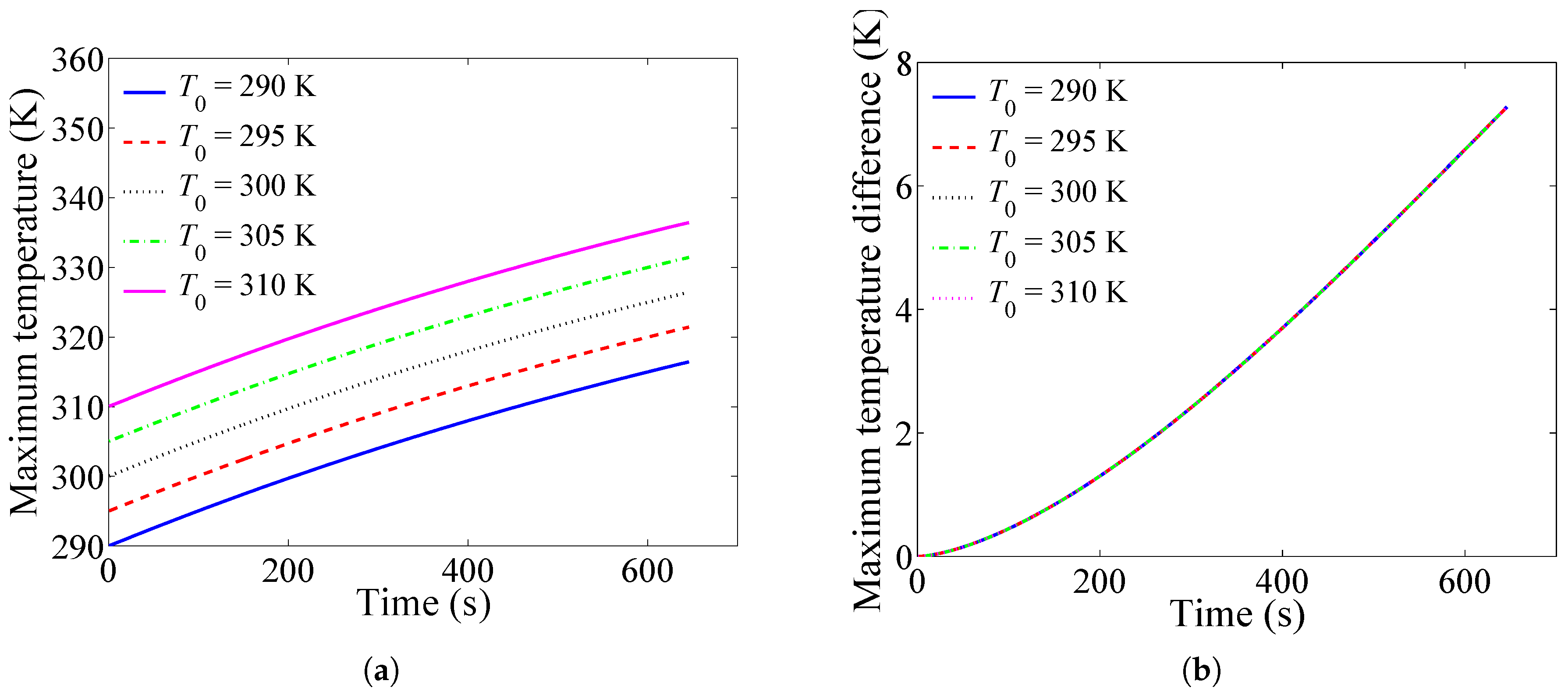
4.2. Influence of the Inlet Air Temperature
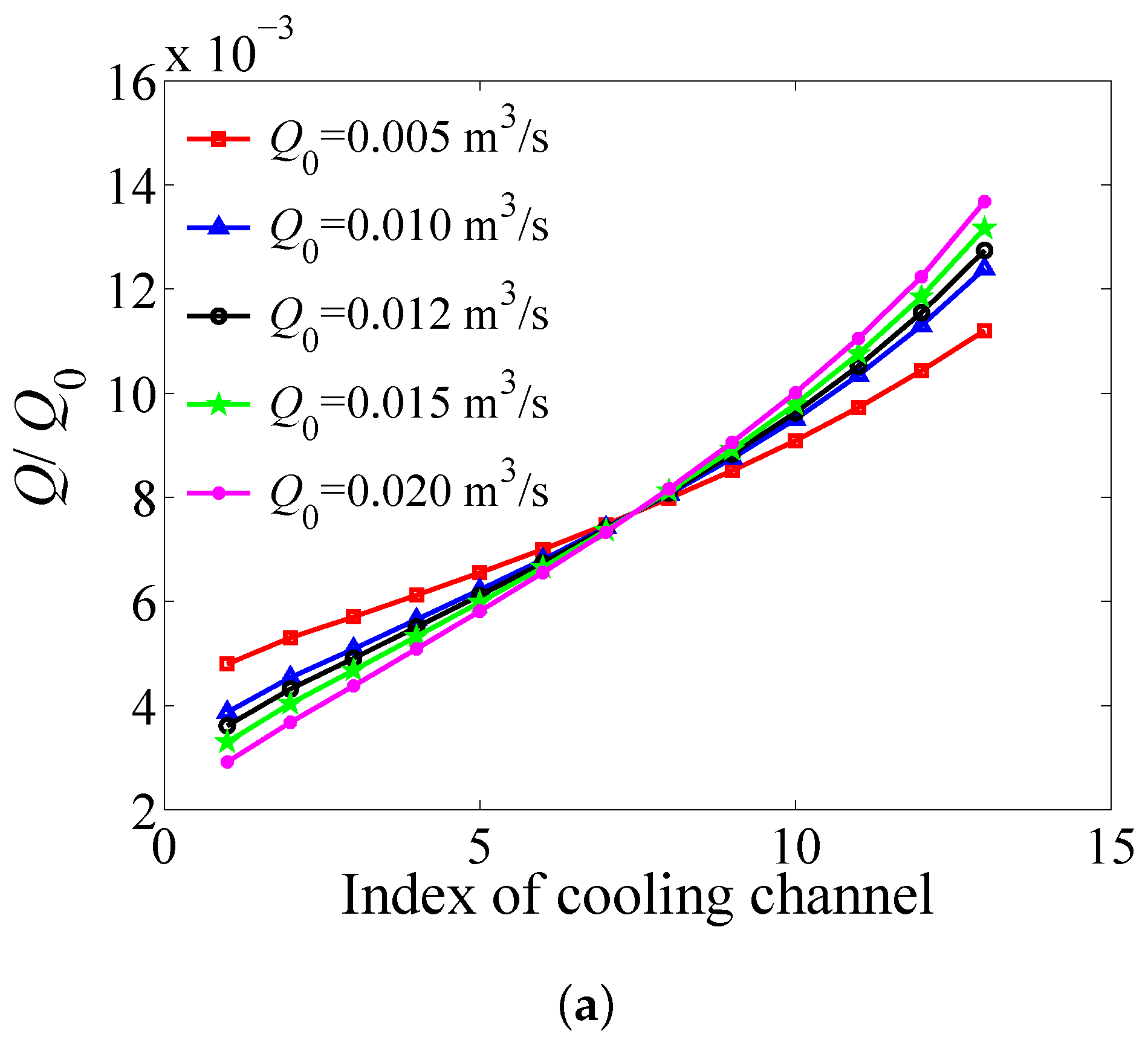
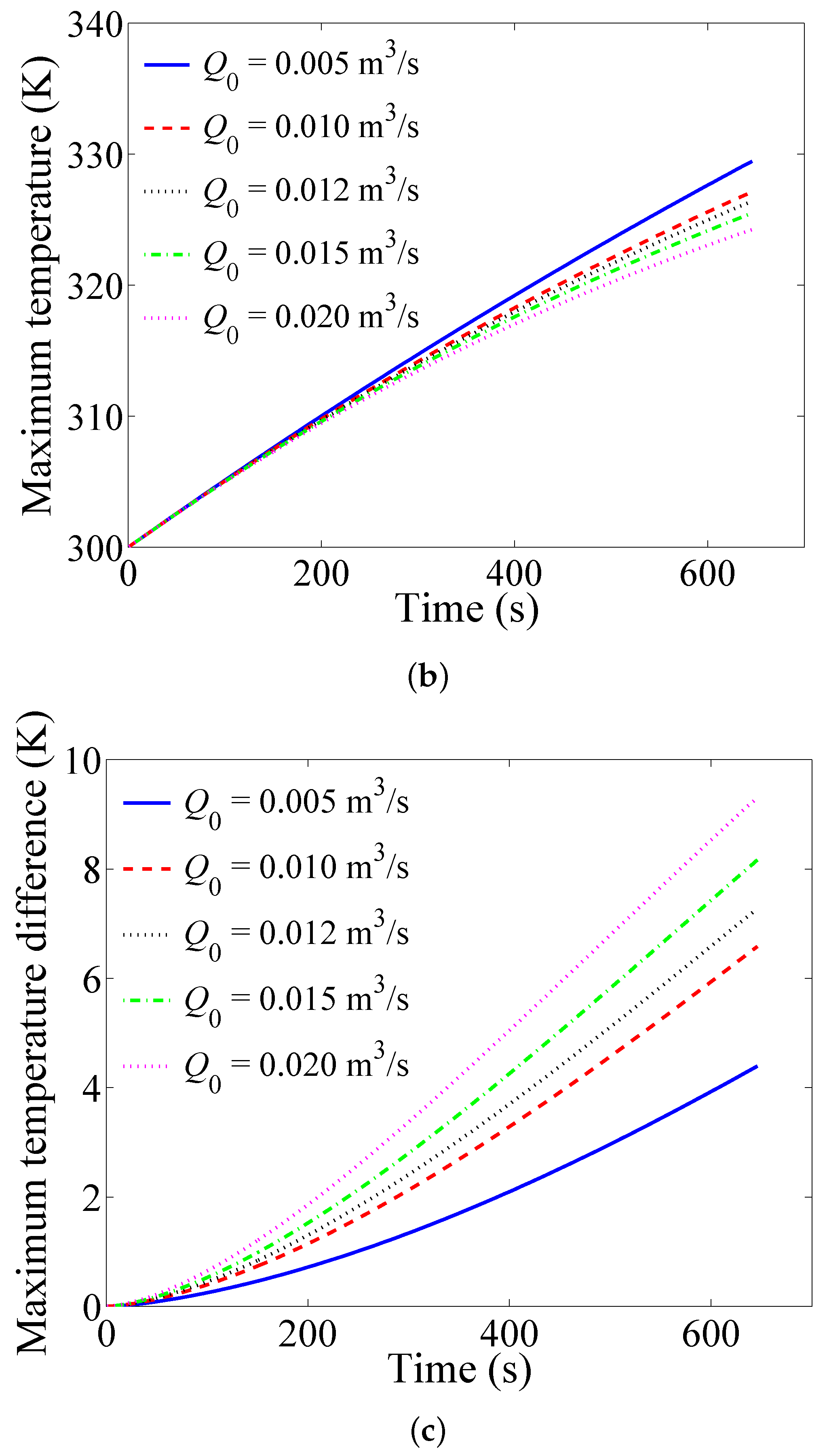
4.3. Influence of the Inlet Airflow Rate
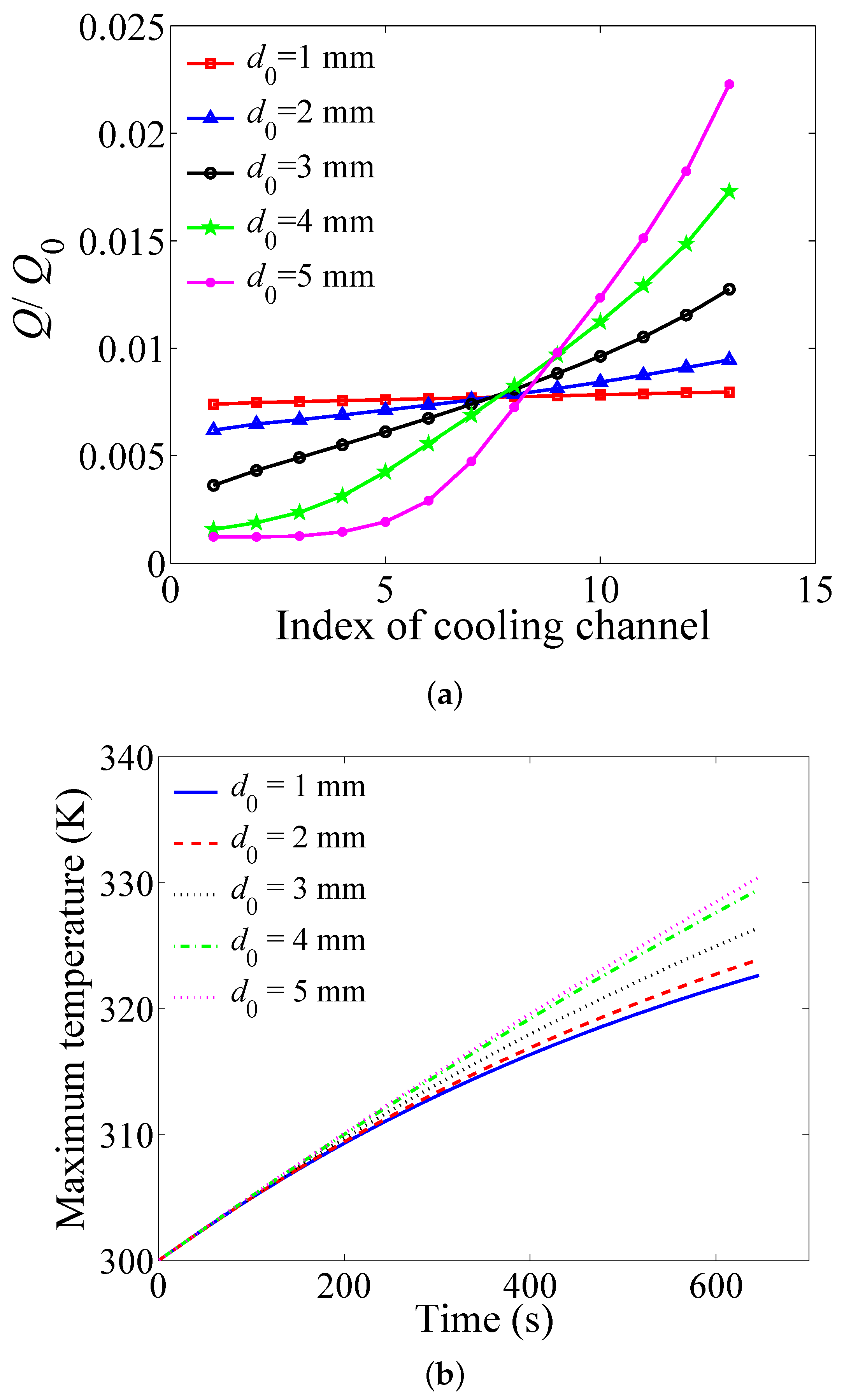
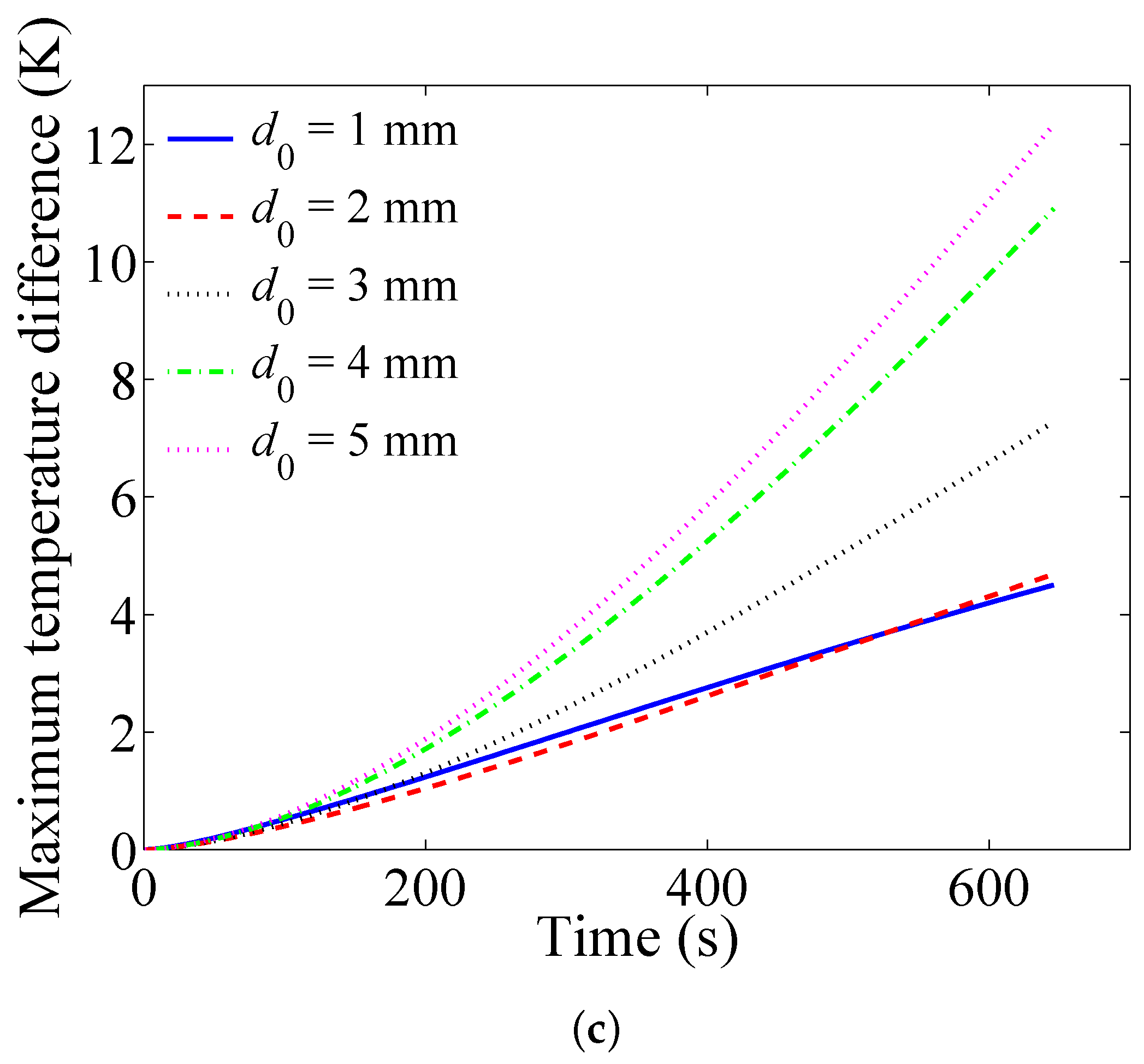
4.4. Influence of Cell Spacing
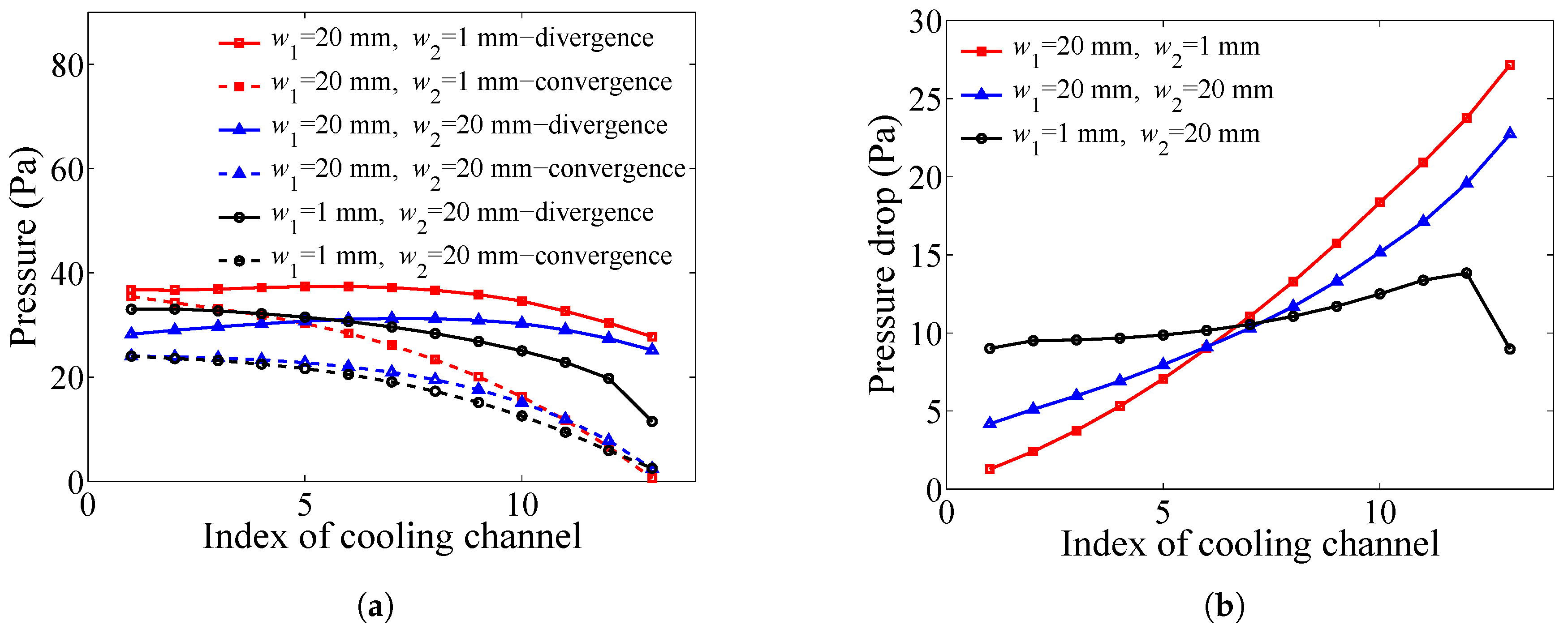
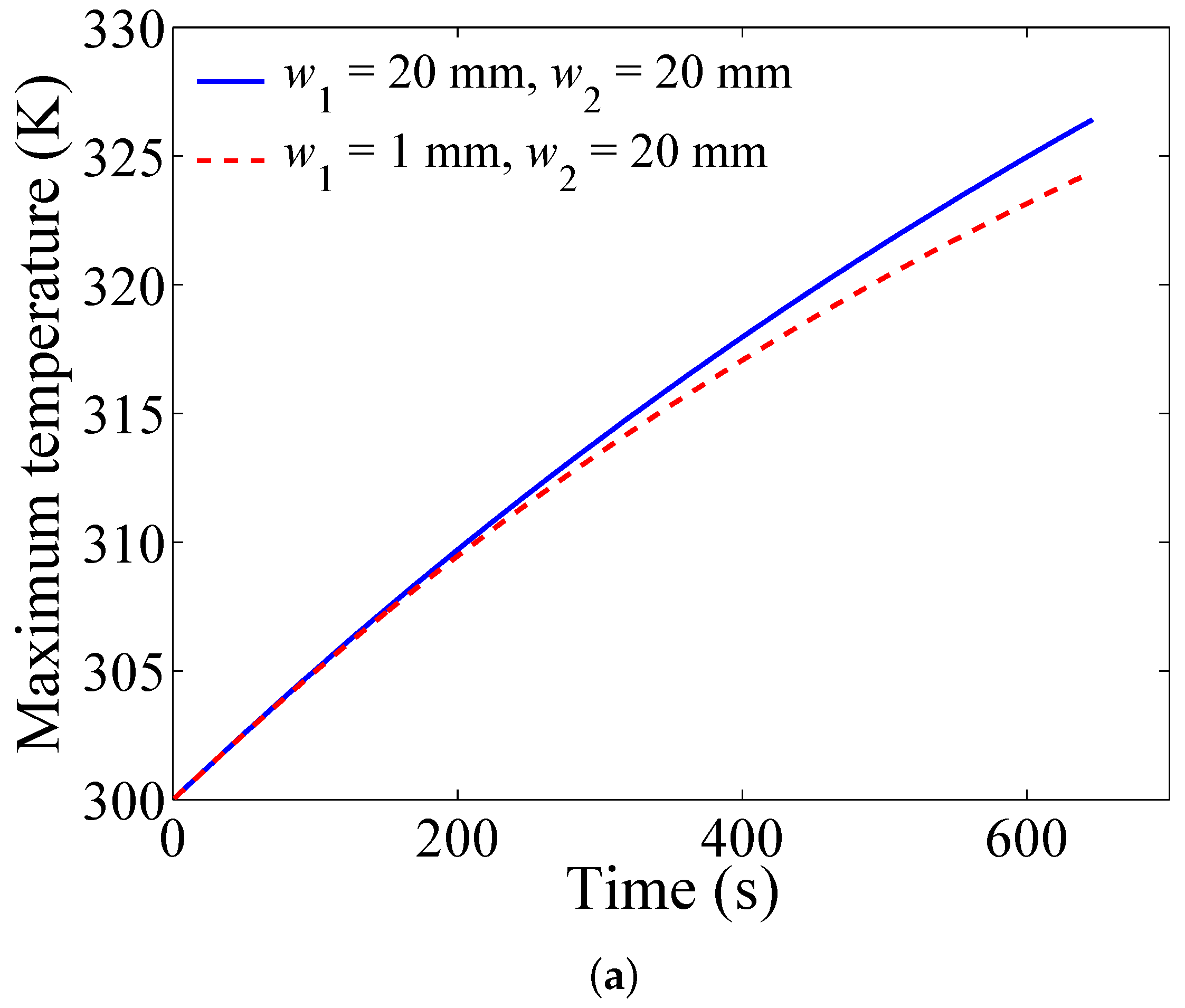
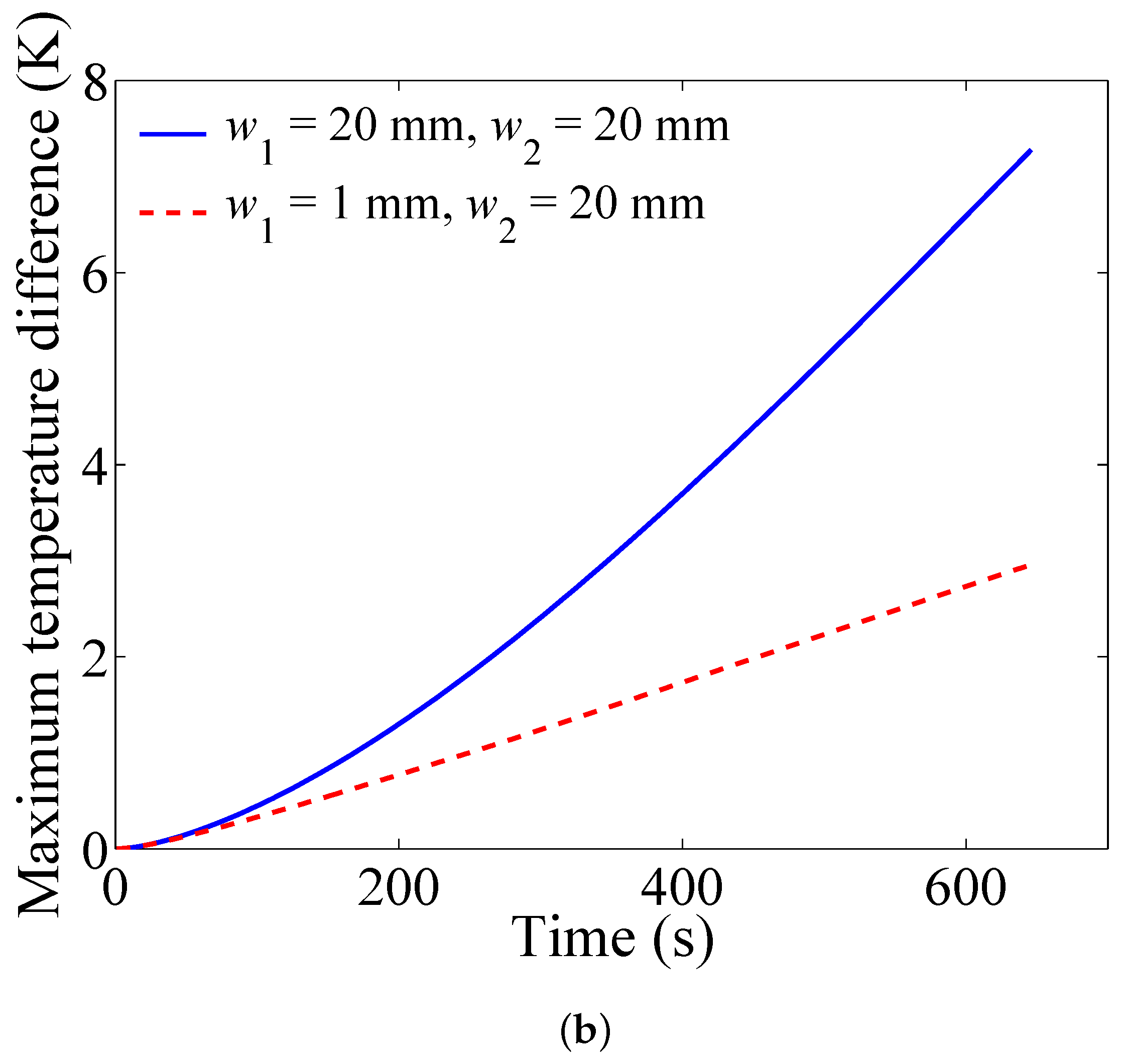
4.5. Influence of the Angles of the Divergence Plenum and Convergence Plenum
- Situation 1: Let mm, and consider the value of as 1 mm, 5 mm, 10 mm, 15 mm and 20 mm, respectively.
- Situation 2: Let , and consider the values as 1 mm, 5 mm, 10 mm, 15 mm and 20 mm, respectively.
- Situation 3: Let mm, and consider the value of as 1 mm, 5 mm, 10 mm, 15 mm and 20 mm, respectively.
4.6. Optimization of Plenum Widths
- Set as the fixed value and set the initial range of as . Calculate the middle point of the range as .
- Let equal , and , respectively. Evaluate the values of of these three BTMSs using the CFD calculation, respectively, denoting them as , and .If ,let , then return to Step 2 and continue the process.else if ,let , then return to Step 2 and continue the process.elsego to Step 3.
- The range for is reduced through using the following strategy. Let and . Evaluate the values of of the two BTMSs with and using CFD calculation, respectively, denoting them as and .If ,let .else if ,let .elselet .
- If and are both smaller than a specified threshold, the optimization process is stopped; otherwise, return to Step 3, and continue the process.
4.7. Performance with Fixed Power Consumption
5. Conclusions
- The temperature rise and the temperature difference of the battery pack increase as the discharge rate increases, but the discharge rate cannot be controlled effectively.
- Reducing the inlet air temperature can reduce the absolute temperature of the battery pack, but cannot effectively reduce the temperature rise and the temperature difference of the system.
- As the inlet airflow rate increases, the maximum temperature of the battery pack is reduced, but the temperature difference of the battery pack and the power consumption to maintain the flow rate are both increased.
- As the cell spacings decrease, the temperature and the temperature difference of the battery pack are both reduced effectively. However, the decrease of the cell spacing increases the power consumption of the system significantly.
- The angles of the plenums remarkably influence the performance of the BTMS. The maximum temperature and the maximum temperature difference of the battery pack can be reduced effectively through optimizing the angles of the plenums, without increasing the total volume and the power consumption of the BTMS.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| parameters of the turbulence model, 1 | |
| parameter of the turbulence model, 1 | |
| heat capacities of the air, | |
| heat capacities of the battery cell, | |
| cell spacing among the battery cells, m | |
| length, width and height of the battery cell, m | |
| I | discharge current of the battery cell, A |
| k | turbulent kinetic energy, |
| M | number of the rows for the battery pack, 1 |
| N | number of the columns for the battery pack, 1 |
| p | Reynolds-averaged pressure, Pa |
| inlet airflow rate, | |
| R | the equivalent resistance of the battery cell, |
| temperature of the inlet airflow, K | |
| temperature of the air, K | |
| temperature of the battery cell, K | |
| maximum temperature of the battery pack, K | |
| maximum temperature difference of the battery pack, K | |
| , | the i-th and the j-th Reynolds-averaged velocity components, m/s |
| volume of the battery cell, | |
| width of the divergence plenum, m | |
| width of the convergence plenum, m | |
| inlet width, m | |
| outlet width, m | |
| power consumption of the BTMS, W | |
| coordinates of the domain, m |
Greek Symbols
| thermal conductivity of the air, | |
| thermal conductivity of the battery cell, | |
| the molecular dynamic viscosity coefficient of the air, | |
| the turbulent dynamic viscosity coefficient, | |
| heat generation rate of the battery cell, | |
| density of the air, | |
| density of the battery cell, | |
| parameter of the turbulence model in the equation, 1 | |
| parameter of the turbulence model in the k equation, 1 | |
| parameter of the turbulence model in the temperature equation, 1 | |
| angle of the divergence plenum, degree | |
| angle of the convergence plenum, degree | |
| turbulent kinetic energy dissipation, |
Subscripts
| battery cell | |
| inlet cross-section | |
| max | maximum |
| outlet cross-section |
References
- Li, X.; He, F.; Ma, L. Thermal management of cylindrical batteries investigated using wind tunnel testing and computational fluid dynamics simulation. J. Power Sources 2013, 238, 395–402. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- He, F.; Li, X.; Ma, L. Combined experimental and numerical study of thermal management of battery module consisting of multiple Li-ion cells. Int. J. Heat Mass Transf. 2014, 72, 622–629. [Google Scholar] [CrossRef]
- Yu, K.; Yang, X.; Cheng, Y.; Li, C. Thermal analysis and two-directional air flow thermal management for lithium-ion battery pack. J. Power Sources 2014, 270, 193–200. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; Zhang, Y. Thermal management optimization of an air-cooled Li-ion battery module using pin-fin heat sinks for hybrid electric vehicles. J. Power Sources 2015, 273, 431–439. [Google Scholar] [CrossRef]
- Jarrett, A.; Kim, I.Y. Design optimization of electric vehicle battery cooling plates for thermal performance. J. Power Sources 2001, 196, 10359–10368. [Google Scholar] [CrossRef]
- Smith, J.; Hinterberger, M.; Hable, P.; Koehler, J. Simulative method for determining the optimal operating conditions for a cooling plate for lithium-ion battery cell modules. J. Power Sources 2014, 267, 784–792. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Y.; Rao, Z. Thermal performance of lithium-ion battery thermal management system by using mini-channel cooling. Energy Convers. Manag. 2016, 126, 622–631. [Google Scholar] [CrossRef]
- Sabbah, R.; Kizilel, R.; Selman, J.R.; Al-Hallaj, S. Active (air-cooled) vs. passive (phase change material) thermal management of high power lithium-ion packs: Limitation of temperature rise and uniformity of temperature distribution. J. Power Sources 2008, 182, 630–638. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, Q.; Huang, C. Investigation of the thermal performance of phase change material/mini-channel coupled battery thermal management system. Appl. Energy 2016, 164, 659–669. [Google Scholar] [CrossRef]
- Alipanah, M.; Li, X. Numerical studies of lithium-ion battery thermal management systems using phase change materials and metal foams. Int. J. Heat Mass Transf. 2016, 102, 1159–1168. [Google Scholar] [CrossRef]
- Wilke, S.; Schweitzer, B.; Khateeb, S.; Al-Hallaj, S. Preventing thermal runaway propagation in lithium ion battery packs using a phase change composite material: An experimental study. J. Power Sources 2017, 340, 51–59. [Google Scholar] [CrossRef]
- Yi, J.; Koo, B.; Shin, C. Three-Dimensional Modeling of the Thermal Behavior of a Lithium-Ion Battery Module for Hybrid Electric Vehicle Applications. Energies 2014, 7, 7586–7601. [Google Scholar] [CrossRef]
- Cho, G.Y.; Choi, J.W.; Park, J.H.; Cha, S.W. Transient modeling and validation of lithium ion battery pack with air cooled thermal management system for electric vehicles. Int. J. Automot. Technol. 2014, 15, 795–803. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M.; Pesaran, A.A. A parametric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles. J. Power Sources 2013, 238, 301–312. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Zhang, J.; Liu, Z. Shortcut computation for the thermal management of a large air-cooled battery pack. Appl. Therm. Eng. 2014, 66, 445–452. [Google Scholar] [CrossRef]
- He, H.; Jia, H.; Huo, W.; Sun, F. Field Synergy Analysis and Optimization of the Thermal Behavior of Lithium Ion Battery Packs. Energies 2017, 10, 811. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Mahamud, R.; Park, C. Reciprocating air flow for Li-ion battery thermal management to improve temperature uniformity. J. Power Sources 2011, 196, 5685–5696. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.J.; Zhao, J.; Wei, Z. Thermal investigation of lithium-ion battery module with different cell arrangement structures and forced air-cooling strategies. Appl. Energy 2014, 134, 229–238. [Google Scholar] [CrossRef]
- Yong, S.C.; Mo, K.D. Prediction of thermal behaviors of an air-cooled lithium-ion battery system for hybrid electric vehicles. J. Power Sources 2014, 270, 273–280. [Google Scholar]
- Park, H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles. J. Power Sources 2013, 239, 30–36. [Google Scholar] [CrossRef]
- Sun, H.; Dixon, R. Development of cooling strategy for an air cooled lithium-ion battery pack. J. Power Sources 2014, 272, 404–414. [Google Scholar] [CrossRef]
- Chen, K.; Wang, S.; Song, M.; Chen, L. Structure optimization of parallel air-cooled battery thermal management system. Int. J. Heat Mass Transf. 2017, 111, 943–952. [Google Scholar] [CrossRef]
- Shahid, S.; Agelin-Chaab, M. Analysis of Cooling Effectiveness and Temperature Uniformity in a Battery Pack for Cylindrical Batteries. Energies 2017, 10, 1157. [Google Scholar] [CrossRef]
- Xu, X.M.; He, R. Research on the heat dissipation performance of battery pack based on forced air cooling. J. Power Sources 2013, 240, 33–41. [Google Scholar] [CrossRef]
- Xu, X.M.; He, R. Review on the heat dissipation performance of battery pack with different structures and operation conditions. Renew. Sustain. Energy Rev. 2014, 29, 301–315. [Google Scholar] [CrossRef]
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal design and simulation of mini-channel cold plate for water cooled large sized prismatic lithium-ion battery. Appl. Therm. Eng. 2017, 22, 80–90. [Google Scholar] [CrossRef]
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Numerical modeling and experimental investigation of a prismatic battery subjected towater cooling. Numer. Heat Transf. Part A Appl. 2017, 71, 626–637. [Google Scholar] [CrossRef]
- Chen, K.; Wang, S.; Song, M.; Chen, L. Configuration optimization of battery pack in parallel air-cooled battery thermal management system using an optimization strategy. Appl. Therm. Eng. 2017, 123, 177–186. [Google Scholar] [CrossRef]
- Wu, W. The Experimental and Simulation Research of Power Batteries Thermal Management Based on PCM. Master’s Thesis, Guangdong University of Technology, Guangzhou, China, 2015. [Google Scholar]
| Property | Air | Battery Cell [22] |
|---|---|---|
| Density () | 1.165 | 2700 |
| Specific heat () | 1005 | 900 |
| Dynamic viscosity () | - | |
| Thermal conductivity () | 0.0267 | 240 |
| Initial temperature (K) | 300 | 300 |
| (mm) | - | 16 |
| (mm) | - | 151 |
| (mm) | - | 65 |
| 3D Calculation | 2D Calculation | ||||
|---|---|---|---|---|---|
| () | (K) | (K) | (K) | (K) | |
| 0.005 | 329.5 | 4.4 | 329.5 | 4.4 | |
| 0.010 | 327.1 | 6.6 | 327.2 | 6.6 | |
| 0.012 | 326.4 | 7.2 | 326.5 | 7.3 | |
| 0.015 | 325.4 | 8.0 | 325.6 | 8.2 | |
| Property | Value [31] |
|---|---|
| Size (mm × mm × mm) | 70 × 27 × 90 |
| Density () | 2335 |
| Specific heat () | 935 |
| Thermal conductivity (, ) | 0.26/0.7/0.26 |
| Equivalent heat generation rate () |
| Discharge Rate | (K) | (K) | (K) |
|---|---|---|---|
| 3C | 313.5 | 308.5 | 5.0 |
| 4C | 320.0 | 313.7 | 6.3 |
| 5C | 326.5 | 319.2 | 7.3 |
| 6C | 333.5 | 325.1 | 8.4 |
| (K) | (K) | (K) | (K) |
|---|---|---|---|
| 290 | 316.5 | 26.5 | 7.3 |
| 295 | 321.5 | 26.5 | 7.3 |
| 300 | 326.5 | 26.5 | 7.3 |
| 305 | 331.5 | 26.5 | 7.3 |
| 310 | 336.5 | 26.5 | 7.3 |
| () | (K) | (K) | (W) |
|---|---|---|---|
| 0.005 | 329.5 | 4.4 | 0.0371 |
| 0.010 | 327.2 | 6.6 | 0.2295 |
| 0.012 | 326.5 | 7.3 | 0.3794 |
| 0.015 | 325.6 | 8.2 | 0.7094 |
| 0.020 | 324.3 | 9.3 | 1.6132 |
| (mm) | (K) | (K) | (W) |
|---|---|---|---|
| 1 | 322.7 | 4.5 | 4.0044 |
| 2 | 324.0 | 4.7 | 0.7023 |
| 3 | 326.5 | 7.3 | 0.3794 |
| 4 | 329.5 | 11.0 | 0.3149 |
| 5 | 330.5 | 12.4 | 0.3056 |
| (mm) | (mm) | (K) | (K) | (W) | |
|---|---|---|---|---|---|
| 20 | 1 | 329.1 | 11.0 | 0.4721 | |
| 20 | 5 | 328.0 | 9.5 | 0.4361 | |
| Situation 1 | 20 | 10 | 327.2 | 8.4 | 0.4097 |
| 20 | 15 | 326.8 | 7.8 | 0.3922 | |
| 20 | 20 | 326.5 | 7.3 | 0.3794 | |
| 1 | 1 | 326.3 | 6.7 | 0.6296 | |
| 5 | 5 | 326.2 | 7.7 | 0.4991 | |
| Situation 2 | 10 | 10 | 326.3 | 7.6 | 0.4379 |
| 15 | 15 | 326.5 | 7.5 | 0.4032 | |
| 20 | 20 | 326.5 | 7.3 | 0.3794 | |
| 1 | 20 | 324.0 | 3.1 | 0.4682 | |
| 5 | 20 | 325.0 | 5.8 | 0.4315 | |
| Situation 3 | 10 | 20 | 325.7 | 6.7 | 0.4063 |
| 15 | 20 | 326.2 | 7.1 | 0.3905 | |
| 20 | 20 | 326.5 | 7.3 | 0.3794 |
| Step | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
(mm) | (K) | (mm) | (K) | (mm) | (K) | (mm) | (K) | (mm) | (K) | |
| 1 | 1.00 | 3.08 | - | - | 3.00 | 5.10 | - | - | 5.00 | 5.80 |
| 2 | 1.00 | 3.08 | - | - | 2.00 | 4.43 | - | - | 3.00 | 5.10 |
| 3 | 1.00 | 3.08 | - | - | 1.50 | 3.92 | - | - | 2.00 | 4.43 |
| 4 | 1.00 | 3.08 | - | - | 1.25 | 3.61 | - | - | 1.50 | 3.92 |
| 5 | 1.00 | 3.08 | - | - | 1.13 | 3.32 | - | - | 1.25 | 3.61 |
| 6 | 1.00 | 3.08 | - | - | 1.06 | 3.21 | - | - | 1.13 | 3.32 |
| Step | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
(mm) | (K) | (mm) | (K) | (mm) | (K) | (mm) | (K) | (mm) | (K) | |
| 1 | 15.00 | 3.45 | - | - | 17.50 | 3.25 | - | - | 20.00 | 3.08 |
| 2 | 17.50 | 3.25 | - | - | 18.75 | 3.16 | - | - | 20.00 | 3.08 |
| 3 | 18.75 | 3.16 | - | - | 19.38 | 3.12 | - | - | 20.00 | 3.08 |
| 4 | 19.38 | 3.12 | - | - | 19.69 | 3.10 | - | - | 20.00 | 3.08 |
| 5 | 19.69 | 3.10 | - | - | 19.84 | 3.09 | - | - | 20.00 | 3.08 |
| 6 | 19.84 | 3.09 | - | - | 19.92 | 3.09 | - | - | 20.00 | 3.08 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Li, Z.; Chen, Y.; Long, S.; Hou, J.; Song, M.; Wang, S. Design of Parallel Air-Cooled Battery Thermal Management System through Numerical Study. Energies 2017, 10, 1677. https://doi.org/10.3390/en10101677
Chen K, Li Z, Chen Y, Long S, Hou J, Song M, Wang S. Design of Parallel Air-Cooled Battery Thermal Management System through Numerical Study. Energies. 2017; 10(10):1677. https://doi.org/10.3390/en10101677
Chicago/Turabian StyleChen, Kai, Zeyu Li, Yiming Chen, Shuming Long, Junsheng Hou, Mengxuan Song, and Shuangfeng Wang. 2017. "Design of Parallel Air-Cooled Battery Thermal Management System through Numerical Study" Energies 10, no. 10: 1677. https://doi.org/10.3390/en10101677
APA StyleChen, K., Li, Z., Chen, Y., Long, S., Hou, J., Song, M., & Wang, S. (2017). Design of Parallel Air-Cooled Battery Thermal Management System through Numerical Study. Energies, 10(10), 1677. https://doi.org/10.3390/en10101677






