A Comparative Study of CFD Models of a Real Wind Turbine in Solar Chimney Power Plants

Abstract

A solar chimney power plant consists of four main parts, a solar collector, a chimney, an energy storage layer, and a wind turbine. So far, several investigations on the performance of the solar chimney power plant have been conducted. Among them, different approaches have been applied to model the turbine inside the system. In particular, a real wind turbine coupled to the system was simulated using computational fluid dynamics (CFD) in three investigations. Gholamalizadeh et al. simulated a wind turbine with the same blade profile as the Manzanares SCPP’s turbine (FX W-151-A blade profile), while a CLARK Y blade profile was modelled by Guo et al. and Ming et al. In this study, simulations of the Manzanares prototype were carried out using the CFD model developed by Gholamalizadeh et al. Then, results obtained by modelling different turbine blade profiles at different turbine rotational speeds were compared. The results showed that a turbine with the CLARK Y blade profile significantly overestimates the value of the pressure drop across the Manzanares prototype turbine as compared to the FX W-151-A blade profile. In addition, modelling of both blade profiles led to very similar trends in changes in turbine efficiency and power output with respect to rotational speed.

1. Introduction

A solar chimney power plant (SCPP) is one of the practical solar thermal power systems that produce electricity from solar energy. A conventional SCPP consists of four main parts: a solar collector, an energy storage medium such as the ground, a chimney, and a wind turbine. Figure 1 shows a schematic diagram of the SCPP and its boundary conditions. The solar radiation freely enters the collector via the collector cover, which is a semi-transparent medium, such as glass, and then is absorbed by the ground. Because the semi-transparent cover is opaque to the long wavelength radiation emitted by the ground, the air inside the collector is heated by the greenhouse effect. Consequently, the temperature of the airflow through the collector increases, which results in a continuous updraft in the chimney due to the upward buoyancy force. This airflow runs a turbine, which is located at the chimney base. Finally, a generator converts the mechanical energy produced by the turbine into the electrical power.

The first SCPP, called the Manzanares prototype, was constructed in Manzanares, Spain, in 1982. This prototype was designed to produce a peak power output of 50 kW, and was tested under continuous operation for a period of seven years [1]. The constructed dimensions of the Manzanares prototype are listed in

Table 1. Constructed dimensions of the Manzanares prototype solar chimney power plant (SCPP).

Parameters	Values
Chimney height	194.6 m
Chimney diameter	10.16 m
Collector radius	122 m
Mean collector height	1.85 m
Number of turbine blades	4
Turbine blade profile	FX W-151-A

.

A mathematical model and preliminary test results of the Manzanares prototype were published by Haaf et al. [2,3]. These results demonstrated the feasibility of the SCPP system for the first time. Afterwards, several studies of the system’s performance were carried out [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Bernardes et al. [20] developed the first numerical code using a finite volume method that solved the Navier-Stokes and energy equations for the natural laminar convection in steady state. Then, Pastohr et al. [21] simulated an SCPP system with the main dimensions of the Manzanares prototype using a commercial computational fluid dynamics (CFD) package. Subsequently, commercial CFD codes were widely employed to simulate the fluid flow and the heat transfer characteristics of an SCPP system. Most of the preliminary simulations were carried out in an axisymmetric system by imposing some non-physical boundary conditions, such as a thin layer as a heat source to model the ground, heat fluxes, specific wall temperatures profiles, and a uniform heat source within the airflow [21,22,23,24]. Gholamalizadeh and Kim [25] developed a more accurate three-dimensional (3-D) model using CFD that predicts heat transfer inside of the solar collector by taking into account the greenhouse effect using discrete ordinates for radiation and a solar load model. A 3-D CFD approach was also carried out by Guo et al. [23] which predicted the maximum value of the turbine pressure drop at a certain solar irradiance.

Simulating an SCPP without the turbine may reveal some information that can be used to evaluate the feasibility and potential energy of the system. However, in the numerical analysis, modelling the turbine has a substantial effect on the predicted system performance. In several investigations, an actuator disc model called “reverse fan boundary condition” was adopted to model the pressure drop across the turbine. This model indeed implements a pre-defined interior pressure jump through a thin surface. Pastohr et al. used the Betz limit to calculate the value of the pressure drop for the reverse fan model [17]. The value of the pressure drop was also estimated by using a parametric study [24,26], and an iterative approach [21].

The main advantage of the reverse fan model was to simulate the pressure jump of the turbine with a computationally low cost. However, the reverse fan model cannot accurately predict the pressure distribution through the system [27]. Hence, modelling a physical wind turbine is of interest from a design point of view since it has a significant influence on the fluid flow and heat transfer characteristics through the SCPP system. Based on a literature review, only a few investigations have been conducted, which modelled a 3-D wind turbine for an SCPP [27,28,29].

A 4-bladed shrouded pressure-staged wind turbine with the FX W-151-A blade profile was installed in the chimney base of the Manzanares prototype [30]. Gholamalizadeh et al. [27] modelled a 4-bladed pressure-staged wind turbine with the same profile as that of the Manzanares prototype (FX W-151-A). Guo et al. [28] and Ming et al. [29] also used a CLARK Y blade profile to simulate 4-bladed and a 3-bladed pressure-staged wind turbines, respectively.

In this paper, in order to examine the effect of the blade profile modelling on the prediction accuracy for a real wind turbine coupled with the SCPP, 3-D simulations for the Manzanares prototype coupled with a wind turbine with the FX W-151-A blade profile were carried out. Then, a comparative study between modelling two different turbine profiles, including FX W-151-A and CLARK Y blade profiles was presented. This will help to obtain a more realistic model for an SCPP, and thus contribute to simulate the fluid flow and heat transfer characteristics of the system more accurately. In addition, for a turbine with FX W-151-A blade profile, the effects of variations in the turbine rotational speed on the mass flow rate, pressure drop across the turbine, the turbine efficiency, and the power output were investigated, and predicted results were compared to those of CLARK Y blade profile.

2. Numerical Methodologies

In [27,28,29], simulations with the constructed dimensions of the Manzanares prototype for steady flow were carried out with the use of the CFD commercial software package ANSYS Fluent (ANSYS Inc., Pittsburgh, PA, USA). The simulations conducted in this investigation used the model developed by Gholamalizadeh et al. [27]. However, in order to compare the results to the results published in other works, the values of the main input parameters were set to be consistent with those in Ref. [28], as listed in

Table 2. Main input parameters of the simulations.

Parameters	Values
Ambient pressure	101,325 Pa
Ambient temperature	302 K
Thermal expansion coefficient	0.00331 (1/K)
Solar irradiance	800 W/m2

. The numerical simulations are based on the following assumptions: (1) For such a small-scale SCPP, the air properties of the environment such as the ambient temperature and the inlet air temperature can be assumed to be constant; (2) the heat loss via wall of the chimney is neglected; (3) since temperature differences through the system are small ($\beta \left(T-T_0\right)\ll 1$), the Boussinesq approximation is assumed to calculate the buoyancy-driven flow.

2.1. Modelling the Fluid Flow and Heat Transfer Inside the System

Table 3. Conservation Equations.

Equation	Gholamalizadeh et al.	Guo et al.	Ming et al.
Continuity	$\frac{\partial }{\partial x_i}\left(\rho u_i\right)=0$			(1)
Momentum	$\frac{\partial }{\partial x_j}\left(\rho u_i{u}_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}{\delta }_{ij}\frac{\partial u_l}{\partial x_l}\right)\right]+\frac{\partial }{\partial x_j}(-\rho \overline{u_i^{\prime }{u}_j^{\prime }})+\rho \overrightarrow{g}$			(2)
Energy	$\nabla ·\left(\overrightarrow{v}\left(\rho E+p\right)\right)=\nabla ·\left({\mathrm{k}}_{eff}\nabla \mathrm{T}-\sum _j{h}_j\overrightarrow{ J_j}+\left({\stackrel{=}{\tau }}_{eff}·\overrightarrow{v}\right)\right)+S_h$			(3)
Radiative Transfer Equation	$\nabla ·(I_{\lambda }(\overrightarrow{r},\overrightarrow{s})\overrightarrow{s})+\left(a_{\lambda }+{\sigma }_s\right)I_{\lambda }(\overrightarrow{r},\overrightarrow{s})=a_{\lambda }{n}^2{I}_{b\lambda }+\frac{{\sigma }_s}{4\pi }{\int }_0^{4\pi }{I}_{\lambda }\left(\overrightarrow{r},{\overrightarrow{s}}^{\prime }\right)\phi \left(\overrightarrow{s}·{\overrightarrow{s}}^{\prime }\right)d\mathsf{\Omega }\prime$		Not Solved	(4)

gives a description of the continuity, momentum, energy, and radiative transfer equations, which were used in the three studies. Gholamalizadeh et al. and also, Guo et al. took into account the radiative transfer equation using the discrete ordinates radiation model, while this equation was not solved in Ming’s simulation. It should be noted that neglecting radiation heat transfer causes the incorrect prediction of temperature distribution [28].

The strength of the buoyancy-induced airflow inside the system was measured using the Rayleigh number. The value of the Rayleigh number for an SCPP with the dimensions of the Manzanares prototype is higher than 10¹⁰, which shows that the airflow should be modelled as a turbulent flow. Guo et al. and Ming et al. used the standard k-ε turbulence closure, while Gholamalizadeh et al. employed the Renormalization-group (RNG) turbulence closure, in which the full buoyancy effect was activated. Scalable wall function is adopted to model the near wall treatment of the turbulent airflow. The simulations conducted in this study used the RNG turbulence closure, which is able to employ the scalable wall functions to capture the boundary layer. The main reason for selecting this method was to reduce the mesh resolution since the computational cost of simulations is high. A multi-block mesh was used to discrete the computational domain consisting of three parts. Unstructured mesh was adopted for the turbine zone, including prismatic inflation layers on the turbine surface, which captured the boundary layer. The meshes of the domains before and after the turbine zone were structural. Three mesh sizes were adopted for the computational domain to obtain a mesh independent solution. Temperature increase inside of the collector and the mass flow rate were captured to obtain the fine mesh. A mesh sensitivity study indicated that attempts to refine the mesh further never achieved more than a relative difference of 1.5%, while it increased the computational cost considerably. Therefore, for the fine mesh, insensitivity of the solution to the mesh was verified. For the fine mesh, numbers of the structural mesh and unstructured mesh were about 2,280,000 and 5,200,000, respectively. Using the fine mesh, simulations were validated by comparing the numerical results with the experimental data of the Manzanares SCPP [3]. At a solar irradiance of 850 W/m², the simulation predicted a pressure drop of 81.5 Pa across the turbine, the inlet chimney velocity of 9 m/s, and the collector temperature increase of 17.2 K, while, according to the measured data, those reached 80 Pa, 8.8 m/s and 17.5 K, respectively.

In Gholamalizadeh et al.’s work, the continuity and momentum equations were coupled together using the pressure-based COUPLED algorithm, while Guo et al.’s used the pressure-based SIMPLEC algorithm. Although the details of the algorithm were not mentioned in Ming et al.’s paper, most probably the pressure-based algorithm was implemented in that work.

The radiation model implemented by Gholamalizadeh et al. and Guo et al. simulated the non-gray radiation for the collector roof cover as a semi-transparent medium, by modelling a gray-band behaviour. Gholamalizadeh et al. and Guo et al. employed the solar load model to describe the solar irradiance that enters the collector, while Ming et al.’s work modelled the solar radiation as a heat flux. All of the investigations used the Boussinesq approximation to implement the buoyancy force through the system.

Table 4. Boundary conditions.

Place	Gholamalizadeh et al.	Guo et al.	Ming et al.
Collector inlet	Pressure inlet (pgage,in = 0)
Chimney outlet	Pressure outlet (pgage,out = 0)
Collector cover	Convection, Solar Irradiation	Convection, Solar Irradiation	TC = f(x, y, z) K
Surface of chimney	Adiabatic (Q = 0)	Undefined	Adiabatic (Q = 0)
Ground-Air interface	Coupled	Coupled	TS = f(x, y, z) K
Bottom of the ground	Constant Temperature T = constant (K)	Constant Temperature T = constant (K)	Undefined

shows the boundary conditions used in the studies. In all of the investigations, the inlet and outlet boundary conditions of the system were set as a pressure inlet and a pressure outlet, respectively. In Gholamalizadeh et al. and Guo et al.’s studies, the collector was covered by a glass, with the boundary condition of convection coupled with radiation, which participates in the solar ray tracing.

They also modelled the energy storage layer with the properties of the ground. The two-sided wall model coupled the fluid and solid regions of the ground-air interface, and the bottom temperature of the energy storage layer was set to be a constant value equal to the ambient temperature. In contrast, the energy storage layer was not simulated by Ming et al. Instead, they imposed parabolic temperature distributions for the ground and the collector surfaces as a function of the collector radius. The chimney was modelled as an adiabatic tube in Gholamalizadeh et al. and Ming et al.’s work, but Guo et al. did not mention this boundary condition.

2.2. Turbine Zone

As mentioned before, the turbine installed at the chimney base of the Manzanares prototype was a 4-bladed pressure-staged wind turbine with the FX W-151-A blade profile [30]. In Ming’s work, a 3-bladed pressure-staged wind turbine in the chimney base was implemented using a CLARK Y blade profile. Guo et al. also adopted a 4-bladed pressure-staged wind turbine with the detailed structural parameters used in Ming’s work. In Gholamalizadeh’s work [27], a 4-bladed wind turbine with the same profile as the Manzanares prototype (FX W-151-A) was modelled in the chimney base. 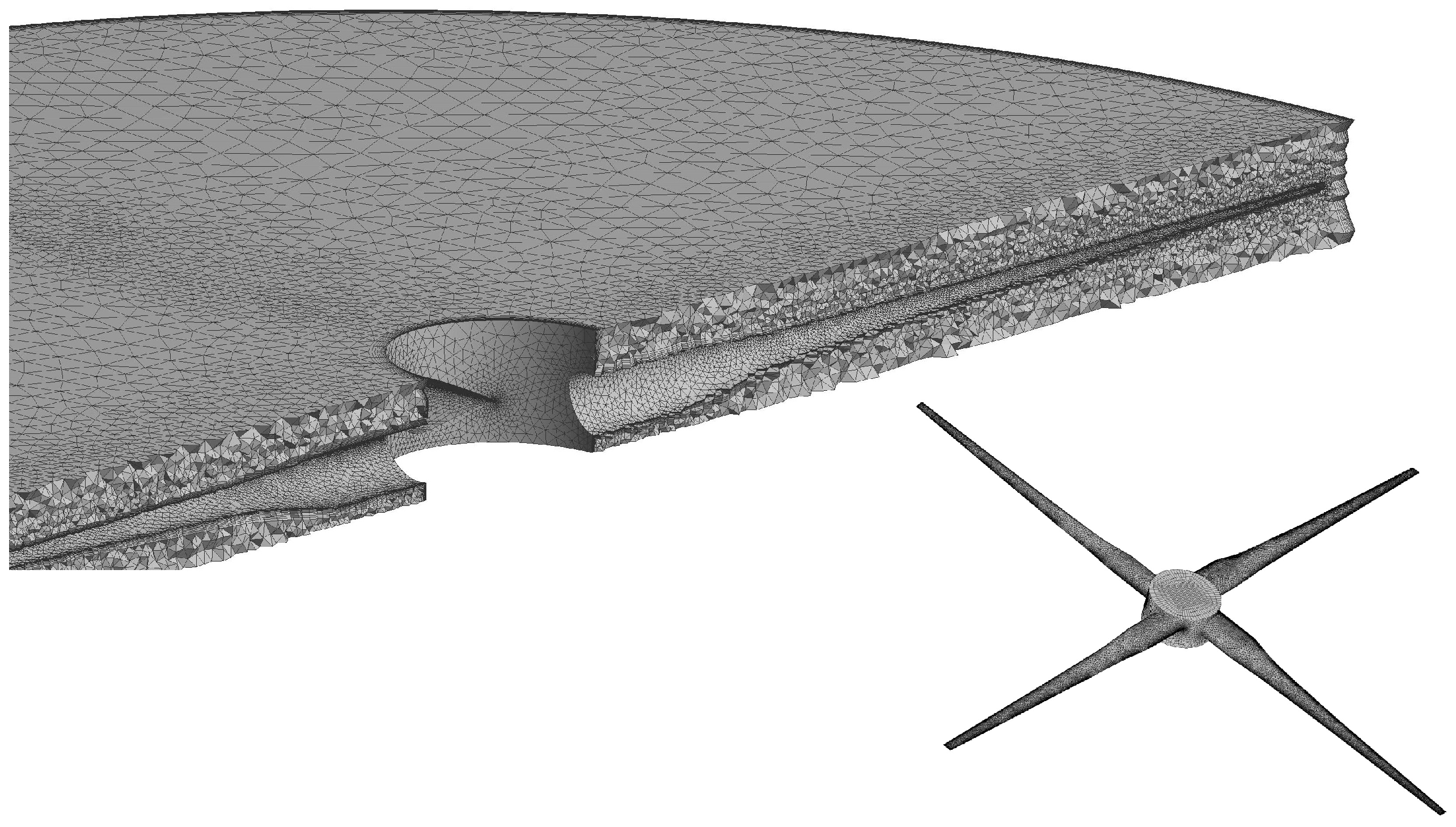Figure 2 illustrates the unstructured mesh adopted for the turbine zone.

In all of the investigations, the turbine-chimney interaction was modelled using the multiple reference frame (MRF) model. The modified equations of motion for the moving zone components are shown in

Table 5. Equations of motion.

Equation	Gholamalizadeh et al.	Guo et al.	Ming et al.
Relative velocity	${\overrightarrow{v}}_r=\overrightarrow{v}-\overrightarrow{\omega }\times \overrightarrow{r}$			(5)
Continuity	$\nabla ·\rho {\overrightarrow{v}}_r=0$			(6)
Momentum	$\nabla ·\left(\rho {\overrightarrow{v}}_r{\overrightarrow{v}}_r\right)+\rho \left(2\overrightarrow{\omega }\times {\overrightarrow{v}}_r+\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}\right)=-\nabla \mathrm{p}+\nabla ·{\stackrel{=}{\tau }}_r$			(7)
Energy	$\nabla ·\left(\rho {\overrightarrow{v}}_r{H}_r\right)=\nabla ·\left(\mathrm{k}\nabla \mathrm{T}+{\stackrel{=}{\tau }}_r·{\overrightarrow{v}}_r\right)$			(8)

.

2.3. System Performance Calculation

All of the investigations used the same approach to predict the performance of the system. The reversible power of the wind turbine was calculated as the product of the turbine pressure drop and the volume flow rate $\left(P_{t,rev}=\Delta p_t·Q\right)$. The power extracted from the rotating shaft was calculated by $P_t=2\pi nT/60$. Then, the efficiency of the turbine was predicted by dividing the shaft power by the reversible value of the shaft power $\left({\eta }_t=P_t/P_{t,rev}\right)$.

3. Results and Discussion

Three different 3-D simulations for the Manzanares prototype SCPP were carried out, taking into account a real physical turbine in the base of the chimney [27,28,29]. The main difference between Gholamalizadeh et al.’s simulations [27] on one side, and those conducted by Guo et al. [28] and Ming et al. [29] on the other hand, was the turbine blade profile. Gholamalizadeh et al. simulated a wind turbine that had the same blade profile as the Manzanares SCPP’s turbine (FX W-151-A blade profile), while the CLARK Y blade profile was modelled in the two other simulations.

In addition, Ming et al.’s work used a considerably more simplified model for modelling heat transfer inside of the collector than those employed by Gholamalizadeh et al. and Guo et al.’s. Moreover, Gholamalizadeh et al. and Guo et al. modelled a 4-bladed turbine while Ming et al. modelled a 3-bladed turbine. The results of all three models were compared with the solar irradiance set to 800 W/m².

Figure 3 shows the mass flow rate of the system at different turbine rotational speeds. In all of the models, the mass flow rate decreases when the rotational speed is increased. This trend shows that the drag force increases significantly when the turbine rotational speed is increased. It is also seen that the mass flow rate values predicted by Guo et al. are slightly higher than those predicted by Gholamalizadeh et al., while Ming et al.’s model predicts considerably higher mass flow rate values. The main reason for this is that the turbine in Ming et al.’s simulations had three blades and consequently, its drag force was lower compared to the 4-bladed turbines simulated in the other studies. Hence, the mass flow rate increased considerably when number of the blades of the turbine was lower.

The values of the pressure drop across the turbine at different rotational speeds are illustrated in Figure 4. Pressure dropped across the turbine increased considerably while the turbine rotational speed was increased. It showed that, at a higher turbine rotational speed, a higher portion of the buoyant force is extracted to run the pressure-staged wind turbine.

In the Manzanares prototype, the pressure drop across the turbine was measured to be about 80 Pa when the turbine rotational speed and the solar irradiance were 100 rpm and 850 W/m², respectively. In [27], Gholamalizadeh et al.’s model predicted a turbine pressure drop of 81.5 Pa for the same conditions, which was in a good agreement with the measured data. According to simulations conducted in this study, the model predicted a turbine pressure drop of about 74.9 Pa at a solar irradiance of 800 W/m². Ming et al.’s model predicted a pressure drop of about 79 Pa, and this pressure drop value is close to that of Gholamalizadeh et al.’s model. However, the turbine in Ming et al.’s model had three blades and therefore, it should be noted that, in Ming et al.’s model, the pressure would drop to a higher value if a 4-bladed turbine had been modelled. Consequently, considering number of blades, this model overestimated the pressure drop.

Guo et al.’s model also considerably overestimated the pressure drop occurring across the turbine in the Manzanares prototype with the predicted value of 106 Pa. While Guo et al. and Ming et al. simulated the same blade profile, it was found that the CLARK Y blade profile considerably overestimates the value of the pressure drop across the turbine when compared to the FX W-151-A blade profile simulated in Gholamalizadeh et al.’s work.

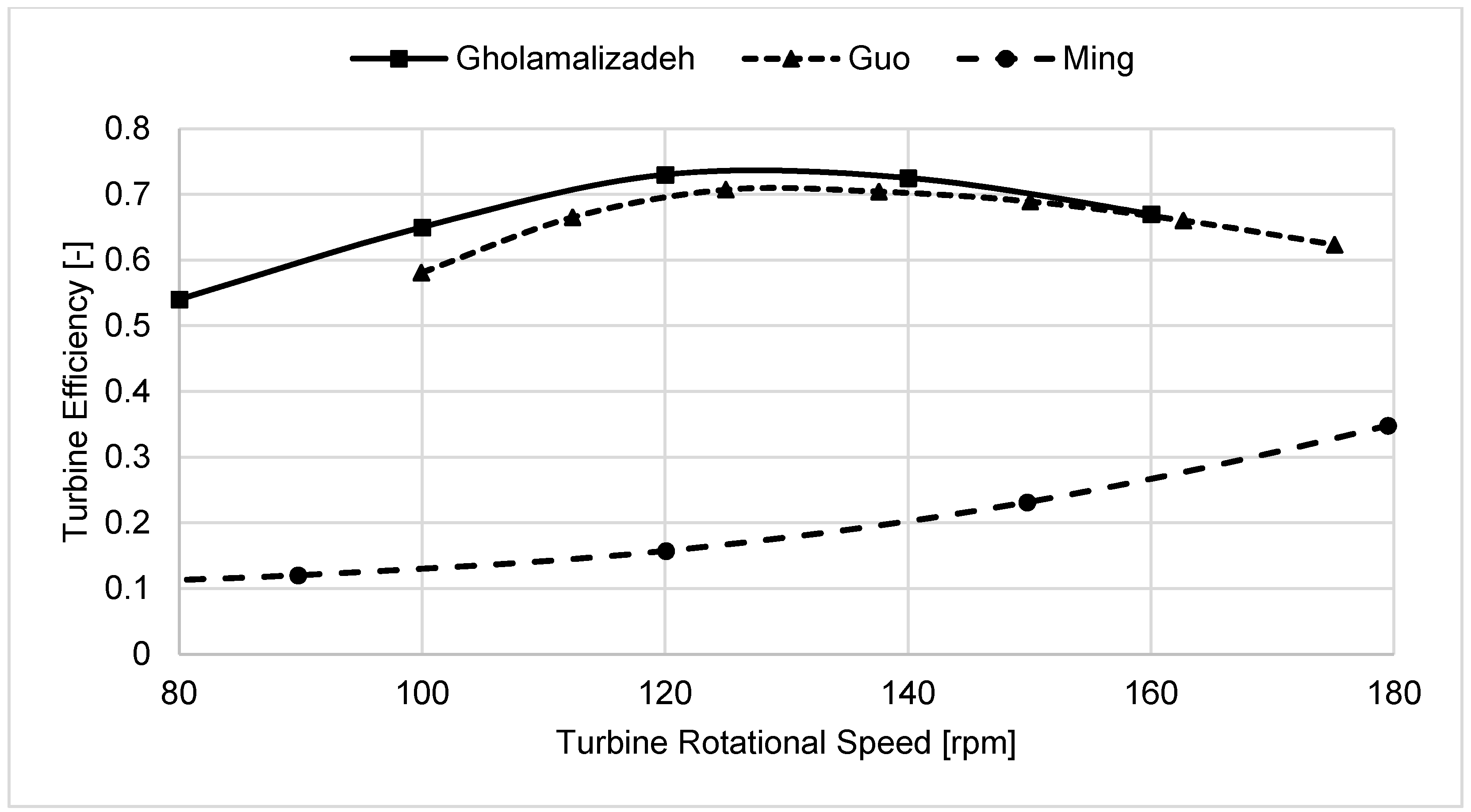
The differences in turbine efficiency with turbine rotational speed are shown in Figure 5. Gholamalizadeh et al. and Guo et al. predicted the same trend for changing turbine efficiency with respect to the turbine rotational speed. In those two investigations, the peak value for turbine efficiency occurs at a rotational speed between 120 rpm and 130 rpm. The maximum values of turbine efficiency predicted by Gholamalizadeh et al. and Guo et al. were about 0.73 and 0.7, respectively. This indicates that a 4-bladed turbine with the FX W-151-A profile has a slightly higher efficiency than that with the CLARK Y profile.

In contrast, in Ming et al.’s simulations, turbine efficiency increases constantly when the rotational speed is increased. The turbine efficiency is also considerably lower at any corresponding turbine rotational speed when compared to other models. The value of turbine efficiency increases from about 0.11 to 0.35 when the rotational speed varies from 80 rpm to 180 rpm. Hence, it is found that installing a 3-bladed turbine is not suitable for an SCPP with the same main dimensions as the Manzanares prototype, due to its low efficiency.

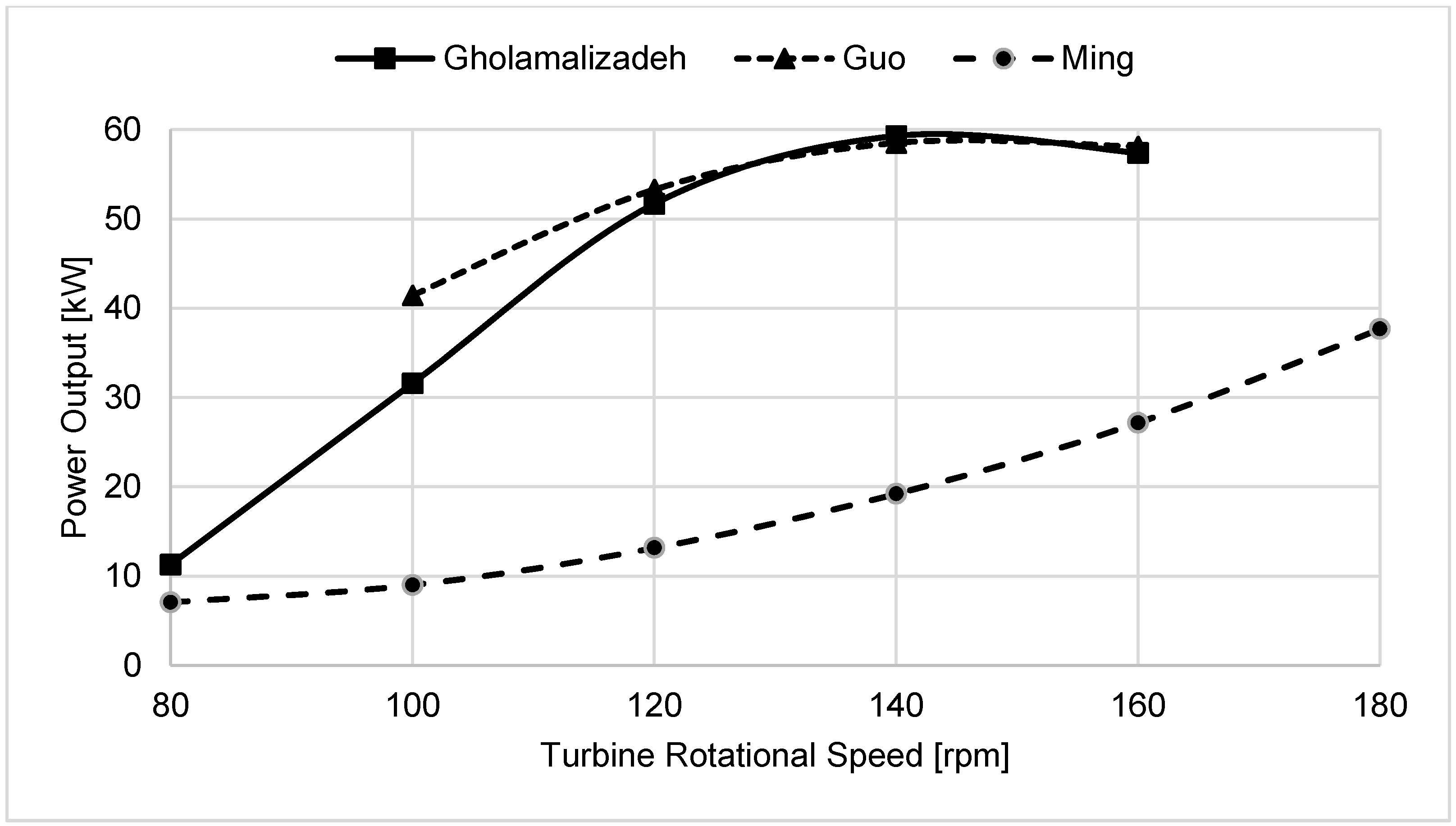
Figure 6 reveals that the power output has a trend similar to turbine efficiency in all of the models. This figure shows that, in Gholamalizadeh et al. and Guo et al.’s work, the maximum power output was calculated when the turbine was working at its optimum rotational speed, between 140 rpm and 150 rpm. In contrast, Ming et al. predicted an increasing trend in power output when the turbine rotational speed was increased. In addition, the power output predicted by Ming et al. is considerably lower than other two models.

4. Conclusions

This paper focused on the influences affecting the modelling of a real wind turbine and predictions of the performance of a solar chimney power plant. To date, three different investigations, conducted by Gholamalizadeh et al., Guo et al., and Ming et al. have simulated a solar chimney power plant with the main dimensions as the Manzanares prototype coupled to a real wind turbine using CFD techniques. The main discrepancy between Gholamalizadeh et al.’s turbine model and those modelled by Guo et al., and Ming et al. was the turbine profile. Gholamalizadeh et al. used an FX W-151-A blade profile (the same blade profile as the Manzanares SCPP’s turbine), while a CLARK Y blade profile was modelled by Guo et al. and Ming et al.

This study carried out 3-D simulations of the Manzanares prototype coupled to a 4-bladed wind turbine with the FX W-151-A blade profile used in Gholamalizadeh et al.’s model. The k-ε turbulence closure, non-gray radiation using discrete ordinates model, and the solar load model were employed. Then, the results were compared to those obtained by the two other investigations at different turbine rotational speeds.

It was found that modelling a wind turbine with the FX W-151-A blade profile could predict the pressure distribution across the turbine of the Manzanares prototype accurately, while a turbine with the CLARK Y blade profile considerably overestimated the value of the pressure drop that occurred across the Manzanares turbine. Results also showed that both blade profiles led to close trends in changes in turbine efficiency and power output with respect to the turbine rotational speed.