Field Synergy Analysis and Optimization of the Thermal Behavior of Lithium Ion Battery Packs
Abstract
:1. Introduction
2. Model Descriptions and Field Synergy Principle
2.1. Electrochemical-Thermal Intercoupling Model
2.2. Field Synergy Principle and Field Synergy Equation Inconvective Heat Transfer Processes
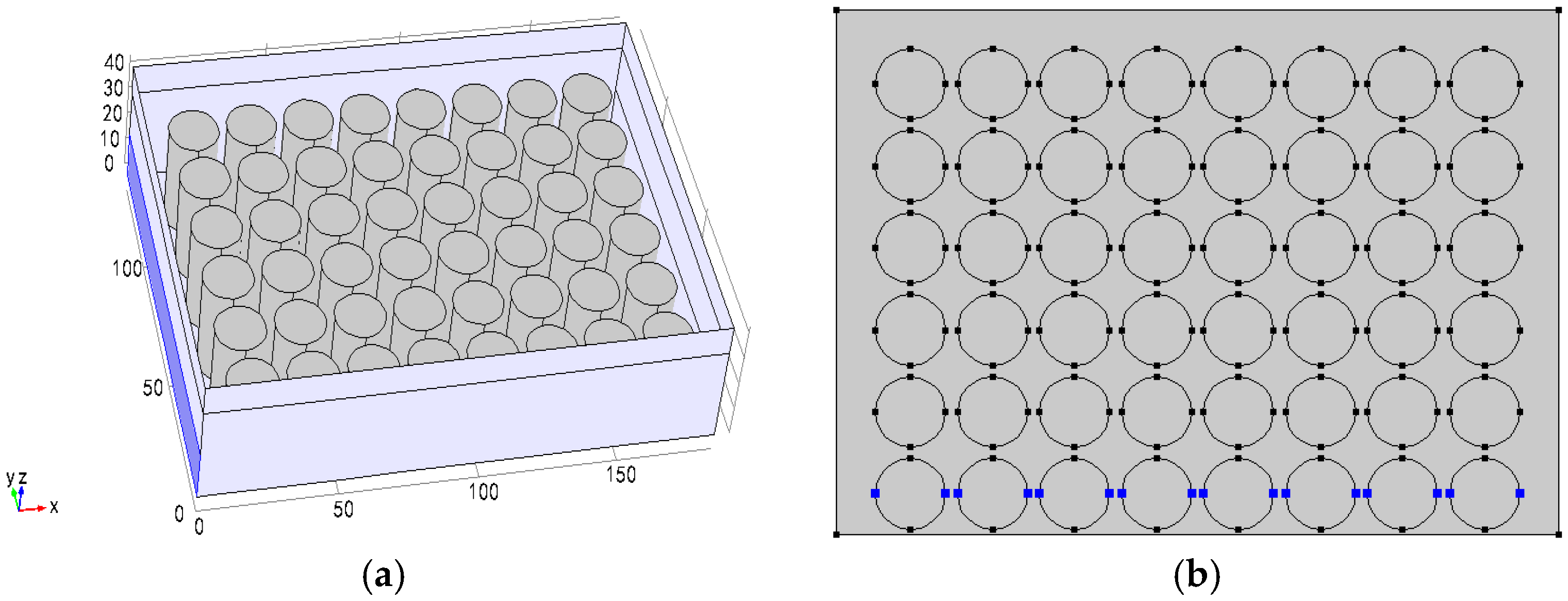
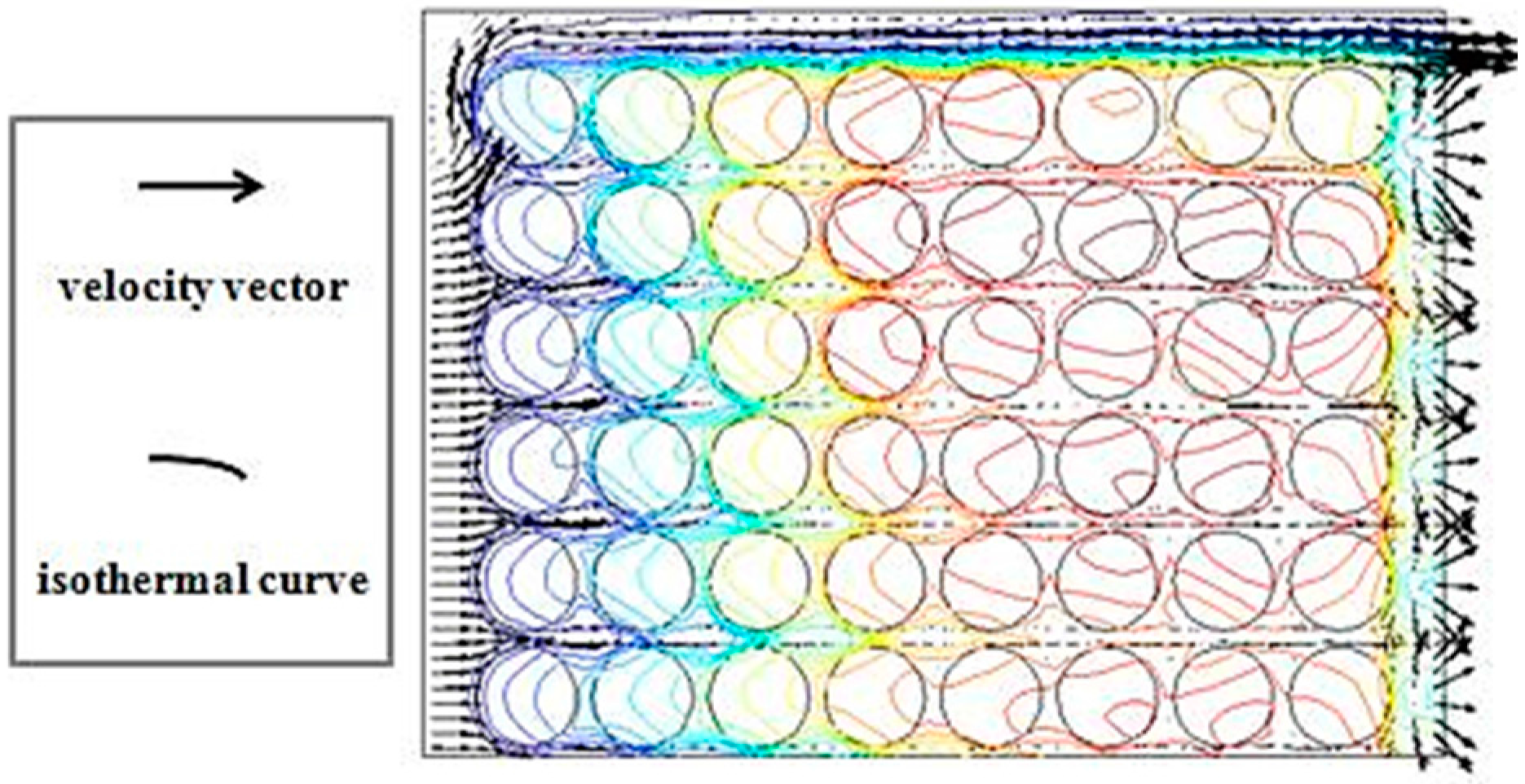
3. Result Numerical Simulation Analysis
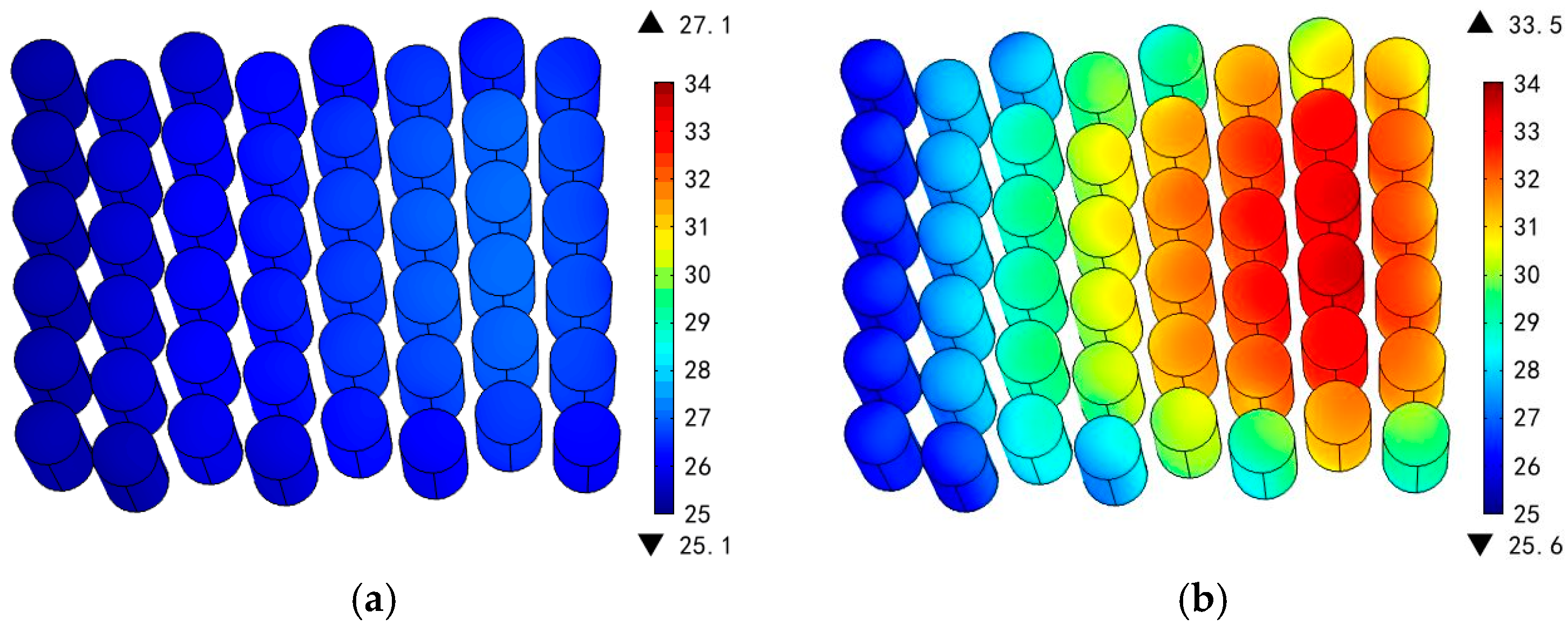
3.1. Various Inlet Air Velocities
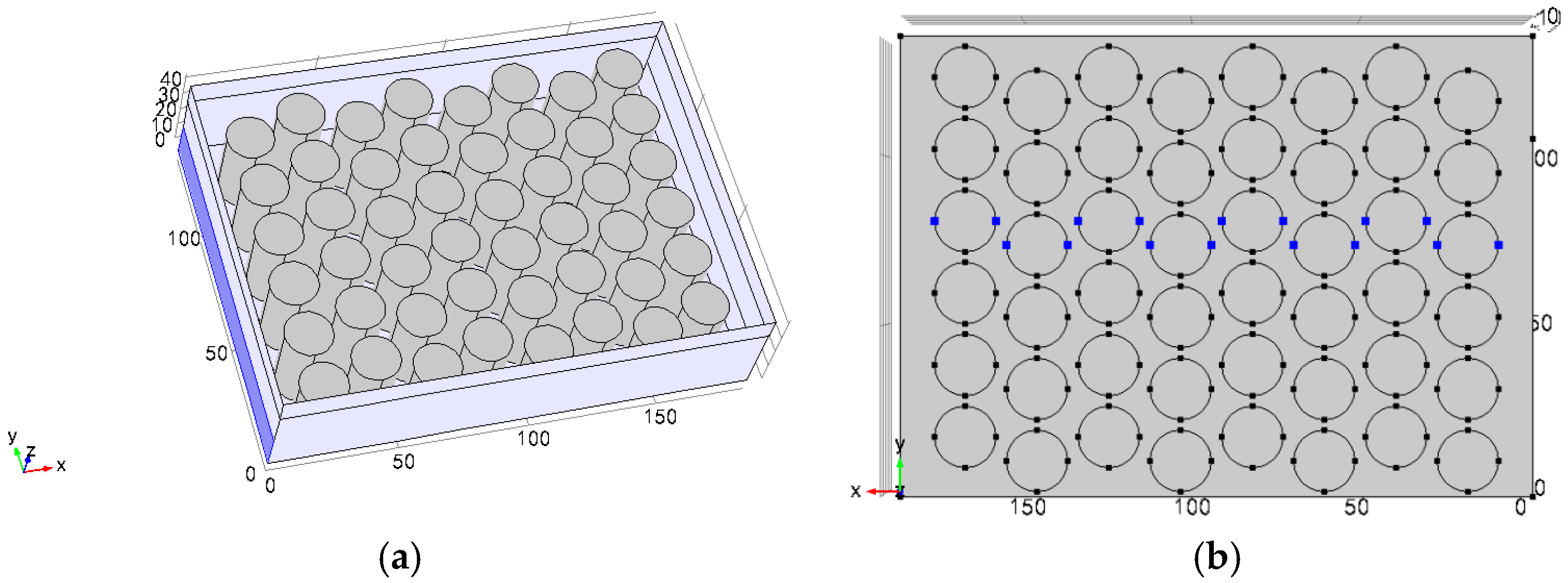
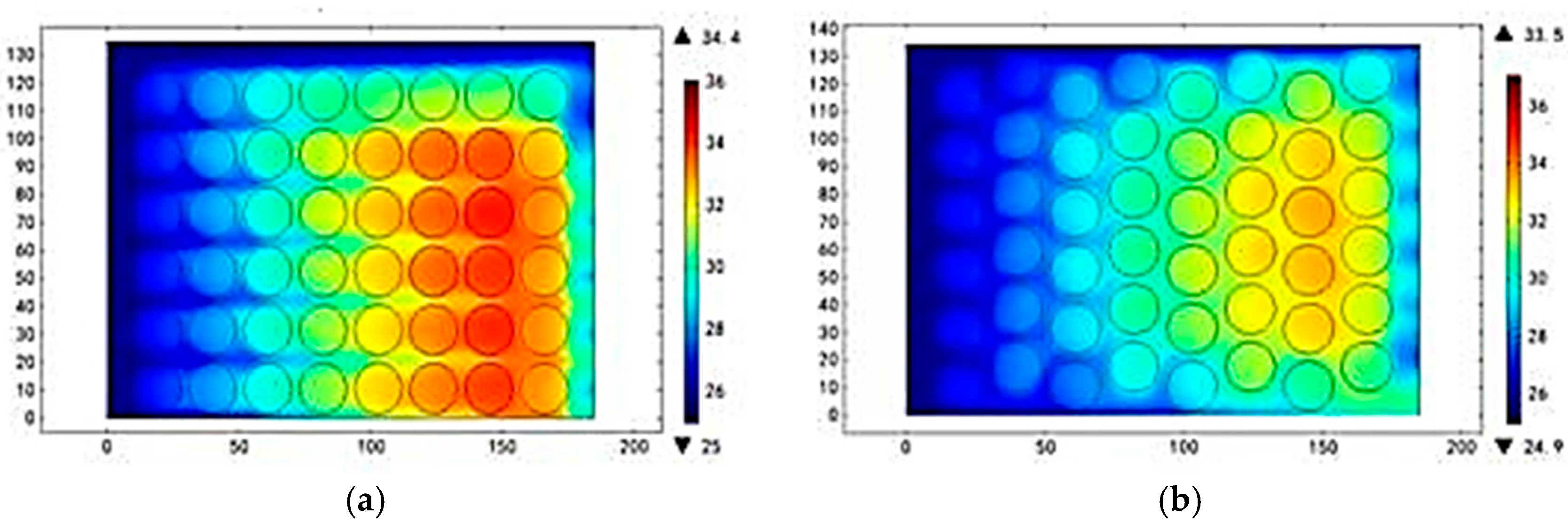
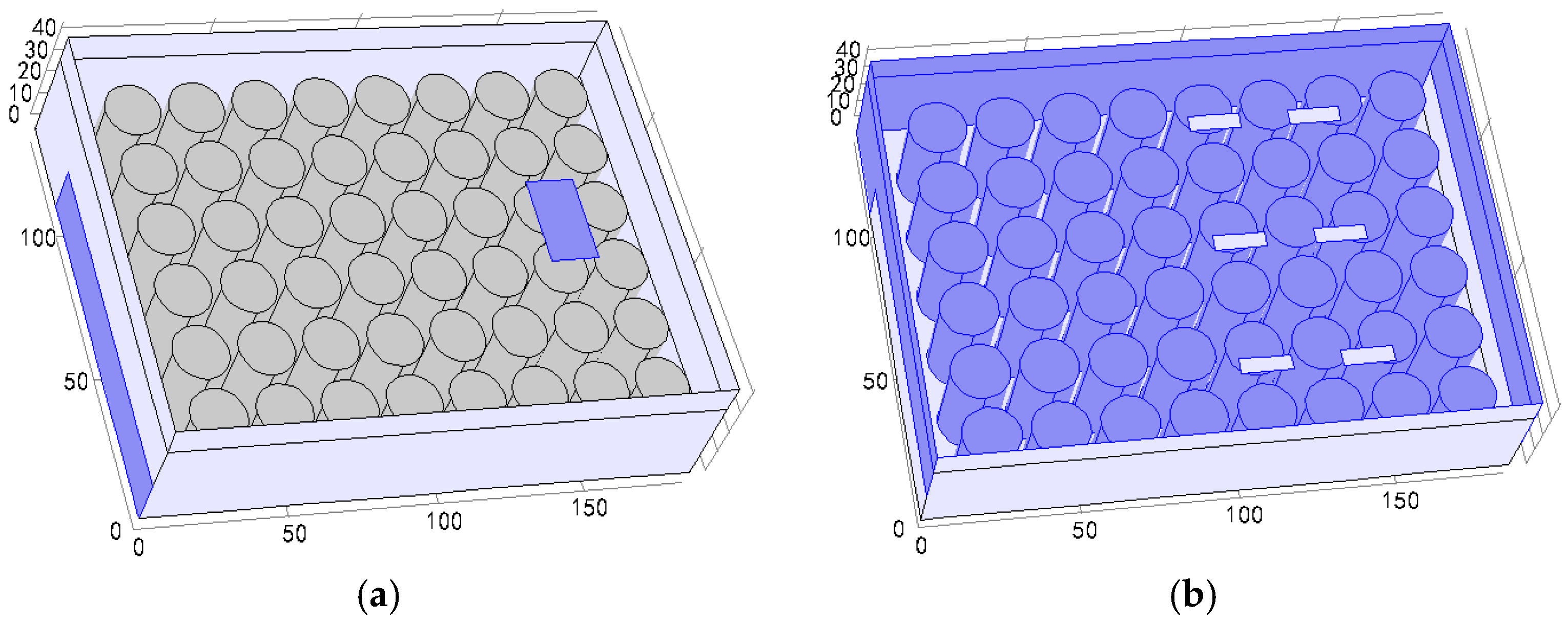
3.2. Different Arrangement Modes
3.3. Different Inlet Modes
3.4. Thermal Responses of the Battery Pack under Different Discharge Mechanisms
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| cp | Specific heat capacity, J·kg−1·K−1 |
| k | Thermal conductivity, W·m−1·K−1 |
| x, y | Cartesian coordinates, m |
| u, v | Velocity component in x-, y-, m·s−1 |
| Thermal boundary layer thickness, m | |
| T | Temperature, K |
| H | Characteristic length |
| U | Velocity vector |
| h | Convective heat-transfer coefficient |
| Flow domain | |
| l | Flow domain boundary |
| ρ | Air density, kg·m−3 |
| v | Coefficient of viscosity |
Subscripts
| w | Wall |
| m | Characteristic |
| avg | Average |
References
- Kwon, K.H.; Shin, C.B.; Kang, T.H.; Kim, C.S. A two-dimensional modeling of a lithium-polymer battery. J. Power Sources 2006, 163, 151–157. [Google Scholar] [CrossRef]
- Guo, M.; White, R.E. A distributed thermal model for a Li-ion electrode plate pair. J. Power Sources 2013, 221, 334–344. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.W.; Sun, F.C.; Liu, X.; Liu, Z. Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Tian, J. Model-based fault diagnosis approach on external short circuit of lithium-ion battery used in electric vehicles. Appl. Energy 2016, 184, 365–374. [Google Scholar] [CrossRef]
- Srinivasan, V.; Wang, C.Y. Analysis of electrochemical and thermal behavior of Li-ion cells. J. Electrochem. Soc. 2003, 150, A98–A106. [Google Scholar] [CrossRef]
- Kim, G.H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Chen, Y.; Evans, J.W. Thermal analysis of lithium polymer electrolyte batteries by a two dimensional model—Thermal behavior and design optimization. Electrochim. Acta 1994, 39, 517–526. [Google Scholar] [CrossRef]
- Forgez, C.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Smith, K.; Kim, G.H.; Darcy, E.; Pesaran, A. Thermal/electrical modeling for abuse-tolerant design of lithium ion modules. Int. J. Energy Res. 2010, 34, 204–215. [Google Scholar] [CrossRef]
- Mills, A.; Al-Hallaj, S. Simulation of passive thermal management system for lithium-ion battery packs. J. Power Sources 2005, 141, 307–315. [Google Scholar] [CrossRef]
- Sabbah, R.; Kizilel, R.; Selman, J.R.; Al-Hallaj, S. Active (air-cooled) vs. passive (phase change material) thermal management of high power lithium-ion packs: Limitation of temperature rise and uniformity of temperature distribution. J. Power Sources 2008, 182, 630–638. [Google Scholar] [CrossRef]
- Kizilel, R.; Sabbah, R.; Selman, J.R.; Al-Hallaj, S. An alternative cooling system to enhance the safety of Li-ion battery packs. J. Power Sources 2009, 194, 1105–1112. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, D.Y.; Wang, B.X. A novel concept for convective heat transfer enhancement. Int. J. Heat Mass Transf. 1998, 41, 2221–2225. [Google Scholar] [CrossRef]
- Tao, W.Q.; Guo, Z.Y.; Wang, B.X. Field synergy principle for enhancing convective heat transfer––Its extension and numerical verifications. Int. J. Heat Mass Transf. 2002, 45, 3849–3856. [Google Scholar] [CrossRef]
- Tao, W.Q.; He, Y.L.; Wang, Q.W.; Qu, Z.G.; Song, F.Q. A unified analysis on enhancing single phase convective heat transfer with field synergy principle. Int. J. Heat Mass Transf. 2002, 45, 4871–4879. [Google Scholar] [CrossRef]
- Cheng, Y.P.; Qu, Z.G.; Tao, W.Q.; He, Y.L. Numericaldesign ofefficientslottedfinsurfacebasedonthe field synergy principle. Numer. Heat Transf. Part A Appl. 2004, 45, 517–538. [Google Scholar] [CrossRef]
- Tao, W.Q.; He, Y.L.; Qu, Z.; Cheng, Y.P. Applications of the field synergy principle in developing new type heat transfer enhanced surfaces. J. Enhanc. Heat Transf. 2004, 11, 435–452. [Google Scholar] [CrossRef]
- Yu, H.; Wen, J.; Xu, G.; Li, H. Theoretically and numerically investigation about the novel evaluating standard for convective heat transfer enhancement based on the entransy theory. Int. J. Heat Mass Transf. 2016, 98, 183–192. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Yuan, F.; Liu, W.; Chen, G. Convective heat transfer optimization in a circular tube based on local exergy destruction minimization. Int. J. Heat Mass Transf. 2015, 90, 49–57. [Google Scholar] [CrossRef]
- Fernández-Gutiérrez, A.; González-Prieto, I.; Parras, L.; Cejudo-López, J.M.; del Pino, C. Experimental and numerical study of a small-scale and low-velocity indoor diffuser coupled with radiant floor cooling. Int. J. Heat Mass Transf. 2015, 87, 71–78. [Google Scholar] [CrossRef]
- Jia, H.; Liu, Z.C.; Liu, W.; Nakayama, A. Convective heat transfer optimization based on minimum entransy dissipation in the circular tube. Int. J. Heat Mass Transf. 2014, 73, 124–129. [Google Scholar] [CrossRef]
- Jia, H.; Liu, W.; Liu, Z. Enhancing convective heat transfer based on minimum power consumption principle. Chem. Eng. Sci. 2012, 69, 225–230. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, L.; Sun, F.C. Constructal optimization of a vertical insulating wall based on a complex objective combining heat flow and strength. Sci. China Technol. Sci. 2010, 53, 2278–2290. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, M.; Guo, Z.Y. Field synergy principle for energy conservation analysis and application. Adv. Mech. Eng. 2010, 2, 129313. [Google Scholar] [CrossRef]
- Chen, Q.; Ren, J.; Guo, Z. The extremum principle of mass entransy dissipation and its application to decontamination ventilation designs in space station cabins. Chin. Sci. Bull. 2009, 54, 2862–2870. [Google Scholar] [CrossRef]
- Mo, J.; Zhang, Y.; Yang, R. Novel insight into VOC removal performance of photocatalytic oxidation reactors. Indoor Air 2005, 15, 291–300. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.Q. The Flow and Heat Transfer Coupling Analysis and Construction Modification of Vehicular Cooling Models Based on Field Synergy Principle; Zhejiang University: Hangzhou, China, 2010. [Google Scholar]
- Jiang, Y. Simulation and Analysis of Heat Transfer Performance of the Slotted Circular Fin Based on Field Synergy Principle; Harbin Engineering University: Harbin, China, 2011. [Google Scholar]
- Yang, M.; Zhao, M.; Zhang, L.X. Field synergy principle and stability of heat convection. J. Eng. Thermophys. 2002, 23, 73–76. [Google Scholar]
- Huo, W.W.; He, H.W.; Sun, F.C. Electrochemical-thermal modeling for a ternary lithium ion battery during discharging and driving cycle testing. RSC Adv. 2015, 5, 57599–57607. [Google Scholar] [CrossRef]

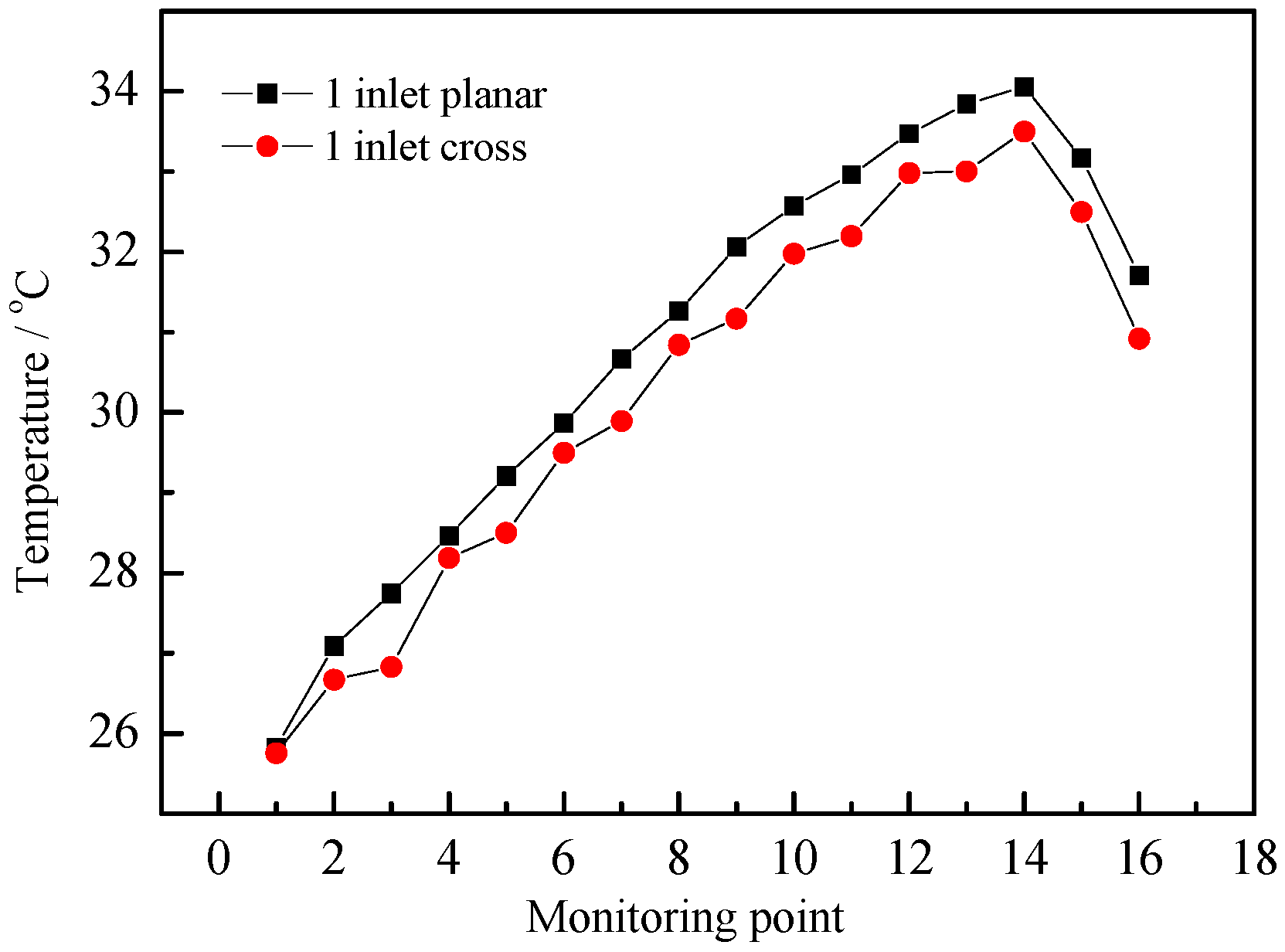
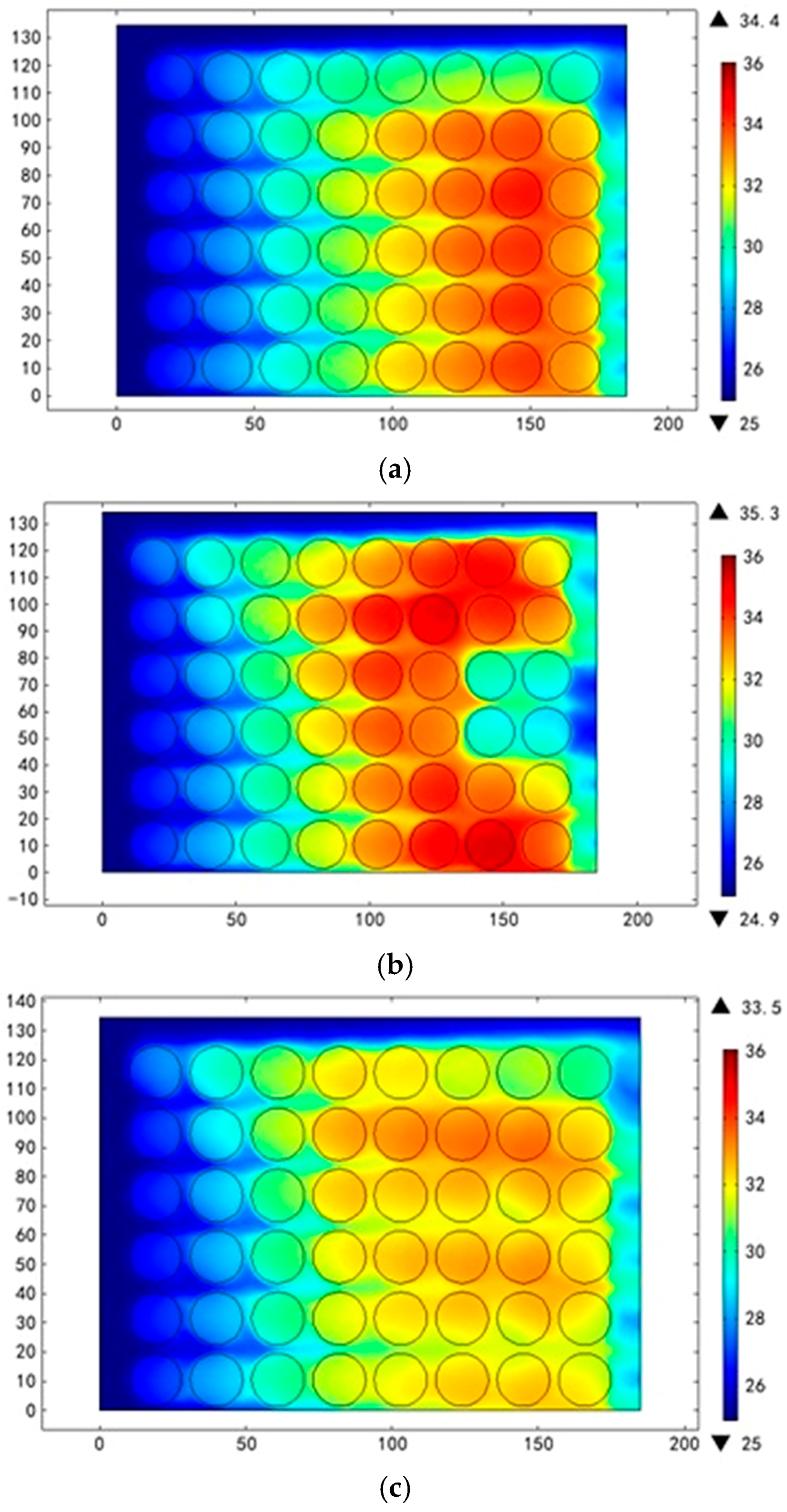
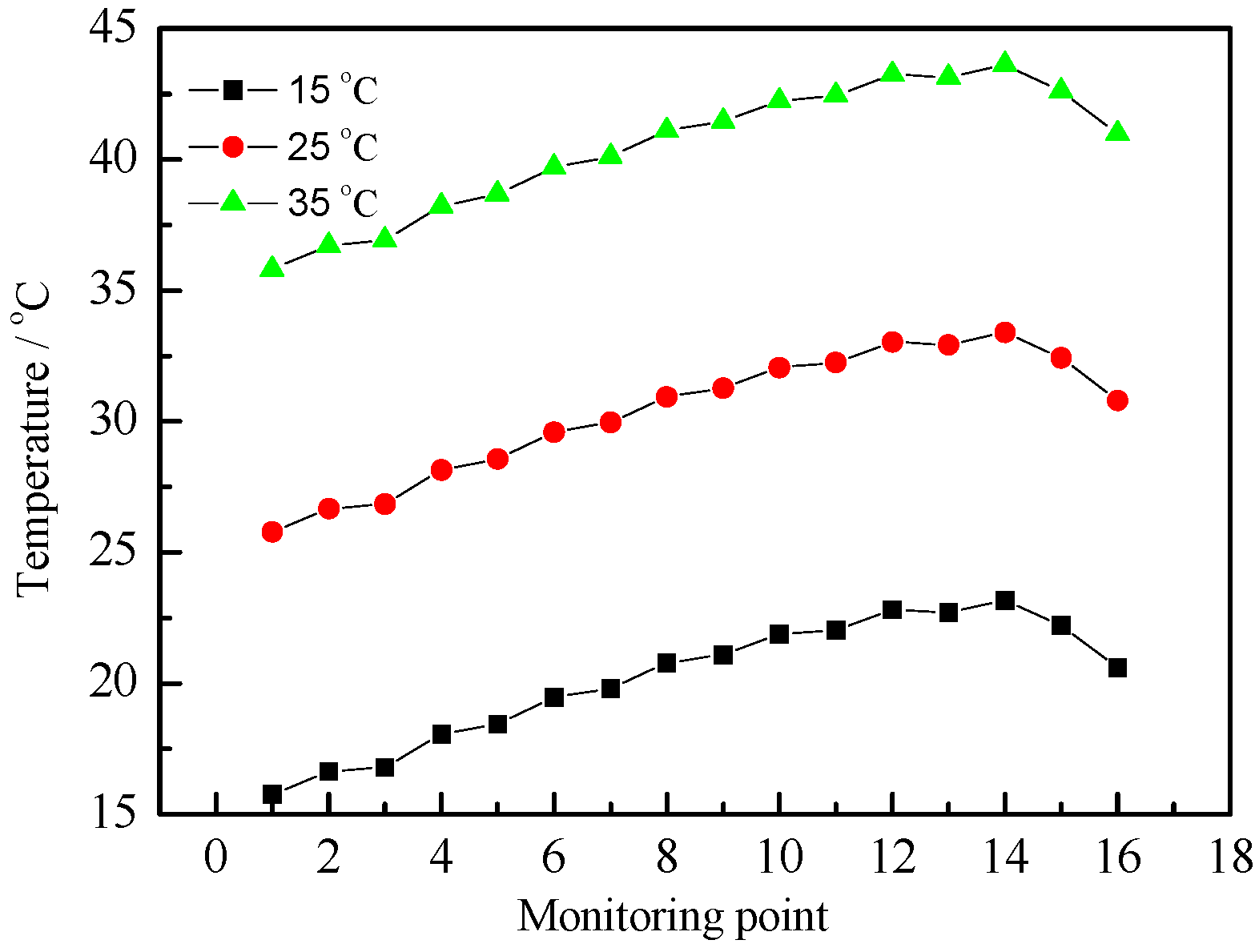
| Air Inlet Velocity (m/s) | Maximum Temperature Rise (°C) | Maximum Temperature Difference (°C) | Average Synergy Angle (°) |
|---|---|---|---|
| 0.7 | 13.1 | 11.3 | 73.17 |
| 0.8 | 11.6 | 10.0 | 73.10 |
| 1.0 | 9.4 | 8.2 | 72.95 |
| 1.1 | 8.6 | 7.5 | 72.88 |
| Air Intake Temperature (°C) | Maximum Temperature Rise (°C) | Maximum Temperature Difference (°C) | Average Synergy Angle (°) |
|---|---|---|---|
| 15 | 9.3 | 6.0 | 73.62 |
| 25 | 8.9 | 5.6 | 73.56 |
| 35 | 8.3 | 5.0 | 73.51 |
| Discharging Rate | Maximum Temperature Rise (°C) | Maximum Temperature Difference (°C) |
|---|---|---|
| 0.5C | 2.1 | 1.2 |
| 1C | 8.5 | 7.6 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Jia, H.; Huo, W.; Sun, F. Field Synergy Analysis and Optimization of the Thermal Behavior of Lithium Ion Battery Packs. Energies 2017, 10, 81. https://doi.org/10.3390/en10010081
He H, Jia H, Huo W, Sun F. Field Synergy Analysis and Optimization of the Thermal Behavior of Lithium Ion Battery Packs. Energies. 2017; 10(1):81. https://doi.org/10.3390/en10010081
Chicago/Turabian StyleHe, Hongwen, Hui Jia, Weiwei Huo, and Fengchun Sun. 2017. "Field Synergy Analysis and Optimization of the Thermal Behavior of Lithium Ion Battery Packs" Energies 10, no. 1: 81. https://doi.org/10.3390/en10010081
APA StyleHe, H., Jia, H., Huo, W., & Sun, F. (2017). Field Synergy Analysis and Optimization of the Thermal Behavior of Lithium Ion Battery Packs. Energies, 10(1), 81. https://doi.org/10.3390/en10010081






