Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application
Abstract
:1. Introduction
2. Battery Cell Model Description
2.1. Equivalent Circuit Model
2.2. Lumped-Capacitance Thermal Model of the Battery Cell
- Convective heat transferThe convective heat transfer from the cell to the surrounding is determined bywhere is the convective heat transfer coefficient, is the area of heat exchange, is the cell temperature and is the ambient temperature.
- Conductive heat transferThe convective heat transfer represents the thermal diffusion through cell to cell electric connector. It can be modeled bywhere and are the temperature of battery cell 2 and battery cell 1, respectively. is the thermal resistance of the connection, which includes the top and bottom connection of the battery cell.
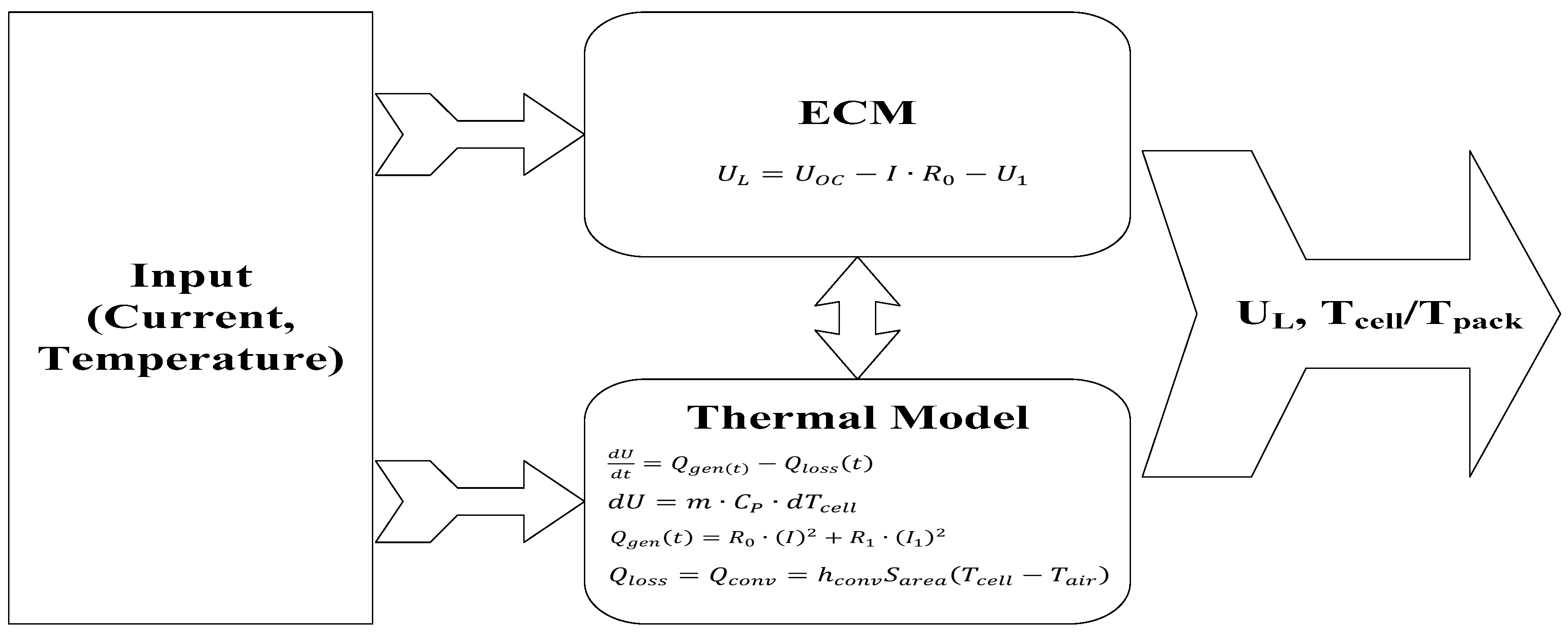
2.3. Coupled Equivalent Circuit Model (ECM) and Thermal Battery Model
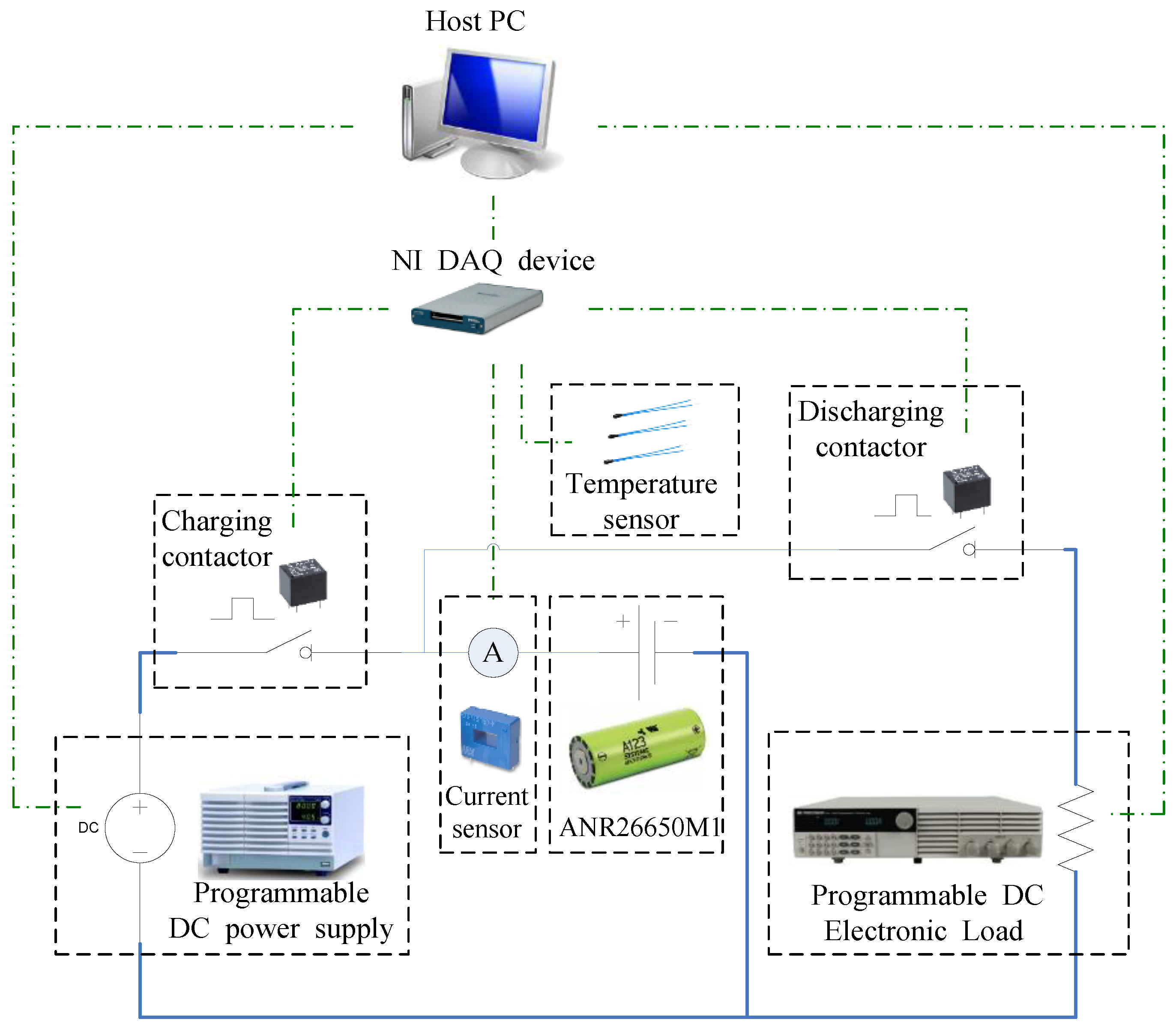
3. Experiment Tests for Battery Characterizations
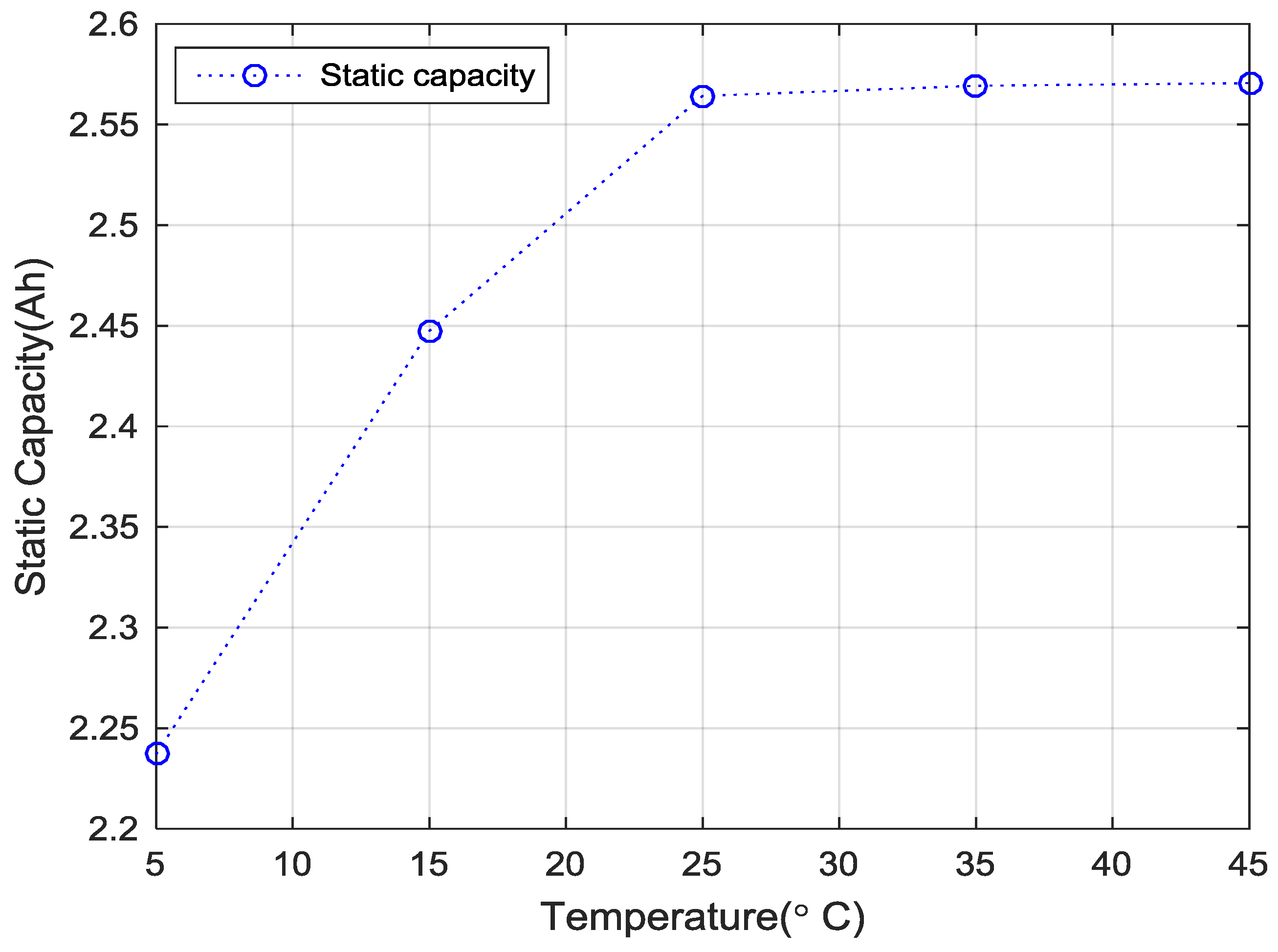
3.1. Static Capacity Test
- Charge the battery at 0.8 C rate (2 A) to the fully charged state in CCCV mode under the specified temperature. The battery is fully charged to 3.6 V when the current reaches 1 mA.
- Apply a 15-hour relaxation period before discharging the battery cell.
- Discharge at a constant current 0.8 C rate until the voltage reaches the battery minimum limit of 2.5 V.
- Record the data and calculate the static capacity as follows.where is the static capacity, is the discharge current in ampere, and is the discharge time in second.
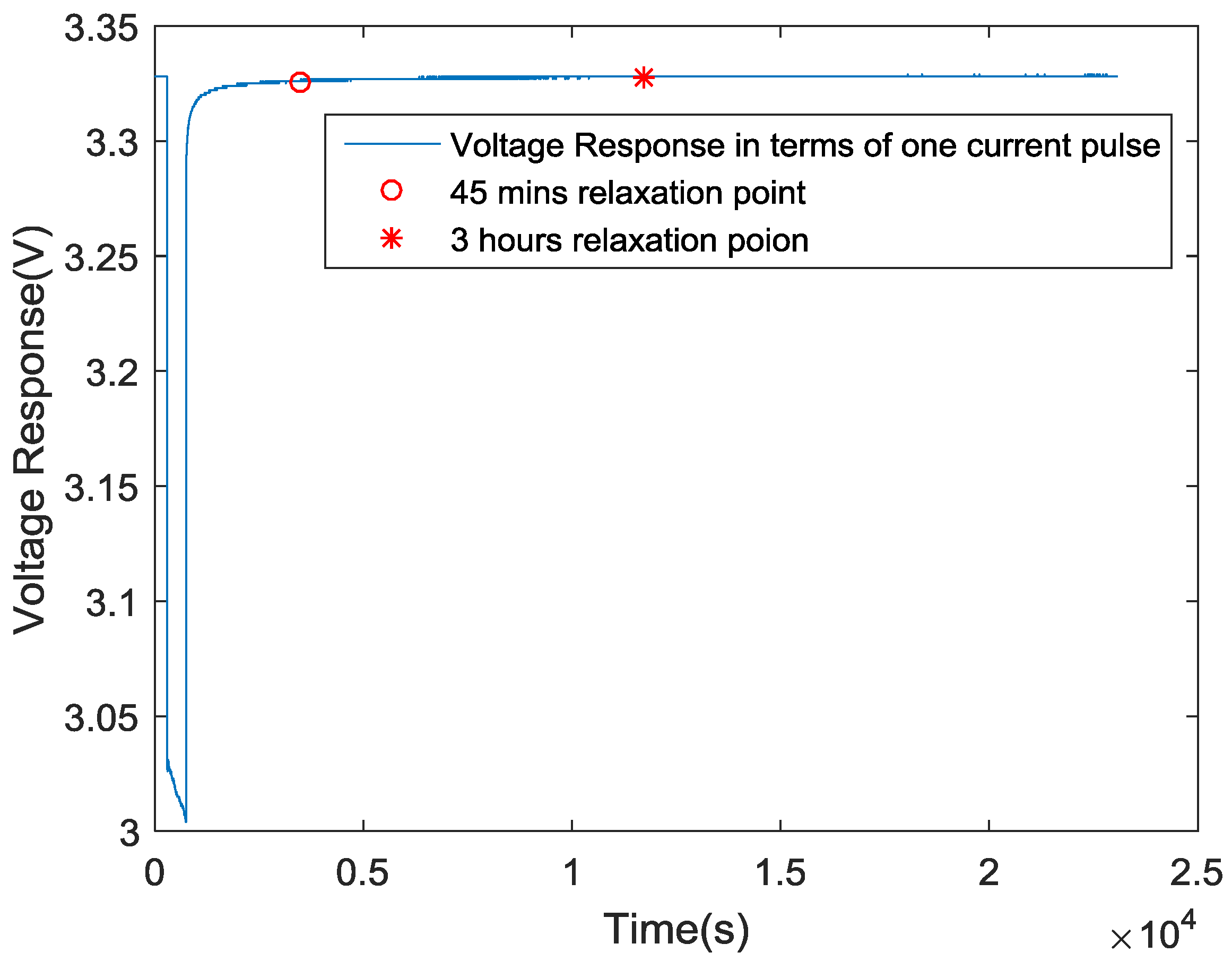
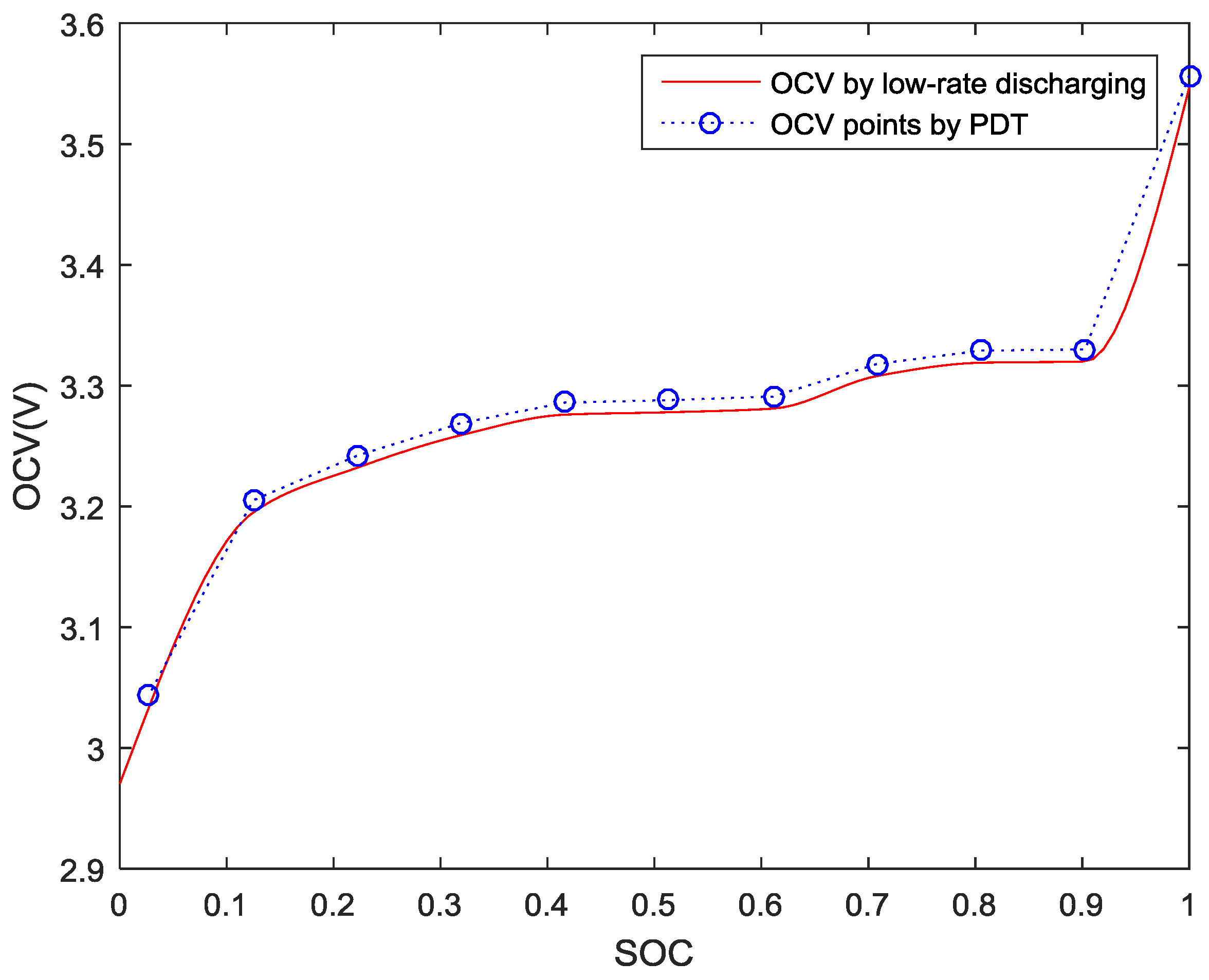
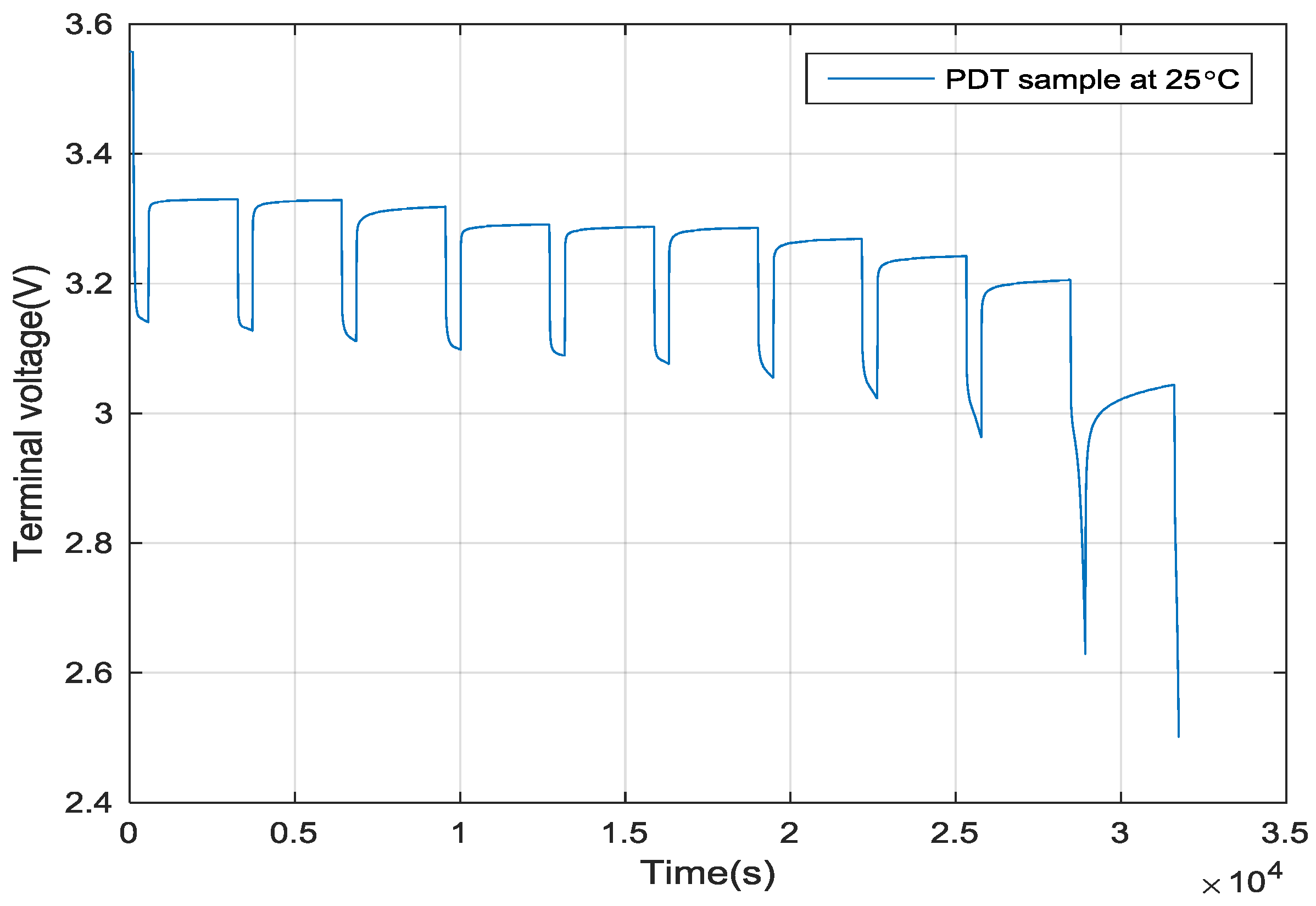
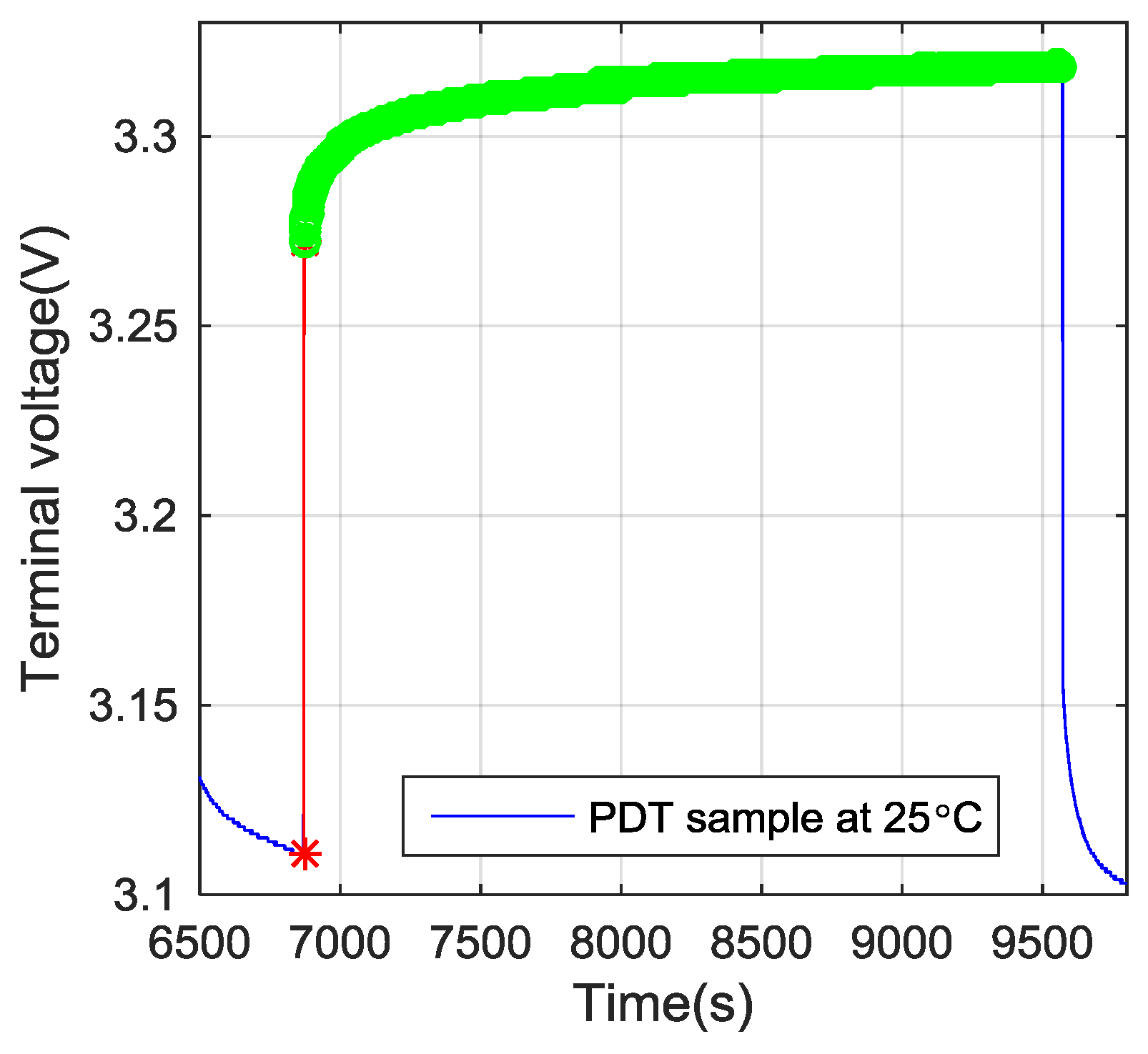
3.2. Pulse Discharge Test
- Charge the battery to a fully charged state, follow step 1 in Section 3.1.
- Apply a 15-hour relaxation period before discharging the battery cell.
- Discharge the battery cell at a pulse current 0.8 C rate with 450 s discharging time and 45 min relaxation period, until the terminal voltage reaches the cut-off voltage 2.5 V.
- Record the data and proceed to model validation and simulation.
3.3. Cycling Aging Test
- Charge the battery to a fully charged state, follow step 1 in Section 3.1.
- Allow the battery to rest for 15 min until its temperature stabilized.
- Discharge at a constant current 0.8 C rate until the voltage reaches the battery minimum limit of 2.5 V.
- Record the data and proceed to another cycle after the battery rests for 15 min.
4. Battery Model Identification and Results
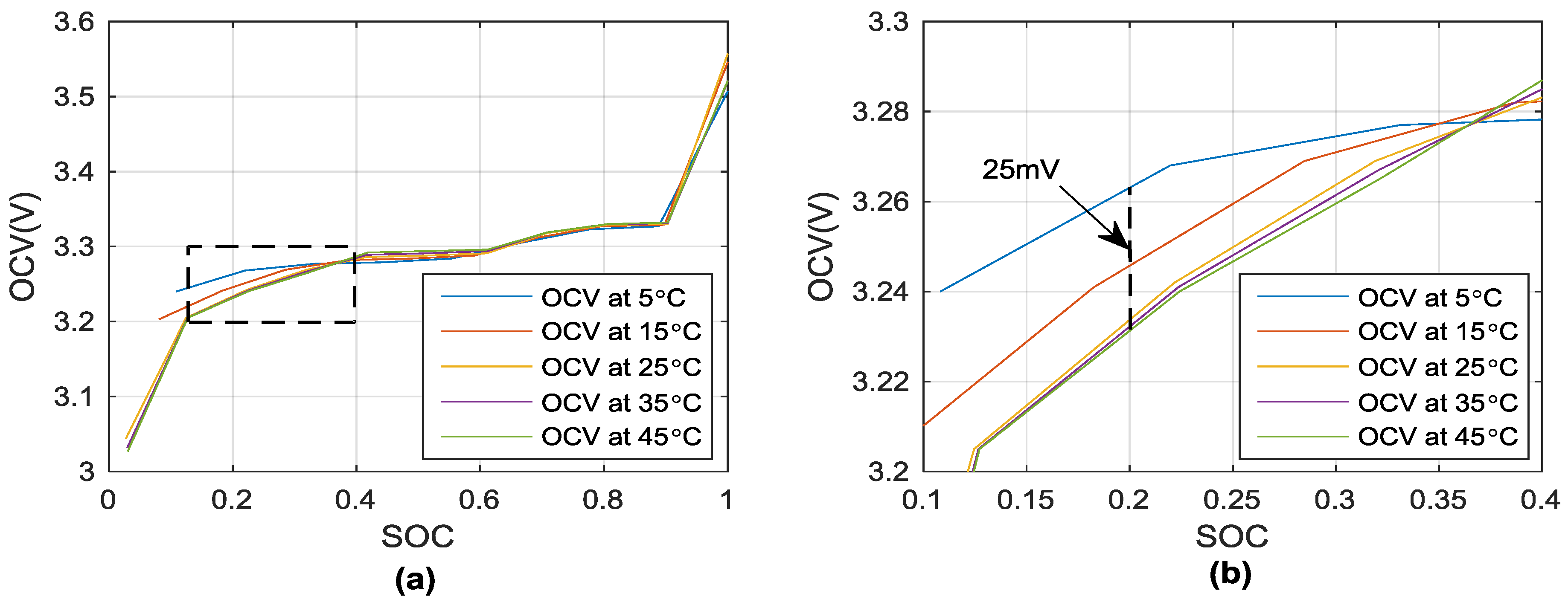
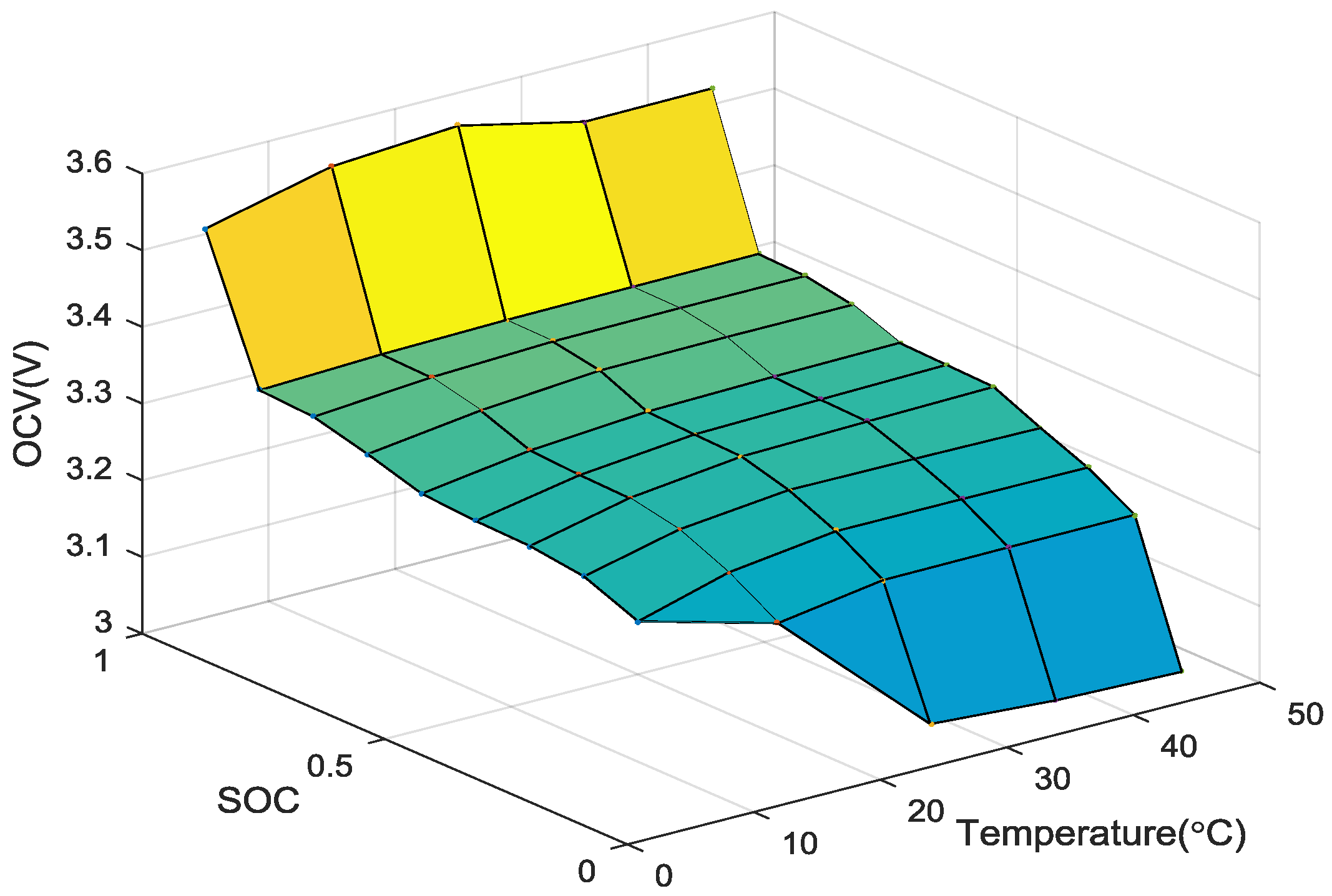
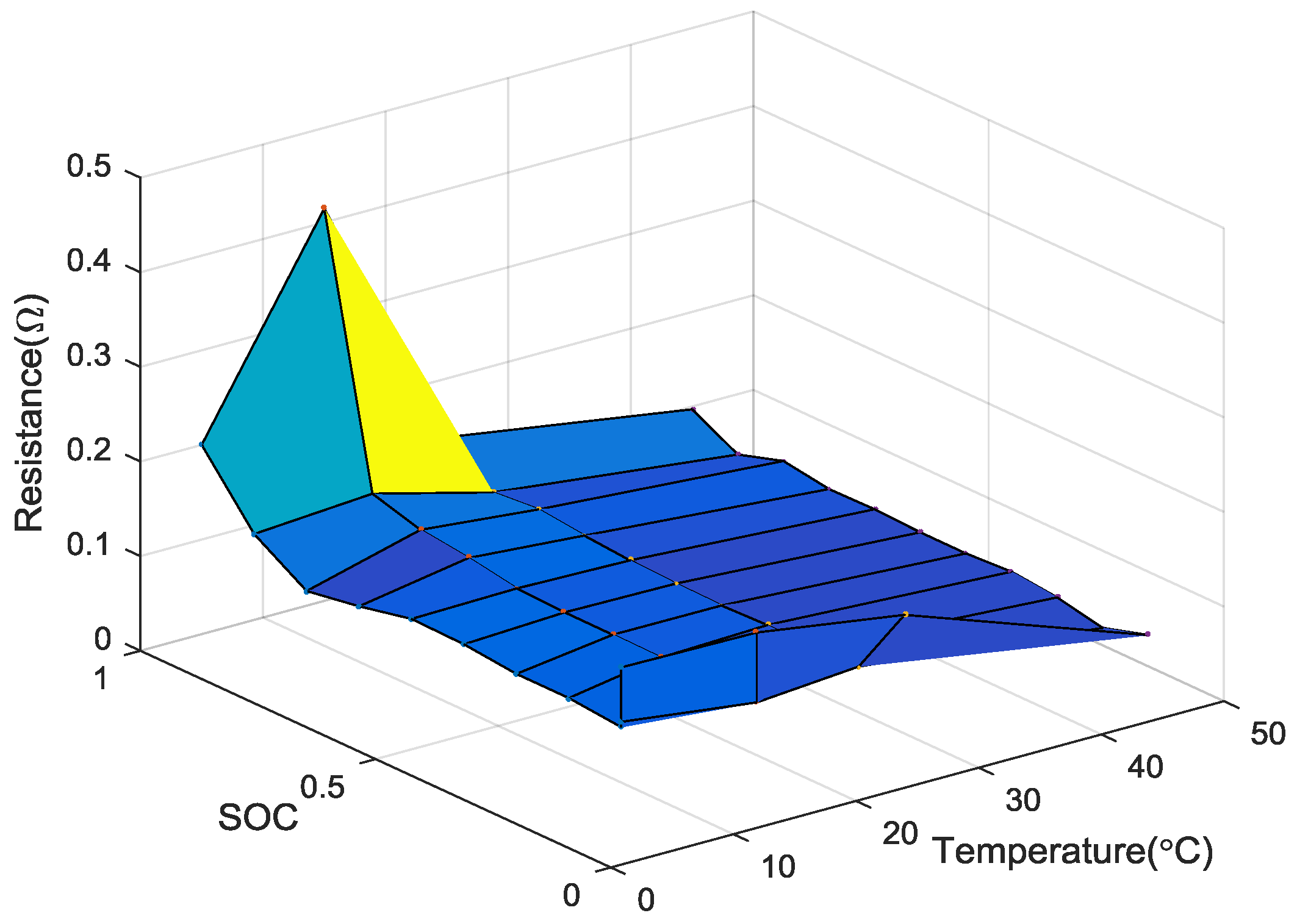
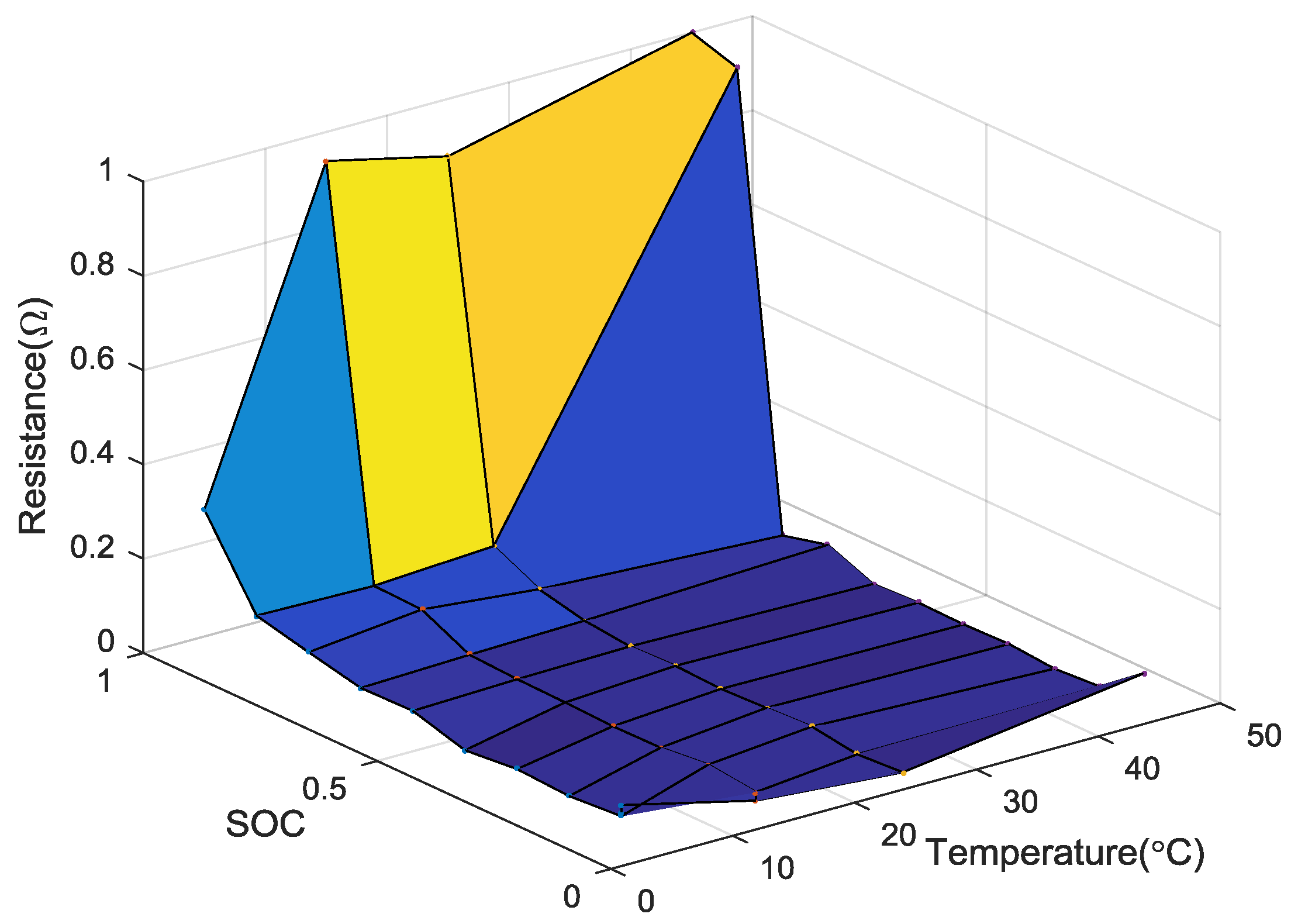
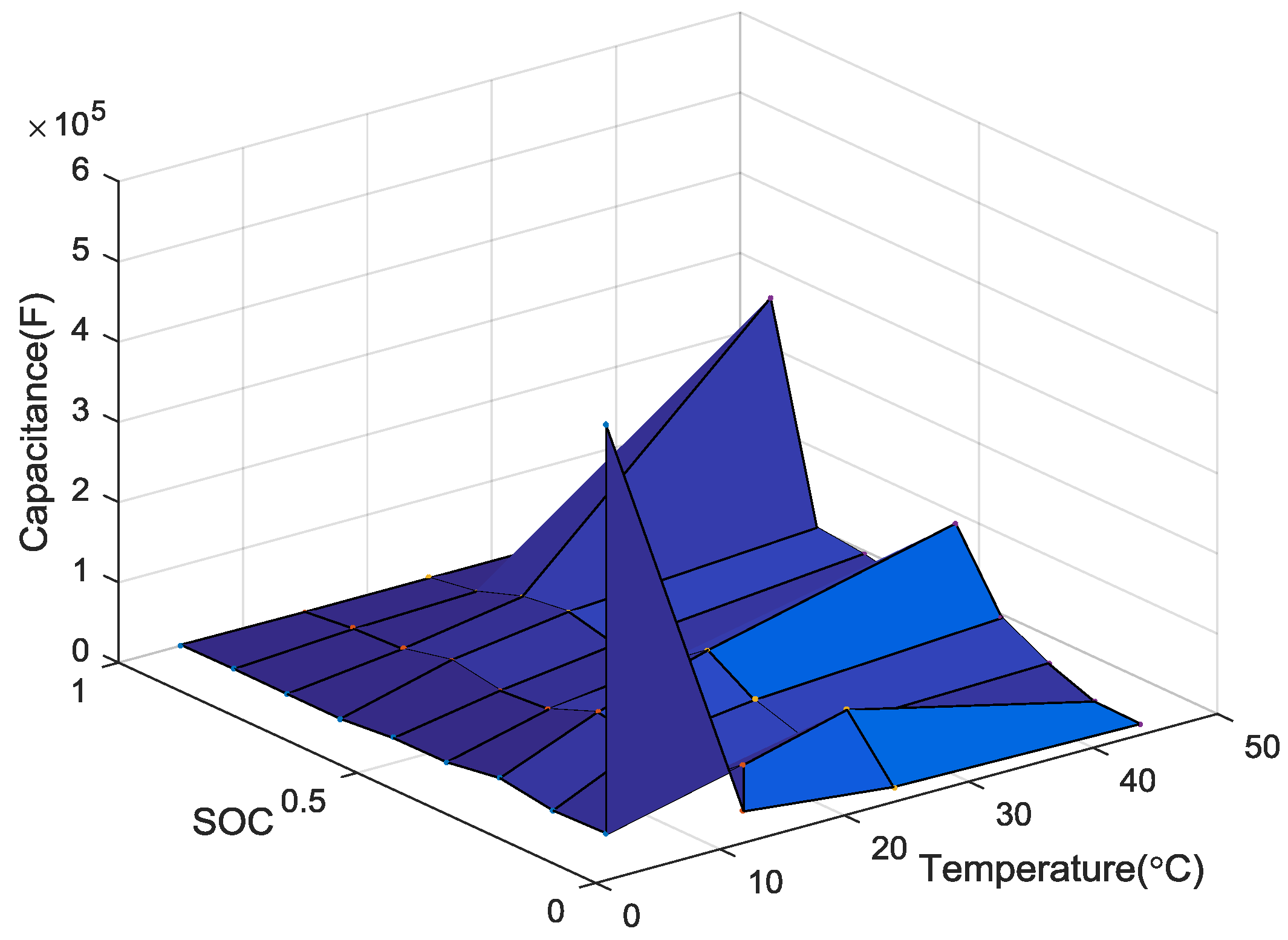
4.1. Temperature-Dependent Battery Cell Parameters Identification
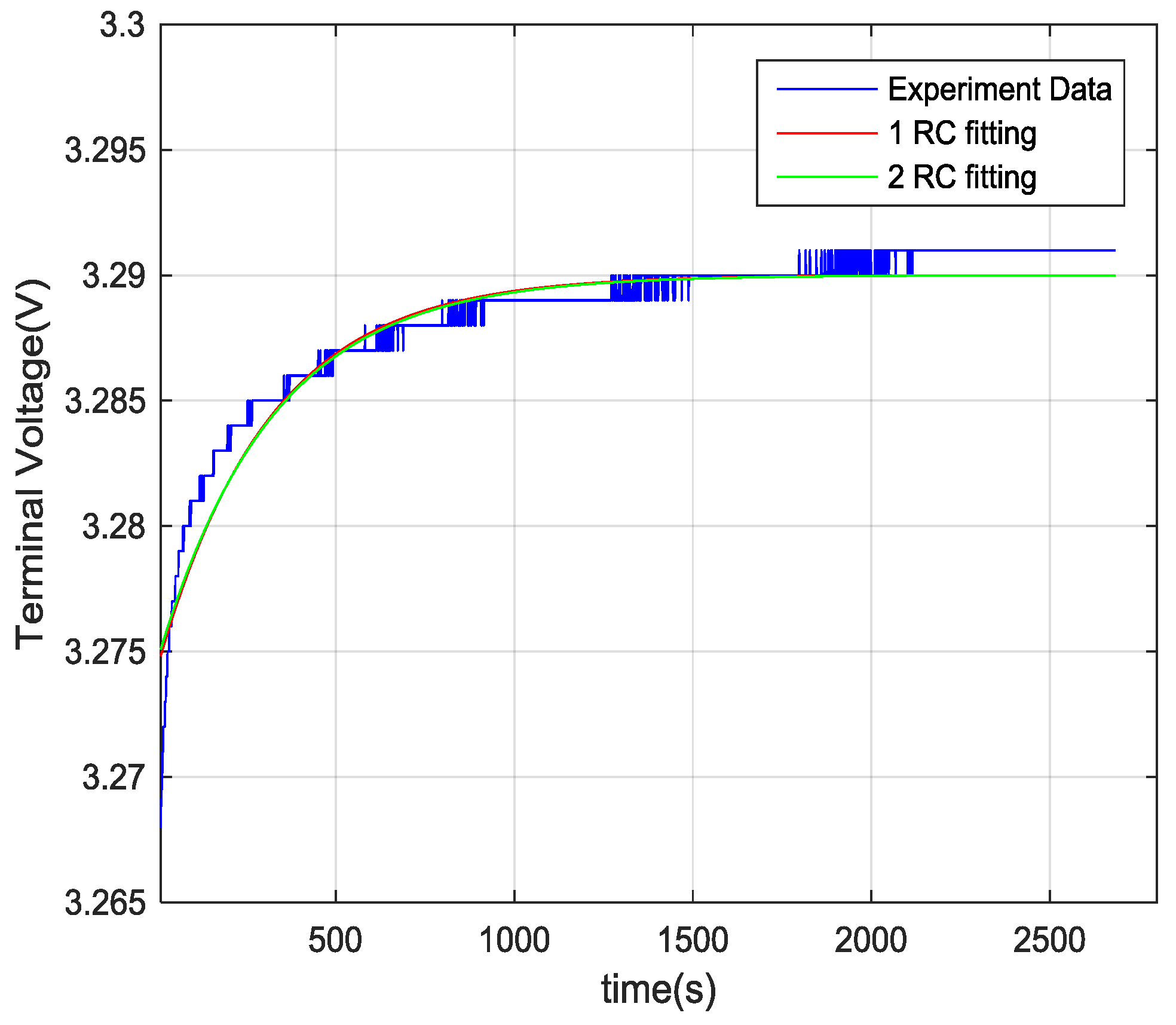
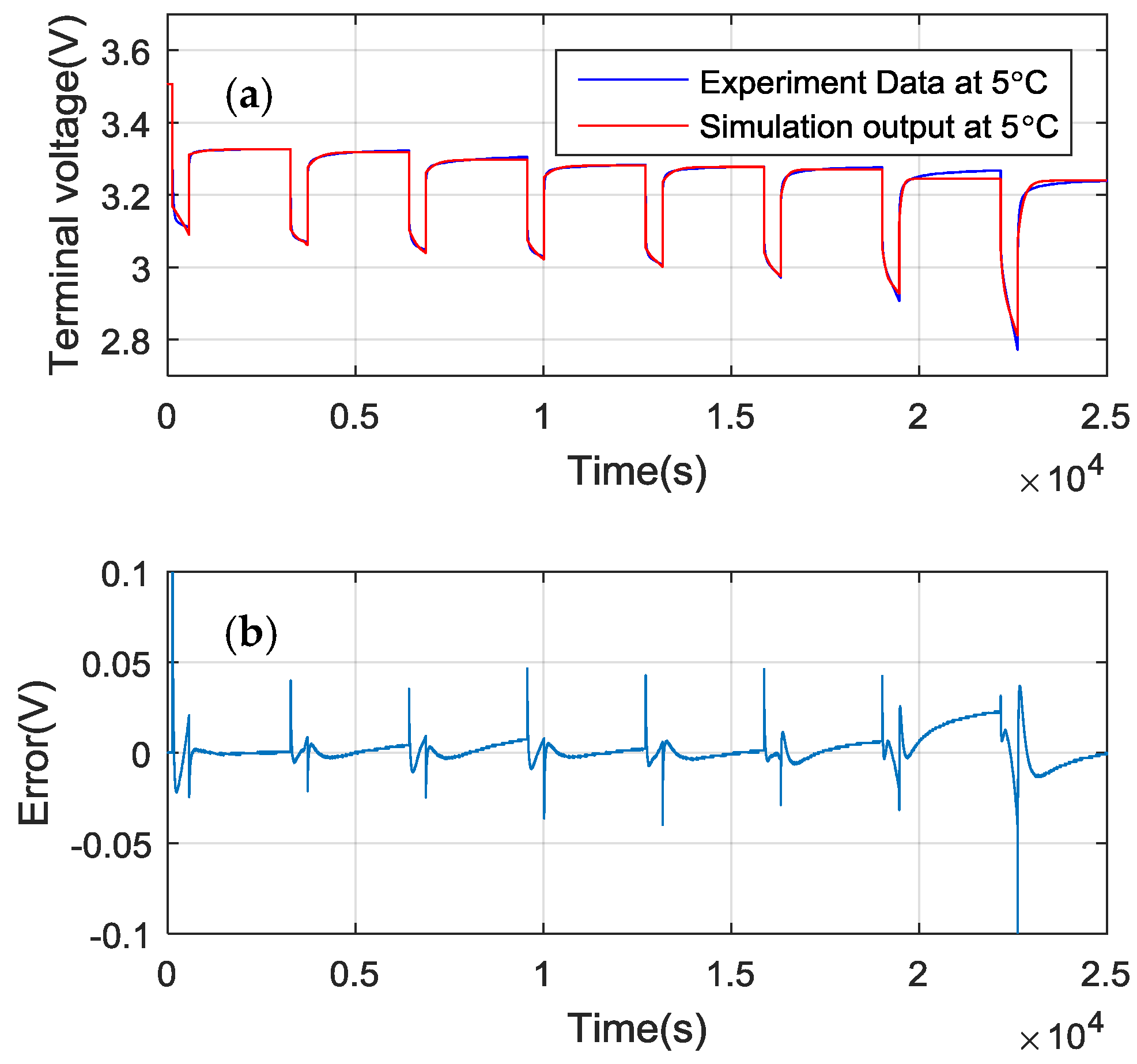
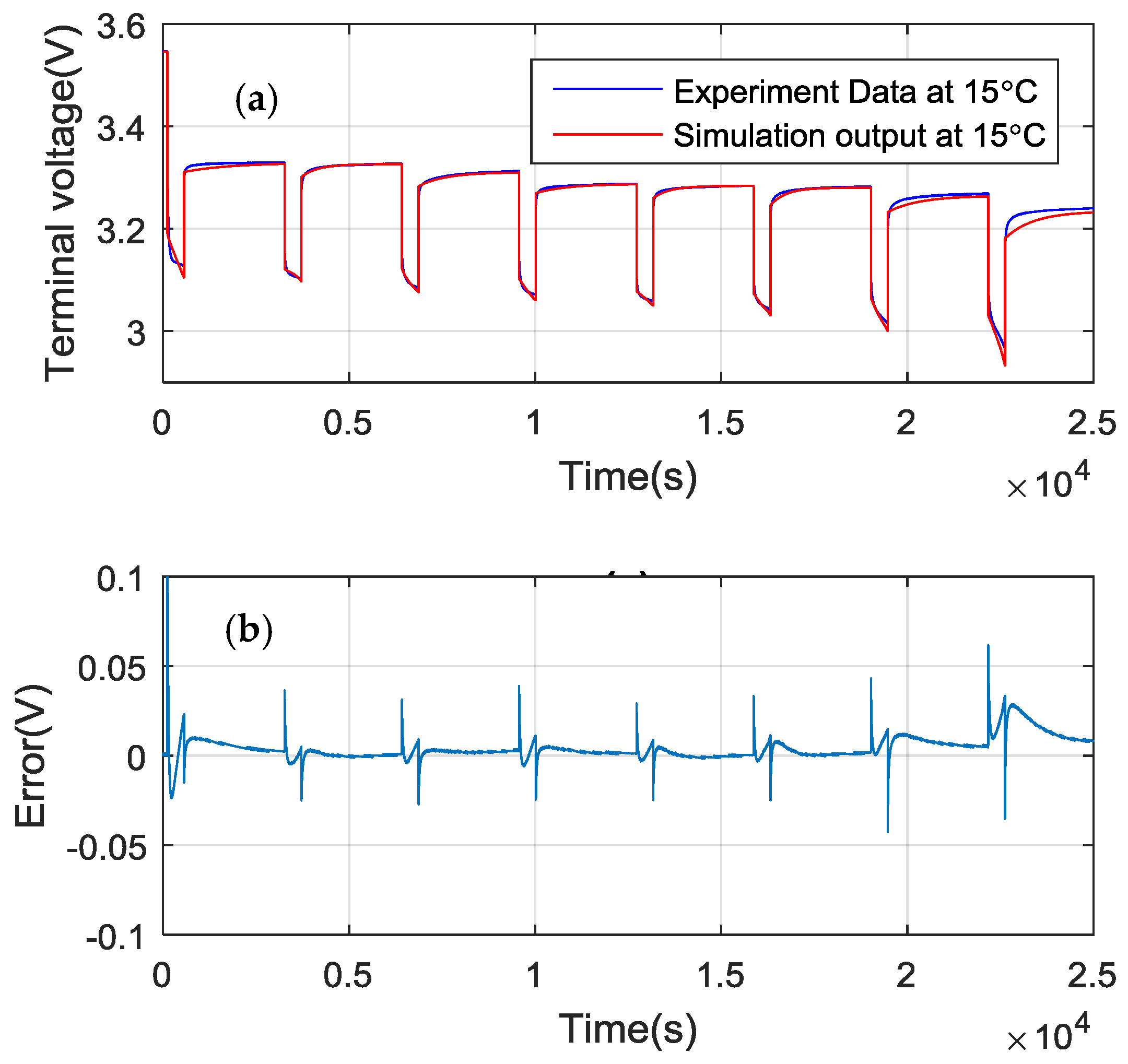
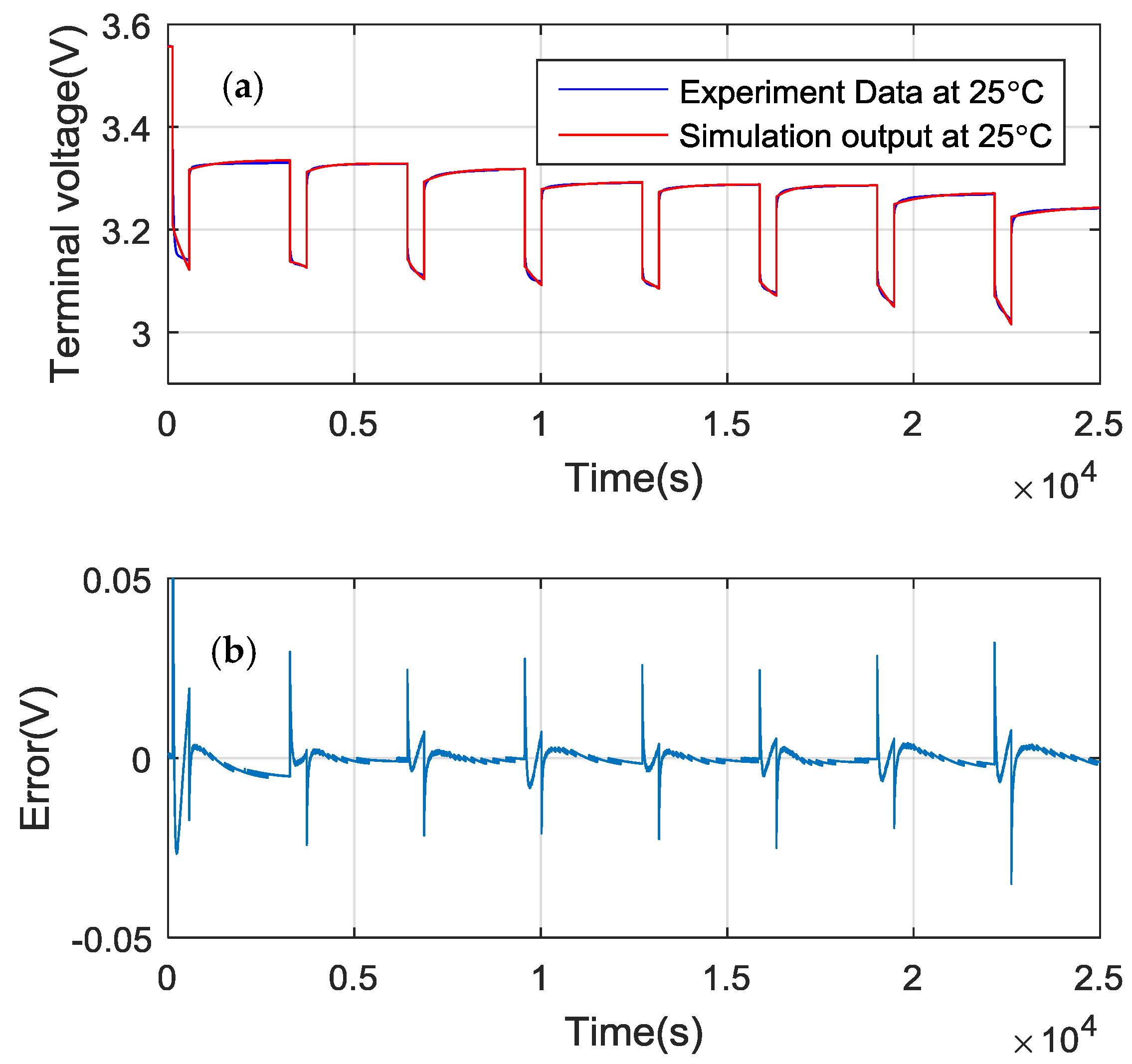
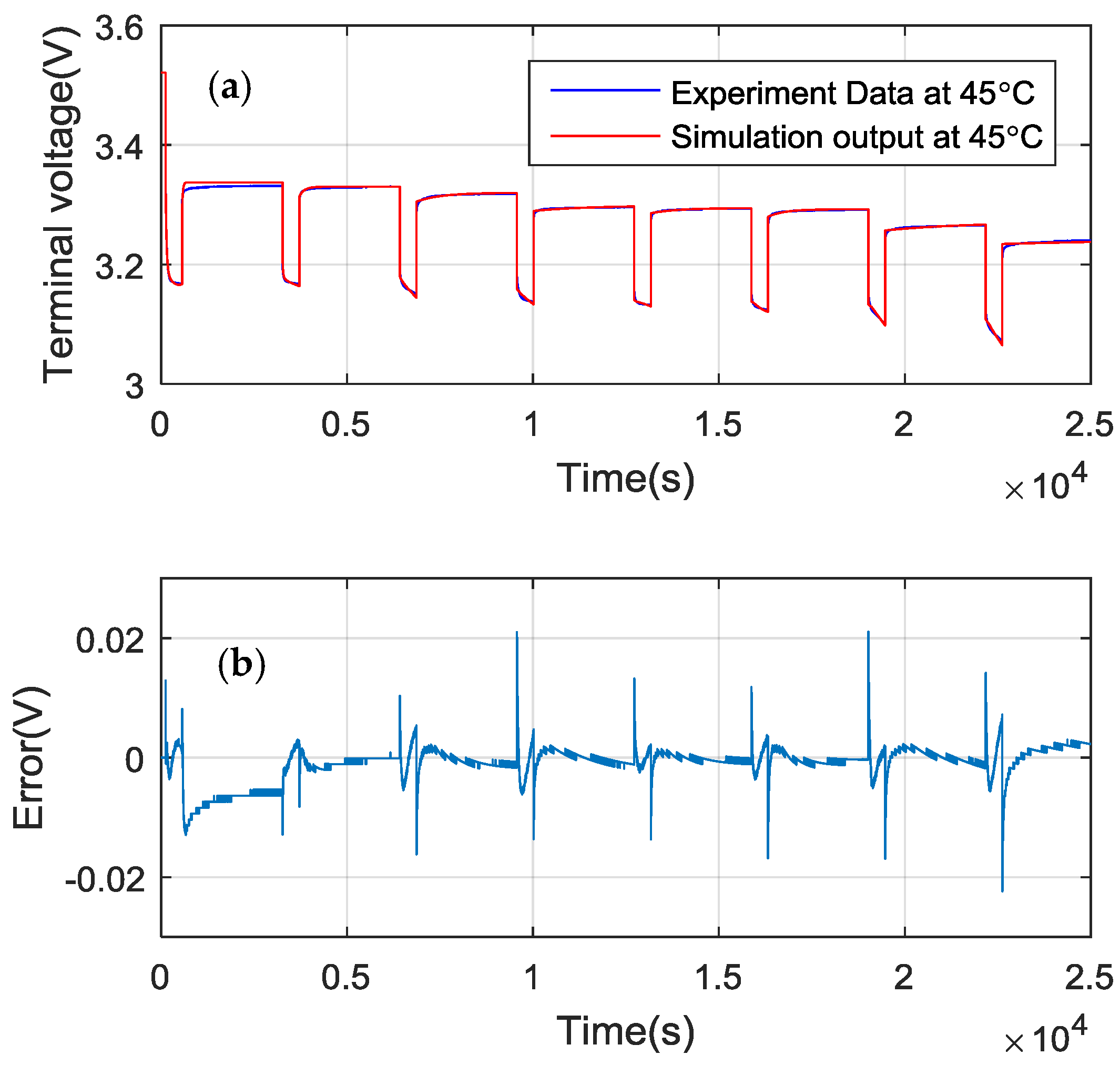
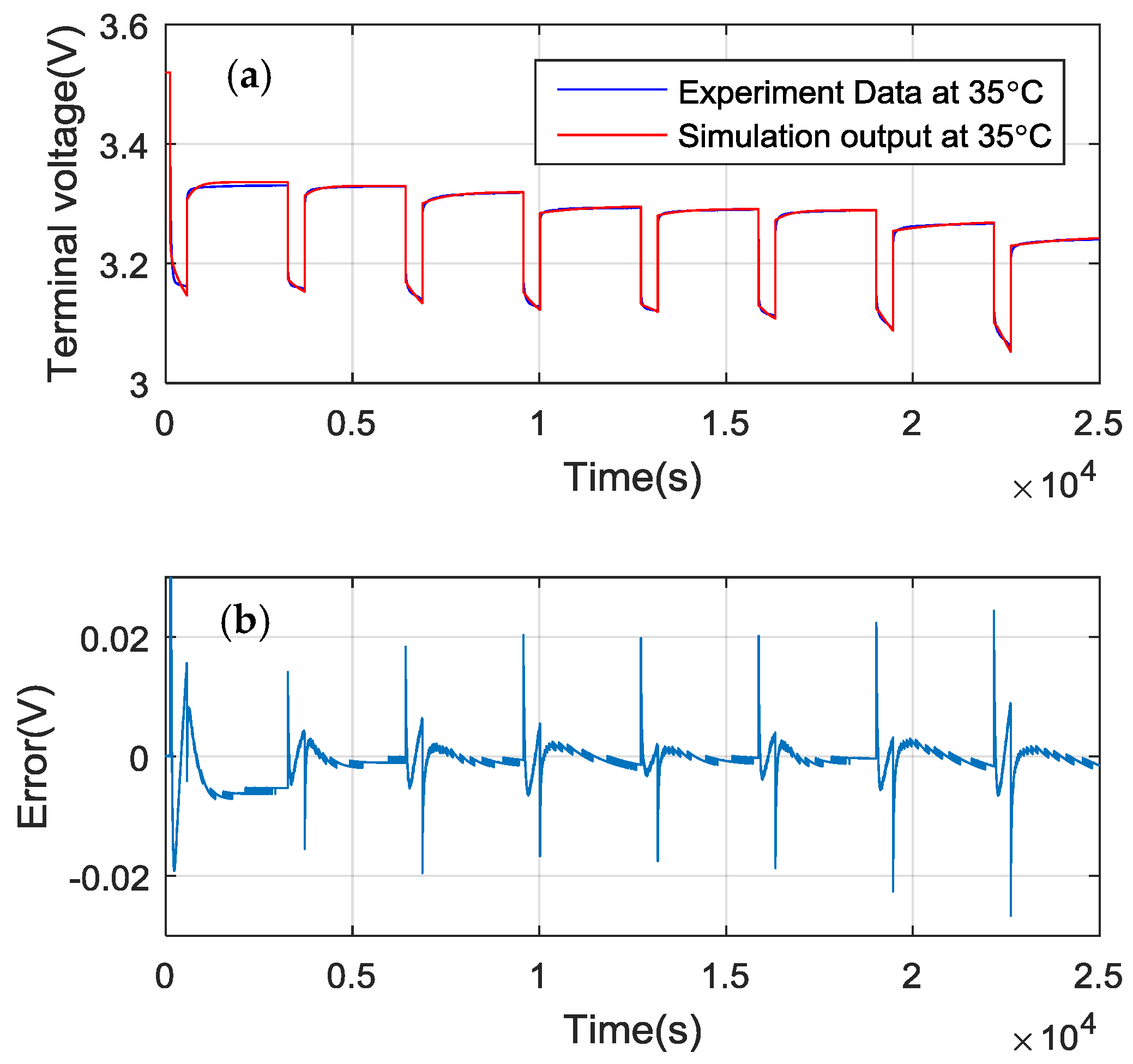
4.2. Temperature-Dependent Battery Cell Parameters Validation
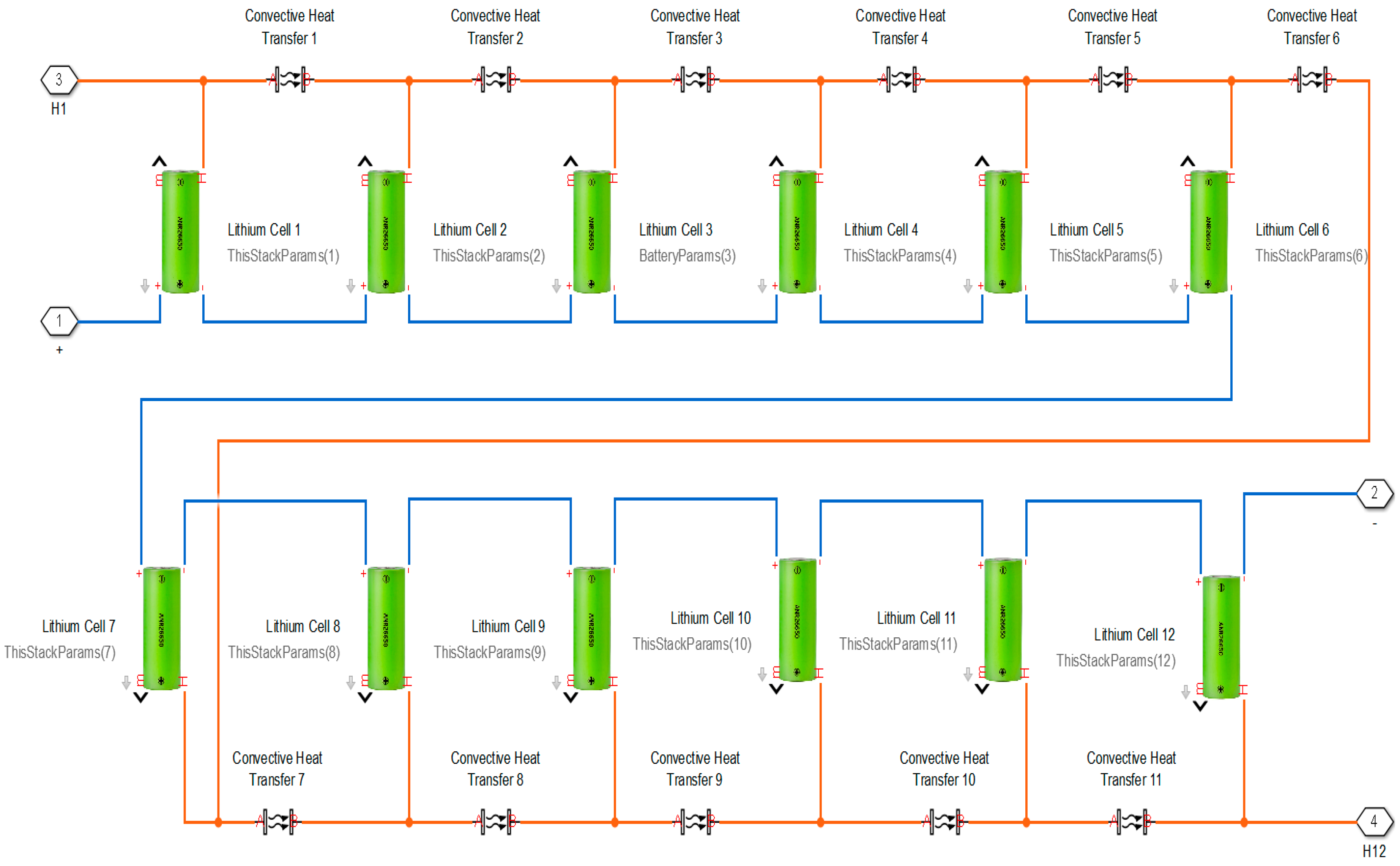
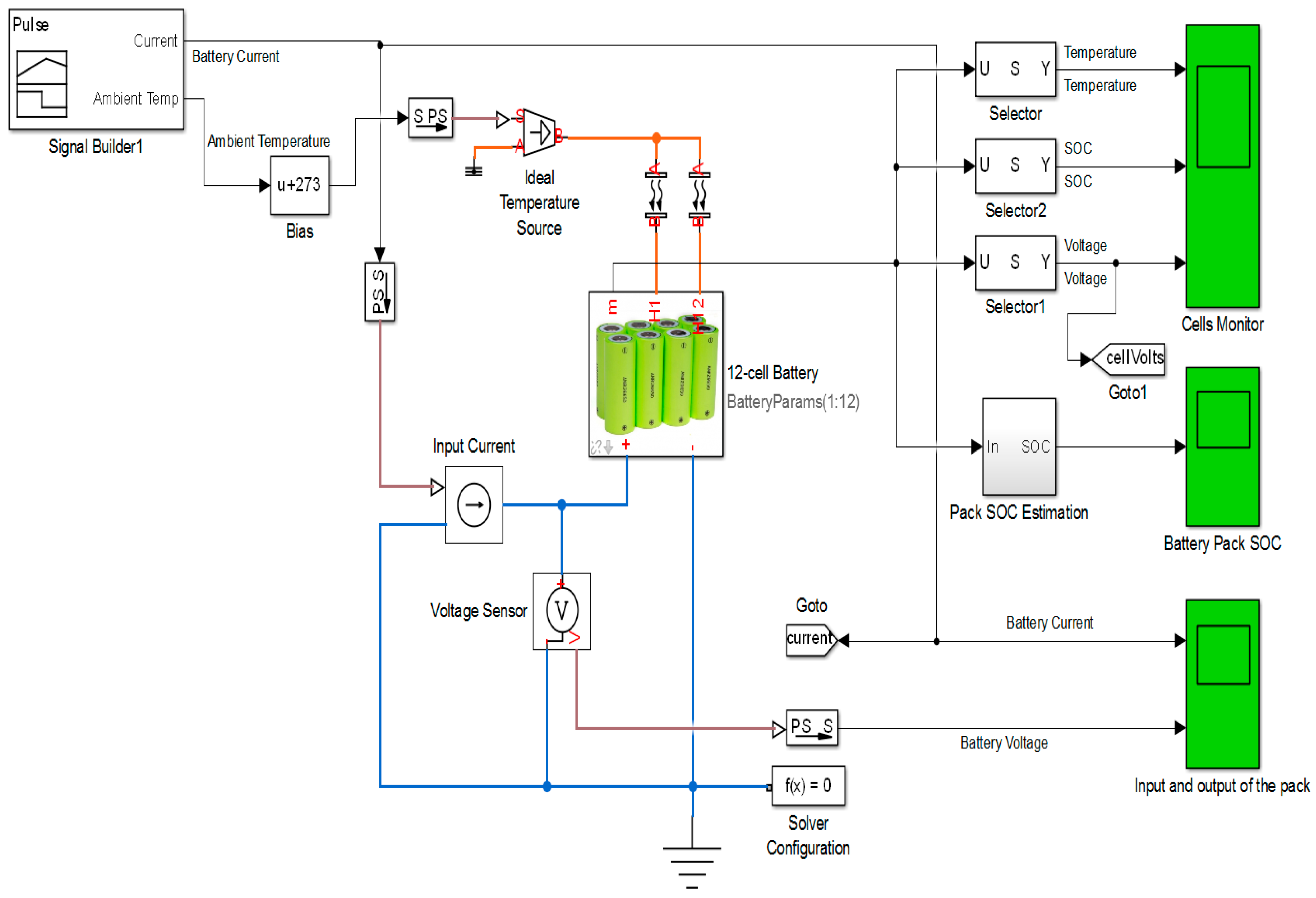
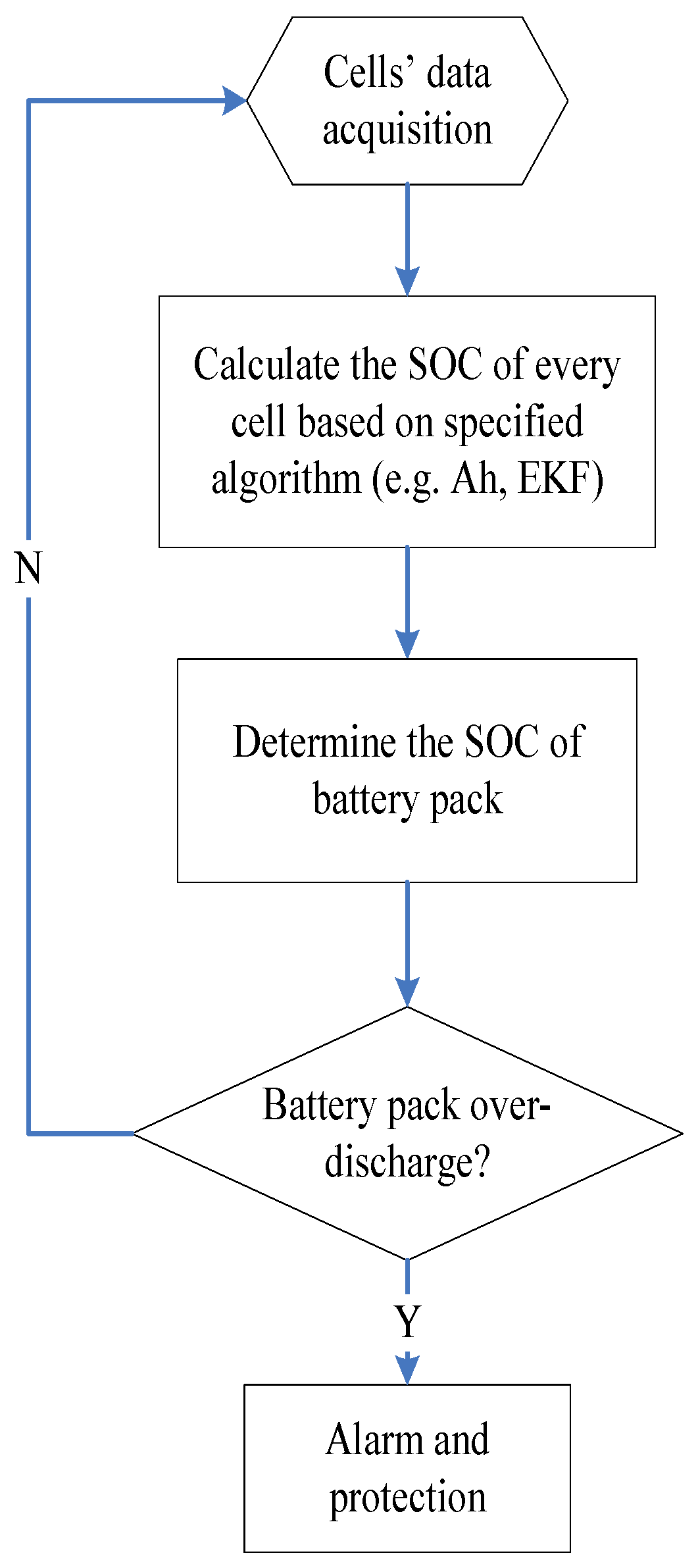
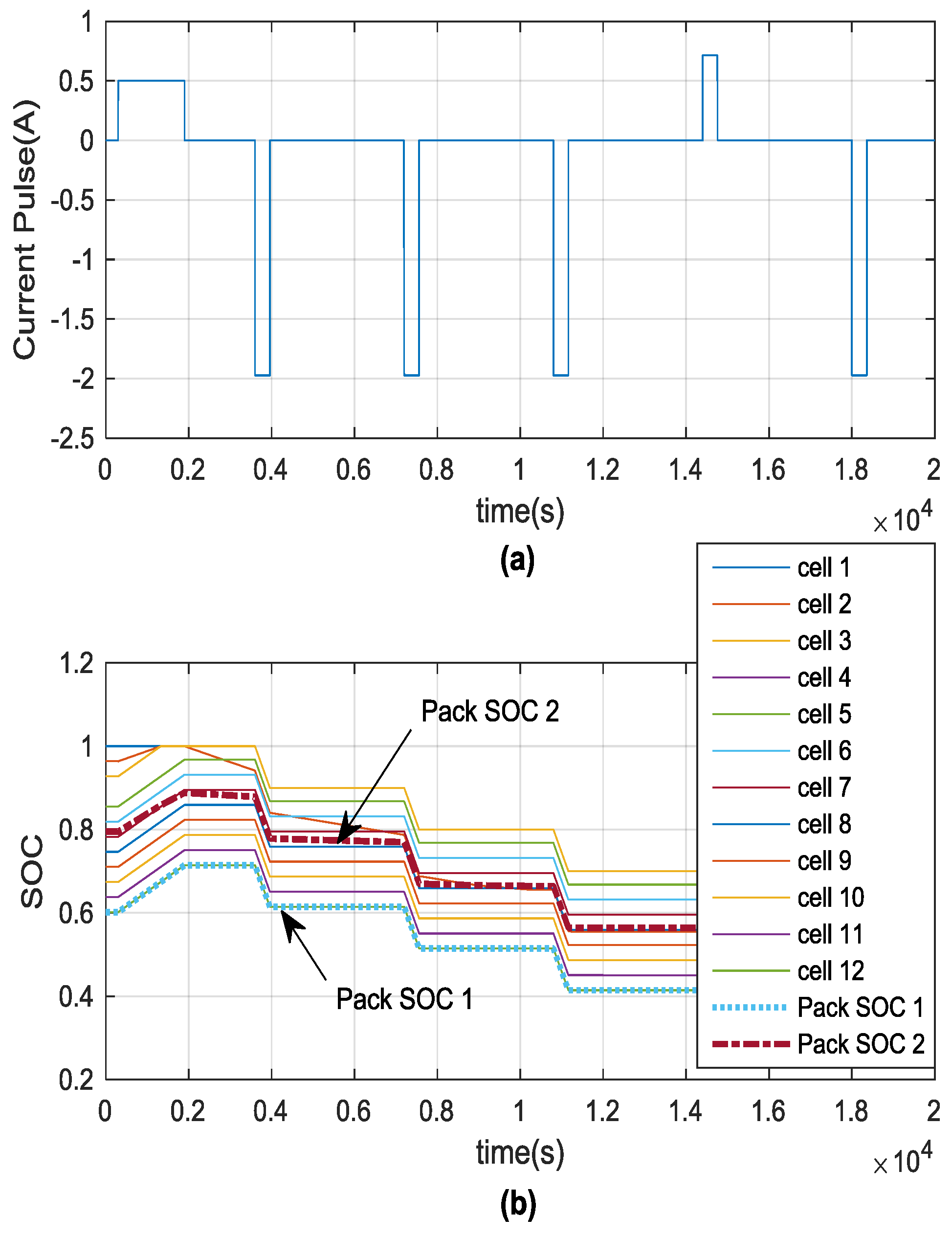
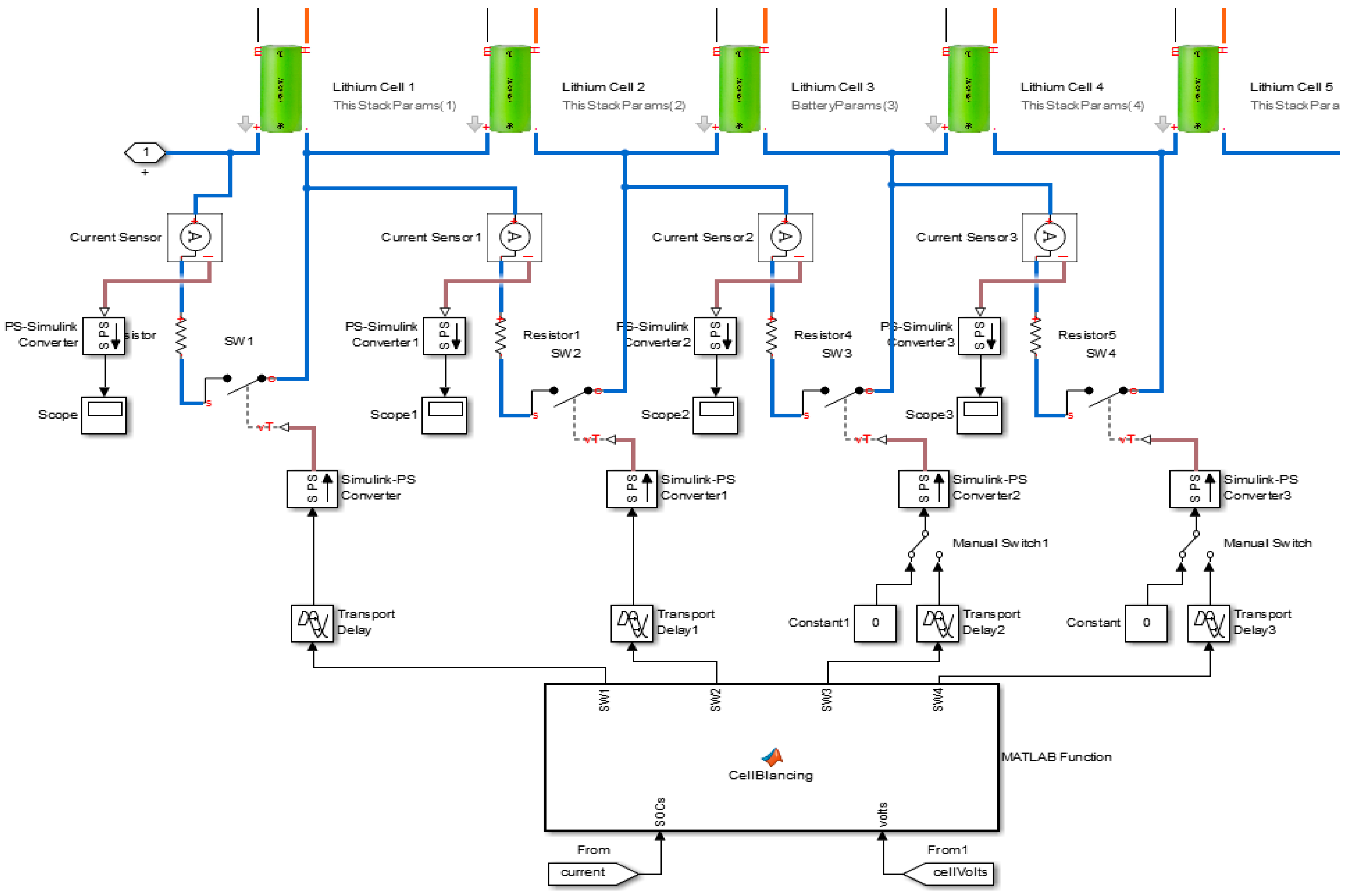
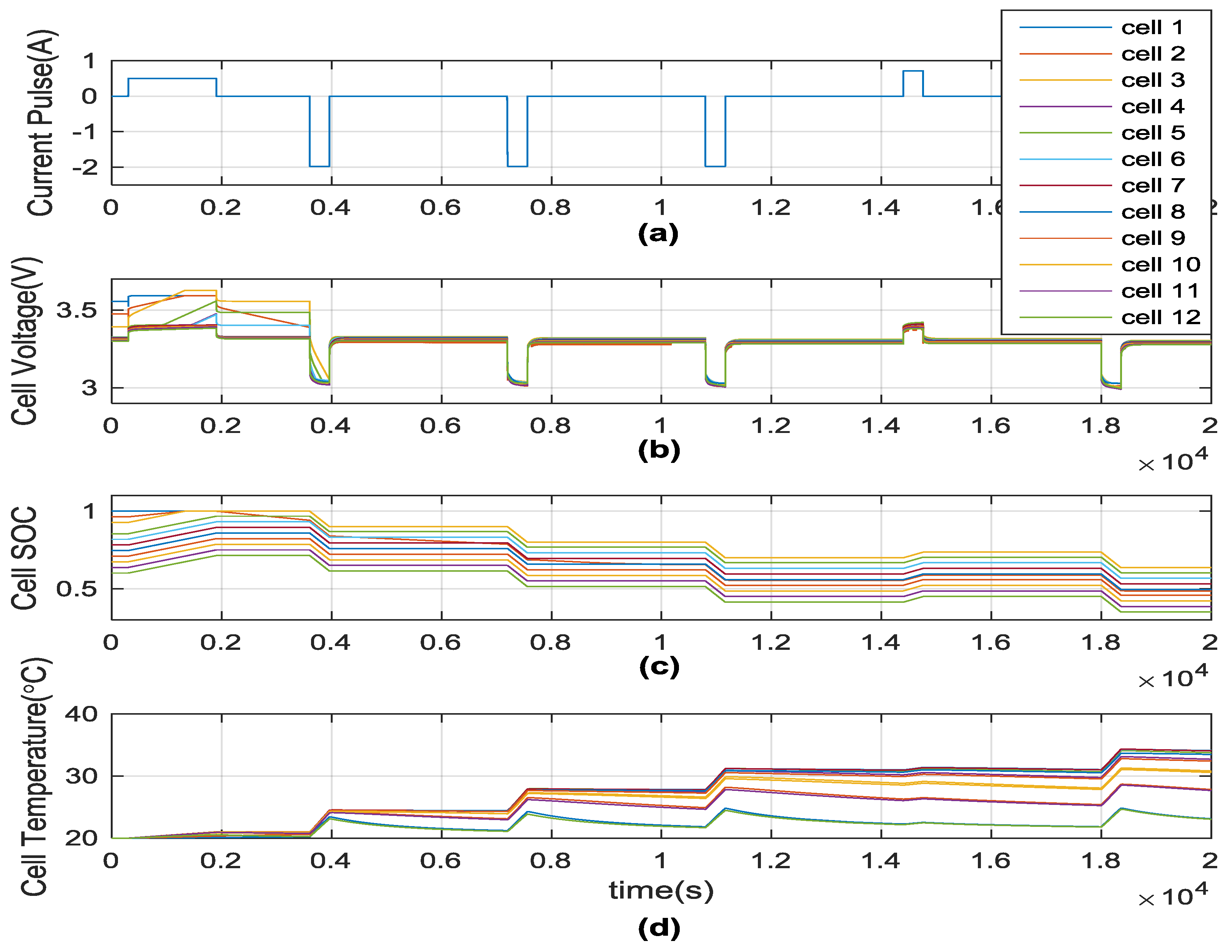
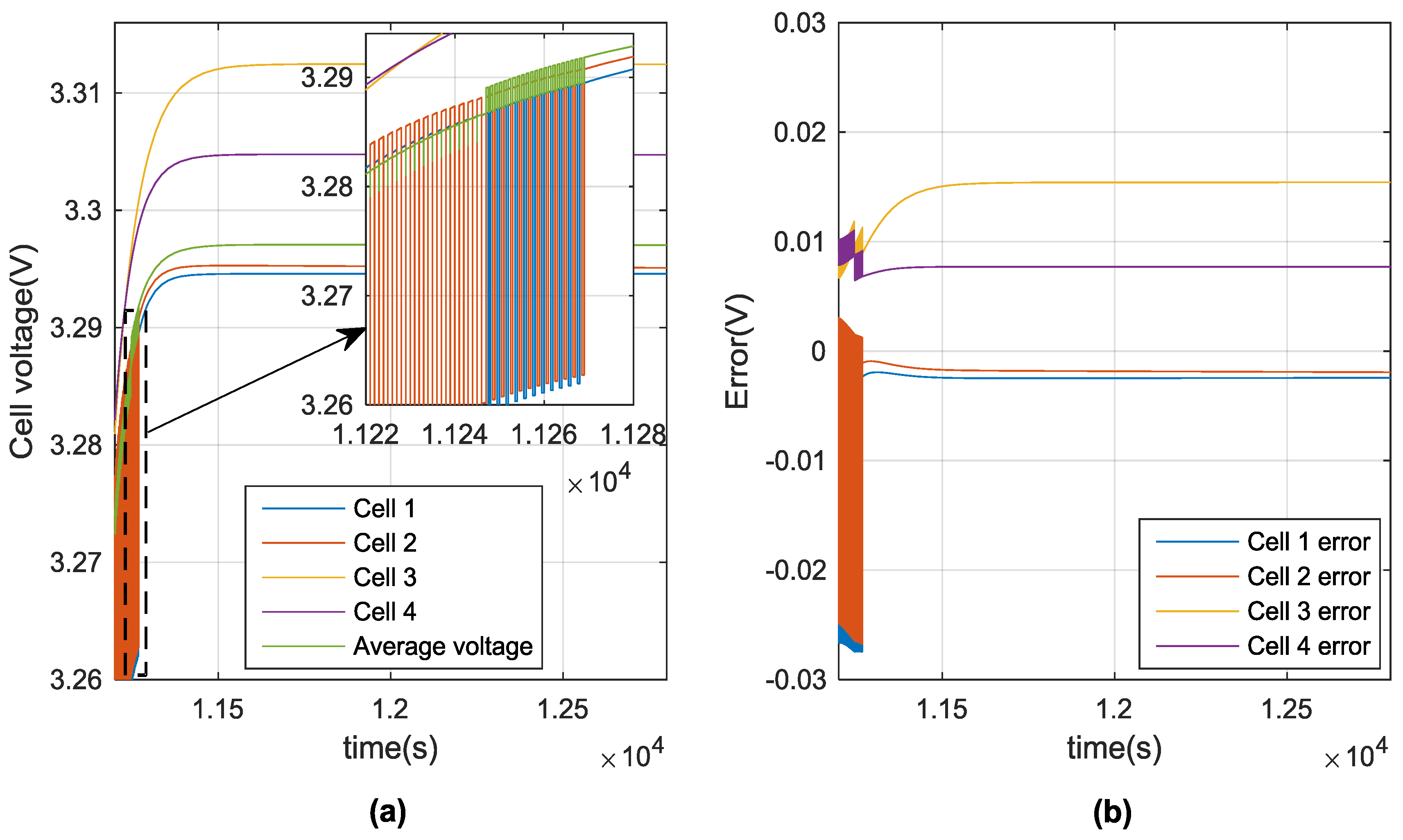
4.3. Temperature-Dependent 12-Cell Battery Model with Convective Heat Transfer Simulation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chang, M.-H.; Huang, H.-P.; Chang, S.-W. A new state of charge estimation method for LiFePO4 battery packs used in robots. Energies 2013, 6, 2007–2030. [Google Scholar] [CrossRef]
- Alhanouti, M.; Gießler, M.; Blank, T.; Gauterin, F. New electro-thermal battery pack model of an electric vehicle. Energies 2016, 9. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Pei, L.; Zhu, C. An integrated approach for real-time model-based state-of-charge estimation of lithium-ion batteries. J. Power Sources 2015, 283, 24–36. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Venkatesh, B. Accuracy improvement of Soc estimation in lithium-ion batteries. J. Energy Storage 2016, 6, 95–104. [Google Scholar] [CrossRef]
- Hansen, T.; Wang, C.-J. Support vector based battery state of charge estimator. J. Power Sources 2005, 141, 351–358. [Google Scholar] [CrossRef]
- Chaoui, H.; Golbon, N.; Hmouz, I.; Souissi, R.; Tahar, S. Lyapunov-based adaptive state of charge and state of health estimation for lithium-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 1610–1618. [Google Scholar] [CrossRef]
- Gandolfo, D.; Brandão, A.; Patiño, D.; Molina, M. Dynamic model of lithium polymer battery—Load resistor method for electric parameters identification. J. Energy Inst. 2015, 88, 470–479. [Google Scholar] [CrossRef]
- Lee, J.L.; Chemistruck, A.; Plett, G.L. Discrete-time realization of transcendental impedance models, with application to modeling spherical solid diffusion. J. Power Sources 2012, 206, 367–377. [Google Scholar] [CrossRef]
- Coleman, M.; Lee, C.K.; Zhu, C.; Hurley, W.G. State-of-charge determination from emf voltage estimation: Using impedance, terminal voltage, and current for lead-acid and lithium-ion batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Hussein, A.A. Capacity fade estimation in electric vehicle Li-ion batteries using artificial neural networks. IEEE Trans. Ind. Appl. 2015, 51, 2321–2330. [Google Scholar] [CrossRef]
- Li, I.H.; Wang, W.Y.; Su, S.F.; Lee, Y.S. A merged fuzzy neural network and its applications in battery state-of-charge estimation. IEEE Trans. Energy Convers. 2007, 22, 697–708. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and ekf. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Gao, Z.; Chin, C.S.; Woo, W.L.; Jia, J.; Toh, W.D. Lithium-ion battery modeling and validation for smart power system. In Proceedings of the 2015 International Conference on Computer, Communications, and Control Technology (I4CT), Kuching, Malaysia, 21–23 April 2015; pp. 269–274.
- Liu, S.; Jiang, J.; Shi, W.; Ma, Z.; Wang, L.Y.; Guo, H. Butler–volmer-equation-based electrical model for high-power lithium titanate batteries used in electric vehicles. IEEE Trans. Ind. Electron. 2015, 62, 7557–7568. [Google Scholar] [CrossRef]
- Melin, P.; Castillo, O. Intelligent control of complex electrochemical systems with a neuro-fuzzy-genetic approach. IEEE Trans. Ind. Electron. 2001, 48, 951–955. [Google Scholar] [CrossRef]
- Lin, H.T.; Liang, T.J.; Chen, S.M. Estimation of battery state of health using the probabilistic neural network. IEEE Trans. Ind. Inform. 2013, 9, 679–685. [Google Scholar] [CrossRef]
- Wang, S.C.; Liu, Y.H. A pso-based fuzzy-controlled searching for the optimal charge pattern of Li-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 2983–2993. [Google Scholar] [CrossRef]
- Kim, J.; Cho, B.H. State-of-charge estimation and state-of-health prediction of a Li-ion degraded battery based on an ekf combined with a per-unit system. IEEE Trans. Veh. Technol. 2011, 60, 4249–4260. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control Syst. Technol. 2015, 23, 357–363. [Google Scholar] [CrossRef]




| Cell Dimensions (mm) | Ø 26 × 65 |
| Cell Weight (g) | 76 |
| Cell Capacity (nominal/minimum) (0.5 C Rate) | 2.5/2.4 |
| Voltage (nominal, V) | 3.3 |
| Recommended Standard Charge Method | 2.5 A to 3.6 V CCCV for 60 min |
| Cycle Life at 20 A Discharge, 100% DOD | >1000 cycles |
| Maximum Continuous Discharge | 50 A |
| Operating Temperature | −30 °C to 55 °C |
| Storage Temperature | −40 °C to 60 °C |
| Specific Heat Capacity of the Cell | 810.53 |
| Convective Heat Transfer Coefficient (W/m2/K) | 5 |
| Surface Area of Heat Exchange (m2) | 0.0149 |
| Ambient Temperature (°C) | 25 |
| Temperature (°C) | 5 | 15 | 25 | 35 | 45 |
|---|---|---|---|---|---|
| Static capacity (Ah) | 2.2369 | 2.4474 | 2.5642 | 2.5693 | 2.5706 |
| R0 | ALS Method | EKF Method | Lookup Table |
|---|---|---|---|
| RMS | 0.0055 | 0.0042 | 0.0058 |
| Computation time | 1.35 s | 1.25 s | 0.021 s |
| Temperature (°C) | 5 | 15 | 25 | 45 |
|---|---|---|---|---|
| RMS error | 6.8736 × 10−5 | 7.2078 × 10−5 | 2.2671 × 10−5 | 9.5907 × 10−6 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Chin, C.S.; Woo, W.L.; Jia, J. Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application. Energies 2017, 10, 85. https://doi.org/10.3390/en10010085
Gao Z, Chin CS, Woo WL, Jia J. Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application. Energies. 2017; 10(1):85. https://doi.org/10.3390/en10010085
Chicago/Turabian StyleGao, Zuchang, Cheng Siong Chin, Wai Lok Woo, and Junbo Jia. 2017. "Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application" Energies 10, no. 1: 85. https://doi.org/10.3390/en10010085
APA StyleGao, Z., Chin, C. S., Woo, W. L., & Jia, J. (2017). Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application. Energies, 10(1), 85. https://doi.org/10.3390/en10010085









