A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter
Abstract
:1. Introduction
2. Mathematical Model
3. Lyapunov Stability Theory-Based Control Strategy
3.1. Current Control Realization
3.2. DC Voltage Control Realization
3.3. NP Voltage Balance through PWM Realization
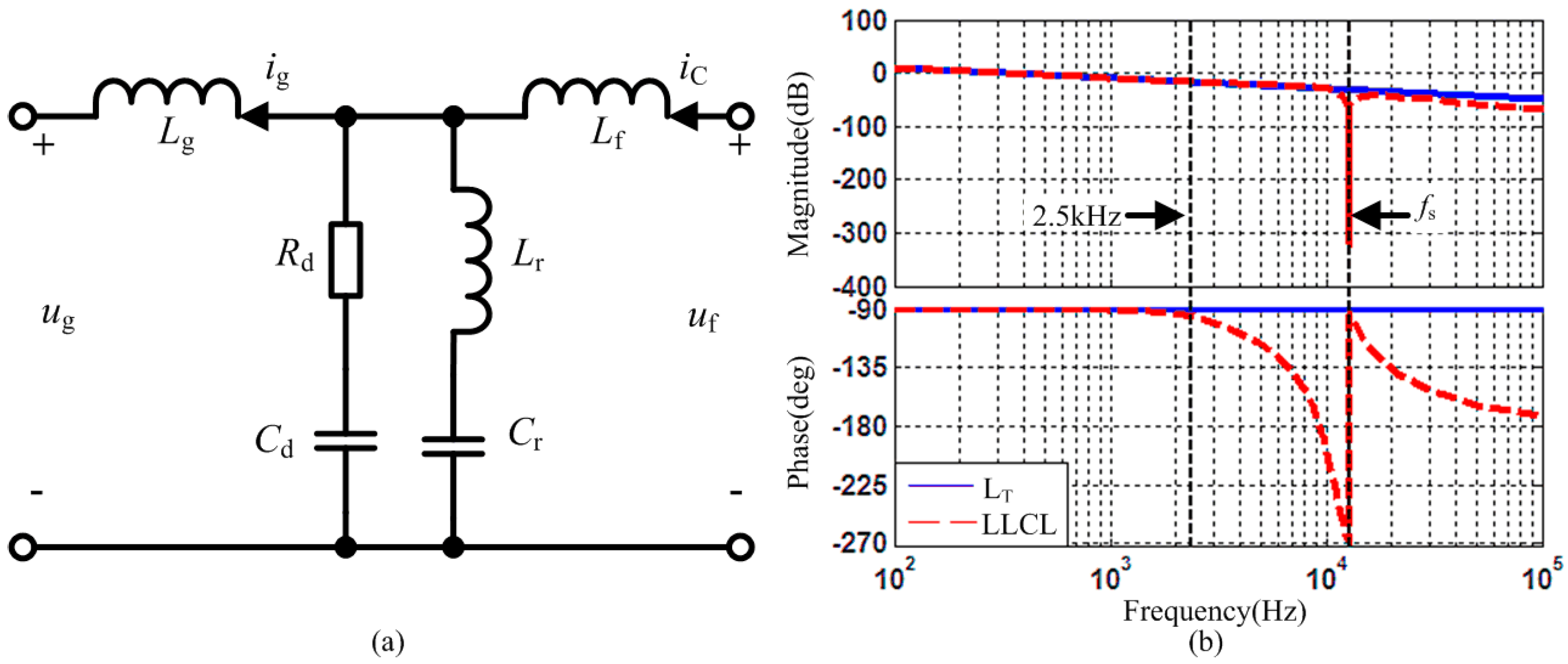
3.4. LCL Type Output Filter Design
- (1)
- In order to ensure the output current follow the highest reference current change rate and limit the output current ripple. LT should meet: , where ΔIc is the output current ripple. fs is the switching frequency (12.8 kHz). uSNm is the amplitude of grid phase voltage. M49 is the 49th harmonic current amplitude which is chosen as 0.5 A. ω49 is the 49th harmonic angular frequency.
- (2)
- Lr and Cr resonates at fs: .
- (3)
- In order to obtain good high frequency attenuate rate and appropriate output bandwidth for NPC-SAPF, Lf, Lg and Ca should meet: Lf ≥ 5Lg and , where fm is the highest compensated frequency (2.5 kHz). Ca = Cd + Cr.
- (4)
- Larger Cd/Cr is helpful to improve the damping performance but increase the power losses [29]. Considering the harmonics characteristics of NPC-SAPF, Cd/Cr = 8 and Rd = 3 are proposed.
4. Comparison Analysis of System Stability
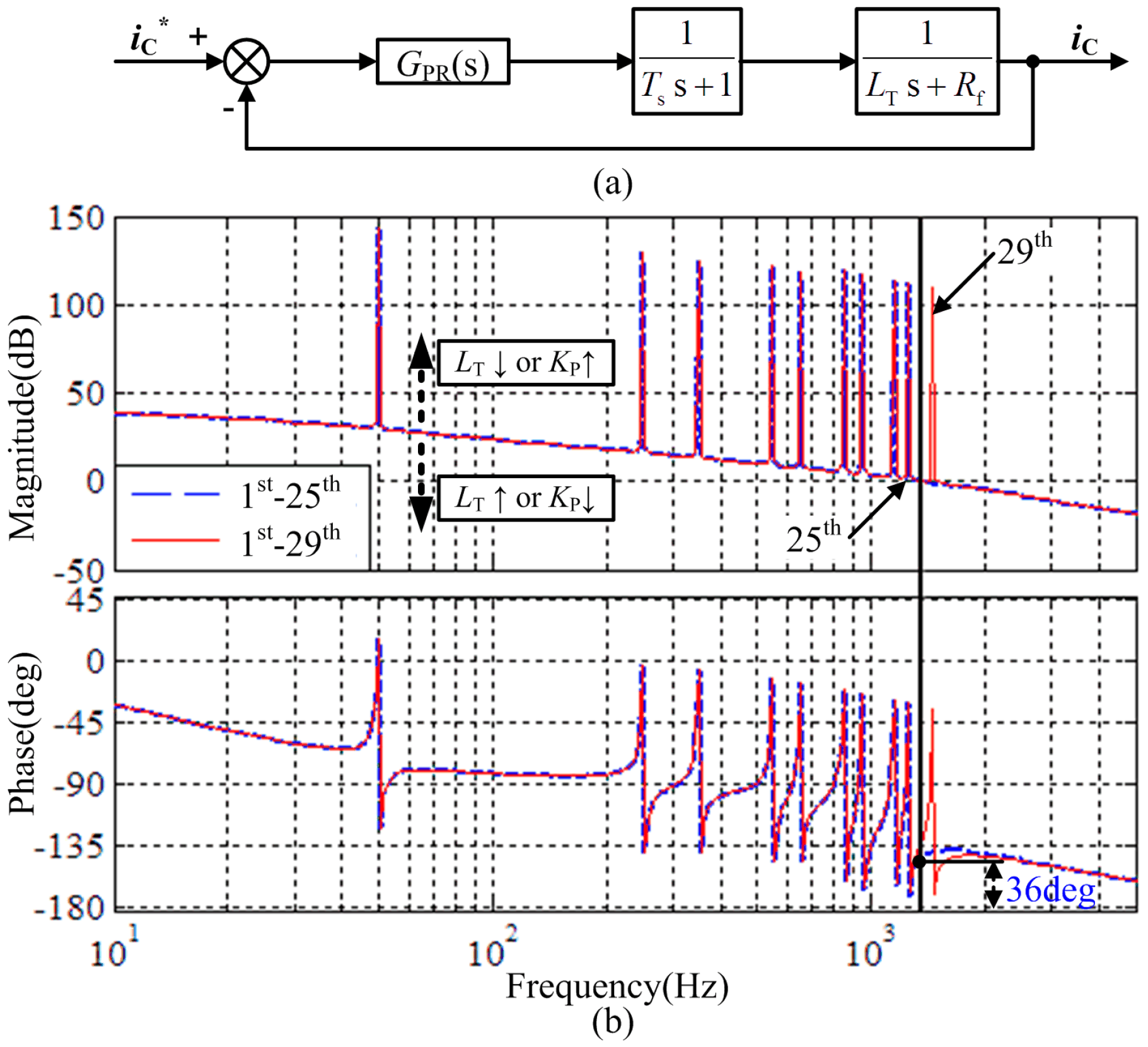
4.1. Stability of the Classical Feedback Control Strategy
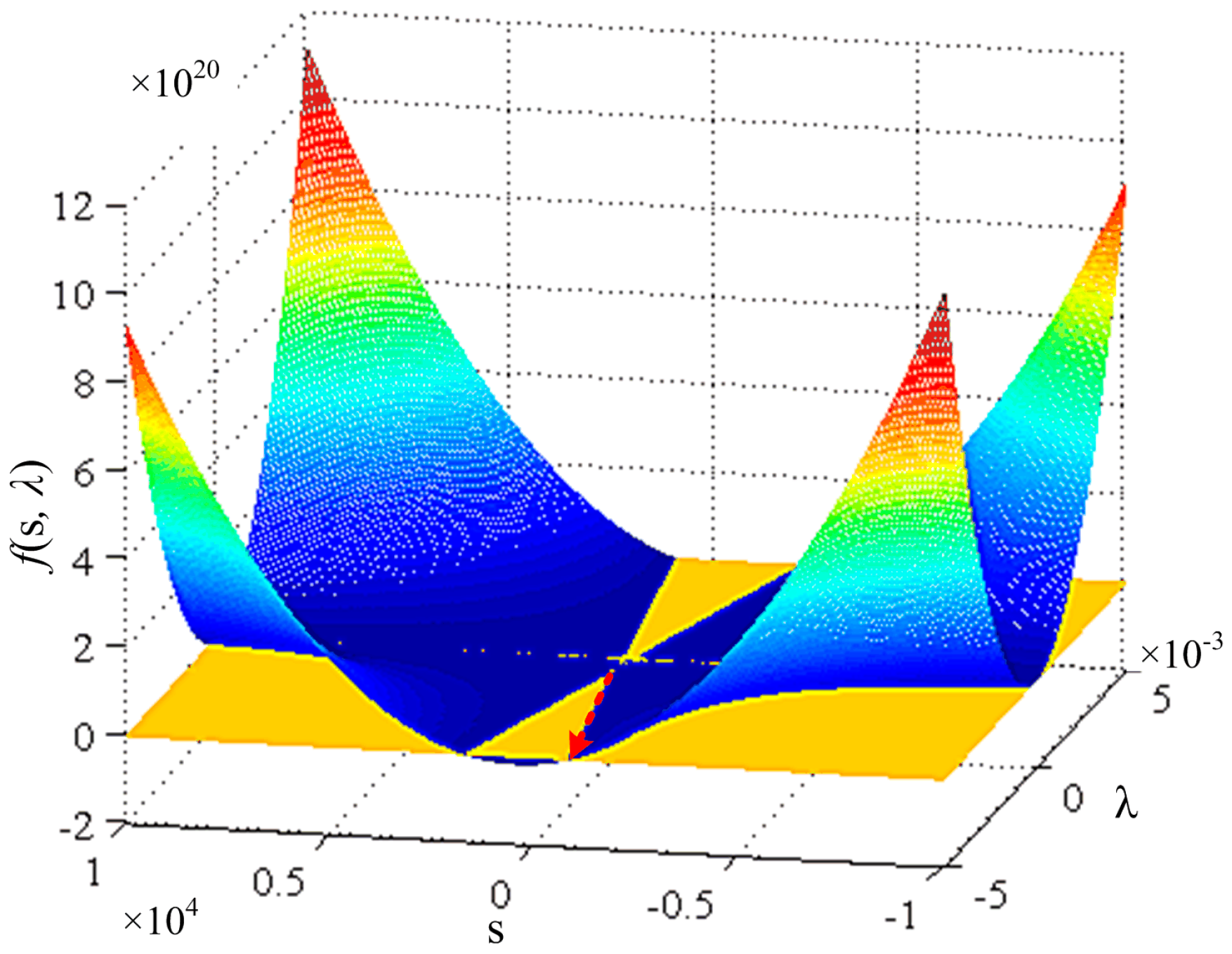
4.2. The Proposed Control Strategy Stability
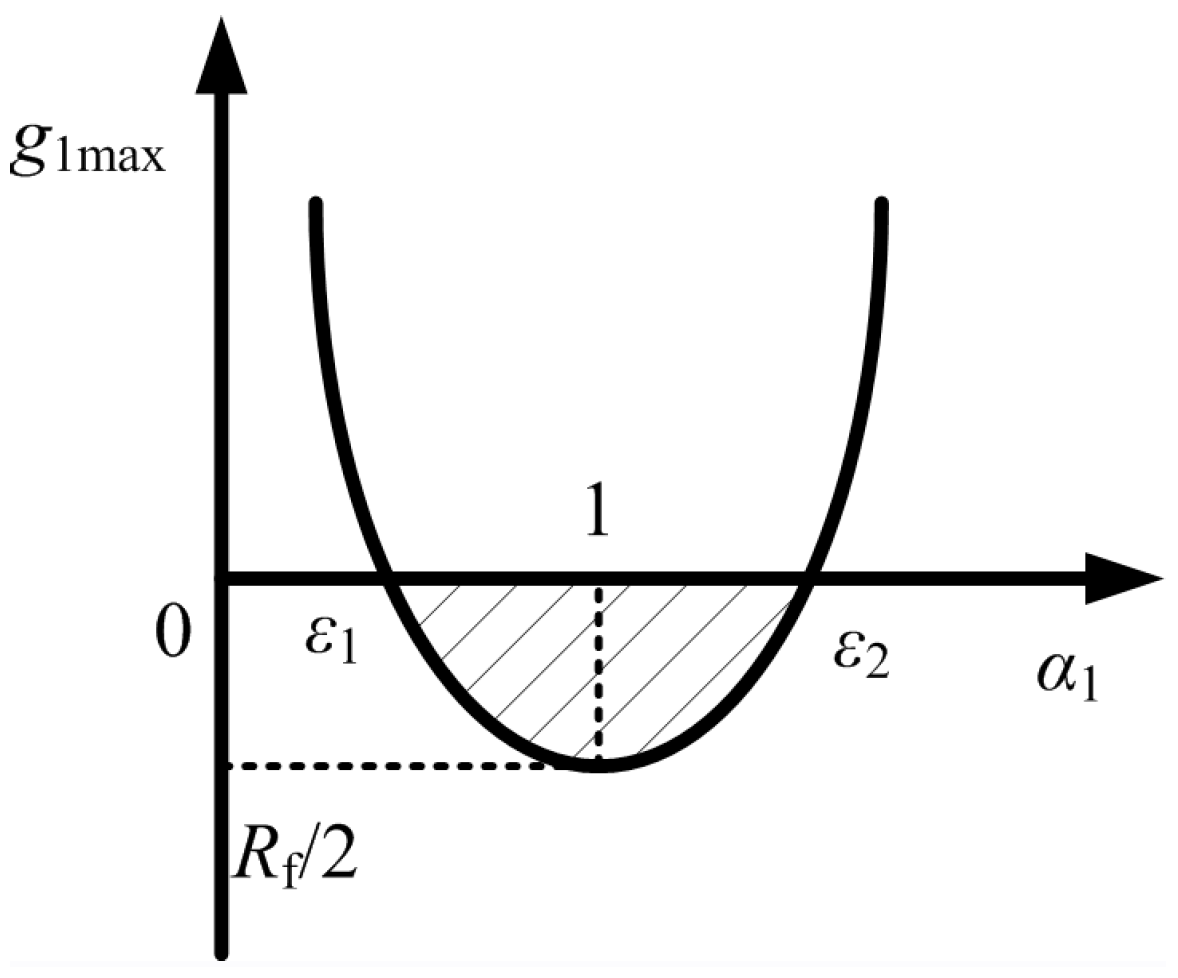
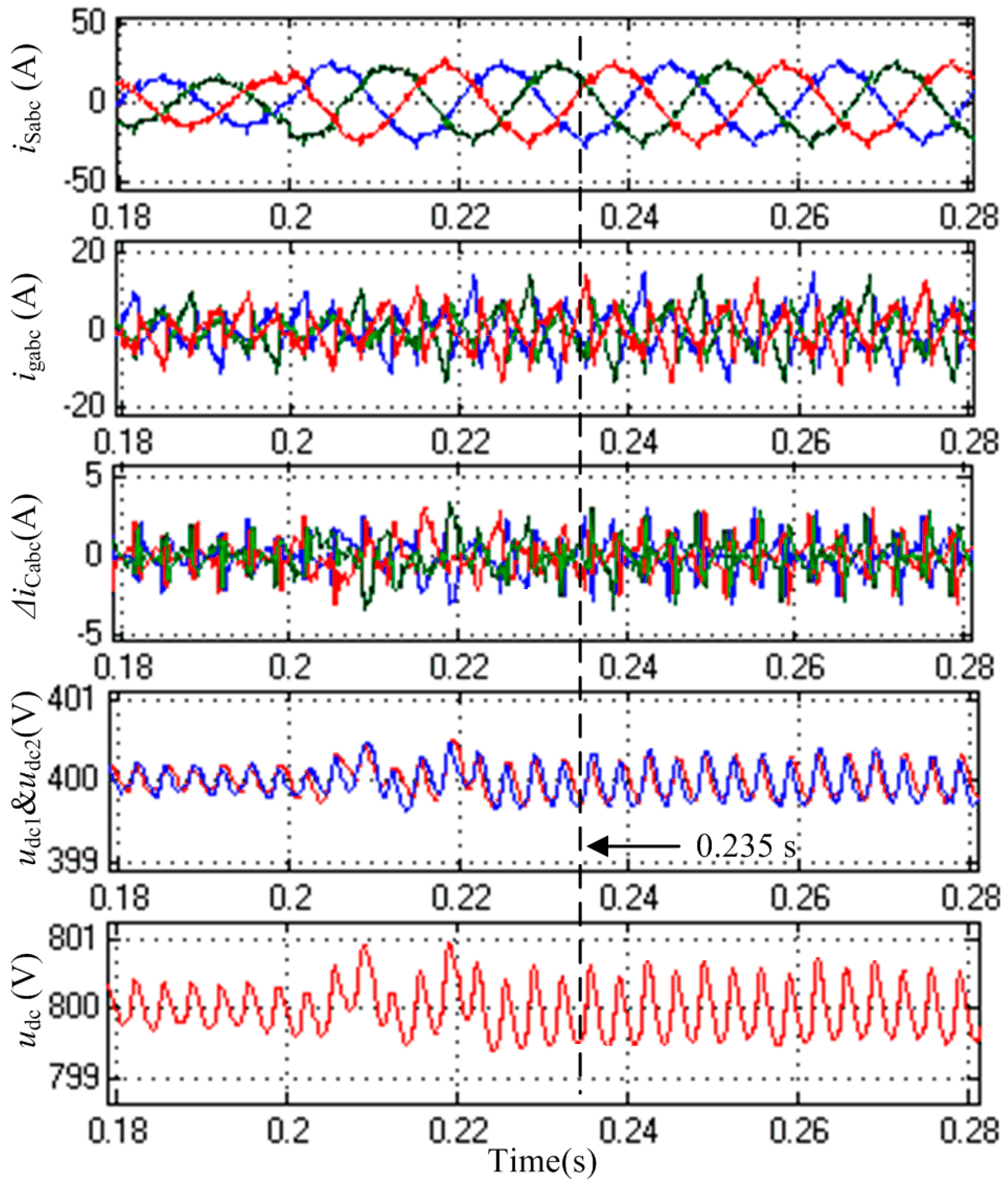
4.3. Tolerance of Inaccurate Model on Stability
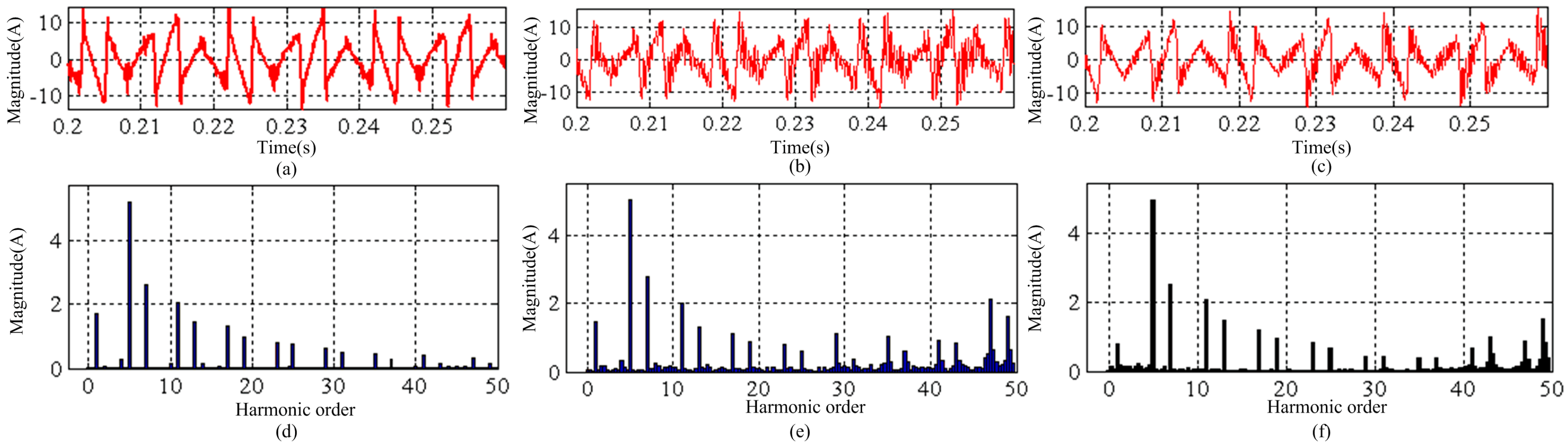
5. Simulation Results
5.1. Comparisons between the Proposed Control Strategy and the Classical Feedback Control Methods
5.2. Dynamic Response of the NPC-SAPF
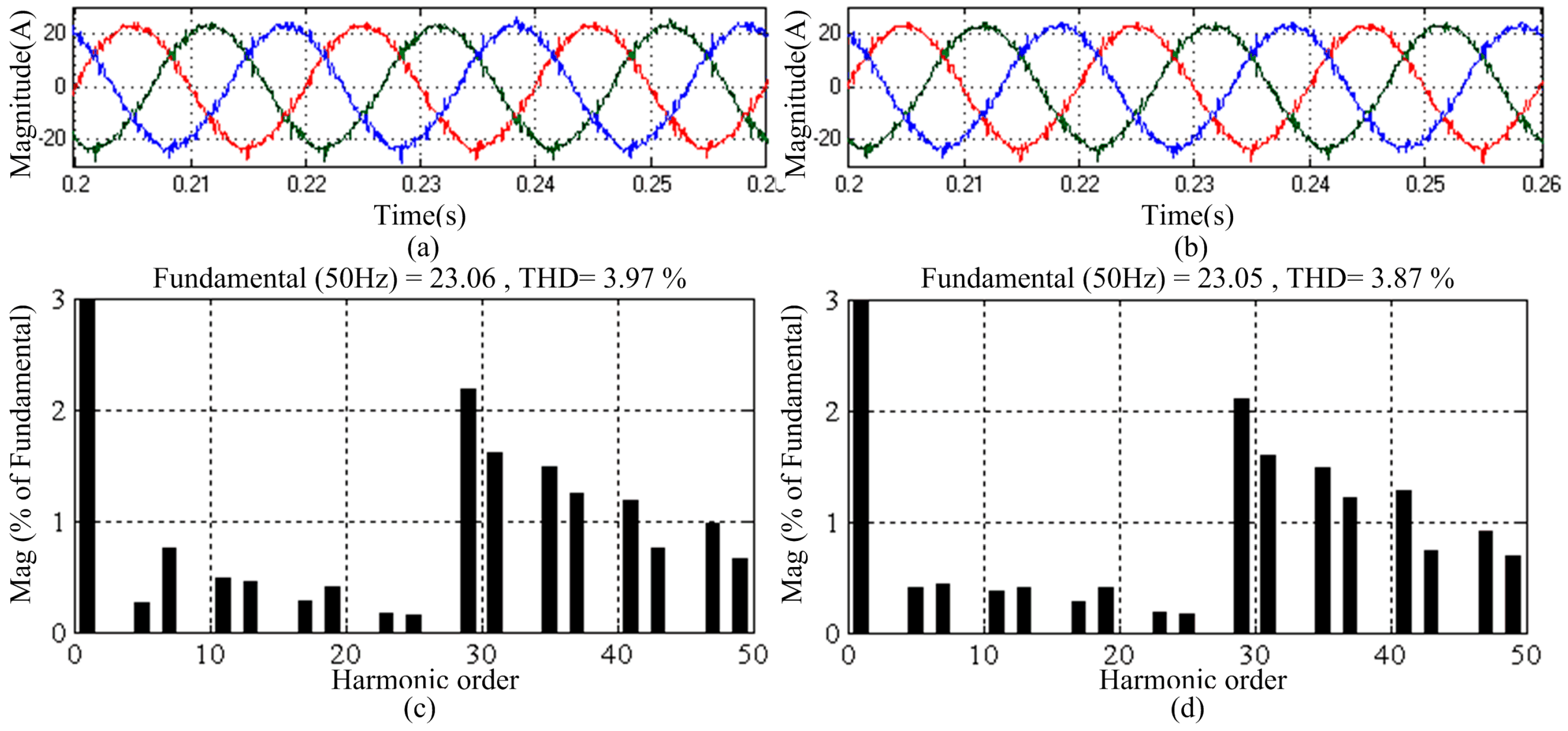
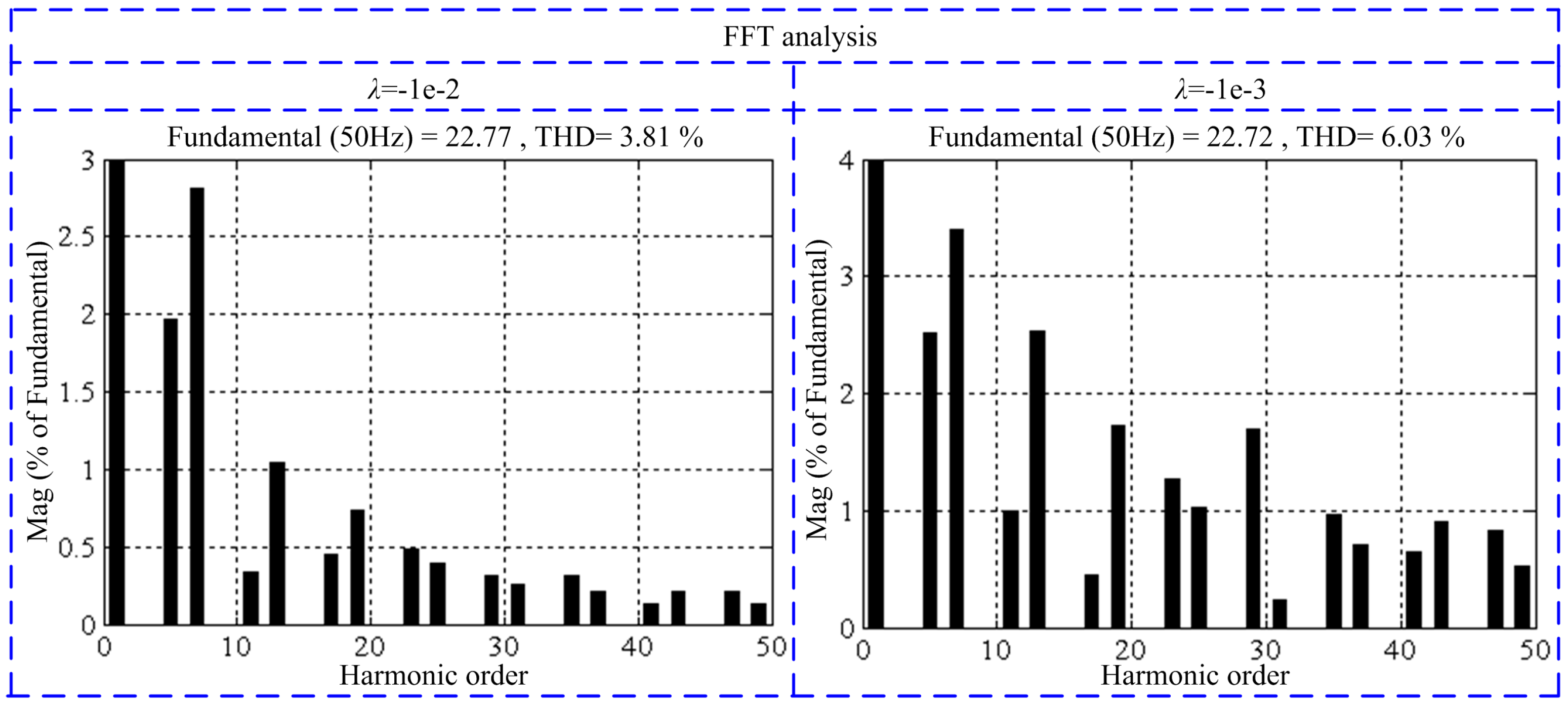
5.3. Steady-State Performance of the NPC-SAPF
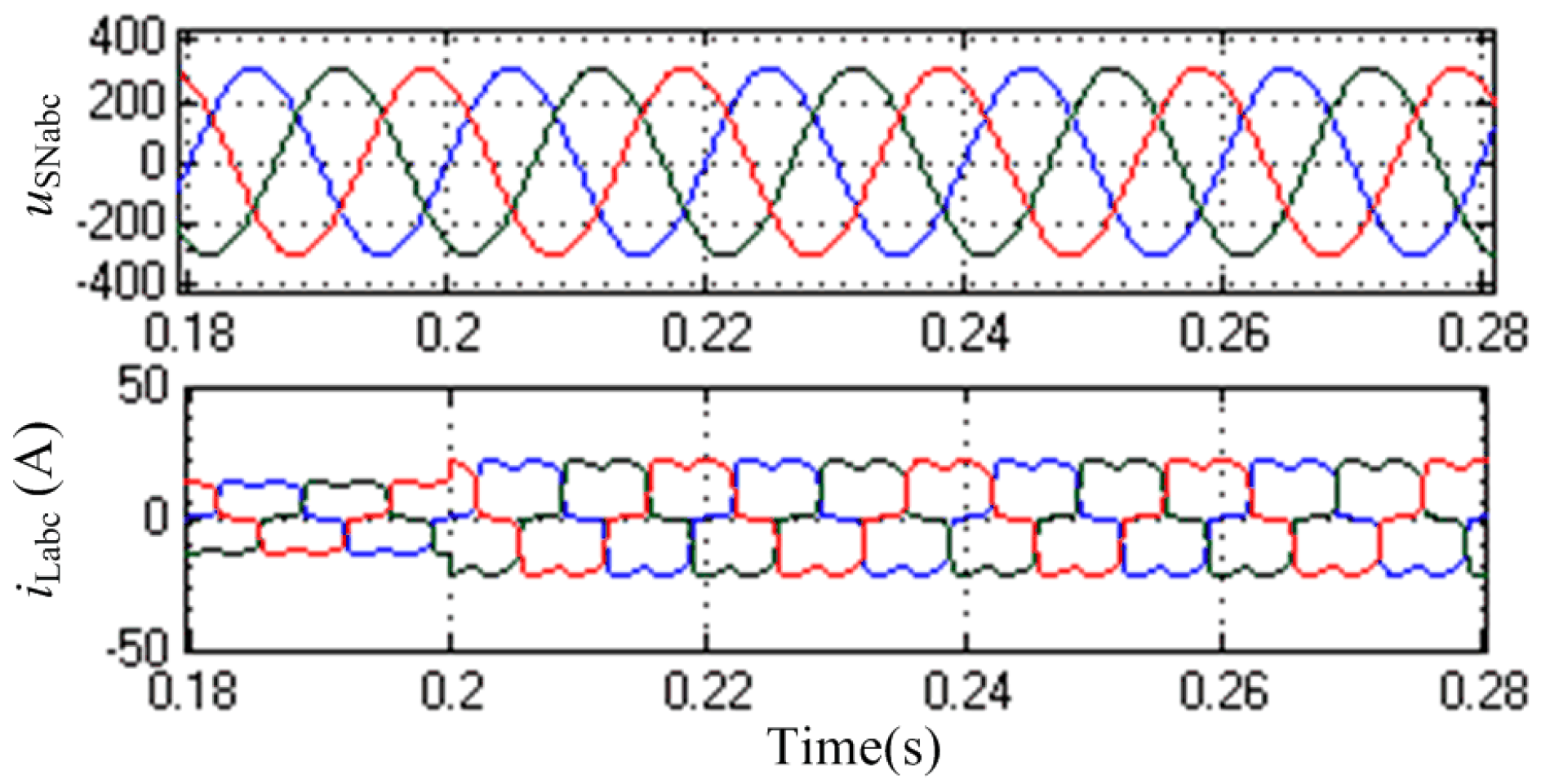
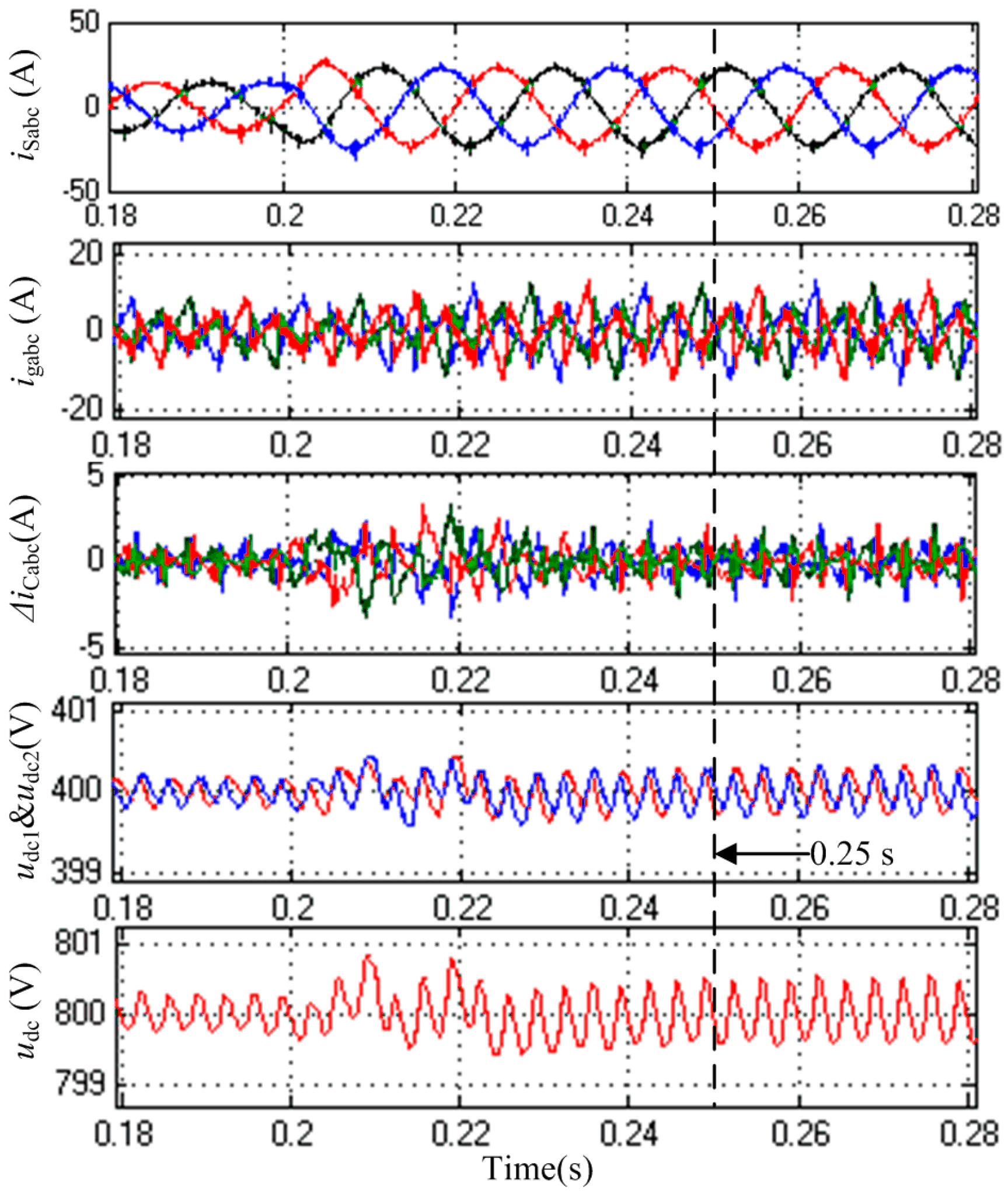
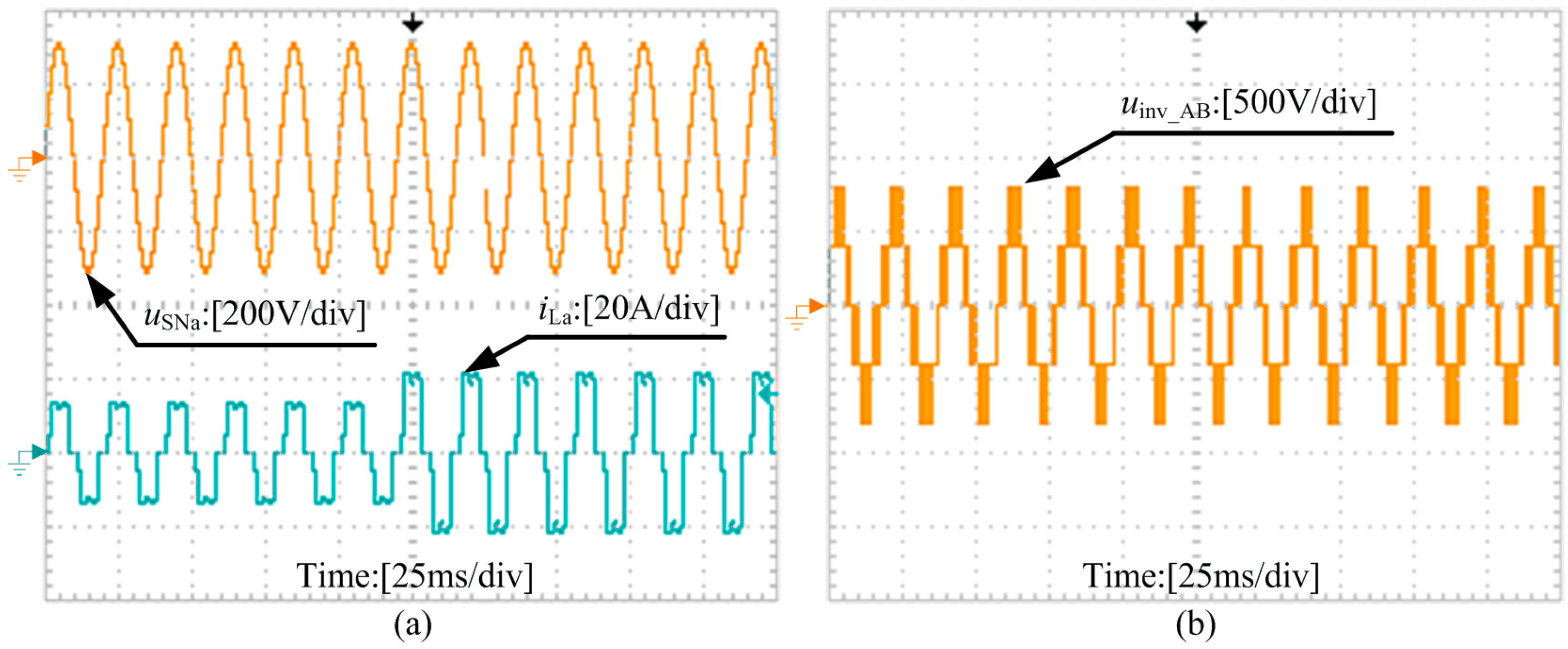
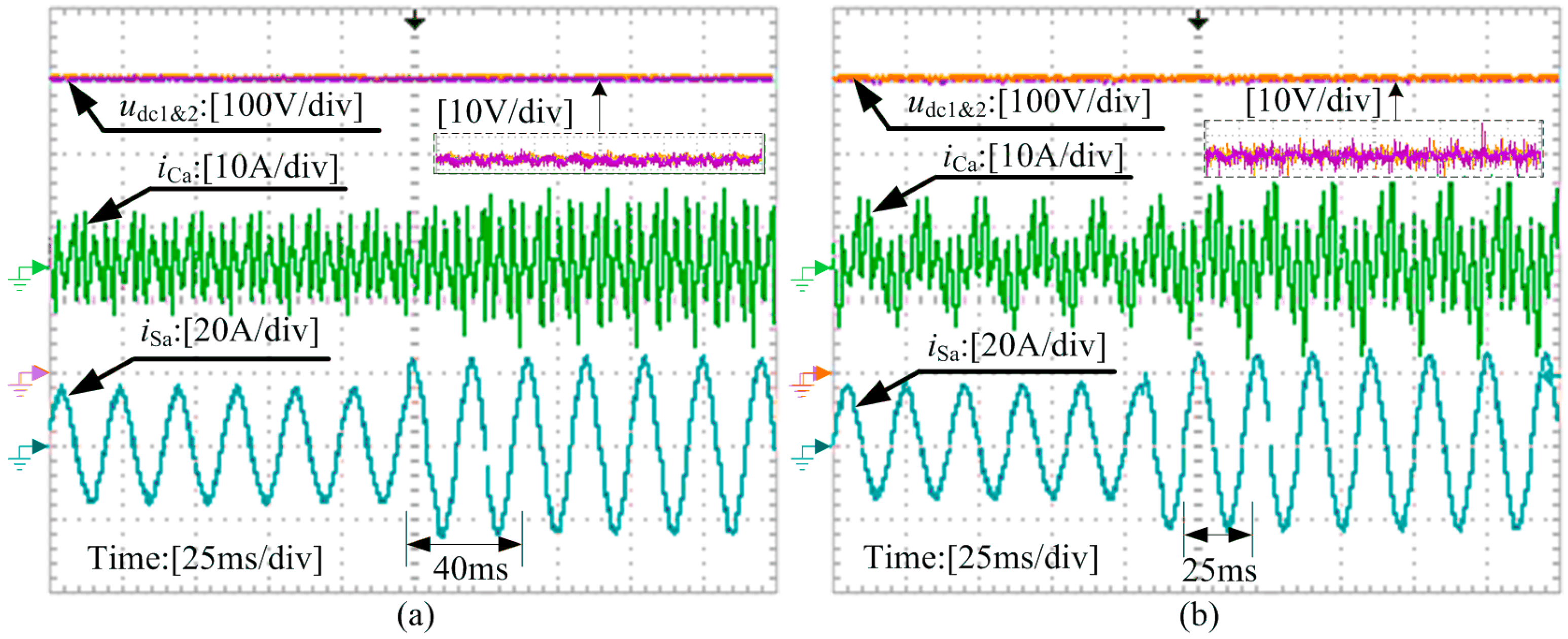
6. Experimental Results
6.1. Dynamic Response of the NPC-SAPF
6.2. Steady-State Performance of the NPC-APF
6.3. Experimental Resultes of PR and VPI Controllers
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Soeiro, T.B.; Kolar, J.W. Analysis of high-efficiency three-phase two- and three-level unidirectional hybrid rectifiers. IEEE Trans. Ind. Electron. 2013, 60, 3589–3601. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Wang, P.; Zhu, H.; Liu, C.; Xu, W. Control of three-phase boost-type PWM rectifier in stationary frame under unbalanced input voltage. IEEE Trans. Power. Electron. 2010, 25, 2521–2530. [Google Scholar] [CrossRef]
- Alejandro, G.Y.; Francisco, D.F.; Jesús, D.G.; Óscar, L. Effects of discretization methods on the performance of resonant controllers. IEEE Trans. Power. Electron. 2010, 25, 1692–1712. [Google Scholar]
- Yi, T.; Poh, C.L.; Peng, W.; Fook, C.H. Generalized design of high performance shunt active power filter with output LCL filter. IEEE Trans. Ind. Electron. 2012, 59, 1443–1452. [Google Scholar]
- Marcos, B.K.; Cursino, B.J. Virtual flux sensorless control for shunt active power filters with Quasi-resonant compensators. IEEE Trans. Power. Electron. 2016, 31, 4818–4830. [Google Scholar]
- Bojoi, R.I.; Griva, G.; Bostan, V.; Guerriero, M. Current control strategy for power conditioners using sinusoidal signal integrators in synchronous reference frame. IEEE Trans. Power. Electron. 2005, 20, 1402–1412. [Google Scholar] [CrossRef]
- Sun, J.J.; Gong, J.W.; Chen, B.F.; Zha, X.M. Analysis and design of repetitive controller based on regeneration spectrum and sensitivity function in active power filter system. IET Power. Electron. 2014, 7, 2133–2140. [Google Scholar] [CrossRef]
- Aurelio, G.C.; Omar, P.A.; Vicente, F.B.; Pedro, R.S. Application of a repetitive controller for a three-phase active power filter. IEEE Trans. Power. Electron. 2007, 22, 237–246. [Google Scholar]
- Zou, Z.X.; Wang, Z.; Cheng, M. Modeling, Analysis, and design of multifunction grid-interfaced inverters with output LCL filter. IEEE Trans. Power. Electron. 2014, 29, 3830–3839. [Google Scholar] [CrossRef]
- Suresh, Y.; Panda, A.K.; Suresh, M. Real-time implementation of adaptive fuzzy hysteresis-band current control technique for shunt active power filter. IET Power. Electron. 2012, 5, 1188–1195. [Google Scholar] [CrossRef]
- Chen, B.S.; Joós, G. Direct power control of active filters with averaged switching frequency regulation. IEEE Trans. Power. Electron. 2008, 23, 2729–2737. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.S.; Wong, M.C.; Dai, N.Y. Non-linear adaptive hysteresis band pulse-width modulation control for hybrid active power filters to reduce switching loss. IET Power. Electron. 2012, 8, 2156–2167. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. High performance current controller for selective harmonic compensation in active power filters. IEEE Trans. Power. Electron. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Q.Y.; Hu, S.J.; Liu, F.; Cao, Y.J.; Luo, L.F.; Rehtanz, C. A virtual impedance comprehensive control strategy for the controllably inductive power filtering system. IEEE Trans. Power. Electron. 2017, 32, 920–926. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Y.J.; Liu, F.; Sidorov, D.; Panasetsky, D.; Liang, C.G.; Luo, L.F.; Cao, Y.J. A controllably inductive filtering method with transformer-integrated linear reactor for power quality improvement of shipboard power system. IEEE Trans. Power Deliv. 2016, PP. [Google Scholar] [CrossRef]
- Yuan, X.; Merk, W.; Stemmler, H.; Allmeling, J. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. IEEE Trans. Ind. Appl. 2002, 38, 523–532. [Google Scholar] [CrossRef]
- IEEE Recommended Practice and Requirements for Harmonic Control in Electrical Power Systems; IEEE Standard 519-2014; IEEE: New York, NY, USA, 2014.
- Komurcugil, H.; Altin, N.; Ozdemir, S.; Sefa, I. An extended Lyapunov-function-based control strategy for single-phase UPS inverters. IEEE Trans. Power. Electron. 2015, 30, 3976–3983. [Google Scholar] [CrossRef]
- Kato, T.; Inoue, K.; Ueda, M. Lyapunov-based digital control of a grid-connected inverter with an LCL filter. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 942–948. [Google Scholar] [CrossRef]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K. A Lyapunov-function-based control for a three-phase shunt hybrid active filter. IEEE Trans. Ind. Electron. 2012, 59, 1418–1429. [Google Scholar] [CrossRef]
- Meza, C.; Biel, D.; Jeltsema, D.; Scherpen, J.M.A. Lyapunov-based control scheme for single-phase grid-connected PV central inverters. IEEE Trans. Control Syst. Technol. 2012, 20, 520–529. [Google Scholar] [CrossRef]
- Komurcugil, H.; Altin, N.; Ozdemir, S. Lyapunov-function and proportional-resonant-based control strategy for single-phase grid-connected VSI with LCL filter. IEEE Trans. Ind. Electron. 2016, 63, 2838–2849. [Google Scholar] [CrossRef]
- Kwak, S.; Yoo, S.J.; Park, J. Finite control set predictive control based on Lyapunov function for three-phase voltage source inverters. IET Power. Electron. 2014, 7, 2726–2732. [Google Scholar] [CrossRef]
- Dasgupta, S.; Mohan, S.N.; Sahoo, S.K. Lyapunov function-based current controller to control active and reactive power flow from a renewable energy source to a generalized three-phase microgrid system. IEEE Trans. Ind. Electron. 2013, 60, 799–813. [Google Scholar] [CrossRef]
- Pou, J.; Zaragoza, J.; Ceballos, S.; Saeedifard, M. A carrier-based PWM strategy with zero sequence voltage injection for a three-level neutral-point-clamped converter. IEEE Trans. Power. Electron. 2012, 27, 642–651. [Google Scholar] [CrossRef]
- Zaragoza, J.; Pou, J.; Ceballos, S. Voltage-Balance compensator for a carrier-based modulation in the neutral-point-clamped converter. IEEE Trans. Ind. Electron. 2009, 56, 305–314. [Google Scholar] [CrossRef]
- López, I.; Ceballos, S.; Pou, J.; Saeedifard, M. Modulation strategy for multiphase neutral-point-clamped converters. IEEE Trans. Power. Electron. 2016, 31, 928–941. [Google Scholar] [CrossRef]
- Wu, W.M.; He, Y.B.; Blaabjerg, F. An LLCL power filter for single-phase grid-tied inverter. IEEE Trans. Power. Electron. 2012, 27, 782–789. [Google Scholar] [CrossRef]
- Wu, W.M.; He, Y.B.; Tang, T.H.; Blaabjerg, F. A new design method for the passive damped LCL and LLCL filter-based single-phase grid-tied inverter. IEEE Trans. Ind. Electron. 2013, 60, 4339–4350. [Google Scholar] [CrossRef]
- Huang, M.; Wang, X.F.; Loh, P.C. Active damping of LLCL-filter resonance based on LC-trap voltage or current feedback. IEEE Trans. Power. Electron. 2016, 31, 2337–2346. [Google Scholar] [CrossRef]
- Wu, W.M.; Sun, Y.J.; Huang, M. A robust passive damping method for LLCL-filter-based grid-tied inverters to minimize the effect of grid harmonic voltages. IEEE Trans. Power. Electron. 2014, 29, 3279–3289. [Google Scholar] [CrossRef]
- Kömürcügil, H.; Kükrer, Ö. A new control strategy for single-phase shunt active power filters using a Lyapunov function. IEEE Trans. Ind. Electron. 2006, 53, 305–312. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| uSNabc | 220 V | Lf | 0.45 mH |
| f0 | 50 Hz | Rf | 0.05 Ω |
| fs | 12.8 kHz | Lg | 0.05 mH |
| 400 V | Lr | 70.28 μH | |
| Ls | 0.02 mH | Cr | 2.2 μF |
| Rs | 0.05 Ω | Cd | 17.6 μF |
| C1(C2) | 4650 μF | Rd | 5 Ω |
| Harmonic Order | Load Current | Grid Current | IEEE Standard 519-2014 | ||
|---|---|---|---|---|---|
| Amplitude (A) | Percent (%) | Amplitude (A) | Percent (%) | Maximum Percent (%) | |
| 1 | 22.61 | 100 | 22.77 | 100 | 100 |
| 5 | 5.11 | 22.59 | 0.45 | 1.97 | 4.0 |
| 7 | 2.45 | 10.85 | 0.64 | 2.81 | 4.0 |
| 11 | 1.94 | 8.60 | 0.08 | 0.34 | 2.0 |
| 13 | 1.28 | 5.67 | 0.24 | 1.04 | 2.0 |
| 17 | 1.10 | 4.87 | 0.10 | 0.45 | 1.5 |
| 19 | 0.78 | 3.46 | 0.17 | 0.74 | 1.5 |
| 23 | 0.69 | 3.06 | 0.11 | 0.48 | 0.6 |
| 25 | 0.50 | 2.20 | 0.09 | 0.39 | 0.6 |
| 29 | 0.45 | 1.98 | 0.07 | 0.31 | 0.6 |
| 31 | 0.32 | 1.40 | 0.06 | 0.26 | 0.6 |
| 35 | 0.29 | 1.29 | 0.07 | 0.31 | 0.3 |
| 37 | 0.20 | 0.87 | 0.05 | 0.21 | 0.3 |
| 41 | 0.19 | 0.85 | 0.03 | 0.13 | 0.3 |
| 43 | 0.12 | 0.53 | 0.05 | 0.21 | 0.3 |
| 47 | 0.13 | 0.60 | 0.06 | 0.26 | 0.3 |
| 49 | 0.07 | 0.32 | 0.03 | 0.13 | 0.3 |
| THD (%) | 28.20 | 3.81 | 5.0 | ||
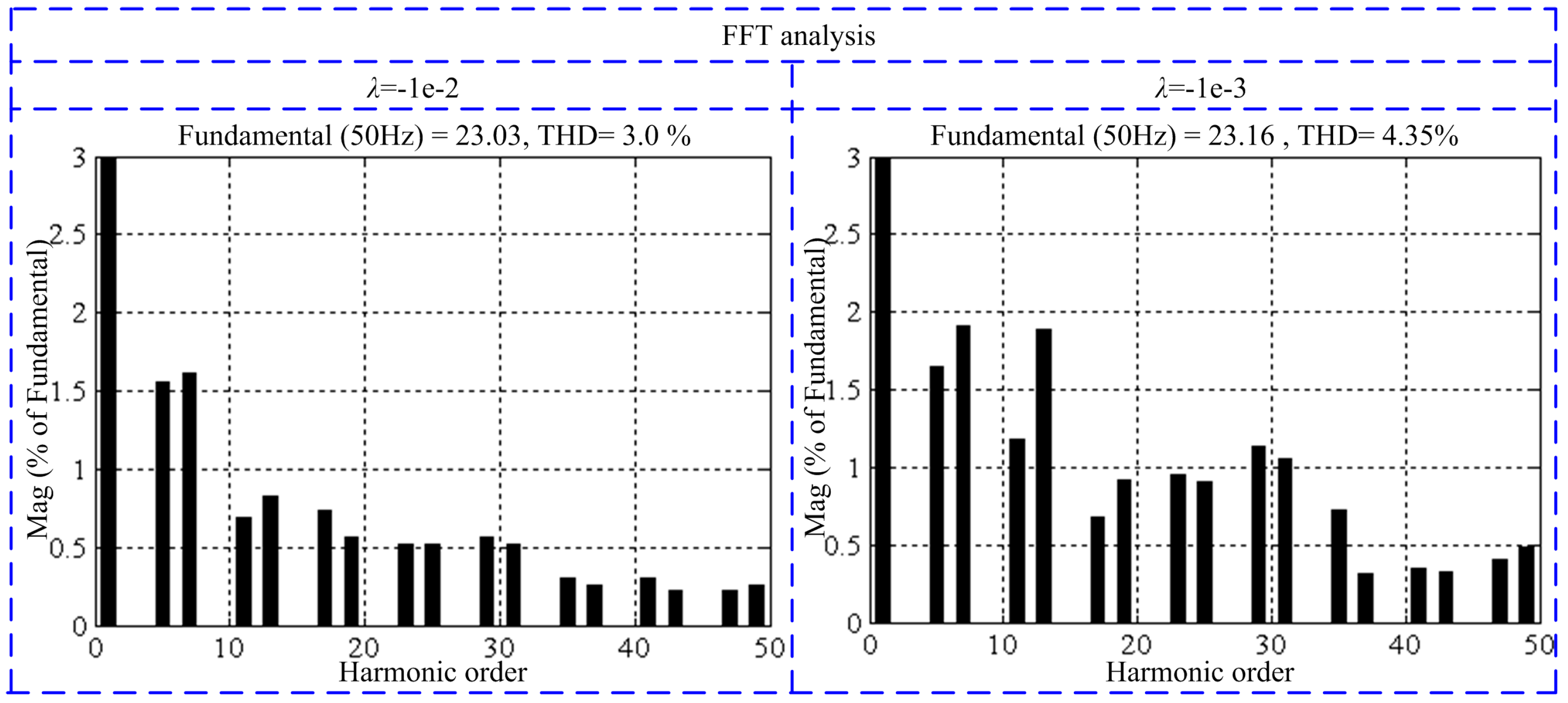
| Harmonic Order | Load Current | Grid Current | ||
|---|---|---|---|---|
| Amplitude (A) | Percent (%) | Amplitude (A) | Percent (%) | |
| 1 | 22.96 | 100 | 23.03 | 100 |
| 5 | 5.08 | 22.10 | 0.36 | 1.56 |
| 7 | 2.39 | 10.41 | 0.37 | 1.61 |
| 11 | 1.92 | 8.36 | 0.16 | 0.69 |
| 13 | 1.25 | 5.44 | 0.19 | 0.83 |
| 17 | 1.10 | 4.79 | 0.17 | 0.74 |
| 19 | 0.75 | 3.27 | 0.13 | 0.56 |
| 23 | 0.66 | 2.87 | 0.12 | 0.52 |
| 25 | 0.48 | 2.09 | 0.12 | 0.52 |
| 29 | 0.46 | 2.00 | 0.13 | 0.56 |
| 31 | 0.31 | 1.35 | 0.12 | 0.52 |
| 35 | 0.30 | 1.31 | 0.07 | 0.30 |
| 37 | 0.20 | 0.87 | 0.06 | 0.26 |
| 41 | 0.18 | 0.78 | 0.07 | 0.30 |
| 43 | 0.12 | 0.52 | 0.05 | 0.22 |
| 47 | 0.12 | 0.52 | 0.05 | 0.22 |
| 49 | 0.07 | 0.30 | 0.06 | 0.26 |
| THD (%) | 27.9 | 3.0 | ||
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Xu, Y.; Li, Y.; Yu, J.; Yu, J. A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter. Energies 2017, 10, 112. https://doi.org/10.3390/en10010112
Cao Y, Xu Y, Li Y, Yu J, Yu J. A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter. Energies. 2017; 10(1):112. https://doi.org/10.3390/en10010112
Chicago/Turabian StyleCao, Yijia, Yong Xu, Yong Li, Jiaqi Yu, and Jingrong Yu. 2017. "A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter" Energies 10, no. 1: 112. https://doi.org/10.3390/en10010112
APA StyleCao, Y., Xu, Y., Li, Y., Yu, J., & Yu, J. (2017). A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter. Energies, 10(1), 112. https://doi.org/10.3390/en10010112






