Pupil Size Affects Measures of Eye Position in Video Eye Tracking: Implications for Recording Vergence Accuracy

Abstract

Video eye trackers rely on the position of the pupil centre. However, the pupil centre can shift when the pupil size changes. This pupillary artefact is investigated for binocular vergence accuracy (i.e., fixation disparity) in near vision where the pupil is smaller in the binocular test phase than in the monocular calibration. A regression between recordings of pupil size and fixation disparity allows correcting the pupillary artefact. This corrected fixation disparity appeared to be favourable with respect to reliability and validity, i.e., the correlation of fixation disparity versus heterophoria. The findings provide a quantitative estimation of the pupillary artefact on measured eye position as function of viewing distance and luminance, both for measures of monocular and binocular eye position.

Introduction

Video eye trackers measure eye movements based on the position of the pupil: the pixel position of the centre of the pupil is converted to the angular rotation of the eye based on the calibration of the eye tracker (Yu, Lin, Tang, Xu, Schmidt, Wang, & Guo, 2015).

However, even if the eye does not rotate, the pupil center may shift horizontally and vertically as a function of pupil size for physiological reasons. The present paper focuses on the horizontal direction. If the pupil contracts (or dilates), the pupil centre shifts nasally (or temporally) in most observers (Walsh, 1988; Wilson, Campbell, & Simonet, 1992; Wyatt, 1995; Yang, Thompson, & Burns, 2002; Camellin, Gambino, & Casaro, 2005; Park, Kim, & Joo, 2009; Tabernero, Atchison, & Markwell, 2009; Wyatt, 2010; Ivanov & Blanche, 2011; Wyatt, 2012; Wildenmann & Schaeffel, 2013; Drewes, Zhu, Hu, & Hu, 2014; Fischinger, Seiler, Schmidinger, & Seiler, 2015; Choe, Blake, & Lee, 2016). The mean of this reported effect is a horizontal pupil centre shift of about 0.05 mm per 1 mm change in pupil size; but individuals differ. If – as in the present study - the location of the pupil centre is directly used to detect eye position, a 0.05 mm pupil shift would appear as a pseudo eye rotation of about 14 min arc = 0.24 deg, as calculated from arc tan (0.05mm/12mm) assuming a 12 mm eye radius; if the pupil centre relative to the first Purkinije image is used, the Hirschberg ratio applies (Wyatt, 2010; Wildenmann & Schaeffel, 2013; Jagini, Vaidyanath, Bharadwaj, 2014). In any case, individual differences require individual calibrations for accurate measurements.

Whether the pupil artefact is relevant depends on the conditions and required accuracy of the experiment. In some conditions, small random variation of pupil size and corresponding random artefacts may average to zero over time or repeated measurements. However, the pupil artefact will induce systematic errors, if the recording includes conditions of different pupil sizes or if the pupil size differs critically between calibration and test phase.

The display luminance is most critical since it directly affects the pupil size. Ivanov & Blanche (2011), Wyatt (2012), and Drewes, Zhu, Hu, & Hu (2014) proposed using calibrations/recordings at different luminance levels – thus, at different pupil sizes - in order to quantify and remove the variance in the measured eye position introduced by the pupil light effect.

The observer’s arousal or the task-related cognitive demand may also affect the pupil; Choe, Blake, & Lee (2016) studied such endogenous factors and proposed a correction based on a regression between recorded gaze position and pupil size as observed during the recording period.

These previous studies of the pupil artefact refer to the position of a single eye, as it is appropriate in research, which is interested in the version position of the eyes (left and right eye separately, or averaged). However, research of the coordination of the two eyes (Howard, 2012) requires measuring the vergence angle between the two eyes (difference in eye position between the two eyes). Here, the pupil artefact induces specific conditions, particularly when the viewing distance is shortened. It is the new approach of the present study to quantify the amount of the pupil artefact on the vergence accuracy (fixation disparity) and to propose a procedure for correction.

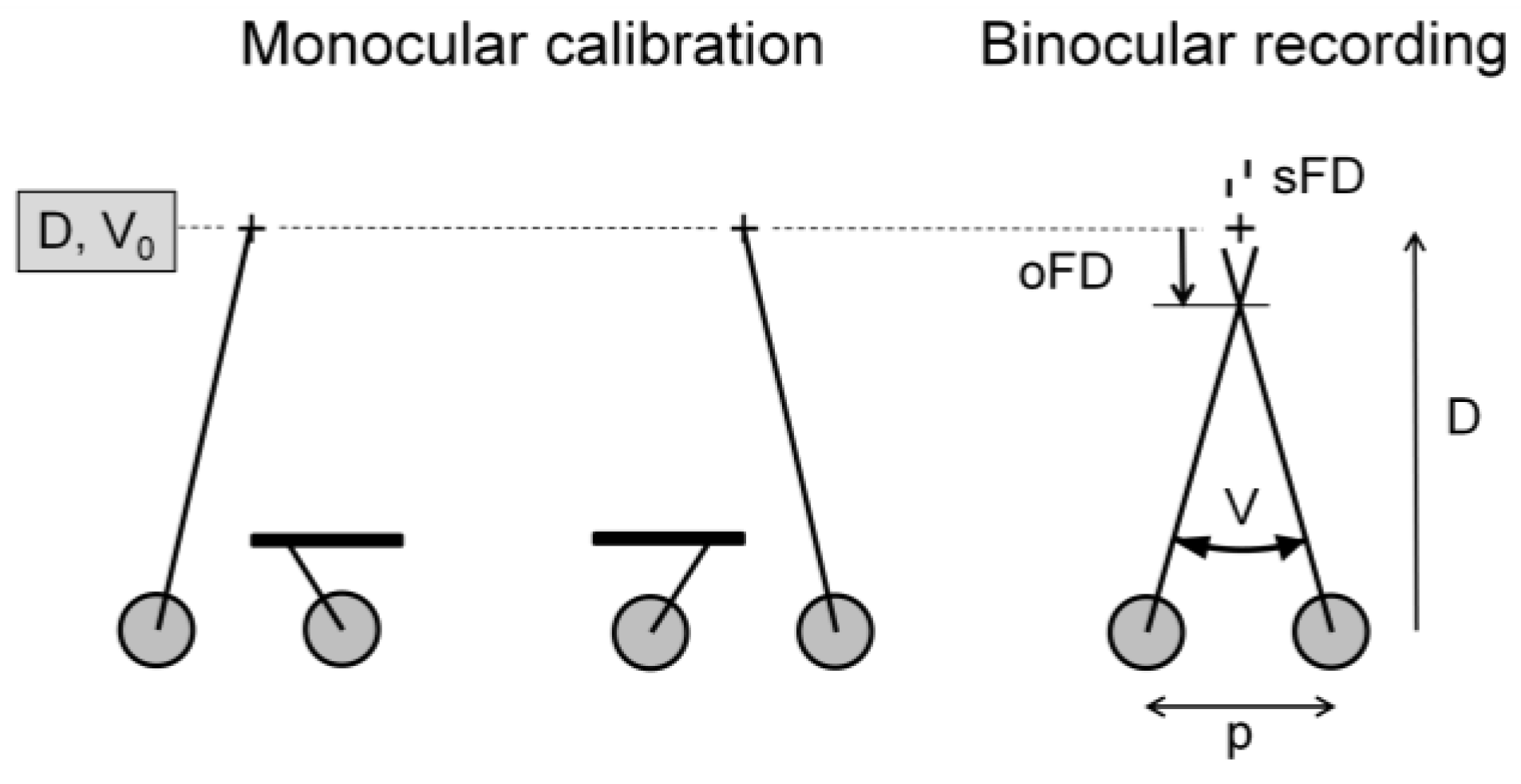
Binocular eye movement research often uses monocular calibrations, i.e. each eye is calibrated while the fellow eye is not provided with a stimulus (Liversedge, White, Findlay, & Rayner, 2006; Švede, Treija, Jaschinski, & Krūmiņa, 2015). In near vision, the pupil is smaller in the binocular test phase than in the monocular calibration due to the concurrent near response of pupil, convergence and accommodation of the eyes (ten Doesschate & Alpern, 1967). The resulting artefact will increase as the viewing distance shortens.

The present study investigates the effect of the pupil artefact on measures of binocular coordination, i. e. on the vergence angle between the two visual axes. Here, the effective artefact is the sum of the artefacts in the two eyes since the pupil center shifts nasally in both eyes. The amount of the artefact may differ between the eyes (Choe, Blake, & Lee, 2016), but assuming an average effect in each eye, the pupil artefact on the vergence angle is twice as large since the recorded center of the pupil shifts nasally in both eyes. With a 1 mm change in pupil size, this could lead to a change in measured vergence of 28 min arc, or about 0.5 deg (see calculation above), on the average. A particular vergence measure is the fixation disparity (Figure 1). The monocular calibration determines the reference eye position, corresponding to the centres of the foveolae in the two eyes. This corresponds to the geometrically expected vergence angle V0 = 2 arctan (p/2D), with the viewing distance D and the interpupil distance p. The objective fixation disparity oFD is the deviation of the current vergence V from the geometrically expected vergence angle V0. In the optimal case, the visual axes of the two eyes intersect at the fixation point and fixation disparity is zero. When the visual axes cross behind or in front of the target, these suboptimal states are referred to as exo or eso fixation disparity, denoted with negative and positive signs, respectively.

Research on fixation disparity in reading and non-reading tasks (e. g., Kirkby, Webster, Blythe, & Liversedge, 2008; Jainta, Hoormann, Kloke, & Jaschinski, 2010; Jainta, Jaschinski, & Wilkins, 2010; Nuthmann, Beveridge, & Shillcock, 2014) has shown that fixation disparity is typically below 1 deg. This small amount is at the limit of the accuracy of video-based eye trackers so that any effort for high accuracy recording is required (Jaschinski, Jainta, & Kloke, 2010) and the pupil artefact should be considered as a source of error. Only more recently, this artefact has been considered for the interpretation of fixation disparity (Schroth, Joos, Jaschinski, 2015).

This study aims to quantify the effect of the pupil artefact on measures of fixation disparity in near vision, i.e. at viewing distances of 40, 30, and 24 cm. In these conditions, one can expect that the difference in pupil size between calibration and test phase increases as the viewing distance shortens. The amount of the pupil artefact is quantified by the regression of measured fixation disparity as a function spontaneous pupil fluctuation during the test phase. This regression allows correcting the pupil artefact on fixation disparity. The benefit of this correction is described in terms of the reliability and validity of fixation disparity measures.

Although this study investigates binocular coordination, some basic findings can be applied to eye movement research that investigates monocular eye position.

Methods

Participants. The 20 young adult subjects aged 19 – 31 years (25 ± 3.5, mean ± SD) and had normal vision without eye glasses. The far visual acuity - in decimal units - was 1.0 or better: 1.5 ± 0.2 and 1.6 ± 0.3, in the left and right eye, respectively. The accommodative near point was 15 cm or better: 12.9 ± 1.8 cm and 12.7 ± 1.6, in the left and right eye, respectively. Thus, the subjects had clear vision at the near displays. This research was approved by the ethic committee of the Leibniz Research Centre of Working Environment and Human Factors (IfADo); the procedures were in accordance with ethic practice and participants signed a written consent.

Study design. Two experimental sessions were made on different days. Each session comprised twelve runs in random order: four repeated runs at each of the three viewing distances of 40, 30, and 24 cm. These viewing distances were chosen in order to have equidistant vergence angles. These were 9, 12, and 15 deg, corresponding to 2.5, 3.3, and 4.2 meter angle; the latter unit of vergence is convenient since it represents the inverse of the viewing distance in meters (Figure 3). It is known that fixation disparity is linearly related to the vergence angle (Jaschinski, 2001); equidistant x-values are advantageous for regression analyses.

This experiment was part of a research that investigated whether vergence accuracy may be improved if observers hold their hands at the visual display; similar effects of hand-proximity are known for cognitive functions, depending on test conditions (e. g., LeBigot & Jaschinski, 2011; LeBigot & Grosjean, 2012; LeBigot & Grosjean, 2015; Vatterott & Vecera, 2013). Therefore, in half of the runs in the present experiment, participants operated response buttons at the display and in the other half they operated a computer mouse hold on their lap. This manipulation, however, did not have an effect on fixation disparity (t = 0.2, p = 0.42, df = 19). Therefore, this factor is ignored in the present methodological study.

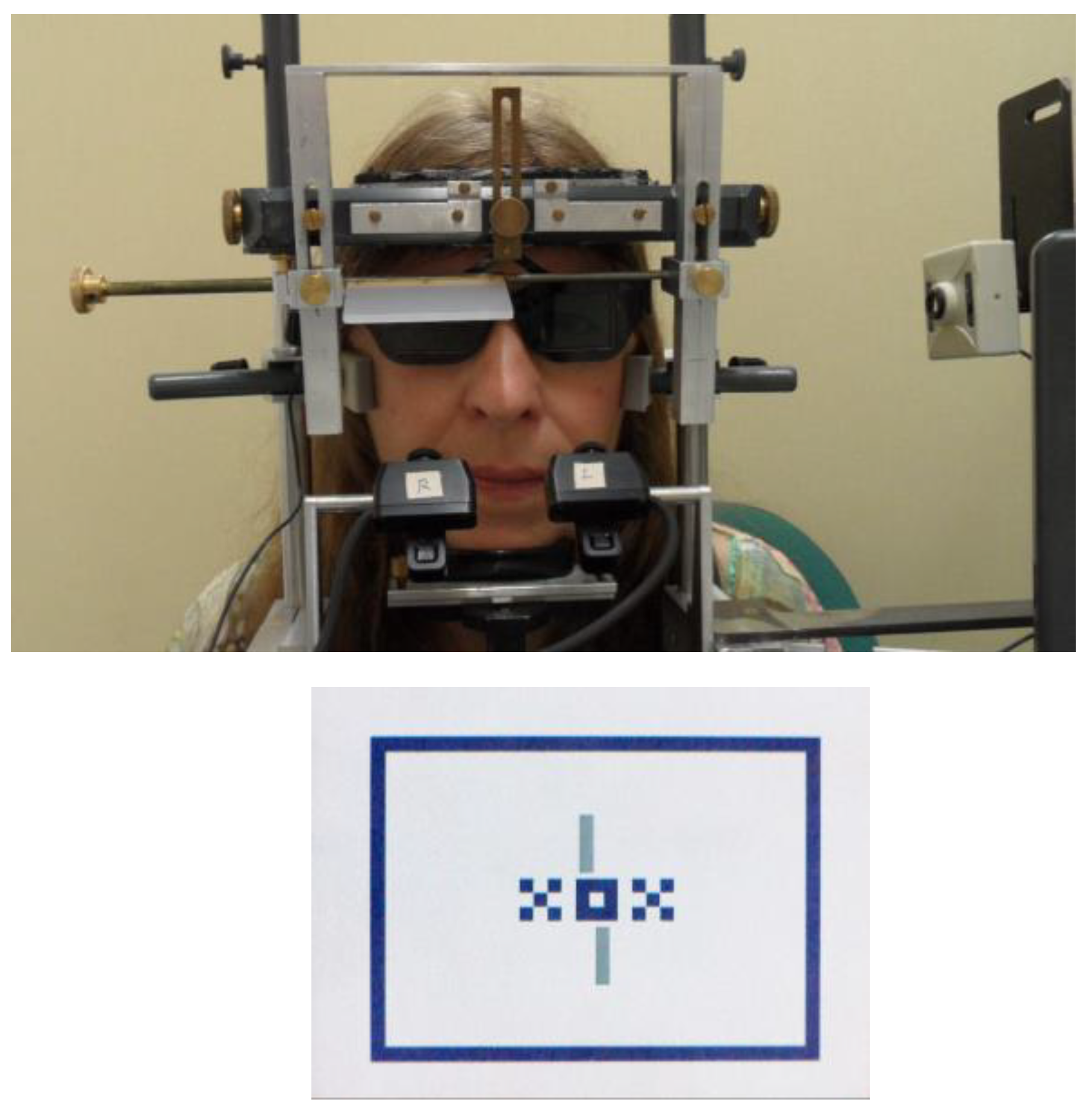
Recording of the dependent measures. Each run consisted of a 1-minute recording period during which the subject fixated a target (Figure 2) that comprised a central and peripheral binocular fusion target (XOX, surrounded by a frame) and two nonius lines. The nonius lines were presented dichoptically, i.e. the upper line to the right eye and the lower to the left eye. The subject shifted the nonius lines horizontally relative to each other until they appeared in alignment. The resulting nonius offset was recorded as a single measure of the subjective fixation disparity and - synchronously - the corresponding pupil size and binocular eye position was recorded. It is assumed that the moments of recording refer to stationary fixation. During one run of 1 minute, the observers typically made a series of 10 to 20 nonius adjustments. This is also the number of single recordings of objective fixation disparity and pupil size; these were averaged to give the mean of a run. The subjective fixation disparity is not part of the present paper, however, the data of pupil size and binocular eye position are analysed in the present paper with respect to the pupil artefact on measured eye position. Therefore, in the present paper, the term “fixation disparity” refers to the binocular eye position measured objectively with the eye tracker.

Display. The stimuli were presented on an OLED-Display (CMEL, diagonal size 2.4 inch, resolution 240 x 320 pixel, RGB, pixel pitch 0.051 x 0.153 mm). The OLED display and shutter glasses were controlled by a purpose-made graphic board to present different stimuli to the two eyes which is necessary for dichoptic nonius lines. The frame rate of the display and shutter glasses was 70 Hz for each eye, which prevented visible flicker at the given screen size and luminance. The OLED display was fixed on a mechanical slide that allowed for precise adjustment of the viewing distance from the centre of the eye. The size of the stimulus was adjusted to have the same angular dimensions at the viewing distances of 24, 30, and 40 cm: a single nonius line subtended 43 min arc. The background luminance was 6 cd/m², measured through the shutter glasses. The OLED-Display was surrounded by a white board (20 cm square) of similar luminance, provided by light panels. The ambient room illumination was constantly dim at about 10 lx in the laboratory without windows.

Eye movement recordings. The video-based EyeLink II (SR Research Ltd, Osgoode ON, Canada) was used with the dark pupil detection mechanism that tracks the centre of the pupil. Recorded data were analyzed based on the raw data, sampled at a rate of 2 ms (500 Hz). The filters of the EyeLink software were switched off.

The conventional EyeLink II procedures were modified in order to improve performance for measuring fixation disparity (Jaschinski, Jainta, & Kloke, 2010). As shown in Figure 2, we used a chin and forehead rest, a band around the head and narrow temporal rests to minimize artefacts due to possible lateral and oblique head movements; a bite bar was not used. The headrest could be adjusted very flexible in order to place the eye at a defined position for all subjects. This correct eye position was controlled by a video camera beside the head. Such precise adjustments are important at the short viewing distances in this experiment. The two EyeLink II cameras were fixed to the headrest. Shutter glasses were installed in front of the eyes for dichoptic presentation of the nonius lines.

Instead of the original EyeLink II calibration mode, we used the raw data and applied the following monocular calibrations before and after the 1-minute recording period that were averaged. The use of shutter glasses is not sufficient for complete monocular vision during the calibration since the mechanical frame of the OLED display may be effective as peripheral fusion target. Therefore, the right eye was covered with an opal occluder for calibrating the left eye and, subsequently, the left eye was covered for calibrating the right eye. The opal occluder was chosen to make all stimuli invisible, but to lower the luminance by only 30 % so that the pupil size is only little reduced by the occlusion. For calibration, subjects were requested to carefully fixate one of three calibration targets (crosses of 10 min arc) that appeared sequentially in the screen centre (zero position) and deviating horizontal positions at 120 min arc. Each of the three calibration targets were presented three times in random order to be able to average across variability in fixation.

Less optimal calibrations introduce an uncertainty into the eye position signal that can be quantified by a standard deviation SD_cal (Fogt & Jones, 1998). We had shown (Hoormann, Jainta, & Jaschinski, 2008) that recording procedures similar to the present ones lead to SD_cal values below 20 min arc in most calibrations. The present analysis does not select recordings based on the quality of calibration; rather, all repeated runs were averaged to reduce random error due to various reasons.

Accuracy of the eye movement recordings. Measurements of fixation disparity below about 1 deg are a challenge for video eye trackers. The physical noise limited resolution of the EyeLink II system is below 1 minutes of arc (as specified by the manufacturer), while the empirical resolution in real eye movement recordings is larger due to physiological variability, head instability, or calibration errors. In a previous study (Jainta, Hoormann, & Jaschinski, 2009) we had evaluated the empirical resolution of our recording procedures: changes in eye position of about 4 – 6 min arc could be resolved, as average of 29 to 41 single eye position recordings. In the present study, one session included 4 runs each with about 10 to 20 single recordings (for each viewing distance); thus, a raw fixation disparity value of each session is the average of 40 to 80 single recordings (depending on how fast the subject made the nonius adjustment for subjective fixation disparity). Further, a Bland-Altman analysis showed that the standard deviation of the difference between fixation disparity of the two sessions was 19.7 and 18.9 min arc at the 40 cm viewing distance for the raw and corrected fixation disparity, respectively (these values increased - for physiological reasons - as the viewing distance was shortened). The test-retest correlations between the two sessions for the raw fixation disparity were 0.77, 0.78, and 0.45 at the three viewing distances of 40, 30, and 24 cm, respectively. For the corrected fixation disparity, these test-test correlations were 0.78, and 0.71, and 0.51, respectively. These values nearly reached the order of magnitude of the test-retest correlations of subjective fixation disparity (0.81, 0.77, 0.87). Note that the subjective fixation disparity is not measured with the eye tracker, rather with dichoptic nonius lines which have a high precision (McKee & Levi, 1987). Thus, the present eye tracker procedures are adequate for this research which aims to identify – despite intra-individual variability - the mean fixation disparity of an observer as an individual characteristic and to investigate its physiological properties.

Monocular fixation is applied during calibration; thus, it is assumed that the target is projected onto the centre of the foveola, i.e. the visual line is directed towards the calibration point. This visual line position is associated with the pixel value of the pupil centre as detected by the EyeLink system. Thus, the calibrated eye positions refer to the visual lines. This description is a simplification since the foveola is not a point, but a non-zero area; moreover, for fusion, fixation disparity does not need to be zero, but must be smaller than Panum’s area. Additionnally, fixational eye movements are always involved. Mircrosaccades are typically up to 30 min arc, but have generally the same direction in both eyes, i.e. the vergence angle tends to be maintained (Otero-Millan, Macknik, & Martinez-Conde, 2015); further, most mircosaccades tend to reduce the fixation disparity by a few minutes of arc (Engbert & Kliegl, 2004). Despite these physiological conditions, test-retest correlations between sessions confirm that a reliable idiosyncratic fixation disparity of an observer can be found based as the average of repeated measurements across random measurement noise and physiological variability.

Measurement of pupil size. The pupil diameter was recorded in subpixels within the image of the eyes as provided by the EyeLink II system, which does not specify the horizontal or vertical meridian. A conversion to real pupil size depends on the position of the camera relative to the eye which sometimes needed to be adjusted between different observers. For calibration of these pupil measures, an artificial pupil of 5 mm (a hole in a thin piece of white metal) was installed at eye position and the corresponding measurement of the EyeLink II system gave a conversion factor to calculate the absolute pupil diameter in mm. This was made for each subject and in each session, so that the pupil size calibration was valid for the session, during which the position of eyes and cameras was controlled to be constant.

For a high accuracy in measuring pupil size, it was important to place the real pupil and the artificial pupil at the correct position in a reproducible way; therefore, a small video camera (not the EyeLink cameras) recorded the eye from side view and the image was displayed continuously on a control monitor; the adjustable headrest allowed to shift the head back and forth relative to the display so that the apex of the cornea was at the correct position as indicated by a marker on the control monitor. This condition was maintained during the eye movement recording. This procedure was confirmed by the high reliability of the pupil size data between the two sessions.

Statistical analyses. Pearson regressions and correlations were used to quantify the pupil artefact and relations between measures. The open-source software R (The R Foundation) was applied for linear mixed effects model to analyse pupil size and fixation disparity as a function of viewing distance (lmer) and for robust regressions (lmrob) to reduce the influence of outliers (Figure 6). One-tailed p-values were used since all hypotheses were one-directional.

Results

The results are presented in several steps.

• Pupil size is analysed as a function of viewing distance, both in binocular vision (during the test phase) and in monocular vision (during the calibration).
• The regression of the measured fixation disparity as a function of spontaneous variations of pupil size is analysed. This regression allows estimating a fixation disparity measure that corrects for the pupil artefact.
• The advantage of the corrected fixation disparity is analysed based on the intra-individual standard deviation, the reliability between sessions, and the physiologically expected correlation between fixation disparity and the heterophoria, i. e. the fusion-free vergence state.

Parameters affecting pupil size

Figure 3 (red insets) shows that – as expected - the pupil is smaller in binocular vision than in monocular vision and that this difference becomes larger as the viewing distance shortens. The viewing distance is plotted in the unit (1/m) since this unit revealed linear functions and corresponds to the vergence angle in the unit “meter angle”. A linear mixed-effects model (lmer) showed three results: (1) when the viewing distance was shortened, the pupil shrank by 0.32 mm/(1/m) or 0.09 mm per degree of vergence stimulus angle (b ± SE = - 0.32 ± 0.05; t = 6.7; p < 0.001); (2) at the centred viewing distance of 30 cm, the pupil was 0.31 mm smaller in binocular than in monocular vision (- 0.31 ± 0.04; t = 8.3; p < 0.001); (3) this binocular-monocular difference increased significantly by a 0.13 mm/(1/m) as the viewing distance was shortened (- 0.13 ± 0.04; t = 2.9; p = 0.003). This also means that at a viewing distance of 3.33 – (0.31/0.13) = 0.95 (1/m) or about 100 cm no difference in pupil size between monocular and binocular vision will occur (red x-intercept in Figure 3).

Effect of pupil size on fixation disparity

Measured fixation disparity versus pupil size in a 1-minute run. The series of nonius adjustments during the recording period of 1 minute gave a time series of paired data of fixation disparity and pupil size, both recorded simultaneously by the EyeLink II system. These two measures may vary independently, or may be correlated due to the pupil artefact. These two measures are plotted relative to each other in Figure 4 with exemplary data of two subjects to calculate a regression that predicts the effect of pupil size on the measured fixation disparity. Each single raw pupil size during the test phase is subtracted by the mean of the pupil size during the corresponding calibration, i. e. ΔP = P_test – mean(P_cal). This is done since the eye tracker calibration coefficients are strictly valid only for the pupil size that is adopted during the calibration phase, i. e. if ΔP = 0. The calibration coefficients result from a complete calibration, i. e. from the series of all fixations during a calibration; this series corresponds to the mean of all pupil sizes, i.e. across all fixations in the pre- and post calibration. The resulting regression lines allows for two conclusions.

First, the slope describes the extent to which the single fixation disparity measures (open circles) depend on the simultaneously measured pupil size. In the examples in Figure 4, this slope ranged from 68 to 81 min arc/mm for subject 1 and from 25 to 36 min arc/mm for subject 2; subject 1 had the largest pupil artefact in the present sample and subject 2 was an average case.

Second, the intercept of the regression line (filled circles on the vertical axis) is a prediction of the fixation disparity when the pupil size is the same in the test and in the calibration (ΔP = 0). Thus, the intercept can be understood as the fixation disparity which is corrected for the pupil artefact. See for example the red data points and regression in Figure 4a: all single measures of fixation disparity (open red circles) give a mean of 111 min arc, which is referred to as raw fixation disparity of a single run (FD_raw). The regression line has an intercept of 46 min arc (closed red circle) which is an estimation of the fixation disparity corrected by the pupil artefact (FD_cor). The typically negative slope of the regression reflects that with decreasing pupil size the recorded eye position shifts more nasally, which corresponds to more eso (positive) measures of fixation disparity. Thus, the intercept - which estimates the corrected fixation disparity - is typically more exo (more negative or less positive) that the raw fixation disparity.

If the data of all 12 runs per session were averaged per subject, a comparison of the two sessions revealed a high test-retest correlation of the slope as shown in Figure 5. The slope had a distribution from about zero up to about – 80 min arc/mm; the significant test-retest correlation suggests that subjects differ considerably in the pupillar artefact on fixations disparity (r = 0.83; p < 0.001). The standard deviation of the difference between the two sessions was 14.3 min arc/mm.

Group averages. The mean (± SD) of the change in fixation disparity with change in pupil size was - 27.4 ± 19.3 min arc/mm (range 4.3 to -74.2) in Session 1 and -26.9 ± 25.5 min arc/mm (range (20.1 to -75.3) in Session 2. The mean values of the raw and the corrected fixation disparity are included in

Table 1. Raw versus corrected fixation disparity: statistical indicators based on the sample of 20 subjects. Significant effects (in bold) appeared at the short viewing distance of 24 cm. 

a: the corrected fixation disparity is more negative, i.e. more exo than the raw fixation disparity, as expected from the direction of the pupil artefact. The difference increases from - 3.6 to -11.7 as the viewing distance shortens from 40 cm to 24 cm. This is related to the fact that the difference in pupil size between the calibration (monocular vision) and the test phase (binocular vision) increases as the viewing distance shortens (Figure 3). A linear mixed-effects model (lmer) was calculated for fixation disparity as a function of the viewing distance, in the unit (1/m): (1) at the centred viewing distance of 30 cm, the fixation disparity was significantly more exo by 7.93 mm due to the correction (b ± SE = - 7.93 ± 2.01; t = 3.9; p < 0.001). Further, this effect of the correction tended to increase by 4.97 min arc/(1/m) as the viewing distance shortened (- 4.97 ± 2.97; t = - 1.68; p = 0.09). This also means that at a viewing distance of 3.33 – (7.93/4.97) = 1.73 (1/m) or about 58 cm no effect of the correction can be expected (see Figure 3).

Advantage of the corrected fixation disparity

The advantage of the corrected fixation disparity is tested with the following measures.

Intra-individual standard deviations. It is hypothesized that the variance of the pupil artefact is included in the raw measures, but not in the corrected fixation disparity. Accordingly, the 8 repeated measures of each subject should result in a smaller intra-individual standard deviation for the corrected fixation disparity: this difference of 1.4 ± 3.3 min arc was significant for the shortest viewing distance of 24 cm (p = 0.0372), but not for longer viewing distances (Table 1b).

Fixation disparity relative to heterophoria. One should expect that the corrected fixation disparity is a more valid measure, in the sense that it should be more favourable when testing physiologically expected hypotheses. In the present experiment, it is possible to test the well known correlation of fixation disparity with heterophoria (Jampolsky, Flom, & Freid, 1957; Jaschinski, 2001; Jaschinski, Jainta, & Kloke, 2010; Jainta & Jaschinski, 2010); heterophoria refers to the vergence error when one eye is covered and the viewing eye fixates and focuses a target, so that accommodation is involved; this condition applies to the calibration phase (see Figure 1). The most critical way to test an advantage of the correction of the pupil artefact is to test the fixation disparity-heterophoria correlation on the individual level, since subjects differ in both the amount of the artefact and in the correlation with heterophoria. For each observer and each viewing distance, 8 measures of heterophoria and fixation disparity were available from both sessions. We found that a fixation disparity-heterophoria correlation did not appear in all 20 observers. This is plausible since for a significant correlation the measures need to have some intra-individual variance: if the two measures are rather stable in the 8 repeated measures, no correlation can exist. Therefore, the following analyses refer only to those subsets of observers, who showed a significant correlation between heterophoria and the corrected fixation disparity (which is hypothesized to give the higher correlations). This was the case in 9 observers at the 24 cm viewing distance. For this subgroup, the heterophoria explained R² = 0.72 ± 0.16 of the variance in corrected fixation disparity, but only R² = 0.61 ± 0.26 of the variance in the raw fixation disparity (mean ± SD, n = 9). This difference of ΔR² = 0.10 ± 0.17 was significant (W = 7, p < 0.05, Wilcoxon test). At the larger viewing distances of 30 and 40 cm, however, the advantage of using the corrected fixation disparity declined to ΔR² = 0.04 and ΔR² = 0.05, respectively, and was insignificant. (see Table 1c).

Reliability of “fixation disparity curves”. Earlier studies (Jaschinski, 1997 & 2001; Jainta & Jaschinski, 2002) also described a further important aspect of fixation disparity, i. e. the change in fixation disparity as a function of the viewing distances, referred to as proximity effect in fixation disparity or fixation disparity curves. Regarding this proximity effect, the test-retest reliability between the sessions was insignificant for the raw fixation disparity (R² = 0.09, r = 0.29, n. s.), but significant for the corrected fixation disparity (R²= 0.25, r = 0.50, p = 0.012), as revealed by robust regressions that reduce the influence of outliers (Figure 6). The standard deviation of the difference between the two sessions was 15.0 min arc and 14.4 min arc for the raw and the corrected fixation disparity, respectively.

Discussion

The methodology of this experiment appears to be adequate for the purposes of this research because of the following findings. The change in viewing distance from 40 to 24 cm (or from 2.5 to 4.2 in the unit (1/m) or a vergence angle from 9 to 15 deg) revealed a shrinking of the pupil by 0.32 mm/(1/m) or 0.09 mm/deg as measured with the present procedure based on EyeLink II recordings. This result is practically identical with previous findings of 0.37 mm/(1/m) or 0.1 mm/deg in Jaschinski (1997) measured with a different technology. The validity of the fixation disparity measures is supported by the physiologically expected correlation with the heterophoria, i. e. the open-loop vergence state in monocular vision. All results were found similarly in two repeated sessions.

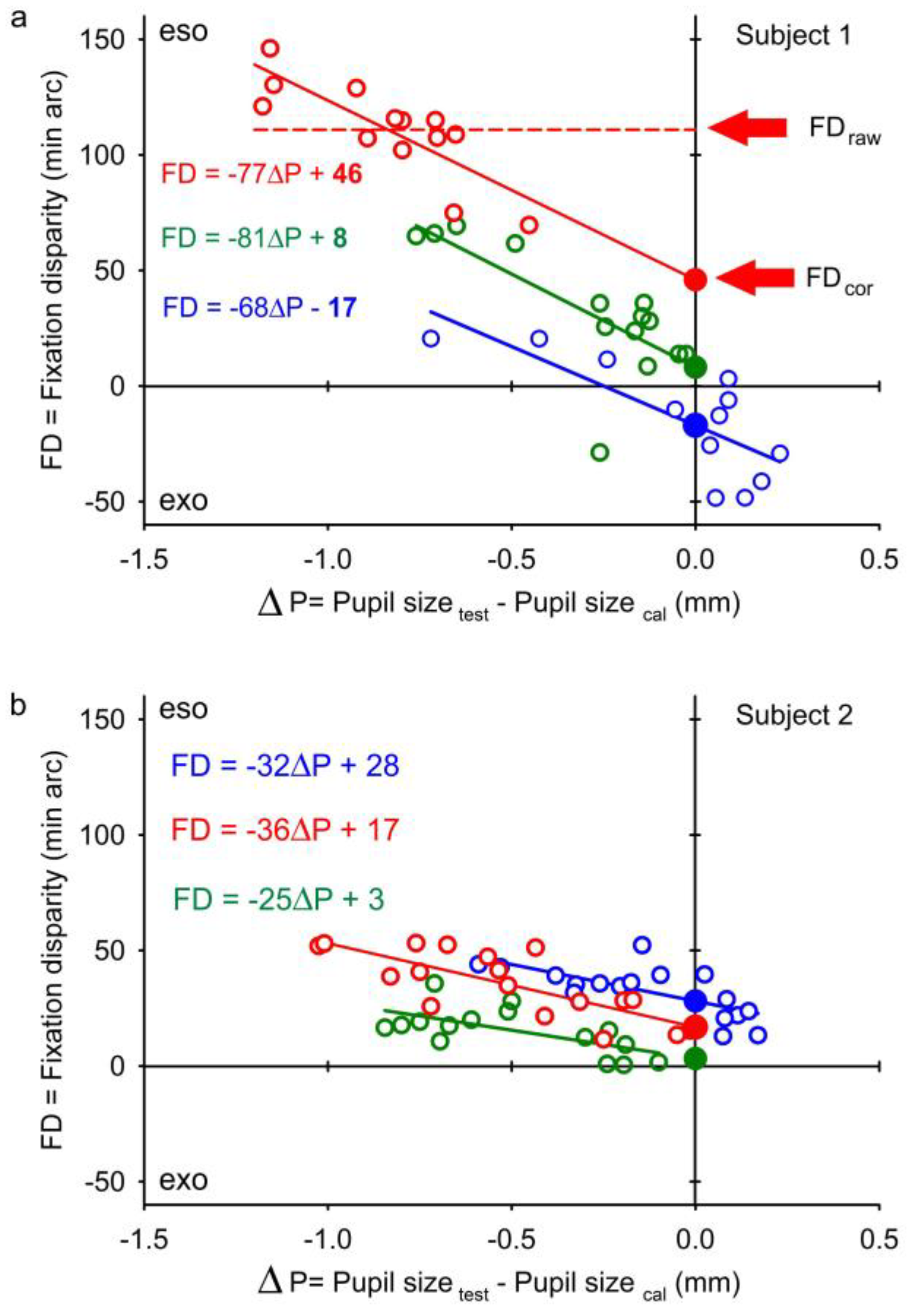
Concerning the pupil centre shift, it has been reported earlier that a reduction in pupil size typically shifts the centre of the pupil nasally (Walsh, 1988; Wilson, Campbell, & Simonet, 1992; Wyatt, 1995; Yang, Thompson, & Burns, 2002; Camellin, Gambino, & Casaro, 2005; Park, Kim, & Joo, 2009; Tabernero, Atchison, & Markwell, 2009; Wyatt, 2010; Ivanov & Blanche, 2011; Wyatt, 2012; Wildenmann & Schaeffel, 2013; Drewes, Zhu, Hu, & Hu, 2014; Fischinger, Seiler, Schmidinger, & Seiler, 2015; Choe, Blake, & Lee, 2016). These earlier reports provide the average estimation that a 1 mm change in pupil size induces a horizontal artefact of a 14 min arc change in measured position of a single eye or a 28 min arc change in binocular vergence (see Introduction). The latter prediction of previous research is quantitatively confirmed in the present study: the average amount of the pupil artefact on fixation disparity was 27 min arc/mm. This resulted from a regression between the measured fixation disparity and spontaneous fluctuations of the pupil size during the 1-minute recording period as shown in Figure 4; these plots as a function of scattering pupil sizes resemble those of Wildenmann & Schaeffel (2013) and Wyatt (2010). In the horizontal direction and for a single eye, the mean pupil artefact of fixation disparity of 27 min arc/mm in the present study corresponds to a shift of the pupil by 0.05 mm per mm change in pupil size; this results from 12 * tan (27/2 min arc), for a 12 mm eye radius. This present finding resembles the mean pupil shift (mm) per mm change in pupil size of 0.03 reported by Wildenmann & Schaeffel (2013) and 0.04 estimated from the graphs in Wyatt (2010).

Random variability of pupil size (and corresponding artefacts on eye position) may not be a serious problem since these may be averaged to zero over a series of trials. But when the pupil size differs systematically between experimental conditions or between calibration and test phase (e.g. by different luminance levels), a systematic bias in eye position can occur. In research of binocular coordination, the binocular test phase typically has a smaller pupil than the monocular calibration phase. Thus, the pupil artefact leads to a systematic bias, i. e. more convergent (eso) measures of fixation disparity, at least in near vision. As proposed in this study, this bias can be corrected based on the regression between the measured fixation disparity and the difference in pupil size between measurement and recording: this regression is based on data of the recording period and allows finding the fixation disparity corresponding to identical pupil sizes in test and calibration phase. Procedures of correcting the pupil artefact on recordings of eye position were mentioned by Wildenmann and Schaeffel (2013) and performed in examples by Wyatt (2010); in the latter examples, the intra-individual standard deviation of eye position was reduced by the correction, as statistically confirmed in the present study. More recently, the proposed correction methods have been elaborated. Ivanov & Blanche (2011), Wyatt (2012), and Drewes, Zhu, Hu, & Hu (2014) suggested different calibrations at a set of luminance levels in order to quantify the artifact of pupil size. Choe, Blake, & Lee (2016) used the spontaneous variations in pupil size during the recording period while the pupil size varied due to endogenous factors as arousal or cognitive demand. These two types of corrections refer to each single eye and Choe, Blake, & Lee (2016) emphasize that the artifact can be substantially different in the two eyes of a single observer. In the present study, the binocular approach does not correct each eye separately, rather the correction is based on the difference between the two eye positions (i.e. left minus right eye position), in order to directly correct the vergence angle, i.e. the resulting fixation disparity, which is the measure of interest in binocular research. This has also the advantage that small residual horizontal head movements are eliminated from the data since these introduce the same horizontal error in the signal of the two eyes.

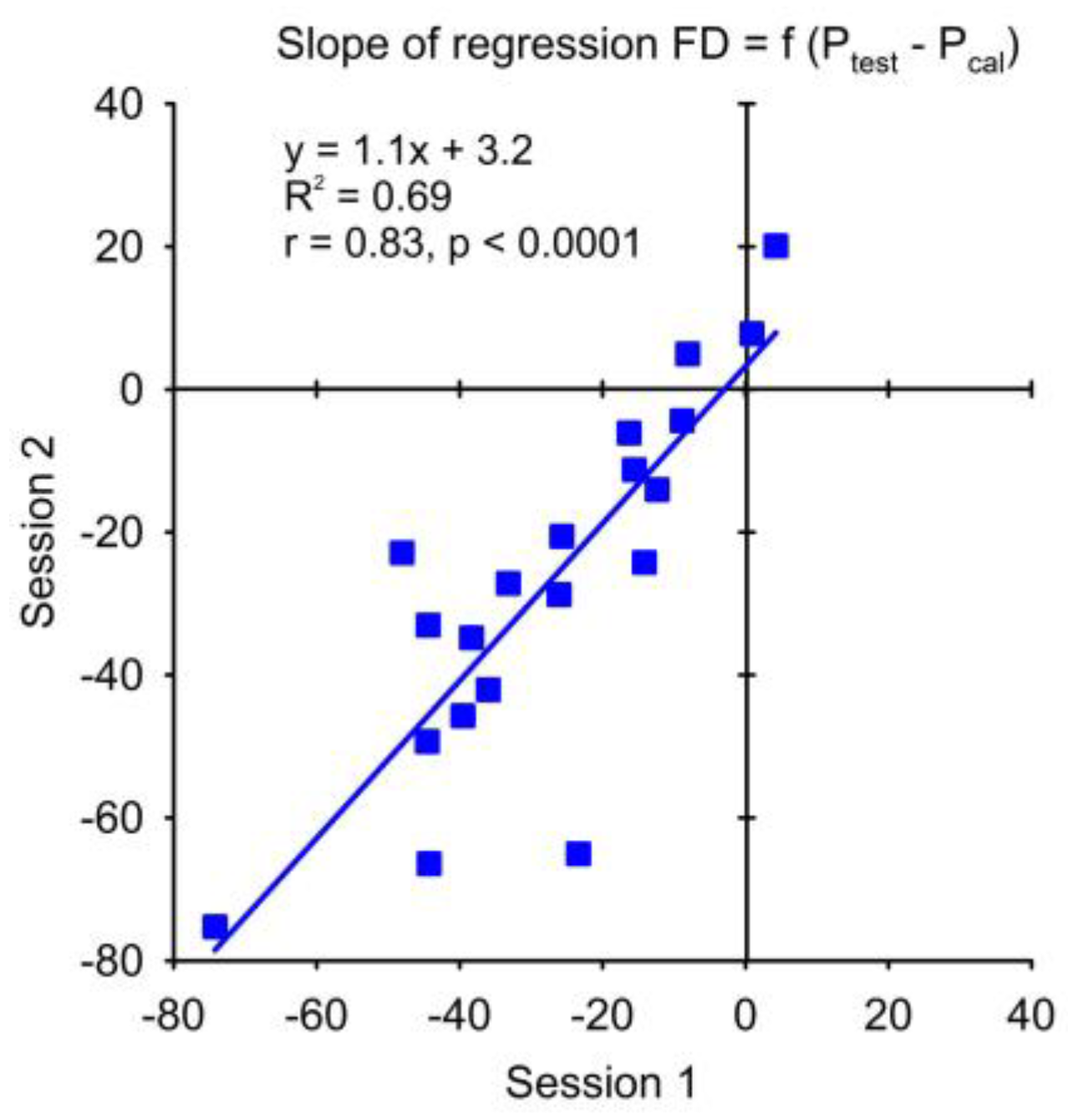
The pupil artefact on fixation disparity depended on the viewing distance: the shorter the viewing distance, the smaller is the pupil in the binocular test phase relative to the monocular calibration and the larger is the artefact in fixation disparity. This function was quantitatively described in the present study (Figure 3) and the linear extrapolation of this function suggests that the pupil artefact becomes negligible at viewing distances beyond about 50 cm, at least on the average. This is the range where most previous research on fixation disparity has been made; thus, retrospectively, it can quantitatively be confirmed that the pupil artefact due to monocular calibrations was negligible at these longer viewing distances. However, the more the viewing distance shortens the larger is the pupil artefact; this is a serious confounder when measuring fixation disparity as a function of viewing distance. This proximity effect in fixation disparity is a relevant characteristic for binocular near vision and its measurement requires the correction of the pupil artefact to eliminate a bias and additional variance due to the pupil size. In the present study, we can conclude that a significant test-retest correlation of the proximity effect in fixation disparity was found for the corrected fixation disparity, but not for the raw fixation disparity (Figure 6). This supports the advantage of using the corrected fixation disparity. The physiological implications of the changes in fixation disparity with viewing distance will be reported elsewhere.

The pupil size in binocular vs. monocular vision does not only depend on the viewing distance, but - more generally - on the vergence stimulus, i. e. the absolute disparity of the two retinal images. This can technically be realized by a horizontal offset of the images on the display (Fogt & Jones, 1998) or by prisms in front of the eyes (Jaschinski, 1997). Also in these conditions, the objective fixation disparity measured with video eye trackers is potentially subject to the pupil artefact, which will increase with the amount of absolute disparity or prism load. These are important test conditions in binocular research.

To test the validity of the corrected fixation disparity versus the raw fixation disparity, one wish to have a direct comparison with a different, high quality eye tracker as the Dual Purkinje or the search coil method, but this is not available in our laboratory. An indirect method to prove the validity is to test a physiologically expected hypothesis with both measures. It is well known that heterophoria is correlated with fixation disparity, both when measured objectively with a video-based eye tracker (Jaschinski, Jainta, & Kloke, 2010; Jainta & Jaschinski, 2010) and subjectively with nonius lines (Jampolsky, Flom, & Freid, 1957; Jaschinski, 2001). In the present study, the heterophoria showed a higher correlation with the corrected fixation disparity than with the raw fixation disparity; and this difference was significant at the short viewing distance of 24 cm where the pupil artefact is largest. Thus, the corrected fixation disparity is favourable for testing physiological hypotheses, at least if the artefact is large.

In the present study, the pupil size differed between monocular and binocular vision in the calibration and test phase, respectively. For other research, it may be interesting to estimate pupil effects due to changes in luminance. For this purpose, one needs to know the amount of change in pupil size with luminance in the visual field. The review of Watson (2012) describes the sigmoid change in pupil size as a function of luminance: in the steepest part of this function, 1 log unit change in luminance produces a 1.25 mm change in pupil size, which is about three times larger than the change in pupil size of 0.42 in the present study due to the change between monocular and binocular vision at the 24 cm viewing distance. Accordingly, the reported effect of 12 min arc at 24 cm can be expected when the luminance changes by 0.42/1.25 = 0.34 log unit (which is a factor of 2.2). This would lead to an average artefact of 12 min arc in fixation disparity.

If a researcher is less interested in binocular vergence, but in the movement of a single eye, half the amount of the pupil artefact in fixation disparity would apply to the monocular eye position. Accordingly, a pupil artefact due to a change in luminance by a factor of 2.2 (0.34 log unit) has an effect on the average monocular eye position of 6 min arc; a factor of ten (1.0 log unit) corresponds to an effect which is 1/0.34 = 2.9 times larger meaning 2.9 * 6 = 18 min arc. These amounts can reach the width of a reading text character which typically subtends 10 – 20 min arc. Wyatt (2010) reported that a 0.8 deg “pseudo” monocular eye movement can appear when the luminance is changed between 0.001 and 54 cd/m². Figure 3 can be used as a quantitative guide for other experimental conditions: for a certain change in pupil size the corresponding change in measured fixation disparity can be seen, or – if half of these values are taken – the corresponding change in measured monocular eye position. Note that the large standard deviations indicate the large inter-individual differences in these effects, e. g. maximal individual effects can be three times the group average. Further, the two eyes may differ considerably in the pupil artefact (Choe, Blake, & Lee, 2016).

In conclusion, the present study provides data in order to estimate the amount of the artefact in measured eye position due the pupil centre shift as a function of pupil size in video-based eye-tracking. In the present conditions, the pupil artefact became relevant when the pupil size changed by about 0.4 mm or more. This can occur with monocular calibrations at a short viewing distance of 24 cm (as tested in the present study of fixation disparity) or with changes in luminance by at least a factor of two, as extrapolated from the present data. In case of doubt, the pupil size should be measured as control variable to be able to correct the data for the pupil artefact.

To summarize, concerning the pupil artefact on fixation disparity in video eye trackers, the binocular vs monocular difference in pupil size is negligible at normal viewing distances larger than about 50 cm, but becomes increasingly relevant as the viewing distance shortens, or – more generally – the absolute disparity of the stimulus increases as it is used in optometric research.