Estimation of a Focused Object Using a Corneal Surface Image for Eye-Based Interaction
Abstract
:Introduction
Related work
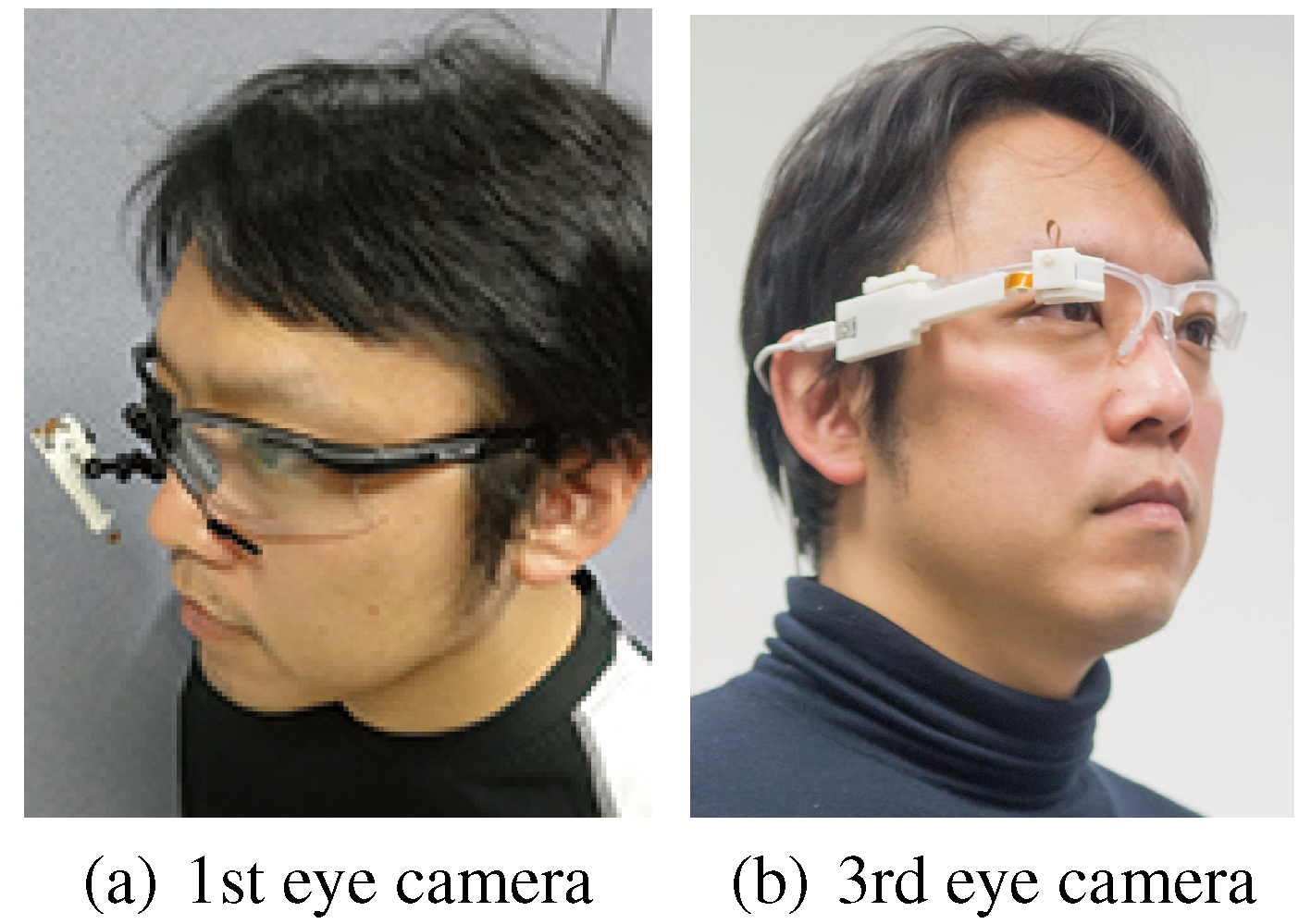
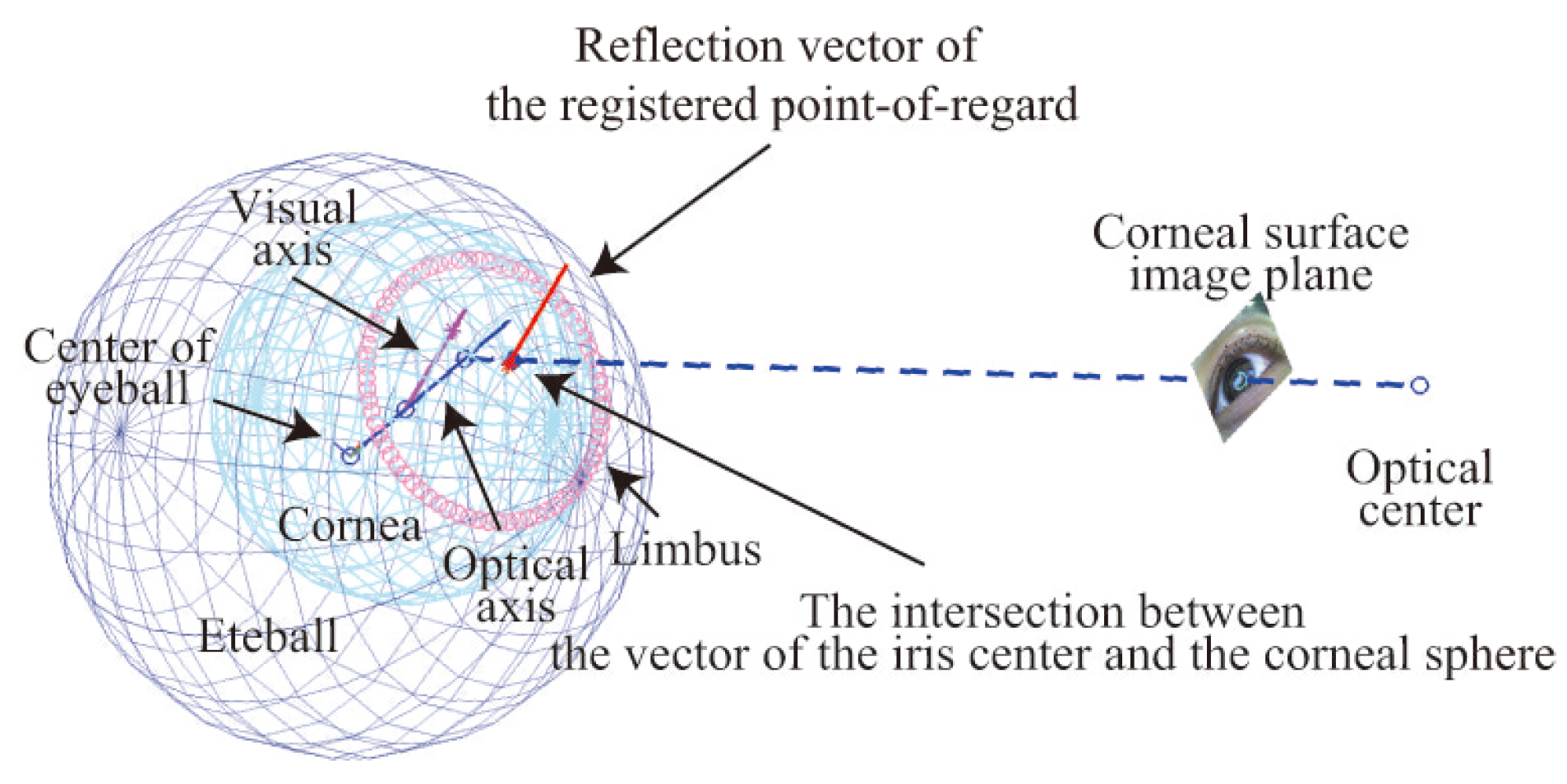
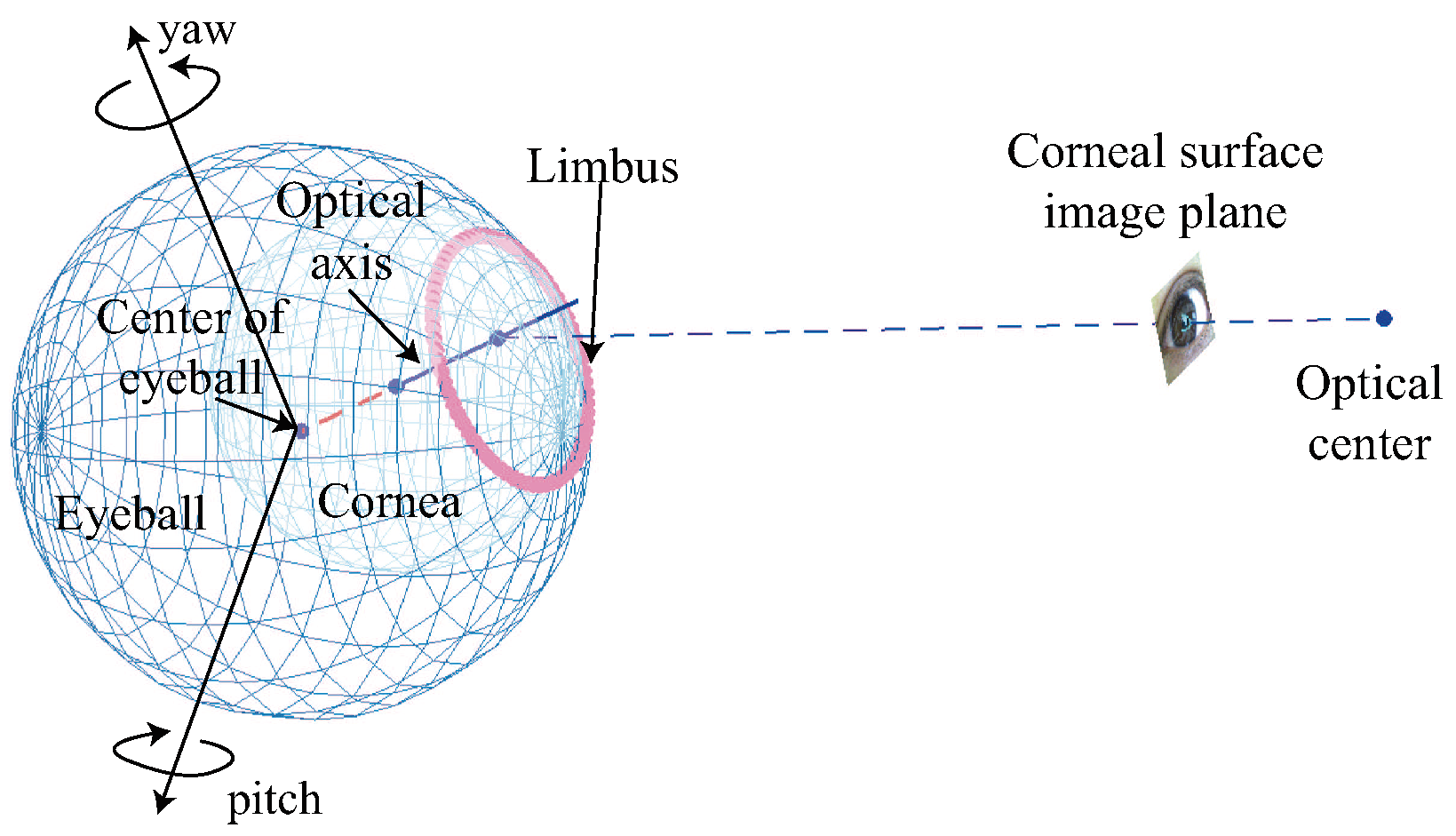
Wearable device for capturing corneal surface images
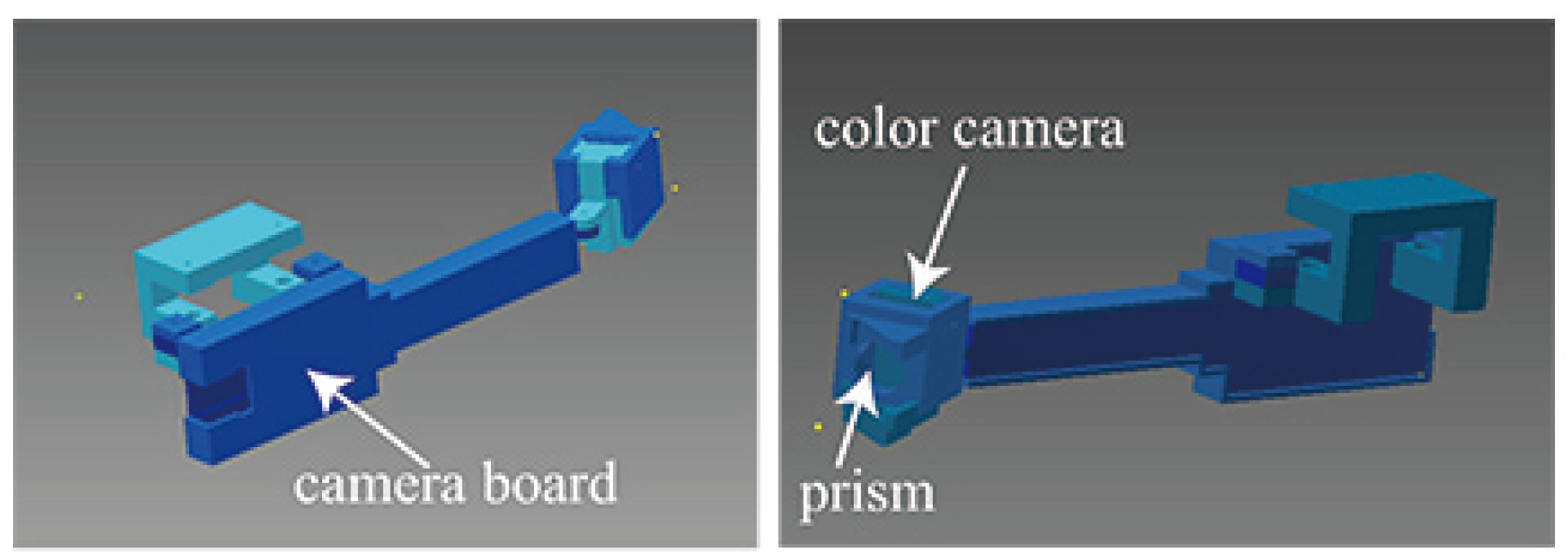
Extracting scene images from corneal surface images
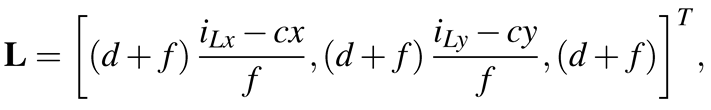 (1)
(1)
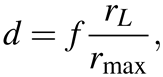 (2)
(2)
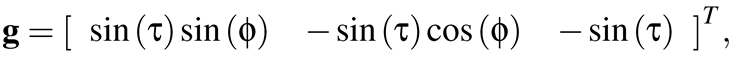 (3)
(3)
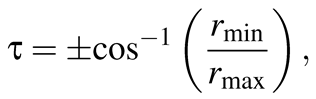 (4)
(4)
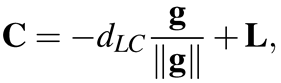 (5)
(5)
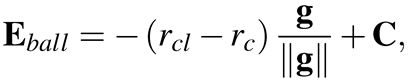 (6)
(6)
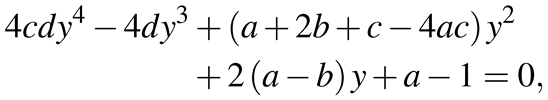 (7)
(7)
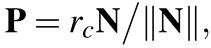 (8)
(8)
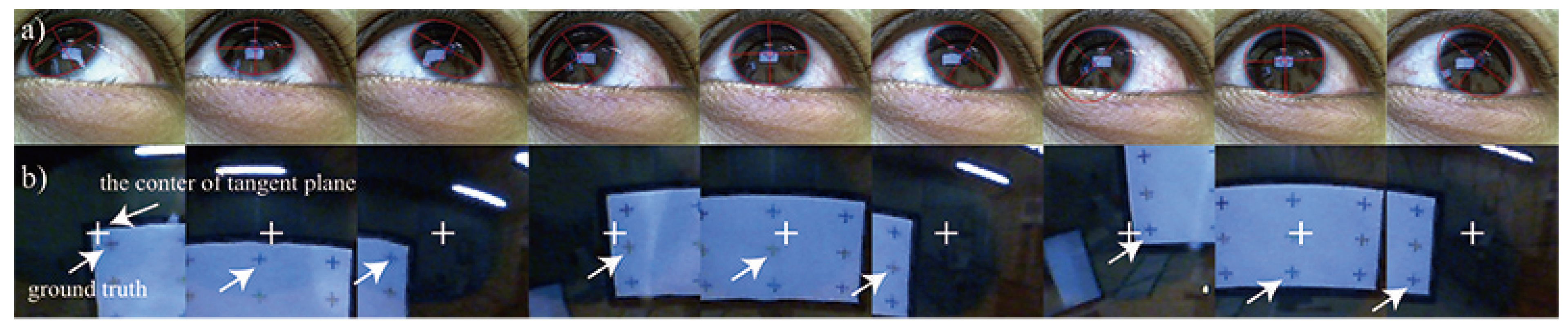
Model-based tracking to generate unwarped images
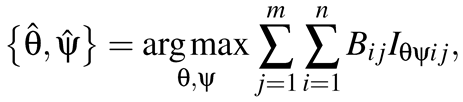 (9)
(9)
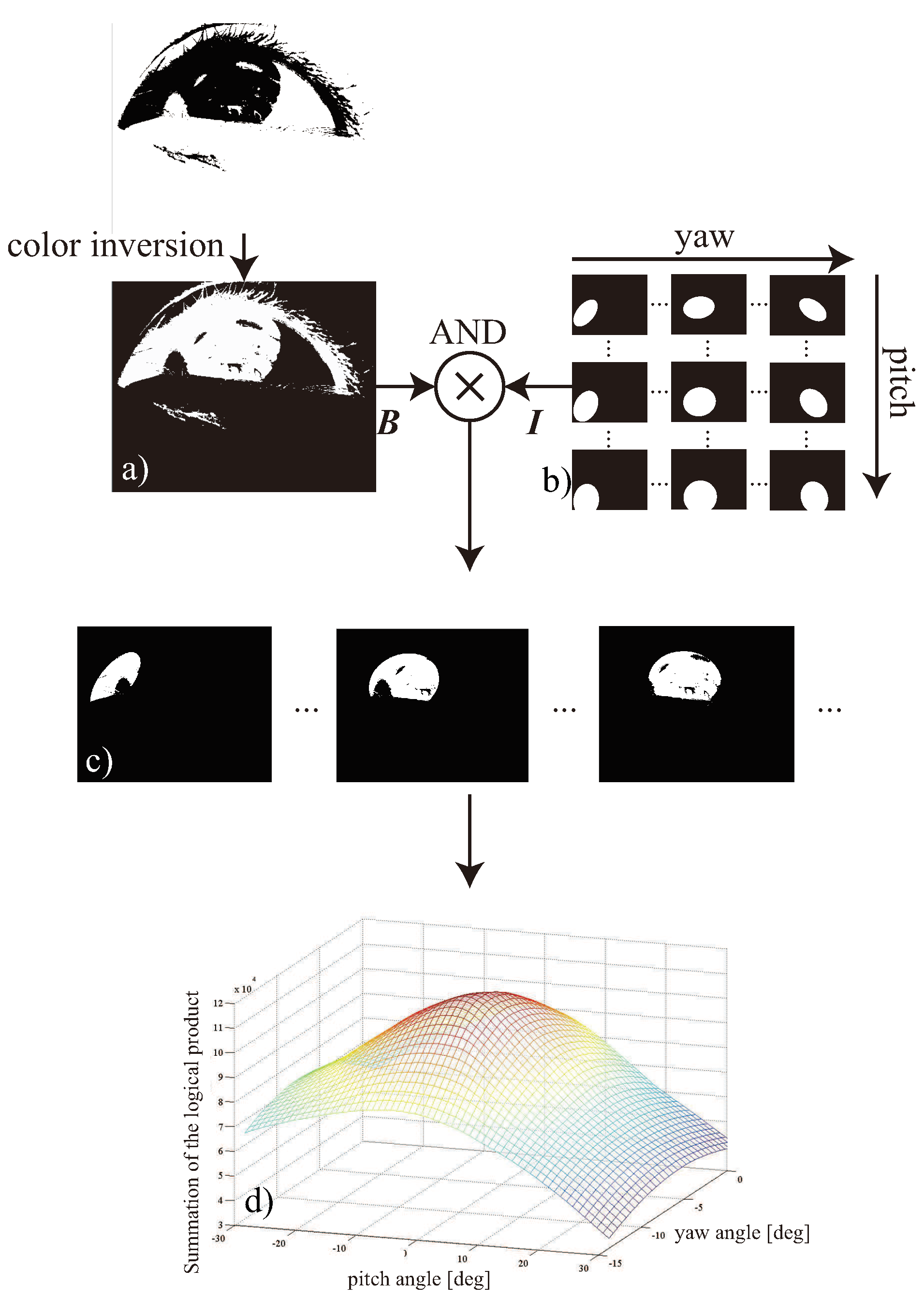
Specific object recognition using the unwarped corneal surface image
 (10)
(10)
Extracting the focused object
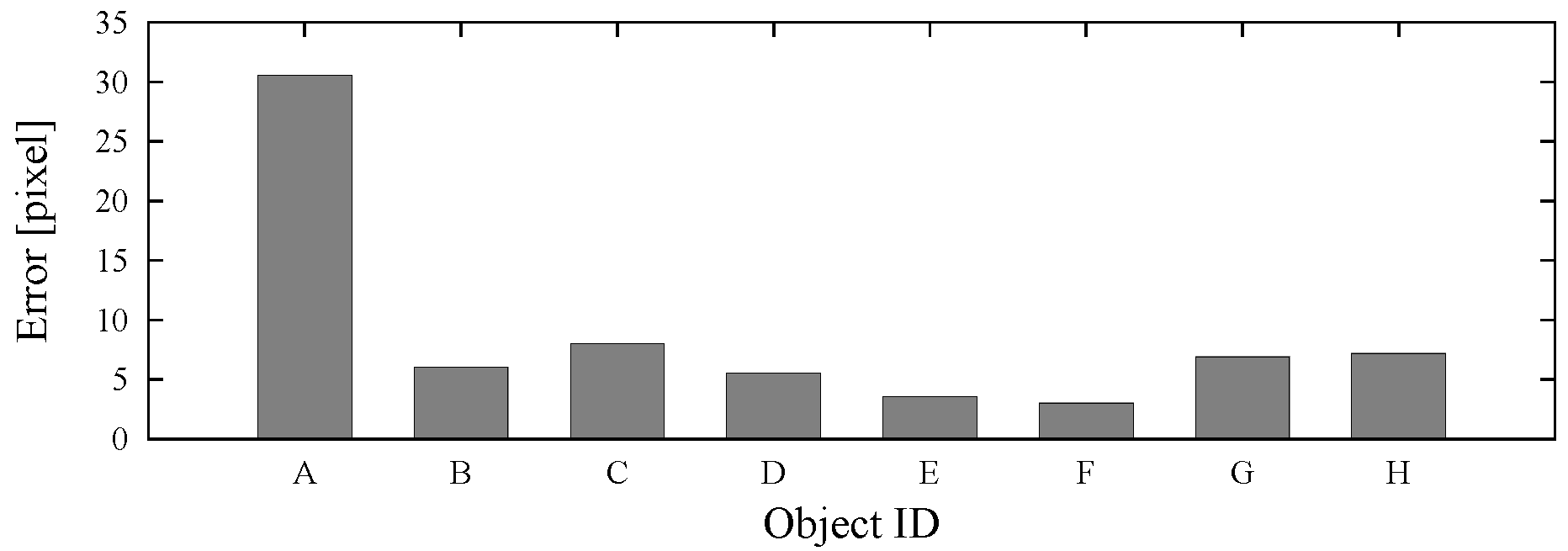
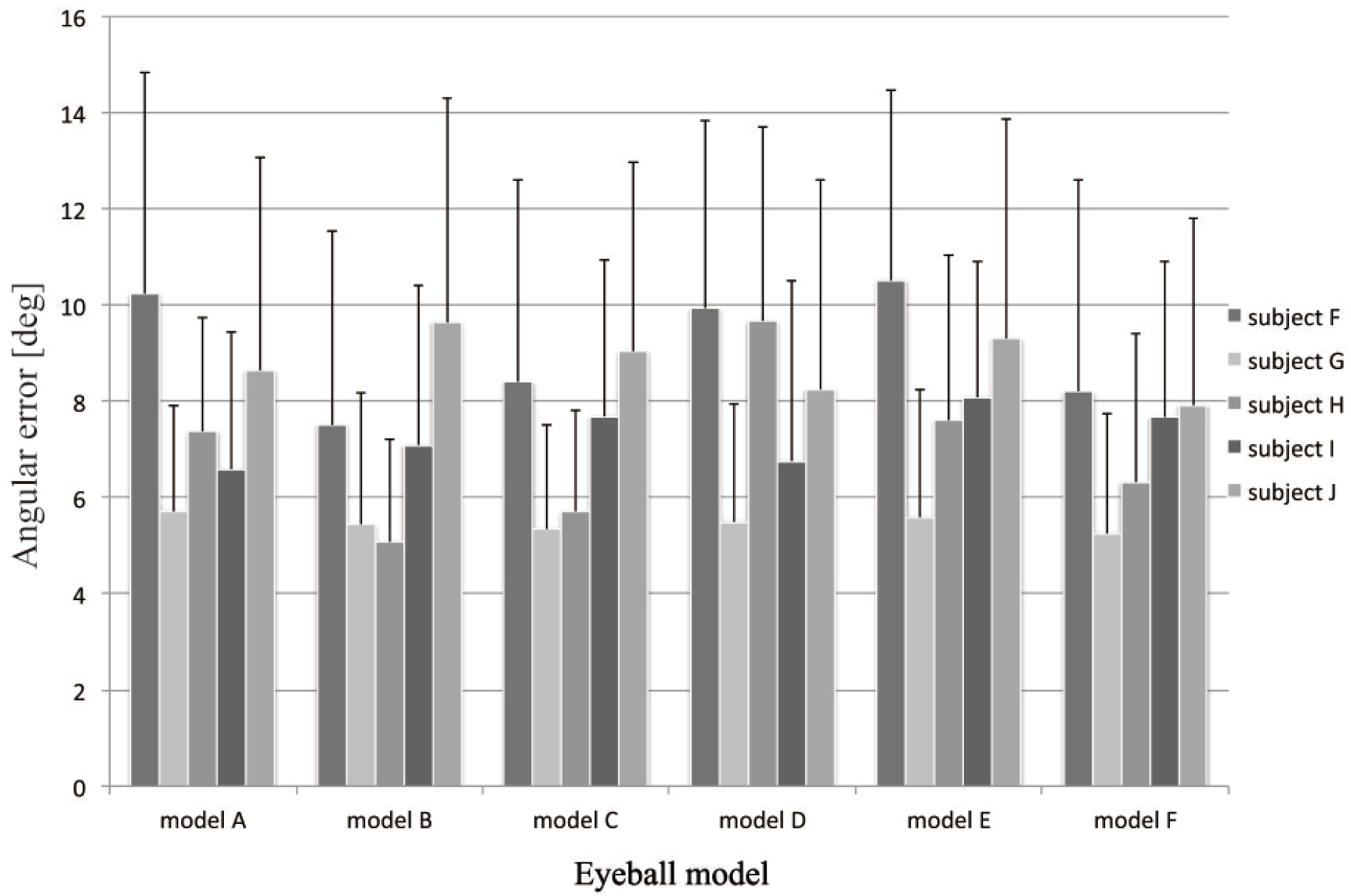
Experimental conditions
Results and discussion
Conclusions
Acknowledgments
References
- Buchsbaum, G. 1980. A spatial processor model for object colour perception. Journal of the Franklin Institute 310, 1: 1–26. [Google Scholar] [CrossRef]
- Bulling, A., D. Roggen, and G. Tröster. 2009. Wearable EOG goggles: Seamless sensing and context-awareness in everyday environments. Journal of Ambient Intelligence and Smart Environments 1, 2: 8386. [Google Scholar]
- Calonder, M., V. Lepetit, C. Strecha, and P. Fua. 2010. Brief: Binary robust independent elementary features. In Proceedings of the 11th european conference on computer vision. pp. 778–792. [Google Scholar]
- Eberly, D. 2008. Computing a point of reflection on a sphere. http://www.geometrictools.com. (Online; accessed 7-Feb-2014).
- Fischler, M. A., and R. C. Bolles. 1981. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM 24, 6: 381–395. [Google Scholar]
- Guestrin, E. D., and E. Eizenman. 2006. General theory of remote gaze estimation using the pupil center and corneal reflections. IEEE Transactions on Biomedical Engineering 53, 6: 1124–1133. [Google Scholar] [PubMed]
- Ishiguro, Y., A. Mujibiya, T. Miyaki, and J. Rekimoto. 2010. Aided eyes: eye activity sensing for daily life. In Proceedings of the 1st augmented human international conference. pp. 25:1–25:7. [Google Scholar]
- Lowe, D. G. 2004. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision 60, 2: 91–110. [Google Scholar]
- Morimoto, C. H., and M. R. M. Mimica. 2005. Eye gaze tracking techniques for interactive applications. Computer Vision Image Understanding 98, 1: 4–24. [Google Scholar] [CrossRef]
- Nagamatsu, T., J. Kamahara, T. Iko, and N. Tanaka. 2008. Onepoint calibration gaze tracking based on eyeball kinematics using stereo cameras. In Proceedings of the 2008 symposium on eye tracking research & applications. pp. 95–98. [Google Scholar]
- Nagamatsu, T., J. Kamahara, and N. Tanaka. 2009. Calibrationfree gaze tracking using a binocular 3d eye model. In Chi ’09 extended abstracts on human factors in computing systems. pp. 3613–3618. [Google Scholar]
- Nishino, K., and S. Nayar. 2004b. The world in an eye. In Proceedings of the 2004 ieee computer society conference on computer vision and pattern recognition. pp. I-444–I-451. [Google Scholar]
- Nishino, K., and S. K. Nayar. 2004a. Eyes for relighting. ACM Trans. Graph. 23, 3: 704–711. [Google Scholar] [CrossRef]
- Nitschke, C., and A. Nakazawa. 2012. Super-resolution from corneal images. In Proceedings of the 23rd british machine vision conference. pp. 22.1–22.12. [Google Scholar]
- Nitschke, C., A. Nakazawa, and H. Takemura. 2011. Displaycamera calibration using eye reflections and geometry constraints. Computer Vision and Image Understanding 115, 6: 835–853. [Google Scholar]
- Ohno, T. 2006. One-point calibration gaze tracking method. In Proceedings of the 2006 symposium on eye tracking research & applications. pp. 34–34. [Google Scholar]
- Ohno, T., and N. Mukawa. 2004. A free-head, simple calibration, gaze tracking system that enables gaze-based interaction. In Proceedings of the 2004 symposium on eye tracking research & applications. pp. 115–122. [Google Scholar]
- Tsukada, A., and T. Kanade. 2012. Automatic acquisition of a 3d eye model for a wearable first-person vision device. In Proceedings of the symposium on eye tracking research & applications. pp. 213–216. [Google Scholar]
- Wang, H., S. Lin, X. Liu, and S. B. Kang. 2005. Separating reflections in human iris images for illumination estimation. In Proceedings of the tenth ieee international conference on computer vision. pp. 1691–1698. [Google Scholar]











 |
Copyright © 2014. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Takemura, K.; Yamakawa, T.; Takamatsu, J.; Ogasawara, T. Estimation of a Focused Object Using a Corneal Surface Image for Eye-Based Interaction. J. Eye Mov. Res. 2014, 7, 1-9. https://doi.org/10.16910/jemr.7.3.4
Takemura K, Yamakawa T, Takamatsu J, Ogasawara T. Estimation of a Focused Object Using a Corneal Surface Image for Eye-Based Interaction. Journal of Eye Movement Research. 2014; 7(3):1-9. https://doi.org/10.16910/jemr.7.3.4
Chicago/Turabian StyleTakemura, Kentaro, Tomohisa Yamakawa, Jun Takamatsu, and Tsukasa Ogasawara. 2014. "Estimation of a Focused Object Using a Corneal Surface Image for Eye-Based Interaction" Journal of Eye Movement Research 7, no. 3: 1-9. https://doi.org/10.16910/jemr.7.3.4
APA StyleTakemura, K., Yamakawa, T., Takamatsu, J., & Ogasawara, T. (2014). Estimation of a Focused Object Using a Corneal Surface Image for Eye-Based Interaction. Journal of Eye Movement Research, 7(3), 1-9. https://doi.org/10.16910/jemr.7.3.4



