Abstract
Infantile nystagmus syndrome (INS) patients occasionally have impaired pursuit. Model and patient data identified relative timing between target motion initiation and INS-waveform saccades as the cause. We used a new stimulus, the “step-pause-ramp” (SPR), to induce saccades proximal to target-velocity onset and test their effect on normal pursuit. Our OMS model predicted that proximal saccades impaired normal ramp responses, as in INS. Eye movements of subjects were calibrated monocularly and recorded binocularly; data were analyzed using OMtools software. Proximal saccades caused lengthened target acquisition times and steady-state position errors, confirming the model’s predictions. Spontaneous pursuit oscillation supported the hypothesis that INS is caused by loss of smooth-pursuit damping. Snooth pursuit may be impaired by saccades overlapping target-motion onset.
Introduction
Ocular motor research and control-system analysis of the infantile nystagmus syndrome (INS) (CEMAS_Working_Group, 2001) and other ocular motor dysfunction has provided a fertile ground for both insights into, and hypothetical mechanisms for, normal ocular motor behavior (Dell’Osso, 1995). Put another way, “buried in the chaos of dysfunction are the keys to the mechanisms of function.” As a result of the first such study, it was hypothesized that the ocular motor system (OMS) could not function as a reflexive, “retinal error” driven system. Instead, it required the use of expected eye movement (efference copy or proprioception) to reconstruct a target-motion signal that would drive the ocular motor response (Dell’Osso, 1968). This more complex mechanism was required by both the absence of oscillopsia (the stable perception of the world) in subjects with nystagmus and their normal behavioral responses to ocular motor stimuli. Subsequent studies of INS and other disorders have resulted in numerous hypotheses relevant to ocular motor control and revealed both mechanisms and limitations not evident from studies of either normal human or animal subjects (Abel, Dell’Osso, & Daroff, 1978; Dell’Osso, 1994; Dell’Osso, Hertle, Williams, & Jacobs, 1999; Dell’Osso, Robinson, & Daroff, 1974; Dell’Osso, Wang, Leigh, & Jacobs, 2006; Dell’Osso & Williams, 1995; Dell’Osso, Williams, Jacobs, & Erchul, 1998; Jacobs, Dell’Osso, Wang, Acland, & Bennett, 2009).
When individuals with INS fixate a stationary target, their eyes oscillate away from and back to the target and foveation occurs during short foveation periods at one extreme of the oscillation, which may take the form of any of several pathognomonic waveforms (Dell’Osso & Daroff, 1975). They do not oscillate to both sides of the target, as was believed in the past and which would preclude the relatively good acuity possible despite the nystagmus. Individuals with INS usually pursue moving targets normally (i.e., with normal pursuit gain) (Dell’Osso, 1986; Dell’Osso, Van der Steen, Steinman, & Collewijn, 1992; Kurzan & Büttner, 1989). However, recent studies demonstrated that target acquisition times were sometimes lengthened and steady-state position errors could appear during pursuit of constant-velocity targets (i.e., ramp responses); this occurred both before and after surgical damping and improvement of the INS (Wang & Dell’Osso, 2009; Z. I. Wang & L. F. Dell’Osso, 2011a). Analysis of each subject’s individual responses revealed that these impaired pursuit responses occurred when one of the intrinsic saccades in the INS waveform occurred near target-motion onset. The main conclusion from these studies was that, despite normal saccadic and pursuit latencies, target acquisition times could be lengthened due to the failure to accurately estimate both target position and velocity in space. Given the wealth of insights into normal function provided by studies of dysfunction (i.e., experiments of nature), the failure of palliative INS therapy to also alleviate these pursuit deficits led us to question whether this was an intrinsic limitation of normal ocular motor control rather than a problem limited to those with INS.
To determine if pursuit in normals (specifically, the ramp response) was similarly impaired, we studied pursuit responses to target motion that occurred near a saccade. In 2009, to ensure that we could elicit such data from normals (who do not exhibit nystagmus under most conditions), we designed a novel stimulus that elicited a saccade whose timing could be varied in relation to the onset of target motion. Two questions are addressed by this study: 1) Does the execution of a saccade in time proximity to the onset of target motion negatively affect the smooth-pursuit response in a normal individual? and 2) Is the saccade generated by a stimulus requiring a voluntary saccade a good model for an intrinsically made saccade, e.g., those found in INS waveforms?
Methods
Recording
A high-speed digital video system was used for the eye-movement recording. The system (EyeLink II, SR Research, Mississauga, ON, Canada) has a linear range of ±30° horizontally and ±20° vertically. System sampling frequency was 500 Hz, and gaze position accuracy was <0.5° on average with a spatial resolution of 0.01°. The data from this system were digitized at 500 Hz with 16-bit resolution. Velocity data for analysis was obtained by differentiation (2-point central difference) of the sampled position data. The signal from each eye was calibrated with the other eye behind cover to obtain position information including tropias and phorias; the foveation periods were used for calibration and the monocular calibrations were applied to the binocular data. Eye positions and velocities (analog differentiation of the position channels) were also displayed on a strip chart recording system (Beckman Type R612 Dynograph). Monocular primary-position adjustments for all methods allowed accurate position information and documentation of small, variable tropias and phorias that may be exhibited by normal subjects. It also ensured that we were always analyzing the fixating eye, especially when the data showed that the subject switched fixation from one eye to the other. All recordings were performed without any refraction because smooth-pursuit gain of a bright laser spot is not affected by a subject’s refraction (also, no accommodation is induced).
Stimuli
In order to simulate the condition of a target motion that occurs in the vicinity of a saccade in normals (as found in INS waveforms), we developed a new stimulus—the step-pause-ramp (SPR), of which the classical step-ramp (SR, Rashbass) (Rashbass, 1961) stimulus is a special case (i.e., pause duration = 0). In normals, this new stimulus can elicit saccades made in close proximity to the onset of ramp motion. As described below, for our analysis of SPR responses, we maintained definitions consistent with those used for step, ramp, and SR responses and (to facilitate comparison), with our studies of the ramp responses of subjects with INS. Despite the simplicity of step, ramp, and step-ramp stimuli and their common classical responses, once the variable pause is introduced, relative timing and ocular motor decision-making may result in more complex responses. For that reason, each component of the SPR stimulus and their expected responses are described mathematically in the Appendix. For any individual response, step (T0) and ramp (R0) onsets or both (for step-ramp stimuli) may be set to 0 to simplify the relationships below, which are expressed in their most general sense owing to the presentation of different stimuli in a sequential manner during each trial.
Classical Step Stimulus. A stationary target steps to a new position by an amount A in a random direction at t = T0. A steady-state position error becomes manifest while the eyes are still. The usual step response is an initial saccade at a latency of SAClat = ts - T0 ≅ 200 – 250 msec that results in accurate eye position on the target, eliminating the initial steady-state position error (see Figure 1, top panel). In this and the following responses, if the initial saccade is slightly incorrect, a short-latency (~150 msec) corrective saccade will bring the eyes onto the target. Target acquisition time (Tat) is the difference between the time the eye is first on target and the time of the step, and remains on target for > 300 – 400 msec. Normally, Tat is approximately SAClat plus the duration of the saccade ≅ 285 msec.
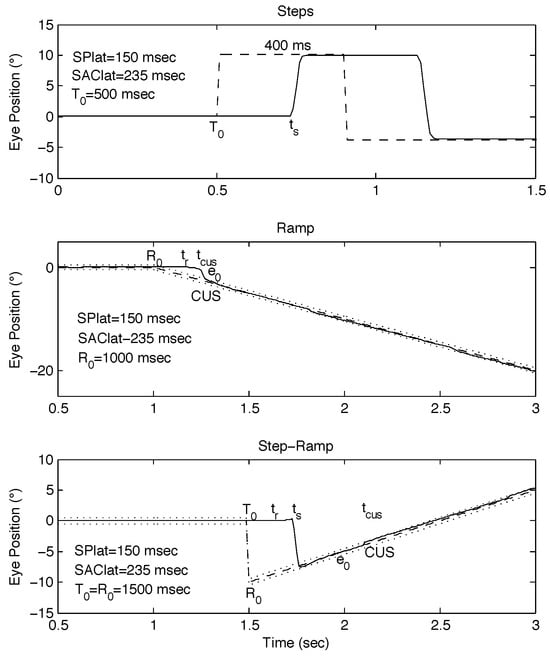
Figure 1.
Examples of classical stimuli and simulated responses using the behavioral OMS model. (top) Positive and negative steps separated by 400 msec. (middle) Negative ramp of -10°/sec. (bottom) Step-ramp (SR, Rashbass, [SR: 0°, -10°, 10°/sec @ 0 msec]). In the middle and bottom panels, dotted lines indicate the foveal extent. In this and the following Figures, T0 = target initiation time; R0 = ramp initiation time; ts = saccade response time, tr = ramp response time; tCUS = catch-up saccade time; e0 = initial eye-position error; SAClat = saccadic latency; SPlat = smooth pursuit latency; dashed lines = target trajectories; rightward motion is positive and leftward, negative.
Classical Ramp Stimulus. A stationary target ramps with a random velocity, Ṫ0 in a random direction at t = R0. A steady-state velocity error becomes manifest while the eyes are still, and a position error begins to build up. The usual ramp response is an initial eye velocity equal to target velocity at a latency of SPlat ≅ 125-175 msec (for simulations, the behavioral OMS model was set at 150 msec) that results in accurate tracking at the target velocity but with an initial steady-state position error. That is followed by a catch-up saccade (CUS) at the saccadic latency (SAClat ≅ 235 msec), which eliminates the position error and allows continued smooth pursuit of the target with no steady-state position error (see Figure 1, middle panel). In this and the following responses, Tat is the difference between the time the eye is first on target and moving with target velocity and the time of the ramp, and remains on target for > 300 – 400 msec. Normally, Tat is approximately SAClat plus the duration of the CUS ≅ 285 msec.
Classical Step-Ramp (Rashbass) Stimulus. A stationary target simultaneously steps to a new position by an amount A at t = T0 in a random direction and ramps with a random velocity, Ṫ0 either in the same or opposite direction as the position change. There is a special use of the SR stimulus whereby by adjusting the velocity of the ramp moving in the opposite direction of the initial step, the target and eye position would coincide at the time of execution of the saccadic step response, and no saccade would result. Since our study was aimed at studying the effects of an initial saccade, for this study, A = ±10° and Ṫ0 = ±10°/sec to preclude saccade-free responses. In this paper, we use a shorthand description of SR stimuli to indicate the initial position, final step position, and ramp velocity (e.g., [SR: 0°, 10°, -10°/sec]).
Both steady-state position and steady-state velocity errors become manifest while the eyes are still and the position error begins to change due to target motion. The usual SR response is an initial eye velocity equal to target velocity at a latency of ≅ 150 msec that results in accurate tracking at the target velocity but with an initial position error. That is followed by a saccade at a latency of SAClat ≅ 235 msec that eliminates the position error and allows continued smooth pursuit of the target with no steady-state position error (see Figure 1, bottom panel). If a CUS is not needed, Tat is approximately SAClat plus the duration of the saccade ≅ 285 msec.
Step-Pause-Ramp Stimulus. A stationary target steps to a new position by an amount A in a random direction at t = T0 and, after a pause (R0 - T0), ramps with a random velocity, Ṫ0, either in the same or opposite direction as the position change. The SPR stimulus is a general mixed stimulus that encompasses the previous three; as the pause is reduced towards 0, it becomes a Rashbass stimulus and as it is increased until the ramp occurs after the saccade, it becomes a classical step stimulus followed by a classical ramp stimulus. However, between these extremes, varying the pause duration in the SPR stimulus provides a new way to study saccade-pursuit interactions. When the pause is adjusted so that the ramp begins in the vicinity of the saccadic response, there is the possibility that the initial saccades made to a stationary target and occurring in close proximity to the onset of target motion (i.e., “proximal saccades”), will interfere with the subsequent ramp response and result in a prolonged Tat. Note that, if R0 < T0, the stimulus becomes the ‘ramp-pause-step’ stimulus, which, can be used to study pursuit-saccade interactions. As for SR stimuli, A = ±10°, Ṫ0 = ±10°/sec, and we use a similar shorthand description of SPR stimuli to indicate the initial position, final step position, ramp velocity, and pause duration (e.g., [SPR: 0°, 10°, -10°/sec @ 300 msec]). The pause intervals were chosen to encompass the subjects’ saccadic latencies so as to produce proximal saccades that might interfere with normal smooth pursuit as has been documented in INS ramp responses (Wang & Dell’Osso, 2009).
A steady-state position error (±A) becomes manifest while the eyes are still. Because of intrasubject variation in saccadic latency, a steady-state velocity error becomes manifest while either:
1) the eyes are still but a saccade is programmed and about to occur;
2) the eyes are in the midst of a saccade and moving at high velocity; or
3) the eyes are slowing just after a saccade.
Prior to our findings that intrinsic saccades in INS can interfere with normal ramp pursuit, the expected normal SPR response should be a saccade of ±A at the normal saccadic latency of ts ≅ 235 msec followed by an initial eye velocity at a latency of SPlat ≅ 150 msec that results in accurate tracking at the target velocity but with an initial position error. That is followed by a CUS at a latency of SAClat ≅ 235 msec that eliminates the position error and allows continued smooth pursuit of the target with no steady-state position error (see “a)” below). If a second CUS is not needed, Tat is approximately duration of the initial saccade plus the latency of the CUS plus the duration of the CUS ≅ 285 – 385 msec.
However, the OMS may not accurately evaluate either the size of the required saccade as target position or the speed of the required smooth pursuit. Therefore, several OMS responses are possible for any of the three stimulus conditions above, depending on the relative timings of the stimulus and the execution of the initial saccade. They may be categorized as follows:
a) there is an initial accurate pursuit at a latency ≥150 msec that results in accurate tracking at the target velocity but with an initial steady-state position error. That is followed by a CUS at a latency ≥ the saccadic latency, and continued smooth pursuit of the target with no steady-state position error (see OMS model simulation shown in Figure 2, top panel). This would be the expected normal response if the saccade did not affect the pursuit response;
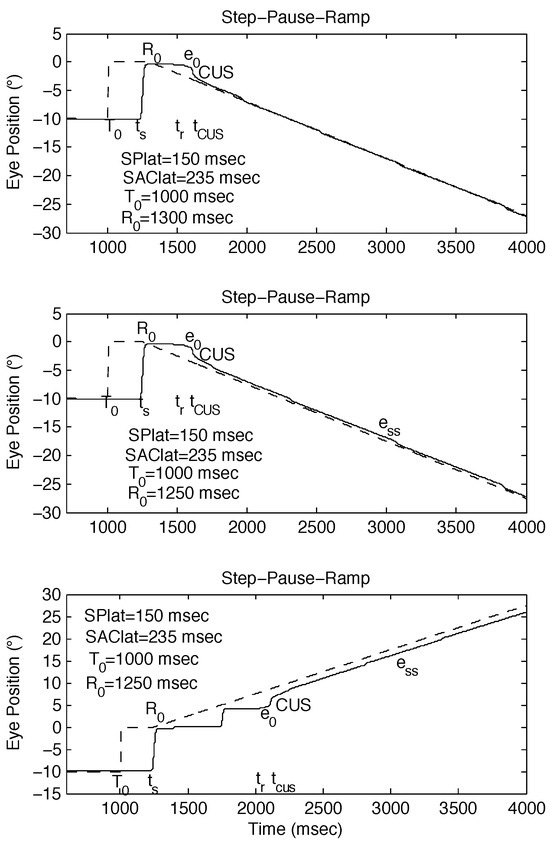
Figure 2.
Examples of SPR stimuli, with R0 set to be approximately equal to ts, and simulated responses using the behavioral OMS model. (top) Expected response to SPR stimulus [SPR: -10°, 0°, -10°/sec @ 300 msec] if no saccade-pursuit interaction (ess = 0). (middle) Possible response to SPR stimulus [SPR: -10°, 0°, -10°/sec @ 250 msec] if tCUS is approximately normal (small ess). (bottom) Possible response to SPR stimulus [SPR: -10°, 0°, 10°/sec @ 250 msec] if tCUS is >> normal (large ess). ess = steady-state eye-position error.
b) there is an initial accurate pursuit at a latency ≥150 msec that results in accurate tracking at the target velocity but with an initial steady-state position error. That is followed by a CUS at a latency ≥ the saccadic latency, and continued smooth pursuit of the target with a steady-state position error (see OMS model simulation shown in Figure 2, middle panel). Note that there is no short-latency corrective saccade to bring the eyes onto the target; or
c) there is no initial pursuit at a latency ≥150 msec that results in no tracking at the target velocity but with an increasing position error equal to the initial position error plus that due to target motion. That is followed by much-delayed CUS’s at a latency much greater than the saccadic latency, with little or no smooth pursuit of the target and some steady-state position error. Finally, accurate pursuit is initiated but a second steady-state position error remains (see OMS model simulation shown in Figure 2, bottom panel). Note that there is no short-latency corrective saccade to bring the eyes onto the target.
If the presence of an initial proximal saccade causes any of the above calculation errors, then Tat could be much longer than 385 msec. For both SR and SPR stimuli, the initial and final positions of the step stimuli were randomly distributed between 0° and ±10° and the ramp velocities were either ±10°/sec. This allowed determination of influences that these parameters might have on the responses.
Protocol
Written consent was obtained from subjects before the testing. All test procedures were carefully explained to the subject before the experiment began, and were reinforced with verbal commands during the trials. Subjects were seated in a chair with headrest, far enough from a projected red laser spot to prevent convergence effects (~5 feet). At this distance the target subtended less than 0.1° of visual angle. The room light could be adjusted from dim down to blackout to minimize extraneous visual stimuli. An experiment consisted of ten trials (3 for calibration and 7 for stimuli), each lasting approximately one minute with time allowed between trials for the subject to rest. A total of 60 SPR and 12 SR stimuli were presented in each experiment.
Subjects
All three subjects (ages 29, 25, and 48 years) were clinically normal with normal visual acuity, stereopsis, and ocular alignment. One, S3, exhibited occasional, small, square-wave jerks (SWJ) during fixation and smooth pursuit; SWJ have been reported in normals and we have documented their occurrence in normals we have recorded over the past 50 years. SWJ do not produce any clinical symptoms; they do not present any perceptual disturbance (e.g., oscillopsia), do not alter the otherwise normal ocular motor responses, and when small and infrequent (as these were), do not indicate cerebellar dysfunction. We included S3 in this study precisely because the sporadic occurrence of these saccades provided a normally occurring condition that closely mimicked the intrinsic saccades of INS.
Analysis and Simulations
Analysis was done with the OMtools software package (downloadable from omlab.org), a toolbox for MATLAB (The MathWorks, Natick, MA) plus a specially developed program, “latpoints” to calculate the initial and final eye velocities. For all stimuli, A = 10° and Ṫ0 = ±10°/sec. We manually identified the following points in the responses: T0, R0, ts, tr, CUS, tcus, and tT, all to an accuracy of 2 msec. We then calculated: SPlat, SAClat, e0, ess, and Tat from the above definitions and the initial and final error velocities. All simulations were done using Simulink. Our behavioral OMS model v1.4 (downloadable from omlab.org) simulates normal responses for pulse, step, ramp, pulse-step, and step-ramp stimuli—see Figure 1 for the three stimuli we used (Jacobs & Dell’Osso, 2004). It also correctly produces short-latency (i.e., less than the visual latency) corrective saccades when initial saccades are hypometric (usually for saccades >15° in normals), generates post-saccadic pursuit velocities greater than target velocity to acquire moving targets, and, as Figure 1, middle and bottom panels show, correctly accounts for target motion in the calculation of required saccades in ramp and SR responses. The above model contains a saccadic pulse generator, a smooth pursuit system that produces damped oscillatory pursuit responses, a fixation system, a final common neural integrator and an ocular motor plant; all are controlled by decisions made in an internal monitor that utilizes efference copy and retinal position and velocity inputs. The default settings for the model were: smooth pursuit gain = 0.95, saccadic latency = 235 msec, and smooth pursuit latency = 150 msec.
The measurement of target acquisition time for SR stimuli is anchored at T0 = R0 since both the step and ramp onsets coincide. The same measurement for the SPR stimuli is made from R0 since T0 precedes the onset of the ramp motion by a variable pause interval. Both measure the time it takes to acquire a moving target, measured from the onset of that motion, allowing comparison to ramp responses in INS (Wang & Dell’Osso, 2009; Z. I. Wang & L. F. Dell’Osso, 2011a). Individuals with INS exhibit nystagmus with one or multiple distinct waveforms. Each INS cycle contains a foveation period, during which eye and target position and velocity coincide within a narrow window. In our studies of target acquisition times in INS, we defined Tat as the time it took for the first foveation period to occur on target, at target velocity, and which was followed by subsequent foveation periods that fulfilled those criteria (Wang & Dell’Osso, 2007, 2009). Thus, for common INS frequencies of 2.5 to 3.5 Hz, where foveation periods are separated by 400 to 286 msec, the target must be accurately tracked for those minimal times; most commonly, they were tracked for several cycles, extending accurate tracking well beyond Tat. To maintain consistency in this study of normals without nystagmus, we used the same criteria for subsequent tracking (i.e., eye velocity at or near target velocity) following Tat. That eliminated instances where one or both eyes only transiently fell into the position and velocity criteria.
Results
Model Simulations
Using our behavioral OMS model in “normal” mode, we simulated responses to SPR stimuli with variable pause intervals. No changes were made in model parameters to produce these different responses; they resulted solely from the differences in stimulus timing. Figure 2 illustrates the responses for different initial saccade times with respect to the onset of the ramp. As Figure 2 (top panel) shows, there was normal smooth pursuit when target motion occurred after the initial saccade. Figure 2 (middle panel) shows that a saccade coincident with the onset of target motion might also result in normal smooth pursuit. However as Figure 2 (bottom panel) illustrates, a proximal saccade commonly could cause both longer target acquisition times and steady-state position errors.
Figure 3 illustrates simulations of additional types of possible responses to SPR stimuli. In Figure 3 (top panel) an accurate pursuit response to an SPR stimulus that produced no proximal saccade; it is similar to that in Figure 2 (top panel) despite the oppositely directed smooth pursuit. Figure 3 (middle panel) shows another accurate response to an SPR stimulus that produced no proximal saccade; it is similar to that in Figure 3 (top panel) despite different initial and final step positions. The target acquisition times for both these responses were slightly delayed due to the need for a second catch-up saccade in each. Figure 3 (bottom panel) shows an inaccurate response to an SPR that did produce a proximal saccade; it is not similar in type to the response shown in Figure 2 (bottom panel) despite the identical pause durations. In Figure 3 (bottom panel) there was a normal sequence of initial pursuit, catch-up saccade and final pursuit with a steady-state error. However, in Figure 2 (bottom panel) this sequence was disrupted and initial pursuit was greatly delayed while the saccadic system attempted to correct the ever-increasing position error. These simulations predicted that, under the same conditions, normal human subjects would also exhibit impaired pursuit.
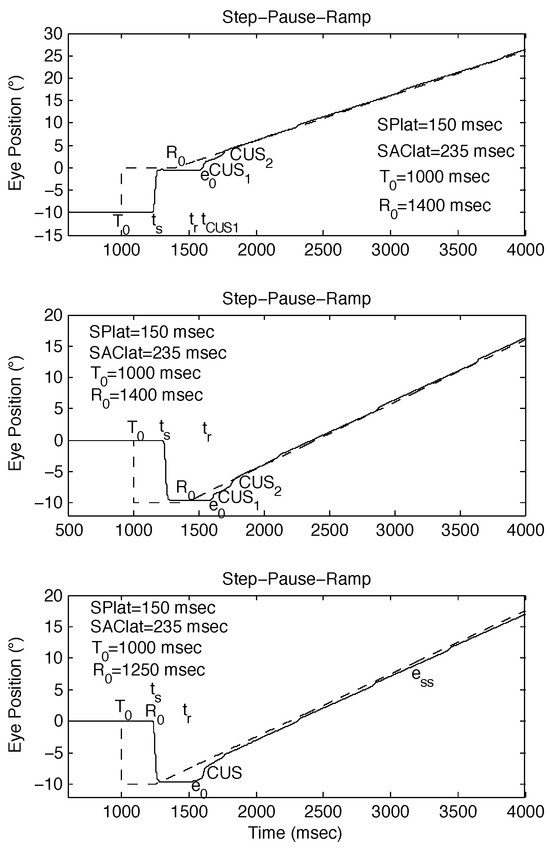
Figure 3.
Examples of the different types of responses to SPR stimuli whose ramp initiation occurs near a saccade. The behavioral OMS model simulations demonstrate how small differences in timing can alter the resulting strategy employed by both the saccadic and pursuit systems. (top) Accurate response to SPR stimulus [SPR: -10°, 0°, 10°/sec @ 400 msec]. (middle) Accurate response to SPR stimulus [SPR: 0°, -10°, 10°/sec @ 400 msec]. (bottom) Inaccurate response to SPR stimulus [SPR: 0°, -10°, 10°/sec @ 250 msec].
Subject Data
We presented the subjects with SR stimuli in addition to SPR stimuli to have a basis to compare the responses between two complex stimuli in addition to comparing the SPR responses to the normal ramp response. Because the behavioral OMS model we used is a unilateral, yoked control model (Dell’Osso, 1994; Jacobs & Dell’Osso, 2004; Z. I. Wang & L. F. Dell’Osso, 2011a; Z. I. Wang & L. F. Dell’Osso, 2011b), the responses it predicted in Figure 1, Figure 2 and Figure 3, are for the fixating eye. However, the data from our subjects were taken during binocular viewing. As the following Figures will show, normal subjects do not always maintain prefect conjugacy during pursuit or fixation, nor do they have a “preferred” eye. The data obtained from the first three subjects we tested were sufficient to answer our two questions. Data from the three subjects (S1, S2, and S3) answered the first and data from the third (S3) answered the second.
The first two normal subjects (S1 and S2) we tested exhibited no spontaneous saccadic intrusions during either fixation or smooth pursuit. Both were able to make the expected (i.e., based on known SR responses) response to the novel SPR stimulus. Figure 4 illustrates S1’s responses to SR stimuli. One of the first observations to be made (in all but the bottom right panel) is that S1 often made disconjugate saccades, with the eyes winding up either slightly converged (for leftward saccades) or diverged (for rightward saccades). Despite this, normal SR responses were possible (top left and middle left panels). The bottom left, top right, and middle right panels illustrate SR responses with longer target acquisition times due to either a required catch-up saccade (top left and middle left panels) or the fixating eye accelerating onto the target (bottom left panel). In the bottom right panel, despite conjugate saccades, the target acquisition time was elongated due to the need for a catch-up saccade and after pursuing the target for about 500 msec, pursuit gain decreased and typical low-gain pursuit resulted. These different types of SR responses were also seen in SPR responses containing proximal saccades.
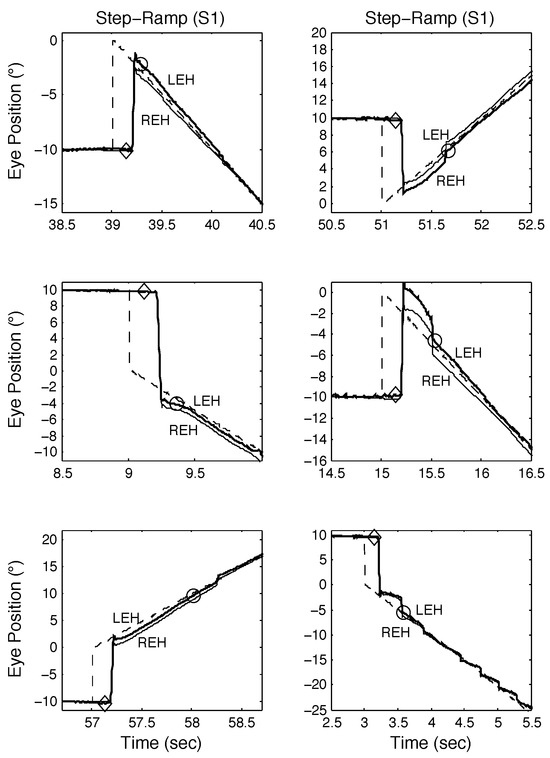
Figure 4.
Examples of SR responses from S1 demonstrating both classical and other types of response, including those containing disconjugate saccades. See text for descriptions. In this and the following figures, the time of pursuit onset is indicated by a diamond, the time the target is acquired, by a circle, and the fixating eye by the heavy tracing. All position and time scales were chosen to best illustrate the components of the response in each panel.
In Figure 5 (top left, middle left, and top right panels), the initial saccade occurred just before the onset of target motion and target acquisition times were longer than normal (disconjugate saccades are also present). In Figure 5 (middle left and bottom right panels), a post-saccadic, high-velocity acquisition of the target replaces a CUS; this OMS decision-making mimics “riding the slow phase” seen in INS patient data and simulations. Acquisition times were similar despite different strategies of using a catch-up saccade (top left and top right panels) or accelerating onto the target (middle left panel). When the timing of the first saccade occurred coincident with the onset of the target motion (bottom left, middle right, and bottom right panels), smooth-pursuit performance could be negatively affected in several ways. In the bottom left panel, the response is similar to that in the top left panel; in the middle right panel, the onset of pursuit was delayed until a catch-up saccade was made; and in the bottom right panel, there was a long steady-state position error.
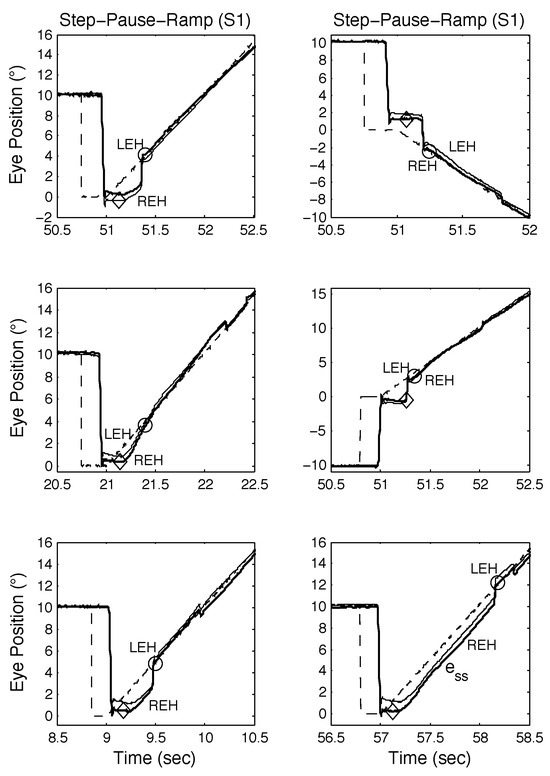
Figure 5.
Examples of SPR responses containing proximal saccades from S1 demonstrating both classical and other types of response, including those containing disconjugate saccades. See text for descriptions.
The responses of S2 to both SR and SPR stimuli are shown in Figure 6 and Figure 7 respectively; as they illustrate, S2 also made convergent and divergent saccades and the saccades also had small dynamic overshoots. For SR stimuli, this did not affect the target acquisition times (see Figure 6, top and middle panels). Saccadic errors could lengthen acquisition times, as Figure 6, bottom panel shows. In Figure 7, top left, middle left, top right, and bottom right panels, the initial saccade occurred just before or during the onset of target motion; the target acquisition times were similar. In the bottom left and middle right panels, the initial saccade occurred either just after or at the same time as target motion onset. The former target acquisition time was less than the latter, which contained a long steady-state error before the eyes accelerated onto the target.
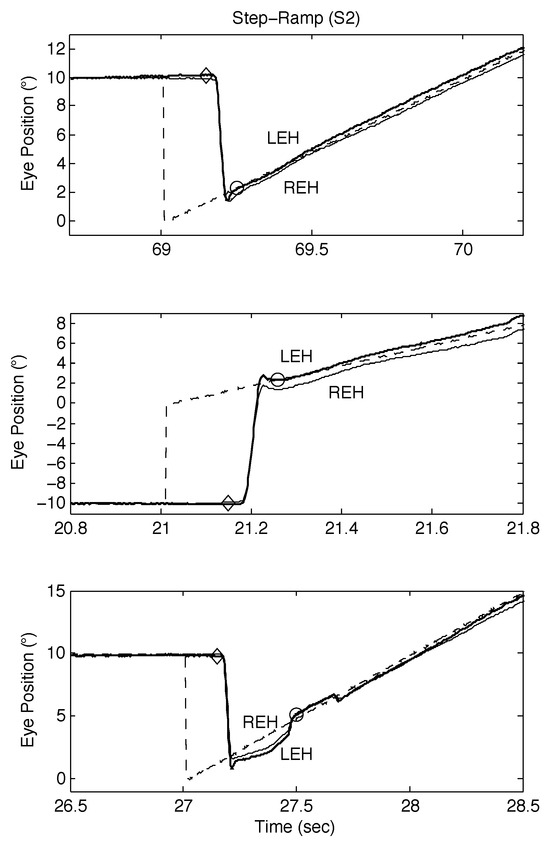
Figure 6.
Examples of SR responses from S2 containing proximal saccades demonstrating both classical and other types of response, including those containing disconjugate saccades. See text for descriptions.
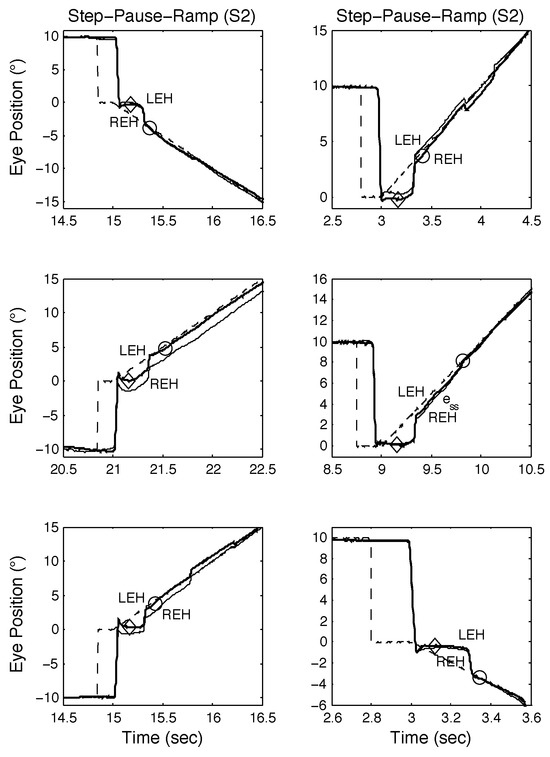
Figure 7.
Examples of SPR responses from S2 containing proximal saccades demonstrating both classical and other types of response, including those containing disconjugate saccades. See text for descriptions.
The third normal subject (S3) we tested exhibited spontaneous saccades (i.e., square-wave jerks, SWJ, or square-wave oscillations, SWO) during both fixation and smooth pursuit. Figure 8 shows responses made in proximity to either SWJ or SWO. The top left panel illustrates a normal SR response. In the other panels, both SWJ and SWO appear in proximity to the initial saccade in SPR responses. There were no cases where either the initial or return saccade in a SWJ appeared in close proximity to the onset of target motion although there were cases where the return saccade in a SWJ should have done so (see Figure 8, middle left, bottom left, top right, and bottom right panels). In all such cases, the return saccade was suppressed and replaced by the initial saccadic response to the SPR stimulus. Subject 3 also made convergent and divergent saccades and exhibited SPR responses that were otherwise similar to those of S1 and S2 unless SWJ and SWO delayed target acquisition times (see Figure 8, bottom right panel).
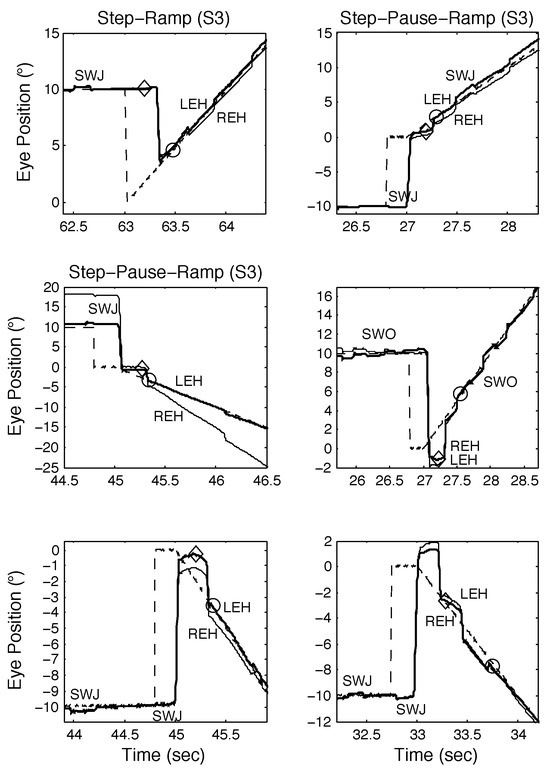
Figure 8.
Examples of SR (top left) and SPR responses from S3 containing proximal saccades demonstrating both classical and other types of response, including those containing disconjugate saccades, square-wave jerks (SWJ), and square-wave oscillations (SWO). See text for descriptions.
To detect the effects of small differences in the overlap of the first saccade in the response and the onset of target ramp motion we plotted the data for SAClat, SPlat, CUSlat, and Tat vs. Overlap. Figure 9 shows a representative plot using S1’s data. As can be seen, SAClat, and SPlat data were tightly arranged across different values of overlap. However both CUSlat and Tat data contained points with large variations from their mean values. Both S1 and S2 had moderate initial error velocities and small final error velocities for both SR and SPR stimuli whereas S3 had larger initial and final error velocities for both.
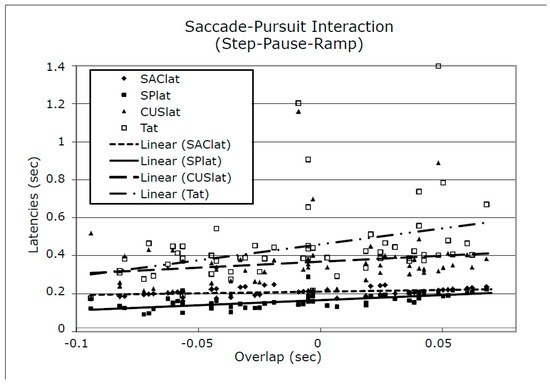
Figure 9.
Plots of SAClat, SPlat, CUSlat, Tat vs. Overlap for S1 (representative of data from all subjects) with linear fits to each data set. CUSlat = catch-up saccade latency; Tat = target acquisition time (tT R0); Overlap = ts - R0. See Methods for definitions of these times.
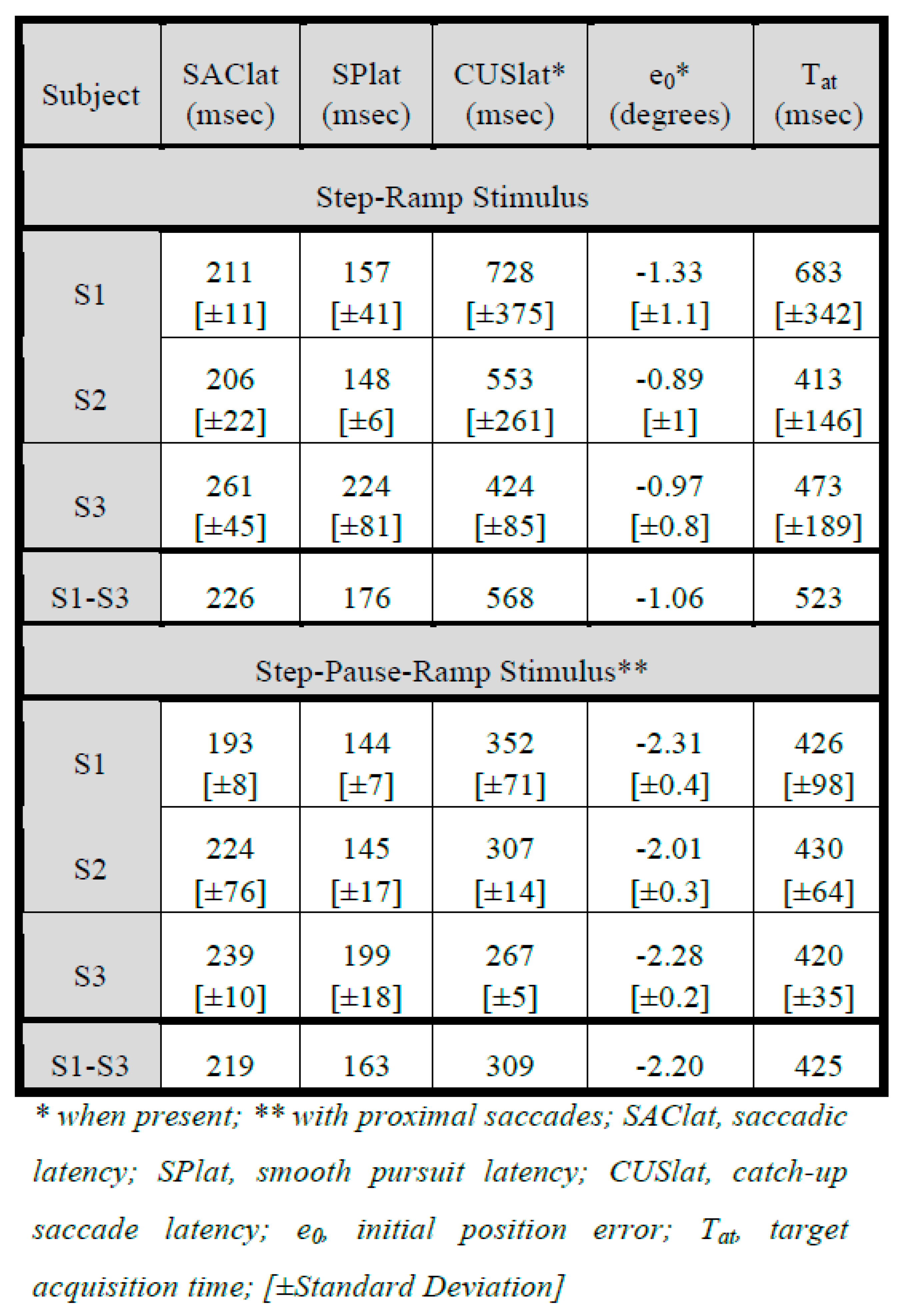
Despite the idiosyncratic differences among the three subjects in response types and the appearance of SWJ and SWO in S3, we were able to obtain averaged target-acquisition times for the pause durations of our SPR stimuli and compare them to those for the SR stimuli. That is, when SWJ or SWO did not interfere with latency measurements, the data from S3, were similar to those of S1 and S2. Table 1 summarizes the average latencies and position errors found for these SR and SPR responses. All saccadic and smooth pursuit latencies were in the normal ranges for both stimuli. Catch-up saccade latencies were longer for SR than SPR stimuli for all three subjects. Initial retinal position errors were greater for SPR than SR stimuli in all subjects; the magnitudes of the initial velocity errors (not shown) were also greater for all subjects. The key outcome measure, target acquisition time (Tat, meas- ured from ramp initiation time, R0), showed idiosyncratic variation, being less for SPR than SR stimuli for S1, greater for S2, and slightly less for S3. The larger value of Tat for S1 responses to SR stimuli was caused by the larger values for CUSlat. When measured from target motion initiation time, T0, all subjects also had approximately equal acquisition times for SPR (626, 663, and 626 msec for S1 through S3). Since the step and ramp initiation times coincided in SR stimuli (T0 = R0), there were no differences in Tat when measured from T0. Note that the standard deviations for Tat and CUSlat were less for SPR than for SR stimuli.

Table 1.
Average Latencies, Errors and Acquisition Times.
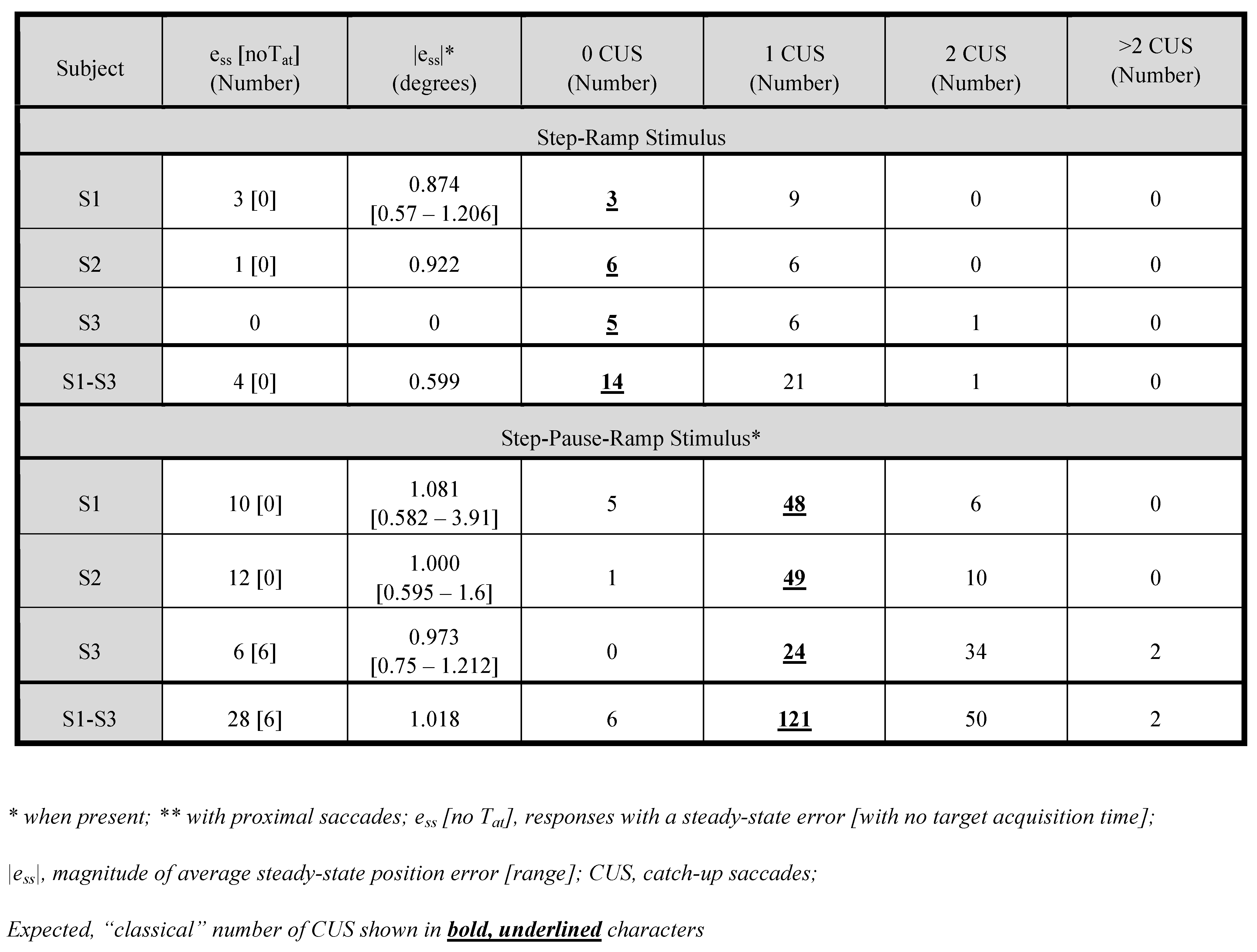
Table 2 compares the number and magnitudes of responses containing steady-state errors and catch-up saccades for both stimuli. Only S1 exhibited some steady-state errors for SR stimuli whereas all three subjects exhibited many such responses for SPR stimuli. When steady-state errors were present, their average magnitudes did not differ between stimuli. However, individual steady-state errors could be much larger for SPR responses (see ranges in Table 2). Although S1 and S2 would eventually acquire the target despite a steady-state error, S3 did not. The number of responses with 1 CUS in SR responses and >1 in SPR responses, demonstrate that the expected, “classical” response to either is not the only type of response or perhaps not the most prevalent. The SPR stimuli resulted in more responses with a second (or even >2 for S3) CUS.

Table 2.
Steady-State Errors (>±0.55°) and Catch-up Saccades.
Examination of individual responses revealed that S2 often exhibited steady-state errors both before CUS1 and after CUS2 in SPR responses whereas for SR responses, they occurred after CUS1. Alternatively, S3 exhibited steady-state errors after all CUS. Also, S3 often suppressed smooth pursuit totally (i.e., eye velocity was 0°/sec) until after CUS1 for both SR and SPR responses. That produced very long values of SPlat; when no suppression occurred, SPlat was normal. Occasionally, responses to both stimuli exhibited low-gain smooth pursuit, necessitating additional, multiple CUS.
We also combined all responses from the three subjects and calculated the group averages for both the SR and SPR stimuli. As expected from the individual averages, both saccadic and pursuit latencies were normal (226 msec and 176 msec respectively for SR and 219 msec and 163 msec respectively for SPR). The group Tat for the SR stimuli was 523 msec and for the SPR stimuli, it was 425 msec; both exceeded the expected Tat = 285 msec for a normal ramp response. Thus, the group average Tat for a ramp made following a proximal saccade was far longer than that expected for a ramp with no confounding prior saccade. The reason that the group average Tat for SR stimuli was greater than for SPR stimuli was due to the extra CUS’s used in SR responses by these subjects.
It has been demonstrated that INS begins with an oscillation unrelated to a prior saccade (Dell’Osso, 2006). Figure 10 shows a rare spontaneous oscillation during smooth pursuit in S3, a normal subject. The frequency of that oscillation was 3.47 Hz, which is consistent with the INS oscillation and provides further support for the hypothesis that the direct cause of INS is an undamped smooth pursuit system.
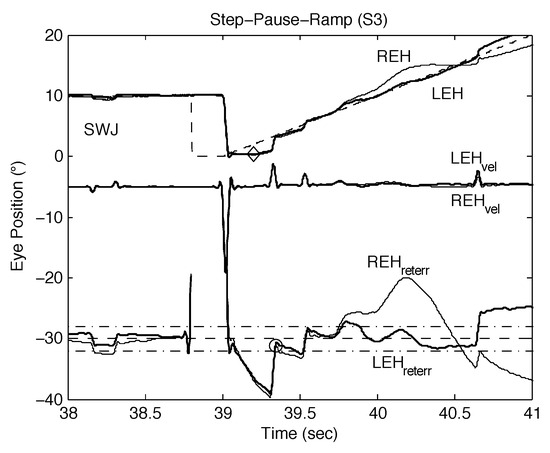
Figure 10.
Plot of S3 data (“latpoints” output) showing a spontaneous, conjugate oscillation during a SPR response by S3. See text for description and significance. REH, right eye horizontal; LEH, left eye horizontal; (REHvel, right eye horizontal velocity; LEHvel, left eye horizontal velocity; REHreterr, right eye retinal error; LEHreterr, left eye retinal error; target shown dashed; foveal extent (±0.5° but scaled up) indicated by the dash-dot lines; velocity traces (scaled down) and retinal error traces (scaled up) are shown shifted for clarity.
Discussion
In subjects with INS, constant target motion is both correctly perceived and accurately tracked despite the oscillatory eye motion (i.e., the retinal slip produced by the oscillation is compensated for and ignored). Occasionally, when target motion coincides with one of the intrinsic, corrective saccades in INS waveforms, target acquisition times are lengthened and steady-state, eye-position errors accompany the otherwise accurate smooth pursuit that occurs during foveation periods.
Our initial demonstration of the effects of proximal saccades on smooth pursuit using our behavioral ocular motor system model was summarized in Figure 2 and Figure 3. Because the same model using fixed internal parameters predicted such disparate responses, we concluded that it was the slight differences in pause length and the resulting differences in the saccade timing vis-à-vis the onset of target motion that affected ocular motor decision-making. That new emergent property of the model was the impetus for applying the SPR paradigm to normal subjects and eliciting proximal saccades that duplicated those in INS waveforms that produced the above pursuit problems.
Because the eyes are at rest during step, ramp, and SR stimuli, the OMS can accurately evaluate the size of the required saccade and the speed of the required smooth pursuit. Furthermore, retinal error position and retinal error velocity (“slip velocity”) would be sufficient to calculate both. However, during the SPN stimuli, as used in this study, the eye is in motion (the proximal saccade) when the target begins to move. This is a fundamentally different condition. Not only must the OMS evaluate the above two retinal inputs and use them to calculate the respective responses, but also, target velocity is not easily discerned from retinal signals alone, neither in normals nor in individuals with INS.
The first observation that stems from the eye-movement data is that the commonly described “classical” responses to SR stimuli are not always those exhibited by normal subjects under normal, binocular conditions. One reason is that individual subjects may make disconjugate saccades, leaving only one eye on target with the other either slightly esotropic or exotropic. Such deviations from perfectly conjugate saccades are to be expected if the ocular motor system computes saccadic responses to each eye individually based on is distinct retinal error signal (Dell’Osso, 1994; Zhou & King, 1997a, 1997b, 1998). Studies in humans or animals performed under conditions of monocular fixation preclude this type of response and may tend to overestimate the number of classical responses that occur under binocular conditions. For the latter, when evaluating responses to either SR or SPR stimuli, accurate, monocular calibration of each eye is necessary to identify which eye is the fixating eye during each response (and, when it changes). Our data also demonstrated different types of responses possible to the same stimuli; i.e., all responses do not always mimic the classical response described in textbooks. This is not unique to our novel SPR stimulus as it was also documented for SR stimuli. The brain must simultaneously evaluate position and velocity data during an SR response and although the relative latencies favor the classical response (i.e., pursuit followed by a saccade), they do not preclude other types of responses secondary to ocular motor decision-making. The same is true for SPR responses where the relative timing of the step and ramp stimuli further facilitate “non-classical” responses. The responses in this study of normals mimicked those in studies of individuals with INS (Wang & Dell’Osso, 2009; Z. I. Wang & L. F. Dell’Osso, 2011a). Indeed, the common observation of INS responses using the ongoing pursuit eye motion to acquire both stationary and moving targets appears to utilize the same mechanisms used by normals. We presume this is accomplished by a velocity-driven fixation subsystem; our behavioral OMS model utilizes such a subsystem.
The data contained large idiosyncratic differences in the responses for the reasons described above; not only were latencies and accuracies variable but also the types of responses differed. The variations in response type confound attempts to draw direct conclusions from simple averaged values of the parameters of interest (e.g., SPlat, SAClat, CUSlat, Tat, etc.). Because response differences reflected different ocular motor mechanisms, decisions, and strategies, we did not limit our analysis to average measurements of each parameter across subjects. Also, different types of responses did not all contain the same latencies and accuracies that could be measured and averaged. Therefore, we have presented the differences exhibited by normal subjects in addition to comparing the average values calculated for the responses. Table 2 presents the number and magnitudes of key parameters that differentiate response types.
The average values compiled in Table 1 reflect not only those expected by the two different types of stimuli (SR and SPR) but also idiosyncratic differences in the number of “classical” responses and strategies for nonclassical responses. Thus, they should not be taken at face value but rather, examined in relation to those differences. As both Tables show, none of the subjects exhibited a majority of the classic responses to SR stimuli or achieved the low values of Tat they would predict (e.g., 285 msec for SR and 285 – 335 msec for SPR stimuli); S1 and S2 did have a majority of classic responses to SPR stimuli. The measured averages of 413 – 683 msec for SR stimuli and 420 – 430 msec for SPR stimuli are the result of non-classical responses that result in longer acquisition times due to additional CUS or slow accelerations onto the target and not longer values of SPlat, which were normal. The tendency for longer acquisition times for the SPR stimuli containing initial saccades made in close proximity to initial target motion, supports the hypothesis that such saccades negatively affect the performance of the normal pursuit system. More striking than the increase in Tat was the greater number of steady-state errors present in SPR responses, for that resulted in the eye being off target for substantial amounts of time, either before or after the final CUS.
There are several other observations from the Tables that deserve comment. Catch-up saccade latencies were longer for SR than SPR stimuli for all three subjects; that probably reflects the fact that CUS are only needed if errors were made in SR responses but are normally part of SPR responses. The larger average value of Tat for S1’s responses to SR stimuli was caused by the larger values for CUSlat. Also, the standard deviations for Tat and CUSlat were less for SPR than for SR stimuli; we believe that this was probably also due to the preponderance of single-CUS (i.e., classical) responses to SPR stimuli whereas those in SR responses represented errors that needed to be corrected (as Table 2 indicates). The initial errors of ~2° in the SPR responses of all subjects reflects the accumulated target motion from the initial saccade (i.e., ~235 msec * 10°/sec = ~2°). Most important is that the average value of Tat across all subjects for the SPR stimuli (425 msec) is greater than that for normal ramp response in the absence of a proximal saccade (285 msec).
As stated in the Introduction, the SPR stimulus was designed to elicit saccades that would precede, interrupt, or follow the onset of target motion. Such saccades are similar to the intrinsic saccades of INS but not exactly the same; the former are a response to eye-position errors due to target motion whereas the latter are a response to eye-position errors due to eye motion (i.e., oscillation). Despite that difference in their genesis, our data demonstrated that saccades made by normals had similar effects on pursuit responses as those found in INS and we conclude that the SPR stimulus was an effective method to elicit them.
The suppression of vision during saccades has been well studied (Latour, 1962; Volkmann, 1962; Volkmann, Schick, & Riggs, 1969; Zuber & Stark, 1966). Normal saccades and intrinsic saccades in INS waveforms have the same similar time-course curves. The threshold of seeing a brief flash of light is significantly elevated if it occurs 30 – 40 msec before, during, or 100 – 120 msec after the saccade. Perisaccadic flash perception studies have demonstrated mislocalization with different spatial patterns depending on the experimental condition (Awater & Lappe, 2006; Hamker, Zirnsak, & Lappe, 2008). It is tempting to attribute the lengthening of Tat to the initial suppression caused by the initial saccades in the responses. However, unlike the brief or dim flash used in saccadic suppression experiments, we used a bright and steady laser beam target. The visibility of the target was well above the visual threshold for all the subjects; after the jump, the target remained visually salient at the new position. Because of that, the predictive performance of the model, which contains no saccadic suppression, and our subjects stating that they could see the target at all times, we do not think the initial saccadic suppression caused by the intrinsic saccades played an important role in longer values of Tat.
More relevant to this study may be prior studies of saccade-pursuit interaction that demonstrated that the initial saccade made during pursuit (specifically of SR stimuli), enhances the pursuit system’s ability to accelerate to match target velocity (Lisberger, 1998). It has also been hypothesized that the saccadic and smooth pursuit systems may be a combined system (i.e., two outcomes of a single sensorimotor process) rather than two separate systems (Krauzlis, 2004, 2005; Liston & Krauzlis, 2005; Orban de Xivry & Lefevre, 2007). Recently, an SPR stimulus was used to study saccadic foveation of a moving target in the rhesus monkey, specifically, the effects on the initial saccade of target displacement preceding that saccade, to examine the “dual drive” and “remapping” hypotheses (Fleuriet, Hugues, Perrinet, & Goffart, 2011).
However, unlike the above studies, the present study did not involve saccade-pursuit interaction secondary to a saccade occurring well after the onset of target motion and usually during pursuit. Rather, the saccades in this study occurred in close proximity to the onset of target motion before pursuit onset. Essentially, we studied how the ramp responses of normals were affected by prior saccades whose time of occurrence might impede the ocular motor system’s ability to calculate target motion and position. In terms of Lisberger’s “pursuit switch,” we hypothesize that although the proximal saccade may have turned it on, the saccadic eye motion may have resulted in inaccurate determination of the subsequent target motion. In terms of the hypothesis of a single sensorimotor process, the proximal saccade may similarly interfere with the subsequent pursuit response. Whatever the actual control-system architecture, the above-referenced results and ours support the conclusion, embodied in our model. That is, saccades and pursuit are not simple reflexive responses but rather involve identification of both target position and motion, followed by decision-making for both saccadic and pursuit responses. That decisionmaking is exemplified by both the intra- and inter-subject response differences we found.
Conclusions
The results of the present study support the hypothesis that SP in INS is “normal” (i.e., foveation-period, smooth-pursuit gain and phase lag are normal despite the ongoing oscillation) (Dell’Osso, 1986; Dell’Osso, et al., 1992; Kurzan & Büttner, 1989). Not only were the expected responses “normal” but, as this study shows, “abnormal” responses (i.e., the smooth-pursuit deficits induced by proximal saccades) were also “‘normal.” We further conclude smooth pursuit in normals may also be impaired when the subject makes a saccade, voluntary or spontaneous, in the vicinity of target-motion onset. Although additional subjects would support the general nature of our results, the model predictions plus the prior INS data provide a firm foundation for them. As has been discussed for individuals with INS (Wang & Dell’Osso, 2009; Z. I. Wang & L. F. Dell’Osso, 2011a), longer target acquisition times and small, steady-state position errors have important implications in real-world situations, especially in sports. If determining target details is important, the diminished acuity of even a small steady-state error is the task-limiting condition. When timing is paramount, longer acquisition times may diminish performance. For example, if a normal batter (i.e., without INS) makes an inappropriate saccade just as the pitcher releases the ball, his ability to determine the position and speed of the ball may be impaired, thereby reducing the accuracy of his prediction of the expected ball position and his subsequent swing. One of the keys to good batting may be the ability to keep one’s eyes still until the pitch is on its way. Unfortunately, for the individual with INS, that is impossible and batting performance may vary based on the relative, and uncontrollable, timing of his intrinsic saccades and the release of the ball by the pitcher.
Acknowledgments
This work was supported in part by the Office of Research and Development, Medical Research Service, Department of Veterans Affairs. Presented in part at the 2010 ARVO meeting.
APPENDIX
The following are the mathematical relationships defining the stimuli and responses described in the Methods.
Classical Step Stimulus. Mathematically, the step stimulus is expressed as, ±Au(t-T0), where u(t) is the unit step.
@ t = T0+: Steady-state position error = ±A (Ė = 0). Initial saccade latency SAClat = ts - T0 ≅ 200 – 250 msec, eliminating the initial steady-state position error (e0 = A).
Normally, Tat ≅ 235 + 50 = 285 msec; the duration the small saccades in this study is approximated as 50 msec.
Classical Ramp Stimulus. Mathematically, the ramp stimulus is expressed as, ± Ṫ0r(t-R0), where r(t) is the unit ramp.
@ t = R0+: Steady-state velocity error = ±Ṫ0 (Ė = 0) and position error, e = ±Ṫ0t. Initial Ė = Ṫ0 at latency SPlat = tr - R0 ≅ 125-175 msec, initial steady-state position error, e0 = 0.150Ṫ0.
Catch-up saccade, CUS, at latency SAClat = tcus - R0 ≅ 235 msec, eliminates e0 and Ė = Ṫ0 with no steady-state position (ess) error.
Normally, Tat ≅ 235 + 50 = 285 msec.
Classical Step-Ramp (Rashbass) Stimulus. Mathematically, the SR stimulus is expressed as, ±Au(t-T0) ± Ṫ0r(t-R0), where R0 = T0 and for this study, A = ±10° and Ṫ0 = ±10°/sec.
@ t = T0+: Ssteady-state position error = ±A and steady-state velocity error = ±Ṫ0 (Ė = 0) and e = ±A ±Ṫ0t.
Size of the required saccade is (±A ±Ṫ0 tcus) ± (Ṫ0(tcus - tr); and required smooth pursuit = Ṫ0. Initial Ė = Ṫ0 at latency SPlat = tr - R0 ≅ 150 msec, initial position error e0 = ±A ± 0.150Ṫ0.
Saccade at latency SAClat = ts - R0 ≅ 235 msec, eliminates e0 and allows Ė = Ṫ0 with no ess.
If a CUS is not needed, Tat ≅ 235 + 50 = 285 msec.
Step-Pause-Ramp Stimulus. Mathematically the SPR stimulus is expressed as, ±Au(t-T0) ± Ṫ0r(t-R0), where R0 ≥ T0. As the pause is reduced towards 0, when (R0 - T0) < (SAClat -50), it becomes a Rashbass stimulus and as it is increased to be >> ts, when (R0 - T0) > (SAClat +50), it is merely a classical step stimulus followed by a classical ramp stimulus. Proximal saccades are produced when (SAClat -50) ≤ (R0 - T0) ≤ (SAClat +50).
@ t = T0+: Steady-state position error = ±A (Ė = 0).
@ t = R0+: Because of intrasubject variation in saccadic latency SAClat = ts - T0, a steady-state velocity error = ±Ṫ0 while either
1) the eyes are still but a saccade is programmed and about to occur;
2) the eyes are in the midst of a saccade and moving at high velocity; or
3) the eyes are slowing just after a saccade.
Expected normal saccade = ±A at the normal saccadic latency ts ≅ 235 msec followed by initial Ė = Ṫ0 at latency SPlat = tr - R0 ≅ 150 msec; accurate tracking with initial position error e0 = ±A ±0.150Ṫ0 followed by CUS at latency SAClat = tcus - R0 ≅ 235 msec, which eliminates e0 and allows Ė = Ṫ0 with no ess (see “a)” below).
If a second CUS is not needed, Tat ≅ (0 – 100) + 235 + 50 = 285 – 385 msec.
However, the OMS may not accurately evaluate either: the size of the required saccade as target position (±A ±Ṫ0(ts - R0)) ± eye position (±A ±Ṫ0(tcus - tr)) or the speed of the required smooth pursuit (±Ṫ0). Several OMS responses are possible for any of the three stimulus conditions above, depending on the relative timings of the stimulus and the execution of the initial saccade. They may be categorized as follows:
a) @ t = tr+, initial Ė = Ṫ0 at latency (tr - R0) ≥150 msec; e0 = ±A ±0.150Ṫ0 followed by CUS at tcus ≥ ts, and no ess.
b) @ t = tr+, initial Ė at a latency (tr - R0) ≥150 msec; e0 = ±A ±0.150Ṫ0 followed by CUS at tcus ≥ ts, and ess or
c) @ t = tr+, no initial pursuit at a latency (tr - R0) ≥150 msec; no tracking but e0 = ±A ±0.150Ṫ0 ±0.150t. Followed by much-delayed CUS’s at a latency >> tr - R0, with little or no smooth pursuit of the target and some steady-state position error. Finally, Ė = Ṫ0 but ess remains.
References
- Abel, L. A., L. F. Dell’Osso, and R. B. Daroff. 1978. Analog model for gaze-evoked nystagmus. Institute of Electrical and Electronics Engineers Transactions of Biomedical Engineering BME, 25: 71–75. [Google Scholar]
- Awater, H., and M. Lappe. 2006. Mislocalization of perceived saccade target position induced by perisaccadic visual stimulation. Journal of Neuroscience 26: 12–20. [Google Scholar] [CrossRef] [PubMed]
- CEMAS_Working_Group. 2001. A National Eye Institute Sponsored Workshop and Publication on The Classification of Eye Movement Abnormalities and Strabismus (CEMAS). In The National Eye Institute Publications (www.nei.nih.gov). Bethesda, MD: National Institutes of Health, National Eye Institute. [Google Scholar]
- Dell’Osso, L. F. 1968. A Dual-Mode Model for the Normal Eye Tracking System and the System with Nystagmus. (Ph.D. Dissertation). University of Wyoming, Laramie. [Google Scholar]
- Dell’Osso, L. F. 1986. Evaluation of smooth pursuit in the presence of congenital nystagmus. Neuro-ophthalmology 6: 383–406. [Google Scholar]
- Dell’Osso, L. F. 1994. Evidence suggesting individual ocular motor control of each eye (muscle). Journal of Vestibular Research 4: 335–345. [Google Scholar] [PubMed]
- Dell’Osso, L. F. 1995. The analysis of ocular motor dysfunction: Insights into disease processes and normal function. Institute of Electrical and Electronics Engineers/Engineering in Medicine and Biology Special Issue: Advances in Vision Research 14: 22–29. [Google Scholar]
- Dell’Osso, L. F. 2006. Biologically relevant models of infantile nystagmus syndrome: the requirement for behavioral ocular motor system models. Seminars in Ophthalmology 21, 2: 71–77. [Google Scholar]
- Dell’Osso, L. F., and R. B. Daroff. 1975. Congenital nystagmus waveforms and foveation strategy. Documenta Ophthalmologica 39: 155–182. [Google Scholar]
- Dell’Osso, L. F., R. W. Hertle, R. W. Williams, and J. B. Jacobs. 1999. A new surgery for congenital nystagmus: effects of tenotomy on an achiasmatic canine and the role of extraocular proprioception. Journal of the American Academy of Pediatric Ophthalmology and Strabismus 3: 166–182. [Google Scholar]
- Dell’Osso, L. F., D. A. Robinson, and R. B. Daroff. 1974. Optokinetic asymmetry in internuclear ophthalmoplegia. Archives of Neurology 31: 138–139. [Google Scholar]
- Dell’Osso, L. F., J. Van der Steen, R. M. Steinman, and H. Collewijn. 1992. Foveation dynamics in congenital nystagmus II: Smooth pursuit. Documenta Ophthalmologica 79: 25–49. [Google Scholar] [CrossRef]
- Dell’Osso, L. F., Z. Wang, R. J. Leigh, and J. B. Jacobs. 2006. Hypothetical explanation for the role of proprioception in the damping of infantile nystagmus by tenotomy surgery: The small-signal gain hypothesis. In Proceedngs of the World Multiconference on Systemics, Cybernetics and Informatics 2006 Conference. Edited by N. Callaos. Orlando, FL: pp. 39–44. [Google Scholar]
- Dell’Osso, L. F., and R. W. Williams. 1995. Ocular motor abnormalities in achiasmatic mutant Belgian sheepdogs: Unyoked eye movements in a mammal. Vision Research 35: 109–116. [Google Scholar] [CrossRef] [PubMed]
- Dell’Osso, L. F., R. W. Williams, J. B. Jacobs, and D. M. Erchul. 1998. The congenital and see-saw nystagmus in the prototypical achiasma of canines: comparison to the human achiasmatic prototype. Vision Research 38: 1629–1641. [Google Scholar] [CrossRef] [PubMed]
- Fleuriet, J., S. Hugues, L. Perrinet, and L. Goffart. 2011. Saccadic foveation of a moving visual target in the rhesus monkey. Journal of Neurophysiology 105, 2: 883–895. [Google Scholar] [CrossRef] [PubMed]
- Hamker, F. H., M. Zirnsak, and M. Lappe. 2008. About the influence of postsaccadic mechanisms for visual stability on peri-saccadic compression of object location. Journal of Vision 8, 14: 1 1–13. [Google Scholar] [CrossRef]
- Jacobs, J. B., and L. F. Dell’Osso. 2004. Congenital nystagmus: hypothesis for its genesis and complex waveforms within a behavioral ocular motor system model. Journal of Vision 4, 7: 604–625. [Google Scholar] [CrossRef]
- Jacobs, J. B., L. F. Dell’Osso, Z. I. Wang, G. M. Acland, and J. Bennett. 2009. Using the NAFX to measure the effectiveness over time of gene therapy in canine LCA. Investigative Ophthalmology and Visual Science 50, 10: 4685–4692. [Google Scholar] [CrossRef]
- Krauzlis, R. J. 2004. Recasting the smooth pursuit eye movement system. Journal of Neurophysiology 91: 591–603. [Google Scholar] [CrossRef]
- Krauzlis, R. J. 2005. The control of voluntary eye movements: new perspectives. Neuroscientist 11, 2: 124–137. [Google Scholar] [CrossRef]
- Kurzan, R., and U. Büttner. 1989. Smooth pursuit mechanisms in congenital nystagmus. Neuro ophthalmology 9: 313–325. [Google Scholar] [CrossRef]
- Latour, P. L. 1962. Visual threshold during eye movements. Vision Research 2: 261–262. [Google Scholar] [CrossRef]
- Lisberger, S. G. 1998. Postsaccadic enhancement of initiation of smooth pursuit eye movements in monkeys. Journal of Neurophysiology 79, 4: 1918–1930. [Google Scholar] [PubMed]
- Liston, D., and R. J. Krauzlis. 2005. Shared decision signal explains performance and timing of pursuit and saccadic eye movements. Journal of Vision 5, 9: 678–689. [Google Scholar] [PubMed]
- Orban de Xivry, J. J., and P. Lefevre. 2007. Saccades and pursuit: two outcomes of a single sensorimotor process. Journal of Physiology 584, Pt 1: 11–23. [Google Scholar]
- Rashbass, C. 1961. The relationship between saccadic and smooth tracking eye movements. Journal of Physiology (London) 159: 326–338. [Google Scholar] [CrossRef]
- Volkmann, F. C. 1962. Vision during voluntary saccadic eye movement. Journal of the Optical Society of America 52: 571–578. [Google Scholar]
- Volkmann, F. C., A. M. L. Schick, and L. A. Riggs. 1969. Time course of visual inhibition during voluntary saccades. Journal of the Optical Society of America 58: 562–569. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. I., and L. F. Dell’Osso. 2007. Being “slow to see” is a dynamic visual function consequence of infantile nystagmus syndrome: Model predictions and patient data identify stimulus timing as its cause. Vision Research 47, 11: 1550–1560. [Google Scholar]
- Wang, Z. I., and L. F. Dell’Osso. 2009. Factors influencing pursuit ability in infantile nystagmus syndrome: Target timing and foveation capability. Vision Research 49: 182–189. [Google Scholar]
- Wang, Z. I., and L. F. Dell’Osso. 2011a. Smooth-pursuit changes after the tenotomy and reattachment procedure for infantile nystagmus syndrome: model predictions and patient data. Journal of Pediatric Ophthalmology and Strabismus 48: 1–8. [Google Scholar]
- Wang, Z. I., and L. F. Dell’Osso. 2011b. A unifying model-based hypothesis for the diverse waveforms of infantile nystagmus syndrome. Journal of Eye Movement Research 4, 1: 1, 1–18. [Google Scholar] [CrossRef]
- Zhou, W., and W. M. King. 1997a. Binocular eye movements not coordinated during REM sleep. Experimental Brain Research 117: 153–160. [Google Scholar] [PubMed]
- Zhou, W., and W. M. King. 1997b. Monocular rather than conjugate saccade burst generators in paramedian pontine reticular formation (PPRF). Society of Neuroscience Abstracts 23: 7. [Google Scholar]
- Zhou, W., and W. M. King. 1998. Premotor commands encode monocular eye movements. Nature 393: 692–695. [Google Scholar] [PubMed]
- Zuber, B. L., and L. Stark. 1966. Saccadic suppression: elevation of visual thresholds associated with saccadic eye movements. Experimental Neurology 16: 65–79. [Google Scholar]
Copyright © 2013. This article is licensed under a Creative Commons Attribution 4.0 International License.