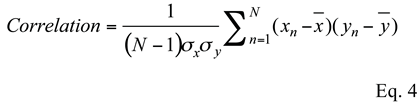Error Correction in Vergence Eye Movements: Evidence Supporting Hering’s Law

Abstract

In pure symmetrical vergence eye movements, a fusion initiating component quickly brings the eyes close to the desired position. A small error usually remains after this response which must be corrected to attain the small final vergence error (i.e., fixation disparity). Error correction will usually involve both version and version movements so possible mechanisms include: small saccades, smooth pursuit, symmetrical vergence, or some combination. Alternatively, an asymmetrical vergence or uniocular slow eye movement could be used to achieve the highly precise final position. Saccade-free late fusion sustaining components during the steady state to a symmetrical vergence step stimulus are analyzed using independent component analysis. Results suggest that fine correction is most likely the product of closely coordinated version and vergence components.

Introduction

Pure vergence stimuli fall strictly along the midline or “cyclopean” axis and while rare in natural viewing, are easy to create in the laboratory. They are particularly useful for studying the neural control of disparity vergence eye movements. Responses to such stimuli should not contain version components, but two factors can lead to transient version components during a symmetrical vergence response. First, vergence responses often contain saccades (Levi et al., 1987; van Leeuwen et al. 1998; Zee et al. 1992; Collewijn, et al., 1995, Semmlow et al. 2008, 2009; Coubard and Koupola, 2008) and even a small saccade will generate a substantial deviation from the midline. Second, even if no saccades are present, responses to pure vergence stimuli are often asymmetrical because one eye moves faster than the other during the fusion initiating (In this manuscript, we use the terms “fusion initiating,” or simply “initiating” for the initial transient component and “fusion sustaining” or “sustaining” for the slow sustaining component.) component of the vergence response ((Horng et al. 1998). Yet in normal subjects with good binocular vision, fixations errors are close to zero (Ogle, 1954), so the late, fusion sustaining portion of the response must contain a compensatory or “fine tuning” component to attain the highly accurate final fixation. In general, the sustaining component will have to be asymmetrical due to the version error produced by the saccade and/or initiating component asymmetry. Historically, the oculomotor response to asymmetrical stimuli has been the subject of much controversy, but has largely formed around two camps: one favoring Hering’s Law (1977) which postulates independent control processes for version and vergence movements and the other centered around Helmholtz’s arguments (1962) for a learned behavior based on independent control of each eye.

Some recent research has reported evidence in favor of Helmholtz’s theory (Cullen & Van Horn, 2011; King, 2011). Zhou and King showed that premotor neurons in the paramedian pontine reticular formation, that were thought to encode for saccadic velocity commands, encoded monocular saccadic commands for the left and right eyes (Zhou & King, 1998). In addition, Van Horn and Cullen suggest that saccadic burst neurons carry monocular vergence-related information during disconjugate saccades, further suggesting evidence of uniocular control (Van Horn & Cullen, 2008). However, Cullen & Van Horn (2011) did not show whether the vergence commands, that are required to drive movements in response to symmetrical disparity vergence stimuli (i.e. when the saccadic burst neurons are silent), utilize uniocular control. King (2011) concludes that while most recent neurophysiological findings favor Helmholtz, there is new evidence for a separate vergence motor pathway (i.e., a separate ‘final common pathway’) which innervates slower extraocular muscle fibers driving disparity vergence and slow corrective movements.

Behavioral studies support a nonlinear interaction between the vergence/saccade systems supporting Herings law. (van Leeuwen, Collewijn, & Erkelens, 1998; Zee, Fitzgibbon, & Optican, 1992) Several models have been proposed to describe the enhancement of vergence peak velocity response induced by saccade- vergence stimuli (i.e. looking between targets side-to- side) that are located in different depths (near to far). These models are based upon: 1) the inhibition of the saccadic omnipause neurons (OPN) (Mays & Gamlin, 1995; Zee et al., 1992); 2) both the saccadic pulse and omnipause neuron inhibition (Kumar, Han, Dell'Osso, Durand, & Leigh, 2005; Kumar et al., 2006); 3) a multiplicative interaction between a weighted saccadic burst signal and vergence motor error (Busettini & Mays, 2005); and 4) dual visual with local feedback mechanisms (Erkelens, 2011).

While most studies have concentrated on the faster eye movements mediated by saccades and asymmetrical vergence, there is behavioral evidence that slower tracking movements, smooth pursuit and the vergence seen in response to ramp stimuli (Also called vergence pursuit), are controlled by separate version and vergence components following Hering’s Law. Semmlow et al. (1998) compared constant velocity tracking driven at the same rate by either pure version or pure vergence stimuli and showed markedly different dynamic behavior. When both stimuli were combined, tracking behavior was consistent with the addition of the two components in proportion to their respective stimuli.

Here we analyze saccade-free fusion sustaining components of oculomotor responses to pure vergence step stimuli. Our objective is to determine whether these late fusion sustaining responses appear to be driven by two separate version and vergence components or the result of independent left-right eye movements (i.e., uniocular control). These movements are particularly important as they are responsible for positioning the eye to their highly accurate final fixations. As King (2011) points out, it is difficult to determine if smooth eye movements are the product of separate version and vergence components since it is always possible to represent these movements as a summation of vergence and version. Stating this summation mathematically (These equations assume that rightward movements are taken as positive.):

Left_Eye = Version + Vergence/2
Right_Eye = Version – Vergence/2

Eqs. 1

The question of interest is do these equations (Eqs. 1) reflect underlying neural control signals? If they do, then the movements of the right and left eyes are indeed (linear) mixtures of two signals: slow version or smooth pursuit and slow vergence.

Alternatively, version and vergence could be just mathematical constructs obtained by adding and subtracting eye movements. That is, version and vergence are mixtures of the separate left and right eye movements.

Stating this mathmatically:

Version = (Left_Eye + Right_Eye)/2
Vergence = Left_Eye – Right_Eye

Eqs. 2

Eqs. 2 Note that Eqs. 1 and 2 are different solutions of the same set of equations. They reflect the fact that there are two signals underlying slow version/vergence motor behavior, but imply different control strategies. Eqs. 1 imply that the motor response is the result of combined version and vergence neural signals: left and right eye movements are just mixtures of these motor componets. Eqs. 2 imply that vergence and version are mixtures of the two signals that independently drive the left and right eyes.

Theoretically there is a straightforward signal processing approach to determine which combination is more likely to be a mixture. Unmixed responses always demonstrate more mathematical independence from each other than mixtures of signals. Intuitively, mixtures are combinations of other signals and have more commonality than independent signals. To determine which of the above sets of equations best describe fusion sustaining vergence response, we can test the independence of version-vergence versus left-right eye movement combinations. The more independent combination indicates which combination better represents underlying neural signals.

There are a number of ways to test independence. One of the most straightforward is independent component analysis (ICA): a statistical method that is designed to un-mix or separate mixtures of signals (Common, 1994; Cardoso, 1994; Hyvarinen & Karhunen, 2001). After un-mixing, the more independent pair will be identified: either left/right or version/vergence signals. ICA is a novel analysis that has been applied over a number of disciplines and in the eye movement field has been used to isolate the fusion initiating from the fusion sustaining component of disparity vergence eye movement ((Semmlow & Yuan 2002). The approach used here will apply ICA to either left and right eye movements or version and vergence (as described below, it really does not matter which combination is used) and allow ICA to un-mix these signals into their most independent representations. If the resultant signals match left and right eye movements, then these are the most independent and best reflect the underlying control signals. Such a result would support Helmholtz’s theory of uniocular control processes for these fusion sustaining movements. Alternatively, if the unmixed signals match version and vergence, then these components best reflect the underlying neural signals supporting Hering’s law. Details of this application are summarized in the next section.

Methods

Stimulus Presentation and Data Recording

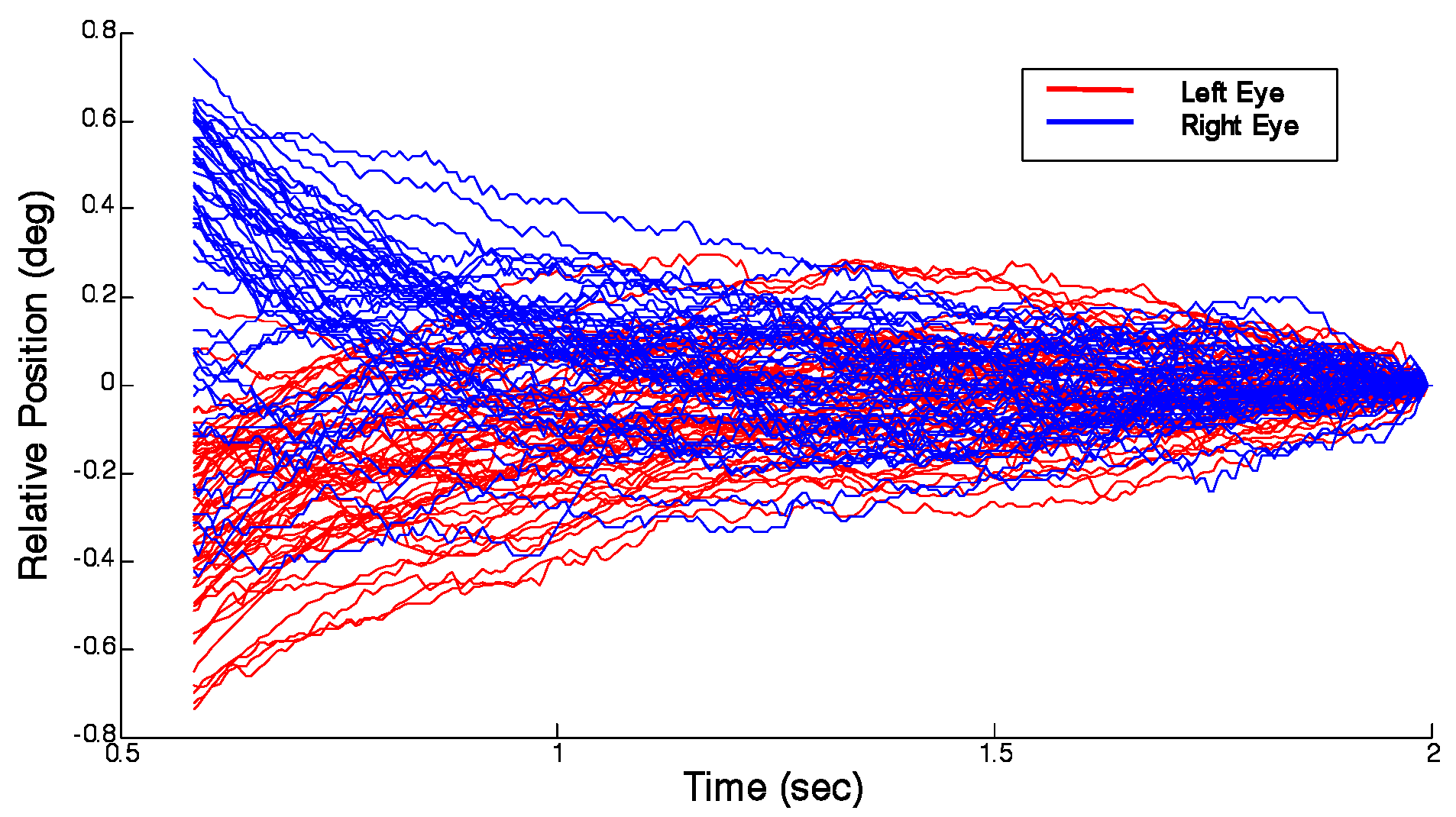
The stimulus was generated by a pair of computer monitors arranged as a haplescope to present separate images to each eye. The stimulus device was calibrated by physical targets viewed directly by the subjects through half silver mirrors. Stimulus generation and data acquisition were under computer control (Guo, Kim, & Alvarez, 2011). The stimulus consisted of pure vergence step changes that occurred at random times and in random directions (convergent and divergent). The responses to 4 deg. convergent steps (between 4 and 8 deg.) were selected for the analysis presented here. The responses of each eye during a 2 sec. period following the stimulus were detected by a Skalar infrared eye movement monitor (Model 6500). A two-point calibration was performed on each eye and for each movement. The final approximately 1.0 sec of the response was extracted for further analysis provided this portion of the response was free of obvious artifacts and saccades. Completely saccade-free vergence responses are rare even in response to pure vergence stimuli; however, the late portion of the response is often saccade- free. Figure 1 shows a collection of 42 responses plotted as vergence responses and Figure 2 shows the excised fusion sustaining portion of these responses plotted as left and right eye movements.

Responses from 7 subjects between the ages of 21 and 40 were analyzed. All subjects had normal binocular vision as assessed by the Randot Stereopsis test and used refractive correction during the experimental trial if needed. All signed informed consent forms and the study and consent were approved by the NJIT Institutional Review Board.

The number of saccade-free and nominally artifact- free late responses obtained from each subject varied between 25 and 42, but not all responses lead to a successful analysis as described below.

Data Analysis

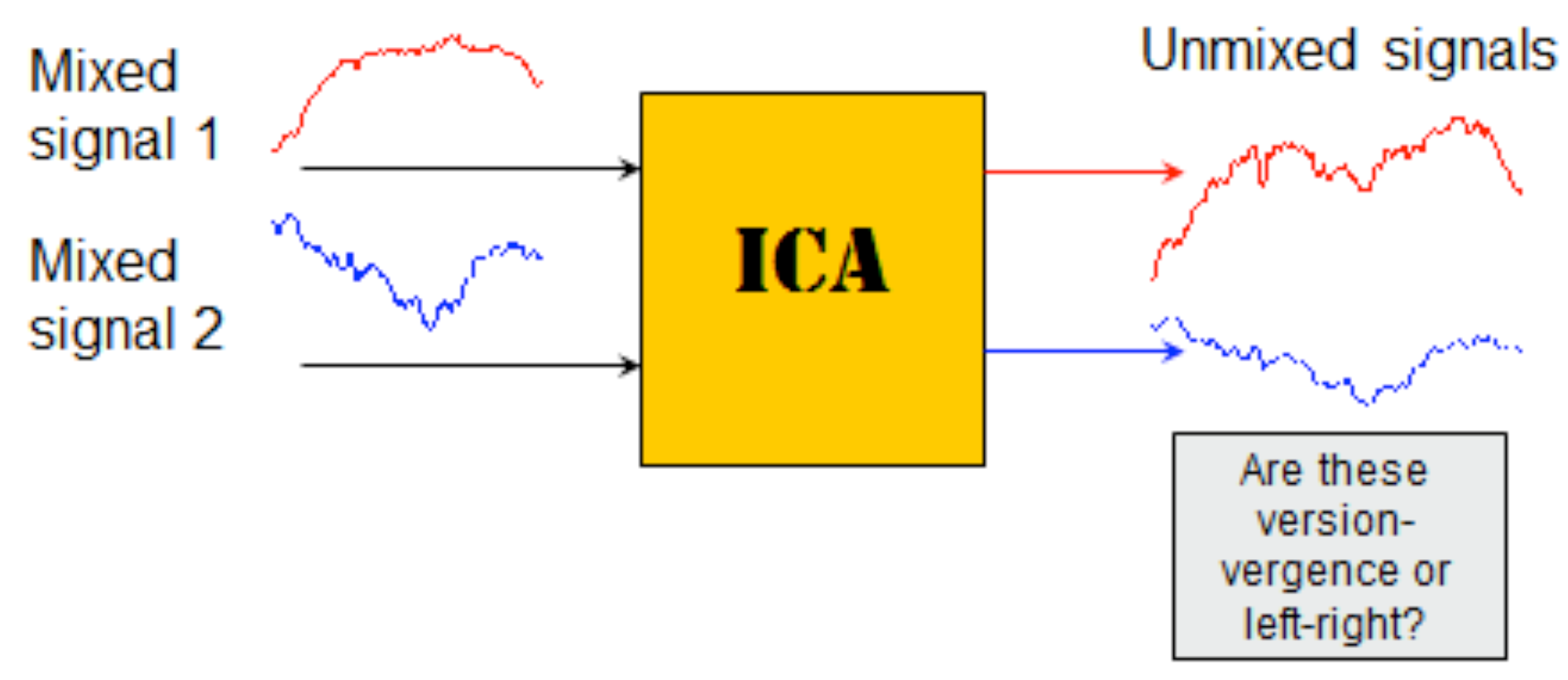
The fusion sustaining portion of a single response is shown in Figure 3 plotted as both left and right eye movements (Figure 3B) and as version and vergence (Figure 3A.) The version and vergence responses were computed from the left and right eye movements using Eq. 2. ICA is applied directly to either of these signal combinations. It really does not matter which signal combination is used since the ICA algorithm first rearranges them into a random combination (i.e., mixture). The ICA algorithm the searches for the combination of two signal that is most independent.

There are a large number of different ICA algorithms, most available from the internet as Matlab files. They all make the assumption that the input signals, x₁ and x₂ are linear mixtures of the actual underlying “source” signals, S₁ and S₂. They all attempt to find an un-mixing matrix A^-1, that produces source signals (S₁ and S₂) that demonstrate the most independence from one another. The general approach is as shown schematically in Figure 4.

Mathematically stated, the original signals can be recovered using:

where x₁ and x₂ are the observed signals that contain mixtures of the source signals, S₁ and S₂, and A^-1 is the un-mixing matrix that uncovers the source signals.

The various algorithms differ in the strategy they use to search for these independent signals (i.e., the specific optimization algorithm) and the approach they use to quantify independence. Common measures of independence include non-Gaussanity (mixtures are always more Gaussian than their unmixed versions), minimum mutual information, and related entropy measures. A number of algorithms were evaluated for this analysis including Jade (Cardoso, 2005), fastICA, and robustica (Zarzoso, 2010).

While all the algorithns gave similar performance, the robustica algorithm was chosen as it showed slightly more reliable algorithm convergence. This algorithm tests for non-Gaussanity based on normalized kurtosis. Kurtosis is a statistical measure computed from the fourth moment of the data and is larger in un-mixed signals (i.e., independent signals) than in signals that are mixtures of other signals. The algorithm searches for signal combinations that result in the largest kurtosis using a computationally efficient iterative technique. Any independent component with non-zero kurtosis can be extracted using this algorithm. This algorithm was applied to the velocity signals since they provide more details on the dynamic behavior of the responses. The derivative operation is a linear operation and will not affect the mixture and theoretically should have no effect on the outcome of an ICA analysis. However, the improvement in dynamic features aids the search algorithm and improves convergence.

All ICA algorithms produce output signals having normalized amplitude. To determine if the unmixed signals best match version/vergence or left/right eye movements, it is necessary to rescale the output signals before making the comparison. Accordingly, the analysis takes each output and attempts to rescale it to maximize the correlation between the output signal and one of the four candidate responses: left eye movement, right eye movement, version movement, or vergence movement. Correlation was computed between the two velocity signals over the full approximately 1 second data period using the standard correlation equation:

where x and y are the two velocity signals, $\stackrel{-}{x}$ and $\stackrel{-}{y}$ are the means, and σ_x and σ_y are the standard deviations of the velocities. This equation scales the correlation coefficient to be between ±1. A correlation greater than 0.95 was considered a match, but usually the correlations of a match were much higher, often approaching 1.0.

Error Sources

The use of independence measures to determine the underlying neural signals can be undermined by artifacts. Artifacts that affect the response of only one eye such as noise in one channel of eye movement monitor eye will make the left and right eye movement signals appear more independent. This could lead to a false identification of left and right eye movement as the independent components. Conversely, binocular artifacts such as lid motion that affect both channels equally will make the individual eye movement signals look more dependent, more like mixtures since both eye movements will contain similar artifacts. Careful eye movement data collection and subsequent editing of eye movements measurements can eliminate obvious artifacts such as blinks, but as we currently have no criteria for identifying subtle artifacts, it not possible to insure that our data are completely artifact free.

Results

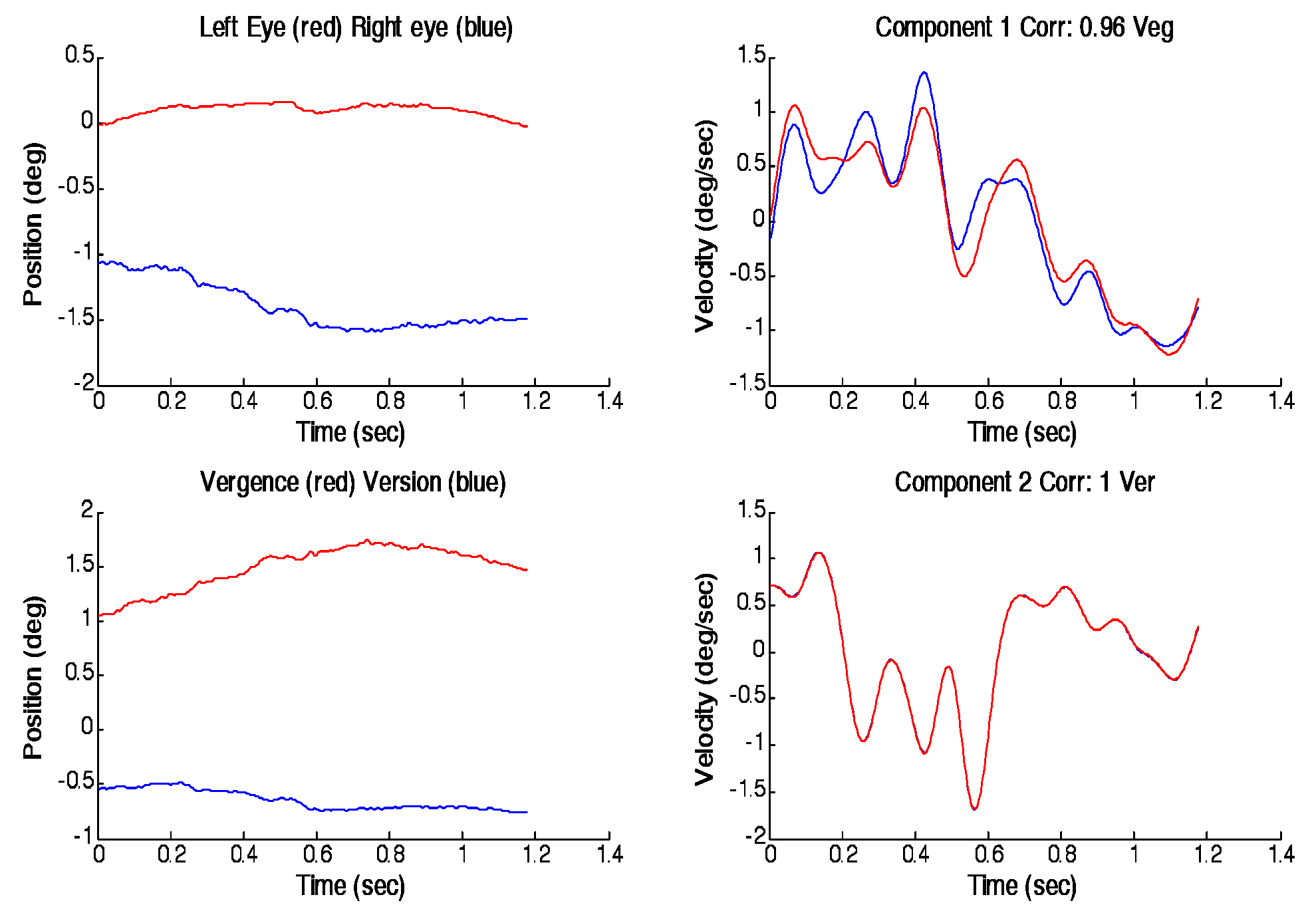
Figure 5 shows a typical fusion sustaining disparity vergence response plotted as left/right and version/vergence responses on the left side with the best matching unmixed velocity traces on the right side. The input to the algorithm was the left and right eye movements, but as noted above, any mixture of left and right eye movements (including version and vergence) gives the same result since the algorithm begins with a random mixture anyway. For this response the best match between ICA and real velocities occurred for a combination of vergence (correlation = 0.96) and version (correlation = 1.0). This match, which occurred most frequently in all subjects, indicates that the slow corrective movements found in the late portion of a disparity vergence fast response are best represented by version and vergence signals in accordance with Hering’s law.

For each subject, a few responses did not converge to stable unmixed velocities and could not be used. Some responses showed the results opposite to those of Figure 6: the best match between the unmixed and actual velocities occurred between left and right movements. An example of such a finding is shown in Figure 6. However, as noted in the Error Sources section of Methods, artifacts that occur in only one channel will cause left and right eye movements to appear more independent. In this response, a comparatively large movement is seen in the right eye only, possibly the result of an error in the eye movement monitor. If this is an artifact, it would explain the anomalous finding, but as we currently have no methodology for definitively classifying artifacts. All subjects had fewer responses for which left and right eye movements were found to be more independent than version and vergence. Some inconsistencies are to be expected given the nature of the analysis, which relies heavily on accurate, noise-free data, and the noise and inaccuracy inherent in eye movement recording (Having considerable experience in both infrared reflection and television-based eye movement monitors, we find that the older infrared method can produce recordings of horizontal eye movements having lower noise in most subjects provided the detectors are carefully aligned by a well-trained operator.).

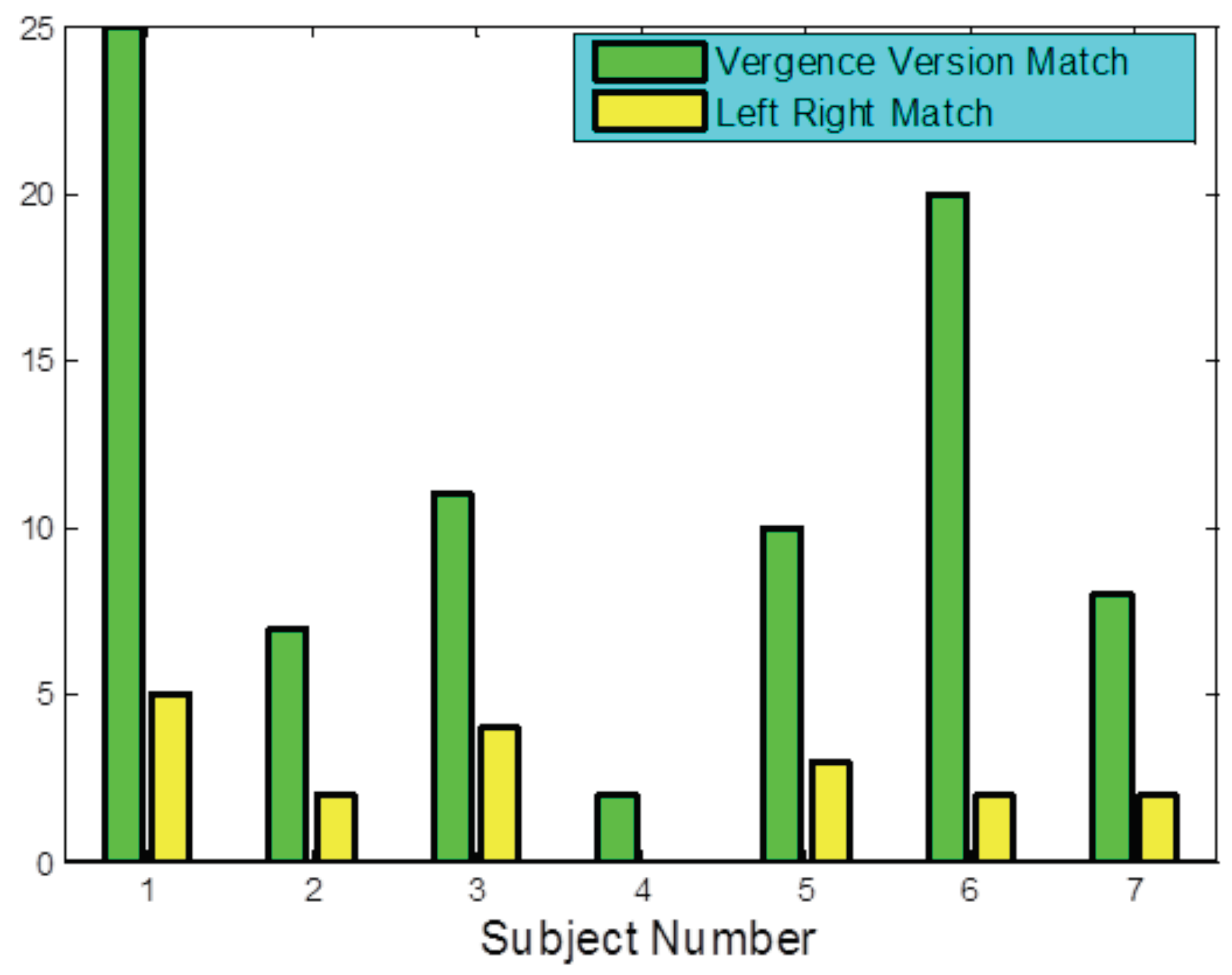
The results of the ICA-based analysis is summarized over all subjects in Figure 7 which shows the number of responses where the best unmixed velocity match occurred between vergence/version velocities (green bars) and left/right velocities (yellow bars). This figure shows that for all subjects, a majority of the responses were found to have version and vergence as the independent components. These differences are stastically significent (p < 0.005) based in a paired right- tailed t-test (since the means of both distributions are positive). This suggests that the slow movements that provide correction of fine tuning following a disparity vergence response are guided by combinations of vergence and version and movements of the left and right eye are actually mixtures of these signals. Those responses that show left and right movements to be more independent could be due to uniocular artifacts which were too small to be identified during editing or could represent a radically different control strategy is employed in some responses.

Discussion

Helmholtz and Herring represent two extremes of eye movement control ranging from pure uniocular to highly coordinated binocular control. With regard to saccade- vergence interactive movements, recent studies support a modified uniocular control from neurophysiological and behavioral evidence (King, 2011; Cullen & VanHorn, 2011, Chen et al, 2011). Yet, the control structure of symmetrical fusion sustaining movements, also called vergence pursuit, is still open to question (Cullen & VanHorn, 2011). A separate set of motorneurons, termed c-group motorneurons, has been found to be active during fusion sustaining vergence in response to symmetrical stimuli. These motorneurons synapse on multiply innervated muscle fibers as opposed to the single innervated twitch fibers that synapse with fast motorneurons (Buttner-Ennever et al., 2001; Wasicky et al., 2004; Ugolini et al., 2006) However, Cullen and VanHorn (2011) report that there is no current evidence for the exclusive use of these motor neurons to drive slow movements. Conversely, they have found motorneurons that respond during periods of both slow and fast (i.e., saccade facilitated) vergence (Sylvestre & Cullen, 2002; Van Horn & Cullen, 2009). It could be that the activation of these special c-group motorneurons and their related muscle fibers depend on the type of slow movement. For example, King (2011) speculates that this motor system could be used for fixation and the fine-tuning of vergence eye position.

The signals analyzed here come at the end of the fusion initiating vergence response and are involved in fine-tuning binocular fixation. Despite their modest dynamics and small size, they are very important in near work as their proper function is needed to reduce eye strain. The responses analyzed here were selected to be saccade-free, but this was not uncommon during the latter portion of the response. In addition, these responses usually involved both conjugate and disconjugate movements. Our ICA-based analysis suggests that in the majority of responses, the movements of the left and right eyes are mixtures of vergence and version, and not the result of fundamental uniocular control signals. Thus, these late fusion sustaining movements are best represented by Eqs. 1, the Hering’s law formulation of binocular control. In a few responses, left and right eye movements are found to be more independent suggesting uniocular control, but these results could have been due to small uniocular artifacts.

In an analysis of eye movement responses to slow version and vergence stimuli, Semmlow et. al. (1998) showed quite different response dynamics depending on which system was controlling the eyes. When a given eye was driven by a smooth disparity vergence ramp stimulus it showed a small oscillatory behavior, but the same eye moving at the same velocity had no oscillation when driven by a purely conjugate ramp stimulus (i.e., smooth pursuit). These experiments evaluated the overall version/vergence slow movement systems including both sensory and motor processes. The significant behavioral differences to the same motor response indicate that they are, at some level, two separate systems. Our ICA-based analysis extends this finding to suggest that slow version and vergence are separate at the motor level.

Conclusion

The disparity vegence response to a symmetrical stimulus consists of an initial, fusion initiating movement followed by a smooth fusion sustaining movement generally composed of version and vergence components. An analysis of the dynamic behavior of isolated fusion sustaining movements, suggests that the individual left and right eye movements are not fundamental, but are the result of a linear addition of version and vergence control components. This supports Hering’s law for the control structure of movements that occur in the latter portion of the disparity vergence response.