The Impact of Fintech Risk on Bank Performance in Africa: The PVAR Approach
Abstract
1. Introduction
2. Literature Review
2.1. Conceptual Framework
2.2. Empirical Review
2.2.1. Studies Related to Financial Innovation and Competition
2.2.2. Studies Related to Competition and Bank Performance/Stability
2.2.3. Studies Related to Financial Innovation and Bank Performance
3. Methodology
3.1. Fintech Financial Stress Indicator Development
3.1.1. Pretest Requirements
Cross-Sectional Dependence Test
Panel Unit Root Test
3.1.2. PVAR Model
4. Empirical Analysis
4.1. Data
4.2. Results and Discussion
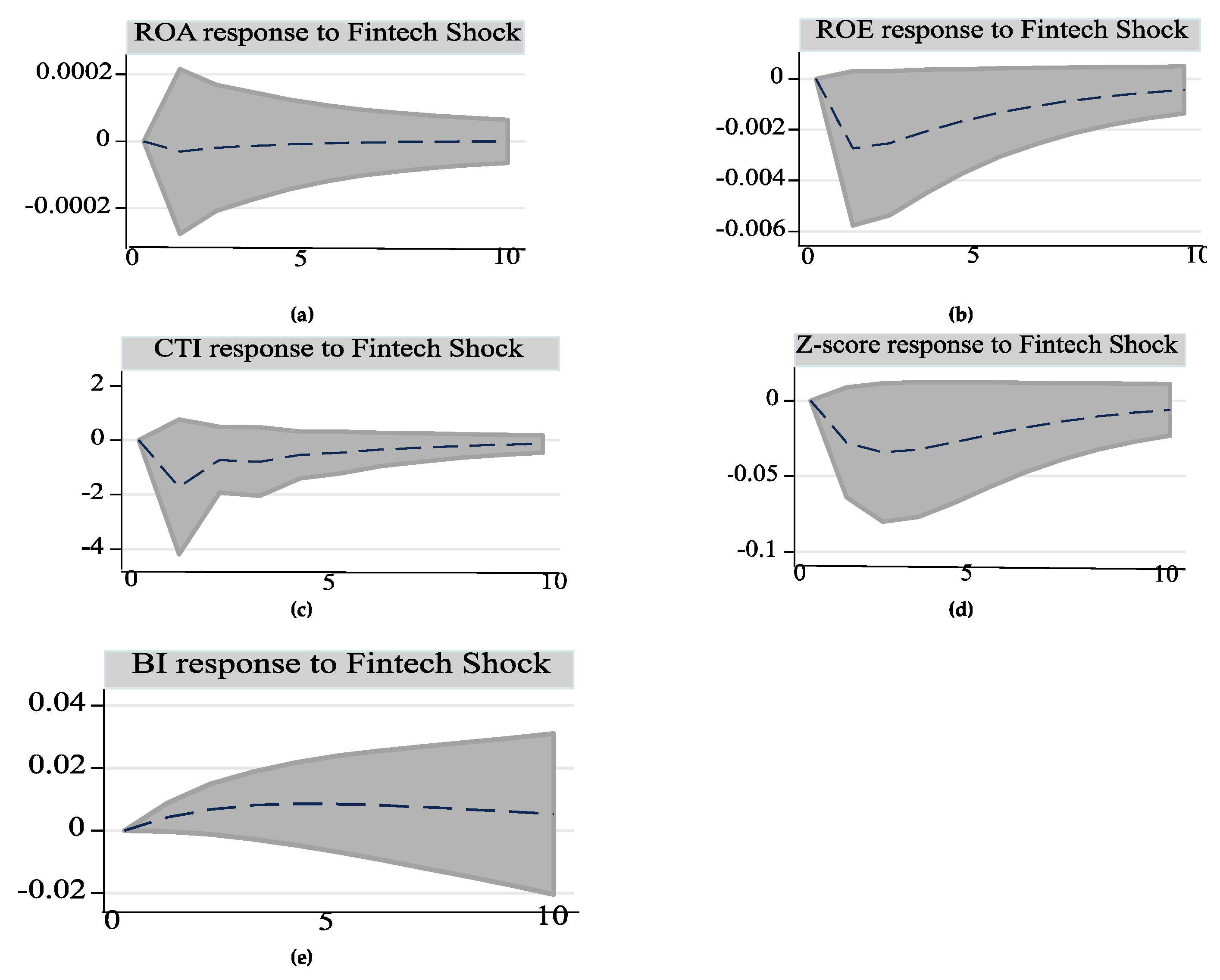
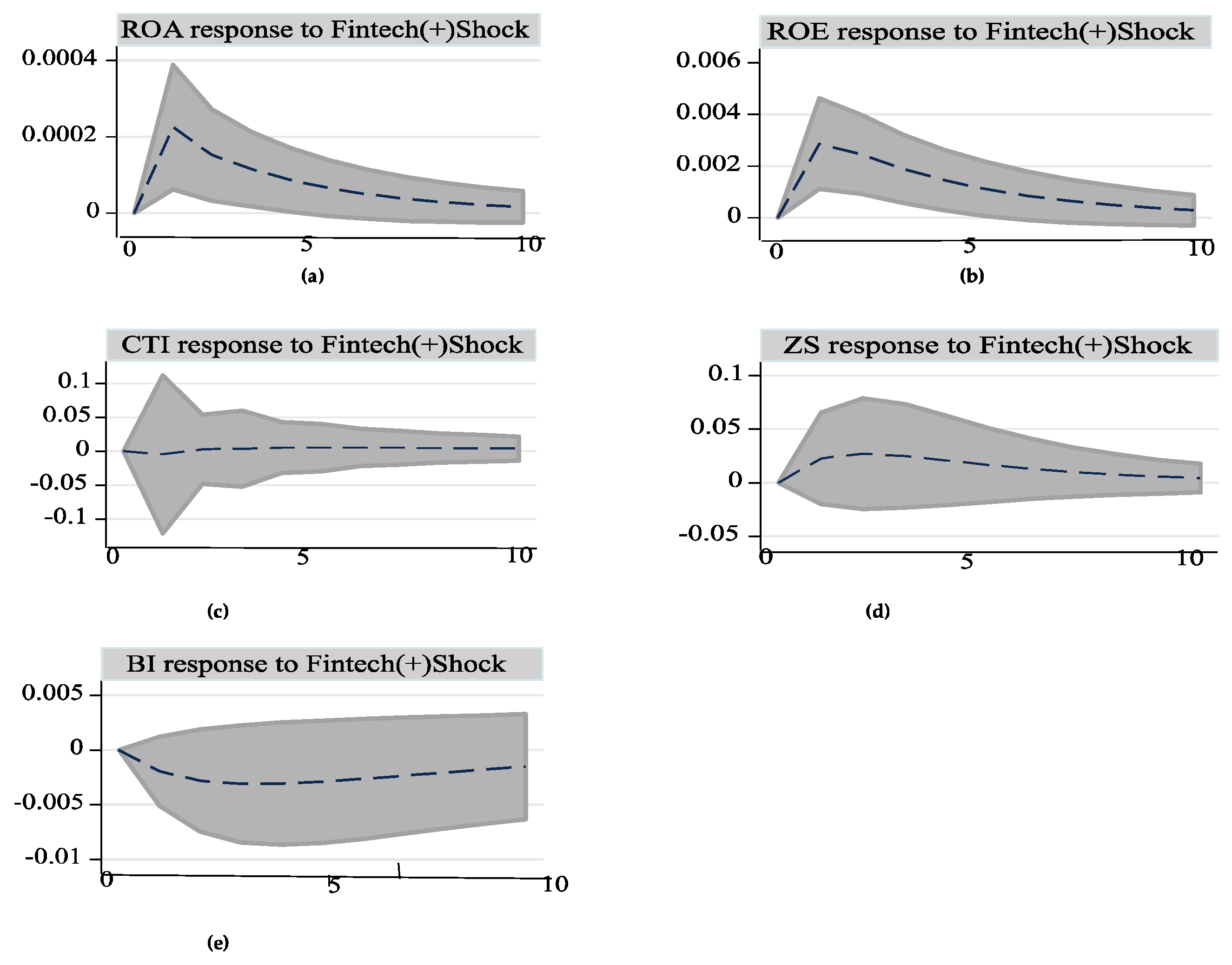
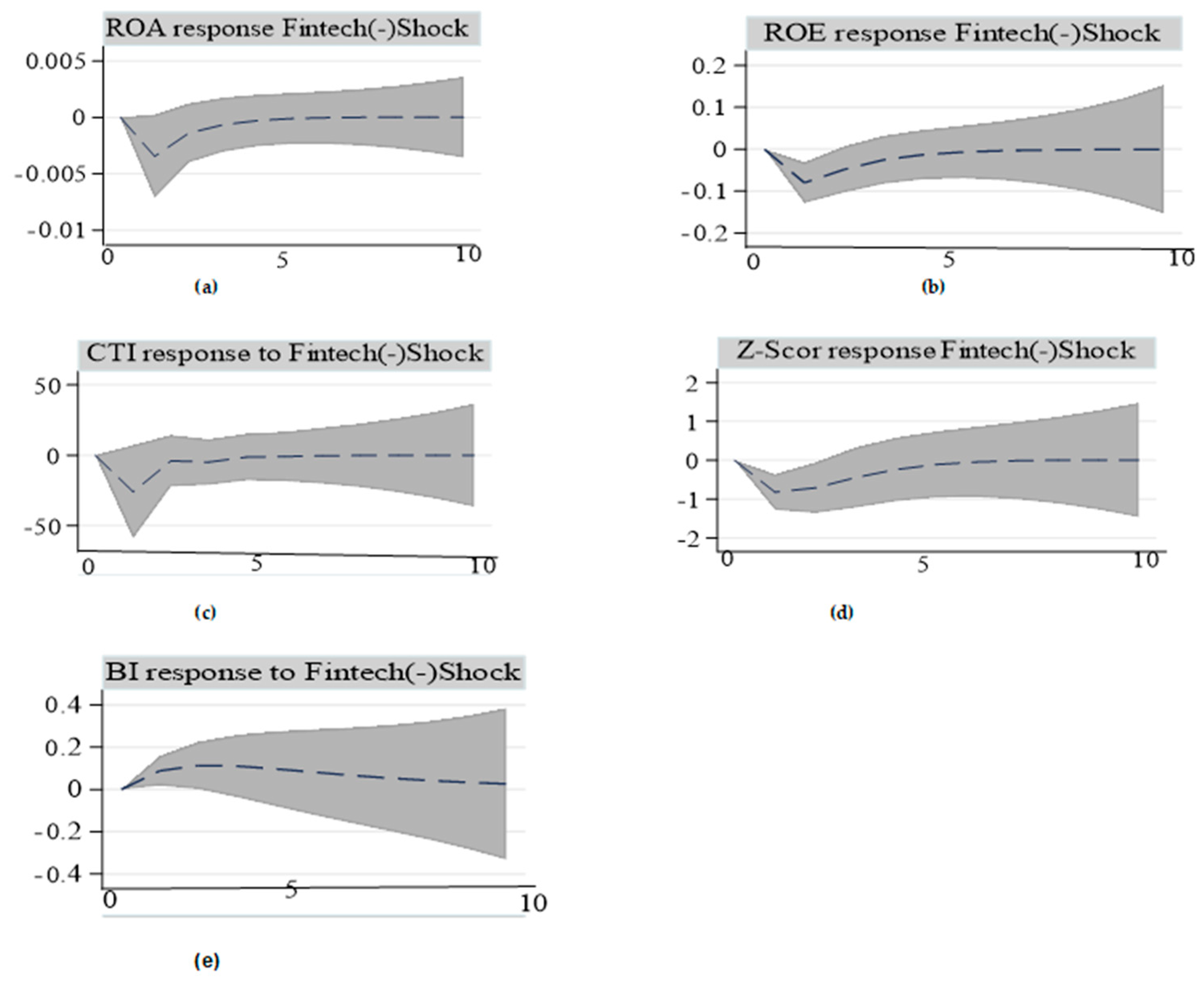
4.2.1. Asymmetric Effects of FFSI on Bank Performance
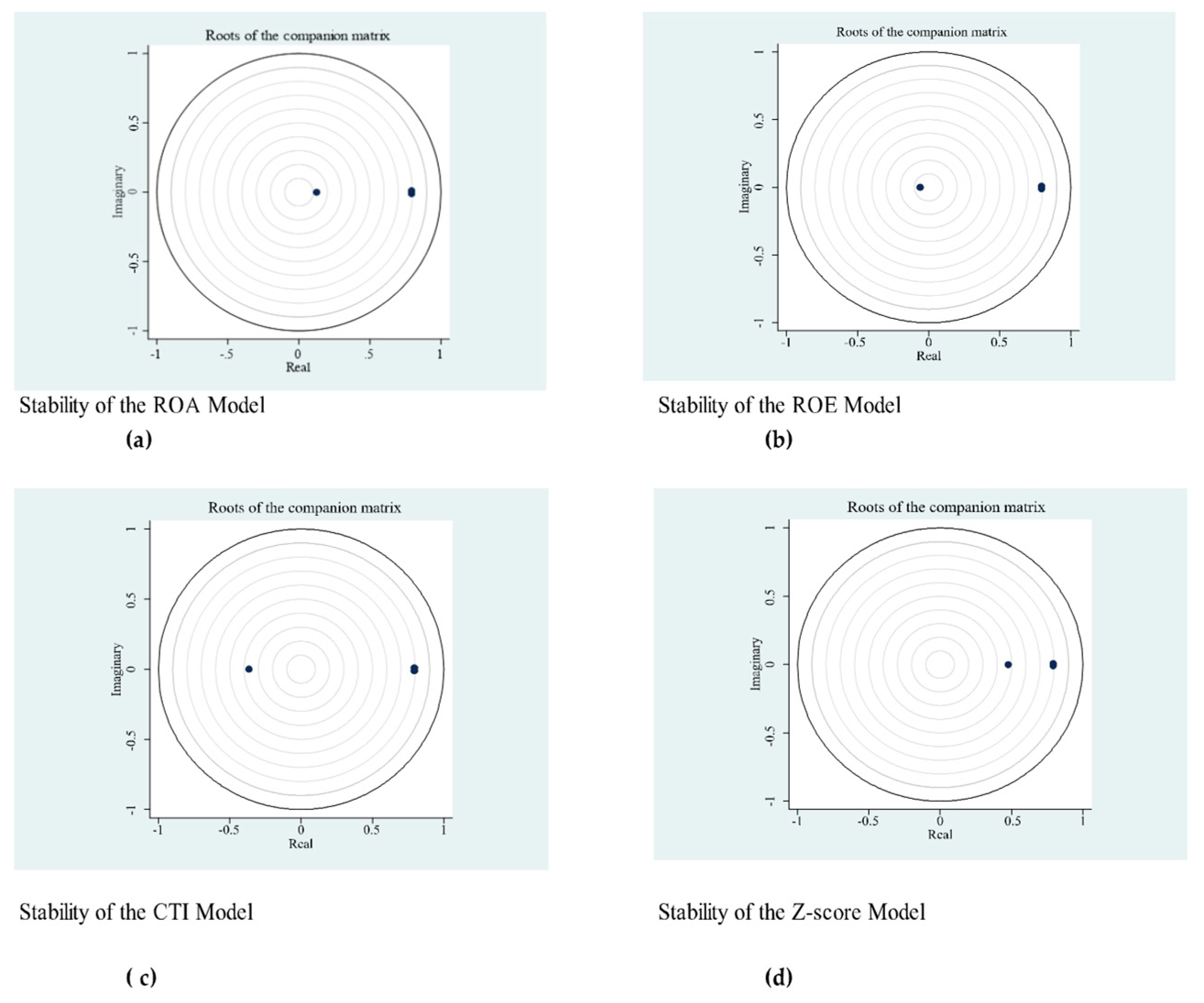
4.2.2. Diagnostic Tests: Stability of the Panel VAR Model
4.2.3. Robustness Check: Granger Non-Causality Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Bank Performance Metrics | ||||
|---|---|---|---|---|
| GMM Estimates | ||||
| ROA | ROE | CTI | Z-Score | |
| ROA (t − 1) | −0.0601 | |||
| (0.106) | ||||
| Fintech (t − 1) | −0.00000784 | −0.000709 * | −0.446 | −0.00715 |
| (0.0000346) | (0.000377) | (0.306) | (0.00544) | |
| BI (t − 1) | 0.000510 | −0.0150 | −2.803 * | 0.0799 |
| (0.00188) | (0.0117) | (1.527) | (0.146) | |
| ROE (t − 1) | 0.125 | |||
| (0.106) | ||||
| CTI (t − 1) | −0.365 ** | |||
| (0.183) | ||||
| Z-Score (t − 1) | 0.473 *** | |||
| (0.0425) | ||||
| GMM Estimates Competition | ||||
| ROA (t − 1) | −0.0388 | |||
| (0.0601) | ||||
| Fintech (t − 1) | 0.00111 * | 0.00110 * | 0.00111 * | 0.00113 * |
| (0.000599) | (0.000598) | (0.000599) | (0.000609) | |
| BI (t − 1) | 0.809 *** | 0.809 *** | 0.809 *** | 0.809 *** |
| (0.124) | (0.124) | (0.124) | (0.123) | |
| ROE (t − 1) | −0.0147 | |||
| (0.0172) | ||||
| CTI (t − 1) | −0.00000172 | |||
| (0.00000921) | ||||
| Z-Score (t − 1) | 0.00242 | |||
| (0.00664) | ||||
| N | 1312 | 1312 | 1312 | 1312 |
| Bank Performance Metrics GMM Estimates | ||||
|---|---|---|---|---|
| ROA | ROE | CTI | Z-Score | |
| ROA (t − 1) | −0.0755 | |||
| (0.0826) | ||||
| FintechP (t − 1) | 0.0000515 * | 0.000657 ** | −0.00104 | 0.00520 |
| (0.0000204) | (0.000213) | (0.0135) | (0.00464) | |
| BI (t − 1) | 0.000161 | −0.0202 | −2.826 | −0.00145 |
| (0.00171) | (0.0128) | (2.031) | (0.122) | |
| ROE (t − 1) | 0.0899 | |||
| (0.0551) | ||||
| CTI (t − 1) | −0.359 * | |||
| (0.179) | ||||
| Z-score (t − 1) | 0.443 *** | |||
| (0.0404) | ||||
| Competition GMM Estimates | ||||
| ROA (t − 1) | −0.00698 | |||
| (0.0268) | ||||
| FintechP (t − 1) | −0.000373 | −0.000367 | −0.000373 | −0.000447 |
| (0.000360) | (0.000360) | (0.000360) | (0.000362) | |
| BI (t − 1) | 0.802 *** | 0.802 *** | 0.802 *** | 0.801 *** |
| (0.103) | (0.103) | (0.103) | (0.103) | |
| ROE (t − 1) | −0.00898 | |||
| (0.00877) | ||||
| CTI (t − 1) | 0.00000735 | |||
| (0.0000126) | ||||
| Z-score (t − 1) | 0.00921 | |||
| (0.00748) | ||||
| N | 1312 | 1312 | 1310 | 1312 |
| Performance Metrics GMM Estimates | ||||
|---|---|---|---|---|
| ROA | ROE | CTI | Z-Score | |
| ROA (t − 1) | −0.0736 | |||
| (0.0819) | ||||
| FintechN (t − 1) | −0.00187 | −0.0432 ** | −14.04 | −0.445 *** |
| (0.000994) | (0.0132) | (9.836) | (0.132) | |
| BI (t − 1) | −0.000573 | −0.0371 | −8.443 | −0.168 |
| (0.00200) | (0.0202) | (6.721) | (0.211) | |
| ROE (t − 1) | 0.105 | |||
| (0.0661) | ||||
| CTI (t − 1) | −0.333 | |||
| (0.178) | ||||
| Z-Score (t − 1) | 0.372 *** | |||
| Competition GMM Estimates | ||||
| ROA (t − 1) | −0.0504 | |||
| (0.0820) | ||||
| FintechN (t − 1) | 0.0478 * | 0.0468 * | 0.0469 * | 0.0565 * |
| (0.0191) | (0.0187) | (0.0187) | (0.0220) | |
| BI (t − 1) | 0.822 *** | 0.821 *** | 0.821 *** | 0.822 *** |
| (0.106) | (0.106) | (0.106) | (0.107) | |
| ROE (t − 1) | −0.0247 | |||
| (0.0226) | ||||
| CTI (t − 1) | −0.0000812 | |||
| (0.0000689) | ||||
| Z-Score (t − 1) | 0.0182 | |||
| (0.00991) | ||||
| N | 1312 | 1312 | 1310 | 1312 |
| 1 | Fintech Partnerships: Synergy in Finance: The Impact of Fintech Partnerships on Nigerian Banks-FasterCapital. |
| 2 | H1a–H4a indicate the alternative hypothesis. |
| 3 | https://www.worldbank.org/en/publication/gfdr/gfdr-2016/background/banking-competition. Accessed on 9 May 2025. |
| 4 | Banking Competition. |
| 5 | Not all indicators featured in Bu et al. (2023) are utilized in this study due to limitations in data availability. Additionally, in contrast to Bu et al. (2023), this research incorporates additional financial inclusion factors, including MoMo platforms and deposits/loans held with credit unions. It is important to note that in certain African regions, credit unions evolved from traditional savings clubs (Stokvel) before formally transitioning into credit unions or deposit taking institutions. |
| 6 | is the characteristic polynomial, and its roots are the eigenvalues. |
| 7 | The eigen vectors are linearly dependent, as for every computed eigenvalue, , we need to solve for non-zero such that . |
| 8 | Where and . Hence the null hypothesis of unit root becomes . Moreover, , subsequently substituting back into Equation (17) one gets: as in Equation (16). |
| 9 | The PVAR models are estimated with a single lag, dictated by the short length of our panel, which precluded the generation of valid statistics for optimal lag length selection. Employing one lag also mitigates the risk of overfitting associated with the inclusion of multiple lags. Furthermore, one lag of the endogenous variable is utilized as an instrumental variable in the GMM estimation to address concerns related to instrument proliferation. |
| 10 | The results can be made available upon request. The results of non-response should be taken with caution due to a small sample size. |
| 11 | The models are also stable for positive and negative FFSI shocks. |
References
- Ahmed, O. N., & Wamugo, L. (2018). Financial innovation and the performance of commercial banks in Kenya. International Journal of Current Aspects in Finance, 4(2), 133–147. [Google Scholar]
- Allen, F., & Gale, D. (2004). Competition and financial stability. Journal of Money, Credit and Banking, 36(3), 453–480. [Google Scholar] [CrossRef]
- Anarigide, D. A., Issahaku, H., & Dary, S. K. (2023). Drivers of financial innovation in sub-Saharan Africa. SN Business & Economics, 3(9), 165. [Google Scholar] [CrossRef]
- Andrews, D. W. K., & Lu, B. (2001). Consistent model and moment selection procedures for GMM estimation with application to dynamic panel data models. Journal of Econometrics, 101, 123–164. [Google Scholar] [CrossRef]
- Andries, A. M., & Capraru, B. (2014). The nexus between competition and efficiency: The European banking industries experience. International Business Review, 23, 566–579. [Google Scholar] [CrossRef]
- Ashiru, O., Balogun, G., & Paseda, O. (2023). Research in globalization financial innovation and bank financial performance: Evidence from Nigerian deposit money banks. Research in Globalization, 6, 100120. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. (2024). Digitalisation of finance. Basel Committee on Banking Supervision. [Google Scholar]
- Bejar, P., Ishi, K., Komatsuzaki, T., Shibata, I., Sin, J., & Tambunlertchai, S. (2022). Can fintech foster competition in the banking system in Latin America and the Caribbean? Latin American Journal of Central Banking, 3(2), 100061. [Google Scholar] [CrossRef]
- Benchimol, J., & Bozou, C. (2024). Desirable banking competition and stability. Journal of Financial Stability, 73, 101266. [Google Scholar] [CrossRef]
- Berger, A. N., & Mester, L. J. (2003). Explaining the dramatic changes in performance of US banks: Technological change, deregulation, and dynamic changes in competition. Journal of Financial Intermediation, 12(1), 57–95. [Google Scholar] [CrossRef]
- Berryman, A. A. (1992). The origins and evolution of predator-prey theory. Ecology, 73(5), 1530–1535. [Google Scholar] [CrossRef]
- Browne, J. (2019). Nigeria’s banking oligopolies: Case for review. Nigerian Tribune. [Google Scholar]
- Bu, Y., Du, X., Li, H., Yu, X., & Wang, Y. (2023). Research on the FFSI early warning based on the MS-VAR model: An empirical analysis in China. Global Finance Journal, 58, 100898. [Google Scholar] [CrossRef]
- Canova, F., & Ciccarelli, M. (2013). Panel vector autoregressive models: A survey (working paper No 1507). European Central Bank. [Google Scholar]
- Chassang, S., & Ortner, J. (2023). Regulating collusion. Annual Review of Economics, 15, 177–204. [Google Scholar] [CrossRef]
- Chipeta, C., & Mapela, L. (2024). The effects of Basel III capital and liquidity (South African reserve bank working paper series-WP/24/17). South African Reserve Bank. [Google Scholar]
- Claessens, S. (2009). Competition in the financial sector: Overview of competition policies. Oxford Journals, 24(1), 83–118. [Google Scholar]
- De Hoyos, R. E., & Sarafidis, V. (2006). Testing for cross-sectional dependence in panel data models. The Stata Journal, 6, 482–496. [Google Scholar] [CrossRef]
- Dong, Q., Du, Q., & Min, A. (2024). Interplay between oil prices, country risks, and stock returns in the context of global conflict: A PVAR approach. Research in International Business and Finance, 72, 102545. [Google Scholar] [CrossRef]
- Dumitrescu, E., & Hurlin, C. (2012). Testing for granger non-causality in heterogeneous panels. Economic Modelling, 29, 1450–1460. [Google Scholar] [CrossRef]
- Emery, D. R., Finnerty, J. D., & Stowe, J. D. (2017). Corporate financial management (5th ed.). Wohl Publishing. [Google Scholar]
- Fang, J., Lau, C. M., Lu, Z., Tan, Y., & Zhang, H. (2019). Bank performance in China: A perspective from bank efficiency, risk-taking and market competition. Pacific-Basin Finance Journal, 56, 290–309. [Google Scholar] [CrossRef]
- Granger, C. W. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424–438. [Google Scholar] [CrossRef]
- Greene, W. H. (2002). Econometric analysis (5th ed.). Prentice Hall. [Google Scholar]
- Im, K. S., Pesaran, M. H., & Shin, Y. (2003). Testing for unit roots in heterogeneous panels. Journal of Econometrics, 115(1), 53–74. [Google Scholar] [CrossRef]
- Jia, K., He, Y., & Mohsin, M. (2023). Digital financial and banking competition network: Evidence from China. Frontiers in Psychology, 13, 1104120. [Google Scholar] [CrossRef] [PubMed]
- Khalaf, B. A., Awad, A. B., Ahmed, O., & Gharios, R. T. (2023). The role of FinTech in determining the performance of banks: The case of Middle East & North Africa (MENA) region. International Journal of Membrane Science and Technology, 10(3), 1525–1535. [Google Scholar] [CrossRef]
- KPMG. (2022). Pulse of fintech H2’21. Available online: https://assets.kpmg.com/content/dam/kpmg/xx/pdf/2022/02/pulse-of-fintech-h2-21.pdf (accessed on 10 February 2024).
- Kulu, E., Opoku, A., Gbolonyo, E., & Kodo, M. A. T. (2022). MoMo transactions and banking sector performance in Ghana. Heliyon, 8, e10761. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z., Feng, Q., & Li, H. (2024). Digital finance, bank competition shocks and operational efficiency of local commercial banks in Western China. Pacific-Basin Finance Journal, 85, 102377. [Google Scholar] [CrossRef]
- Lopez, L., & Weber, S. (2017). Testing for granger causality in panel data. The Stata Journal, 17(4), 972–984. [Google Scholar] [CrossRef]
- Lütkepohl, H. (2005). New introduction to multiple time series analysis. Springer. [Google Scholar]
- Mabe, Q. M., & Simo-Kengne, B. D. (2023). Relative importance of time, country and bank-specific effects on bank performance: A three-level hierarchical approach. African Review of Economics and Finance, 15, 1–25. [Google Scholar]
- Mas-Colell, A., Whinston, M. D., & Green, J. R. (1995). Microeconomic theory. Oxford University Press. [Google Scholar]
- Mhlongo, N., Kunjal, D., & Muzindutsi, P.-F. (2025). The influence of fintech innovations on bank competition and performance in South Africa. Modern Finance, 3(2), 1–12. [Google Scholar] [CrossRef]
- Murinde, V., Rizopoulos, E., & Zachariadis, M. (2022). International review of financial analysis the impact of the FinTech revolution on the future of banking: Opportunities and risks. International Review of Financial Analysis, 81, 102103. [Google Scholar] [CrossRef]
- Mushonga, M., Arun, T. G., & Marwa, N. W. (2018). Technological forecasting & social change drivers, inhibitors and the future of co-operative financial institutions: A Delphi study on South African perspective. Technological Forecasting & Social Change, 133, 254–268. [Google Scholar] [CrossRef]
- Nekesa, S. M., & Olweny, T. (2018). Effect of financial innovation on financial performance: A case study of deposit-taking savings and credit cooperative societies in Kajiado county. International Journal of Social and Information Technology, V(IV). [Google Scholar]
- Niehans, J. (1983). Financial innovation, multinational banking and monetary policy. Journal of Banking and Finance, 7, 537–551. [Google Scholar] [CrossRef]
- Okapor, C. (2023). Top fintech companies in Africa. Business Insider Africa. [Google Scholar]
- Oriji, O., Shonibare, M. A., Daraojimba, R. E., Abitoye, O., & Darojimba, C. (2023). Financial technology evolution in Africa: A comprehensive review of legal frameworks and implications for AI-driven financial services. International Journal of Management and Entrepreneurship Research, 5(12), 929–951. [Google Scholar] [CrossRef]
- Pesaran, M. H. (2004). General diagnostic tests for cross section dependence in panels (Cambridge working papers in economics No. 0435). University of Cambridge, Faculty of Economics. [Google Scholar]
- Petersen, F. (2019). SA’s banking oligopoly and the forex cartel, IOL. Available online: https://www.iol.co.za/sundayindependent/analysis/sas-banking-oligopoly-and-the-forex-cartel-2654b258-1ebc-464e-9174-41352bc7ce68 (accessed on 19 February 2025).
- Shehadeh, M., Alshurafat, H., & Arabiat, O. (2024). Inverting the paradigm: Digital transformation’s impact on firm performance and the counterintuitive role of gender. Competitiveness Review: An International Business Journal, 35(2), 371–390. [Google Scholar] [CrossRef]
- Silber, W. L. (1983). The process of financial. American Economic Association, 73(2), 89–95. [Google Scholar]
- Simo-Kengne, B. D., Gupta, R., & Bittencourt, M. (2013). The impact of house prices on consumption in South Africa: Evidence from provincial-level panel VARs. Housing Studies, 28(8), 1133–1154. [Google Scholar] [CrossRef]
- Stata Corp. (2023). Stata statistical software: Release 18. STATA reference manual. StataCorp LLC. [Google Scholar]
- Stigler, G. J. (1964). A theory of oligopoly. Journal of Political Economy, 72(1), 44–61. [Google Scholar] [CrossRef]
- Timm, S. (2019). Here are eight SA fintechs that local banks are working with. Ventureburn. [Google Scholar]
- Walyaula, A. (2007). List of fintech startups in Kenya, Kahawa Tungu. Available online: https://kahawatungu.com/list-of-fintech-startups-in-kenya (accessed on 9 April 2025).
- Wang, W., Feng, C., & Dang, X. (2021). Research on the impact of market competition on the operating performance of rural commercial banks—Path inspection based. In J. Xu, F. P. García Márquez, M. H. Ali Hassan, G. Duca, A. Hajiyev, & F. Altiparmak (Eds.), Proceedings of the fifteenth international conference on management science and engineering management (pp. 788–811). Springer International Publishing. [Google Scholar] [CrossRef]
- Werker, C. (2003). Innovation, market performance, and competition: Lessons from a product life cycle model. Technovation, 23, 281–290. [Google Scholar] [CrossRef]
- Xu, F., Kasperskaya, Y., & Sagarra, M. (2025). The impact of FinTech on bank performance: A systematic literature review. Digital Business, 5(2), 100131. [Google Scholar] [CrossRef]
- Zamil, R., & Lawson, A. (2022). Gatekeeping the gatekeepers: When big techs and fintechs own banks—Benefits, risks and policy options. Bank for International Settlements, Financial Stability Institute. [Google Scholar]
- Zhao, J., Li, X., Yu, C., Chen, S., & Lee, C. (2022). Riding the FinTech innovation wave: FinTech, patents and bank performance. Journal of International Money and Finance, 122, 102552. [Google Scholar] [CrossRef]
- Zhu, K., & Guo, L. (2024). Financial technology, inclusive finance and bank performance. Finance Research Letters, 60, 104872. [Google Scholar] [CrossRef]
- Zribi, W., Boufateh, T., Lahouel, B. B., & Urom, C. (2024). Uncertainty shocks, investor sentiment and environmental performance: Novel evidence from a PVAR approach. International Review of Financial Analysis, 93, 103196. [Google Scholar] [CrossRef]

| Model Parameters | Interpretations and Assumptions |
|---|---|
| The growth rate of cartel customers. | |
| The diminishing rate of cartel customers when they interact with the violator customers. | |
| The percentage rate of cartel customers who leave the cartel bank without any interaction with the violating banks’ customers. The assumption is that customers who leave banks that conform to the cartel agreement become the violators’ customers. | |
| The death rate of the violators’ customers or customers who switch to mattress banking. | |
| The growth rate of the violators’ customers when they interact with the cartels’ customers. |
| Metric Type | Level 1 Indicators | Secondary Indicators |
|---|---|---|
| Fintech companies | Market risk | MoMo growth rate |
| Stoxx Global Fintech volatility | ||
| Internet use | ||
| Deposits and loans with credit unions | ||
| Banking-financial institutions | Digital operational risk | ATM growth rate |
| Branch growth rate | ||
| Operational risk | Non-performing loan ratio | |
| Capital adequacy ratio | ||
| Provision for loan loss reserves | ||
| Market risk | Liquidity ratio | |
| Net interest margin | ||
| Financial market volatility | ||
| Non-banking financial institutions | Securities market cycle risk | Treasury bill rates |
| Peripheral services | Economic environment | Year-on-year CPI |
| GDP growth rate | ||
| Finance | Financial environment | Net loans-to-total deposits of financial institutions |
| External environment | Technological environment | Secured internet servers R&D growth rate |
| Network environment/cyber crime | Crime rate |
| Description | Variable | Source |
|---|---|---|
| The ratio of net income to equity | ROE | Thomson Reuters |
| The ratio of net income to total assets | ROA | Thomson Reuters |
| Cost-to-income ratio | CTI | Thomson Reuters |
| The difference between ROA and its mean over the standard deviation of ROA | Z-score | Derived by the author |
| Fintech Financial Stress Index | FFSI | Derived by the author |
| Variable | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| ROA | 1394 | 0.009 | 0.054 | −1.310 | 0.623 |
| ROE | 1394 | 0.188 | 0.412 | −10.000 | 1.392 |
| CTI | 1394 | −2.167 | 61.257 | −1379.000 | 327.528 |
| Z-score | 1394 | 0.000 | 0.986 | −5.066 | 4.902 |
| FFSI | 1394 | 0.387 | 19.072 | −26.753 | 67.461 |
| BI | 1394 | −0.205 | 0.366 | −2.578 | 0.240 |
| Factors | Component 1 |
|---|---|
| Loan to deposit ratio | 0.3589 |
| Leverage ratio | 0.2129 |
| Liquidity (current liability: current assets) | 0.2652 |
| Non-performing loans | −0.2713 |
| Net interest margin | 0.0741 |
| Tier 1 capital ratio | −0.299 |
| Loan loss reserves | −0.0029 |
| Market volatility | −0.0022 |
| Fin tech volatility | 0.0164 |
| Rate of change of MoMo transactions | −0.0833 |
| Rate of change in the number of bank branches | 0.2643 |
| Rate of change in the number of ATMs | 0.3254 |
| Internet use per 100 individuals | −0.3095 |
| Treasury bill rates | −0.2165 |
| Consumer price index (CPI) | 0.2552 |
| GDP | 0.2223 |
| Rate of change in the number of secured internet servers | −0.0939 |
| Crime rate | −0.2709 |
| Research and development | 0.0219 |
| Deposits in credit unions | 0.2308 |
| Loans issued by credit unions | −0.1046 |
| ROA | ROE | CTI | Z-Score | FFSI | BI | |
|---|---|---|---|---|---|---|
| ROA | 1.000 | |||||
| ROE | 0.8165 * | 1.000 | ||||
| CTI | 0.019 | −0.012 | 1.000 | |||
| Z-score | 0.3214 * | 0.2259 * | −0.039 | 1.000 | ||
| FFSI | 0.003 | −0.011 | 0.0704 * | −0.008 | 1.000 | |
| BI | 0.018 | 0.0713 * | −0.036 | −0.006 | 0.1910 * | 1.000 |
| Models | Pesaran Test Statistic | Probability |
|---|---|---|
| ROA | 3.535 *** | 0.0004 |
| ROE | 3.973 *** | 0.0001 |
| CTI | 9.649 *** | 0.0000 |
| Z-Score | 3.135 *** | 0.0017 |
| BI | 21.212 *** | 0.0000 |
| Variables | Statistics | p-Value | Order of Integration |
|---|---|---|---|
| ROA | −21.65 *** | 0.0000 | I(0) |
| ROE | −17.037 *** | 0.0000 | I(0) |
| CTI | −22.29 *** | 0.0000 | I(0) |
| Z-score | −12.11 *** | 0.0000 | I(0) |
| FFSI | −10.03 *** | 0.0300 | I(0) |
| BI | −9.71 *** | 0.0000 | I(0) |
| ROA | ROE | CTI | Z-Score | ||||
|---|---|---|---|---|---|---|---|
| Hypothesis | Hypothesis | Hypothesis | Hypothesis | ||||
| BI ROA | 0.074 | BI ROE | 1.65 | BI CTI | 3.37 * | BI Z-score | 0.302 |
| Fintech ROA | 0.051 | Fintech ROE | 3.537 * | Fintech CTI | 2.118 | Fintech Z-score | 1.729 |
| ROA BI | 0.416 | ROE BI | 0.733 | CTI BI | 0.035 | Z-score BI | 0.133 |
| Fintech BI | 3.44 * | Fintech BI | 3.389 * | Fintech BI | 3.427 | Fintech BI | 3.427 * |
| ROA Fintech | 0.089 | ROE Fintech | 0.201 | CTI Fintech | 0.165 | Z-score Fintech | 0.512 |
| BI Fintech | 0.93 | BI Fintech | 0.916 | BI Fintech | 0.932 | BI Fintech | 1.23 |
| Positive Fintech | Positive Fintech | Positive Fintech | Positive Fintech | ||||
| BI ROA | 0.009 | BI ROE | 2.497 | BI CTI | 1.936 | BI Z-score | 0.002 |
| Fintech ROA | 6.394 *** | Fintech ROE | 9.542 ** | Fintech CTI | 0.006 | Fintech Z-score | 1.255 |
| ROA BI | 0.068 | ROE BI | 1.049 | CTI BI | 0.338 | Z-score BI | 1.515 |
| Fintech BI | 1.074 | Fintech BI | 1.041 | Fintech BI | 1.075 | Fintech BI | 1.522 |
| ROA Fintech | 1.507 | ROE Fintech | 1.661 | CTI Fintech | 2.165 | Z-score Fintech | 0.042 |
| BI Fintech | 0.215 | BI Fintech | 0.292 | BI Fintech | 0.243 | BI Fintech | 0.042 |
| Negative Fintech | Negative Fintech | Negative Fintech | Negative Fintech | ||||
| BI ROA | 0.082 | BI ROE | 3.367 * | BI CTI | 1.578 | BI Z-score | 0.639 |
| Fintech ROA | 3.527 * | Fintech ROE | 10.664 ** | Fintech CTI | 2.038 | Fintech Z-score | 11.297 *** |
| ROA BI | 0.378 | ROE BI | 1.195 | CTI BI | 1.386 | Z-score BI | 3.367 * |
| Fintech BI | 6.262 *** | Fintech BI | 6.271 ** | Fintech BI | 6.28 ** | Fintech BI | 6.591 *** |
| ROA Fintech | 0.24 | ROE Fintech | 0.105 | CTI Fintech | 0.041 | Z-score Fintech | 0.113 |
| BI Fintech | 1.193 | BI Fintech | 1.25 | BI Fintech | 1.235 | BI Fintech | 1.174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mabe, Q.M.; Simo-Kengne, B.D. The Impact of Fintech Risk on Bank Performance in Africa: The PVAR Approach. J. Risk Financial Manag. 2025, 18, 456. https://doi.org/10.3390/jrfm18080456
Mabe QM, Simo-Kengne BD. The Impact of Fintech Risk on Bank Performance in Africa: The PVAR Approach. Journal of Risk and Financial Management. 2025; 18(8):456. https://doi.org/10.3390/jrfm18080456
Chicago/Turabian StyleMabe, Queen Magadi, and Beatrice Desiree Simo-Kengne. 2025. "The Impact of Fintech Risk on Bank Performance in Africa: The PVAR Approach" Journal of Risk and Financial Management 18, no. 8: 456. https://doi.org/10.3390/jrfm18080456
APA StyleMabe, Q. M., & Simo-Kengne, B. D. (2025). The Impact of Fintech Risk on Bank Performance in Africa: The PVAR Approach. Journal of Risk and Financial Management, 18(8), 456. https://doi.org/10.3390/jrfm18080456






