Hedging via Perpetual Derivatives: Trinomial Option Pricing and Implied Parameter Surface Analysis
Abstract
1. Introduction
2. The Perpetual Derivative
3. Trinomial Tree Model
4. Parameter Calibration and Continuous-Time Limits
4.1. Estimation of and
4.2. Estimation of Extreme Values for and
5. Application to Empirical Data
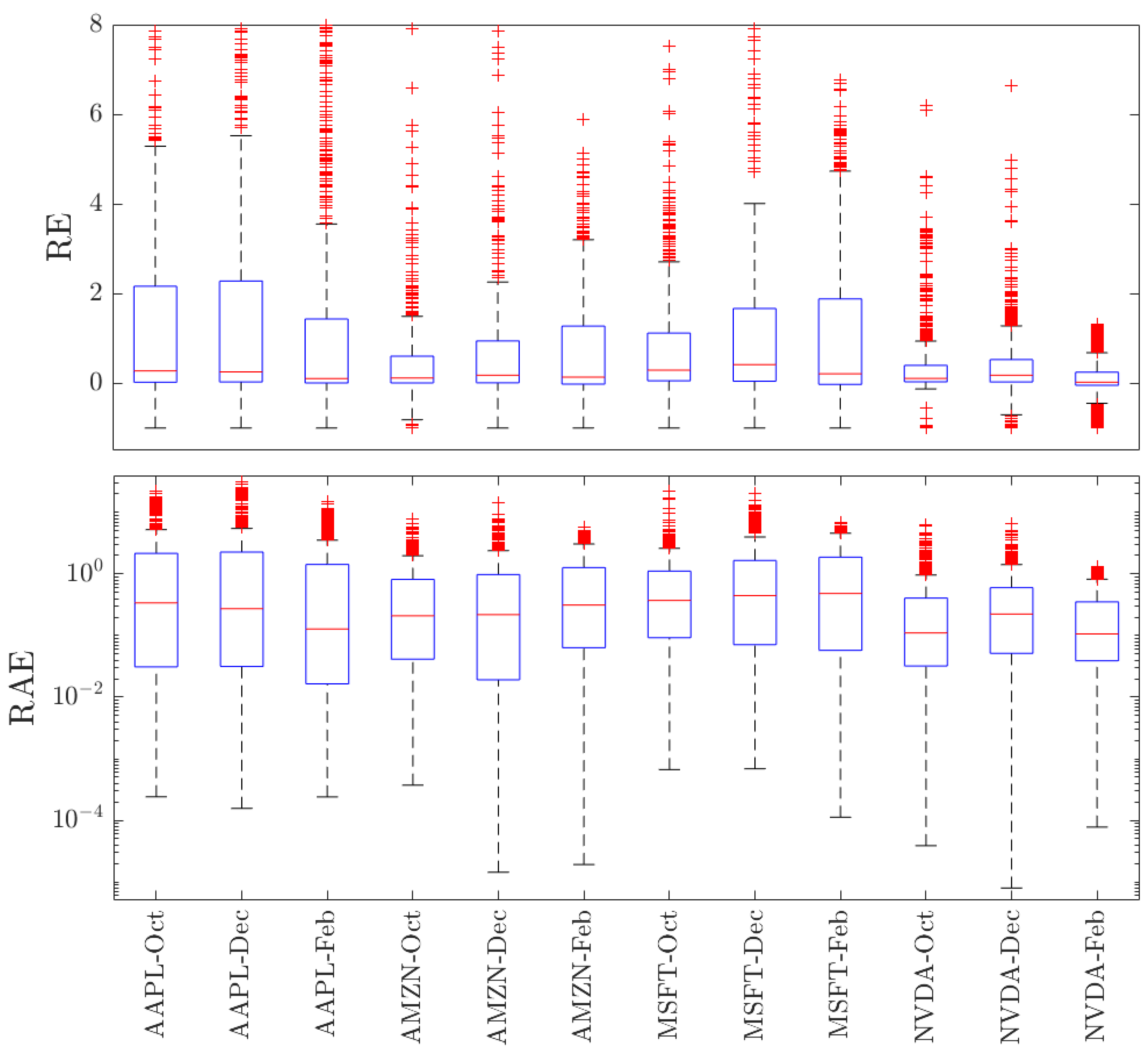
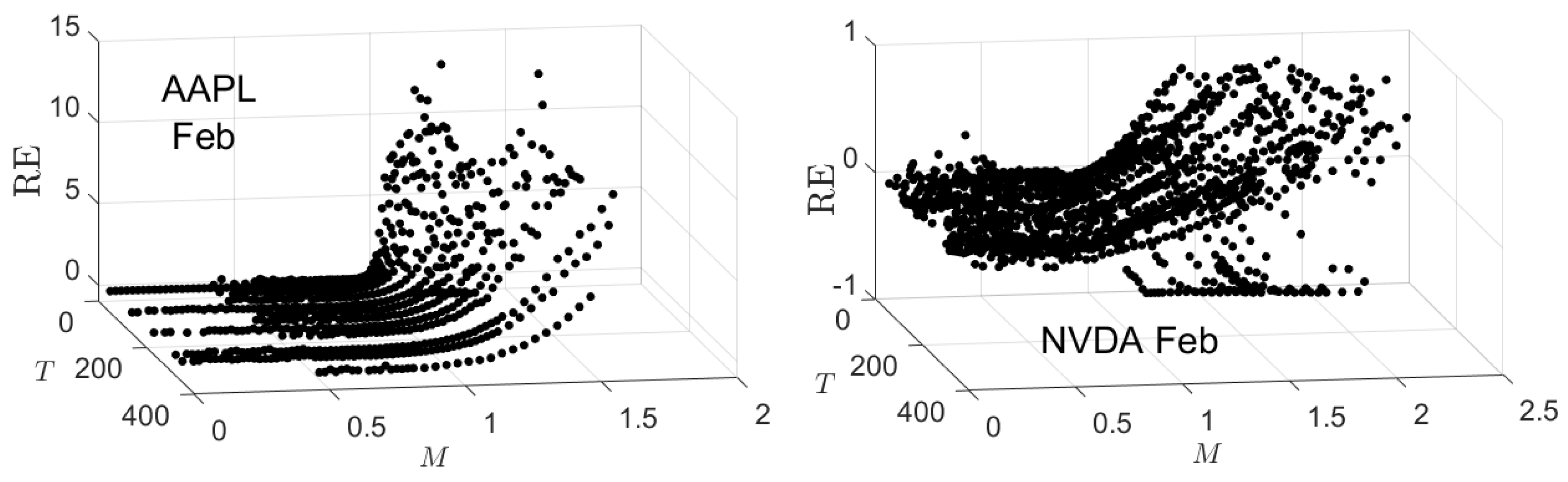
5.1. Option Prices
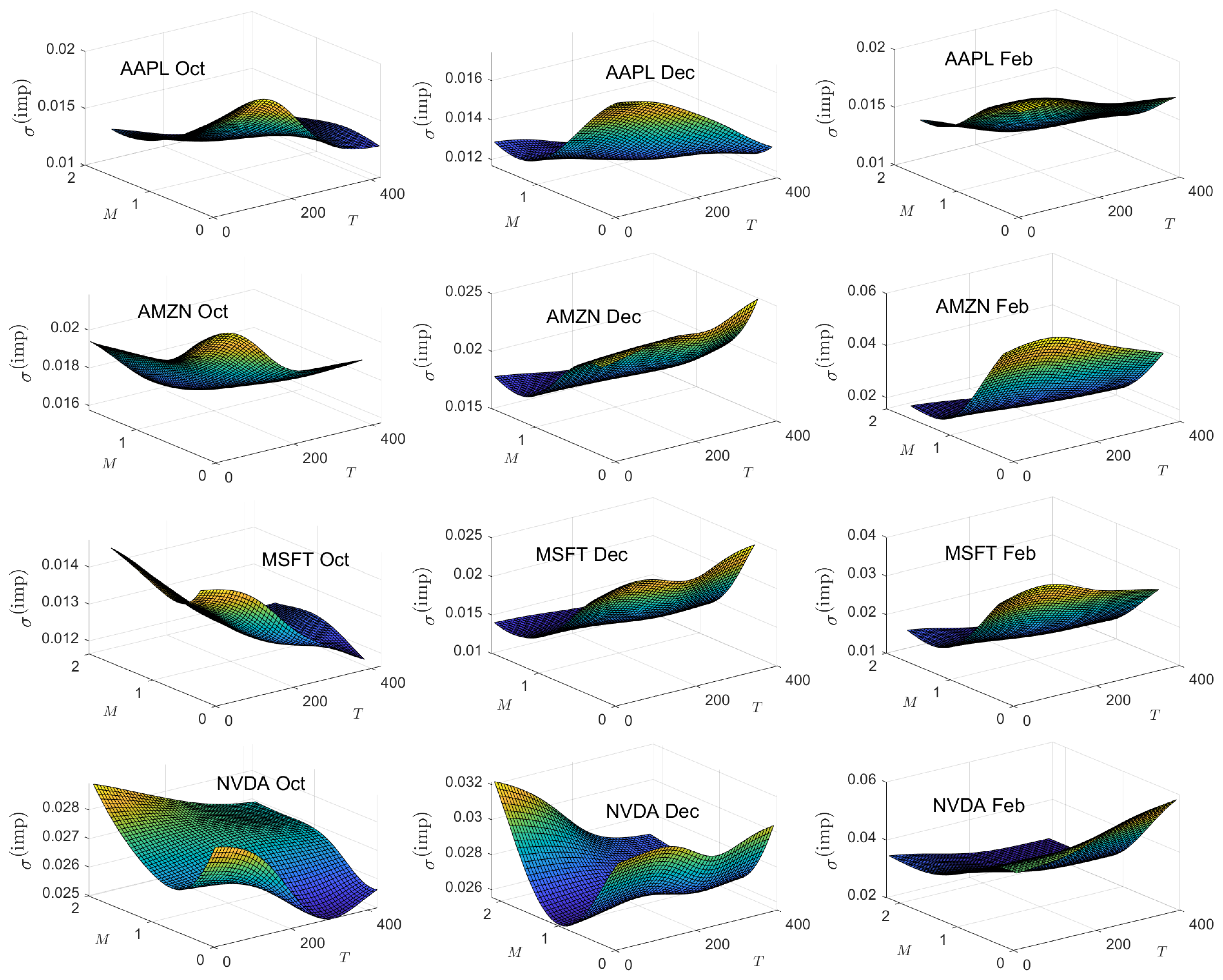
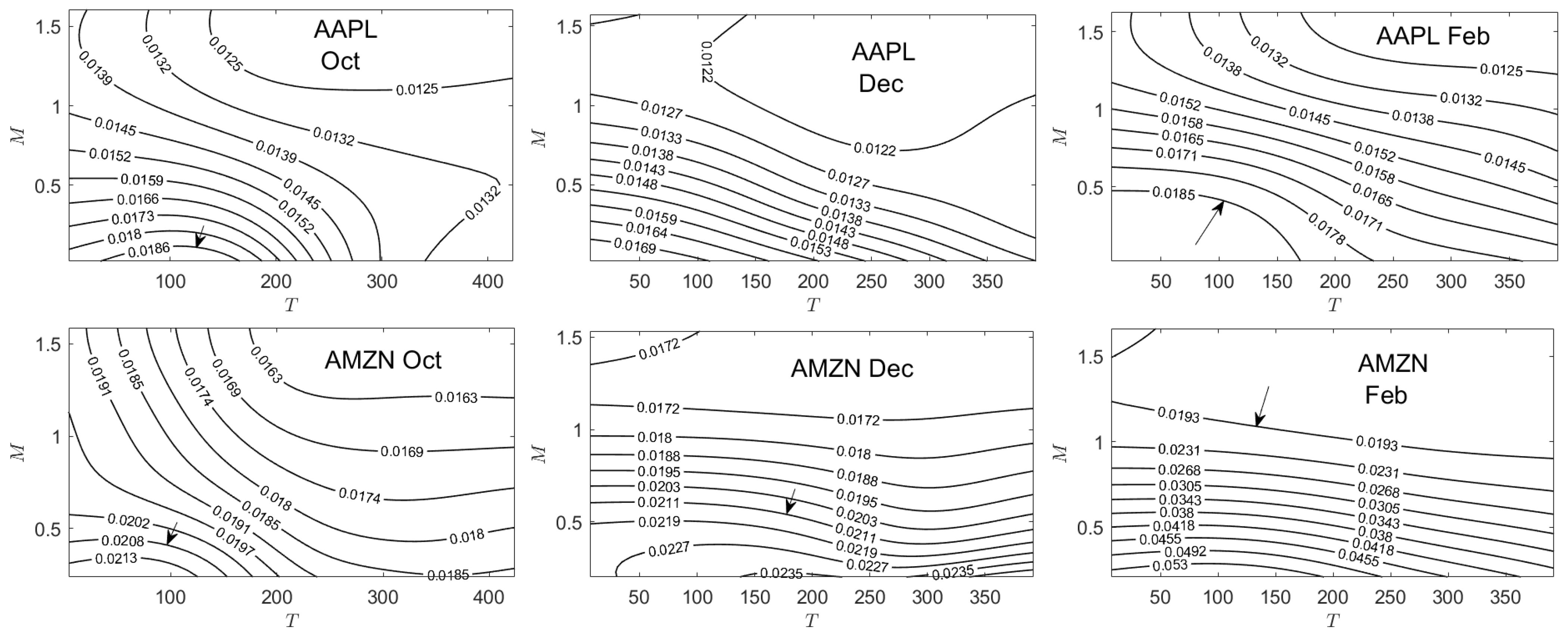
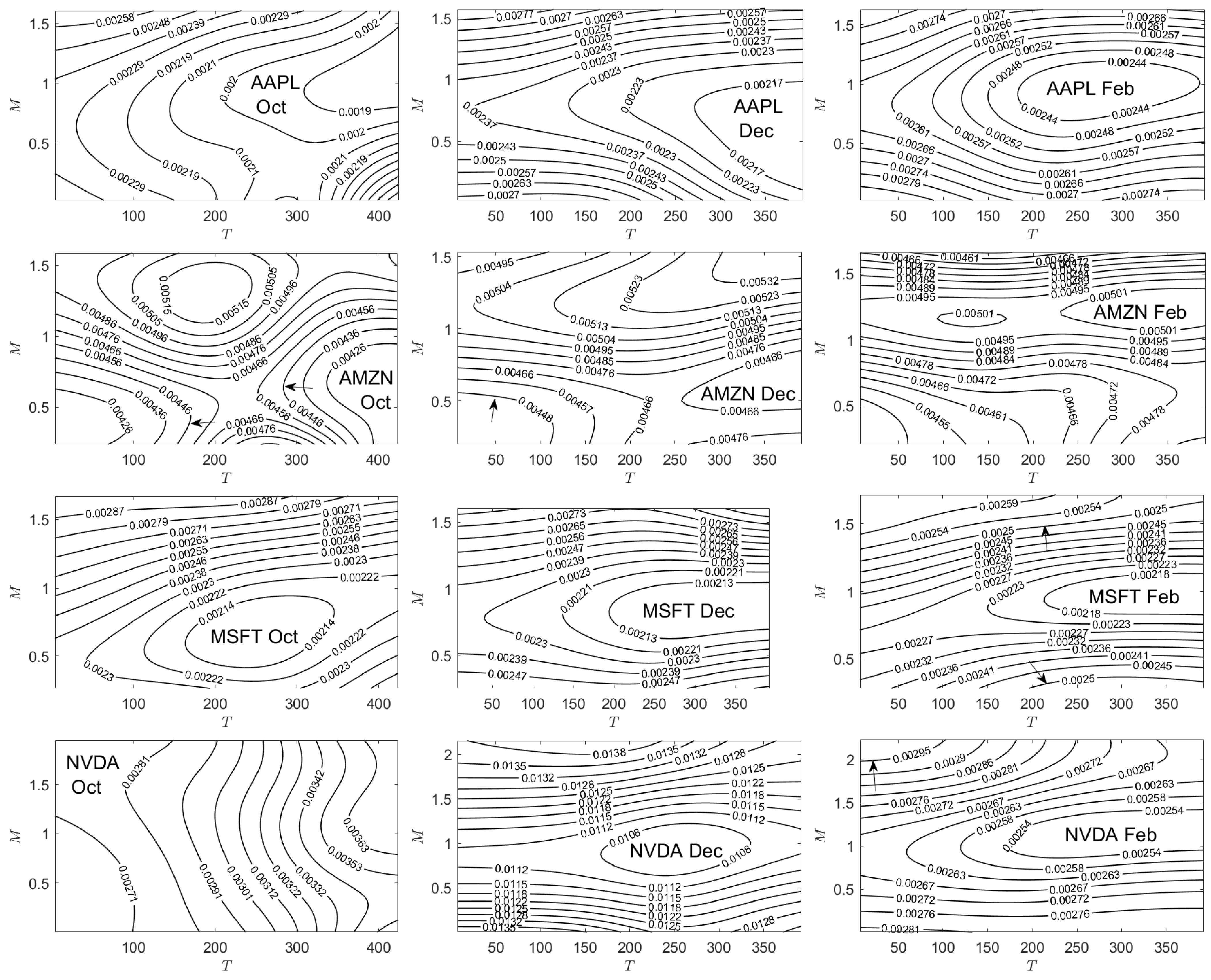
5.2. Implied Volatility
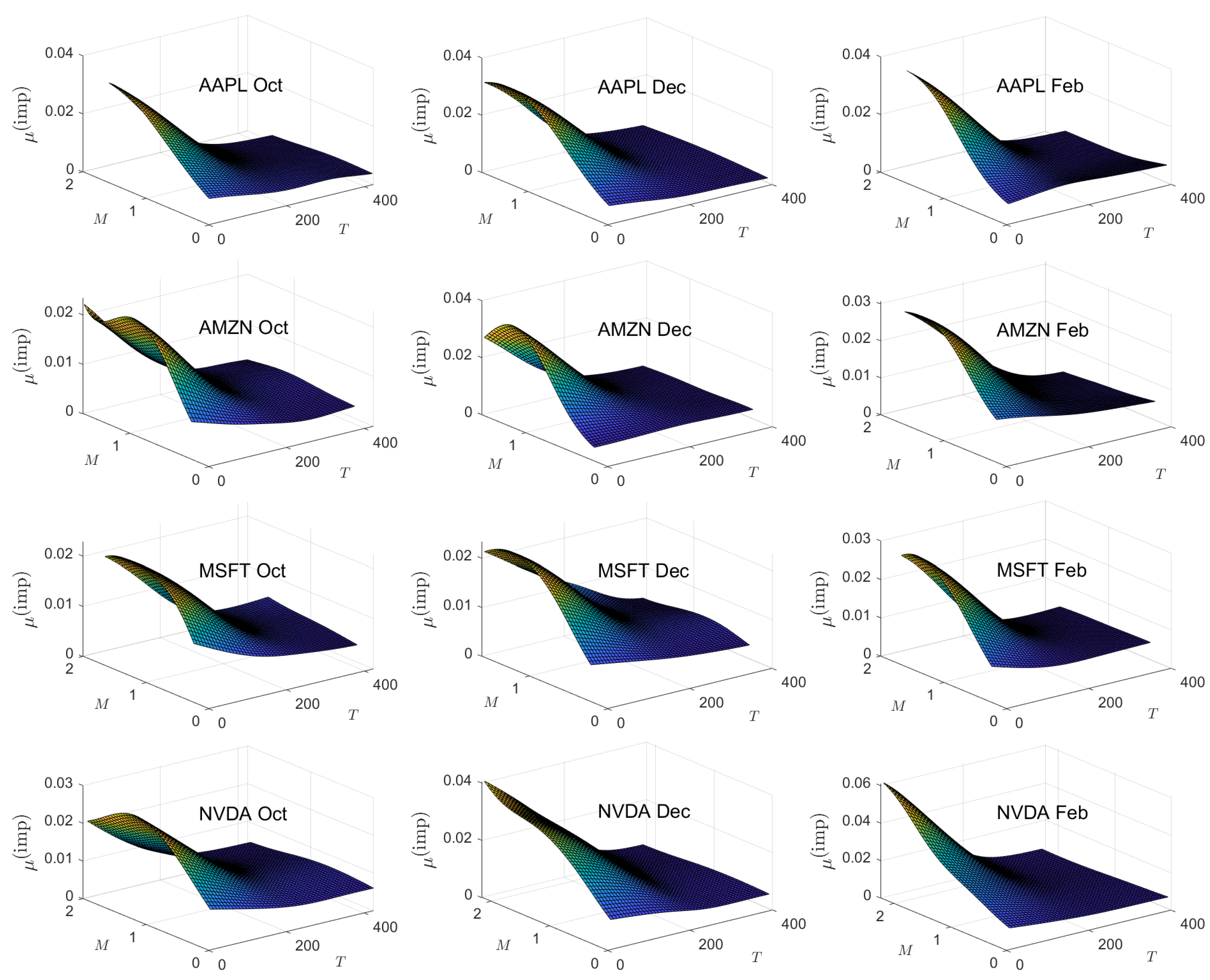
5.3. Implied Mean
5.4. Implied Risk-Free Rate
5.5. Implied Price-Change Probability
5.5.1. Implied
5.5.2. Implied
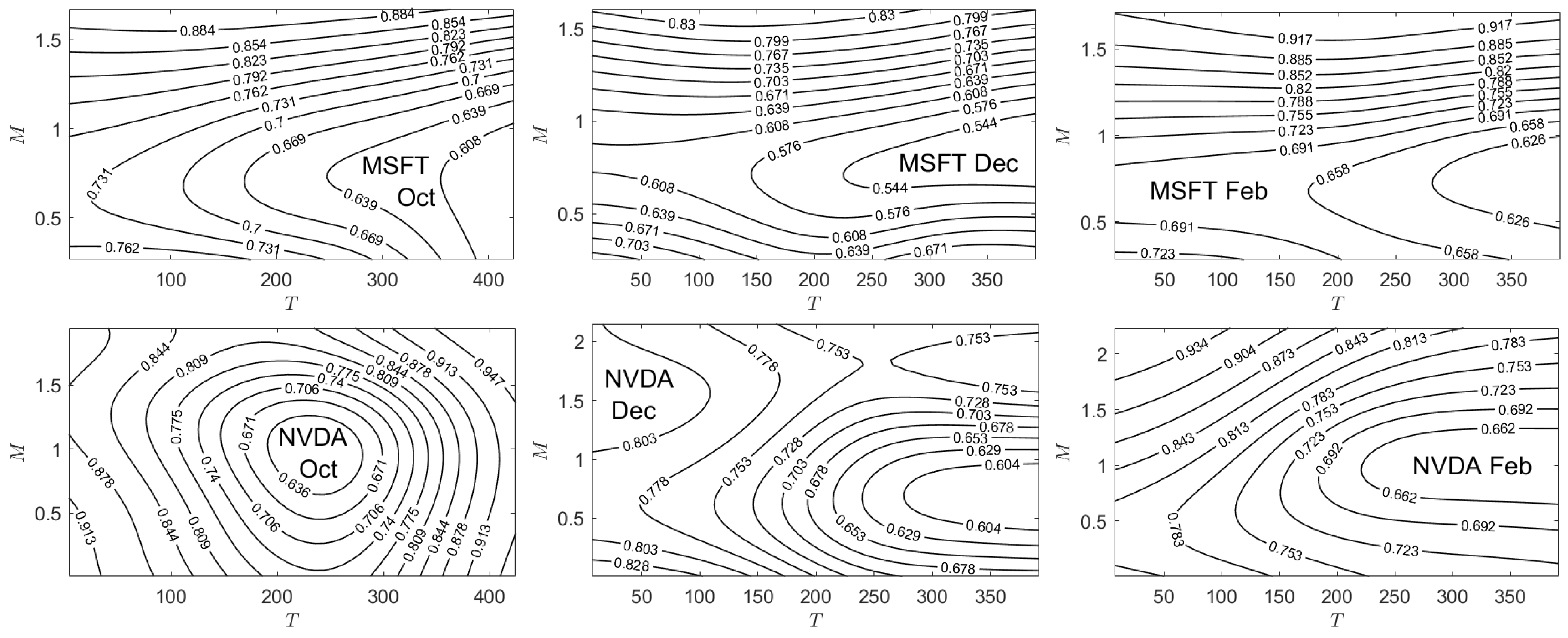
5.6. Implied Extreme Price Change Probabilities
5.6.1. Implied
5.6.2. Implied
6. Conclusions
- We have developed a market-complete trinomial pricing model in which completeness is ensured by a market consisting of a stock and its perpetual derivative as risky assets; a riskless asset (bond); and a European option. The use of the perpetual derivative ensures that the number of Brownian motions driving price stochastics does not increase, thus ensuring the completeness of the market.
- Our model is developed in the natural world and, through the construction of a replicating portfolio, we derive the risk-neutral price dynamics of all four assets. This methodology thus captures the relationship between the risk-neutral and natural-world parameters.
- We derive a new approach for calibrating the probabilities and for price movements in the natural-world model to empirical data. The approach is based upon hypothesis testing on sub-sample mean values.
- As a result of capturing the explicit relationship between the risk-neutral and natural-world parameters, using call option data from four of the “Magnificent Seven” technology stocks, we compute implied surfaces for all parameters in the model. Examination of the contour levels of an implied parameter surface may split the surface into two regimes —“above and below” the historical value for that parameter—allowing for a comparison of the views of option and spot traders relative to the future performance of that parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Determination of rthr Values
| AAPL | AMZN | |||||||
| 0.05 | NS * | 0 | NS | 0 | NS | 0 | 1 | 1.97 |
| 0.01 | −1 | −2.77 | NS | 0 | −1 | −2.36 | 1 | 1.97 |
| 0.005 | −1 | −2.77 | NS | 0 | −1 | −2.36 | 1 | 1.97 |
| 0.001 | −2 | −6.13 | NS | 0 | −1 | −2.36 | 1 | 1.97 |
| 0.0005 | −2 | −6.13 | 1 | 4.20 | −1 | −2.36 | 1 | 1.97 |
| 0.0001 | −3 | −10.6 | 1 | 4.20 | −2 | −8.06 | 2 | 9.36 |
| MSFT | NVDA | |||||||
| 0.05 | NS | 0 | NS | 0 | NS | 0 | NS | 0 |
| 0.01 | −1 | −1.46 | 1 | 1.62 | NS | 0 | NS | 0 |
| 0.005 | −1 | −1.46 | 1 | 1.62 | −1 | −4.07 | 2 | 5.75 |
| 0.001 | −1 | −1.46 | 1 | 1.62 | −2 | −6.19 | 2 | 5.75 |
| 0.0005 | −1 | −1.46 | 1 | 1.62 | −3 | −11.5 | 3 | 11.5 |
| 0.0001 | −2 | −6.59 | 1 | 1.62 | −3 | −11.5 | 4 | 16.3 |
Appendix B. Empirical and Theoretical Option Price Plots
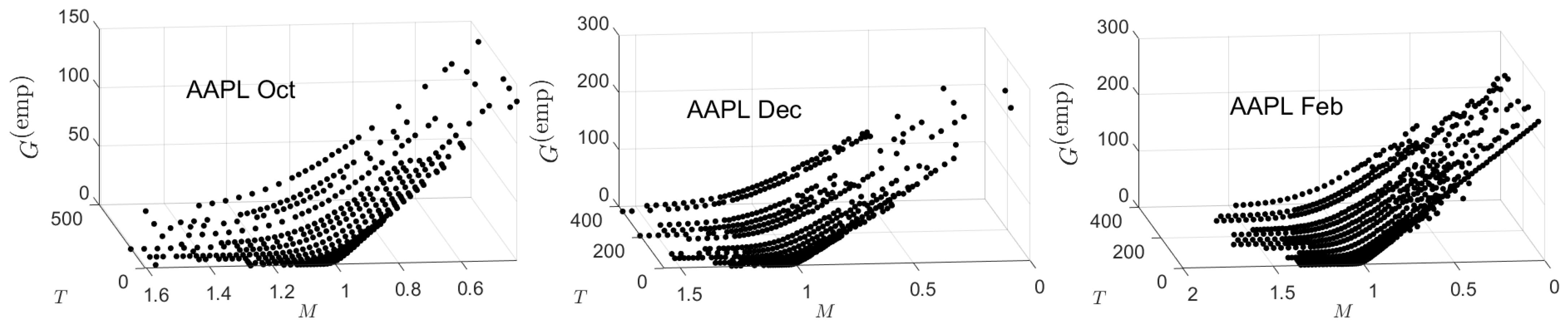
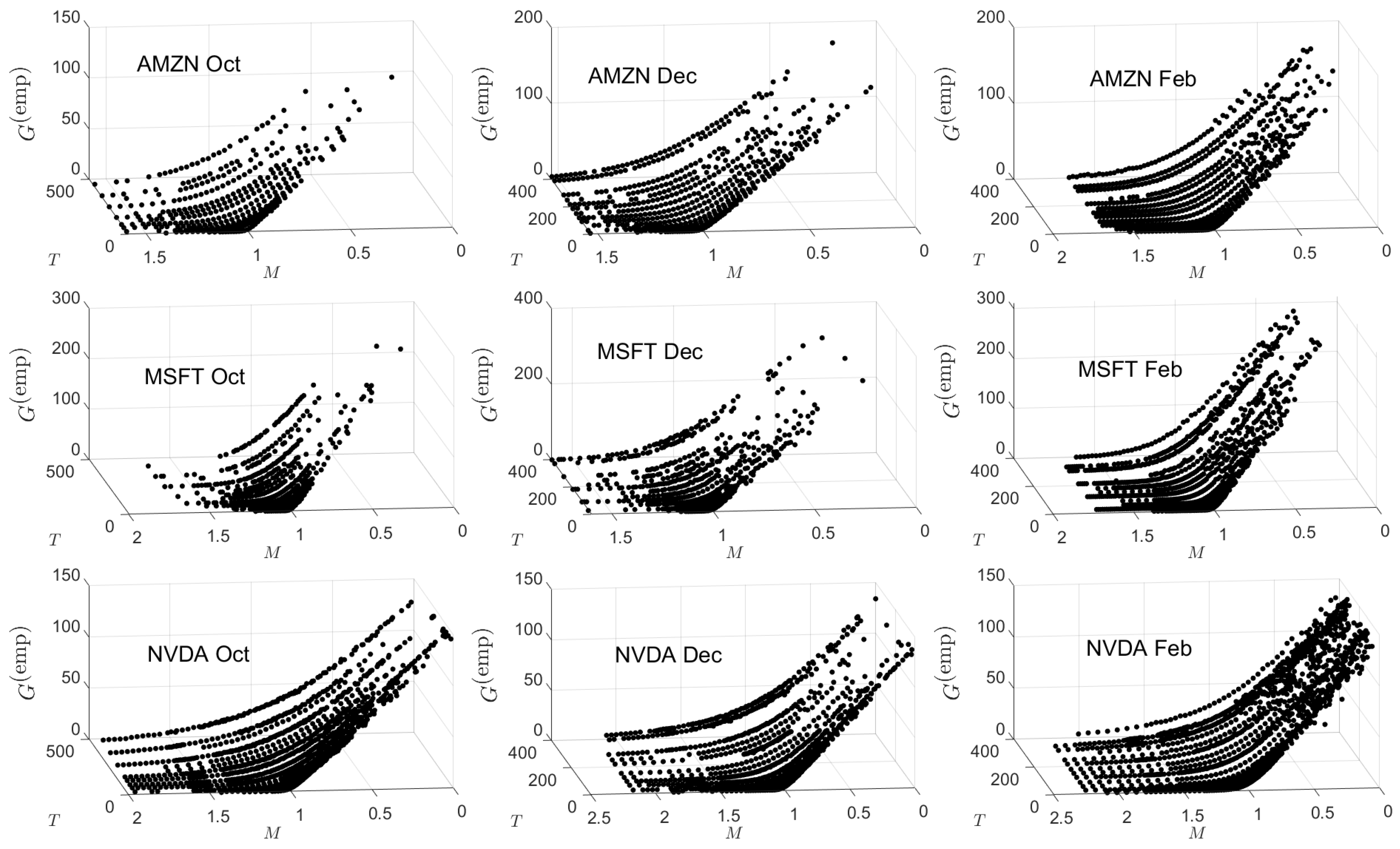
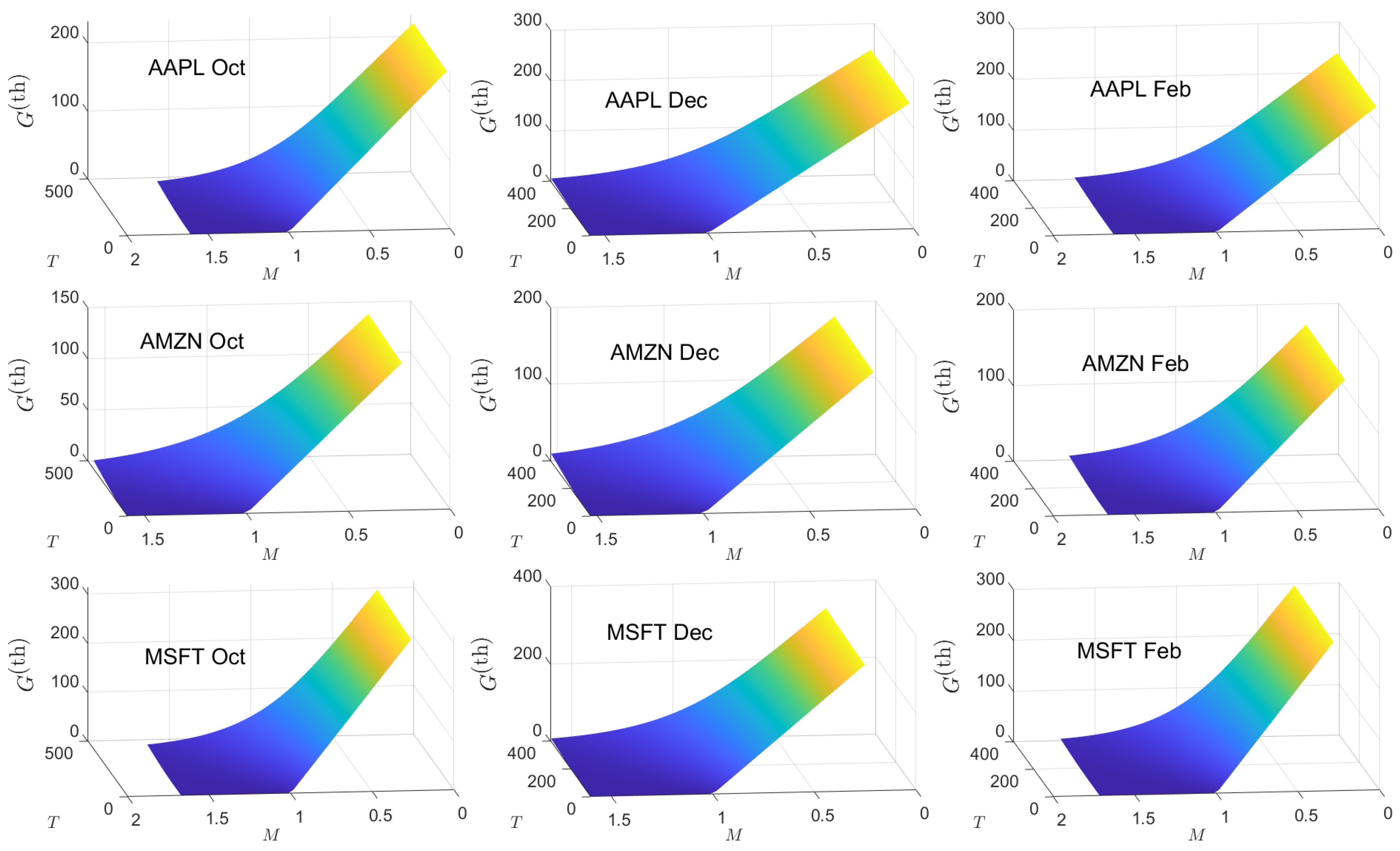
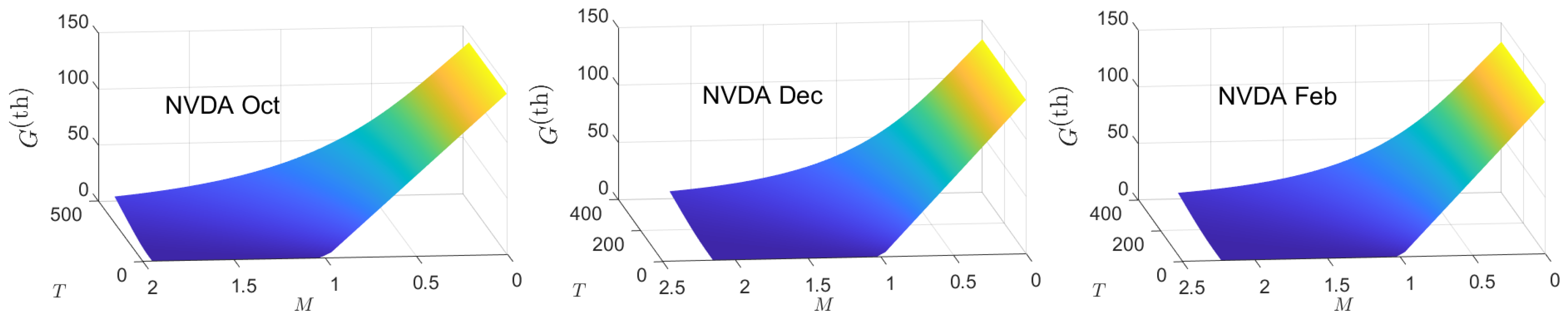
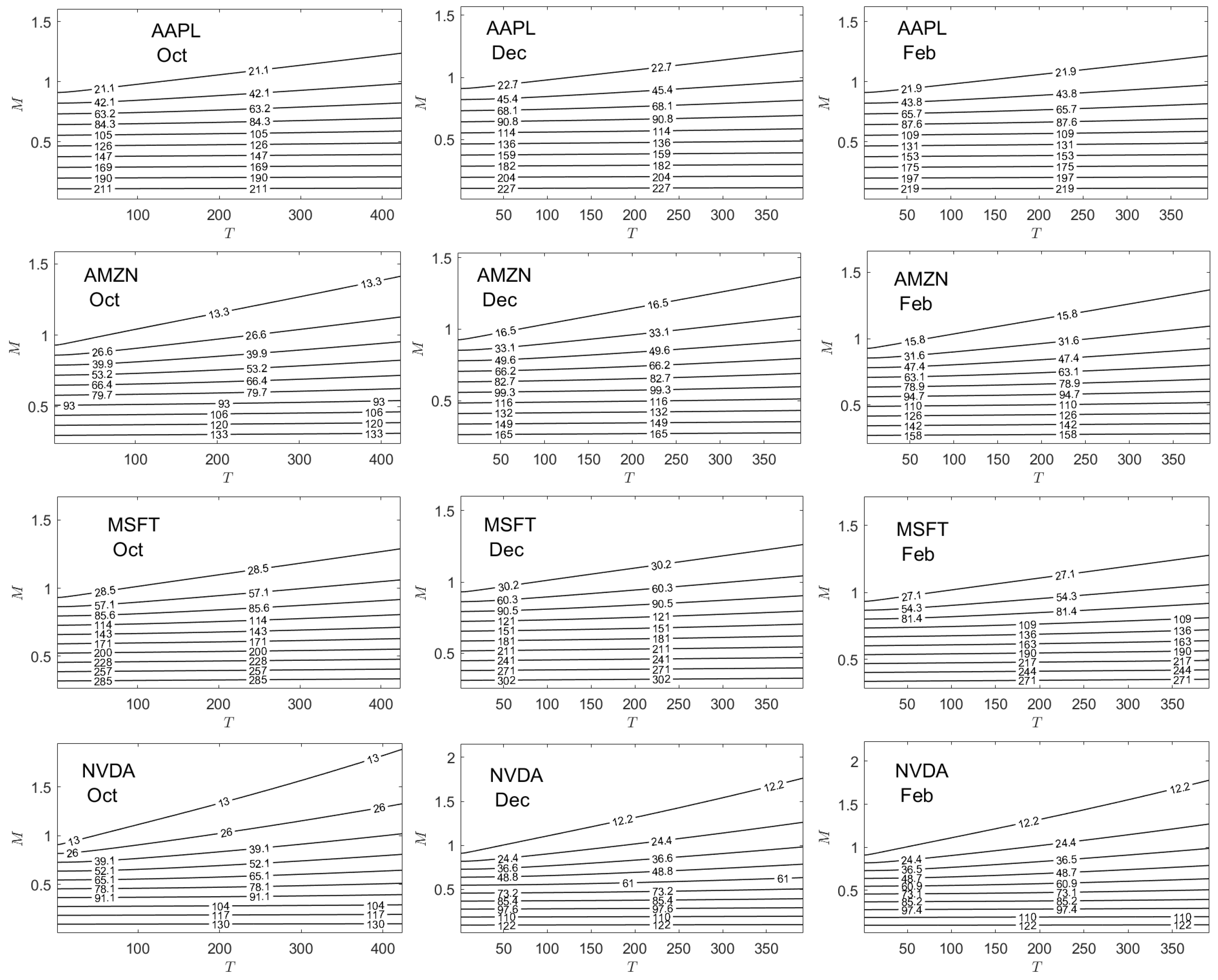
Appendix C. Implied Parameter Plots

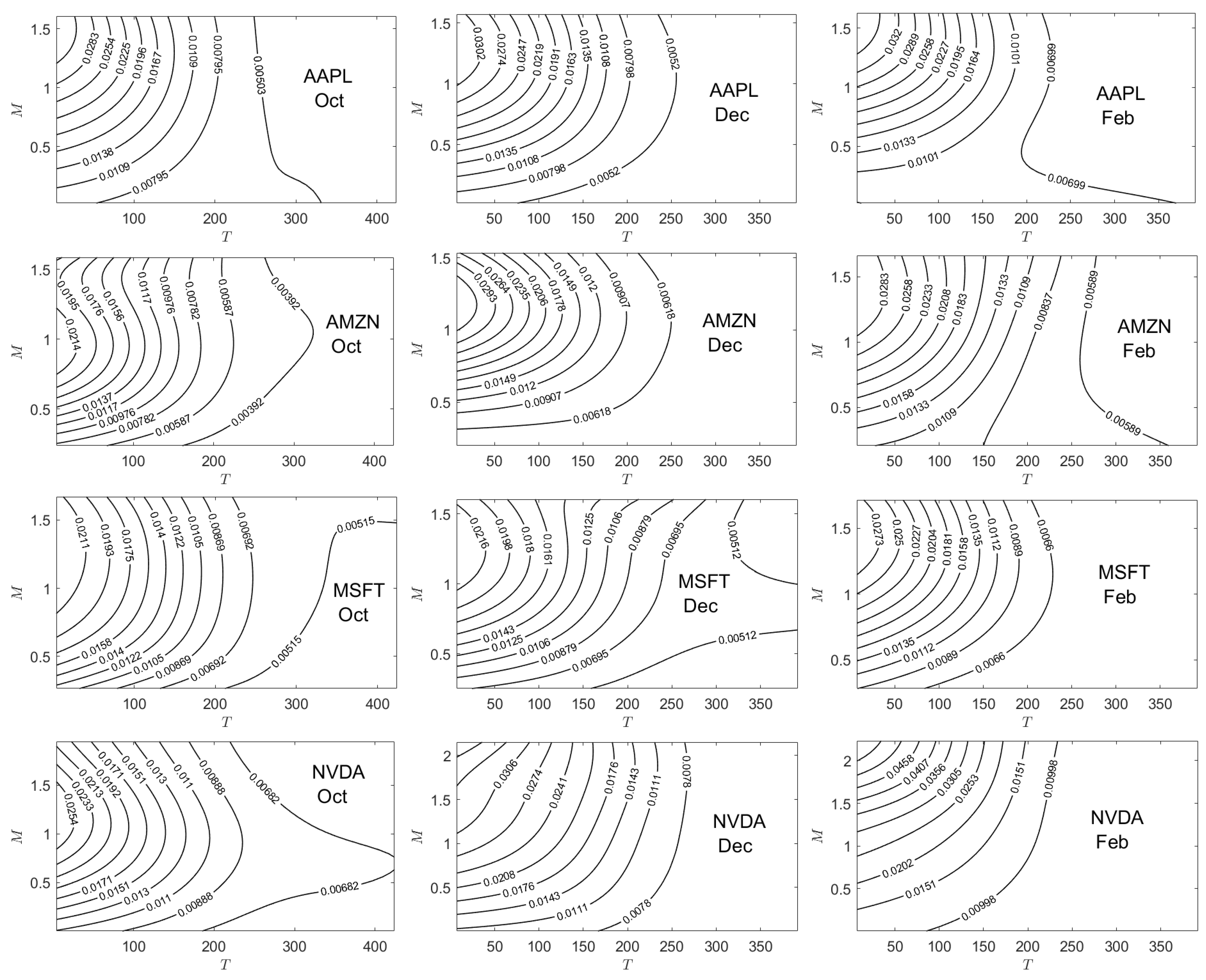

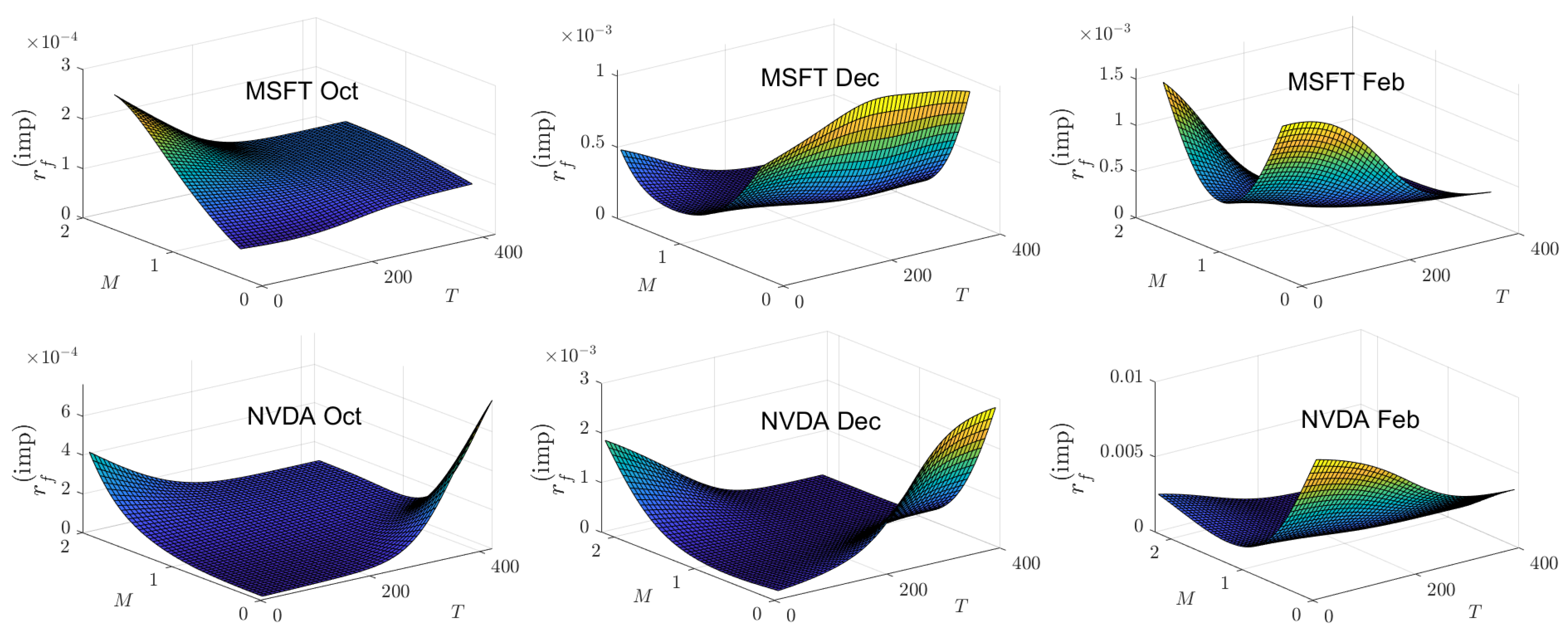

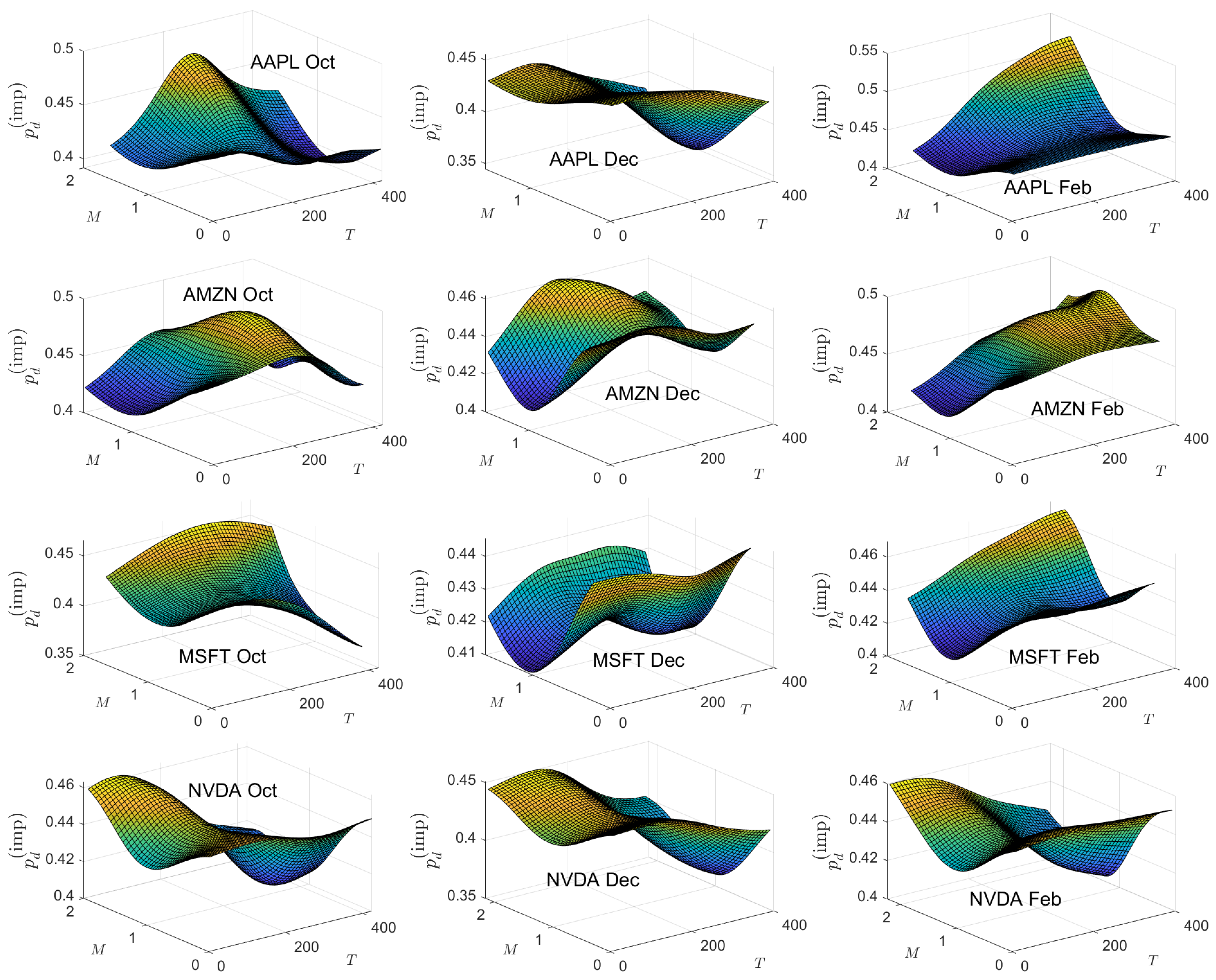
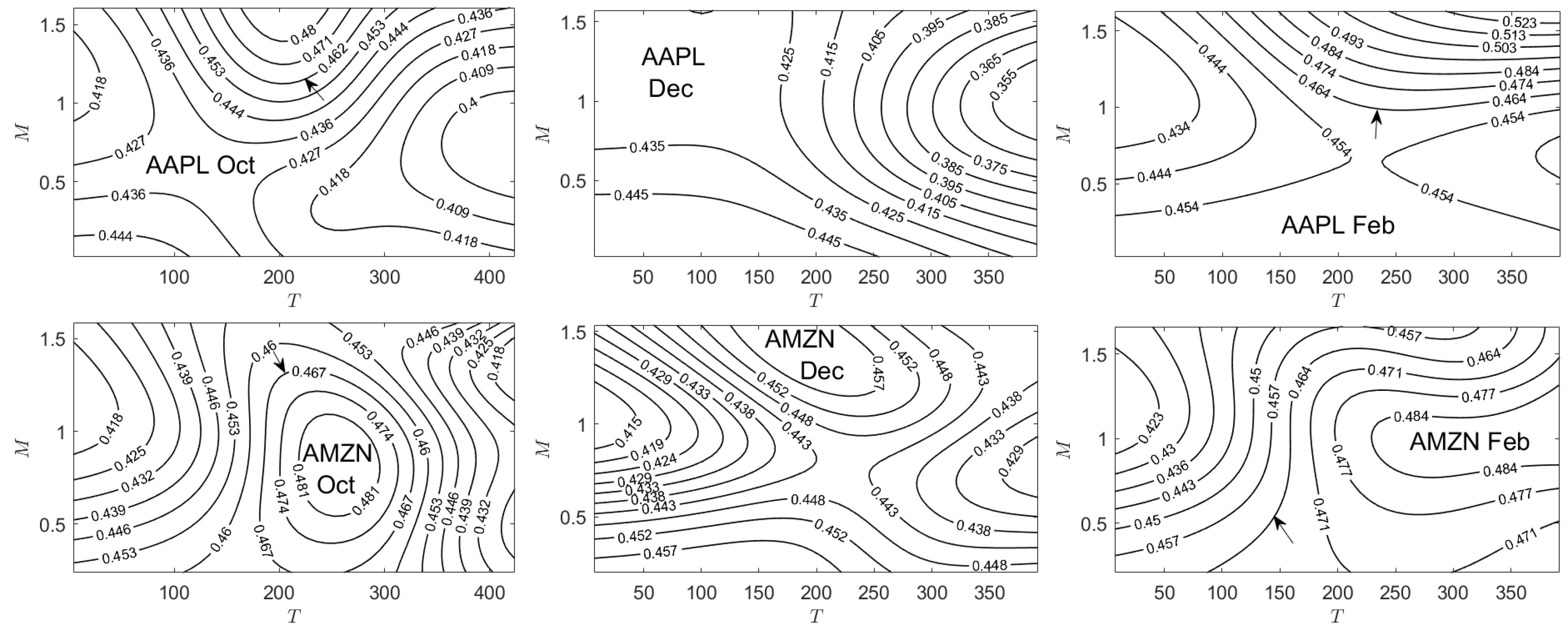

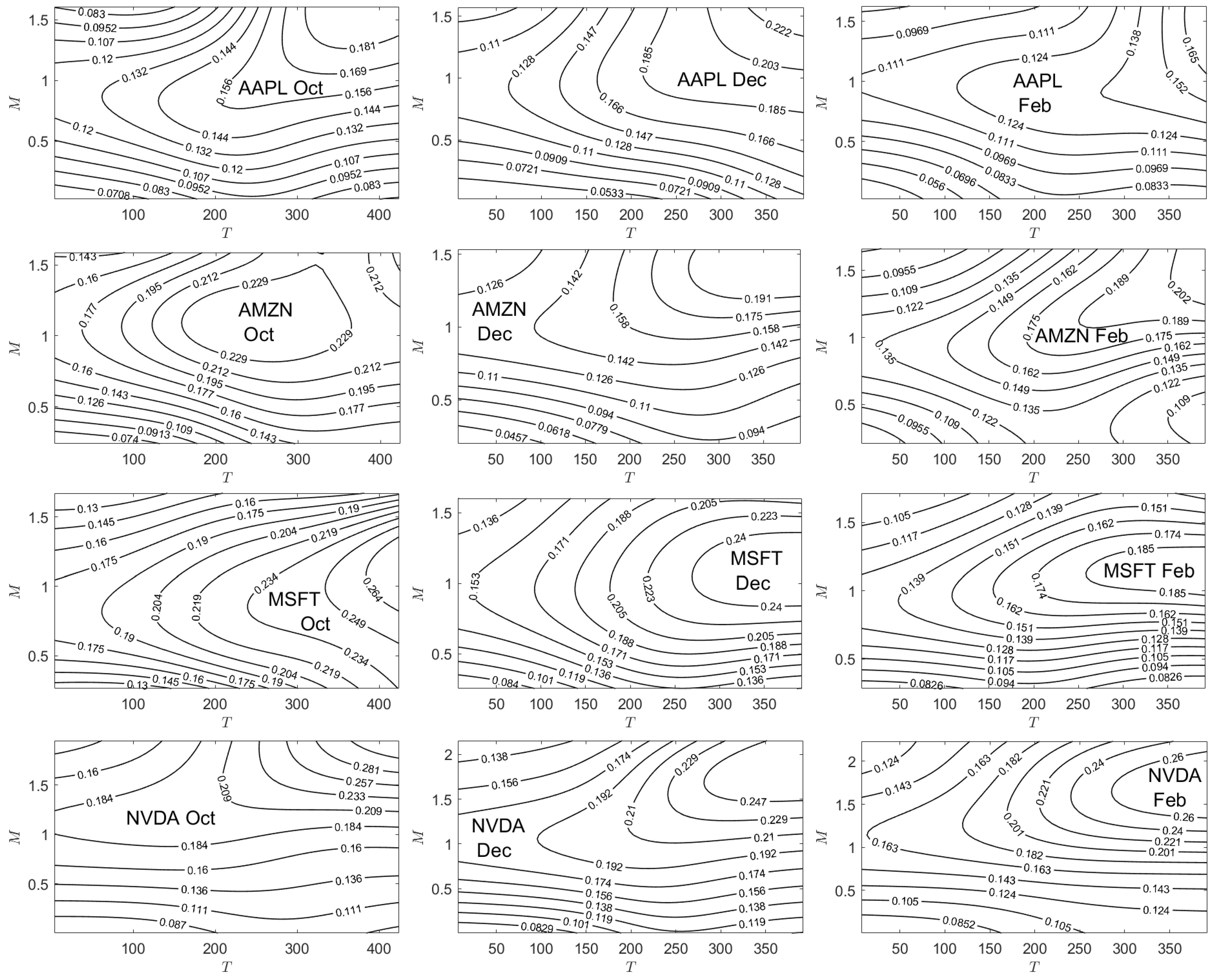
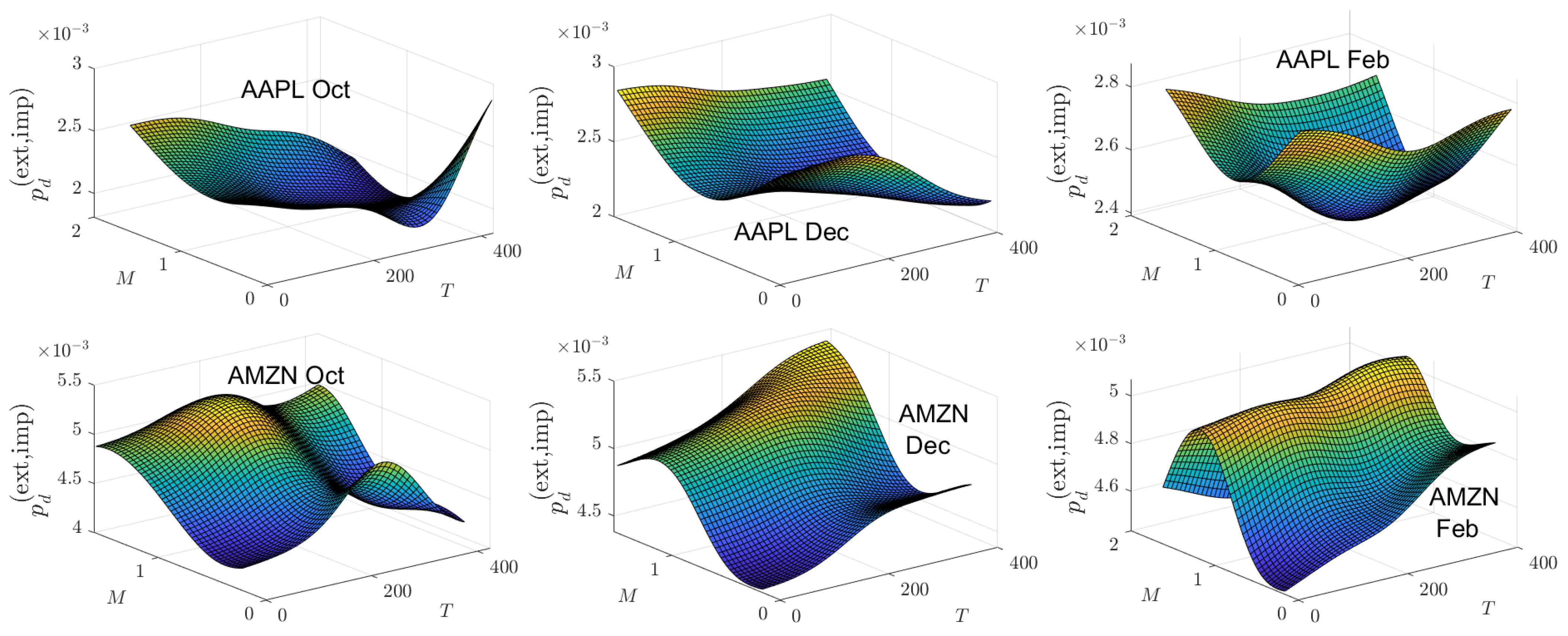
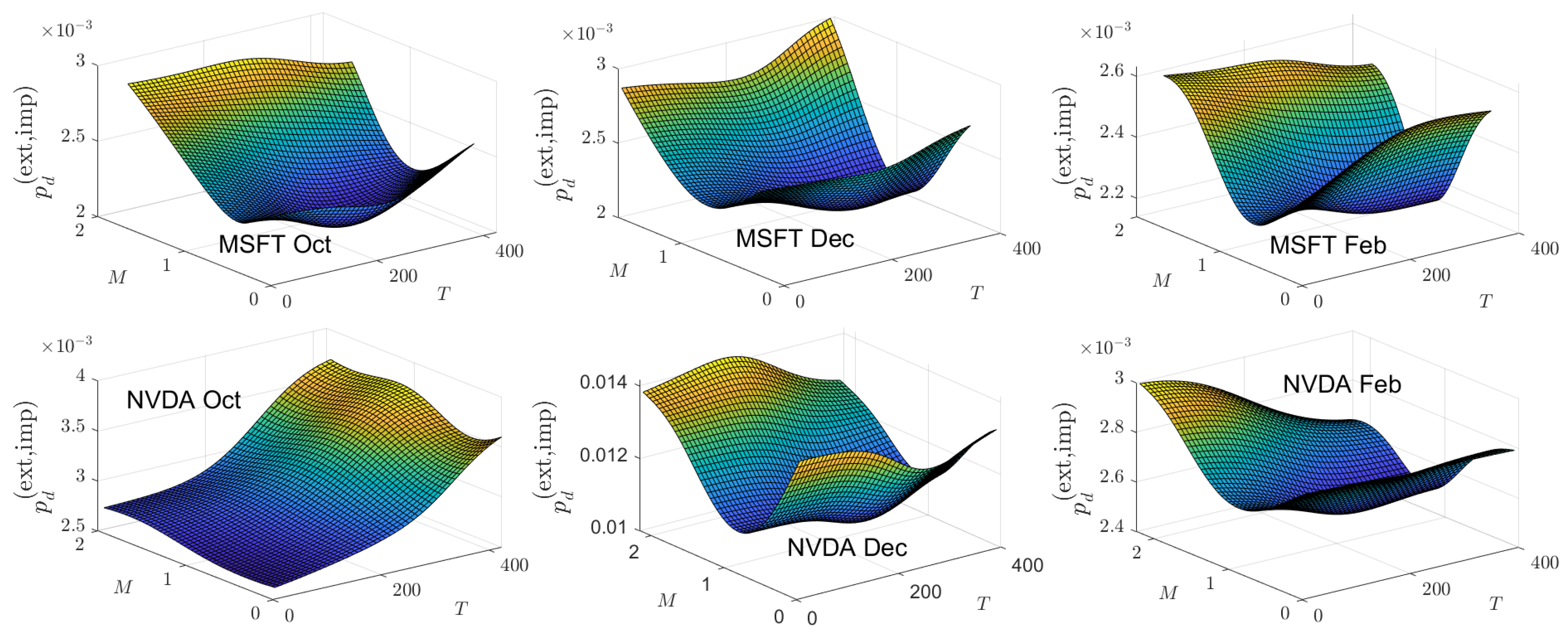


| 1 | See, however, the results of Chan et al. (2009) which show that the Tian third-order moment binomial tree model outperforms eight other trinomial tree models. |
| 2 | Let be a parameter and denote a perpetual derivative having the price process , where . Then, the price process discounted by a riskless bond rate is a martingale under the EMM and thus the security can be traded within the BSM market model. The log-return of this perpetual derivative is a linear combination of the log-returns of the underlying stock and the bond . When , then and the perpetual derivative price becomes independent of the bond price. |
| 3 | This is often referred to as a “single period” tree. However, a single period tree would imply . We prefer the designation fundamental unit, as the tree is assembled by replication of this unit. In the binomial tree literature, it has become convention to adopt and as the generic price changes. This convention does not extend naturally to multinomial trees. We prefer the level indexing , and employed here as it extends naturally to multinomial (including binomial) trees. To be consistent with a general multinomial tree nomenclature, our price change probabilities should be written , and . We confess to being inconsistent in adopting the most general notation. |
| 4 | We impose sufficient conditions. |
| 5 | For notational consistency, and should be labeled and to indicate the historical window with which they are associated—just as is performed with , and . For notational brevity, we omit the time dependence for and . |
| 6 | Use of the t-test for sample means assumes that the center of the distribution of returns is well approximated by a normal distribution. |
| 7 | The procedure adopted here was motivated by the computation of VaR and CVaR values. The value is analogous to a VaR value, while is analogous to the related CVaR value. In this view, is the largest “CVaR” value for which the null hypothesis is not rejected. |
| 8 | We focus on rather than as investors react more strongly to market downturns than to market upturns. |
| 9 | We ignore the convention that defines values of conditional value at risk corresponding to losses as positive. |
| 10 | When we computed implied parameter values, we used empirical prices for American options. As call option prices for European and American options are identical, but put option prices differ, we considered only call option prices and implied parameter values based on those call options. |
| 11 | Option price data were obtained from Bloomberg Professional Services. (Data accessed over the period 19–22 February 2025). The range of this time period reflects historical option prices available to us under our Bloomberg Services license. |
| 12 | Specifically the historical windows spanned 21 October 2016 through 21 October 2024; 20 December 2016 through 20 December 2024; and 21 February 2017 through 21 February 2025. |
| 13 | Stock price data were obtained from Bloomberg Professional Services. (Data accessed over the period 19–22 February 2025). |
| 14 | Note that the theoretical option prices are computed for a denser set of maturity times, , compared to the empirical maturity times . |
| 15 | To avoid repetition in the manuscript, we note here that, for each implied parameter optimization, we computed implied values for all points for which there are empirical data. A Gaussian kernel smoother was then used to interpolate implied values for all possible coordinate pairs. |
| 16 | An alternative is to specify contours that correspond to all the US Treasury bill, note and bond yield rates for the appropriate date. However, this can yield to cases of very closely spaced contours. |
| 17 | The implied surfaces of are just inverted surfaces of while the contour plots of both look identical with values of the contours given by (28). |
| 18 | The implied values of are computed assuming is fixed at the historical value. |
| 19 |
References
- Ahn, J., & Song, M. (2007). Convergence of the trinomial tree method for pricing European/American options. Applied Mathematics and Computation, 189(1), 575–582. [Google Scholar]
- Bates, D. S. (1996). Jumps and stochastic volatility: Exchange rate processes implicit in Deutsche Mark options. Review of Financial Studies, 9, 69–108. [Google Scholar] [CrossRef]
- Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654. [Google Scholar]
- Boyle, P. P. (1986). Option valuation using a tree-jump process. International Options Journal, 3, 7–12. [Google Scholar]
- Boyle, P. P. (1988). A lattice framework for option pricing with two state variables. Journal of Financial and Quantitative Analysis, 23(1), 1–12. [Google Scholar]
- Boyle, P. P., Evnine, J., & Gibbs, S. (1989). Numerical evaluation of multivariate contingent claims. Review of Financial Studies, 2, 241–251. [Google Scholar]
- Boyle, P. P., & Lau, S. H. (1994). Bumping up against the barrier with the binomial method. Journal of Derivatives, 1, 6–14. [Google Scholar]
- Chan, J. H., Joshi, M., Tang, R., & Yang, C. (2009). Trinomial or binomial: Accelerating American put option price on trees. Journal of Futures Markets, 29(9), 797–893. [Google Scholar]
- Cox, J. C., Ross, S. A., & Rubinstein, M. (1979). Option pricing: A simplified approach. Journal of Financial Economics, 7(3), 229–263. [Google Scholar]
- Davydov, Y., & Rotar, V. (2008). On a non-classical invariance principle. Statistics & Probability Letters, 78, 2031–2038. [Google Scholar]
- Deutsch, H.-P. (2009). Derivatives and internal models (4th ed.). Palgrave Macmillan. [Google Scholar]
- Florescu, I., & Viens, F. (2008). Stochastic volatility: Option pricing using a multinomial recombining tree. Applied Mathematical Finance, 15, 151–181. [Google Scholar]
- Hilliard, J. E., & Schwartz, A. (1996). Binomial option pricing under stochastic volatility and correlated state variables. Journal of Derivatives, 4(1), 23–39. [Google Scholar]
- Hu, Y., Shirvani, A., Lindquist, W. B., Fabozzi, F. J., & Rachev, S. T. (2020). Option pricing incorporating factor dynamics in complete markets. Journal of Risk and Financial Management, 13(12), 321. [Google Scholar]
- Jarrow, R., & Rudd, A. (1983). Option pricing. Dow Jones-Irwin. [Google Scholar]
- Josheski, D., & Apostolov, M. (2020). A review of the binomial and trinomial models for option pricing and their convergence to the Black-Scholes model determined option prices. Econometrics, 24(2), 53–85. [Google Scholar] [CrossRef]
- Kamrad, B., & Ritchen, P. (1991). Multinomial approximating models for options with k state variables. Management Science, 37, 1640–1652. [Google Scholar]
- Kim, Y. S., Stoyanov, S. V., Rachev, S. T., & Fabozzi, F. J. (2019). Enhancing binomial and trinomial equity option pricing models. Finance Research Letters, 28, 185–190. [Google Scholar]
- Langat, K. K., Mwaniki, J. I., & Kiprop, G. K. (2019). Pricing options using trinomial lattice method. Journal of Finance and Economics, 7, 81–87. [Google Scholar]
- Leisen, D. P. J., & Reimer, M. (1996). Binomial models for option valuation—Examining and improving convergence. Applied Mathematical Finance, 3(4), 319–346. [Google Scholar]
- Lilyana, D., Subartini, B., Riaman, R., & Supriatna, A. K. (2021). Calculation of call option using trinomial tree method and Black-Scholes method: Case study of Microsoft Corporation. Journal of Physics: Conference Series, 1722, 012064. [Google Scholar]
- Lindquist, W. B., & Rachev, S. T. (2025). Alternatives to classical option pricing. Annals of Operations Research, 346, 489–509. [Google Scholar]
- Ma, J., & Zhu, T. (2015). Convergence rates of trinomial tree methods for option pricing under regime-switching models. Applied Mathematics Letters, 39, 13–18. [Google Scholar]
- Madan, D. B., Milne, F., & Shefrin, H. (1989). The multinomial option pricing model and its Brownian and Poisson limits. Review of Financial Studies, 2, 251–265. [Google Scholar]
- Merton, R. C. (1973). Theory of rational option pricing. The Bell Journal of Economics and Management Science, 4(1), 141–183. [Google Scholar]
- Rubinstein, M. (1998). Edgeworth binomial trees. The Journal of Derivatives, 5(3), 20–27. [Google Scholar]
- Sharpe, W. F. (1978). Investments. Prentice-Hall. [Google Scholar]
- Shirvani, A., Stoyanov, S. V., Rachev, S. T., & Fabozzi, F. J. (2020). A new set of financial instruments. Frontiers in Applied Mathematics and Statistics, 6, 606812. [Google Scholar]
- Skorokhod, A. V. (2005). Basic principles and applications of probability theory. Springer. [Google Scholar]
- Tian, Y. (1993). A modified lattice approach to option pricing. The Journal of Futures Markets (1986–1998), 13, 563–577. [Google Scholar]
- Yuen, F. L., & Yang, H. (2010). Option pricing with regime switching by trinomial tree method. Journal of Computational and Applied Mathematics, 233(8), 1821–1833. [Google Scholar]





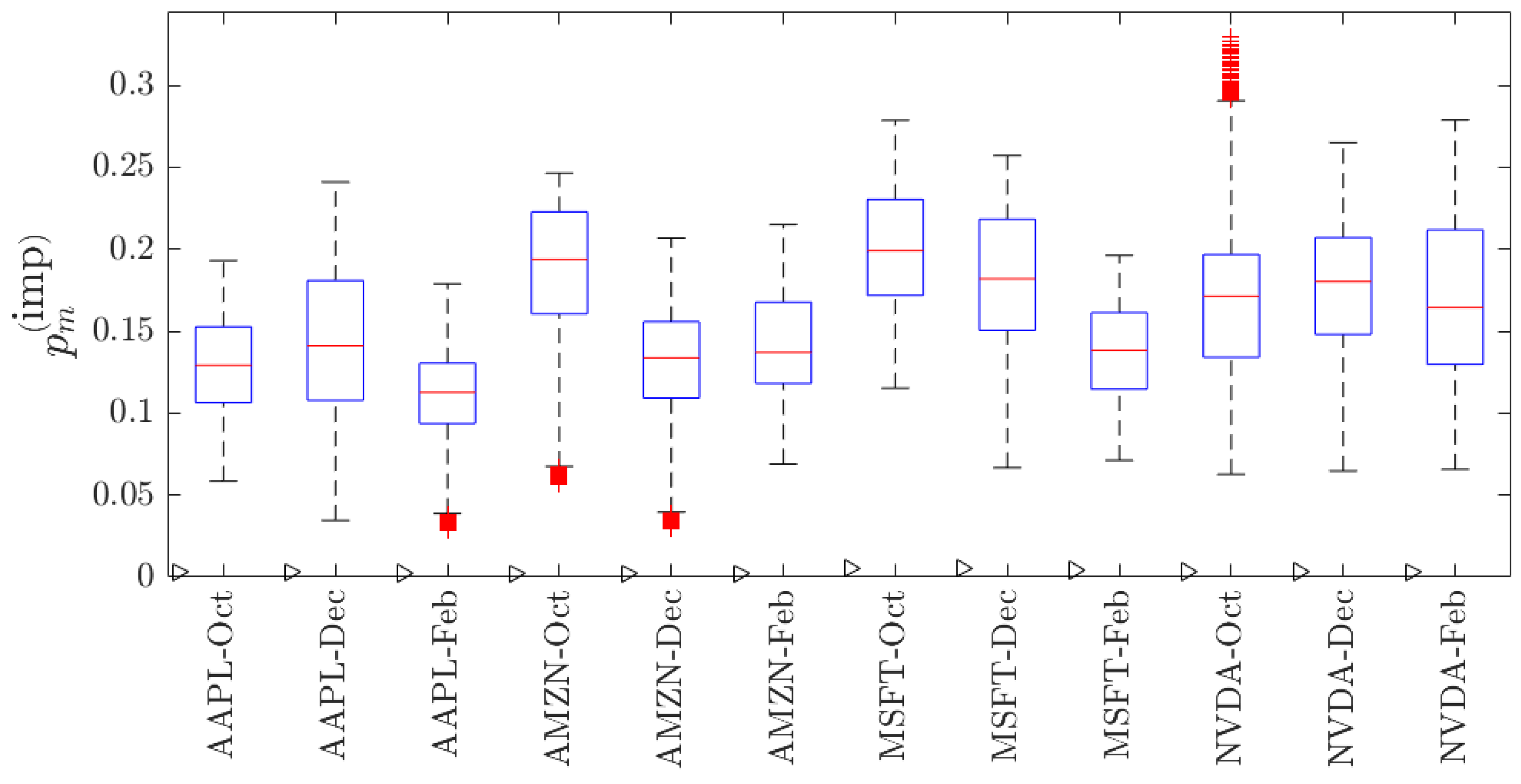
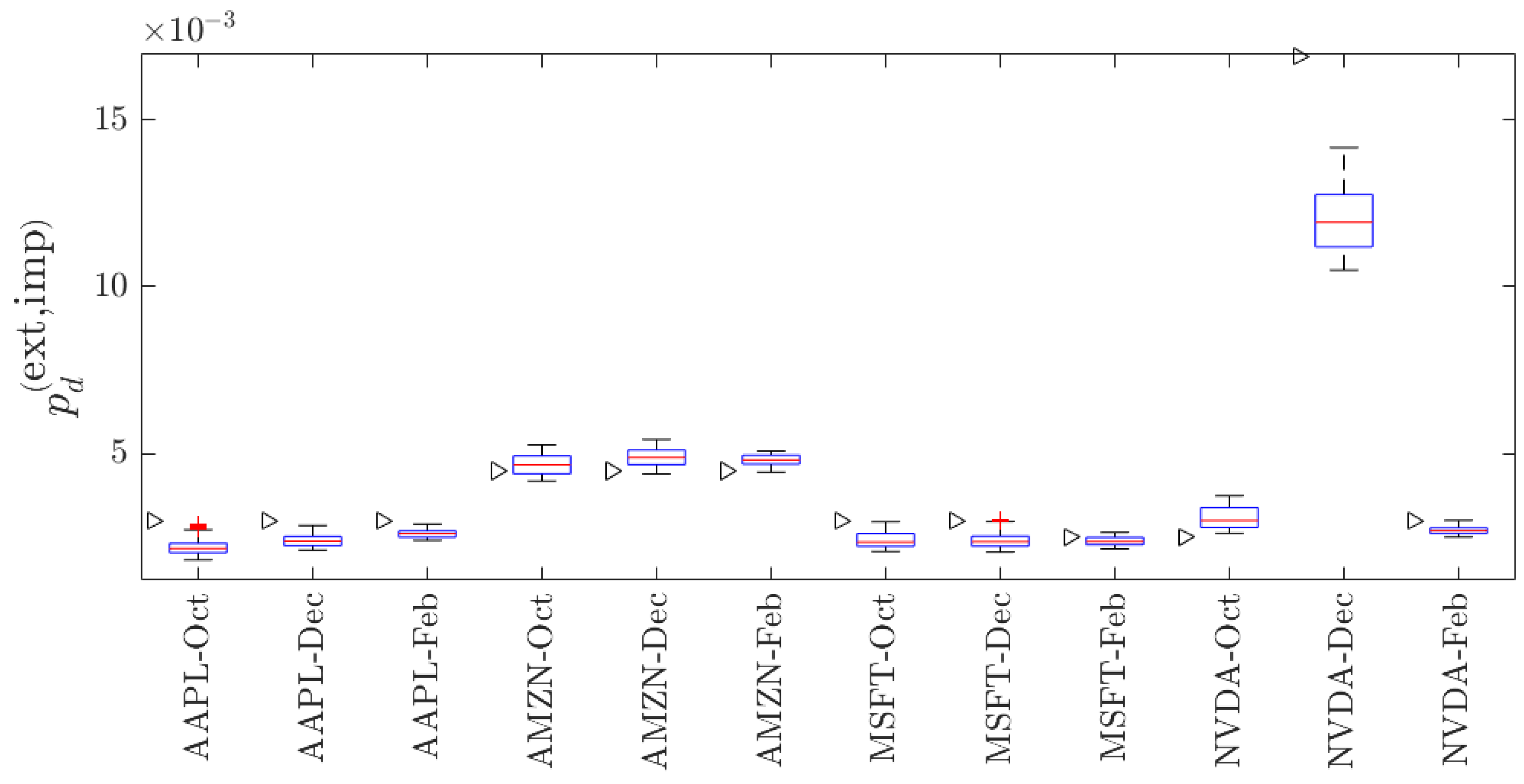

| Stock | Yearly | Daily | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 21 October 2024 | |||||||||
| AAPL | 236.48 | 1.21 | 1.84 | 0.461 | 2.98 | 0.537 | 3 Mo | 4.73 | 5.08 |
| AMZN | 189.07 | 0.976 | 2.08 | 0.465 | 1.99 | 0.533 | 10 Yr | 4.19 | 1.12 |
| MSFT | 418.78 | 1.12 | 1.73 | 0.459 | 5.47 | 0.536 | |||
| NVDA | 143.71 | 2.73 | 3.25 | 0.454 | 3.48 | 0.543 | |||
| 20 December 2024 | |||||||||
| AAPL | 254.49 | 1.24 | 1.84 | 0.459 | 2.98 | 0.538 | 3 Mo | 4.34 | 4.67 |
| AMZN | 224.92 | 1.09 | 2.08 | 0.463 | 1.99 | 0.535 | 10 Yr | 4.52 | 1.21 |
| MSFT | 436.60 | 1.11 | 1.73 | 0.456 | 5.46 | 0.539 | |||
| NVDA | 134.70 | 2.46 | 3.17 | 0.456 | 3.48 | 0.541 | |||
| 21 February 2025 | |||||||||
| AAPL | 245.55 | 1.15 | 1.85 | 0.462 | 2.49 | 0.535 | 3 Mo | 4.32 | 4.65 |
| AMZN | 216.58 | 1.02 | 2.09 | 0.467 | 1.99 | 0.531 | 10 Yr | 4.42 | 1.19 |
| MSFT | 408.21 | 1.07 | 1.75 | 0.455 | 4.47 | 0.540 | |||
| NVDA | 134.43 | 2.44 | 3.20 | 0.456 | 2.98 | 0.541 | |||
| Stock | |||||
|---|---|---|---|---|---|
| 21 October 2024 | |||||
| AAPL | −6.69 | 7.37 | 2.98 | 0.9935 | 3.48 |
| AMZN | −7.28 | 8.13 | 4.47 | 0.9925 | 2.98 |
| MSFT | −6.09 | 7.06 | 2.98 | 0.9935 | 3.48 |
| NVDA | −10.4 | 13.1 | 2.49 | 0.9940 | 3.48 |
| 20 December 2024 | |||||
| AAPL | −6.69 | 7.37 | 2.98 | 0.9935 | 3.48 |
| AMZN | −7.28 | 8.15 | 4.47 | 0.9926 | 2.98 |
| MSFT | −6.17 | 7.06 | 2.98 | 0.9935 | 3.48 |
| NVDA * | −6.89 | 7.44 | 16.9 | 0.9697 | 13.4 |
| 21 February 2025 | |||||
| AAPL | −6.69 | 7.32 | 2.98 | 0.9935 | 3.48 |
| AMZN | −7.28 | 8.15 | 4.47 | 0.9925 | 2.98 |
| MSFT | −6.26 | 7.06 | 2.49 | 0.9940 | 3.48 |
| NVDA | −10.8 | 12.1 | 2.98 | 0.9935 | 3.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gnawali, J.; Lindquist, W.B.; Rachev, S.T. Hedging via Perpetual Derivatives: Trinomial Option Pricing and Implied Parameter Surface Analysis. J. Risk Financial Manag. 2025, 18, 192. https://doi.org/10.3390/jrfm18040192
Gnawali J, Lindquist WB, Rachev ST. Hedging via Perpetual Derivatives: Trinomial Option Pricing and Implied Parameter Surface Analysis. Journal of Risk and Financial Management. 2025; 18(4):192. https://doi.org/10.3390/jrfm18040192
Chicago/Turabian StyleGnawali, Jagdish, W. Brent Lindquist, and Svetlozar T. Rachev. 2025. "Hedging via Perpetual Derivatives: Trinomial Option Pricing and Implied Parameter Surface Analysis" Journal of Risk and Financial Management 18, no. 4: 192. https://doi.org/10.3390/jrfm18040192
APA StyleGnawali, J., Lindquist, W. B., & Rachev, S. T. (2025). Hedging via Perpetual Derivatives: Trinomial Option Pricing and Implied Parameter Surface Analysis. Journal of Risk and Financial Management, 18(4), 192. https://doi.org/10.3390/jrfm18040192








