Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method
Abstract
:1. Introduction
2. Mathematical Formulation of the Problem
3. Approximate Analytical Expression of the Concentration and Effectiveness Factor Using Akbari-Ganji’s Method
4. Numerical Simulation
5. Discussion
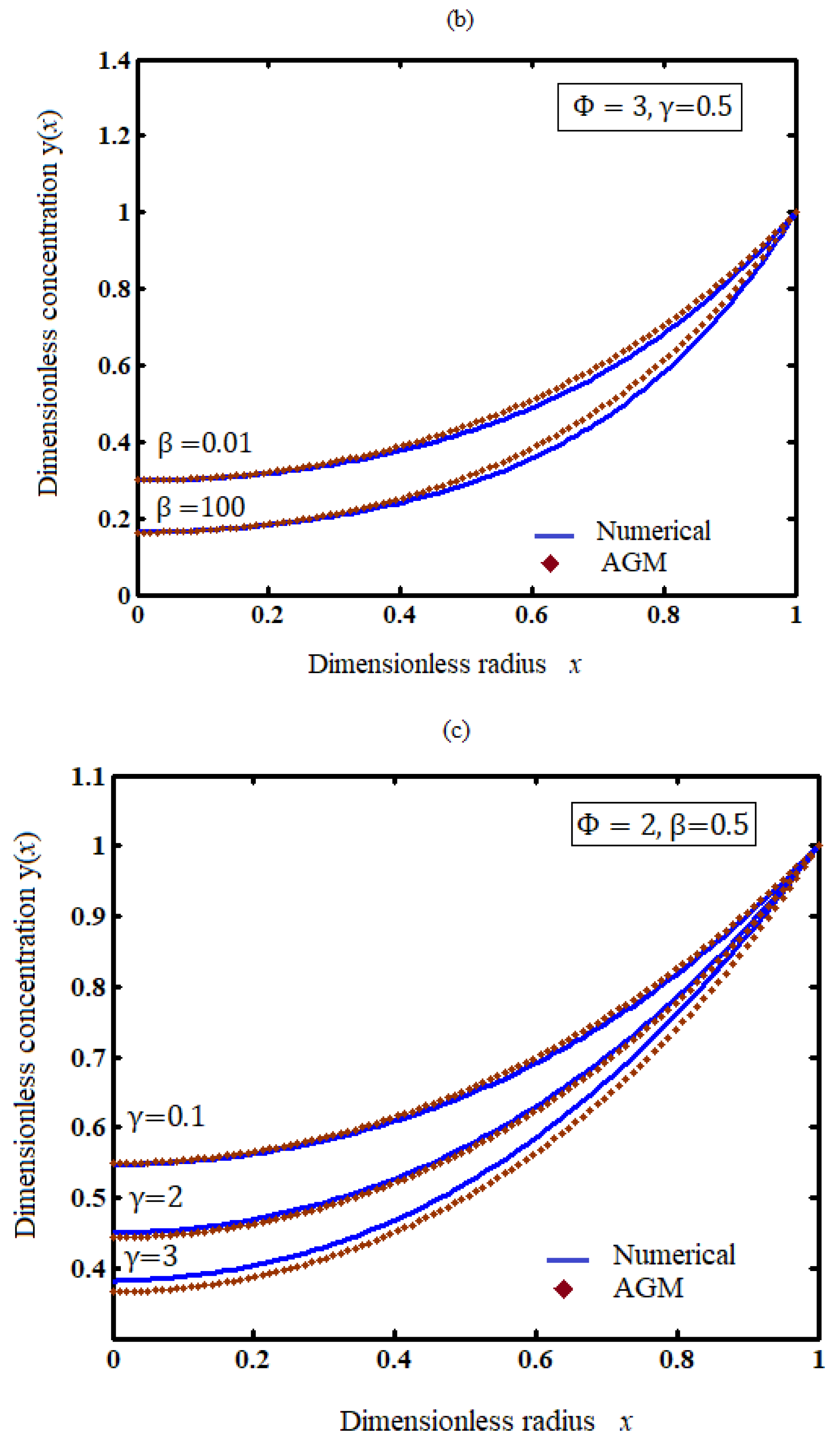
5.1. Influence of the Parameters (Thiele Modulus, Heat of the Reaction, and Activation Energy) on the Concentration Profile
5.2. Influence of the Parameters (Thiele Modulus, Heat of the Reaction, and Activation Energy) on the Effectiveness Factor
5.3. A limiting Case: The Dimensionless Heat of Reaction Is Zero
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| Concentration of reactant inside the catalyst pellet | |
| Concentration of reactant at the surface of catalyst pellet | |
| Effective diffusivity inside the catalyst pellet | |
| Activation energy | |
| Reference reaction constant | |
| Effective thermal conductivity inside the catalyst pellet | |
| Arrhenius reaction rate | |
| Radius of a sphere | |
| Gas constant | |
| Temperature inside the catalyst pellet | |
| Reference temperature | |
| Temperature at the surface of catalyst pellet | |
| Dimensionless radius of the spherical catalyst pellet | |
| Dimensionless concentration | |
| Heat of reaction | |
| Thiele modulus | |
| Dimensionless heat of reaction | |
| Dimensionless activation energy | |
| Effectiveness factor | |
| Flux |
Appendix A. Physicochemical Formulation of the Problem
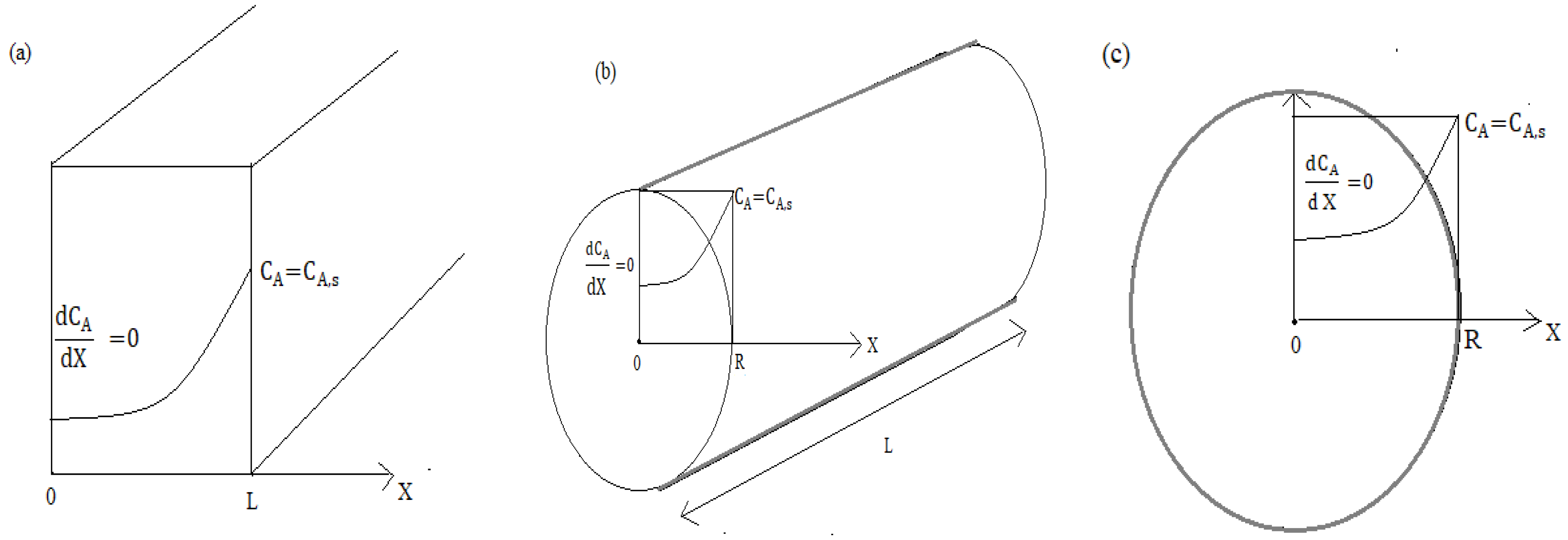
Appendix B. Approximate Analytical Expression of a Substrate Concentration in Species
Appendix C. Approximate Analytical Solution of Nonlinear Equation (6)
Appendix D. MATLAB Code for Numerical Solution of the Non-Linear Equation (1)
References
- Walsh, F. A First Course in Electrochemical; The Electrochemical Consultancy: Hants, UK, 1993. [Google Scholar]
- Sedahmed, G.H.; Shemilt, L.W. Forced convection mass transfer at rough surfacesin annuli. Lett. Heat Mass Transf. 1976, 3, 499–511. [Google Scholar] [CrossRef]
- Bird, R.; Stewart, W.; Lightfoot, E. Transport Phenomena, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Treybal, R.E. Mass Transfer Operations; McGraw Hill: New York, NY, USA, 1980; p. 466. [Google Scholar]
- Zaki, M.; Nirdosh, I.; Sedahmed, G.H. Effect of surface roughness induced bywoven metallic screens wrapped on the inner surface of an annulus on the rate of turbulent flow mass transfer. Ind. Eng. Chem. Res. 1996, 35, 4354–4359. [Google Scholar] [CrossRef]
- El-Sherbiny, M.F.; Zatout, A.A.; Hussien, M.; Sedahmed, G.H. Mass transfer at the gas evolving inner electrode of a concentric cylinder reactor. J. Appl. Electrochem. 1991, 21, 537–542. [Google Scholar] [CrossRef]
- Fahidy, T.Z. Electrolysis in an annular flow cell with gas generation. J. Appl. Electrochem. 1979, 9, 101–108. [Google Scholar] [CrossRef]
- Sedahmed, G.H.; Hosny, A.Y.; Fadally, O.A.; El-Mekkawy, I.M. Mass transfer at rough gas-sparged electrodes. J. Appl. Electrochem. 1994, 24, 139–144. [Google Scholar] [CrossRef]
- de Sa, M.S.; Shemilt, L.W.; Soegiarto, I.V. Mass transfer in the entrance region for axial and swirling annular flow. Can. J. Chem. Eng. 1991, 69, 294–299. [Google Scholar] [CrossRef]
- Legentilhomme, P.; Legrand, J. Overall mass transfer in swirling decaying flow in an annular electrochemical cells. J. Appl. Electrochem. 1990, 20, 216–222. [Google Scholar] [CrossRef]
- Zaki, M.M.; Nirdosh, I.; Sedahmed, G.H. Mass transfer behavior of annular ducts under developing flow with superimposed pulsating flow. Chem. Eng. Technol. 2011, 34, 475–481. [Google Scholar] [CrossRef]
- Storck, A.; Coeuret, F. Mass transfer between a flowing liquid and a wall or animmersed surface in fixed and fluidized beds. Chem. Eng. J. 1980, 20, 149–154. [Google Scholar] [CrossRef]
- Hutin, D.; Storck, A.; Coeuret, F. Local study of wall to liquid mass transfer influidized and packed beds. II. Mass transfer in packed beds. J. Appl. Electrochem. 1979, 9, 361–367. [Google Scholar] [CrossRef]
- Ramana Rao, M.V.; Rao, C.V. Mass transfer in square channels. Part II–ionic mass transfer in packed beds. Ind. J. Technol. 1970, 8, 44–47. [Google Scholar]
- Paterson, W.R.; Cresswell, D.L. A simple method for the calculation of effectiveness factors. Chem. Eng. Sci. 1971, 26, 605–616. [Google Scholar] [CrossRef]
- Tavera, E.M. Analytical expression for the non-isothermal effectiveness factor: The nth-order reaction in a slab geometry. Chem. Eng. Sci. 2005, 60, 907–916. [Google Scholar] [CrossRef]
- Thiele, E.W. Relation between catalytic activity and size of particle. Ind. Eng. Chem. 1936, 31, 916–920. [Google Scholar] [CrossRef]
- Weisz, P.; Hicks, J. The behaviour of porous catalyst particles in view of internal mass and heat diffusion effects. Chem. Eng. 1962, 17, 265–275. [Google Scholar] [CrossRef]
- Ishida, M.; Wen, C.; Shirai, T. Comparison of zone-reaction model and unreacted-core shrinking model in solid-gas reactions—II non-isothermal analysis. Chem. Eng. Sci. 1971, 26, 1043–1048. [Google Scholar] [CrossRef]
- Kimura, S.; Tone, S.; Otake, T. Reaction order in the grain model with grain size distribution. J. Chem. Eng. Jpn. 1981, 14, 491–493. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.C.; Wen, C.Y. Experimental evaluation of nonisotheral solid-gas reaction model. AIChE J. 1972, 18, 1231–1238. [Google Scholar] [CrossRef]
- Weisz, P.B.; Goodwin, R.D. Combustion of carbonaceous deposits within porous catalyst particles I. Diffusion-controlled kinetics. J. Catal. 1963, 2, 397–404. [Google Scholar] [CrossRef]
- Cannon, K.J.; Denbigh, K.G. Studies on gas-solid reactions—I: The oxidation rate of zinc sulphide. Chem. Eng. Sci. 1957, 6, 145–154. [Google Scholar] [CrossRef]
- Costa, E.C.; Smith, J.M. Kinetics of noncatalytic, nonisothermal, gas-solid reactions: Hydrofluorination of uranium dioxide. AIChE J. 1971, 17, 947–957. [Google Scholar] [CrossRef]
- Shettigar, U.R.; Hughues, R. Prediction of transient temperature distribution in gas—Solid reactions. Chem. Eng. J. 1972, 3, 93–99. [Google Scholar] [CrossRef]
- Lucia, A.; Gattupalli, R.R. A barrier-terrain methodology for global optimization. Ind. Eng. Chem. Res. 2008, 47, 2666–2680. [Google Scholar] [CrossRef]
- Renugadevi, M.; Sevukaperumal, S.; Rajendran, L. The Approximate analytical solution of non-linear equation for simultaneous internal mass and heat diffusion effects. Nat. Sci. 2016, 8, 284–294. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, M.; He, J.H. The homotopy perturbation method for fractional differential equations: Part 2, two-scale transform. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 559–567. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions for Helmholtz-Fangzhu oscillator. Int. J. Mod. Phys. B 2021, 35, 2150244. [Google Scholar] [CrossRef]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Lyons, M.E.G. Amperometric biosensors and coupled enzyme nonlinear reactions processes: A complete theoretical and numerical approach. Electrochim. Acta 2022, 415, 140236. [Google Scholar] [CrossRef]
- Hasan, Y.Q.; Zhu, L.M. A note on the use of modified Adomian decomposition method for solving singular boundary value problems of higher-order ordinary differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 3261–3265. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Kannan, M.; Rajendran, L. Approximate analytical solutions of biofilm reactor problem in applied biotechnology. Theor. Found. Chem. Eng. 2021, 55, 851–861. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Abukhaled, M.; Kannan, M. Semi-analytical expressions for the concentrations and effectiveness factor for the three general catalyst shapes. React. Kinet. Mech. Catal. 2022, 135, 1739–1754. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Variational iteration method: New development and applications. Comput. Math. Appl. 2007, 54, 881–894. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A comparison between the variational iteration method and Adomian decomposition method. J. Comput. Appl. Math. 2007, 207, 129–136. [Google Scholar] [CrossRef] [Green Version]
- Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology. J. Math. 2013, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Solving nonlinear reaction–diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. J. Math. Chem. 2021, 59, 1332–1347. [Google Scholar] [CrossRef]
- He, J.H. Taylor series solution for a third order boundary value problem arising in Architectural Engineering. Ain Shams Eng. J. 2022, 11, 1411–1414. [Google Scholar] [CrossRef]
- Manimegalai, B.; Lyons, M.E.G.; Rajendran, L. A kinetic model for amperometric immobilized enzymes at planar, cylindrical and spherical electrodes: The Akbari-Ganji method. J. Electroanal. Chem. 2021, 880, 114921. [Google Scholar] [CrossRef]
- Salomi, R.J.; Sylvia, S.V.; Rajendran, L.; Abukhaled, M. Electric potential and surface oxygen ion density for planar, spherical and cylindrical metal oxide grains. Sens. Actuators B Chem. 2020, 321, 128576. [Google Scholar] [CrossRef]
- Saranya, K.; Mohan, V.; Rajendran, L. Steady-state concentrations of carbon dioxide absorbed into phenyl glycidyl ether solutions by residual method. J. Math. Chem. 2020, 58, 1230–1246. [Google Scholar] [CrossRef]
- Akbari, M.R.; Akbari, S.; Kalantari, E.; Ganji, D.D. Akbari-Ganji’s method “AGM” to chemical reactor design for non-isothermal and non-adiabatic of mixed flow reactors. J. Chem. Eng. Mater. Sci. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Mary, M.L.C.; Devi, M.C.; Meena, A.; Rajendran, L.; Abukhaled, M. Mathematical modeling of immobilized enzyme in porous planar, cylindrical, and spherical particle: A reliable semi-analytical approach. React. Kinet. Mech. Catal. 2021, 134, 641–651. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Lyons, M. Reaction-diffusion in a packed-bed reactors: Enzymatic isomerization with Michaelis-Menten Kinetics. J. Electroanal. Chem. 2022, 910, 116184. [Google Scholar] [CrossRef]
- Salomi, R.J.; Rajendran, L. Cyclic voltammetric response of homogeneous catalysis of electrochemical reactions: Part 1. A theoretical and numerical approach for EE’C scheme. J. Electroanal. Chem. 2022, 918, 116429. [Google Scholar] [CrossRef]
- Lakshmi Narayanan, K.; Shanthi, R.; Usha Rani, R.; Lyons, M.E.G.; Rajendran, L. Mathematical modelling of forced convection in a porous medium for a general geometry: Solution of thermal energy equation via Taylor’s series with Ying Buzu algorithms. Int. J. Electrochem. Sci. 2022, 17, 220623. [Google Scholar] [CrossRef]
- Manimegalai, B.; Swaminathan, R.; Lyons, M.E.G.; Rajendran, L. Application of Taylor’s series with Ying Buzu Shu algorithm for the nonlinear problem in amperometric biosensors. Int. J. Electrochem. Sci. 2022, 17, 22074. [Google Scholar] [CrossRef]
- Fucik, S.; Kufner, A. Nonlinear Differential Equations; Elsevier: Prague, Czech Republic, 2014; pp. 1–136. [Google Scholar]
- Hermann, M.; Seravi, M. Nonlinear Ordinary Differential Equations; Springer: New Delhi, India, 2016. [Google Scholar]
- Akbari, M.R.; Ganji, D.D.; Nimafar, M.; Ahmadi, A.R. Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Front. Mech. Eng. 2014, 9, 390–401. [Google Scholar] [CrossRef]



| Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.9983 | 0.9983 | 0.0000 | 0.0663 | 0.0625 | 5.7315 | 0.0007 | 0.0007 | 0.0000 |
| 0.2 | 0.9984 | 0.9984 | 0.0000 | 0.0783 | 0.0774 | 1.1494 | 0.0016 | 0.0016 | 0.0000 |
| 0.4 | 0.9986 | 0.9986 | 0.0000 | 0.1222 | 0.1290 | 5.2713 | 0.0062 | 0.0062 | 0.0000 |
| 0.6 | 0.9989 | 0.9989 | 0.0000 | 0.2282 | 0.2246 | 1.5776 | 0.0315 | 0.0302 | 4.1269 |
| 0.8 | 0.9994 | 0.9994 | 0.0000 | 0.4727 | 0.4795 | 1.4385 | 0.1802 | 0.1739 | 3.4961 |
| 1 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 |
| Average error (%) | 0.0000 | Average error (%) | 2.5280 | Average error (%) | 1.2705 | ||||
| Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.9981 | 0.9981 | 0.0000 | 0.0045 | 0.0040 | 11.111 | 0.0000 | 0.0000 | 0.0000 |
| 0.2 | 0.9982 | 0.9982 | 0.0000 | 0.0069 | 0.0068 | 1.4493 | 0.0000 | 0.0000 | 0.0000 |
| 0.4 | 0.9985 | 0.9984 | 0.0100 | 0.0187 | 0.0189 | 1.0695 | 0.0001 | 0.0001 | 0.0000 |
| 0.6 | 0.9988 | 0.9988 | 0.0000 | 0.0656 | 0.0649 | 1.0671 | 0.0026 | 0.0024 | 7.6923 |
| 0.8 | 0.9994 | 0.9993 | 0.0100 | 0.2581 | 0.2548 | 1.2786 | 0.0532 | 0.0531 | 0.1880 |
| 1 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 |
| Average error (%) | 0.0033 | Average error (%) | 2.6626 | Average error (%) | 1.3134 | ||||
| Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.9983 | 0.9983 | 0.0000 | 0.0673 | 0.0651 | 3.2689 | 0.0000 | 0.0000 | 0.0000 |
| 0.2 | 0.9984 | 0.9984 | 0.0000 | 0.0794 | 0.0802 | 1.0075 | 0.0017 | 0.0017 | 0.0000 |
| 0.4 | 0.9986 | 0.9986 | 0.0000 | 0.1235 | 0.1228 | 0.5668 | 0.0064 | 0.0064 | 0.0000 |
| 0.6 | 0.9989 | 0.9989 | 0.0000 | 0.2296 | 0.2264 | 1.3937 | 0.0320 | 0.0335 | 4.6875 |
| 0.8 | 0.9994 | 0.9994 | 0.0000 | 0.4738 | 0.4649 | 1.8784 | 0.1813 | 0.1908 | 5.2399 |
| 1 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 |
| Average error (%) | 0.0000 | Average error (%) | 1.3525 | Average error (%) | 1.6546 | ||||
| Num. | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | Num | Approximate Analytical Equation (5) | Error% Equation (5) | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.9983 | 0.9983 | 0.0000 | 0.0071 | 0.0068 | 4.2253 | 0.0000 | 0.0000 | 0.0000 |
| 0.2 | 0.9984 | 0.9984 | 0.0000 | 0.0108 | 0.0101 | 6.4615 | 0.0000 | 0.0000 | 0.0000 |
| 0.4 | 0.9986 | 0.9986 | 0.0000 | 0.0289 | 0.0289 | 0.0000 | 0.0002 | 0.0002 | 0.0000 |
| 0.6 | 0.9989 | 0.9989 | 0.0000 | 0.0981 | 0.0956 | 2.5484 | 0.0038 | 0.0033 | 13.158 |
| 0.8 | 0.9994 | 0.9994 | 0.0000 | 0.3460 | 0.3401 | 1.7052 | 0.0780 | 0.0713 | 8.5874 |
| 1 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 |
| Average error (%) | 0.0000 | Average error (%) | 2.4906 | Average error (%) | 3.6242 | ||||
| Geometry | Exact Result | This Work (Approximate Analytical Result) | ||
|---|---|---|---|---|
| Concentration | Effectiveness Factor | Concentration | Effectiveness Factor | |
| Spherical ) | (11) | (12) | (17) where m is obtained by solving the equation (18) | (19) |
| ) | (13) | (14) | ||
| Slab) | (15) | (16) | ||
| Exact Equation (13) | This Work Equation (17) | Error% | Exact Equation (13) | This Work Equation (17) | Error% | Exact Equation (13) | This Work Equation (17) | Error% | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.9975 | 0.9975 | 0.0000 | 0.0367 | 0.0351 | 4.3697 | 0.0003 | 0.0003 | 0.0000 |
| 0.2 | 0.9976 | 0.9976 | 0.0000 | 0.0465 | 0.0469 | 0.8602 | 0.0008 | 0.0008 | 0.0000 |
| 0.4 | 0.9979 | 0.9979 | 0.0000 | 0.0837 | 0.0821 | 1.9116 | 0.0040 | 0.0045 | 12.500 |
| 0.6 | 0.9984 | 0.9984 | 0.0000 | 0.1792 | 0.1753 | 2.1763 | 0.0239 | 0.0236 | 1.2552 |
| 0.8 | 0.9991 | 0.9991 | 0.0000 | 0.4149 | 0.4174 | 0.7231 | 0.1518 | 0.1607 | 5.8629 |
| 1 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | 0.0000 |
| Average error (%) | 0.0000 | Average error (%) | 1.6735 | Average error (%) | 3.2697 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G.; Abukhaled, M. Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method. Electrochem 2022, 3, 699-712. https://doi.org/10.3390/electrochem3040046
Jeyabarathi P, Rajendran L, Lyons MEG, Abukhaled M. Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method. Electrochem. 2022; 3(4):699-712. https://doi.org/10.3390/electrochem3040046
Chicago/Turabian StyleJeyabarathi, Ponraj, Lakshmanan Rajendran, Michael E. G. Lyons, and Marwan Abukhaled. 2022. "Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method" Electrochem 3, no. 4: 699-712. https://doi.org/10.3390/electrochem3040046
APA StyleJeyabarathi, P., Rajendran, L., Lyons, M. E. G., & Abukhaled, M. (2022). Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method. Electrochem, 3(4), 699-712. https://doi.org/10.3390/electrochem3040046







