Robust Variable Selection Based on Relaxed Lad Lasso
Abstract
:1. Introduction
2. Relaxed Lad Lasso
2.1. Definition
2.2. Algorithm
| Algorithm 1 The algorithm for relaxed lad lasso |
| Input: Design matrix , response vector , parameter , iteration number k, stepsize |
| Output: The relaxed lad lasso estimator |
| Initialization: Define |
| Compute |
|
| Repeat |
|
| Until convergence |
3. The Asymptotic Properties of Relaxed Lad Lasso
4. Simulation
4.1. Setup
- We consider the following regression model in this simulation. The predictor matrix is generated from a p-dimension multivariate normal distribution where the covariance matrix with . is derived from several heavy-tailed distributions. The density function of the t-distribution shows a heavy tail compared to the standard normal distribution. Therefore, we set to follow t-distribution with 5 degrees of freedom df() and the standard t-distribution with 3 degrees of freedom df().
- We set the fixed dimension and vary to compare the performances of four methods under different sample sizes.
- The true regression cofficient is an eight-dimension vector where its first four elements are important variables taking nonzero coefficients and otherwise set as 0.
- The value of is adjusted to achieve different theoretical SNR values. We discuss and in order to test the effects of strong and weak SNR values on the results.
- The parameter is selected by the five-fold cross-validation, and the mean absolute error is applied for the loss of cross-validation. In addition, 100 simulation iterations are completed for each situation to test the performance of relaxed lad lasso.
4.2. Evaluation Metrics
4.3. Summary of Results
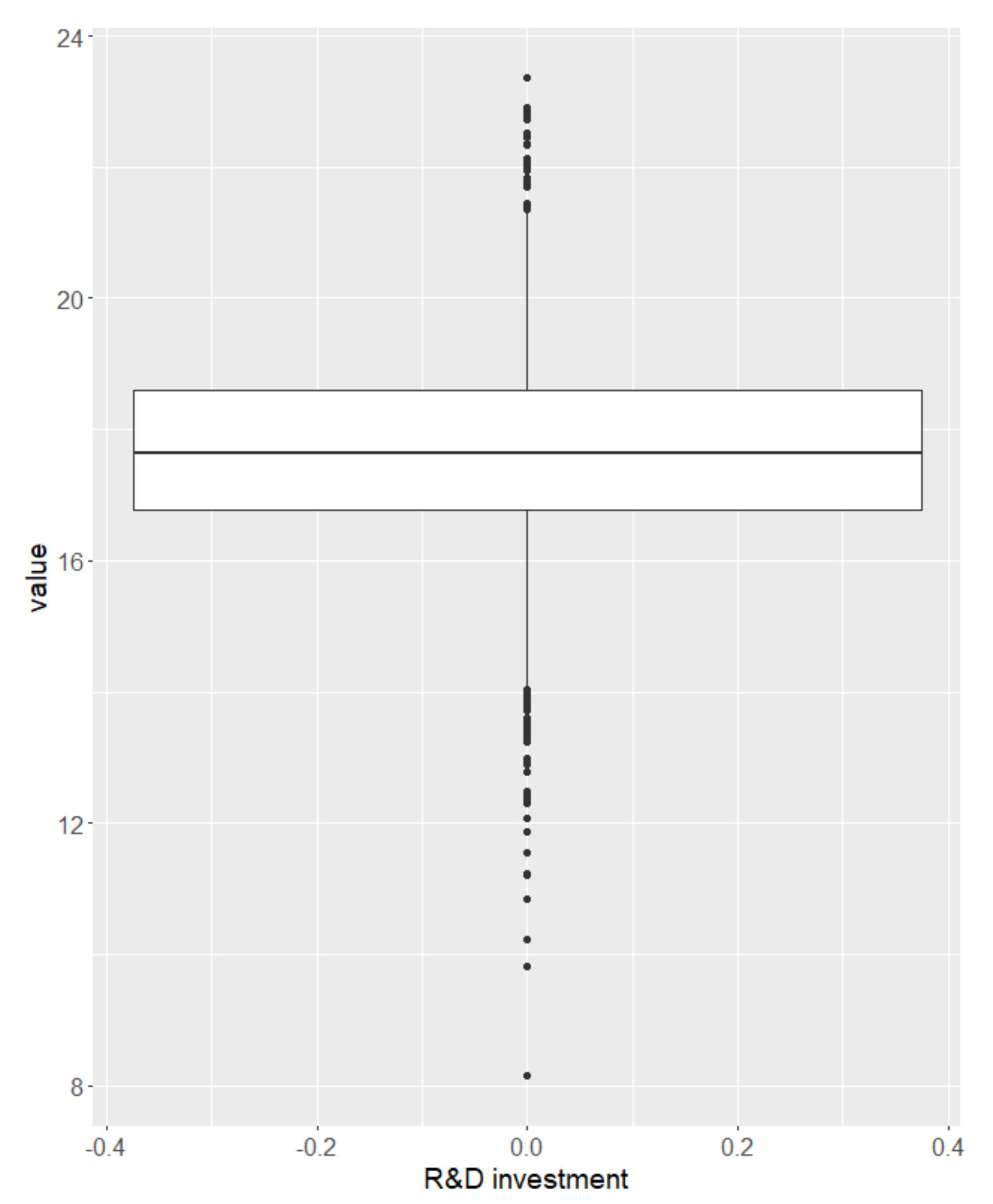
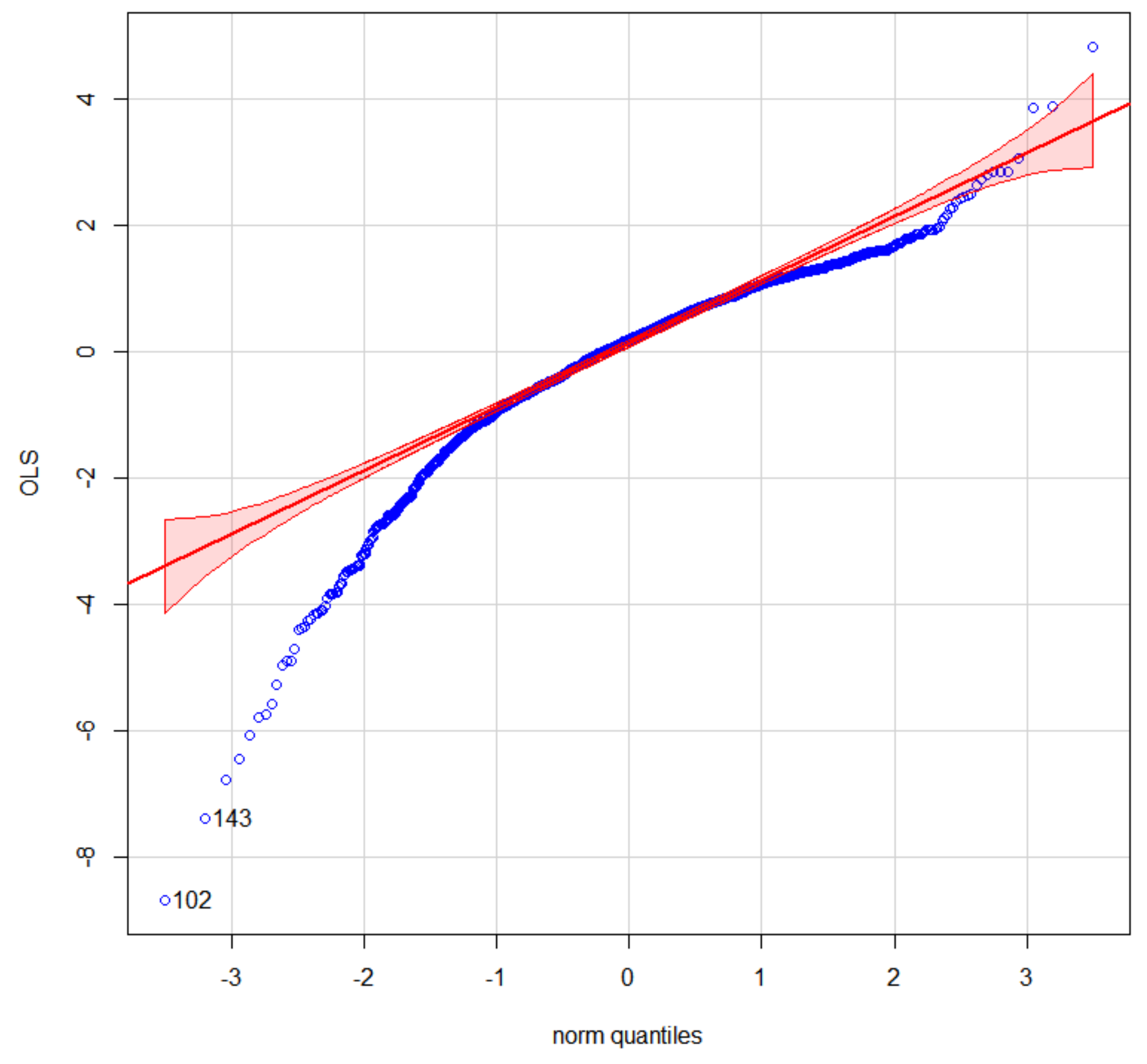
5. Application to Real Data
5.1. Dataset
5.2. Analysis Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Appendix Proof of Lemma 1
Appendix B. Appendix Proof of Theorem 1
Appendix C. Appendix Proof of Theorem 2
Appendix D. Appendix Proof of Theorem 3
Appendix E. Appendix Proof of Theorem 4
References
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Briefings Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uraibi, H.S. Weighted Lasso Subsampling for HighDimensional Regression. Electron. J. Appl. Stat. Anal. 2019, 12, 69–84. [Google Scholar]
- Meinshausen, N. Relaxed lasso. Comput. Stat. Data Anal. 2007, 52, 374–393. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Tibshirani, R.J. Extended comparisons of best subset selection, forward stepwise selection, and the lasso. arXiv 2017, arXiv:1707.08692. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Tibshirani, R.J. Rejoinder: Best Subset, Forward Stepwise or Lasso? Analysis and Recommendations Based on Extensive Comparisons. Stat. Sci. 2020, 35, 625–626. [Google Scholar] [CrossRef]
- Mentch, L.; Zhou, S. Randomization as regularization: A degrees of freedom explanation for random forest success. J. Mach. Learn. Res. 2020, 21, 1–36. [Google Scholar]
- Bloise, F.; Brunori, P.; Piraino, P. Estimating intergenerational income mobility on sub-optimal data: A machine learning approach. J. Econ. Inequal. 2021, 19, 643–665. [Google Scholar] [CrossRef]
- He, Y. The Analysis of Impact Factors of Foreign Investment Based on Relaxed Lasso. J. Appl. Math. Phys. 2017, 5, 693–699. [Google Scholar] [CrossRef] [Green Version]
- Gao, X. Estimation and Selection Properties of the LAD Fused Lasso Signal Approximator. arXiv 2021, arXiv:2105.00045. [Google Scholar]
- Wang, H.; Li, G.; Jiang, G. Robust regression shrinkage and consistent variable selection through the LAD-Lasso. J. Bus. Econ. Stat. 2007, 25, 347–355. [Google Scholar] [CrossRef]
- Gao, X.; Huang, J. Asymptotic analysis of high-dimensional LAD regression with LASSO. Stat. Sin. 2010, 20, 1485–1506. [Google Scholar]
- Xu, J.; Ying, Z. Simultaneous estimation and variable selection in median regression using Lasso-type penalty. Ann. Inst. Stat. Math. 2010, 62, 487–514. [Google Scholar] [CrossRef] [Green Version]
- Arslan, O. Weighted LAD-LASSO method for robust parameter estimation and variable selection in regression. Comput. Stat. Data Anal. 2012, 56, 1952–1965. [Google Scholar] [CrossRef]
- Rahardiantoro, S.; Kurnia, A. Lad-lasso: Simulation study of robust regression in high dimensional data. Forum Statistika dan Komputasi. 2020, 20. [Google Scholar]
- Zhou, X.; Liu, G. LAD-lasso variable selection for doubly censored median regression models. Commun. Stat. Theory Methods 2016, 45, 3658–3667. [Google Scholar] [CrossRef]
- Li, Q.; Wang, L. Robust change point detection method via adaptive LAD-LASSO. Stat. Pap. 2020, 61, 109–121. [Google Scholar] [CrossRef]
- Croux, C.; Filzmoser, P.; Pison, G.; Rousseeuw, P.J. Fitting multiplicative models by robust alternating regressions. Stat. Comput. 2003, 13, 23–36. [Google Scholar] [CrossRef]
- Giloni, A.; Simonoff, J.S.; Sengupta, B. Robust weighted LAD regression. Comput. Stat. Data Anal. 2006, 50, 3124–3140. [Google Scholar] [CrossRef] [Green Version]
- Xue, F.; Qu, A. Variable selection for highly correlated predictors. arXiv 2017, arXiv:1709.04840. [Google Scholar]
- Gao, X.; Feng, Y. Penalized weighted least absolute deviation regression. Stat. Interface 2018, 11, 79–89. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Zhang, J.; Xie, B.; Liao, J.; Liao, W. Outlier detection and robust variable selection via the penalized weighted LAD-LASSO method. J. Appl. Stat. 2021, 48, 234–246. [Google Scholar] [CrossRef]
- Fu, W.; Knight, K. Asymptotics for lasso-type estimators. Ann. Stat. 2000, 28, 1356–1378. [Google Scholar] [CrossRef]
- Pesme, S.; Flammarion, N. Online robust regression via sgd on the l1 loss. Adv. Neural Inf. Process. Syst. 2020, 33, 2540–2552. [Google Scholar]
- Contreras-Reyes, J.E.; Arellano-Valle, R.B.; Canales, T.M. Comparing growth curves with asymmetric heavy-tailed errors: Application to the southern blue whiting (Micromesistius australis). Fish. Res. 2014, 159, 88–94. [Google Scholar] [CrossRef]
| n | Method | Mean MAPE | Median MAPE | Number of Nonzeros | Number of Zeros | ||
|---|---|---|---|---|---|---|---|
| Incorrect | Corerect | ||||||
| 0.5 | 50 | Lasso | 0.150 | 0.148 | 4.3 | 0.02 | 3.67 |
| Ladlasso | 0.176 | 0.163 | 2.8 | 1.23 | 4.00 | ||
| Rlasso | 0.142 | 0.139 | 3.7 | 0.38 | 3.95 | ||
| Rladlasso | 0.133 | 0.131 | 4.1 | 0.12 | 3.77 | ||
| 100 | Lasso | 0.145 | 0.141 | 4.2 | 0.00 | 3.76 | |
| Ladlasso | 0.158 | 0.152 | 3.0 | 1.01 | 4.00 | ||
| Rlasso | 0.137 | 0.131 | 3.8 | 0.19 | 3.98 | ||
| Rladlasso | 0.133 | 0.127 | 4.2 | 0.00 | 3.78 | ||
| 200 | Lasso | 0.138 | 0.130 | 4.1 | 0.00 | 3.88 | |
| Ladlasso | 0.151 | 0.124 | 3.1 | 0.88 | 4.00 | ||
| Rlasso | 0.129 | 0.125 | 4.0 | 0.03 | 4.00 | ||
| Rladlasso | 0.128 | 0.125 | 4.2 | 0.00 | 3.79 | ||
| 1 | 50 | Lasso | 0.307 | 0.306 | 4.1 | 0.25 | 3.65 |
| Ladlasso | 0.314 | 0.313 | 2.3 | 1.74 | 4.00 | ||
| Rlasso | 0.298 | 0.292 | 3.1 | 1.00 | 3.93 | ||
| Rladlasso | 0.279 | 0.280 | 3.9 | 0.43 | 3.69 | ||
| 100 | Lasso | 0.277 | 0.272 | 4.1 | 0.10 | 3.80 | |
| Ladlasso | 0.269 | 0.265 | 2.8 | 1.21 | 4.00 | ||
| Rlasso | 0.267 | 0.262 | 3.3 | 0.76 | 3.96 | ||
| Rladlasso | 0.258 | 0.255 | 4.0 | 0.20 | 3.79 | ||
| 200 | Lasso | 0.251 | 0.249 | 4.1 | 0.02 | 3.86 | |
| Ladlasso | 0.248 | 0.247 | 3.0 | 1.01 | 4.00 | ||
| Rlasso | 0.248 | 0.243 | 3.3 | 0.70 | 4.00 | ||
| Rladlasso | 0.239 | 0.235 | 4.1 | 0.06 | 3.83 | ||
| n | Method | Mean MAPE | Median MAPE | Number of Nonzeros | Number of Zeros | ||
|---|---|---|---|---|---|---|---|
| Incorrect | Corerect | ||||||
| 0.5 | 50 | Lasso | 0.184 | 0.178 | 4.2 | 0.10 | 3.68 |
| Ladlasso | 0.205 | 0.198 | 2.7 | 1.33 | 4.00 | ||
| Rlasso | 0.172 | 0.170 | 3.4 | 0.62 | 3.96 | ||
| Rladlasso | 0.157 | 0.154 | 4.1 | 0.17 | 3.75 | ||
| 100 | Lasso | 0.172 | 0.166 | 4.3 | 0.02 | 3.65 | |
| Ladlasso | 0.175 | 0.171 | 3.0 | 0.99 | 4.00 | ||
| Rlasso | 0.164 | 0.159 | 3.6 | 0.36 | 4.00 | ||
| Rladlasso | 0.154 | 0.150 | 4.2 | 0.00 | 3.79 | ||
| 200 | Lasso | 0.162 | 0.160 | 4.1 | 0.00 | 3.88 | |
| Ladlasso | 0.170 | 0.171 | 3.1 | 0.89 | 4.00 | ||
| Rlasso | 0.153 | 0.153 | 3.9 | 0.15 | 4.00 | ||
| Rladlasso | 0.147 | 0.146 | 4.2 | 0.00 | 3.85 | ||
| 1 | 50 | Lasso | 0.339 | 0.324 | 3.8 | 0.59 | 3.58 |
| Ladlasso | 0.340 | 0.320 | 2.1 | 1.89 | 4.00 | ||
| Rlasso | 0.325 | 0.314 | 3.0 | 1.12 | 3.92 | ||
| Rladlasso | 0.299 | 0.290 | 3.8 | 0.54 | 3.70 | ||
| 100 | Lasso | 0.317 | 0.311 | 3.9 | 0.29 | 3.82 | |
| Ladlasso | 0.292 | 0.288 | 2.8 | 1.23 | 4.00 | ||
| Rlasso | 0.303 | 0.286 | 3.0 | 1.02 | 4.00 | ||
| Rladlasso | 0.280 | 0.274 | 4.0 | 0.22 | 3.80 | ||
| 200 | Lasso | 0.308 | 0.308 | 4.0 | 0.10 | 3.90 | |
| Ladlasso | 0.286 | 0.283 | 3.0 | 1.00 | 4.00 | ||
| Rlasso | 0.295 | 0.293 | 3.0 | 0.96 | 4.00 | ||
| Rladlasso | 0.279 | 0.276 | 4.1 | 0.06 | 3.89 | ||
| Variables | Description | Symbols |
|---|---|---|
| R&D investment | Research and Development Costs | Y |
| Profitability | Finance Costs , Payback On Assets , Operating Costs , … | |
| Business Capability | Net Accounts Receivable , Business Cycle , Current Assets , … | |
| Assets and Liabilities | Total Current Liabilities , Taxes Payable , Accounts Payable , … | |
| Profits | Operating Profit , Total Comprehensive Income , … | |
| Cash Flow | Cash Paid For Goods , Net Cash Flows From Investing Activities , … |
| Method | Lasso | Ladlasso | Rlasso | Rladlasso |
|---|---|---|---|---|
| MAPE | 0.203 | 0.201 | 0.191 | 0.184 |
| Order Number | Explanatory Variable | Coefficient |
|---|---|---|
| Net Accounts Receivable | 0.297 | |
| Basic Earnings Per Share | 0.023 | |
| Interest Income | 0.115 | |
| Other Income | 0.197 | |
| Gains and Losses from Asset Disposition | 0.154 | |
| Funds Paid to and for Staff | 0.251 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xu, X.; Lu, Y.; Yu, X.; Zhao, T.; Zhang, R. Robust Variable Selection Based on Relaxed Lad Lasso. Symmetry 2022, 14, 2161. https://doi.org/10.3390/sym14102161
Li H, Xu X, Lu Y, Yu X, Zhao T, Zhang R. Robust Variable Selection Based on Relaxed Lad Lasso. Symmetry. 2022; 14(10):2161. https://doi.org/10.3390/sym14102161
Chicago/Turabian StyleLi, Hongyu, Xieting Xu, Yajun Lu, Xi Yu, Tong Zhao, and Rufei Zhang. 2022. "Robust Variable Selection Based on Relaxed Lad Lasso" Symmetry 14, no. 10: 2161. https://doi.org/10.3390/sym14102161
APA StyleLi, H., Xu, X., Lu, Y., Yu, X., Zhao, T., & Zhang, R. (2022). Robust Variable Selection Based on Relaxed Lad Lasso. Symmetry, 14(10), 2161. https://doi.org/10.3390/sym14102161






