Water Dynamics in Cancer Cells: Lessons from Quasielastic Neutron Scattering
Abstract
1. Introduction
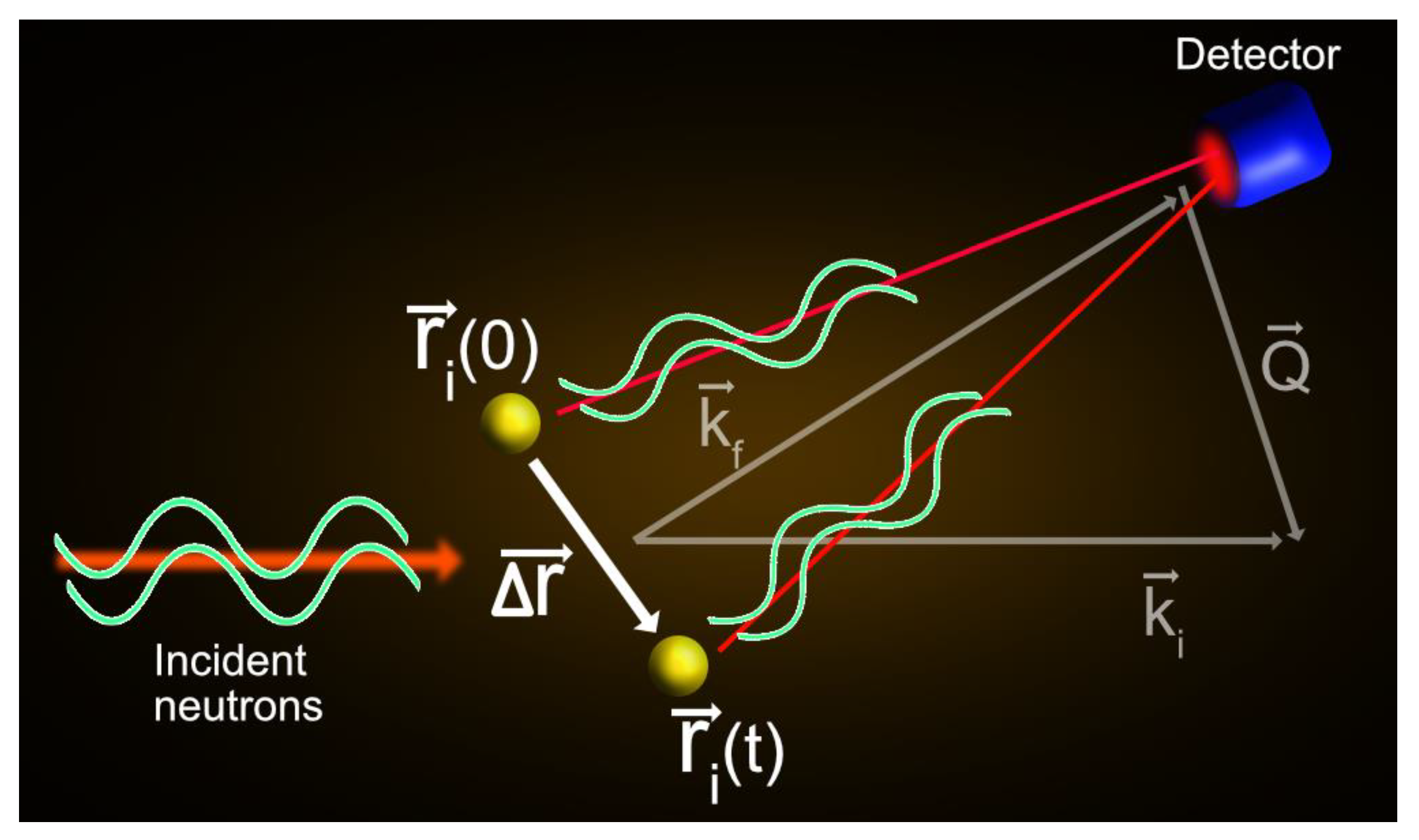
2. The QENS Technique: A Brief Overview
2.1. Basic Concepts of QENS
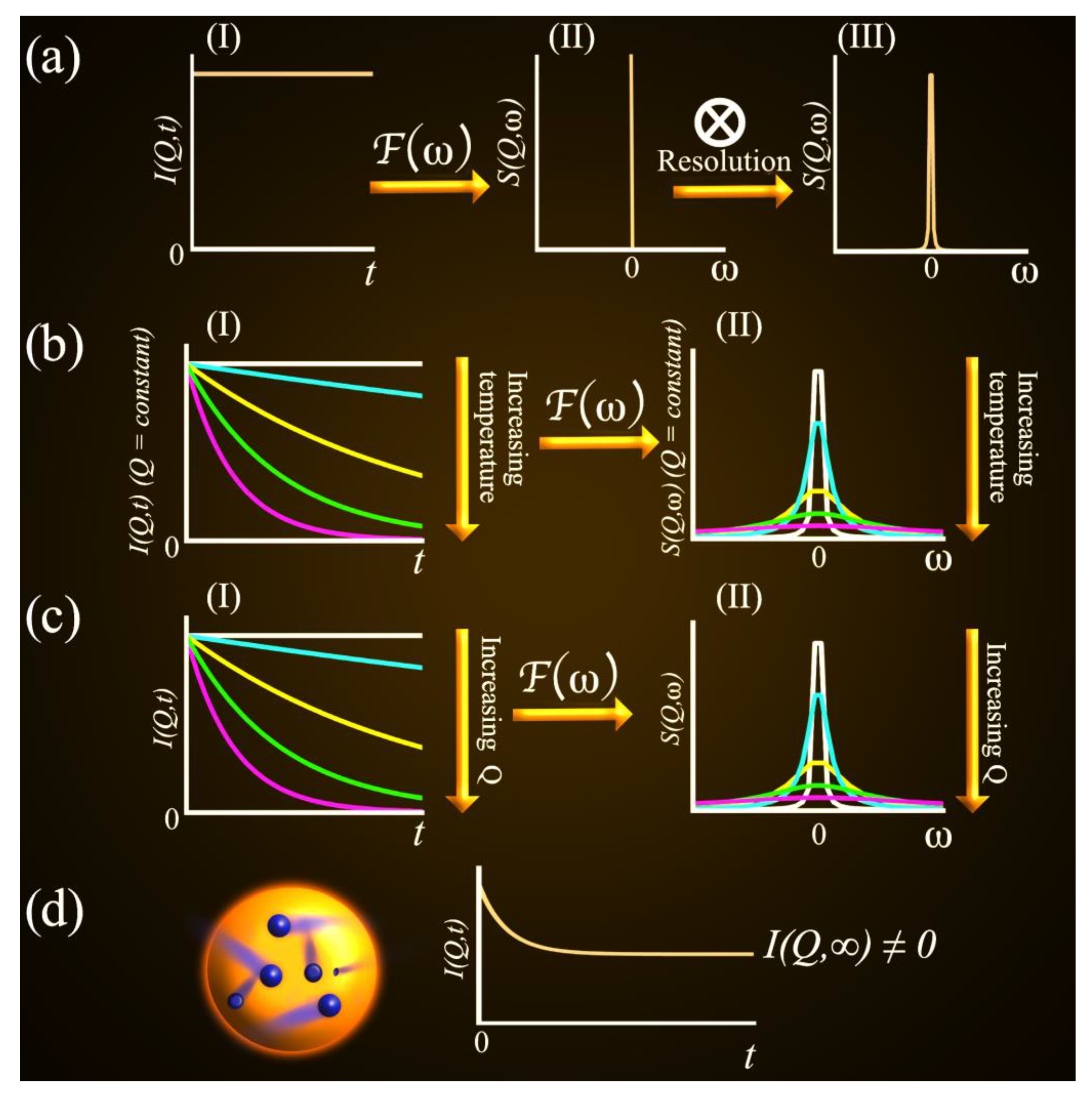
2.2. QENS Data Analysis
3. QENS and Cancer Cells
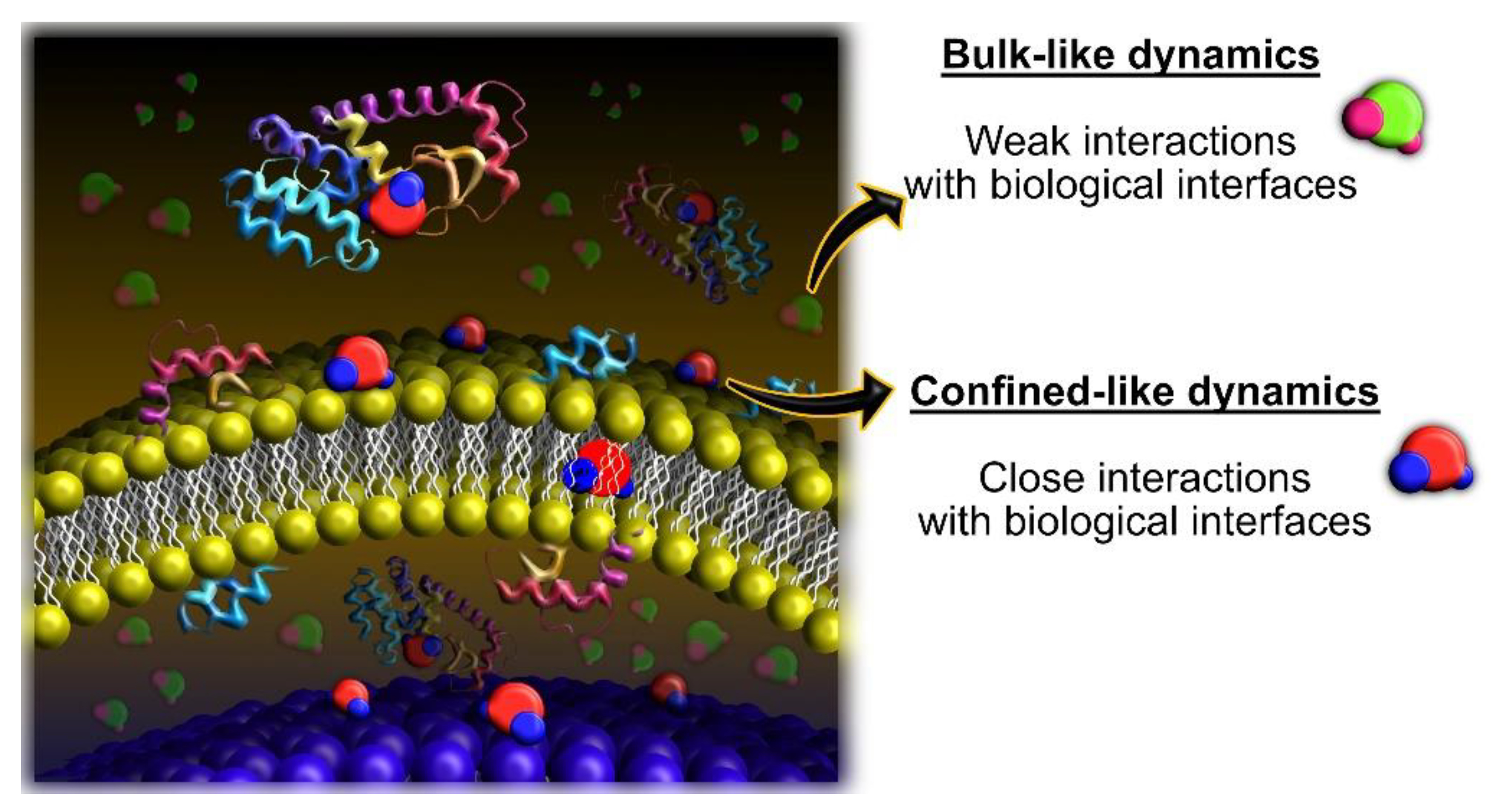
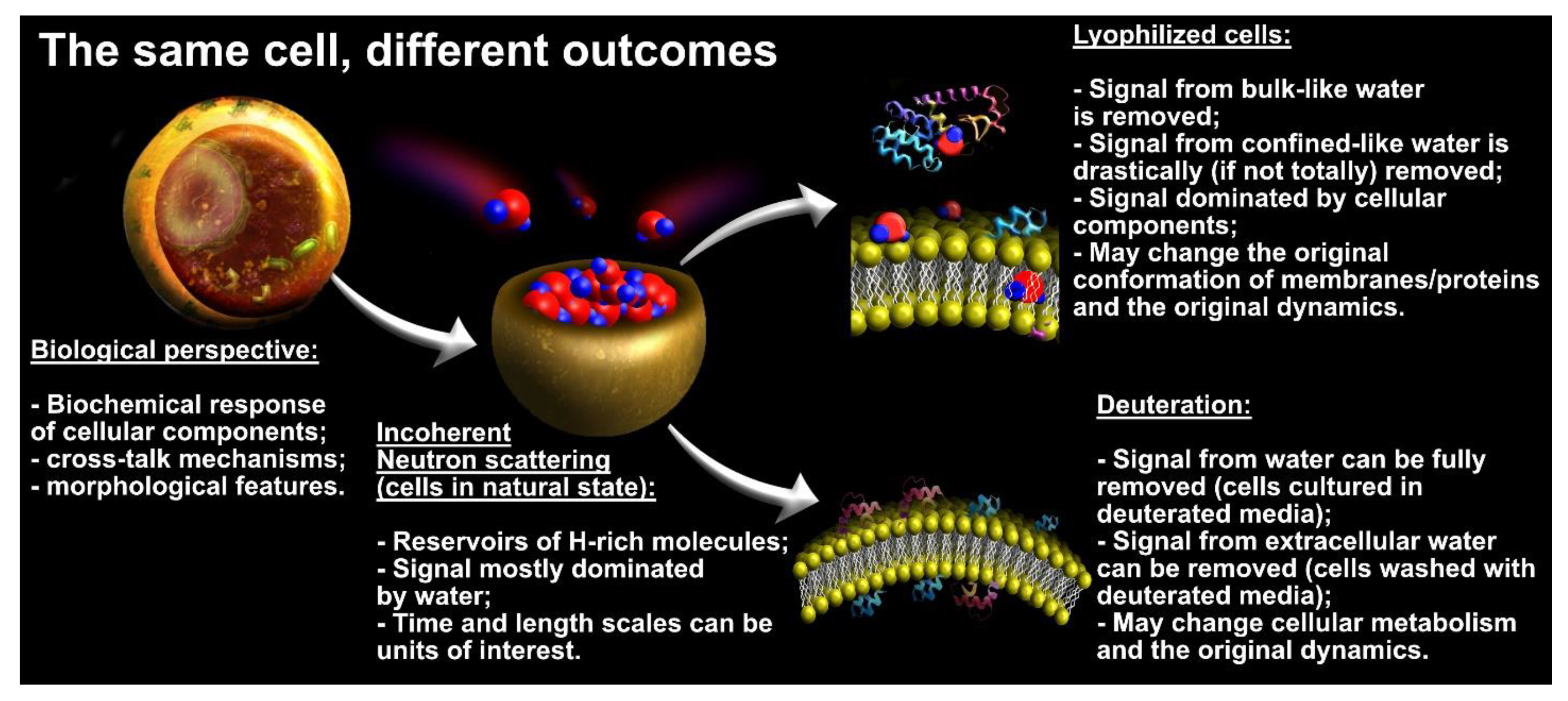
3.1. Experimental Considerations
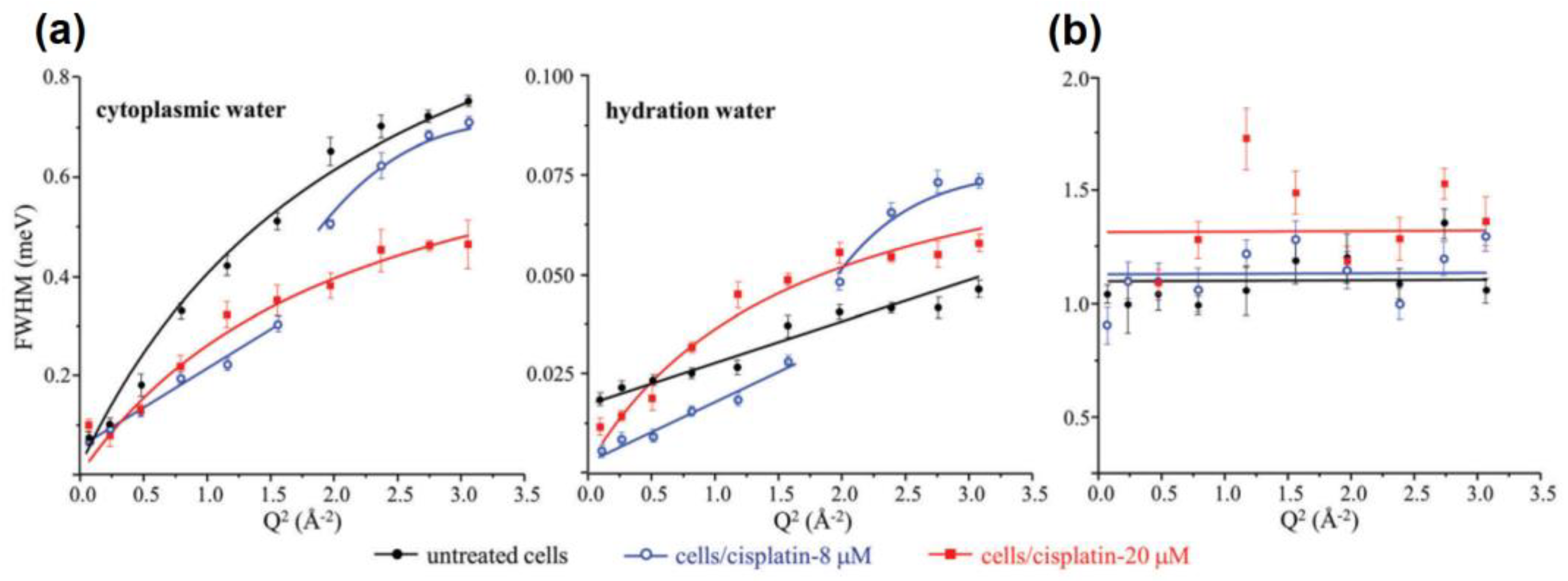
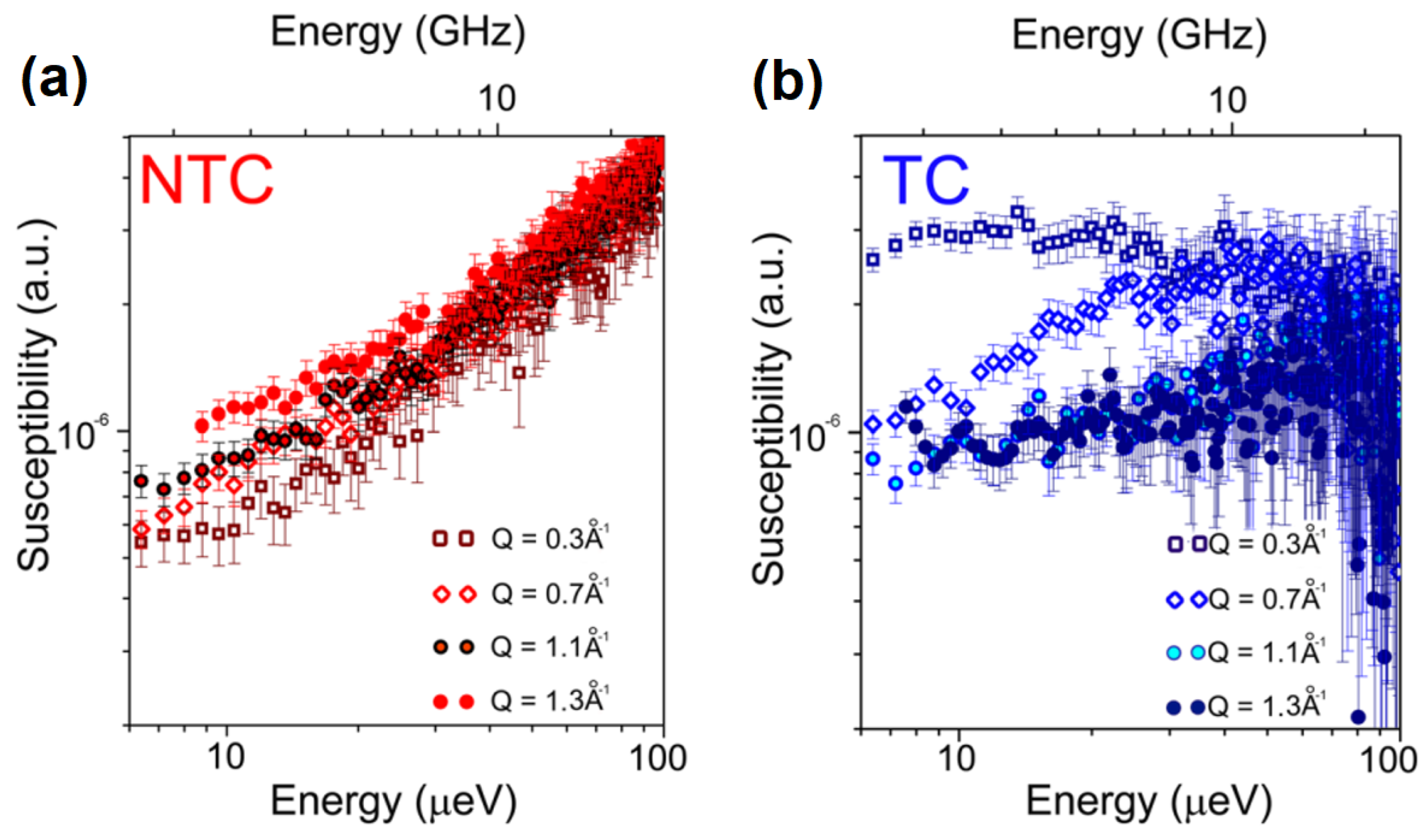
3.2. What Have We Learned So Far with QENS and Cancer Cells?
4. Perspectives for the Future
5. Final Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.D.; Fidler-Benaoudia, M.; Keegan, T.H.; Hipp, H.S.; Jemal, A.; Siegel, R.L. Cancer statistics for adolescents and young adults, 2020. CA Cancer J. Clin. 2020, 70, 443–459. [Google Scholar] [CrossRef] [PubMed]
- Ajabnoor, G.M.A.; Crook, T.; Coley, H.M. Paclitaxel resistance is associated with switch from apoptotic to autophagic cell death in MCF-7 breast cancer cells. Cell Death Dis. 2012, 3, e260. [Google Scholar] [CrossRef] [PubMed]
- Eramo, A.; Ricci-Vitiani, L.; Zeuner, A.; Pallini, R.; Lotti, F.; Sette, G.; Pilozzi, E.; Larocca, L.M.; Peschle, C.; De Maria, R. Chemotherapy resistance of glioblastoma stem cells. Cell Death Differ. 2006, 13, 1238–1241. [Google Scholar] [CrossRef]
- Barker, H.E.; Paget, J.T.E.; Khan, A.A.; Harrington, K.J. The tumour microenvironment after radiotherapy: Mechanisms of resistance and recurrence. Nat. Rev. Cancer 2015, 15, 409–425. [Google Scholar] [CrossRef]
- Wu, P.H.; Aroush, D.R.B.; Asnacios, A.; Chen, W.C.; Dokukin, M.E.; Doss, B.L.; Durand-Smet, P.; Ekpenyong, A.; Guck, J.; Guz, N.V.; et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 2018, 15, 491–498. [Google Scholar] [CrossRef]
- Hussein, M.; Awwad, F.; Jithin, D.; El Hasasna, H.; Athamneh, K.; Iratni, R. Breast cancer cells exhibits specific dielectric signature in vitro using the open-ended coaxial probe technique from 200 MHz to 13.6 GHz. Sci. Rep. 2019, 9, 4681. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Cai, K.; Yu, H.; Zhou, D.; Lu, D.; Xin, S.X. Dielectric Properties of Normal and Metastatic Lymph Nodes Ex Vivo From Lung Cancer Surgeries. Bioelectromagnetics 2020, 41, 148–155. [Google Scholar] [CrossRef]
- Patterson, D.M.; Padhani, A.R.; Collins, D.J. Technology Insight: Water diffusion MRI—a potential new biomarker of response to cancer therapy. Nat. Clin. Pract. Oncol. 2008, 5, 220–233. [Google Scholar] [CrossRef]
- Amornsiripanitch, N.; Bickelhaupt, S.; Shin, H.J.; Dang, M.; Rahbar, H.; Pinker, K.; Partridge, S.C. Diffusion-weighted MRI for Unenhanced Breast Cancer Screening. Radiology 2019, 293, 504–520. [Google Scholar] [CrossRef]
- Feng, B.; Sosa, R.P.; Mårtensson, A.K.F.; Jiang, K.; Tong, A.; Dorfman, K.D.; Takahashi, M.; Lincoln, P.; Bustamante, C.J.; Westerlund, F.; et al. Hydrophobic catalysis and a potential biological role of DNA unstacking induced by environment effects. Proc. Natl. Acad. Sci. USA 2019, 116, 17169–17174. [Google Scholar] [CrossRef] [PubMed]
- Bellissent-Funel, M.-C.; Hassanali, A.; Havenith, M.; Henchman, R.; Pohl, P.; Sterpone, F.; van der Spoel, D.; Xu, Y.; Garcia, A.E. Water Determines the Structure and Dynamics of Proteins. Chem. Rev. 2016, 116, 7673–7697. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S.; Mukherjee, S.; Bagchi, B. Protein Hydration Dynamics: Much Ado about Nothing? J. Phys. Chem. Lett. 2017, 8, 4878–4882. [Google Scholar] [CrossRef] [PubMed]
- Jensen, H.H.; Login, F.H.; Koffman, J.S.; Kwon, T.-H.; Nejsum, L.N. The role of aquaporin-5 in cancer cell migration: A potential active participant. Int. J. Biochem. Cell Biol. 2016, 79, 271–276. [Google Scholar] [CrossRef]
- Auciello, O.; Scott, J.F.; Ramesh, R. The Physics of Ferroelectric Memories. Phys. Today 1998, 51, 22–27. [Google Scholar] [CrossRef]
- Martins, M.L.; Dinitzen, A.B.; Mamontov, E.; Rudić, S.; Pereira, J.E.M.; Hartmann-Petersen, R.; Herwig, K.W.; Bordallo, H.N. Water dynamics in MCF-7 breast cancer cells: A neutron scattering descriptive study. Sci. Rep. 2019, 9, 8704. [Google Scholar] [CrossRef]
- Cerveny, S.; Swenson, J. Water dynamics in the hydration shells of biological and non-biological polymers. J. Chem. Phys. 2019, 150, 234904. [Google Scholar] [CrossRef]
- Martins, M.L.; Bordallo, H.N.; Arrese-Igor, S.; Alegría, A.; Colmenero de Leon, J. Effect of Paclitaxel in the Water Dynamics of MCF-7 Breast Cancer Cells Revealed by Dielectric Spectroscopy. ACS Omega 2020, 5, 18602–18607. [Google Scholar] [CrossRef]
- Stadler, A.M.; Embs, J.P.; Digel, I.; Artmann, G.M.; Unruh, T.; Büldt, G.; Zaccai, G. Cytoplasmic Water and Hydration Layer Dynamics in Human Red Blood Cells. J. Am. Chem. Soc. 2008, 130, 16852–16853. [Google Scholar] [CrossRef]
- Frölich, A.; Gabel, F.; Jasnin, M.; Lehnert, U.; Oesterhelt, D.; Stadler, A.M.; Tehei, M.; Weik, M.; Wood, K.; Zaccai, G. From shell to cell: Neutron scattering studies of biological water dynamics and coupling to activity. Faraday Discuss. 2008, 141, 117–130. [Google Scholar] [CrossRef]
- Jasnin, M.; Moulin, M.; Haertlein, M.; Zaccai, G.; Tehei, M. Down to atomic-scale intracellular water dynamics. EMBO J. 2008, 9, 543–547. [Google Scholar] [CrossRef] [PubMed]
- Jasnin, M.; Stadler, A.; Teheiw Cd, M.; Zaccaiw, G. Specific cellular water dynamics observed in vivo by neutron scattering and NMR. Phys. Chem. Chem. Phys. 2010, 12, 10154–10160. [Google Scholar] [CrossRef] [PubMed]
- Natali, F.; Dolce, C.; Peters, J.; Gerelli, Y.; Stelletta, C.; Leduc, G. Water Dynamics in Neural Tissue. J. Phys. Soc. JPN 2012, 82, 17. [Google Scholar] [CrossRef][Green Version]
- Natali, F.; Gerelli, Y.; Stelletta, C.; Peters, J. Anomalous proton dynamics of water molecules in neural tissue as seen by quasi-elastic neutron scattering. Impact on medical imaging techniques. AIP Conf. Proc. 2013, 1518, 551–557. [Google Scholar]
- Bordallo, H.N.; Zakharov, B.A.; Boldyreva, E.V.; Johnson, M.R.; Koza, M.M.; Seydel, T.; Fischer, J. Application of Incoherent Inelastic Neutron Scattering in Pharmaceutical Analysis: Relaxation Dynamics in Phenacetin. Mol. Pharm. 2012, 9, 2434–2441. [Google Scholar] [CrossRef]
- Martins, M.L.; Eckert, J.; Jacobsen, H.; dos Santos, É.C.; Ignazzi, R.; de Araujo, D.R.; Bellissent-Funel, M.C.; Natali, F.; Koza, M.M.; Matic, A.; et al. Probing the dynamics of complexed local anesthetics via neutron scattering spectroscopy and DFT calculations. Int. J. Pharm. 2017, 524, 397–406. [Google Scholar] [CrossRef]
- Martins, M.L.; Ignazzi, R.; Jacobsen, H.; de Araujo, D.R.; Yokaichiya, F.; Saeki, M.J.; de Paula, E.; Bordallo, H.N. Encapsulation effects on the structure-dynamics on drug carriers revealed by neutron scattering. Neutron News 2014, 25, 16–19. [Google Scholar] [CrossRef]
- Martins, M.L.; Ignazzi, R.; Eckert, J.; Watts, B.; Kaneno, R.; Zambuzzi, W.F.; Daemen, L.; Saeki, M.J.; Bordallo, H.N. Restricted mobility of specific functional groups reduces anti-cancer drug activity in healthy cells. Sci. Rep. 2016, 6, 22478. [Google Scholar] [CrossRef]
- Martins, M.L.; Orecchini, A.; Aguilera, L.; Eckert, J.; Embs, J.; Matic, A.; Saeki, M.J.; Bordallo, H.N. Encapsulation of paclitaxel into a bio-nanocomposite. A study combining inelastic neutron scattering to thermal analysis and infrared spectroscopy. EPJ Web Conf. 2015, 83, 02011. [Google Scholar] [CrossRef]
- Zaccai, G. Molecular dynamics in cells: A neutron view. Biochim. Biophys. Acta-Gen. Subj. 2020, 1864, 129475. [Google Scholar] [CrossRef]
- Martins, M.L.; Sacci, R.L.; Sanders, N.C.; Tyler, J.L.; Matsumoto, R.; Popov, I.; Guo, W.; Dai, S.; Cummings, P.T.; Sokolov, A.P.; et al. Addition of Chloroform in a Solvent-in-Salt Electrolyte: Outcomes in the Microscopic Dynamics in Bulk and Confinement. J. Phys. Chem. C 2020, 124, 22366–22375. [Google Scholar] [CrossRef]
- Martins, M.L.; Sacci, R.L.; Lin, X.; Matsumoto, R.; Popov, I.; Cui, J.; Kobayashi, T.; Tyagi, M.; Guo, W.; Dai, S.; et al. Beyond Simple Dilution: Superior Conductivities from Cosolvation of Acetonitrile/LiTFSI Concentrated Solution with Acetone. J. Phys. Chem. C 2022, 126, 2788–2796. [Google Scholar] [CrossRef]
- Farmer, T.O.; Markvardsen, A.J.; Rod, T.H.; Bordallo, H.N.; Swenson, J. Dynamical Accuracy of Water Models on Supercooling. J. Phys. Chem. Lett. 2020, 11, 7469–7475. [Google Scholar] [CrossRef] [PubMed]
- Osti, N.C.; Van Aken, K.L.; Thompson, M.W.; Tiet, F.; Jiang, D.; Cummings, P.T.; Gogotsi, Y.; Mamontov, E. Solvent Polarity Governs Ion Interactions and Transport in a Solvated Room-Temperature Ionic Liquid. J. Phys. Chem. Lett. 2017, 8, 167–171. [Google Scholar] [CrossRef]
- Bridges, C.A.; Martins, M.L.; Jafta, C.J.; Sun, X.G.; Paranthaman, M.P.; Liu, J.; Dai, S.; Mamontov, E. Dynamics of Emim+ in [Emim][TFSI]/LiTFSI Solutions as Bulk and under Confinement in a Quasi-liquid Solid Electrolyte. J. Phys. Chem. B 2021, 125, 5443–5450. [Google Scholar] [CrossRef]
- Mamontov, E.; Smith, R.W.; Billings, J.J.; Ramirez-Cuesta, A.J. Simple analytical model for fitting QENS data from liquids. Phys. B Condens. Matter 2019, 566, 50–54. [Google Scholar] [CrossRef]
- Teixeira, J.; Bellissent-Funel, M.-C. Dynamics of water studied by neutron scattering. J. Phys. Condens. Matter 1990, 2, SA105–SA108. [Google Scholar] [CrossRef]
- Mamontov, E.; Luo, H.; Dai, S. Proton Dynamics in N,N,N′,N′-Tetramethylguanidinium Bis(perfluoroethylsulfonyl)imide Protic Ionic Liquid Probed by Quasielastic Neutron Scattering. J. Phys. Chem. B 2009, 113, 159–169. [Google Scholar] [CrossRef]
- Petersen, M.H.; Vernet, N.; Gates, W.P.; Villacorta, F.J.; Ohira-Kawamura, S.; Kawakita, Y.; Arai, M.; Kneller, G.; Bordallo, H.N. Assessing Diffusion Relaxation of Interlayer Water in Clay Minerals Using a Minimalist Three-Parameter Model. J. Phys. Chem. C 2021, 125, 15085–15093. [Google Scholar] [CrossRef]
- Jasnin, M.; Moulin, M.; Haertlein, M.; Zaccai, G.; Tehei, M. In vivo measurement of internal and global macromolecular motions in Escherichia coli. Biophys. J. 2008, 95, 857–864. [Google Scholar] [CrossRef][Green Version]
- Liberton, M.; Page, L.E.; O’Dell, W.B.; O’Neill, H.; Mamontov, E.; Urban, V.S.; Pakrasi, H.B. Organization and flexibility of cyanobacterial thylakoid membranes examined by neutron scattering. J. Biol. Chem. 2013, 288, 3632–3640. [Google Scholar] [CrossRef] [PubMed]
- Colas de la Noue, A.; Natali, F.; Fekraoui, F.; Gervais, P.; Martinez, N.; Perrier-Cornet, J.-M.; Peters, J. The molecular dynamics of bacterial spore and the role of calcium dipicolinate in core properties at the sub-nanosecond time-scale. Sci. Rep. 2020, 10, 8265. [Google Scholar] [CrossRef] [PubMed]
- Zeller, D.; Tan, P.; Hong, L.; Bari, D.D.; Sakai, V.G.; Peters, J. Differences between calcium rich and depleted alpha-lactalbumin investigated by molecular dynamics simulations and incoherent neutron scattering. Phys. Rev. E 2020, 101, 32415. [Google Scholar] [CrossRef] [PubMed]
- Natali, F.; Dolce, C.; Peters, J.; Stelletta, C.; Demé, B.; Ollivier, J.; Boehm, M.; Leduc, G.; Piazza, I.; Cupane, A.; et al. Anomalous water dynamics in brain: A combined diffusion magnetic resonance imaging and neutron scattering investigation. J. R. Soc. Interface 2019, 16, 20190186. [Google Scholar] [CrossRef]
- Natali, F.; Dolce, C.; Peters, J.; Stelletta, C.; Demé, B.; Ollivier, J.; Leduc, G.; Cupane, A.; Barbier, E.L. Brain lateralization probed by water diffusion at the atomic to micrometric scale. Sci. Rep. 2019, 9, 14694. [Google Scholar] [CrossRef]
- Mamontov, E. Microscopic diffusion processes measured in living planarians. Sci. Rep. 2018, 8, 4–11. [Google Scholar] [CrossRef]
- Mamontov, E.; Osti, N.C.; Tyagi, M. Temperature dependence of nanoscale dynamic processes measured in living millipedes by high resolution inelastic and elastic neutron scattering. Sci. Rep. 2019, 9, 11646. [Google Scholar] [CrossRef]
- Mamontov, E. Non-monotonic temperature dependence of nanoscopic dynamics measured in living housefly larvae. Phys. B Condens. Matter 2019, 566, 23–29. [Google Scholar] [CrossRef]
- Merivaara, A.; Zini, J.; Koivunotko, E.; Valkonen, S.; Korhonen, O.; Fernandes, F.M.; Yliperttula, M. Preservation of biomaterials and cells by freeze-drying: Change of paradigm. J. Control. Release 2021, 336, 480–498. [Google Scholar] [CrossRef]
- Zhang, M.; Oldenhof, H.; Sydykov, B.; Bigalk, J.; Sieme, H.; Wolkers, W.F. Freeze-drying of mammalian cells using trehalose: Preservation of DNA integrity. Sci. Rep. 2017, 7, 6198. [Google Scholar] [CrossRef]
- Kampmeyer, C.; Johansen, J.V.; Holmberg, C.; Karlson, M.; Gersing, S.K.; Bordallo, H.N.; Kragelund, B.B.; Lerche, M.H.; Jourdain, I.; Winther, J.R.; et al. Mutations in a Single Signaling Pathway Allow Cell Growth in Heavy Water. ACS Synth. Biol. 2020, 9, 733–748. [Google Scholar] [CrossRef] [PubMed]
- Marques, M.P.M.; Batista de Carvalho, A.L.M.; Mamede, A.P.; Rudić, S.; Dopplapudi, A.; García Sakai, V.; Batista de Carvalho, L.A.E. Intracellular water as a mediator of anticancer drug action. Int. Rev. Phys. Chem. 2020, 39, 67–81. [Google Scholar] [CrossRef]
- Marques, M.P.M.; Batista de Carvalho, A.L.M.; Sakai, V.G.; Hatter, L.; Batista de Carvalho, L.A.E. Intracellular water—An overlooked drug target? Cisplatin impact in cancer cells probed by neutrons. Phys. Chem. Chem. Phys. 2017, 19, 2702–2713. [Google Scholar] [CrossRef] [PubMed]
- Marques, M.P.M.; Batista de Carvalho, A.L.M.; Mamede, A.P.; Dopplapudi, A.; García Sakai, V.; Batista de Carvalho, L.A.E. Role of intracellular water in the normal-to-cancer transition in human cells—Insights from quasi-elastic neutron scattering. Struct. Dyn. 2020, 7, 054701. [Google Scholar] [CrossRef] [PubMed]
- Marques, M.P.M.; Batista de Carvalho, A.L.M.; Mamede, A.P.; Santos, I.P.; García Sakai, V.; Dopplapudi, A.; Cinque, G.; Wolna, M.; Gardner, P.; Batista de Carvalho, L.A.E. Chemotherapeutic Targets in Osteosarcoma: Insights from Synchrotron-MicroFTIR and Quasi-Elastic Neutron Scattering. J. Phys. Chem. B 2019, 123, 6968–6979. [Google Scholar] [CrossRef] [PubMed]
- Mamontov, E.; Herwig, K.W. A time-of-flight backscattering spectrometer at the Spallation Neutron Source, BASIS. Rev. Sci. Instrum. 2011, 82, 085109. [Google Scholar] [CrossRef]
- Shibata, K.; Takahashi, N.; Kawakita, Y.; Matsuura, M.; Yamada, T.; Tominaga, T.; Kambara, W.; Kobayashi, M.; Inamura, Y.; Nakatani, T.; et al. The Performance of TOF near Backscattering Spectrometer DNA in MLF, J-PARC. In Proceedings of the 2nd International Symposium on Science at J-PARC—Unlocking the Mysteries of Life, Matter and the Universe—Journal of the Physical Society of Japan, Tsukuba, Japan, 12–15 July 2014. [Google Scholar]
- Frick, B.; Mamontov, E.; Eijck, L.; van Seydel, T. Recent Backscattering Instrument Developments at the ILL and SNS. Zeitschrift für Phys. Chem. 2010, 224, 33–60. [Google Scholar] [CrossRef]
- Appel, M.; Frick, B.; Magerl, A. First results with the neutron backscattering and TOF spectrometer option BATS on IN16B. Phys. B Condens. Matter 2019, 562, 6–8. [Google Scholar] [CrossRef]
- Tsapatsaris, N.; Willendrup, P.K.; Lechner, R.E.; Bordallo, H.N. From BASIS to MIRACLES: Benchmarking and perspectives for high-resolution neutron spectroscopy at the ESS. EPJ Web Conf. 2015, 83, 03015. [Google Scholar] [CrossRef]
- Tsapatsaris, N.; Lechner, R.E.; Markó, M.; Bordallo, H.N. Conceptual design of the time-of-flight backscattering spectrometer, MIRACLES, at the European Spallation Source. Rev. Sci. Instrum. 2016, 87, 085118. [Google Scholar] [CrossRef]
- Villacorta, F.J.; Rodríguez, D.M.; Bertelsen, M.; Bordallo, H.N. Optimization of the Guide Design of MIRACLES, the Neutron Time-of-Flight Backscattering Spectrometer at the European Spallation Source. Quantum Beam Sci. 2021, 6, 3. [Google Scholar] [CrossRef]
- Mamontov, E.; Boone, C.; Frost, M.J.; Herwig, K.W.; Huegle, T.; Lin, J.Y.Y.; McCormick, B.; McHargue, W.; Stoica, A.D.; Torres, P.; et al. A concept of a broadband inverted geometry spectrometer for the Second Target Station at the Spallation Neutron Source. Rev. Sci. Instrum. 2022, 93, 045101. [Google Scholar] [CrossRef] [PubMed]
- Berg, M.C.; Benetti, A.R.; Telling, M.T.F.; Seydel, T.; Yu, D.; Daemen, L.L.; Bordallo, H.N. Nanoscale Mobility of Aqueous Polyacrylic Acid in Dental Restorative Cements. ACS Appl. Mater. Interfaces 2018, 10, 9904–9915. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, M.L.; Bordallo, H.N.; Mamontov, E. Water Dynamics in Cancer Cells: Lessons from Quasielastic Neutron Scattering. Medicina 2022, 58, 654. https://doi.org/10.3390/medicina58050654
Martins ML, Bordallo HN, Mamontov E. Water Dynamics in Cancer Cells: Lessons from Quasielastic Neutron Scattering. Medicina. 2022; 58(5):654. https://doi.org/10.3390/medicina58050654
Chicago/Turabian StyleMartins, Murillo L., Heloisa N. Bordallo, and Eugene Mamontov. 2022. "Water Dynamics in Cancer Cells: Lessons from Quasielastic Neutron Scattering" Medicina 58, no. 5: 654. https://doi.org/10.3390/medicina58050654
APA StyleMartins, M. L., Bordallo, H. N., & Mamontov, E. (2022). Water Dynamics in Cancer Cells: Lessons from Quasielastic Neutron Scattering. Medicina, 58(5), 654. https://doi.org/10.3390/medicina58050654






