Development of a Knee Joint CT-FEM Model in Load Response of the Stance Phase During Walking Using Muscle Exertion, Motion Analysis, and Ground Reaction Force Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participant
2.2. Gait Analysis
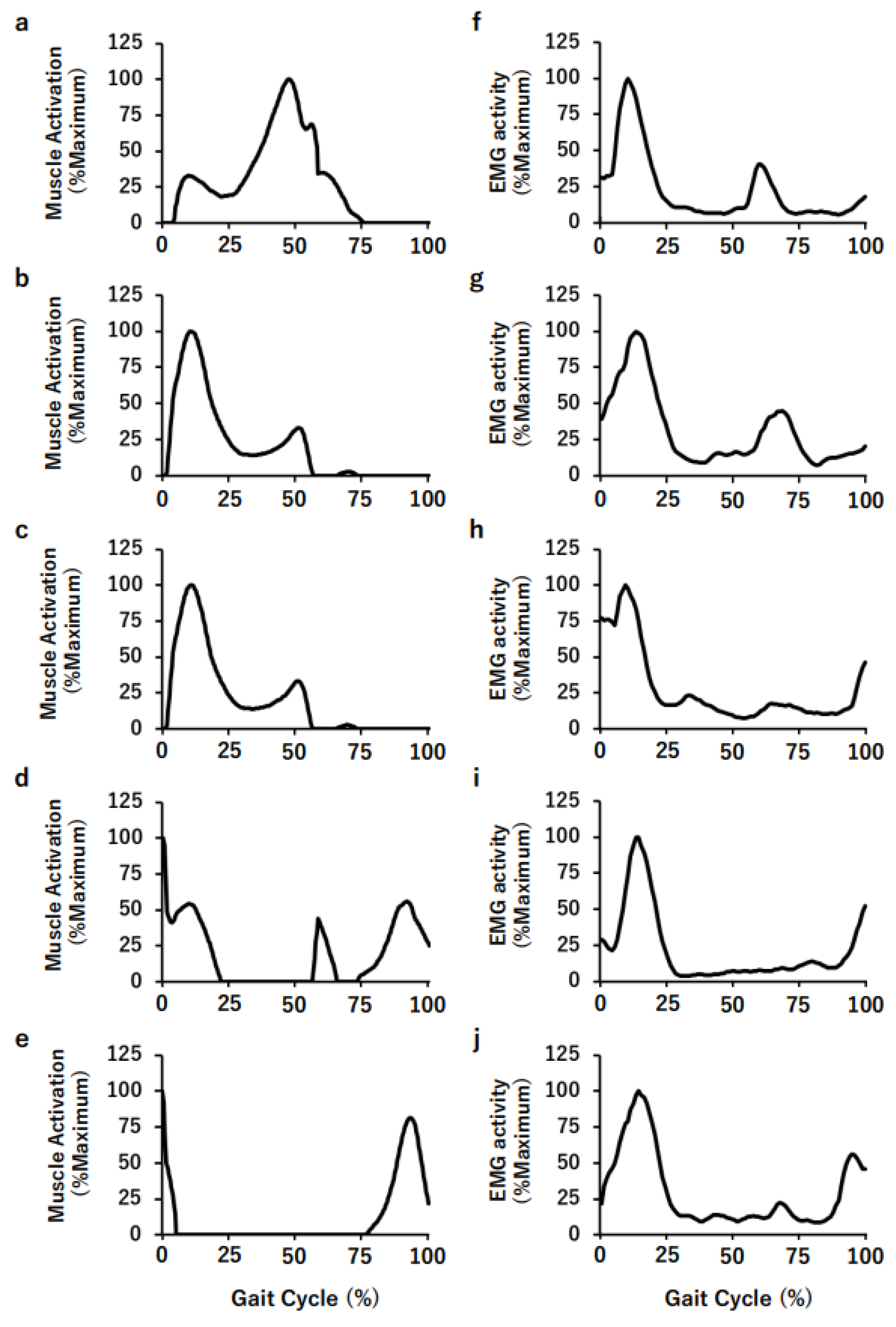
2.2.1. Motion Analysis
2.2.2. Electromyography (EMG)
2.3. Outline of the Model and Calculation Method
2.3.1. CT Value (HU: Hounsfield Unit) Density Conversion Formula
2.3.2. Young’s Modulus
2.3.3. Young’s Modulus Conversion Formula
2.3.4. Poisson’s Ratio
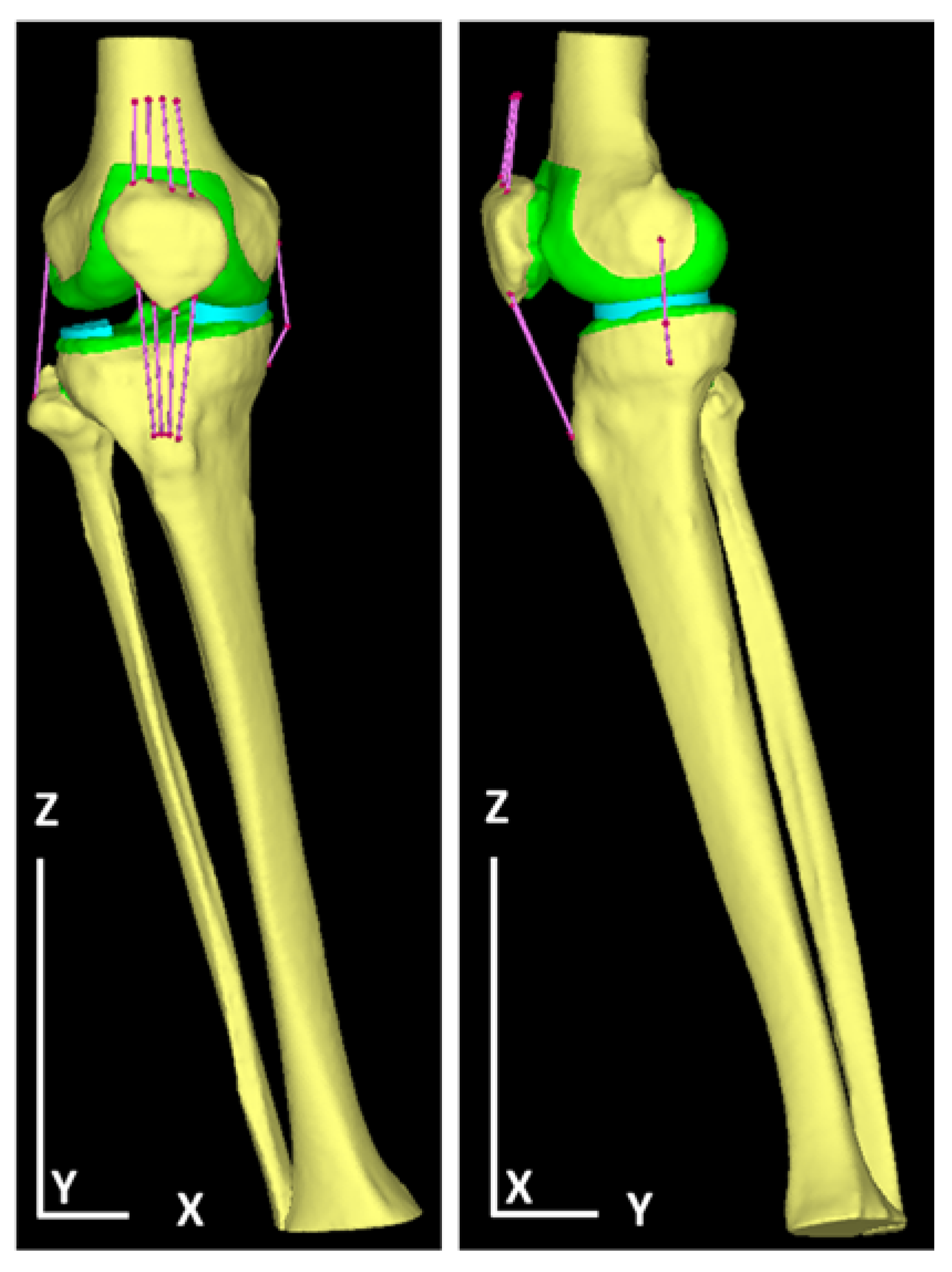
2.4. Modeling Construction and Procedure
2.4.1. Determination of Material Properties
2.4.2. Determination of Walking Posture
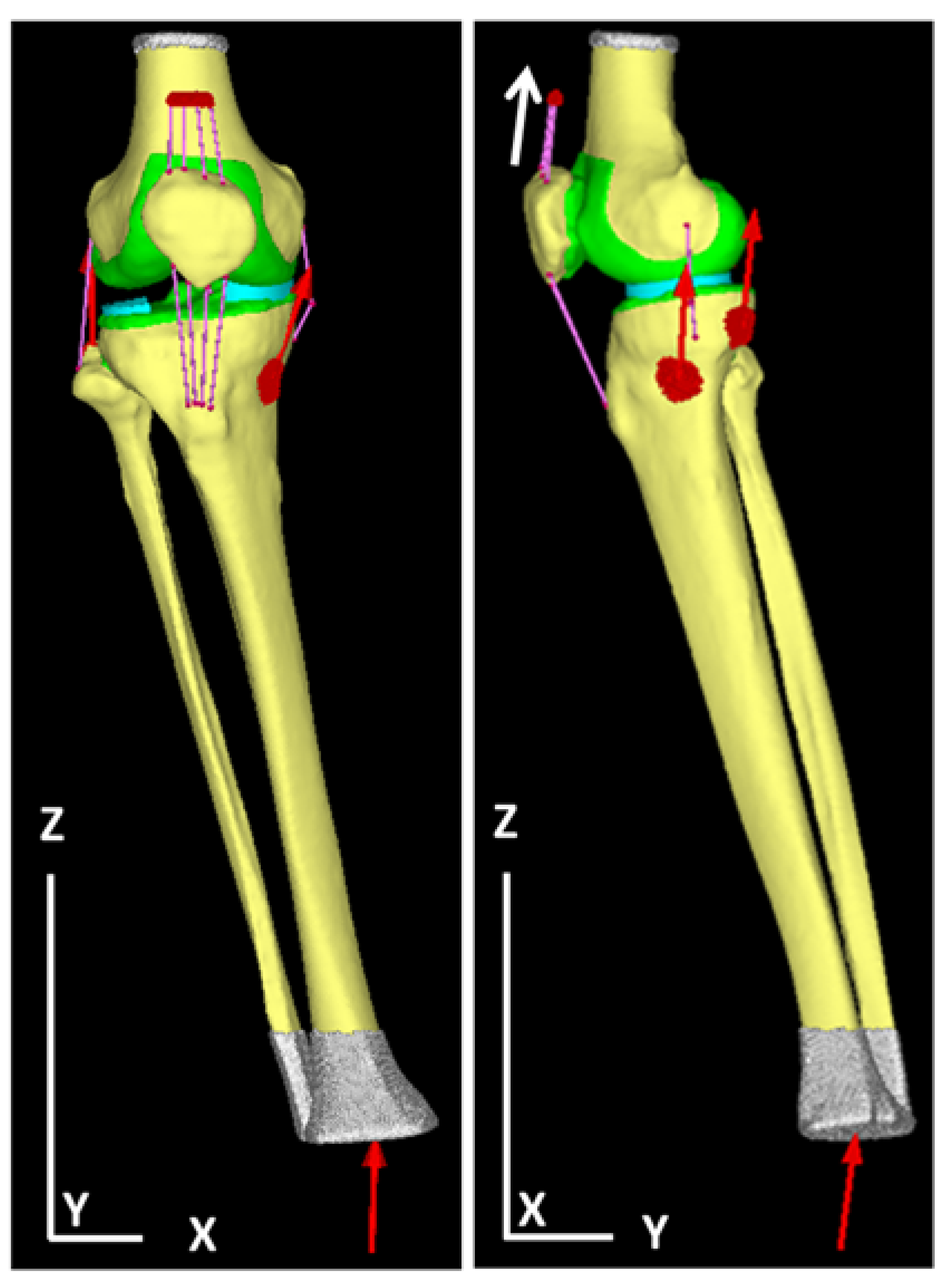
2.4.3. Determination of Load and Restraint Conditions
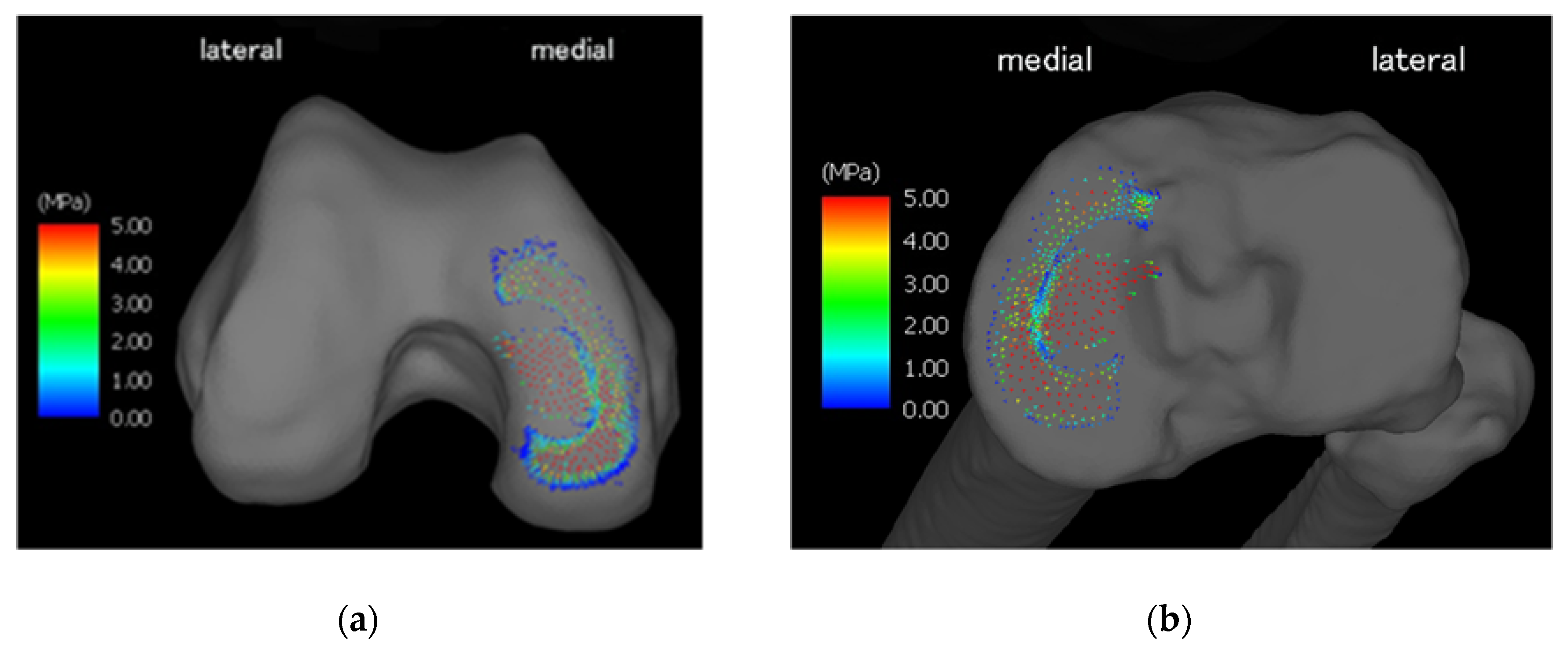
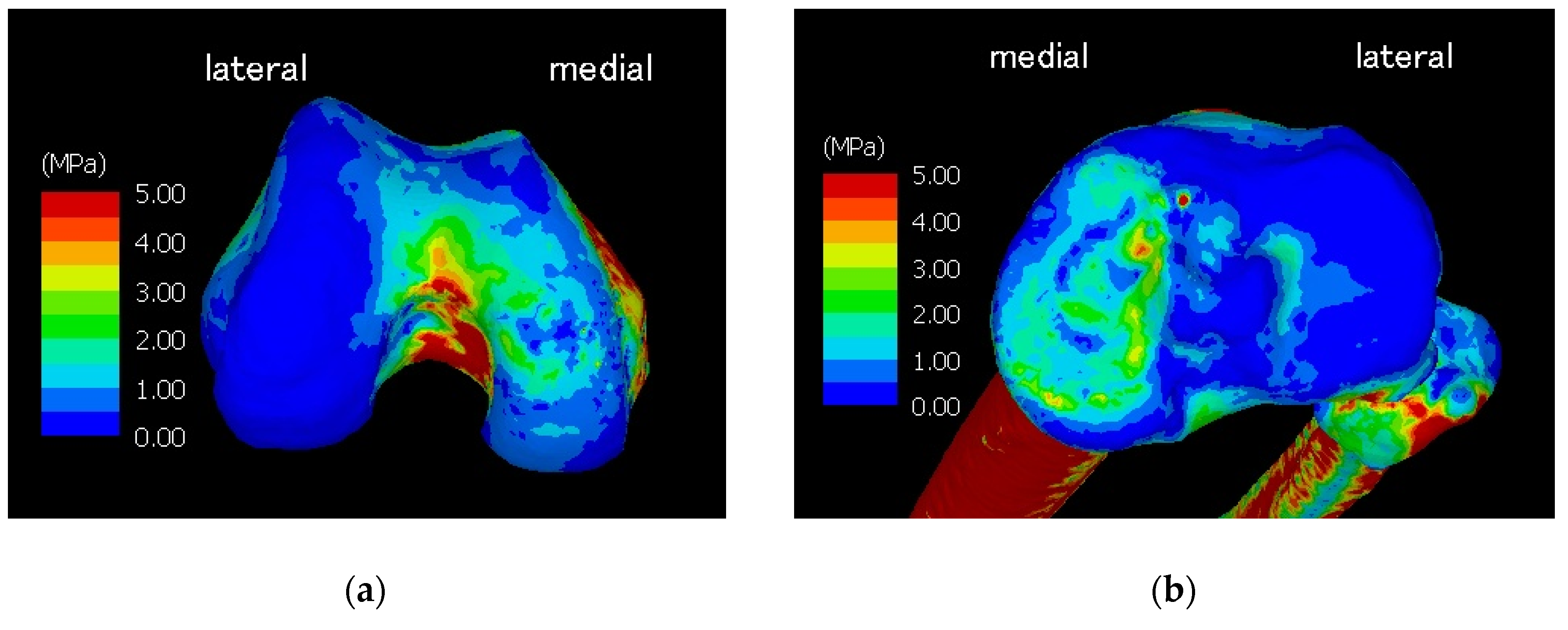
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ackroyd, R.T. Finite Element Methods for Particle Transport; Research Studies Press: Taunton, Somerset, UK, 1997; pp. 8–12. [Google Scholar]
- Jiang, B. The Least-Squares Finite Element Method; Springer: New York, NY, USA, 1998; pp. 3–10. [Google Scholar]
- Bessho, M.; Ohnishi, I.; Matsumoto, T.; Ohashi, S.; Matsuyama, J.; Tobita, K.; Kaneko, M.; Nakamura, K. Prediction of proximal femur strength using a CT-based nonlinear finite element method: Differences in predicted fracture load and site with changing load and boundary conditions. Bone 2009, 45, 226–231. [Google Scholar] [CrossRef] [PubMed]
- Brune, A.; Stiesch, M.; Eisenburger, M.; Greuling, A. The effect of different occlusal contact situations on peri-implant bone stress—A contact finite element analysis of indirect axial loading. Mater. Sci. Eng. C Mater. Biol. Appl. 2019, 99, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Hingsammer, L.; Pommer, B.; Hunger, S.; Stehrer, R.; Watzek, G.; Insua, A. Influence of implant length and associated parameters upon biomechanical forces in finite element analyses: A systematic review. Implant Dent. 2019, 28, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Zysset, P.K.; Dall’ara, E.; Varga, P.; Pahr, D.H. Finite element analysis for prediction of bone strength. Bonekey Rep. 2013, 2, 386. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wanq, Z. Intervertebral disc biomechanical analysis using the finite element modeling based on medical images. Comput. Med. Imaging Graph. 2006, 30, 363–370. [Google Scholar] [CrossRef]
- Erdem, I.; Truumees, E.; van der Meulen, M.C. Simulation of the behaviour of the L1 vertebra for different material properties and loading conditions. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 736–746. [Google Scholar] [CrossRef]
- Halonen, K.S.; Mononen, M.E.; Jurvelin, J.S.; Töyräs, J.; Klodowski, A.; Kulmala, J.P.; Korhonen, R.K. Importance of patella, quadriceps forces, and depthwise cartilage structure on knee joint motion and cartilage response during gait. J. Biomech. Eng. 2016, 138, 071002. [Google Scholar] [CrossRef]
- Miura, M.; Nakamura, J.; Matsuura, Y.; Wako, Y.; Suzuki, T.; Hagiwara, S.; Orita, S.; Inage, K.; Kawarai, Y.; Sugano, M.; et al. Prediction of fracture load and stiffness of the proximal femur by CT-based specimen specific finite element analysis: Cadaveric validation study. BMC Musculoskelet. Disord. 2017, 18, 536. [Google Scholar] [CrossRef]
- Allaire, B.T.; Lu, D.; Johannesdottir, F.; Kopperdahl, D.; Keaveny, T.M.; Jarraya, M.; Guermazi, A.; Bredella, M.A.; Samelson, E.J.; Kiel, D.P.; et al. Prediction of incident vertebral fracture using CT-based finite element analysis. Osteoporos. Int. 2019, 30, 323–331. [Google Scholar] [CrossRef]
- Kawabata, Y.; Matsuo, K.; Nezu, Y.; Kamiishi, T.; Inaba, Y.; Saito, T. The risk assessment of pathological fracture in the proximal femur using a CT-based finite element method. J. Orthop. Sci. 2017, 22, 931–937. [Google Scholar] [CrossRef]
- Henak, C.R.; Ellis, B.J.; Harris, M.D.; Anderson, A.E.; Peters, C.L.; Weiss, J.A. Role of the acetabular labrum in load support across the hip joint. J. Biomech. 2011, 44, 2201–2206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuchs, S.; Kullmer, G.; Richard, H.A. Designing the construction of an FE model exemplified by the knee joint. Biomed. Tech. 1997, 42, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Chantarapanich, N.; Nanakorn, P.; Chernchujit, B.; Sitthiseripratip, K. A finite element study of stress distributions in normal and osteoarthritic knee joints. J. Med. Assoc. Thail. 2009, 92, 97–103. [Google Scholar]
- Bae, J.Y.; Park, K.S.; Seon, J.K.; Kwak, D.S.; Jeon, L.; Song, E.K. Biomechanical analysis of the effects of medial meniscectomy on degenerative osteoarthritis. Med. Biol. Eng. Comput. 2012, 50, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Jeon, I.; Bae, J.Y.; Park, J.H.; Yoon, T.R.; Todo, M.; Mawatari, M.; Hotokebuchi, T. The biomechanical effect of the collar of a femoral stem on total hip arthroplasty. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 103–112. [Google Scholar] [CrossRef]
- Osano, K.; Nagamine, R.; Todo, M.; Kawasaki, M. The effect of malrotation of tibial component of total knee arthroplasty on tibial insert during high flexion using a finite element analysis. Sci. World J. 2014, 2014, 695028. [Google Scholar] [CrossRef]
- Anuar, M.A.; Todo, M.; Nagamine, R.; Hirokawa, S. Dynamic finite element analysis of mobile bearing type knee prosthesis under deep flexional motion. Sci. World J. 2014, 2014, 586921. [Google Scholar]
- Marouane, H.; Shirazi-Adl, A.; Hashemi, J. Quantification of the role of tibial posterior slope in knee joint mechanics and ACL force in simulated gait. J. Biomech. 2015, 48, 1899–1905. [Google Scholar] [CrossRef]
- Bendjaballah, M.Z.; Shirazi-Adl, A.; Zukor, D.J. Biomechanics of the human knee joint in compression: Reconstruction, mesh generation and finite element analysis. Knee 1995, 2, 69–79. [Google Scholar] [CrossRef]
- Shirazi, R.; Shirazi-Adl, A.; Hurtig, M. Role of cartilage collagen fibrils networks in knee joint biomechanics under compression. J. Biomech. 2008, 41, 3340–3348. [Google Scholar] [CrossRef]
- Adouni, M.; Shirazi-Adl, A. Consideration of equilibrium equations at the hip joint alongside those at the knee and ankle joints has mixed effects on knee joint response during gait. J. Biomech. 2003, 46, 619–624. [Google Scholar] [CrossRef] [PubMed]
- Tammy, L.; Donahue, H.; Hull, M.L.; Rashid, M.M.; Jacobs, C.R. A Finite Element Model of the Human Knee Joint for the Study of Tibio-Femoral Contact. J. Biomech. Eng. 2002, 124, 273–280. [Google Scholar]
- Ferrari, A.; Benedetti, M.G.; Pavan, E.; Frigo, C.; Bettinelli, D.; Rabuffetti, M.; Crenna, P.; Leardini, A. Quantitative comparison of five current protocols in gait analysis. Gait Posture 2008, 28, 207–216. [Google Scholar] [CrossRef]
- Grood, E.S.; Suntay, W.J. A joint coordinate system for the clinical description of three-dimensional motions: Application to the knee. J. Biomech. Eng. 1983, 105, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Perry, J.; Burnfield, J. Gait Analysis: Normal and Pathological Function; SLACK Incorporated: Thorofare, NJ, USA, 1992; pp. 89–108. [Google Scholar]
- Research Center of Computational Mechanics. Research Center of Computation Mechanics: User’s Manual for Mechanical Finder Ver.10.0; RCCM: Tokyo, Japan, 2018; pp. 170–174. [Google Scholar]
- Keyak, J.H.; Rossi, S.A.; Jones, K.A.; Skinner, H.B. Prediction of femoral fracture load using automated finite element modelling. J. Biomech. 1998, 31, 125–133. [Google Scholar] [CrossRef]
- Keyak, J.H.; Sigurdsson, S.; Karlsdottir, G.; Oskaradottir, D.; Siqmarsdottir, A.; Zhao, S.; Kornak, J.; Harris, T.B.; Siqurdsson, G.; Jonsson, B.Y.; et al. Male-female differences in the association between incident hip fracture and proximal femoral strength: A finite element analysis study. Bone 2011, 48, 1239–1245. [Google Scholar] [CrossRef] [Green Version]
- Imai, K.; Ohnishi, I.; Yamamoto, S.; Nakamura, K. In vivo assessment of lumbar vertebral strength in elderly women using computed tomography-based nonlinear finite element model. Spine 2008, 33, 27–32. [Google Scholar] [CrossRef]
- Tawara, D.; Sakamoto, J.; Oda, J. Finite Element Analysis Considering Material Inhomogeneousness of Bone Using “ADVENTURE System”. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2005, 48, 292–298. [Google Scholar] [CrossRef] [Green Version]
- Silva, M.J.; Keaveny, T.M.; Hayes, W.C. Load sharing between the shell and centrum in the lumbar vertebral body. Spine 1997, 22, 140–150. [Google Scholar] [CrossRef]
- Takano, H.; Yonezawa, I.; Todo, M. Biomechanical study of vertebral compression fracture using finite element analysis. J. Appl. Math. Phys. 2017, 5, 953–965. [Google Scholar] [CrossRef] [Green Version]
- Matsuura, Y.; Giambini, H.; Ogawa, Y.; Fanq, Z.; Thoreson, A.R.; Yaszemski, M.J.; Lu, L.; An, K.N. Specimen-specific nonlinear finite element modeling to predict vertebrae fracture loads after vertebroplasty. Spine (Phila Pa 1976) 2014, 39, E1291–E1296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hayashi, S. Quantitative analysis of lateral force of floor reactions in normal and above-knee prosthetic gait. Nihon Seikeigeka Gakkai Zasshi 1983, 57, 1911–1921. [Google Scholar] [PubMed]
- Maly, M.R.; Acker, S.M.; Totterman, S.; Tamez-Pena, J.; Stratford, P.W.; Callaqhan, J.P.; Adachi, J.D.; Beattie, K.A. Knee adduction moment relates to medial femoral and tibial cartilage morphology in clinical knee osteoarthritis. J. Biomech. 2015, 48, 3495–3501. [Google Scholar] [CrossRef] [PubMed]
- Zevenbergen, L.; Smith, C.R.; Van Rossom, S.; Thelen, D.G.; Famaey, N.; Vander Sloten, J.; Jonkers, I. Cartilage defect location and stiffness predispose the tibiofemoral joint to aberrant loading conditions during stance phase of gait. PLoS ONE 2018, 13, e0205842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenhart, R.L.; Kaiser, J.; Smith, C.R.; Thelen, D.G. Prediction and validation of load-dependent behavior of the tibiofemoral and patellofemoral joints during movement. Ann. Biomed. Eng. 2015, 43, 2675–2685. [Google Scholar] [CrossRef] [Green Version]
- Halonen, K.S.; Mononen, M.E.; Jurvelin, J.S.; Töyräs, J.; Salo, J.; Korhonen, R.K. Deformation of articular cartilage during static loading of a knee joint--experimental and finite element analysis. J. Biomech. 2014, 47, 2467–2474. [Google Scholar] [CrossRef]
- Oatis, C.A. Kinesiology: The Mechanics & Pathomechanics of Human Movement; LWW: Philadelphia, PA, USA, 2004; pp. 861–863. [Google Scholar]
- Levangie, P.K.; Norkin, C.C. Joint Structure and Function: A Comprehensive Analysis, 4th ed.; F.A. Davis: Philadelphia, PA, USA, 2005; pp. 395–397. [Google Scholar]
- Derrick, T.R.; Edwards, W.B.; Fellin, R.E.; Seay, J.F. An integrative modeling approach for the efficient estimation of cross sectional tibial stresses during locomotion. J. Biomech. 2016, 49, 429–435. [Google Scholar] [CrossRef]
| Anatomy Element | Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| Femur, tibia, fibula, patella | Keyak’s conversion formula | 0.4 |
| Cartilage | 20 (100 only on the fibula) | 0.4 |
| Meniscal | 20 | 0.4 |
| Ligament | 0.1 | 0.4 |
| The angle between the leg bone and the floor (deg.) | ||
| Inversion direction 11.5 | Bending direction 13.3 | Inward direction 7.7 |
| The angle between the femur and tibia (deg.) | ||
| Inversion direction 12.21 | Bending direction 14.62 | Inward direction −3.28 |
| Anatomical Element | Strain Range | Tension (N) |
|---|---|---|
| Cruciate ligament, collateral ligament | ε < 0.0 0.0 < ε | 0.0 1000ε |
| Patellar ligament, quadriceps tendon | ε < 0.0 0.0 < ε < 0.005 0.005 < ε | 0.0 172754ε 863.77 |
| Floor reaction force (N) | |
| Inward direction | 26.08 |
| Forward direction | −112.00 |
| Upward direction | 808.95 |
| Muscle traction (N) | |
| Quadriceps | 863.77 |
| Biceps femoris | 266.26 |
| Semimembranosus | 99.99 |
| Semitendinosus + gracilis | 61.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, K.; Mutsuzaki, H.; Fukaya, T.; Aoyama, T.; Nakajima, S.; Sekine, N.; Mori, K. Development of a Knee Joint CT-FEM Model in Load Response of the Stance Phase During Walking Using Muscle Exertion, Motion Analysis, and Ground Reaction Force Data. Medicina 2020, 56, 56. https://doi.org/10.3390/medicina56020056
Watanabe K, Mutsuzaki H, Fukaya T, Aoyama T, Nakajima S, Sekine N, Mori K. Development of a Knee Joint CT-FEM Model in Load Response of the Stance Phase During Walking Using Muscle Exertion, Motion Analysis, and Ground Reaction Force Data. Medicina. 2020; 56(2):56. https://doi.org/10.3390/medicina56020056
Chicago/Turabian StyleWatanabe, Kunihiro, Hirotaka Mutsuzaki, Takashi Fukaya, Toshiyuki Aoyama, Syuichi Nakajima, Norio Sekine, and Koichi Mori. 2020. "Development of a Knee Joint CT-FEM Model in Load Response of the Stance Phase During Walking Using Muscle Exertion, Motion Analysis, and Ground Reaction Force Data" Medicina 56, no. 2: 56. https://doi.org/10.3390/medicina56020056




