Efficient Approaches for Solving Systems of Nonlinear Time-Fractional Partial Differential Equations

Abstract

In this work, we present a modified generalized Mittag–Leffler function method (MGMLFM) and Laplace Adomian decomposition method (LADM) to get an analytic-approximate solution for nonlinear systems of partial differential equations (PDEs) of fractional-order in the Caputo derivative. We apply the MGMLFM and LADM on systems of nonlinear time-fractional PDEs. Precisely, we consider some important fractional-order nonlinear systems, namely Broer–Kaup (BK) and Burgers, which have found major significance because they arise in many physical applications such as shock wave, wave processes, vorticity transport, dispersal in porous media, and hydrodynamic turbulence. The analysis of these methods is implemented on the BK, Burgers systems and solutions have been offered in a simple formula. We show our results in figures and tables to demonstrate the efficiency and reliability of the used methods. Furthermore, our outcome converges rapidly to the given exact solutions.

1. Introduction

Mathematical models within fractional calculus (FC) have been widely used in various fields of natural science and engineering. In the last few decades, throughout much of the literature, we can find the concept of “memory” as the main advantage to process a system of fractional differential equations. This property has a significant impact on the behavior of the solutions for the considered models (see, e.g., [1,2]). The non-locality property of the fractional derivatives [3,4] that gives preference to utilizing FC, means calculating a time-fractional derivative of a function $f\left(t\right)$ at some time $t=t_1$ and requires all the previous history. This effect justifies the use of FC to better explain real-life models. In general, these models actually made more progress than those without the memory concept [5,6,7]. Recently, some authors have added a significant amount of research in the area of FC and its applications in various branches of engineering and natural science, such as electrodynamics [8], nano-technology [9], finance [10], mathematical biology [11,12], and control theory [13,14].

There are numerous phenomena in physics, biology, chemistry, engineering, finance, and other applied sciences that are represented by differential equations. In recent years, there have been a special interest in fractional partial differential equations (FPDEs), especially nonlinear ones, because of their influence in many applied sciences, such as diffusion of biological populations, fluid flow, electromagnetic waves, control theory of dynamical systems, and so on (see, e.g., [15,16,17,18,19] and the references therein). The majority of scientific problems in physics, engineering, and biological systems are nonlinear and their exact solutions are not easy to find. For example, physical problems are mostly modeled using higher nonlinear FPDEs. In fact, it is challenging to find the exact solutions to such problems. Consequently, numerical and approximate techniques must be applied. Many useful approaches have been utilized to solve nonlinear and linear fractional differential equations (FDEs), such as the Adomian decomposition method (ADM) [20], variational iteration method (VIM) [21,22], homotopy analysis method (HAM) [23,24,25,26], homotopy perturbation method (HPM) [27,28,29].

The Mittag–Leffler function (MLF) has acquired major significance because its participation in solving numerous applications of FDEs. The generalized MLF method (GMLFM) is utilized to solve ordinary FDEs [30]. The GMLFM is applied to find analytical and approximate solutions for nonlinear systems that have applications such as the smoking model [31,32], Lorenz system [33], Riccati differential equations [34], and so on. The efficiency and eligibility of the GMLFM derive from the fact that its results converge promptly to the exact solution, and that it also provides solutions in simple and convenient procedures. Moreover, the GMLFM can be modified to solve FPDES, where the MLF undetermined coefficient method contributes to solve the homogeneous FPDEs [35]. The modification of the GMLFM was applied to solve time-fractional Korteweg–de Vries (KdV) and Korteweg–de Vries–Burgers (KdVB) equations [36]. Furthermore, this modification has been used to illustrate the dynamics of predator–prey population as in [37].

The Adomian decomposition method (ADM) is an effective analytical method, that was first introduced by Adomian in the 1980s (see, e.g., [38,39]) to solve differential equations describing physical phenomena [40]. Furthermore, the ADM was developed by using Laplace transformation. Briefly, the LADM has been developed using the Laplace transform and ADM. Thus, we can say that the LADM demonstrates how the Laplace transform may be combined with the ADM to obtain an analytic approximate solution of nonlinear differential equations. Precisely, we used the LDAM because the calculations are easy to follow and understand. Additionally, the LADM is able to converge to the exact solutions faster than the ADM. For more advantages of the LADM over ADM and the comparison between them, see, e.g., [41]. Numerous phenomena that are described by PDE and FPDEs have been solved using the LADM, like Swift–Hohenberg (SH) equation [42], Keller–Segel equation [43], time-fractional model of Navier–Stokes equation [44], Fisher’s equation [45], fractional-order telegraph equations [46], and third-order dispersive FPDEs [47].

In this article, we intend to obtain the analytical solution of the following nonlinear fractional partial differential equations (NFPDEs):

• Broer–Kaup (BK) sytem [48] of fractional order $0<\alpha <1$

  $$\left\{\begin{array}{c}{}_{}^C{\mathfrak{D}}_t^{\alpha }U+U{U}_x+V_x=0,\hfill \\ \\ {}_{}^C{\mathfrak{D}}_t^{\alpha }V+U_x+{\left(UV\right)}_x+U_{xxx}=0,\hfill \end{array}\right.$$

  (1)

  with the initial conditions (ICs)

  $$U(x,0)=1+2tanh\left(x\right)V(x,0)=1-2tan{h}^2\left(x\right).$$

  (2)
• Burgers’ system [49] of fractional order $0<\alpha <1$

  $$\left\{\begin{array}{c}{}_{}^C{\mathfrak{D}}_t^{\alpha }U(x,t)=U_{xx}+2U{U}_x-U{V}_x-V{U}_x,\hfill \\ \\ {}_{}^C{\mathfrak{D}}_t^{\alpha }V(x,t)=V_{xx}+2V{V}_x-U{V}_x-V{U}_x,\hfill \end{array}\right.$$

  (3)

  with the ICs

  $$U(x,0)=sin\left(x\right),V(x,0)=sin\left(x\right).$$

  (4)
• Burgers’ system [49]:

  $$\left\{\begin{array}{c}{}_{}^C{\mathfrak{D}}_t^{\alpha }U(x,y,t)=W_x{V}_y-W_y{V}_x-U,\hfill \\ \\ {}_{}^C{\mathfrak{D}}_t^{\alpha }V(x,y,t)=V-U_y{W}_x-U_x{W}_y,\hfill \\ \\ {}_{}^C{\mathfrak{D}}_t^{\alpha }W(x,y,t)=W-V_y{U}_x-V_x{U}_y,\hfill \end{array}\right.$$

  (5)

  with the ICs

  $$U(x,y,0)=e^{x+y},V(x,y,0)=e^{x-y},W(x,y,0)=e^{-x+y}.$$

  (6)

The motivation of this study was to introduce two analytical techniques called MGMLFM and LADM to solve a full general NFPDE. In order to determine the efficacy and accuracy of the used methods, we applied them to solve the previous nonlinear systems of FPDEs and compared the obtained results with known exact solutions and solutions obtained by other methods. Precisely, to the best knowledge of the authors, analytical solutions of Broer–Kaup and Burgers’ systems of fractional orders by the proposed methods have not previously been reported in the literature, which strongly motivated this work.

The rest of this article is structured as: Section 2, we present some necessary concepts of FC, helping us to understand the main results in this article. In Section 3, we introduce the analysis of the proposed methods to solve a general system of FPDEs. Section 4 is devoted to applying the MGMLFM and LADM to the construction of approximate solutions of some illustrative examples of nonlinear systems of FPDEs. Moreover, we offer numerical simulations to compare our results with the exact solution, in order to prove the accuracy and efficacy of our methodology. Finally, our conclusion is presented in Section 5.

2. Preliminaries

In this section, we give a brief overview of the most important definitions and concepts related to this article (see, e.g., [50,51,52]).

Definition 1.

The Riemann–Liouville fractional integral of order $\alpha >0$ of a function $f\left(t\right),$ can be defined as

$$\begin{array}{ccc}\hfill {}_{}{\mathfrak{I}}_t^{\alpha }f\left(t\right)& =& \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\zeta )}^{\alpha -1}f\left(\zeta \right)d\zeta ,t>0,\hfill \\ \hfill {}_{}{\mathfrak{I}}_t^{0}f\left(t\right)& =& f\left(t\right),\hfill \end{array}$$

where $\mathrm{\Gamma }(·)$ is the Euler gamma function, defined as follows:

$$\mathrm{\Gamma }\left(\xi \right)={\int }_0^{\infty }{t}^{\xi -1}{e}^{-t}dt,(Re\left(\xi \right)>0).$$

Definition 2.

The Caputo fractional partial derivative of a function $f(x,t)$ of order α is defined as

$$\begin{array}{ccc}\hfill {}_{}^C{\mathfrak{D}}_t^{\alpha }f(x,t)& =& \frac{1}{\mathrm{\Gamma }(m-\alpha )}{\int }_0^t{(t-\zeta )}^{m-\alpha -1}\frac{{\partial }^{m}f(x,\zeta )}{\partial {\zeta }^m}d\zeta ,t>0,\hfill \end{array}$$

for $m-1<\alpha \le m,$$m\in \mathbb{N}.$ In particular, for $0<\alpha <1,$ the Caputo fractional partial derivative becomes

$$\begin{array}{ccc}\hfill {}_{}^C{\mathfrak{D}}_t^{\alpha }f(x,t)& =& \frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-\zeta )}^{-\alpha }\frac{\partial f(x,\zeta )}{\partial \zeta }d\zeta ,t>0.\hfill \end{array}$$

Theorem 1.

Let $f(x,t)$ be a differentiable function in the interval $[0,T]$, $m-1<\alpha \le m,$$m\in \mathbb{N}$. Then,

$$\begin{array}{ccc}\hfill {}_{}^C{\mathfrak{D}}_t^{\alpha }{}_{}{\mathfrak{I}}_t^{\alpha }f(x,t)& =& f(x,t),\hfill \\ \hfill {}_{}{\mathfrak{I}}_t^{\alpha }{}_{}^C{\mathfrak{D}}_t^{\alpha }f(x,t)& =& f(x,t)-\sum _{k=0}^{m-1}\frac{{\partial }^{k}f(x,t)}{\partial t^k}{|}_{t=0}\frac{t^k}{k!}.\hfill \end{array}$$

Proposition 1.

For $m-1<\alpha \le m,$$m\in \mathbb{N}$ and $\beta >-1$, we have:

$$\begin{array}{ccc}\hfill {}_{}^C{\mathfrak{D}}_t^{\alpha }{t}^{\beta }& =& \frac{\mathrm{\Gamma }(\beta +1)}{\mathrm{\Gamma }(\beta -\alpha +1)}{t}^{\beta -\alpha },\hfill \\ \hfill {}_{}{\mathfrak{I}}_t^{\alpha }{t}^{\beta }& =& \frac{\mathrm{\Gamma }(\beta +1)}{\mathrm{\Gamma }(\beta +\alpha +1)}{t}^{\beta +\alpha }.\hfill \end{array}$$

Definition 3.

Let $F(x,s)$ be the Laplace transform of the function $f(x,t)$. Then, the Laplace transform of the Caputo fractional partial derivative is given by [53]

$$\begin{array}{c}\hfill \mathcal{L}{\{}_{}^C{\mathfrak{D}}_t^{\alpha }f\left(t\right),s\}=s^{\alpha }F\left(s\right)-\sum _{i=0}^{n-1}{s}^{\alpha -i-1}{f}^{\left(i\right)}\left(0\right),(n-1<\alpha \le n);n\in \mathbb{N}.\end{array}$$

Definition 4.

The two-parameter MLF is defined by:

$$E_{\alpha ,\beta }\left(x\right)=\sum _{n=0}^{\infty }\frac{x^n}{\mathrm{\Gamma }(n\alpha +\beta )},\alpha ,\beta >0.$$

If $\beta =1$, this function is denoted by $E_{\alpha }(·),$ and if $\alpha =\beta =1$ this function represents $e^x$.

Lemma 1.

The fractional derivative of the GMLF is given as:

$${}_{}^C{\mathfrak{D}}_t^{\alpha }{E}_{\alpha }\left(\lambda t^{\alpha }\right){=}_{}^C{\mathfrak{D}}_t^{\alpha }\left(\sum _{n=0}^{\infty }{\displaystyle \frac{{\lambda }^n{t}^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}}\right)=\sum _{n=1}^{\infty }{\displaystyle \frac{{\lambda }^n{t}^{(n-1)\alpha }}{\mathrm{\Gamma }\left(\right(n-1)\alpha +1)}}=\sum _{n=0}^{\infty }{\displaystyle \frac{{\lambda }^{n+1}{t}^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}}=\lambda E_{\alpha }\left(\lambda t^{\alpha }\right).$$

Theorem 2.

Assume that a nonlinear function $N\left(u\right)$ and $u={\sum }_{l=0}^{\infty }{\xi }^l{u}_l,$ then (see, e.g., [54])

$$\frac{{\partial }^n}{\partial {\xi }^n}N{\left(u\right)}_{\xi =0}=\frac{{\partial }^n}{\partial {\xi }^n}N{\left(\sum _{l=0}^{\infty }{\xi }^l{u}_l\right)}_{\xi =0}=\frac{{\partial }^n}{\partial {\xi }^n}N{\left(\sum _{l=0}^n{\xi }^l{u}_l\right)}_{\xi =0}.$$

3. Idea of the Used Methods

In this section, we introduce the idea behind the analysis of the proposed methods and how these methods were implemented to solve a general form of NFPDEs. For more details on the convergence analysis of these methods, we encourage the reader to consult [30,31,32,33,55].

3.1. Analysis of the MGMLFM

In this subsection, we discuss the methodology of the MGMLFM to solve a general FPDEs. To this end, we consider a system of fractional-order nonlinear PDEs of the following general form

$$\begin{array}{c}\hfill {}_{}^C{\mathfrak{D}}_t^{\alpha }\mathbf{u}(\mathbf{\xi },t)=L\left(\mathbf{u}(\mathbf{\xi },t)\right)+N\left(u(\mathbf{\xi },t)\right),\end{array}$$

(7)

with the ICs

$$\begin{array}{c}\hfill \mathbf{u}(\mathbf{\xi },0)=\mathbf{\varphi }\left(\mathbf{\xi }\right),\end{array}$$

(8)

where ${}_{}^C{\mathfrak{D}}_t^{\alpha }\mathbf{u}(\mathbf{\xi },t)$ is the Caputo fractional derivative of order $p-1<\alpha \le p$ for the function $\mathbf{u}(\mathbf{\xi },t)$, such that $\mathbf{u}={(u_1,u_2,\cdots ,u_m)}^T$, $\mathbf{\varphi }={({\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_m)}^T$ and $\mathbf{\xi }=({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\in {\mathbb{R}}^n,$$p,m,n\in \mathbb{N}.$ The nonlinear and linear operator of the function $\mathrm{u}(\mathbf{\xi },t)$ are represented by L and N, respectively.

The MGMLFM assumes that the solution of $\mathbf{u}(\mathbf{\xi },t)$ in Equation (7) can be written as an infinite series as follows:

$$\begin{array}{ccc}\hfill u_1(\mathbf{\xi },t)& =& w_1\left(\mathbf{\xi }\right)E_{\alpha }\left(A_1{t}^{\alpha }\right)=\sum _{j=0}^{\infty }{w}_1\left(\mathbf{\xi }\right)A_1^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}},\hfill \\ \hfill u_2(\mathbf{\xi },t)& =& w_2\left(\mathbf{\xi }\right)E_{\alpha }\left(A_2{t}^{\alpha }\right)=\sum _{j=0}^{\infty }{w}_2\left(\mathbf{\xi }\right)A_2^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}},\hfill \\ & ⋮& \hfill \\ \hfill u_m(\mathbf{\xi },t)& =& w_m\left(\mathbf{\xi }\right)E_{\alpha }\left(A_m{t}^{\alpha }\right)=\sum _{j=0}^{\infty }{w}_m\left(\mathbf{\xi }\right)A_m^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}},\hfill \end{array}$$

(9)

where $A_1,A_2,\cdots ,A_m$ are undetermined coefficients and $w_1\left(\mathbf{\xi }\right),w_2\left(\mathbf{\xi }\right),\cdots ,w_m\left(\mathbf{\xi }\right)$ are functions of the variable $\mathbf{\xi }.$ By using ICs (8), we have

$$w_1\left(\mathbf{\xi }\right)={\varphi }_1\left(\mathbf{\xi }\right),w_2\left(\mathbf{\xi }\right)={\varphi }_2\left(\mathbf{\xi }\right),\cdots ,w_m\left(\mathbf{\xi }\right)={\varphi }_m\left(\mathbf{\xi }\right).$$

Following to Lemma 1, Equations (9), (7) and ICs (8), we get:

$$\sum _{j=0}^{\infty }{\varphi }_m\left(\mathbf{\xi }\right)A_m^{j+1}{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}}=L\left(\sum _{j=0}^{\infty }{\varphi }_m\left(\mathbf{\xi }\right)A_m^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}}\right)+N\left(\sum _{j=0}^{\infty }{\varphi }_m\left(\mathbf{\xi }\right)A_m^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}}\right),m=1,2,....$$

(10)

Therefore, the linear term can be decomposed as

$$\begin{array}{ccc}\hfill L\left(\mathbf{u}\right(\mathbf{\xi },t\left)\right)& =& L\left(\sum _{j=0}^{\infty }{\varphi }_m\left(\mathbf{\xi }\right)A_m^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}}\right)=L\left({\varphi }_m\left(\mathbf{\xi }\right)\right)\sum _{j=0}^{\infty }{A}_m^j\frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}\hfill \\ & =& {\lambda }_m^{*}{\varphi }_m\left(\mathbf{\xi }\right)\sum _{j=0}^{\infty }{A}_m^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}},\hfill \end{array}$$

(11)

where ${\lambda }_m^{*}$ is a constant. From He’s polynomials [54,56,57] and Theorem 2, the $N\left(\mathbf{u}\right(\mathbf{\xi },t\left)\right)$ can be decomposed as:

$$\begin{array}{c}\hfill N\left(\mathbf{u}(\mathbf{\xi },t)\right)=N\left(\sum _{j=0}^{\infty }{\varphi }_m\left(\mathbf{\xi }\right)A_m^j{\displaystyle \frac{t^{j\alpha }}{\mathrm{\Gamma }(j\alpha +1)}}\right)=N\left({\varphi }_m\left(\mathbf{\xi }\right)\right)N\left(\sum _{j=0}^m{u}_j(\mathbf{\xi },t)\right).\end{array}$$

(12)

Substituting Equations (11) and (12) into Equation (10), we can specify the recurrence relation (RR) and obtain the $A_m$, therefore we can get the solution of the NFPDEs.

3.2. LADM for System of FDEs

Here, we explain the basic idea of the LADM for solving Equations (7) and (8). By applying the Laplace transform to both sides of Equation (7) and using the linear property of this transformation, the result is

$$\begin{array}{c}\hfill \mathcal{L}{[}_{}^C{\mathfrak{D}}_t^{\alpha }\mathbf{u}(\mathbf{\xi },t)]=\mathcal{L}\left[L\left(\mathbf{u}(\mathbf{\xi },t)\right)\right]+\mathcal{L}[N\left(\mathbf{u}(\mathbf{\xi },t)\right].\end{array}$$

Using Definition 3 and applying the formulas of the Laplace transform, we get:

$$\begin{array}{cc}\hfill s^{\alpha }\mathcal{L}\left[\mathbf{u}(\mathbf{\xi },t)\right]& =s^{\alpha -1}\mathbf{u}(\mathbf{\xi },0)+\mathcal{L}\left[L\left(\mathbf{u}(\mathbf{\xi },t)\right)\right]+\mathcal{L}\left[N\left(\mathbf{u}(\mathbf{\xi },t)\right)\right],\hfill \\ \hfill \\ \hfill \mathcal{L}\left[\mathbf{u}\right(\mathbf{\xi },t\left)\right]& ={\displaystyle \frac{\mathbf{\varphi }\left(\mathbf{\xi }\right)}{s}}+\frac{1}{s^{\alpha }}\left(\mathcal{L}\left[L\right(\mathbf{u}(\mathbf{\xi },t)\left)\right]+\mathcal{L}\left[N\right(\mathbf{u}(\mathbf{\xi },t)\left)\right]\right).\hfill \end{array}$$

(13)

The LADM represents the solution as an infinite series

$$\begin{array}{c}\hfill \mathbf{u}(\mathbf{\xi },t)=\sum _{r=0}^{\infty }{\mathbf{u}}_r(\mathbf{\xi },t),\end{array}$$

(14)

and the nonlinear terms in Equation (7) decompose as

$$\begin{array}{c}\hfill N(\mathbf{u}(\mathbf{\xi },t)=\sum _{r=0}^{\infty }{A}_r,\end{array}$$

(15)

where $A_r$ are Adomian polynomials and they can be calculated by the following formula:

$$\begin{array}{c}\hfill {\mathrm{A}}_r=\frac{1}{r!}\frac{d^r}{d{\lambda }^r}\left[N\sum _{i=0}^{\infty }\left({\lambda }^i{\mathbf{u}}_i\right)\right]{|}_{\lambda =0},r=0,1,2....\end{array}$$

(16)

Substituting Equations (14) and (15) in Equation (16), we have:

$$\begin{array}{c}\hfill \mathcal{L}\left[\sum _{r=0}^{\infty }{\mathbf{u}}_r(\mathbf{\xi },t)\right]={\displaystyle \frac{\mathbf{\varphi }\left(\mathbf{\xi }\right)}{s}}+{\displaystyle \frac{1}{s^{\alpha }}}\left(\mathcal{L}\left[L\left(\sum _{r=0}^{\infty }{\mathbf{u}}_r(\mathbf{\xi },t)\right)\right]+\mathcal{L}\left[\sum _{r=0}^{\infty }{\mathrm{A}}_r\right]\right).\end{array}$$

Then, we can write:

$$\begin{array}{cc}\hfill \mathcal{L}\left[{\mathbf{u}}_0(\mathbf{\xi },t)\right]& ={\displaystyle \frac{\mathbf{\varphi }\left(\mathbf{\xi }\right)}{s}},\hfill \\ \hfill ⋮\\ \hfill \mathcal{L}\left[{\mathbf{u}}_r(\mathbf{\xi },t)\right]& ={\displaystyle \frac{1}{s^{\alpha }}}\left(\mathcal{L}\left[L\left({\mathbf{u}}_{r-1}(\mathbf{\xi },t)\right)\right]+\mathcal{L}\left[A_{r-1}\right]\right),r\ge 1.\hfill \end{array}$$

(17)

Then, applying the inverse Laplace transform to Equation (17), we obtain the values $u_r(\mathbf{\xi },t)$ recursively.

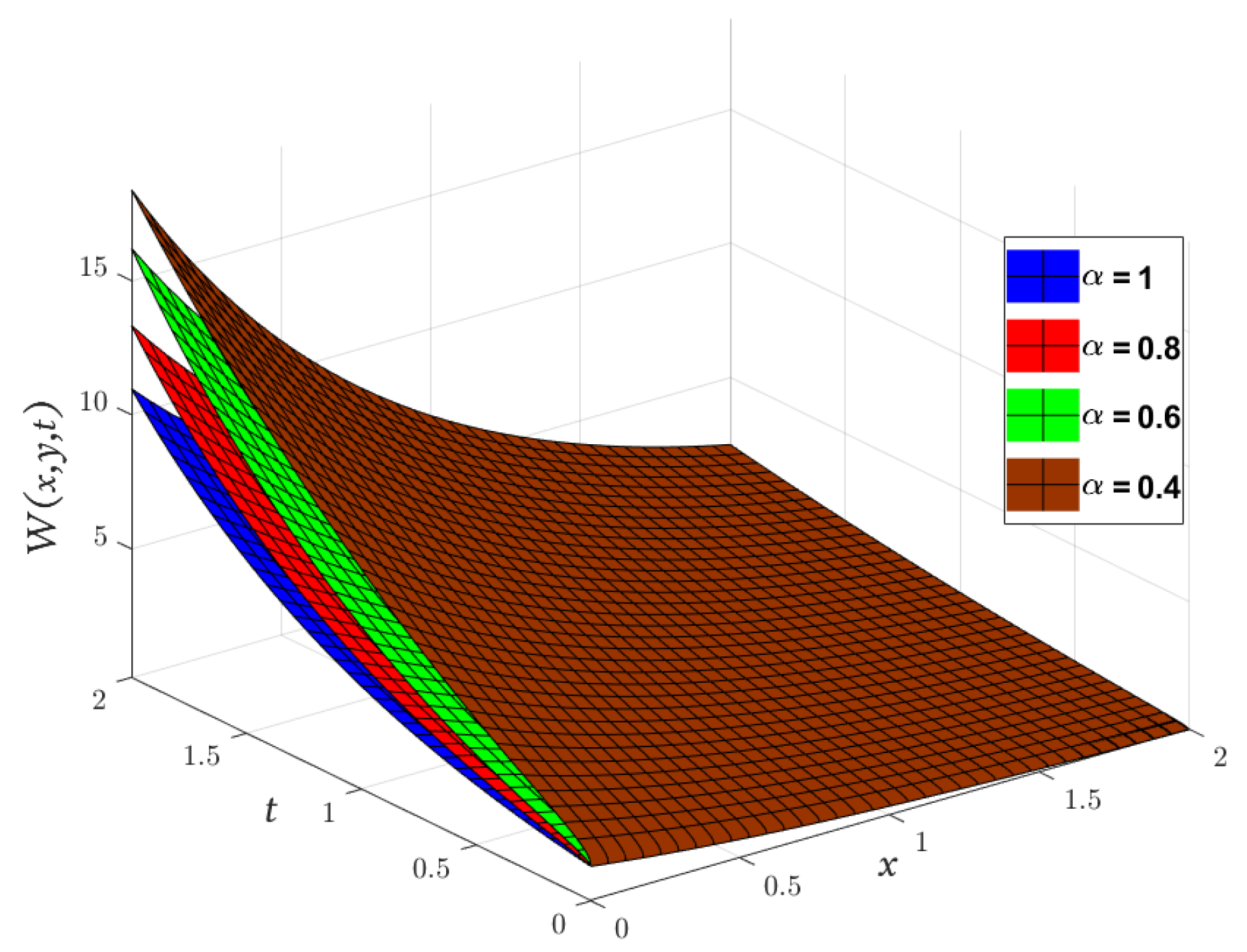
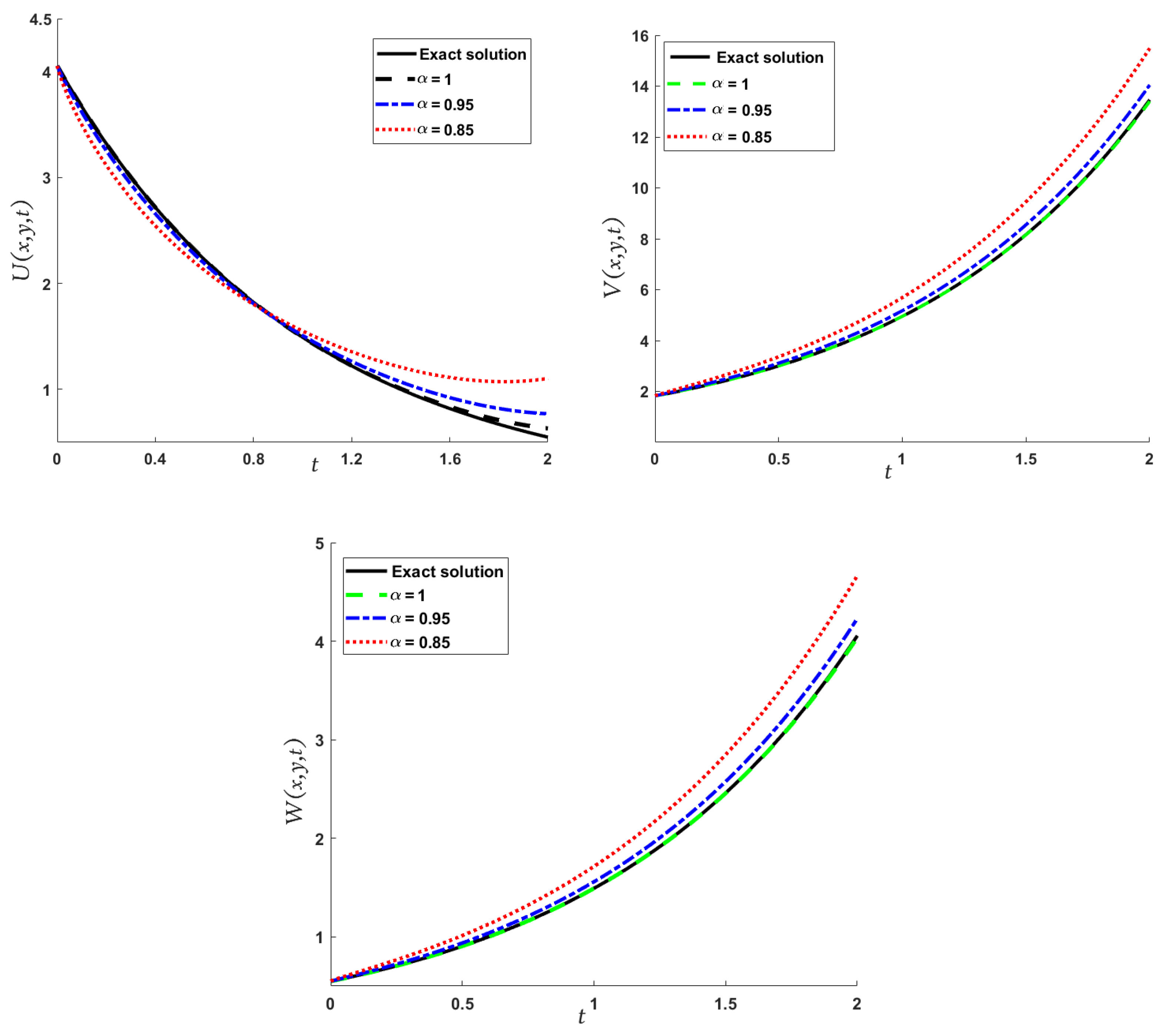
4. Applications and Results

Here, we apply the MGMLFM and LADM on Equations (1), (3), and (5) and provide a comparison of the obtained results with the given exact solutions to present the accuracy and advantages of the used approaches.

Example 1.

Let the system of NFPDEs (1) subject to ICs (2) and the known exact solutions of this system when $\alpha =1$ are given as [48]:

$$U(x,t)=1-2tanh(t-x)V(x,t)=1-2tan{h}^2(t-x).$$

(18)

• Applying the MGMLFM, as the suggestions in equation (9). Let

  $$\begin{array}{ccc}\hfill U(x,t)& =& \sum _{n=0}^{\infty }{F}_1\left(x\right)A^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \end{array}$$

  (19)

  $$\begin{array}{ccc}\hfill V(x,t)& =& \sum _{n=0}^{\infty }{F}_2\left(x\right)B^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \end{array}$$

  (20)
  where $A,B$ are coefficients. From ICs (2), we have $F_1\left(x\right)=U_0=1+2tanh\left(x\right)$ and $F_2\left(x\right)=V_0=1-2tan{h}^2\left(x\right).$ By using Equation (11), we write the linear term of (1) as follows:

  $$\begin{array}{ccc}\hfill L\left(U\right)& =& -\frac{\partial (1-2tan{h}^2\left(x\right))}{\partial x}=4sec{h}^2\left(x\right)tanh\left(x\right),\hfill \\ \hfill L\left(V\right)& =& -\frac{\partial (1+2tanh(x\left)\right)}{\partial x}-\frac{{\partial }^3(1+2tanh\left(x\right))}{\partial x^3}=2sec{h}^2\left(x\right)(1-6tan{h}^2\left(x\right)).\hfill \end{array}$$
  Similarly, the nonlinear term of Equation (1) is given as

  $$\begin{array}{ccc}\hfill N\left(U\right)& =& -(1+2tanh\left(x\right))\frac{\partial (1+2tanh(x\left)\right)}{\partial x}=-2sec{h}^2\left(x\right)(1+2tanh\left(x\right)),\hfill \\ \hfill N\left(V\right)& =& -(1+2tanh\left(x\right))\frac{\partial (1-2tan{h}^2\left(x\right)}{\partial x}-(1-2tan{h}^2\left(x\right)\frac{\partial (1+2tanh(x\left)\right)}{\partial x}\hfill \\ & =& 2sec{h}^2\left(x\right)(-1+2tanh\left(x\right)+6tan{h}^2\left(x\right)).\hfill \end{array}$$
  By using Equations (1) and (10), we get

  $$\begin{array}{ccc}\hfill & & \sum _{n=0}^{\infty }(U_0{A}^{n+1}-2sec{h}^2\left(x\right)(2tanh\left(x\right)B^n-(1+2tanh\left(x\right))C^n\mathrm{\Gamma }(n\alpha +1)))\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}=0,\hfill \\ \\ \hfill & & \sum _{n=0}^{\infty }(V_0{B}^{n+1}-2sec{h}^2\left(x\right)((1-6tan{h}^2\left(x\right))A^n+(-1+2tanh\left(x\right)\hfill \\ & & +6tan{h}^2\left(x\right))C_{*}^n\mathrm{\Gamma }(n\alpha +1)\left)\right)\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}=0,\hfill \end{array}$$
  where

  $$\begin{array}{c}\hfill C^n=\sum _{k=0}^n\frac{A^k{A}^{n-k}}{\mathrm{\Gamma }(k\alpha +1)\mathrm{\Gamma }\left(\right(n-k)\alpha +1)}and{C}_{*}^n=\sum _{k=0}^n\frac{A^k{B}^{n-k}}{\mathrm{\Gamma }(k\alpha +1)\mathrm{\Gamma }\left(\right(n-k)\alpha +1)}.\end{array}$$
  Then, the RR are given by

  $$\begin{array}{ccc}\hfill A^{n+1}& =& \frac{2sec{h}^2\left(x\right)}{U_0}(2tanh\left(x\right)B^n-(1+2tanh\left(x\right))C^n\mathrm{\Gamma }(n\alpha +1)),\hfill \\ \\ \hfill B^{n+1}& =& \frac{2sec{h}^2\left(x\right)}{V_0}((1-6tan{h}^2\left(x\right))A^n+(-1+2tanh\left(x\right)+6tan{h}^2\left(x\right))C_{*}^n\mathrm{\Gamma }(n\alpha +1)).\hfill \end{array}$$

  (21)
  Substituting the values of n and doing some computation, we obtain the following:

  $$\begin{array}{ccc}\hfill A^0& =& 1,B^0=1,\hfill \\ \hfill A^1& =& -\frac{2sec{h}^2\left(x\right)}{U_0},B^1=\frac{4sec{h}^2\left(x\right)tanh\left(x\right)}{V_0}.\hfill \end{array}$$
  Similarly, we can obtain additional coefficients by replacing various values of n in Equation (21). From Equations (19) and (20), we obtain the approximate solutions as follows:

  $$\begin{array}{ccc}\hfill U(x,t)& =& U_0(A^0+\frac{A^1{t}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{A^2{t}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}+\frac{A^3{t}^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots ),\hfill \\ \hfill V(x,t)& =& V_0(B^0+\frac{B^1{t}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{B^2{t}^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}+\frac{B^3{t}^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots ).\hfill \end{array}$$
• To implement the LADM, we take the Laplace transform of Equation (1); then,

  $$\left\{\begin{array}{c}\mathcal{L}{[}_{}^C{\mathfrak{D}}_t^{\alpha }U]+\mathcal{L}[U{U}_x+V_x]=0,\hfill \\ \\ \mathcal{L}{[}_{}^C{\mathfrak{D}}_t^{\alpha }V]+\mathcal{L}[U_x+{\left(UV\right)}_x+U_{xxx}]=0,\hfill \end{array}\right.$$
  and by using the differential property of the Laplace transform, we have:

  $$\left\{\begin{array}{c}\mathcal{L}{[}_{}^C{\mathfrak{D}}_t^{\alpha }U]=\frac{1}{s}U(x,0)-\frac{1}{s^{\alpha }}\mathcal{L}[U{U}_x+V_x],\hfill \\ \\ \mathcal{L}{[}_{}^C{\mathfrak{D}}_t^{\alpha }V]=\frac{1}{s}V(x,0)-\frac{1}{s^{\alpha }}\mathcal{L}[U_x+{\left(UV\right)}_x+U_{xxx}].\hfill \end{array}\right.$$

  (22)
  As in the LADM, the solution can be represented as an infinite series

  $$\begin{array}{c}\hfill \mathrm{U}(x,t)=\sum _{r=0}^{\infty }{\mathrm{U}}_r(x,t);\mathrm{U}={(U,V)}^T,\end{array}$$

  (23)
  and the nonlinear term in Equation (1) can be decomposed as

  $$\begin{array}{c}\hfill N_1\mathrm{U}(x,t)=\sum _{r=0}^{\infty }{\mathcal{A}}_r,N_2\mathrm{U}(x,t)=\sum _{r=0}^{\infty }{\mathcal{B}}_r,\end{array}$$
  where ${\mathcal{A}}_r$ and ${\mathcal{B}}_r$ are Adomian polynomials, which can be calculated by the following formulas:

  $$\left\{\begin{array}{c}{\mathcal{A}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_1\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},\hfill \\ \\ {\mathcal{B}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_2\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0}.\hfill \end{array}\right.$$

  (24)
  Substitution Equations (23) and (24) with ICs (2) into Equation (22) yields:

  $$\left\{\begin{array}{c}\mathcal{L}\left[\sum _{r=0}^{\infty }{U}_r(x,t)\right]=\frac{1}{s}(1+2tanh\left(x\right))-\frac{1}{s^{\alpha }}\mathcal{L}[N_1+{\partial }_x\left(\sum _{r=0}^{\infty }{V}_r(x,t)\right)],\hfill \\ \\ \mathcal{L}\left[\sum _{r=0}^{\infty }{V}_r(x,t)\right]=\frac{1}{s}(1-2tan{h}^2\left(x\right))-\frac{1}{s^{\alpha }}\mathcal{L}[{\partial }_x\left(\sum _{r=0}^{\infty }{U}_r(x,t)\right)+N_2\hfill \\ +{\partial }_{xxx}\left(\sum _{r=0}^{\infty }{U}_r(x,t)\right)].\hfill \end{array}\right.$$

  (25)
  By applying the inverse Laplace transform on both sides of Equation (25), we obtain

  $$\left\{\begin{array}{c}{U}_{r+1}=-{\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[{\mathcal{A}}_r+V_x]\right],\hfill \\ \\ V_{r+1}=-{\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[U_x+{\mathcal{B}}_r+U_{xxx}]\right],\hfill \end{array}\right.$$

  (26)
  where

  $$\left\{\begin{array}{c}{U}_0=1+2tanh\left(x\right),\hfill \\ \\ V_0=1-2tan{h}^2\left(x\right).\hfill \end{array}\right.$$
  The nonlinear terms ${\mathcal{A}}_r$ and ${\mathcal{B}}_r$ can be written as:

  $${\mathcal{A}}_0=U_0{U}_{0x},{\mathcal{A}}_1=U_{0x}{U}_1+U_0{U}_{1x},{\mathcal{A}}_2=U_{0x}{U}_2+U_{1x}{U}_1+U_0{U}_{2x},...$$

  (27)

  $${\mathcal{B}}_0={\left(U_0{V}_0\right)}_x,{\mathcal{B}}_1={(U_0{V}_1+V_0{U}_1)}_x,{\mathcal{B}}_2={(U_0{V}_2+U_1{V}_1+V_0{U}_2)}_x,....$$

  (28)
  In order to obtain the other terms of the projected solutions, we substitute the values of Equations (27) and (28) into Equation (26), yielding:

  $$\left\{\begin{array}{c}{U}_1=-2{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}sec{h}^2\left(x\right),U_2=-4{\displaystyle \frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}sec{h}^2\left(x\right)tanh\left(x\right),...\hfill \\ \\ V_1=4{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}sec{h}^2\left(x\right)tanh\left(x\right),V_2=4{\displaystyle \frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}[cosh\left(2x\right)-2]sec{h}^4\left(x\right),....\hfill \end{array}\right.$$
  Finally, we approximate the analytic solution $U(x,t)$ and $V(x,t)$ by

  $$\begin{array}{cc}\hfill U(x,t)& =\underset{r\to \infty }{lim}{U}_r(x,t)=U_0+U_1+U_3+...,\hfill \\ \hfill V(x,t)& =\underset{r\to \infty }{lim}{V}_r(x,t)=V_0+V_1+V_3+....\hfill \end{array}$$

In

Table 1. Values of approximate solutions obtained by the MGMLFM, exact solution, and absolute errors of $U(x,t)$ for system (1) with various values of $\alpha ,t$ and x.

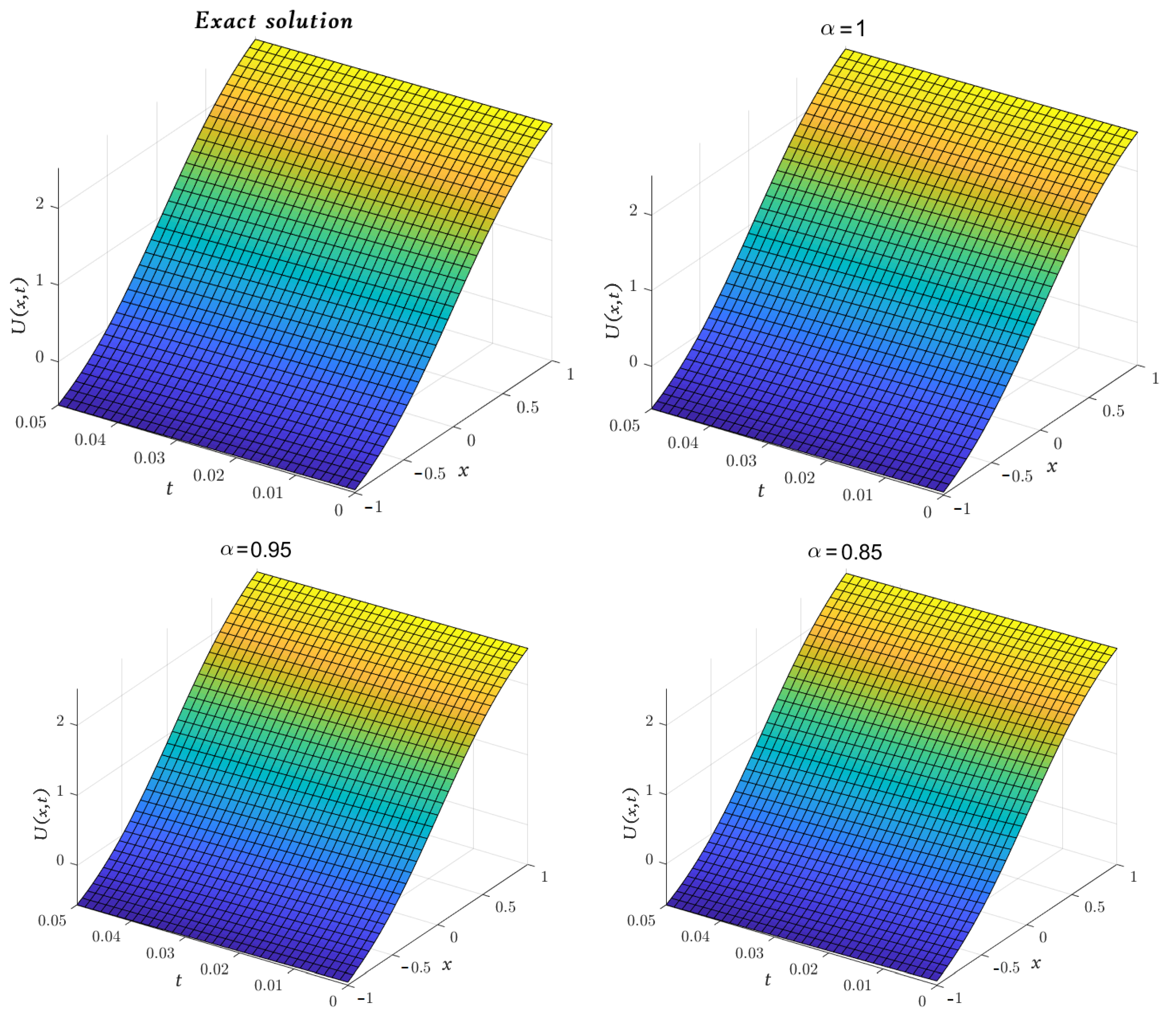
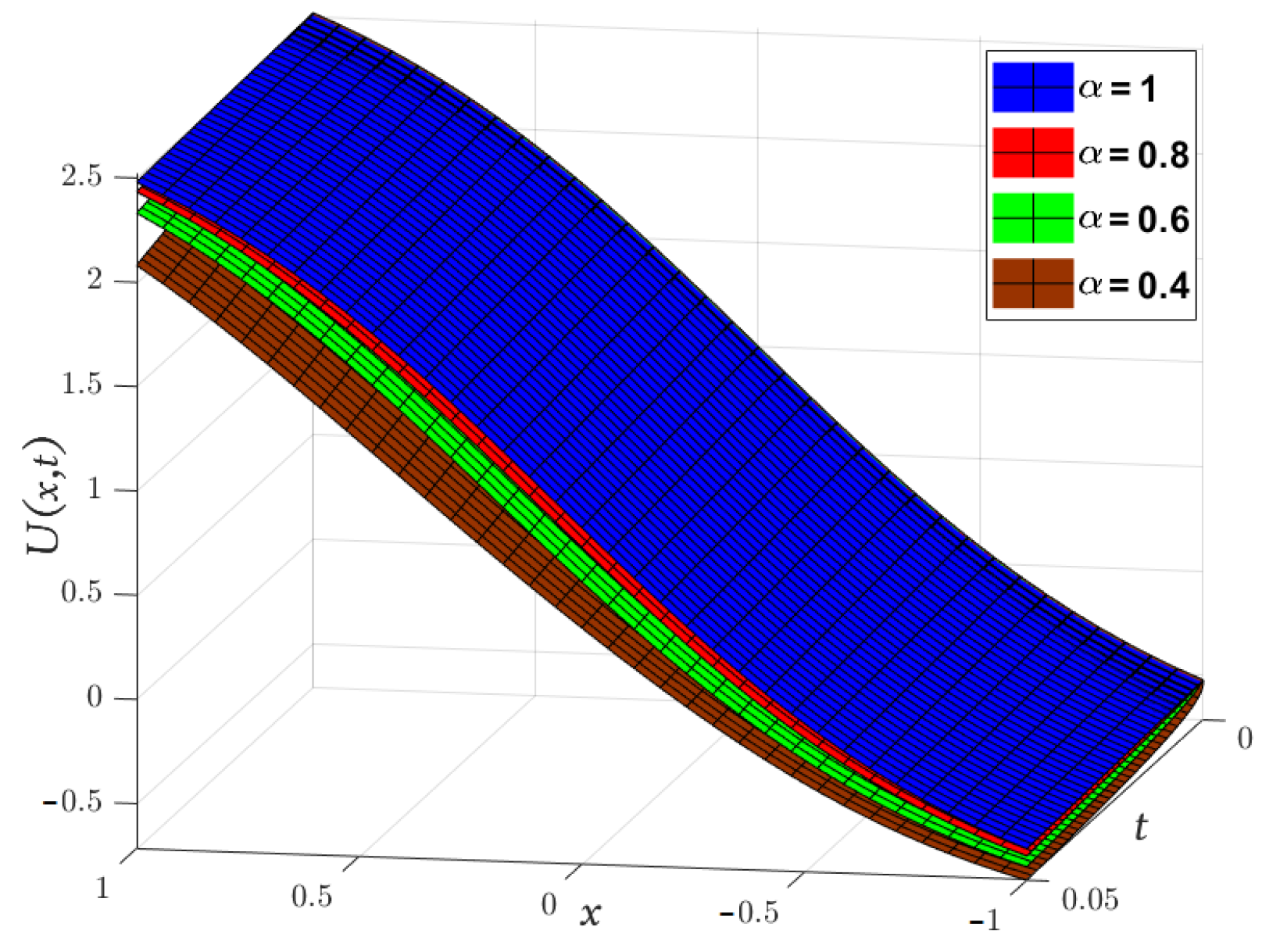
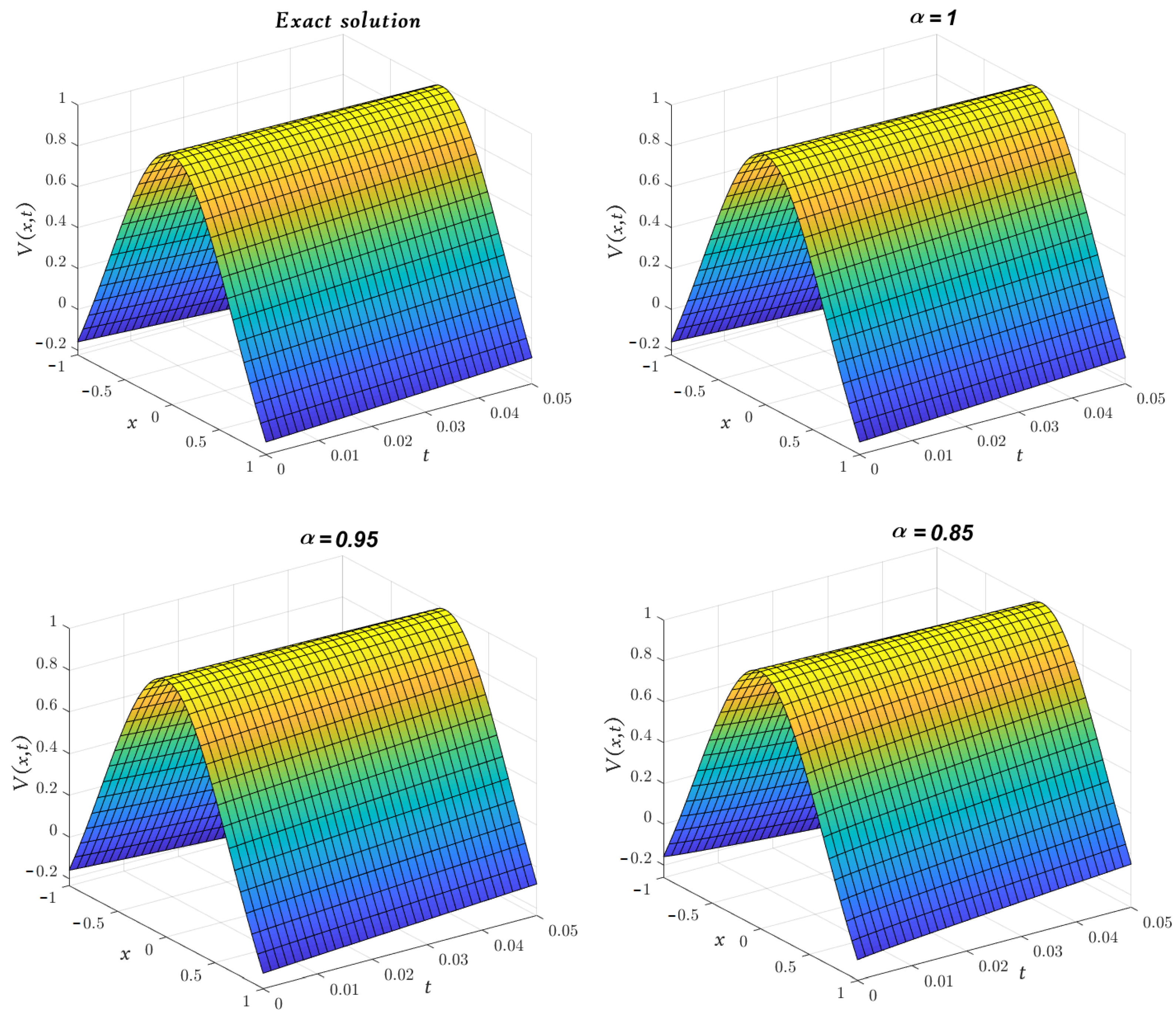
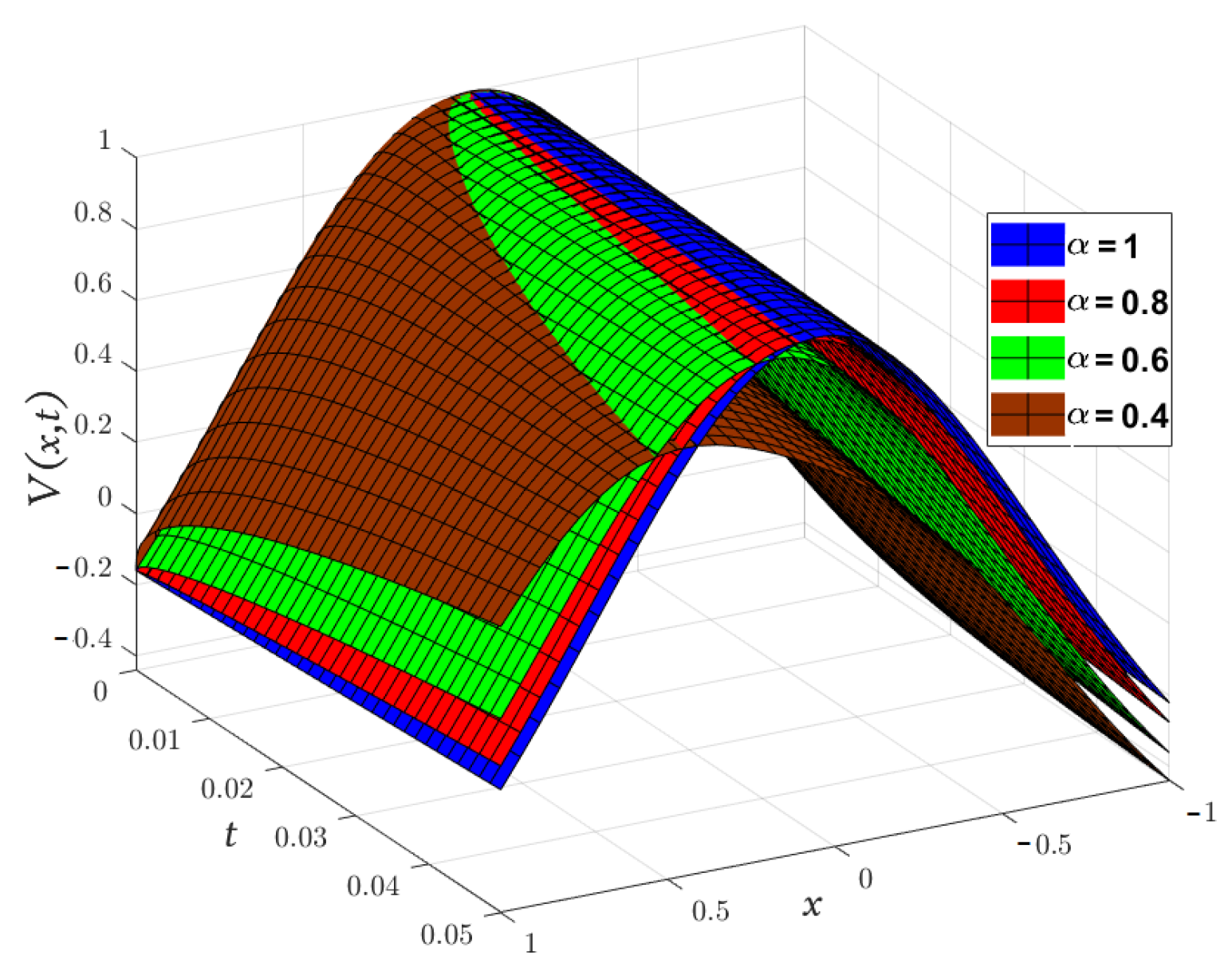
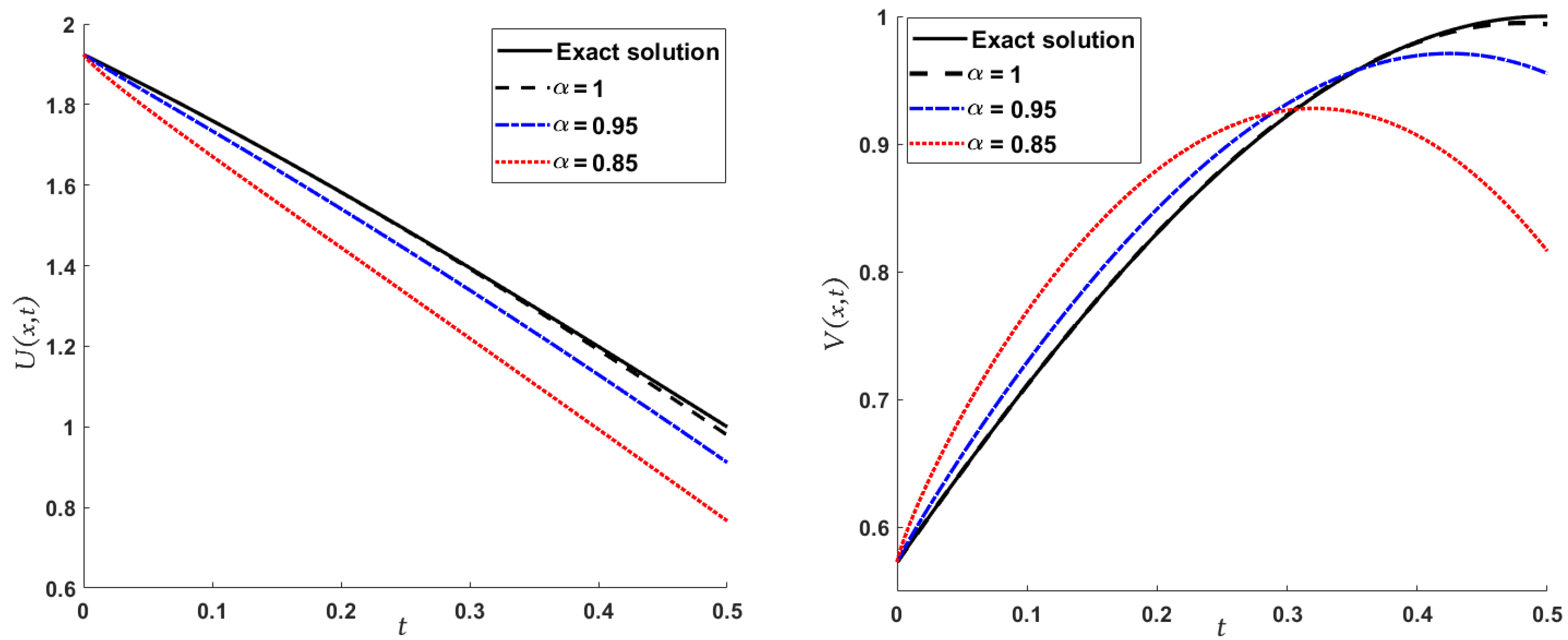
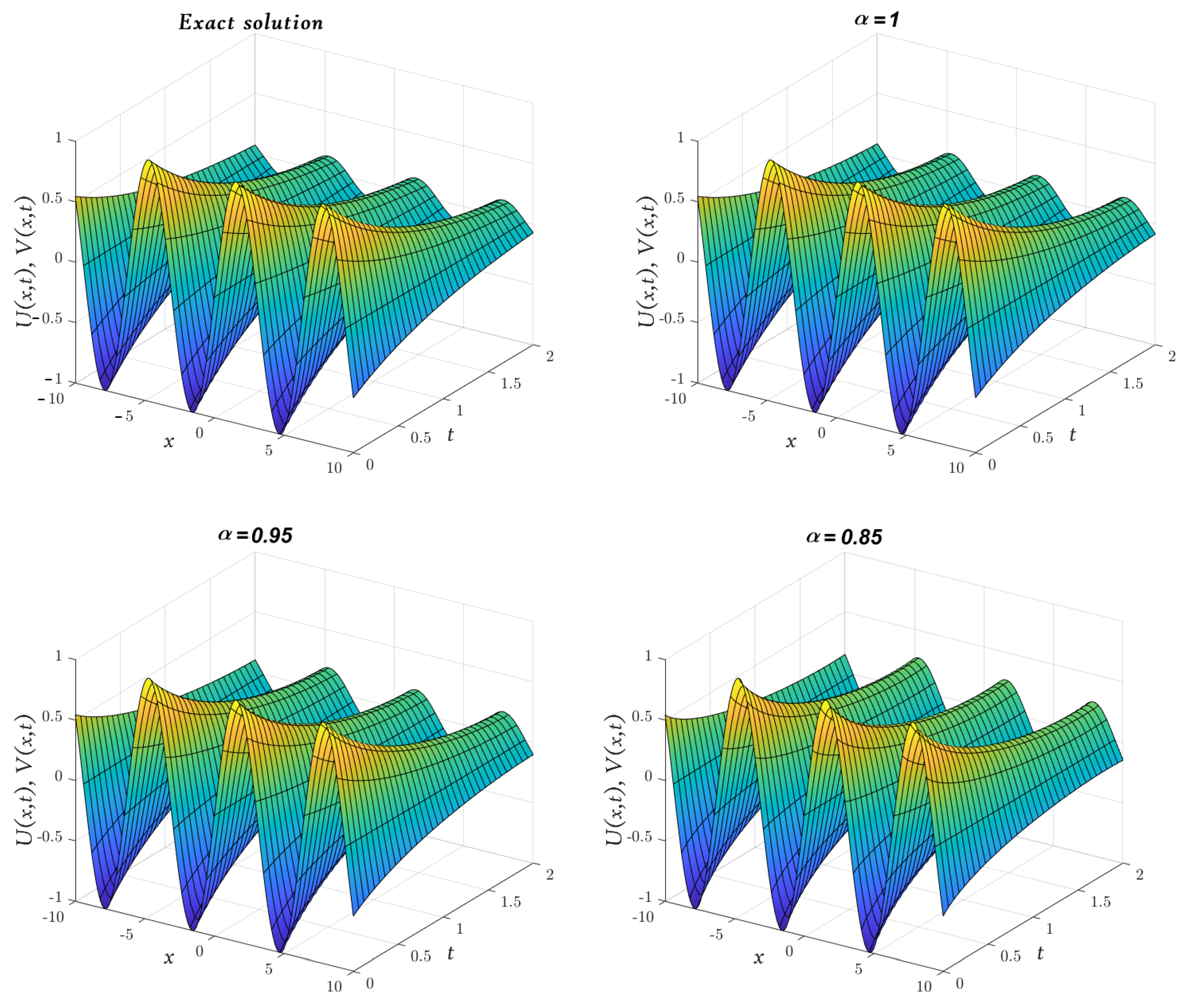
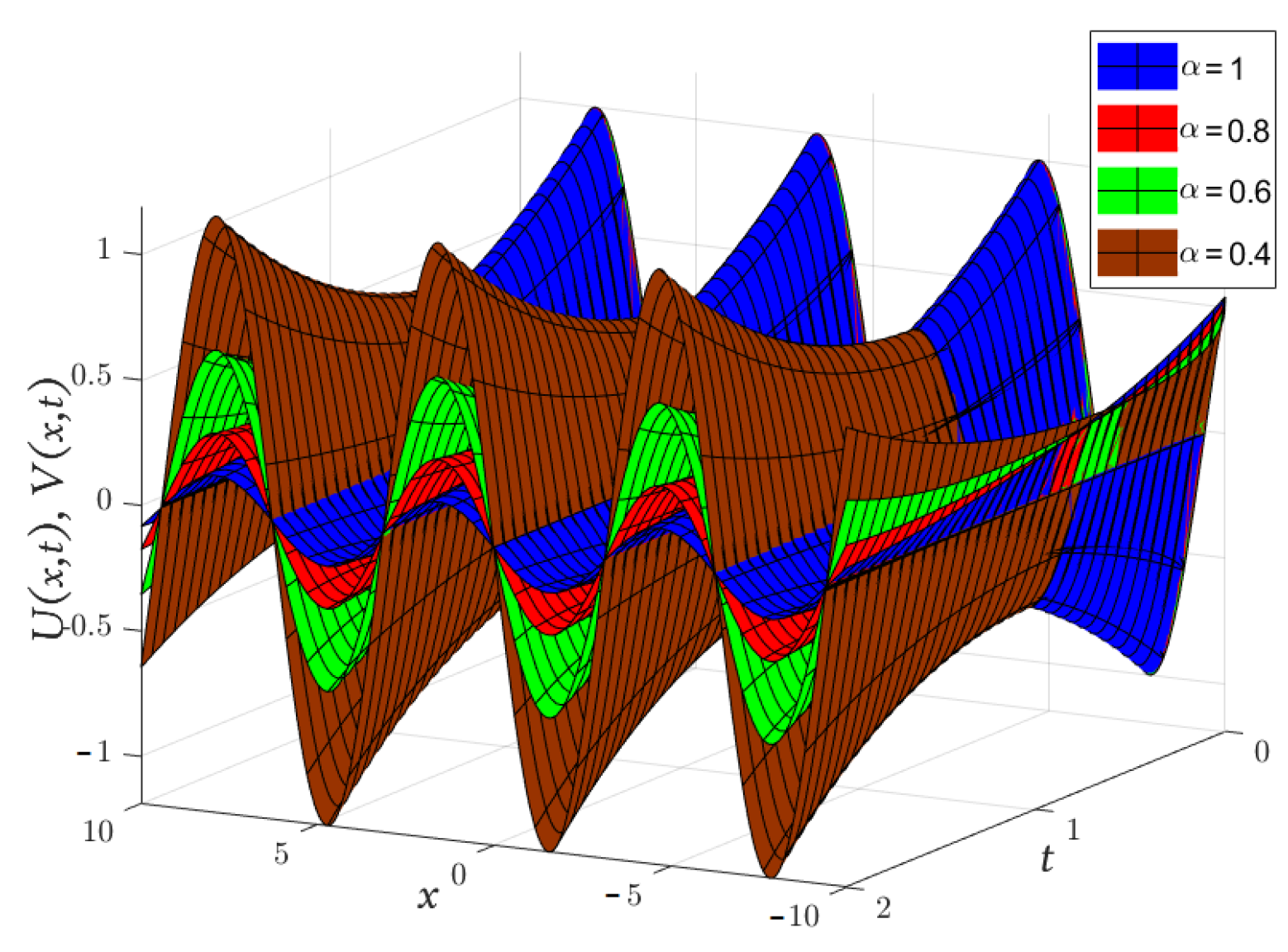
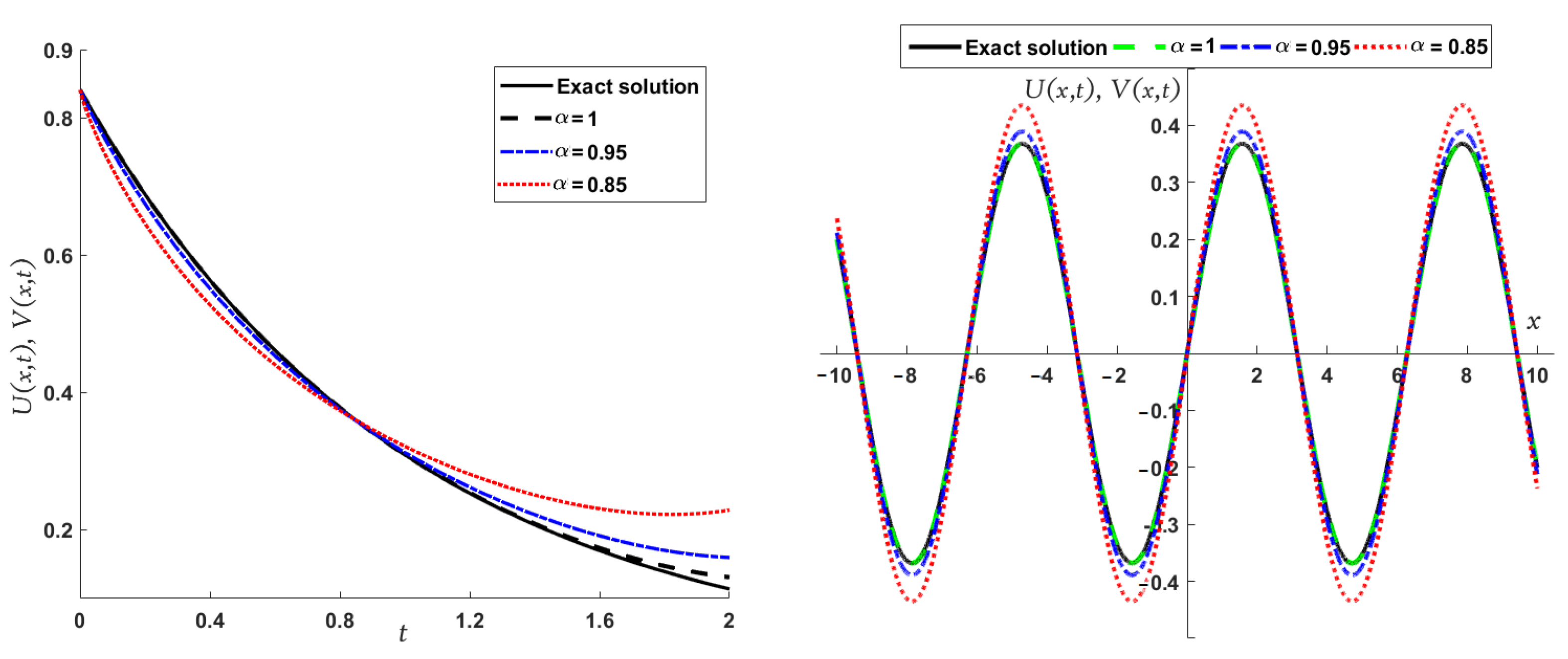
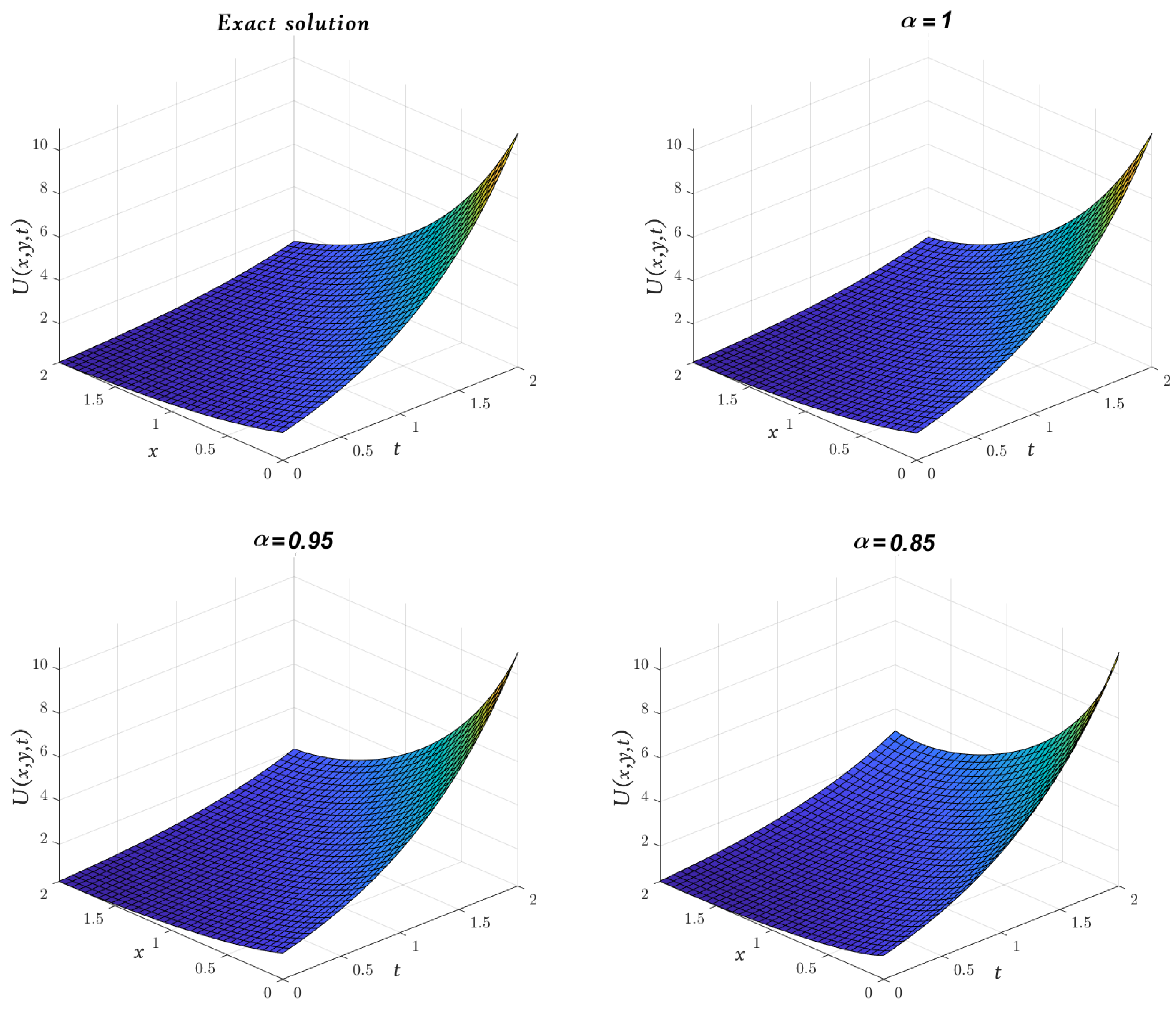
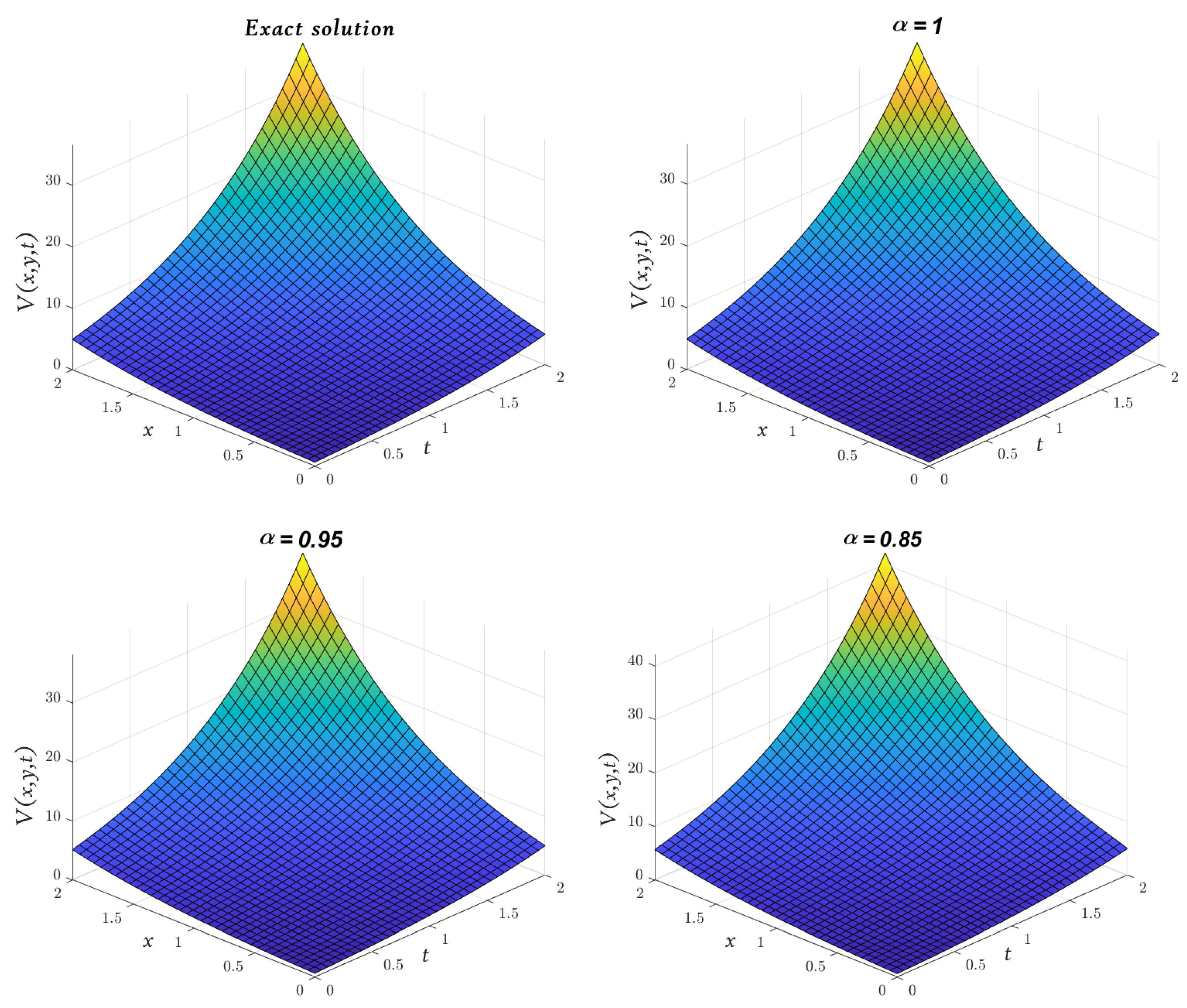
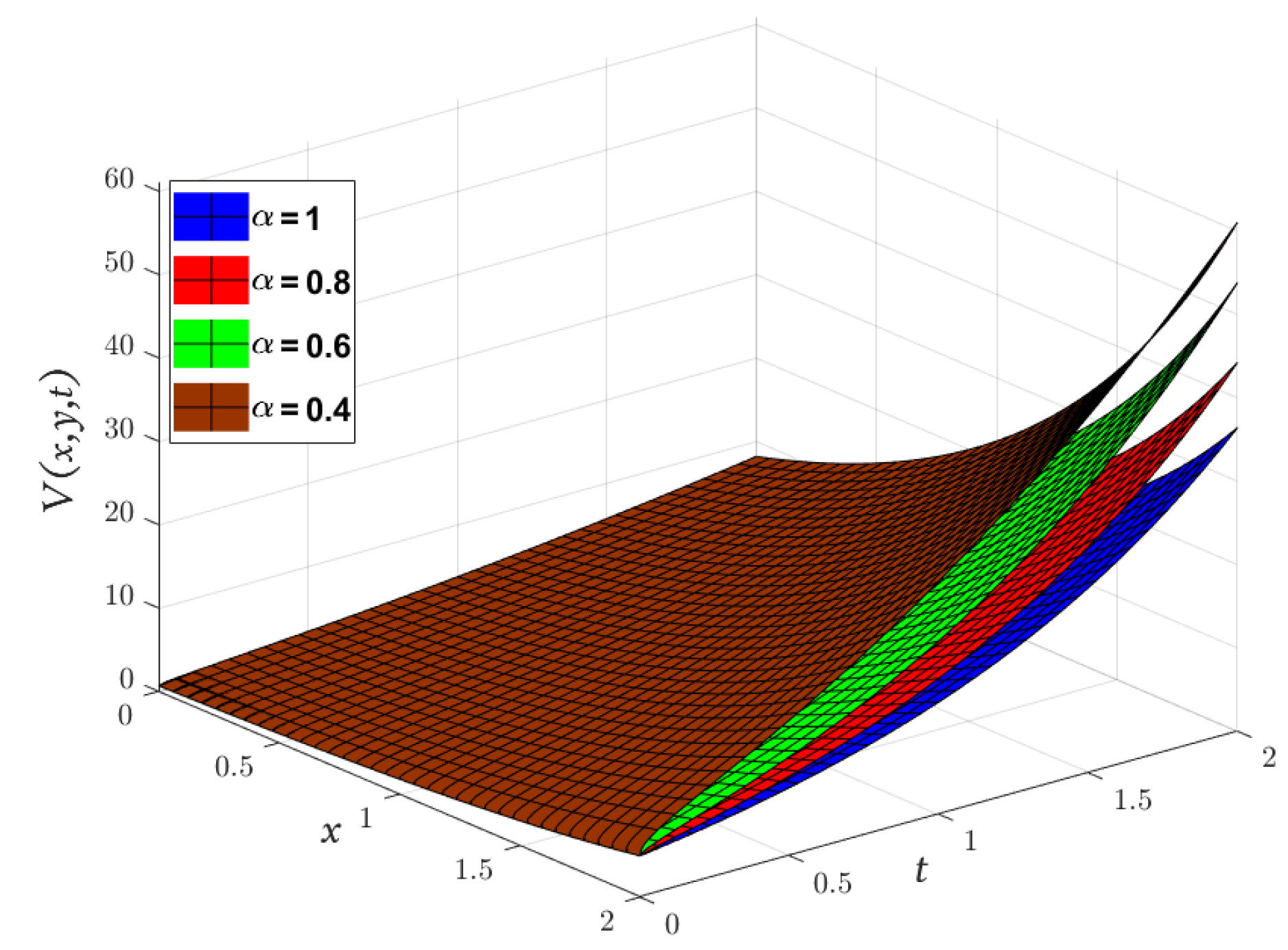
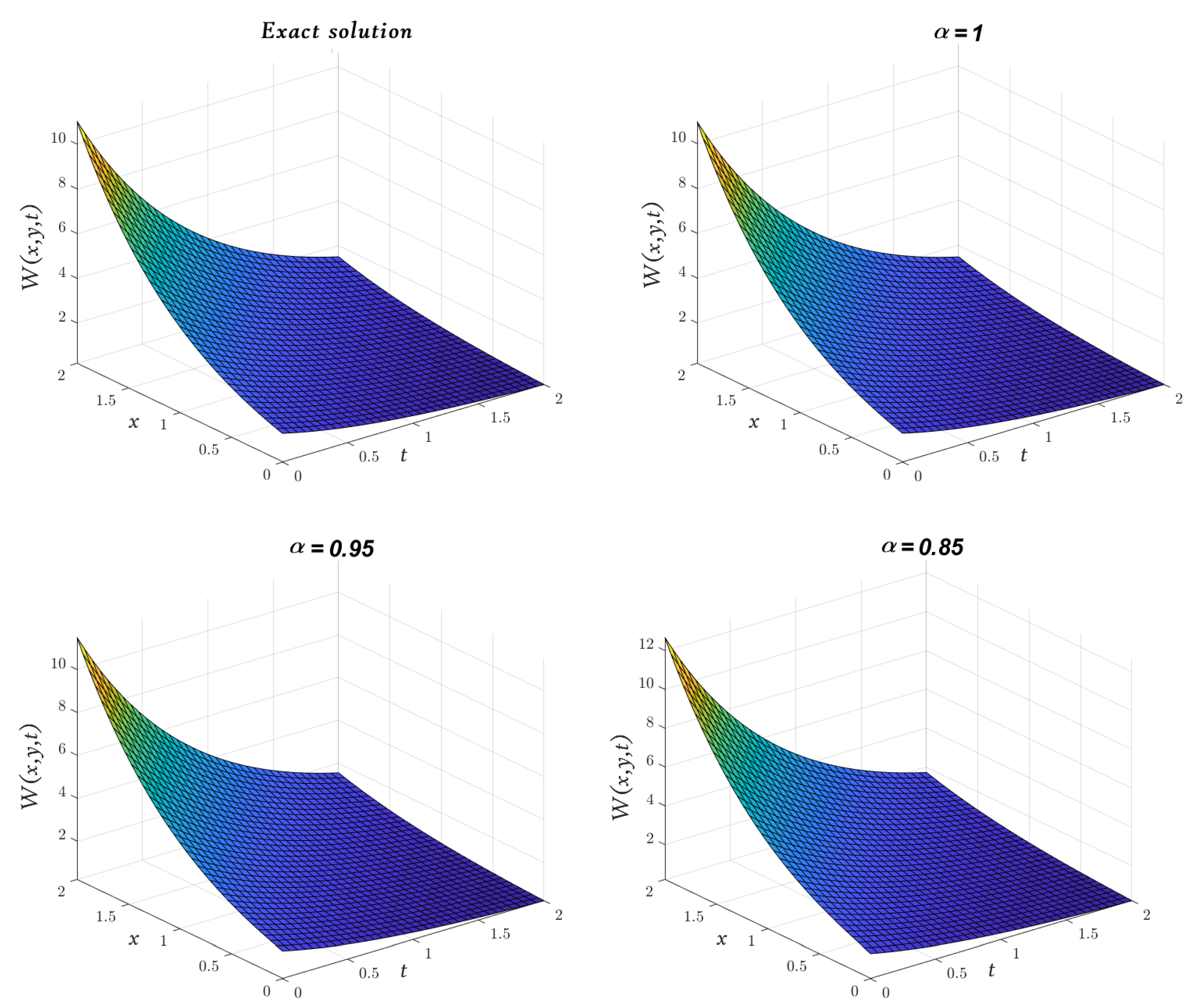
x	t	$\mathit{\alpha }=0.8$	$\mathit{\alpha }=0.9$	$\mathit{\alpha }=1$	Exact [48]	Absolute Error
		MGMLFM	MGMLFM	MGMLFM
−1	0.003	−0.532386	−0.528021	−0.525748	−0.525702	4.51907$\times {10}^{-5}$
	0.006	−0.539882	−0.547092	−0.528385	−0.528205	1.79812$\times {10}^{-4}$
	0.009	−0.547092	−0.536834	−0.531099	−0.530696	4.02448$\times {10}^{-4}$
−0.5	0.003	0.0600753	0.0671357	0.0710849	0.0710535	3.13711$\times {10}^{-5}$
	0.006	0.0489784	0.0598679	0.0664763	0.0663545	1.21755$\times {10}^{-4}$
	0.009	0.0392715	0.0531238	0.0619344	0.0616686	2.65732$\times {10}^{-4}$
0.5	0.003	1.90859	1.91561	1.91955	1.91951	4.53038$\times {10}^{-5}$
	0.006	1.8977	1.90838	1.91495	1.91477	1.80805$\times {10}^{-4}$
	0.009	1.88838	1.90171	1.91043	1.91002	4.05897$\times {10}^{-4}$
1	0.003	2.51404	2.51836	2.52063	2.52066	3.28798$\times {10}^{-5}$
	0.006	2.50673	2.51397	2.518	2.51813	1.2751$\times {10}^{-4}$
	0.009	2.49988	2.50966	2.5153	2.51558	2.78165$\times {10}^{-4}$

and

Table 2. Values of approximate solutions obtained by the MGMLFM, exact solution, and absolute errors of $V(x,t)$ for system (1) with various values of $\alpha ,t$ and x.

x	t	$\mathit{\alpha }=0.8$	$\mathit{\alpha }=0.9$	$\mathit{\alpha }=1$	Exact [48]	Absolute Error
		MGMLFM	MGMLFM	MGMLFM
−1	0.003	−0.172947	−0.167111	−0.16387	−0.163884	1.3969$\times {10}^{-5}$
	0.006	−0.182166	−0.173109	−0.16765	−0.167705	5.5459$\times {10}^{-5}$
	0.009	−0.190232	−0.178702	−0.171392	−0.171515	1.23872$\times {10}^{-4}$
−0.5	0.003	0.559953	0.56534	0.56868	0.568529	1.50951$\times {10}^{-4}$
	0.006	0.552808	0.559654	0.564751	0.564153	5.98079$\times {10}^{-4}$
	0.009	0.548031	0.554961	0.5611	0.559767	1.33332$\times {10}^{-3}$
0.5	0.003	0.588096	0.581064	0.577273	0.577252	2.14755$\times {10}^{-5}$
	0.006	0.599675	0.588242	0.581683	0.581597	8.62386$\times {10}^{-5}$
	0.009	0.610335	0.595142	0.586127	0.585932	1.94798$\times {10}^{-4}$
1	0.003	−0.148477	−0.153365	−0.156333	−0.156208	1.25863$\times {10}^{-4}$
	0.006	−0.141644	−0.148238	−0.152846	−0.152353	4.93352$\times {10}^{-4}$
	0.009	−0.136498	−0.143877	−0.149575	−0.148487	1.08802$\times {10}^{-3}$

, the MGMLFM approximate solutions of Example 1 are shown for various values of α and compared with the exact solution. The tabled results below seem to coincide with the values of the exact solution (18), which means that the MGMLFM is a more accurate technique than those methods that give a solution as an infinite series.

In Figure 1 and Figure 2 the LADM approximate solutions of $U(x,t)$ and $V(x,t)$ at various values of α are plotted in the domain $-1<x<1,0<t<0.05$; Moreover, a 3D graph with comparative results at $\alpha =1,0.8,0.6,0.4$ is shown.

Figure 3 represents the 2D graphs of the exact solution and the LADM solutions of $U(x,t)$ and $V(x,t)$ for $\alpha =1,0.95,0.85$, and $x=0.5$.

Example 2.

Consider the system of NFPDEs (3) subject to ICs (4) and the known exact solutions of this system when $\alpha =1$ are given as [49]:

$$U(x,t)=sin\left(x\right)e^{-t},V(x,t)=sin\left(x\right)e^{-t}.$$

(29)

• We apply the MGMLFM, using the suggestions stated in (9); let

  $$\begin{array}{ccc}\hfill U(x,t)& =& \sum _{n=0}^{\infty }{F}_1\left(x\right)A^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \end{array}$$

  (30)

  $$\begin{array}{ccc}\hfill V(x,t)& =& \sum _{n=0}^{\infty }{F}_2\left(x\right)B^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \end{array}$$

  (31)
  From ICs (4), we have $F_1\left(x\right)=sin\left(x\right)$ and $F_2\left(x\right)=sin\left(x\right).$ By using Equation (11), we obtain the linear term of Equation (3) as follows:

  $$\begin{array}{ccc}\hfill forU(x,t)\to L\left(sin\right(x\left)\right)& =& \frac{{\partial }^{2}sin\left(x\right)}{\partial x^2}=-sin\left(x\right)\Rightarrow {\lambda }_1^{*}=-1,\hfill \\ \hfill forV(x,t)\to L\left(sin\right(x\left)\right)& =& \frac{{\partial }^{2}sin\left(x\right)}{\partial x^2}=-sin\left(x\right)\Rightarrow {\lambda }_2^{*}=-1.\hfill \end{array}$$
  Similarly, the nonlinear term of Equation (3) can be written as:

  $$\begin{array}{ccc}\hfill forU(x,t)\to N\left(sin\right(x\left)\right)& =& 2sin\left(x\right)\frac{\partial sin\left(x\right)}{\partial x}-sin\left(x\right)\frac{\partial sin\left(x\right)}{\partial x}-sin\left(x\right)\frac{\partial sin\left(x\right)}{\partial x}=0,\hfill \\ \hfill forV(x,t)\to N\left(sin\right(x\left)\right)& =& 2sin\left(x\right)\frac{\partial sin\left(x\right)}{\partial x}-sin\left(x\right)\frac{\partial sin\left(x\right)}{\partial x}-sin\left(x\right)\frac{\partial sin\left(x\right)}{\partial x}=0.\hfill \end{array}$$
  By using Equations (3) and (10), we get:

  $$\begin{array}{ccc}\hfill sin\left(x\right)\sum _{n=0}^{\infty }(A^{n+1}+A^n)\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}& =& 0,\hfill \\ \\ \hfill sin\left(x\right)\sum _{n=0}^{\infty }(B^{n+1}+B^n)\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}& =& 0.\hfill \end{array}$$
  Then, the RR are given by:

  $$\begin{array}{c}\hfill A^{n+1}=-A^n,B^{n+1}=-B^n.\end{array}$$
  By substituting values of n, we have:

  $$\begin{array}{ccc}\hfill A^0& =& 1,B^0=1,\hfill \\ \hfill A^1& =& -1,B^1=-1,\hfill \\ \hfill A^2& =& 1,B^2=1\hfill \\ \hfill A^3& =& -1,B^3=-1.\hfill \end{array}$$
  From Equations (30) and (31), we get:

  $$\begin{array}{ccc}\hfill U(x,t)& =& sin\left(x\right)(1-\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}-\frac{t^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots )=sin\left(x\right)E_{\alpha }(-t^{\alpha }),\hfill \\ \hfill V(x,t)& =& sin\left(x\right)(1-\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}-\frac{t^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots )=sin\left(x\right)E_{\alpha }(-t^{\alpha }).\hfill \end{array}$$
• To implement the LADM, we take the Laplace transform of both sides of Equation (3); then,

  $$\left\{\begin{array}{c}\mathcal{L}{[}^C{\mathfrak{D}}_t^{\alpha }U(x,t)]=\mathcal{L}[U_{xx}+2U{U}_x-{\left(UV\right)}_x],\hfill \\ \\ \mathcal{L}{[}^C{\mathfrak{D}}_t^{\alpha }V(x,t)]=\mathcal{L}[V_{xx}+2V{V}_x-{\left(UV\right)}_x],\hfill \end{array}\right.$$
  using the properties of the Laplace transform, we obtain:

  $$\left\{\begin{array}{c}\mathcal{L}\left[U(x,t)\right]=\frac{1}{s}U(x,0)+\frac{1}{s^{\alpha }}\mathcal{L}[U_{xx}+2U{U}_x-{\left(UV\right)}_x],\hfill \\ \\ \mathcal{L}\left[V(x,t)\right]=\frac{1}{s}V(x,0)+\frac{1}{s^{\alpha }}\mathcal{L}[V_{xx}+2V{V}_x-{\left(UV\right)}_x].\hfill \end{array}\right.$$
  The next step in the LADM is to represent the solution as Equation (23), and the nonlinear terms $U{U}_x,V{V}_x$ and ${\left(UV\right)}_x$ are decomposed as

  $$\begin{array}{c}\hfill N_1\mathrm{U}(x,t)=\sum _{r=0}^{\infty }{\mathcal{A}}_r,N_2\mathrm{U}(x,t)=\sum _{r=0}^{\infty }{\mathcal{B}}_r,N_3\mathrm{U}(x,t)=\sum _{n=0}^{\infty }{\mathcal{C}}_n,\end{array}$$
  where ${\mathcal{A}}_r,{\mathcal{B}}_r$ and ${\mathcal{C}}_r$ are Adomian polynomials and their components are defined as:

  $$\left\{\begin{array}{c}{\mathcal{A}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_1\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},\hfill \\ \\ {\mathcal{B}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_2\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},\hfill \\ \\ {\mathcal{C}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_3\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0}.\hfill \end{array}\right.$$

  (32)
  From Equations (23) and (32) with ICs (4), we have:

  $$\left\{\begin{array}{c}\mathcal{L}\left[\sum _{r=0}^{\infty }{U}_r(x,t)\right]=\frac{1}{s}sin\left(x\right)+\frac{1}{s^{\alpha }}\mathcal{L}[{\partial }_{xx}\left(\sum _{r=0}^{\infty }{U}_r(x,t)\right)+2N_1-N_3],\hfill \\ \\ \mathcal{L}\left[\sum _{r=0}^{\infty }{V}_r(x,t)\right]=\frac{1}{s}sin\left(x\right)+\frac{1}{s^{\alpha }}\mathcal{L}[{\partial }_{xx}\left(\sum _{r=0}^{\infty }{V}_r(x,t)\right)+2N_2-N_3].\hfill \end{array}\right.$$

  (33)
  Applying the inverse Laplace transform on both sides of Equation (33), we get

  $$\left\{\begin{array}{c}{U}_{r+1}={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[U_{rxx}+2{\mathcal{A}}_r-{\mathcal{C}}_r]\right],\hfill \\ \\ V_{r+1}={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[V_{rxx}+2{\mathcal{B}}_r-{\mathcal{C}}_r]\right],\hfill \end{array}\right.$$
  where

  $$\left\{\begin{array}{c}{U}_0=sin\left(x\right),\hfill \\ \\ V_0=sin\left(x\right).\hfill \end{array}\right.$$
  For the other terms, we can write:

  $$\left\{\begin{array}{c}{U}_1=-{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}sin\left(x\right),U_2={\displaystyle \frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}sin\left(x\right),...\hfill \\ \\ V_1={\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}sin\left(x\right),V_2={\displaystyle \frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}}sin\left(x\right),....\hfill \end{array}\right.$$

  (34)
  Finally, we approximate the analytic solution $U(x,t)$ and $V(x,t)$ by

  $$\begin{array}{cc}\hfill U(x,t)& =\underset{r\to \infty }{lim}{U}_r(x,t)=U_0+U_1+U_3+...,\hfill \\ \hfill V(x,t)& =\underset{r\to \infty }{lim}{V}_r(x,t)=V_0+V_1+V_3+....\hfill \end{array}$$

Obviously, the results in

Table 3. Values of approximate solutions obtained by MGMLFM, FNDM, exact solution, and absolute errors of $U(x,t)$ and $V(x,t)$ for system (3) with various values of $\alpha ,t,x$ and $y=0.4$.

x	t	$\mathit{\alpha }=0.75$		$\mathit{\alpha }=0.9$		$\mathit{\alpha }=1$		Exact	Absolute Error
		FNDM [49]	MGMLFM	FNDM [49]	MGMLFM	FNDM [49]	MGMLFM
−10	0.2	0.403596	0.3985421	0.429046	0.4274714	0.446097	0.4454068	0.445407	1.3478525$\times {10}^{-9}$
	0.4	0.349827	0.3275878	0.358413	0.3487726	0.369934	0.3646684	0.364668	1.6838537$\times {10}^{-7}$
−5	0.2	0.711403	0.7024943	0.756262	0.7534867	0.786318	0.7851008	0.785101	2.3758057$\times {10}^{-9}$
	0.4	0.616625	0.5774259	0.63176	0.6147676	0.652069	0.6427865	0.642786	2.9680616$\times {10}^{-7}$
5	0.2	−0.711403	−0.7024943	−0.756262	−0.7534867	−0.786318	−0.7851008	−0.785101	2.3758057$\times {10}^{-9}$
	0.4	−0.616625	−0.5774259	−0.63176	−0.6147676	−0.652069	−0.6427865	−0.642786	2.9680616$\times {10}^{-7}$
10	0.2	−0.403596	−0.3985421	−0.429046	−0.4274714	−0.446097	−0.4454068	−0.445407	1.3478525$\times {10}^{-9}$
	0.4	−0.349827	−0.3275878	−0.358413	−0.3487726	−0.369934	−0.3646684	−0.364668	1.6838537$\times {10}^{-7}$

are very close to the exact solution shown earlier in Equation (29) when $\alpha =1,$ which means that the approximate solutions obtained by the MGMLFM are rapidly converging to the exact solutions. Now, the LADM solutions for system (3) with ICs (4) are illustrated by the following simulation.

In Figure 4, we compare the obtained solutions by the LADM for $U(x,t)$ and $V(x,t)$ with the exact solution (29). Moreover, this figure illustrates the results obtained by the LADM for $U(x,t)$ and $V(x,t)$ with $\alpha =1,0.8,0.6,0.4$.

Further, in Figure 5, we display the comparison between exact and approximate solutions in two dimensions with time $0<t<2,x=1,$ (right figure) and with various values of space $-10<x<10,t=1,$ (left figure). Finally, it is noticeable that the LADM and MGMLFM approximate solutions overlap (for any interval of the variables $x,t$) and have a high degree of accuracy when compared to the exact solution.

Example 3.

Consider the system (5) subject to ICs (6) and the known exact solutions of this system when $\alpha =1$ are given as [49,58]:

$$U(x,y,t)=e^{x+y-t},V(x,y,t)=e^{x-y+t},W(x,y,t)=e^{-x+y+t}.$$

(35)

• To apply the MGMLFM, we assume

  $$\begin{array}{ccc}\hfill U(x,y,t)& =& \sum _{n=0}^{\infty }{F}_1(x,y)A^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \\ \hfill V(x,y,t)& =& \sum _{n=0}^{\infty }{F}_2(x,y)B^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \\ \hfill W(x,y,t)& =& \sum _{n=0}^{\infty }{F}_3(x,y)S^n\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)},\hfill \end{array}$$
  where $A,B$, and S are undetermined coefficients. From ICs (6), we have $F_1(x,y)=e^{x+y},$$F_2(x,y)=e^{x-y},$ and $F_3(x,y)=e^{-x+y}.$ Similarly, as in Example 2, we calculate the linear and nonlinear parts of the system (5) and using Equation (10), we get

  $$\begin{array}{c}\hfill \begin{array}{ccc}\sum _{n=0}^{\infty }(A^{n+1}-{\lambda }_1^{*}{A}^n)\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}\hfill & =\hfill & 0,\hfill \\ \\ \sum _{n=0}^{\infty }(B^{n+1}-{\lambda }_2^{*}{B}^n)\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}\hfill & =\hfill & 0,\hfill \\ \\ \sum _{n=0}^{\infty }(S^{n+1}-{\lambda }_3^{*}{S}^n)\frac{t^{n\alpha }}{\mathrm{\Gamma }(n\alpha +1)}\hfill & =\hfill & 0,\hfill \end{array}\end{array}$$

  (36)
  where ${\lambda }_1^{*}=-1,$${\lambda }_2^{*}=1,$ and ${\lambda }_3^{*}=1.$ Then, the RR are given by

  $$\begin{array}{c}\hfill \begin{array}{ccc}{A}^{n+1}\hfill & =\hfill & {\lambda }_1^{*}{A}^n,\hfill \\ \\ B^{n+1}\hfill & =\hfill & {\lambda }_2^{*}{B}^n,\hfill \\ \\ S^{n+1}\hfill & =\hfill & {\lambda }_3^{*}{S}^n.\hfill \end{array}\end{array}$$
  By substituting different values of n and using Equation (36) we get the approximate solutions in the following:

  $$\begin{array}{ccc}\hfill U(x,y,t)& =& e^{x+y}(1-\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}-\frac{t^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots )=e^{x+y}{E}_{\alpha }(-t^{\alpha }),\hfill \\ \hfill V(x,y,t)& =& e^{x-y}(1+\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}+\frac{t^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots )=e^{x-y}{E}_{\alpha }\left(t^{\alpha }\right),\hfill \\ \hfill W(x,y,t)& =& e^{-x+y}(1+\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}+\frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}+\frac{t^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1)}+\cdots )=e^{-x+y}{E}_{\alpha }\left(t^{\alpha }\right).\hfill \end{array}$$
• To implement the LADM, we take the Laplace transform of Equation (5),

  $$\left\{\begin{array}{c}\mathcal{L}{[}^C{\mathfrak{D}}_t^{\alpha }U(x,y,t)]=\mathcal{L}[W_x{V}_y-W_y{V}_x-U],\hfill \\ \\ \mathcal{L}{[}^C{\mathfrak{D}}_t^{\alpha }V(x,y,t)]=\mathcal{L}[V-U_y{W}_x-U_x{W}_y],\hfill \\ \\ \mathcal{L}{[}^C{\mathfrak{D}}_t^{\alpha }W(x,y,t)]=\mathcal{L}[W-V_y{U}_x-V_x{U}_y],\hfill \end{array}\right.$$
  using the Laplace transform of the Caputo derivative, we have

  $$\left\{\begin{array}{c}\mathcal{L}\left[U(x,y,t)\right]=\frac{1}{s}U(x,y,0)+\frac{1}{s^{\alpha }}\mathcal{L}[W_x{V}_y-W_y{V}_x-U],\hfill \\ \\ \mathcal{L}\left[V(x,y,t)\right]=\frac{1}{s}V(x,y,0)+\frac{1}{s^{\alpha }}\mathcal{L}[V-U_y{W}_x-U_x{W}_y],\hfill \\ \\ \mathcal{L}\left[W(x,y,t)\right]=\frac{1}{s}W(x,y,0)+\frac{1}{s^{\alpha }}\mathcal{L}[W-V_y{U}_x-V_x{U}_y].\hfill \end{array}\right.$$

  (37)
  Representing the solution $U(x,y,t),V(x,y,t)$, and $W(x,y,t)$ as an infinite series, as follows,

  $$\begin{array}{c}\hfill \mathrm{U}(x,y,t)=\sum _{r=0}^{\infty }{\mathrm{U}}_r(x,y,t);\mathrm{U}={(U,V,W)}^T,\end{array}$$

  (38)
  the nonlinear terms included in Equation (5) can be decomposed as

  $$\begin{array}{c}\hfill N_1\mathrm{U}(x,y,t)=\sum _{r=0}^{\infty }{\mathcal{A}}_r,N_2\mathrm{U}(x,y,t)=\sum _{r=0}^{\infty }{\mathcal{A}}_r^{*},\\ \hfill N_3\mathrm{U}(x,y,t)=\sum _{n=0}^{\infty }{\mathcal{B}}_n,N_4\mathrm{U}(x,y,t)=\sum _{r=0}^{\infty }{\mathcal{B}}_r^{*},\\ \hfill N_4\mathrm{U}(x,y,t)=\sum _{n=0}^{\infty }{\mathcal{C}}_n,N_5\mathrm{U}(x,y,t)=\sum _{r=0}^{\infty }{\mathcal{C}}_r^{*},\end{array}$$
  where ${\mathcal{A}}_r,{\mathcal{A}}_r^{*},{\mathcal{B}}_r,{\mathcal{B}}_r^{*},{\mathcal{C}}_r$ and ${\mathcal{C}}_r^{*}$ are Adomian polynomials defined as:

  $$\left\{\begin{array}{c}{\mathcal{A}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_1\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},{\mathcal{A}}_r^{*}={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_2\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},\hfill \\ \\ {\mathcal{B}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_3\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},{\mathcal{B}}_r^{*}={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_4\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},\hfill \\ \\ {\mathcal{C}}_r={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_5\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0},{\mathcal{C}}_r^{*}={\displaystyle \frac{1}{r!}}{\displaystyle \frac{d^r}{d{\lambda }^r}}{N}_6\left(\sum _{i=0}^{\infty }{\lambda }^i{\mathrm{U}}_i\right){|}_{\lambda =0}.\hfill \end{array}\right.$$

  (39)
  From Equations (38) and (39) with ICs (6), Equation (37) becomes:

  $$\left\{\begin{array}{c}\mathcal{L}\left[\sum _{r=0}^{\infty }{U}_r(x,y,t)\right]=\frac{1}{s}{e}^{x+y}+\frac{1}{s^{\alpha }}\mathcal{L}[N_1-N_2-\sum _{r=0}^{\infty }{U}_r(x,y,t)],\hfill \\ \\ \mathcal{L}\left[\sum _{r=0}^{\infty }{V}_r(x,y,t)\right]=\frac{1}{s}{e}^{x-y}+\frac{1}{s^{\alpha }}\mathcal{L}[\sum _{r=0}^{\infty }{V}_r(x,y,t)-N_3-N_4],\hfill \\ \\ \mathcal{L}\left[\sum _{r=0}^{\infty }{W}_r(x,y,t)\right]=\frac{1}{s}{e}^{-x+y}+\frac{1}{s^{\alpha }}\mathcal{L}[\sum _{r=0}^{\infty }{W}_r(x,y,t)-N_5-N_6].\hfill \end{array}\right.$$

  (40)
  by apply the inverse Laplace transform to Equation (40), we get

  $$\left\{\begin{array}{c}{U}_{r+1}={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[{\mathcal{A}}_r-{\mathcal{A}}_r^{*}-U_r]\right],\hfill \\ \\ V_{r+1}={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[V_r-{\mathcal{B}}_r-{\mathcal{B}}_r^{*}]\right],\hfill \\ \\ W_{r+1}={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[W_r-{\mathcal{C}}_r-{\mathcal{C}}_r^{*}]\right],\hfill \end{array}\right.$$
  where

  $$\left\{\begin{array}{c}{U}_0=e^{x+y},\hfill \\ \\ V_0=e^{x-y},\hfill \\ \\ W_0=e^{-x+y}.\hfill \end{array}\right.$$
  Then, it follows that for the remaining terms we obtain the solution

  $$\left\{\begin{array}{c}{U}_1={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[{\mathcal{A}}_0-{\mathcal{A}}_0^{*}-U_0]\right]=-e^{x+y}{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}},\hfill \\ \\ V_1={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[V_0-{\mathcal{B}}_0-{\mathcal{B}}_0^{*}]\right]=e^{x-y}{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}},\hfill \\ \\ W_1={\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}[W_0-{\mathcal{C}}_0-{\mathcal{C}}_0^{*}]\right]=e^{-x+y}{\displaystyle \frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}.\hfill \end{array}\right.$$
  The other terms of $U_2,U_3,...,$ $V_2,V_3,...$ and $W_2,W_3,...,$ can be computed, respectively, in the same way and according to the ADM the solution is as follows:

  $$\begin{array}{cc}\hfill U(x,y,t)& =\underset{r\to \infty }{lim}{U}_r(x,y,t)=U_0+U_1+U_3+...,\hfill \\ \hfill V(x,y,t)& =\underset{r\to \infty }{lim}{V}_r(x,y,t)=V_0+V_1+V_3+...,\hfill \\ \hfill W(x,y,t)& =\underset{r\to \infty }{lim}{W}_r(x,y,t)=W_0+W_1+W_3+....\hfill \end{array}$$

The results in

Table 4. Values of approximate solutions obtained by MGMLFM, FNDM, exact solution, and absolute errors of U for system (5) with various values of $\alpha ,t,x$ and $y=0.4$.

x	t	$\mathit{\alpha }=0.75$		$\mathit{\alpha }=0.9$		$\mathit{\alpha }=1$		Exact	Absolute Error
		FNDM [49]	MGMLFM	FNDM [49]	MGMLFM	FNDM [49]	MGMLFM
0.5	0.3	1.6256	1.6241897	1.74178	1.74158	1.82217	1.8221189	1.82212	1.0285638$\times {10}^{-7}$
	0.6	1.27791	1.2607914	1.31047	1.3063996	1.35131	1.3498715	1.34986	1.27012$\times {10}^{-5}$
	0.9	1.10414	1.033497	1.02931	1.0058445	1.0105	1.00021	1	2.09565$\times {10}^{-4}$
1	0.3	2.68017	2.6778362	2.8717	2.871385	3.00424	3.0041662	3.00417	1.695815$\times {10}^{-7}$
	0.6	2.10692	2.0786935	2.1606	2.1538889	2.22793	2.225562	2.22554	2.09407$\times {10}^{-5}$
	0.9	1.82042	1.7039486	1.69705	1.6583572	1.66603	1.649067	1.64872	3.45514$\times {10}^{-4}$
1.5	0.3	4.41885	4.4150055	4.73464	4.7341143	4.95316	4.9530327	4.95303	2.7959262$\times {10}^{-7}$
	0.6	3.47372	3.4271863	3.56223	3.5511624	3.6323	3.6693312	3.6693	3.45253$\times {10}^{-5}$
	0.9	3.00136	2.809336	2.79796	2.7341689	2.74682	2.718851	2.71828	5.69657$\times {10}^{-4}$

,

Table 5. Values of approximate solutions obtained by MGMLFM, FNDM, exact solution, and absolute errors of V for system (5) with various values of $\alpha ,t,x$ and $y=0.4$.

x	t	$\mathit{\alpha }=0.75$		$\mathit{\alpha }=0.9$		$\mathit{\alpha }=1$		Exact	Absolute Error
		FNDM [49]	MGMLFM	FNDM [49]	MGMLFM	FNDM [49]	MGMLFM
0.5	0.3	1.76307	1.7638956	1.58084	1.5809426	1.4918	1.4918246	1.49182	4.9816688$\times {10}^{-8}$
	0.6	2.48848	2.5004130	2.17346	2.1758721	2.01296	2.0137461	2.01375	6.6314571$\times {10}^{-6}$
	0.9	3.40244	3.4604711	2.95156	2.9672968	2.71191	2.7181639	2.71828	1.17976$\times {10}^{-4}$
1	0.3	2.90682	2.9081722	2.60637	2.6065337	2.45956	2.4596030	2.4596	8.2133832$\times {10}^{-8}$
	0.6	4.10281	4.1224841	3.58343	3.5874066	3.31881	3.3201059	3.32012	1.0933424$\times {10}^{-5}$
	0.9	5.60968	5.7053523	4.86629	4.8922453	4.47118	4.4814946	4.48169	1.9450873$\times {10}^{-4}$
1.5	0.3	4.79253	4.7947653	4.29717	4.2974475	4.05514	4.0551998	4.0552	1.3541579$\times {10}^{-7}$
	0.6	6.76439	6.7968273	5.90808	5.9146336	5.47179	5.4739294	5.47395	1.8026169$\times {10}^{-5}$
	0.9	9.2488	9.4065356	8.02316	8.0659489	7.37174	7.3887354	7.38906	3.2069069$\times {10}^{-4}$

and

Table 6. Values of approximate solutions obtained by MGMLFM, FNDM, exact solution, and absolute errors of W for system (5) with various values of $\alpha ,t,x$ and $y=0.4$.

x	t	$\mathit{\alpha }=0.75$		$\mathit{\alpha }=0.9$		$\mathit{\alpha }=1$		Exact	Absolute Error
		FNDM [49]	MGMLFM	FNDM [49]	MGMLFM	FNDM [49]	MGMLFM
0.5	0.3	1.44348	1.4441556	1.29428	1.2943663	1.22138	1.2214027	1.2214	4.0786454$\times {10}^{-8}$
	0.6	2.0374	2.0471650	1.77948	1.7814534	1.64807	1.6487158	1.64872	5.4293779$\times {10}^{-6}$
	0.9	2.78569	2.8331941	2.41653	2.4294171	2.22032	2.2254443	2.22554	9.65902$\times {10}^{-5}$
1	0.3	0.875516	0.8759246	0.785023	0.7850729	0.740807	0.7408182	0.740818	2.4738235$\times {10}^{-8}$
	0.6	1.23574	1.2416684	1.07931	1.0805061	0.999606	0.9999967	1	3.2930841$\times {10}^{-6}$
	0.9	1.6896	1.7184191	1.4657	1.4735159	1.34669	1.3498002	1.34986	5.8584905$\times {10}^{-5}$
1.5	0.3	0.531027	0.5312751	0.47614	0.4761708	0.449322	0.4493289	0.449329	1.5004498$\times {10}^{-8}$
	0.6	0.749516	0.7531099	0.654634	0.6553601	0.606291	0.6065287	0.606531	1.9973565$\times {10}^{-6}$
	0.9	1.0248	1.0422739	0.888992	0.8937326	0.816812	0.8186952	0.818731	3.5533541$\times {10}^{-5}$

coincide with the exact solutions described in Equation (35) when $\alpha =1$. This confirms that the approximate solutions obtained by the MGMLFM are rapidly converging to the exact solutions and this is explained in the following tables.

In Figure 6, Figure 7, Figure 8, we compare the approximate solution obtained by the LADM for $U(x,y,t)$, $V(x,y,t)$, and $W(x,y,t)$ with the exact solution. Furthermore, Figure 9 represents the solutions obtained by the LADM for $U(x,y,t)$, $V(x,y,t)$, and $W(x,y,t)$ with various values of α, $y=0.4$ and $x=1$.

5. Conclusions

In this article, the MGMLFM and LADM were successfully used to find analytic-approximate solutions for the NFPDEs. Moreover, we focused on solving fractional-order Broer–Kaup and Burgers’ systems that arise in many physical applications, and displayed our contributions in tables and figures for different domains of $x,t$. The LADM and MGMLFM solutions were presented at different values of $\alpha$ and also for classical case (i.e., $\alpha =1$), which showed a highly coincide with the exact solutions for all considered problems. The analysis and computations confirmed that the approximate solutions offered by the MGMLFM and LADM had rapid convergence, required low computational cost, and provided highly accurate results compared to other analytical methods. Briefly, the obtained results together with their graphical simulations revealed the complete efficiency and accuracy of the proposed methods.

Our results motivate us to deal with other types of NFPDEs. For example, in the future, the used methods can be implemented to get the analytic-approximate solution for systems of NFPDEs that arise widely in the mathematical formulation of epidemiological models for different populations.