Stability of Generalized Proportional Caputo Fractional Differential Equations by Lyapunov Functions
Abstract
:1. Introduction
2. Notes on Fractional Calculus
3. Statement of the Problem
- Stable if for every , there exist such that for any , the inequality implies for ;
- Attractive if there exists such that for any with and for every , there exists such that for ;
- Asymptotically stable if the zero solution is stable and attractive.
4. Comparison Results
- 1.
- The function is a solution of (9) defined on , where , and is a given constant, ;
- 2.
- The function ;
- 3.
- The function ; the generalized proportional Caputo fractional derivative exists for any point , and the inequality:holds;
- 4.
- The function is the maximal solution of (11) on .Then, the inequality implies for
5. Main Result
6. Applications
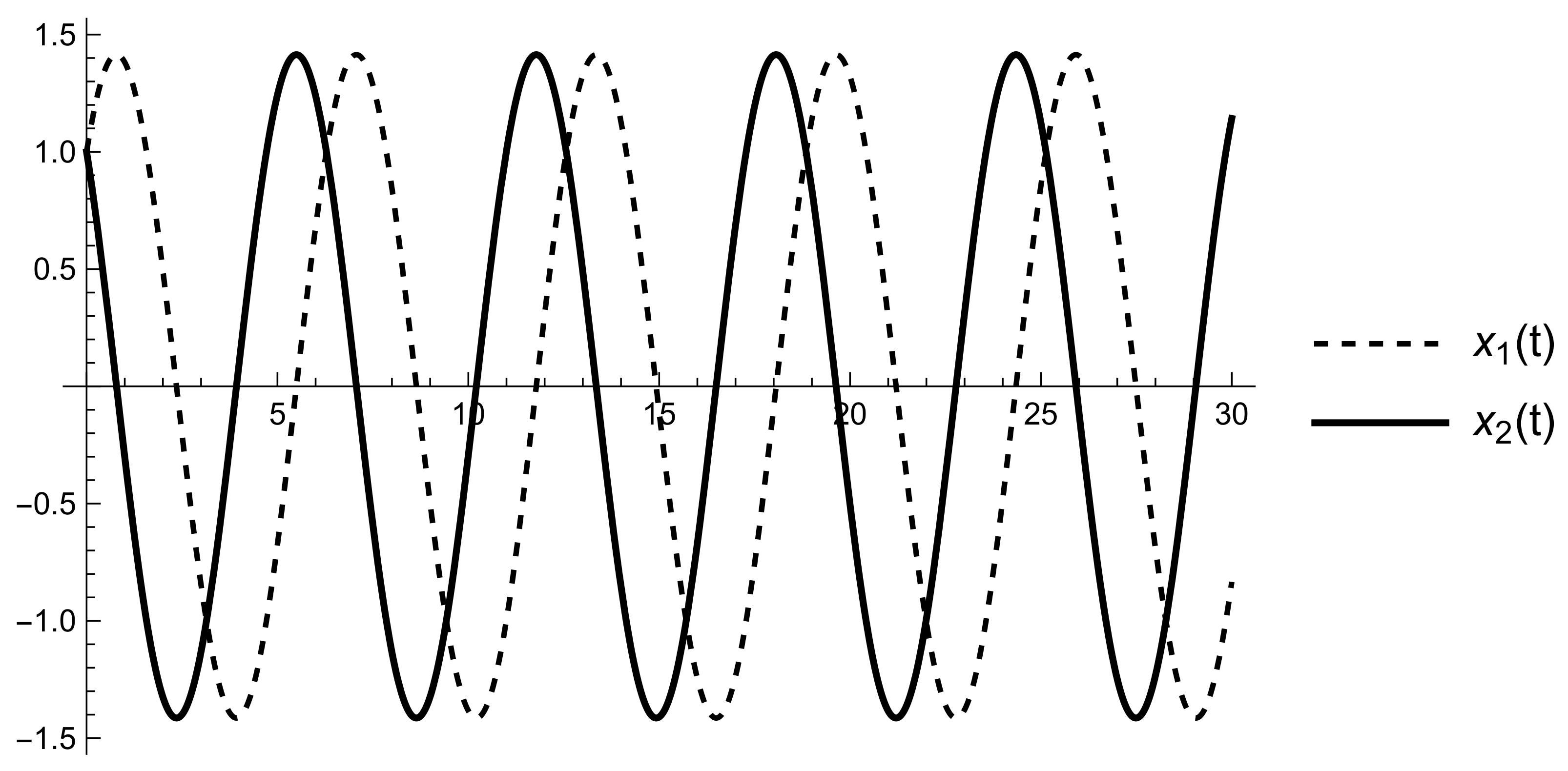
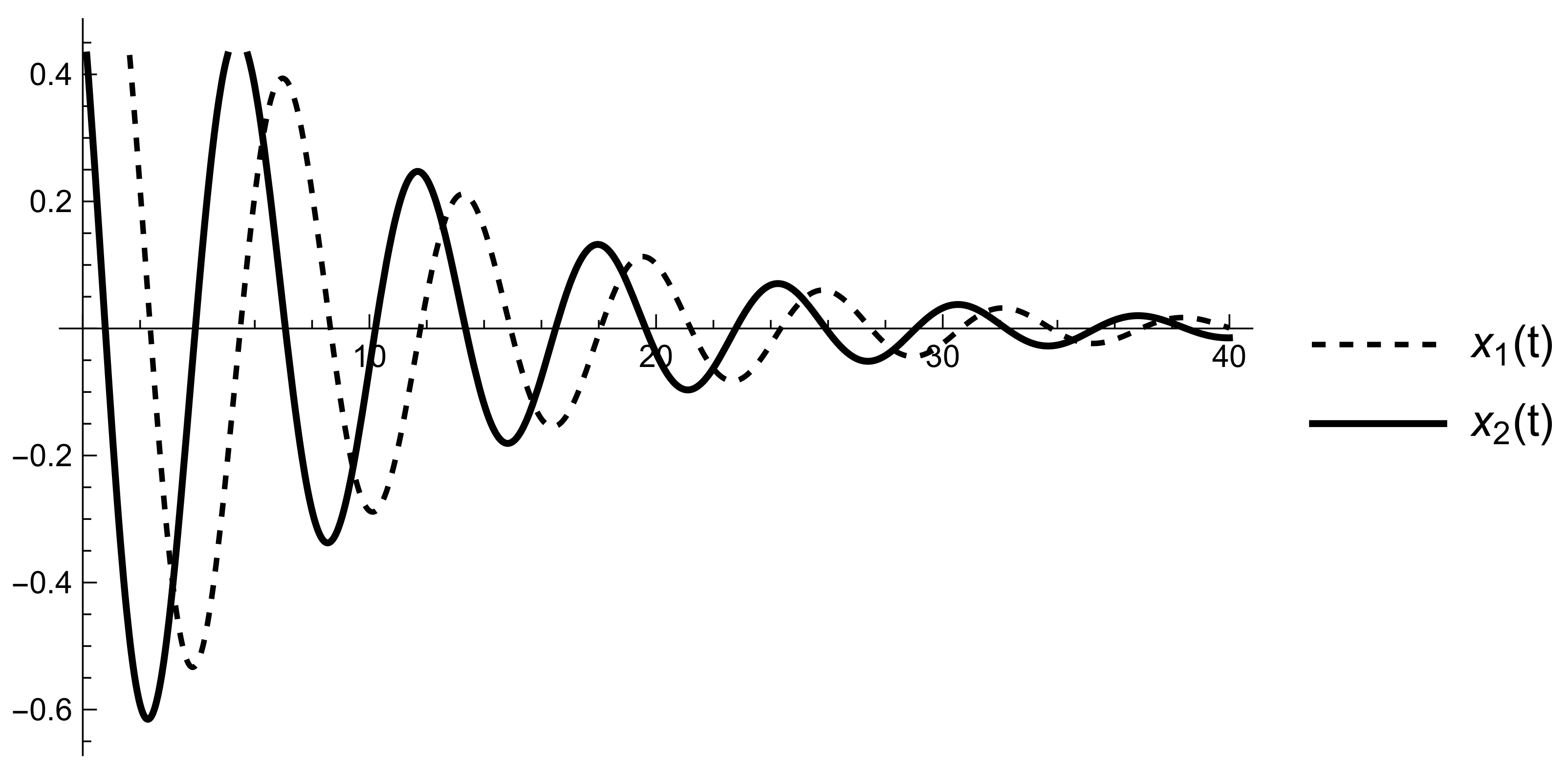
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Comm. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Burton, T.A. Fractional Differential equations and Lyapunov functionals. Nonlinear Anal. Theory Methods Appl. 2011, 74, 5648–5662. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Hu, J.B.; Lu, G.P.; Zhang, S.B.; Zhao, L.-D. Lyapunov stability theorem about fractional system without and with delay. Commun. Nonlinear Sci. Numer. Simulat. 2015, 20, 905–913. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef] [Green Version]
- Li, C.P.; Zhang, F.R. A survey on the stability of fractional differential equations. Eur. Phys. J. Spec. Top. 2011, 193, 27–47. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Alzabut, J. Generalized fractional derivatives generated by a class of local proportional derivatives. Eur. Phys. J. Spec. Top. 2017, 226, 3457–3471. [Google Scholar] [CrossRef]
- Abbas, M.I.; Ragusa, M.A. On the hybrid fractional differential equations with fractional proportional derivatives of a function with respect to a certain function. Symmetry 2021, 13, 264. [Google Scholar] [CrossRef]
- Alzabut, J.; Abdeljawad, T.; Jarad, F.; Sudsutad, W. A Gronwall inequality via the generalized proportional fractional derivative with applications. J. Ineq. Appl. 2019, 2019, 101. [Google Scholar] [CrossRef] [Green Version]
- Hristova, S.; Abbas, M.I. Explicit solutions of initial-value problems for fractional generalized proportional differential equations with and without impulses. Symmetry 2021, 13, 996. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discret. Contin. Dyn. Syst.-S 2020, 13, 709–722. [Google Scholar] [CrossRef] [Green Version]
- Laadjal, Z.; Abdeljawad, T.; Jarad, F. On existence-uniqueness results for proportional fractional differential equations and incomplete gamma functions. Adv. Differ. Equ. 2020, 2020, 641. [Google Scholar] [CrossRef]
- Almeida, R.; Agarwal, R.P.; Hristova, S.; O’Regan, D. Quadratic Lyapunov functions for stability of generalized proportional fractional differential equations with applications to neural networks. Axioms 2021, 10, 322. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo Derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Mustafa, O.G. On the global existence of solutions to a class of fractional differential equations. Comput. Math. Appl. 2010, 59, 1835–1841. [Google Scholar] [CrossRef] [Green Version]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Philadelphia, PA, USA, 1993. [Google Scholar]
- Abbas, M.I.; Hristova, S. Existence results of nonlinear generalized proportional fractional differential inclusions via the diagonalization technique. AIMS Math. 2021, 6, 12832–12844. [Google Scholar] [CrossRef]
- Abbas, M.I.; Hristova, S. On the Initial Value Problems for Caputo-Type Generalized Proportional Vector-Order Fractional Differential Equations. Mathematics 2021, 9, 2720. [Google Scholar] [CrossRef]
- Simon, T. Mittag–Leffler functions and complete monotonicity. Integral Transf. Spec. 2015, 26, 36–50. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarwal, R.; Hristova, S.; O’Regan, D. Stability of Generalized Proportional Caputo Fractional Differential Equations by Lyapunov Functions. Fractal Fract. 2022, 6, 34. https://doi.org/10.3390/fractalfract6010034
Agarwal R, Hristova S, O’Regan D. Stability of Generalized Proportional Caputo Fractional Differential Equations by Lyapunov Functions. Fractal and Fractional. 2022; 6(1):34. https://doi.org/10.3390/fractalfract6010034
Chicago/Turabian StyleAgarwal, Ravi, Snezhana Hristova, and Donal O’Regan. 2022. "Stability of Generalized Proportional Caputo Fractional Differential Equations by Lyapunov Functions" Fractal and Fractional 6, no. 1: 34. https://doi.org/10.3390/fractalfract6010034
APA StyleAgarwal, R., Hristova, S., & O’Regan, D. (2022). Stability of Generalized Proportional Caputo Fractional Differential Equations by Lyapunov Functions. Fractal and Fractional, 6(1), 34. https://doi.org/10.3390/fractalfract6010034







