Scale-Agnostic Models Based on Dimensionless Quality by Design as Pharmaceutical Development Accelerator
Abstract
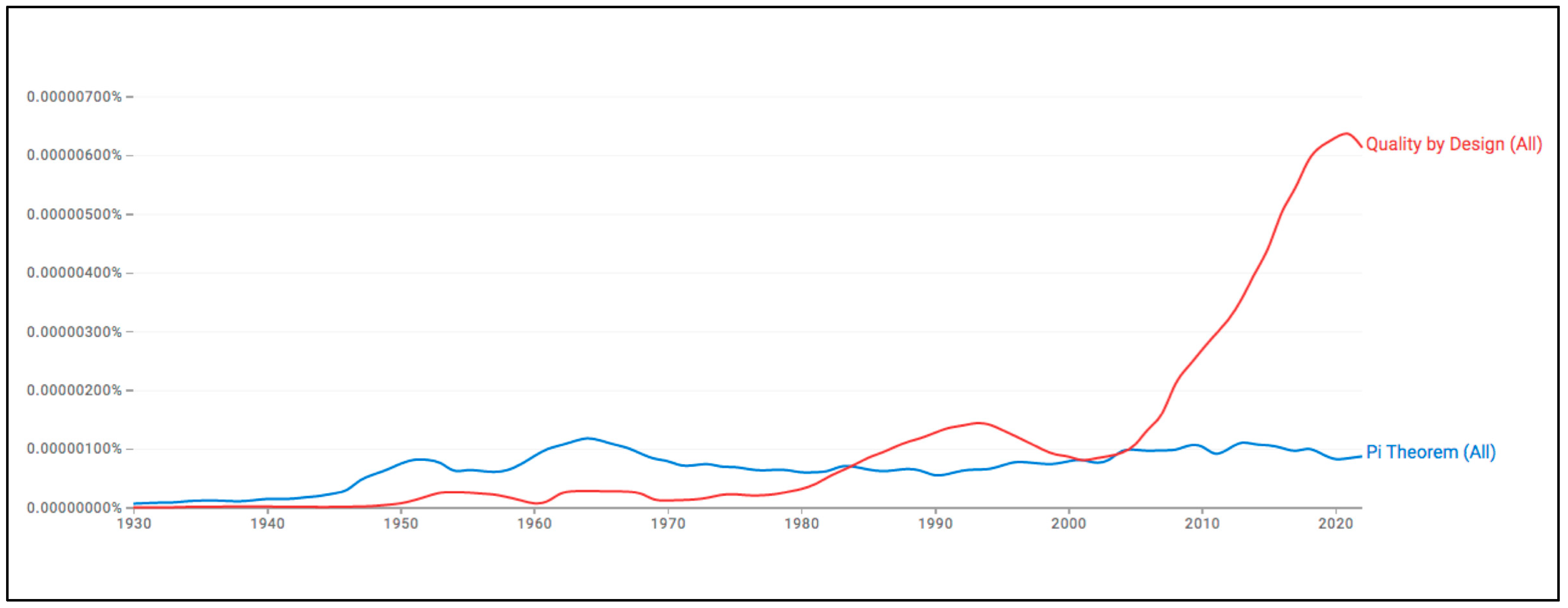
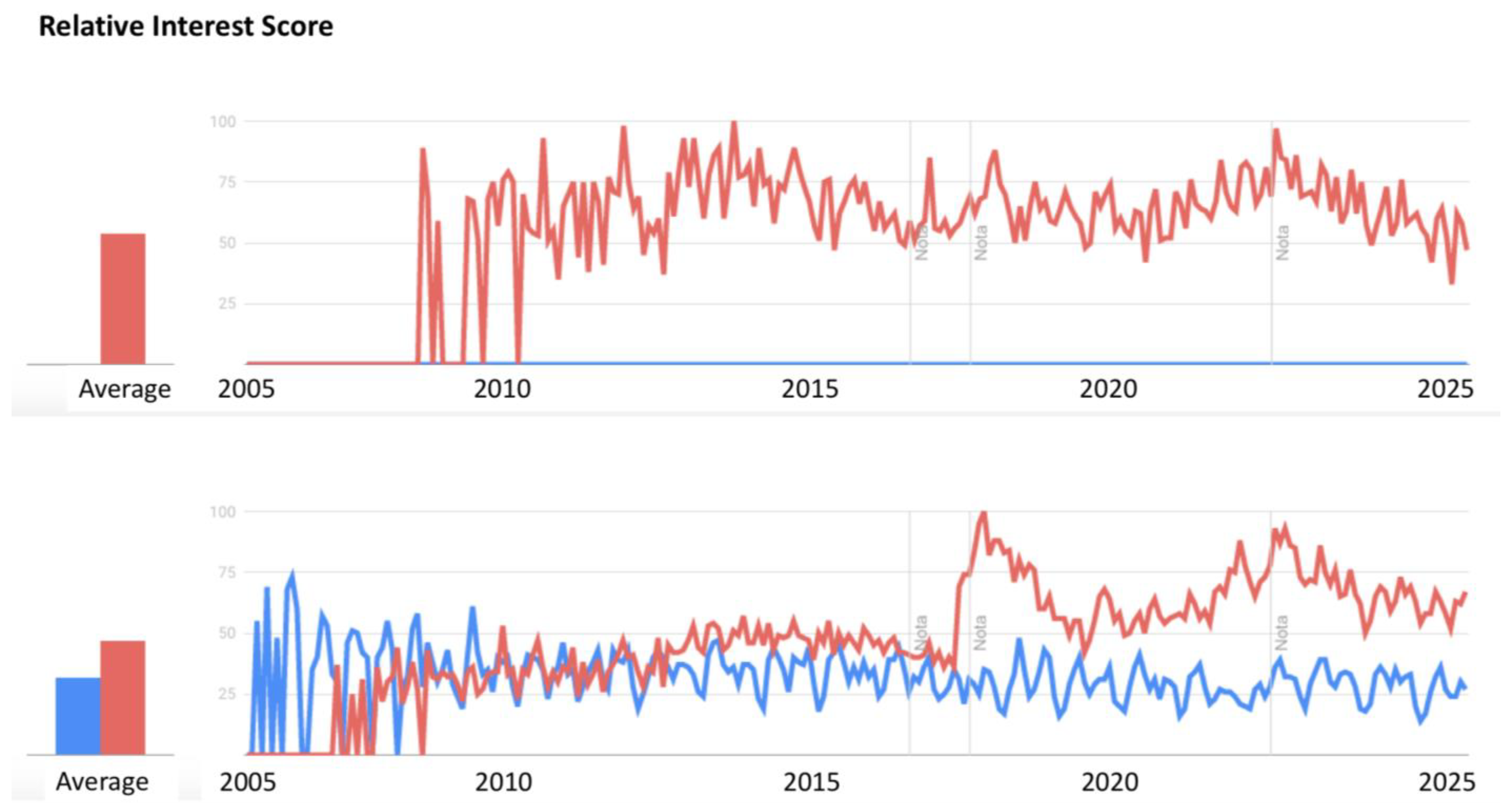
1. Advantages and Opportunities of Combining Quality by Design with the Pi–Buckingham Theorem
2. State of the Art in the Pharmaceutical Industry and Other Sectors
3. Traditional QbD Framework
3.1. Key Elements of QbD
3.2. Risk Assessment
3.3. Experimental Design
3.4. Design Space Definition and Process Optimization
3.5. Monitoring and Continuous Improvement
4. Pi–Buckingham Theorem
4.1. Applications in Physics and Engineering
4.2. Conceptual Pi–Buckingham Theorem Framework
4.3. Use Case Examples
4.3.1. Tablet Coating in a Conventional Pan Coating System
4.3.2. Bioprocess Scaling Up
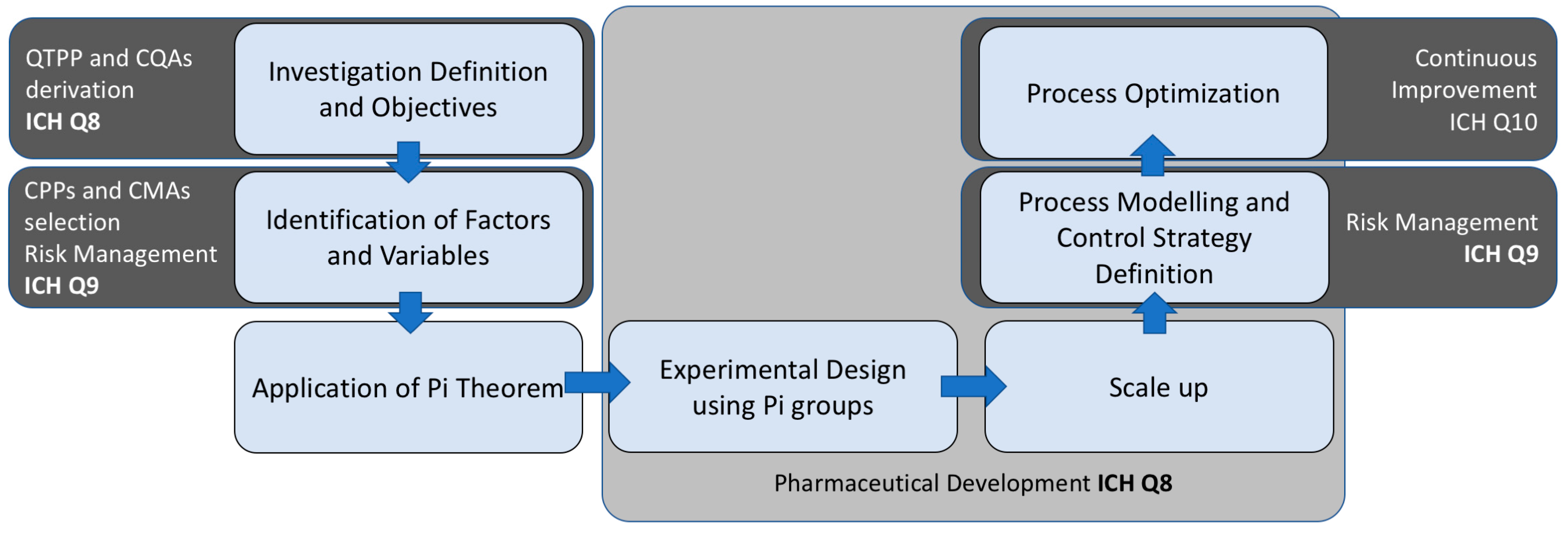
5. Synergistic Use of QbD and Buckingham Pi Theorem
6. Enhancing Product Development Through Synergy
6.1. Benefits
6.2. Challenges and Considerations
6.3. Continuous Improvement and Adaptability
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AQbD | Analytical Quality by Design |
| CMA | Critical Material Attributes |
| CPP | Critical Process Parameters |
| CQA | Critical Quality Attributes |
| DoE | Design of Experiments |
| DS | Design Space |
| EMA | European Medicines Agency |
| FDA | Food and Drug Administration |
| FMEA | Failure Mode and Effects Analysis |
| ICH | International Council for Harmonization |
| PAT | Process Analytical Technology |
| QbD | Quality by Design |
| QTPP | Quality Target Product Profile |
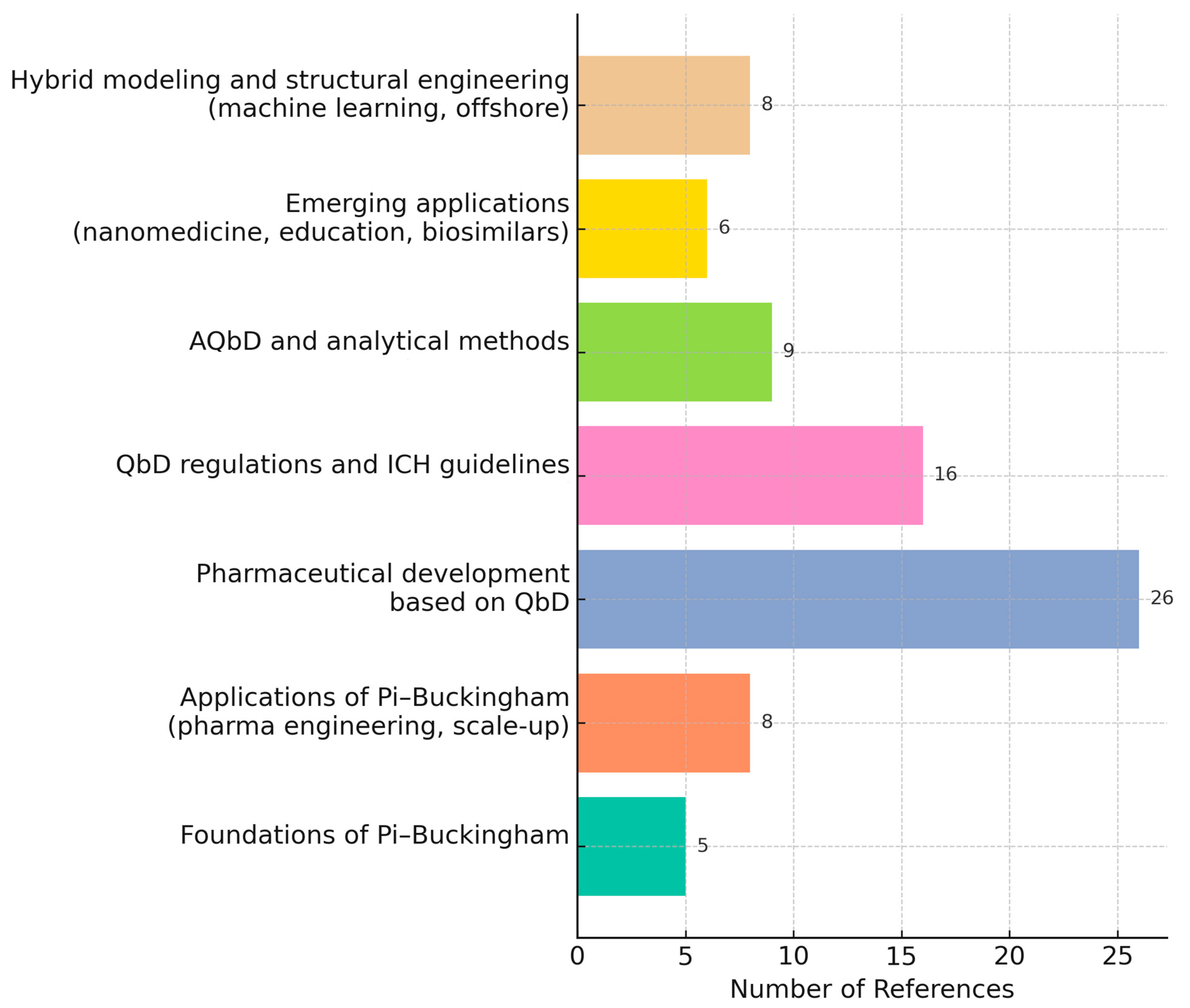
References
- Wang, Z.; Escotet-Espinoza, M.S.; Ierapetritou, M. Process Analysis and Optimization of Continuous Pharmaceutical Manufacturing Using Flowsheet Models. Comput. Chem. Eng. 2017, 107, 77–91. [Google Scholar] [CrossRef]
- Shen, W.; Davis, T.; Lin, D.K.J.; Nachtsheim, C.J. Dimensional Analysis and Its Applications in Statistics. J. Qual. Technol. 2014, 46, 185–198. [Google Scholar] [CrossRef]
- Dilip Bhoir, A.; Mohire, N.C.; Vite, M.H.; Bhoir, J.P.; Pharm, B. A Review on Quality by Design. IJFMR Int. J. Multidiscip. Res. 2023, 5, IJFMR230610684. [Google Scholar] [CrossRef]
- Barrera Jiménez, A.A.; Matsunami, K.; Ghijs, M.; Van Hauwermeiren, D.; Peeters, M.; Stauffer, F.; De Beer, T.; Nopens, I. Model Development and Calibration of Two-Dimensional Population Balance Model for Twin-Screw Wet Granulation Based on Particle Size Distribution and Porosity. Powder Technol. 2023, 419, 118334. [Google Scholar] [CrossRef]
- Bano, G.; Wang, Z.; Facco, P.; Bezzo, F.; Barolo, M.; Ierapetritou, M. A Novel and Systematic Approach to Identify the Design Space of Pharmaceutical Processes. Comput. Chem. Eng. 2018, 115, 309–322. [Google Scholar] [CrossRef]
- International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use. ICH Harmonised Tripartite Guideline. Pharmaceutical Development Q8 (R2). 2009. Available online: https://database.ich.org/sites/default/files/Q8_R2_Guideline.pdf (accessed on 7 July 2025).
- International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use. ICH Harmonised Tripartite Guideline. Development and Manufacture of Drug Substances (Chemical Entities and Biotechnological/Biological Entities) Q11. 2012. Available online: https://database.ich.org/sites/default/files/Q11%20Guideline.pdf (accessed on 7 July 2025).
- European Medicines Agency. Quality by Design. Available online: https://www.ema.europa.eu/en/human-regulatory-overview/research-development/quality-design (accessed on 11 May 2025).
- Juran, J.M. Juran on Quality by Design: The New Steps for Planning Quality into Goods and Services; Free Press: New York, NY, USA; Maxwell Macmillan Canada: Toronto, ON, Canada; Maxwell Macmillan International: New York, NY, USA, 1992. [Google Scholar]
- Mallikarjun, P.N.; Kumari, P.; Kumar, S.M.; Sowmya, G. An Overview on Quality by Design in Pharmaceutical Product Development. J. Chem. Health Risks 2025, 15, 326–332. [Google Scholar] [CrossRef]
- Cong, P.; Wang, J. Suggestion of a New Dimensionless Number for Predicting the Dynamic Response of Structures Subjected to Impact Loading. Structures 2024, 64, 106604. [Google Scholar] [CrossRef]
- Patil, D.R.; Patil, D.K.; Patil, S.A. A Review on Quality by Design. Res. J. Pharmacol. Pharmacodyn. 2024, 16, 119–122. [Google Scholar] [CrossRef]
- Wanegaonkar, A.M.; Chaudhari, M.; Jadhav, K.R.; Kadam, V.J. Quality by Design: An Over View in Pharma Industry. Res. J. Pharm. Technol. 2024, 17, 3492–3498. [Google Scholar] [CrossRef]
- Jones, J.; Zhang, B.; Zhang, X.; Konings, P.; Hansson, P.; Backmark, A.; Serrano, A.; Künzel, U.; Novick, S. Quality by Design for Preclinical In Vitro Assay Development. Pharm. Stat. 2024, 24, e2430. [Google Scholar] [CrossRef]
- Aru, P.B.; Gulhane, M.S.; Katekar, V.A.; Deshmukh, S.P. Corresponding Author: Pratik B. Aru Quality by Design (QbD) in Pharmaceutical Development: A Comprehensive Review. GSC Biol. Pharm. Sci. 2024, 2024, 328–340. [Google Scholar] [CrossRef]
- Murari, A.; Spolladore, L.; Rossi, R.; Gelfusa, M. Combining Dimensional and Statistical Analysis for Efficient Data Driven Modelling of Complex Systems. Inf. Sci. 2023, 644, 119243. [Google Scholar] [CrossRef]
- Raikwar, A. Quality By Design: Concept and Applications. Int. J. Pharma Prof. Res. (IJPPR) 2023, 14, 109–123. [Google Scholar] [CrossRef]
- Patil, H.D.; Patil, C.B.; Patil, V.V.; Patil, P.S. An Overview on Quality by Design. Asian J. Res. Pharm. Sci. 2023, 13, 49–55. [Google Scholar] [CrossRef]
- Chiarentin, L.; Gonçalves, C.; Augusto, C.; Miranda, M.; Cardoso, C.; Vitorino, C. Drilling into “Quality by Design” Approach for Analytical Methods. Crit. Rev. Anal. Chem. 2023, 54, 3478–3519. [Google Scholar] [CrossRef] [PubMed]
- Sanjay, V.D.; Sanjay, N.T.; Bandal, R.S.; Jadhav, S.G. Quality by Design Approach-to Analytical Method Validation. IJFMR Int. J. Multidiscip. Res. 2023, 5, IJFMR23021903. [Google Scholar] [CrossRef]
- Mehrotra, S.; Salwa; Kumar, L. Implementation of Quality by Design in the Formulation and Development of Nanocarrier-Based Drug Delivery Systems. Crit. Rev. Trade Ther. Drug Carr. Syst. 2023, 40, 1–46. [Google Scholar] [CrossRef]
- Pawar, S.S.; Mahale, Y.S.; Kalamkar, P.A.; Satdive, R.A.; Sonawane, S.K.; Bhapkar, S.P. Quality by Design (QbD): A Comprehensive Understanding and Implementation in Pharmaceuticals Development. Curr. Pharm. Anal. 2023, 19, 677–686. [Google Scholar] [CrossRef]
- Savitha, S.; Devi, K. Quality By Design: A Review. J. Drug Deliv. Ther. 2022, 12, 234–239. [Google Scholar] [CrossRef]
- Xie, X.; Samaei, A.; Guo, J.; Liu, W.K.; Gan, Z. Data-Driven Discovery of Dimensionless Numbers and Governing Laws from Scarce Measurements. Nat. Commun. 2022, 13, 7562. [Google Scholar] [CrossRef]
- Daniel, S.; Kis, Z.; Kontoravdi, C.; Shah, N. Quality by Design for Enabling RNA Platform Production Processes. Trends Biotechnol. 2022, 40, 1213–1228. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Henríquez, L.; Murillo-Castillo, B.; Chaves-Siles, L.; Mora-Román, J.J.; Ramírez-Arguedas, N.; Hernández-Mora, É.; Vega-Baudrit, J. Quality by Design: A Suitable Methodology in Industrial Pharmacy for Costa Rican Universities. Sci. Pharm. 2022, 90, 34. [Google Scholar] [CrossRef]
- Alshaer, W.; Nsairat, H.; Lafi, Z.; Hourani, O.M.; Al-Kadash, A.; Esawi, E.; Alkilany, A.M. Quality by Design Approach in Liposomal Formulations: Robust Product Development. Molecules 2022, 28, 10. [Google Scholar] [CrossRef] [PubMed]
- Katekar, V.; Sangule, D.; Bhurbhure, O.; Ingle, P.; Dhage, S.; Jadhav, K. A Review on Quality by Design Approach in Analytical Methods. J. Drug Deliv. Ther. 2022, 12, 255–261. [Google Scholar] [CrossRef]
- Jagtap, K.; Chaudhari, B.; Redasani, V. Quality by Design (QbD) Concept Review in Pharmaceuticals. Asian J. Res. Chem. 2022, 15, 303–307. [Google Scholar] [CrossRef]
- Zlota, A.A. Recommendations for Effective and Defendable Implementation of Quality by Design. Org. Process Res. Dev. 2021, 26, 899–914. [Google Scholar] [CrossRef]
- Choo, M.J.; Kim, J.Y.; Chow, S.-C.; Lee, S.J. Methodologies in Biosimilar Product Development; Chapter: Quality by Design; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021; ISBN 9781003205807. [Google Scholar]
- Choudhary, V. Design and Conduct of Clinical Studies by Integration of Quality by Design (QbD) into Quality Management System (QMS)—A Pragmatic Approach. Clin. Res. Open Access 2021, 7, 1–6. [Google Scholar] [CrossRef]
- Rajora, A.; Chhabra, G. Quality by Design Approach: Regulatory Need, Current, and Future Perspective. Asian J. Pharm. Clin. Res. 2021, 14, 29–35. [Google Scholar] [CrossRef]
- Ramalinagm, P.; Basha, S.; Bhaddraya, K.; Beg, S. Risk assessment and design space consideration in analytical quality by design. In Handbook of Analytical Quality by Design; Beg, S., Hasnain, M.S., Rahman, M., Almalki, W.H., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 167–189. [Google Scholar] [CrossRef]
- Rendón-Castrillón, L.; Ramírez-Carmona, M.; Ocampo-López, C.; Gómez-Arroyave, L. Mathematical Model for Scaling up Bioprocesses Using Experiment Design Combined with Buckingham Pi Theorem. Appl. Sci. 2021, 11, 11338. [Google Scholar] [CrossRef]
- Grangeia, H.B.; Silva, C.; Simões, S.P.; Reis, M.S. Quality by Design in Pharmaceutical Manufacturing: A Systematic Review of Current Status, Challenges and Future Perspectives. Eur. J. Pharm. Biopharm. 2020, 147, 19–37. [Google Scholar] [CrossRef]
- Kalyane, D.; Raval, N.; Polaka, S.; Tekade, R.K. Quality by Design as an Emerging Concept in the Development of Pharmaceuticals. In The Future of Pharmaceutical Product Development and Research; Academic Press: Cambridge, MA, USA, 2020; pp. 1–25. [Google Scholar] [CrossRef]
- Lloyd, D.K.; Bergum, J.; Wang, Q. Application of Quality by Design to the Development and Validation of Analytical Methods. In Specification of Drug Substances and Products: Development and Validation of Analytical Methods, Second Edition; Elsevier: Amsterdam, The Netherlands, 2020; pp. 59–99. [Google Scholar] [CrossRef]
- Zsófia, N.; Dorina, D.; Edina, P.; Ildikó, C. Quality by Design-Based Approach to Liposomal Development. Symp. Young Res. Pharm. Technol. Biotechnol. Regul. Sci. 2020, 2, 13. [Google Scholar] [CrossRef]
- Shirazian, S.; Ismail, H.Y.; Singh, M.; Shaikh, R.; Croker, D.M.; Walker, G.M. Multi-Dimensional Population Balance Modelling of Pharmaceutical Formulations for Continuous Twin-Screw Wet Granulation: Determination of Liquid Distribution. Int. J. Pharm. 2019, 566, 352–360. [Google Scholar] [CrossRef] [PubMed]
- Saint-Marcoux, J.F. Dimensionless Numbers as an Effective Tool for Validation & Verification. In Proceedings of the Annual Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar] [CrossRef]
- Purohit, D.; Saini, M.; Pandey, P.; Tripathy, S.; Dureja, H. Implementation of Quality by Design: A Review. Appl. Clin. Res. Clin. Trials Regul. Aff. 2019, 6, 99–111. [Google Scholar] [CrossRef]
- Kengar, D.M.; Tamboli, A.J.; Magdum, S.C. Quality by Design—A Review. PharmaTutor 2019, 7, 48–51. [Google Scholar]
- Sarwar, B.; Hasnain, M.S. Introduction to Quality by Design (QbD): Fundamentals, Principles, and Applications. In Pharmaceutical Quality by Design: Principles and Applications; Beg, S., Hasnain, M.S., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 1–17. ISBN 978-0-12-815799-2. [Google Scholar]
- Swain, S.; Parhi, R.; Jena, B.R.; Babu, S.M. Quality by Design: Concept to Applications. Curr. Drug Discov. Technol. 2018, 16, 240–250. [Google Scholar] [CrossRef]
- Nayak, A.K.; Ahmed, S.A.; Beg, S.; Tabish, M.; Hasnain, M.S. Application of Quality by Design for the Development of Biopharmaceuticals. In Pharmaceutical Quality by Design; Academic Press: Cambridge, MA, USA, 2019; pp. 399–411. [Google Scholar] [CrossRef]
- Girija, D.; Venkateswara Reddy, B.; Siva Krishna, C.; Kalyan kumar, R.; Lakshmi, G.; Mahesh, S. Emerging Achievements of Quality by Design in Pharmaceutical Industry. WJPLS World J. Pharm. Life Sci. 2019, 5, 208–213. [Google Scholar]
- Deepak Kumar, D.; Ancheria, R.; Shrivastava, S.; Soni, S.L.; Sharma, M. Review on Pharmaceutical Quality by Design (QbD). Asian J. Pharm. Res. Dev. 2019, 7, 78–82. [Google Scholar] [CrossRef]
- Sachin, L.D. A Review on Quality by Design. Int. J. Pharm. Chem. Anal. 2020, 5, 1–6. [Google Scholar] [CrossRef]
- Nagaich, U. Pharmaceutical “Quality by Design” Approach. J. Adv. Pharm. Technol. Res. 2018, 9, 1. [Google Scholar] [CrossRef]
- FDA. FDA Report from the EMA-FDA QbD Pilot Program. 2017. Available online: https://www.fda.gov/media/104371/download (accessed on 7 July 2025).
- Barhate, C.L.; Regalado, E.L.; Contrella, N.D.; Lee, J.; Jo, J.; Makarov, A.A.; Armstrong, D.W.; Welch, C.J. Ultrafast Chiral Chromatography as the Second Dimension in Two-Dimensional Liquid Chromatography Experiments. Anal. Chem. 2017, 89, 3545–3553. [Google Scholar] [CrossRef]
- Hazyuk, I.; Budinger, M.; Sanchez, F.; Gogu, C. Optimal Design of Computer Experiments for Surrogate Models with Dimensionless Variables. Struct. Multidiscip. Optim. 2017, 56, 663–679. [Google Scholar] [CrossRef]
- Zhang, L.; Mao, S. Application of Quality by Design in the Current Drug Development. Asian J. Pharm. Sci. 2017, 12, 1–8. [Google Scholar] [CrossRef]
- Sangshetti, J.N.; Deshpande, M.; Zaheer, Z.; Shinde, D.B.; Arote, R. Quality by Design Approach: Regulatory Need. Arab. J. Chem. 2017, 10, S3412–S3425. [Google Scholar] [CrossRef]
- Niblett, D.; Porter, S.; Reynolds, G.; Morgan, T.; Greenamoyer, J.; Hach, R.; Sido, S.; Karan, K.; Gabbott, I. Development and Evaluation of a Dimensionless Mechanistic Pan Coating Model for the Prediction of Coated Tablet Appearance. Int. J. Pharm. 2017, 528, 180–201. [Google Scholar] [CrossRef]
- Mogal, V.; Dusane, J.; Borase, P.; Thakare, P.; Khirsagar, S.J. A Review on Quality by Design. Pharm. Biol. Eval. 2016, 3, 313–319. [Google Scholar]
- Chavan, S.D.; Pimpodkar, N.V.; Kadam, A.S.; Gaikwad, P.S. Quality by Design. Asian J. Res. Pharm. Sci. 2016, 6, 45–50. [Google Scholar] [CrossRef][Green Version]
- Yu, L.X.; Amidon, G.; Khan, M.A.; Hoag, S.W.; Polli, J.; Raju, G.K.; Woodcock, J. Understanding Pharmaceutical Quality by Design. AAPS J. 2014, 16, 771–783. [Google Scholar] [CrossRef]
- Bala, I.; Verma, S.; Namdev, K.K. A Review on Process Variables Effects of an Oral Dosage Form by Using “Quality by Design”. Int. J. Drug Deliv. Technol. 2014, 5, 1–14. [Google Scholar] [CrossRef][Green Version]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Riabouchinsky, D. Méthode Des Variables de Dimension Zéro, et Son Application En Aérodynamique; L’Aérophile: Chantilly, France, 1911. [Google Scholar]
- Vaschy, A. Sur Les Lois de Similitude En Physique. Ann. Télégraphiques 1892, 19, 25–28. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero-Obon, M.; Sancho-Ochoa, V.; Rouaz-El-Hajoui, K.; Pérez-Lozano, P.; Suñé-Pou, M.; Suñé-Negre, J.M.; García-Montoya, E. Scale-Agnostic Models Based on Dimensionless Quality by Design as Pharmaceutical Development Accelerator. Pharmaceuticals 2025, 18, 1033. https://doi.org/10.3390/ph18071033
Romero-Obon M, Sancho-Ochoa V, Rouaz-El-Hajoui K, Pérez-Lozano P, Suñé-Pou M, Suñé-Negre JM, García-Montoya E. Scale-Agnostic Models Based on Dimensionless Quality by Design as Pharmaceutical Development Accelerator. Pharmaceuticals. 2025; 18(7):1033. https://doi.org/10.3390/ph18071033
Chicago/Turabian StyleRomero-Obon, Miquel, Virginia Sancho-Ochoa, Khadija Rouaz-El-Hajoui, Pilar Pérez-Lozano, Marc Suñé-Pou, Josep María Suñé-Negre, and Encarna García-Montoya. 2025. "Scale-Agnostic Models Based on Dimensionless Quality by Design as Pharmaceutical Development Accelerator" Pharmaceuticals 18, no. 7: 1033. https://doi.org/10.3390/ph18071033
APA StyleRomero-Obon, M., Sancho-Ochoa, V., Rouaz-El-Hajoui, K., Pérez-Lozano, P., Suñé-Pou, M., Suñé-Negre, J. M., & García-Montoya, E. (2025). Scale-Agnostic Models Based on Dimensionless Quality by Design as Pharmaceutical Development Accelerator. Pharmaceuticals, 18(7), 1033. https://doi.org/10.3390/ph18071033










