Dissolution Thermodynamics of the Solubility of Sulfamethazine in (Acetonitrile + 1-Propanol) Mixtures
Abstract
1. Introduction

2. Results and Discussion
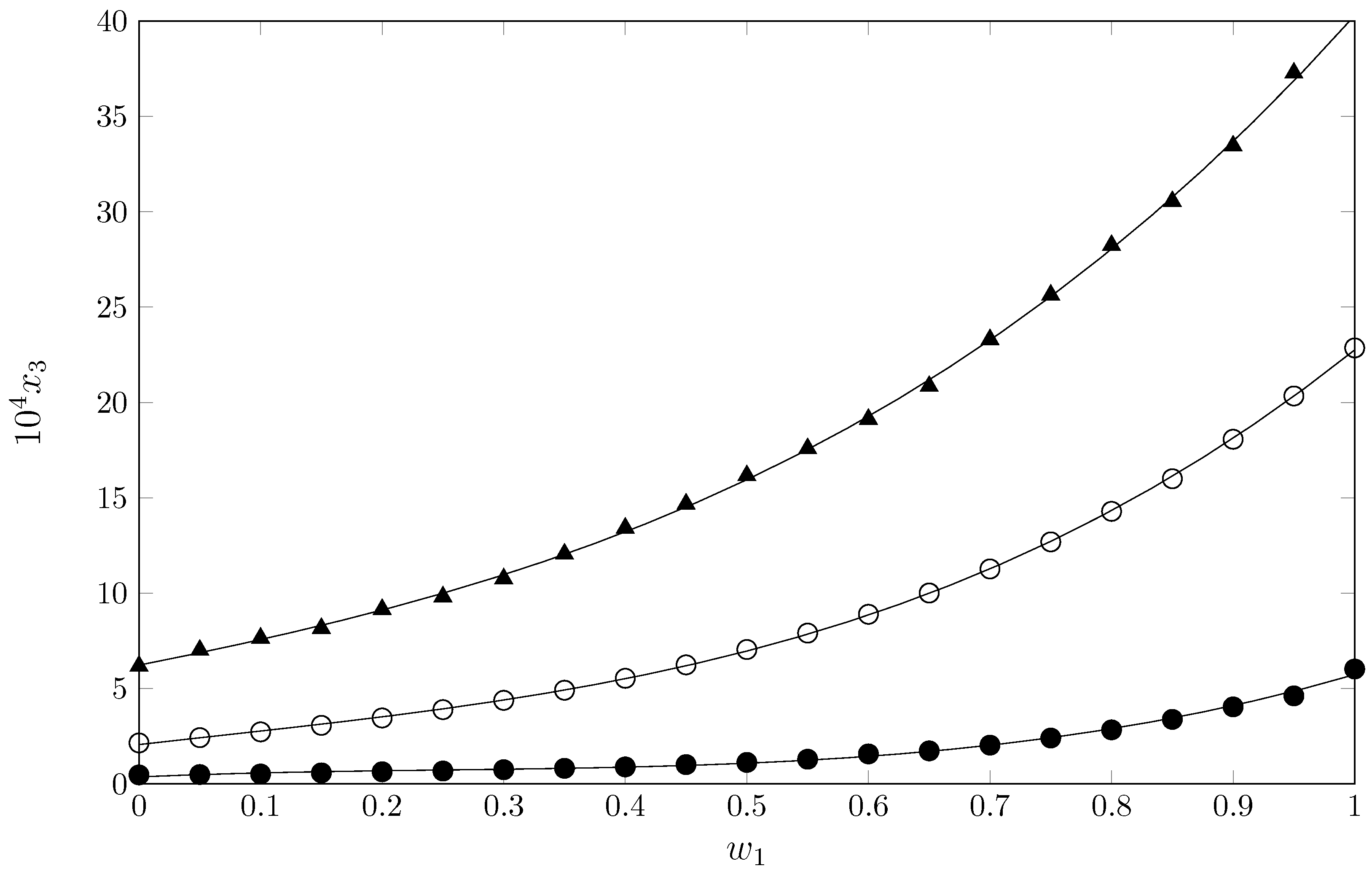
2.1. Experimental Mole Fraction Solubility
| w1 a,b | Temperature/K b | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 278.15 | 283.15 | 288.15 | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | |
| 0.00 | 3.17 | 3.75 | 4.42 | 5.32 | 6.18 | 7.08 | 8.40 | 10.1 | 11.5 |
| 0.05 | 3.51 | 4.14 | 4.93 | 5.95 | 7.01 | 7.94 | 9.46 | 11.3 | 13.0 |
| 0.10 | 3.82 | 4.52 | 5.40 | 6.50 | 7.65 | 8.65 | 10.4 | 12.4 | 14.3 |
| 0.15 | 4.20 | 4.97 | 5.87 | 7.13 | 8.16 | 9.56 | 11.4 | 13.7 | 15.9 |
| 0.20 | 4.54 | 5.46 | 6.49 | 7.82 | 9.15 | 10.6 | 12.5 | 15.1 | 17.4 |
| 0.25 | 4.93 | 5.93 | 7.06 | 8.47 | 9.81 | 11.7 | 13.9 | 16.6 | 19.3 |
| 0.30 | 5.42 | 6.45 | 7.69 | 9.28 | 10.8 | 12.8 | 15.3 | 18.4 | 21.2 |
| 0.35 | 5.89 | 7.08 | 8.49 | 10.3 | 12.1 | 14.2 | 16.8 | 20.2 | 23.4 |
| 0.40 | 6.45 | 7.72 | 9.28 | 11.1 | 13.4 | 15.8 | 18.5 | 22.4 | 25.9 |
| 0.45 | 6.96 | 8.51 | 10.1 | 12.2 | 14.7 | 17.2 | 20.4 | 24.5 | 28.5 |
| 0.50 | 7.69 | 9.15 | 11.2 | 13.4 | 16.2 | 19.0 | 22.4 | 26.9 | 31.4 |
| 0.55 | 8.31 | 10.1 | 12.2 | 14.9 | 17.6 | 21.0 | 24.7 | 29.7 | 35.0 |
| 0.60 | 9.05 | 11.0 | 13.4 | 16.1 | 19.1 | 23.6 | 27.3 | 32.8 | 38.4 |
| 0.65 | 9.91 | 12.0 | 14.5 | 17.3 | 20.9 | 25.6 | 30.0 | 36.0 | 42.2 |
| 0.70 | 10.8 | 13.2 | 16.1 | 19.1 | 23.3 | 28.4 | 33.2 | 40.0 | 46.6 |
| 0.75 | 11.7 | 14.4 | 17.6 | 21.0 | 25.6 | 30.1 | 36.0 | 43.7 | 51.5 |
| 0.80 | 13.0 | 15.6 | 19.0 | 23.6 | 28.2 | 34.1 | 40.4 | 48.0 | 57.1 |
| 0.85 | 14.0 | 17.1 | 20.8 | 25.7 | 30.5 | 36.9 | 44.1 | 53.1 | 62.8 |
| 0.90 | 15.1 | 18.8 | 23.0 | 27.8 | 33.5 | 40.5 | 48.9 | 58.5 | 68.3 |
| 0.95 | 16.7 | 20.6 | 25.2 | 30.6 | 37.3 | 45.2 | 53.1 | 64.9 | 76.3 |
| 1.00 c | 17.8 | 22.0 | 27.1 | 33.1 | 40.2 | 48.8 | 58.1 | 70.0 | 83.1 |
| Ideal c | 101.4 | 118.4 | 137.9 | 160.1 | 185.5 | 214.4 | 247.2 | 284.3 | 326.3 |

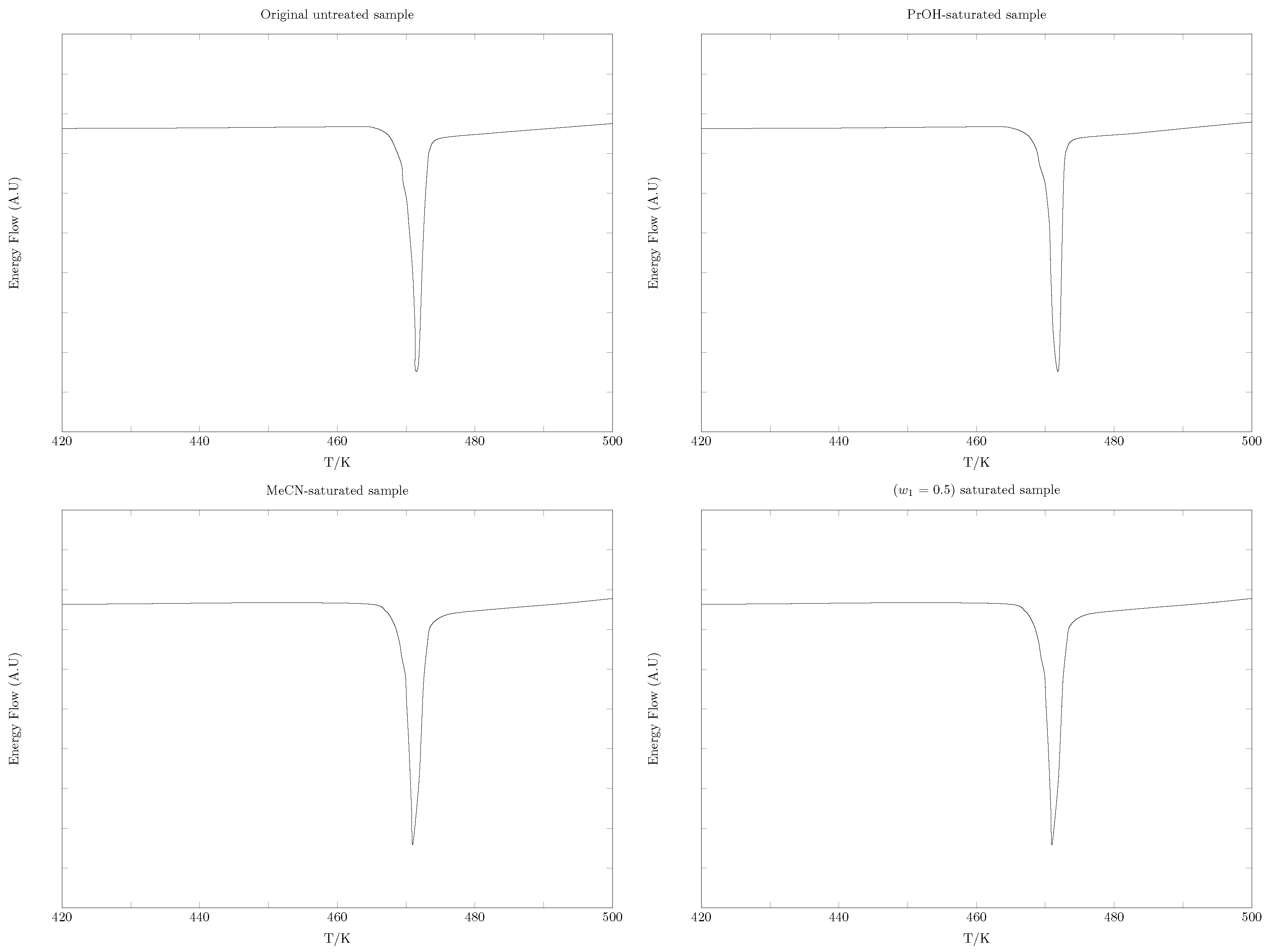
2.2. SMT Solid Phases DSC Analysis
2.3. Activity Coefficients of SMT in Mixed Solvents
| Temperature/K bc | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 278.15 | 283.15 | 288.15 | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | |
| 0.00 | 32.0 | 31.5 | 31.2 | 30.1 | 30.0 | 30.3 | 29.4 | 28.1 | 28.3 |
| 0.05 | 28.9 | 28.6 | 28.0 | 26.9 | 26.5 | 27.0 | 26.1 | 25.2 | 25.1 |
| 0.10 | 26.5 | 26.2 | 25.6 | 24.6 | 24.2 | 24.8 | 23.8 | 23.0 | 22.8 |
| 0.15 | 24.2 | 23.8 | 23.5 | 22.5 | 22.7 | 22.4 | 21.6 | 20.7 | 20.5 |
| 0.20 | 22.3 | 21.7 | 21.2 | 20.5 | 20.3 | 20.3 | 19.7 | 18.8 | 18.7 |
| 0.25 | 20.6 | 20.0 | 19.5 | 18.9 | 18.9 | 18.3 | 17.7 | 17.1 | 16.9 |
| 0.30 | 18.7 | 18.4 | 17.9 | 17.3 | 17.2 | 16.7 | 16.2 | 15.5 | 15.4 |
| 0.35 | 17.2 | 16.7 | 16.3 | 15.6 | 15.4 | 15.1 | 14.7 | 14.0 | 13.9 |
| 0.40 | 15.7 | 15.3 | 14.9 | 14.5 | 13.8 | 13.6 | 13.4 | 12.7 | 12.6 |
| 0.45 | 14.6 | 13.9 | 13.6 | 13.1 | 12.6 | 12.5 | 12.1 | 11.6 | 11.4 |
| 0.50 | 13.2 | 12.9 | 12.3 | 12.0 | 11.5 | 11.3 | 11.0 | 10.6 | 10.4 |
| 0.55 | 12.2 | 11.8 | 11.3 | 10.8 | 10.6 | 10.2 | 10.0 | 9.6 | 9.3 |
| 0.60 | 11.2 | 10.8 | 10.3 | 10.0 | 9.7 | 9.1 | 9.0 | 8.7 | 8.5 |
| 0.65 | 10.2 | 9.8 | 9.5 | 9.3 | 8.9 | 8.4 | 8.2 | 7.9 | 7.7 |
| 0.70 | 9.4 | 9.0 | 8.6 | 8.4 | 8.0 | 7.5 | 7.4 | 7.1 | 7.0 |
| 0.75 | 8.7 | 8.2 | 7.8 | 7.6 | 7.2 | 7.1 | 6.9 | 6.5 | 6.3 |
| 0.80 | 7.8 | 7.6 | 7.3 | 6.8 | 6.6 | 6.3 | 6.1 | 5.9 | 5.7 |
| 0.85 | 7.2 | 6.9 | 6.6 | 6.2 | 6.1 | 5.8 | 5.6 | 5.4 | 5.2 |
| 0.90 | 6.7 | 6.3 | 6.0 | 5.8 | 5.5 | 5.3 | 5.1 | 4.9 | 4.8 |
| 0.95 | 6.1 | 5.8 | 5.5 | 5.2 | 5.0 | 4.7 | 4.7 | 4.4 | 4.3 |
| 1.00 c | 5.7 | 5.4 | 5.1 | 4.8 | 4.6 | 4.4 | 4.3 | 4.1 | 3.9 |
2.4. Apparent Dissolution Thermodynamics
2.5. Apparent Mixing Thermodynamics
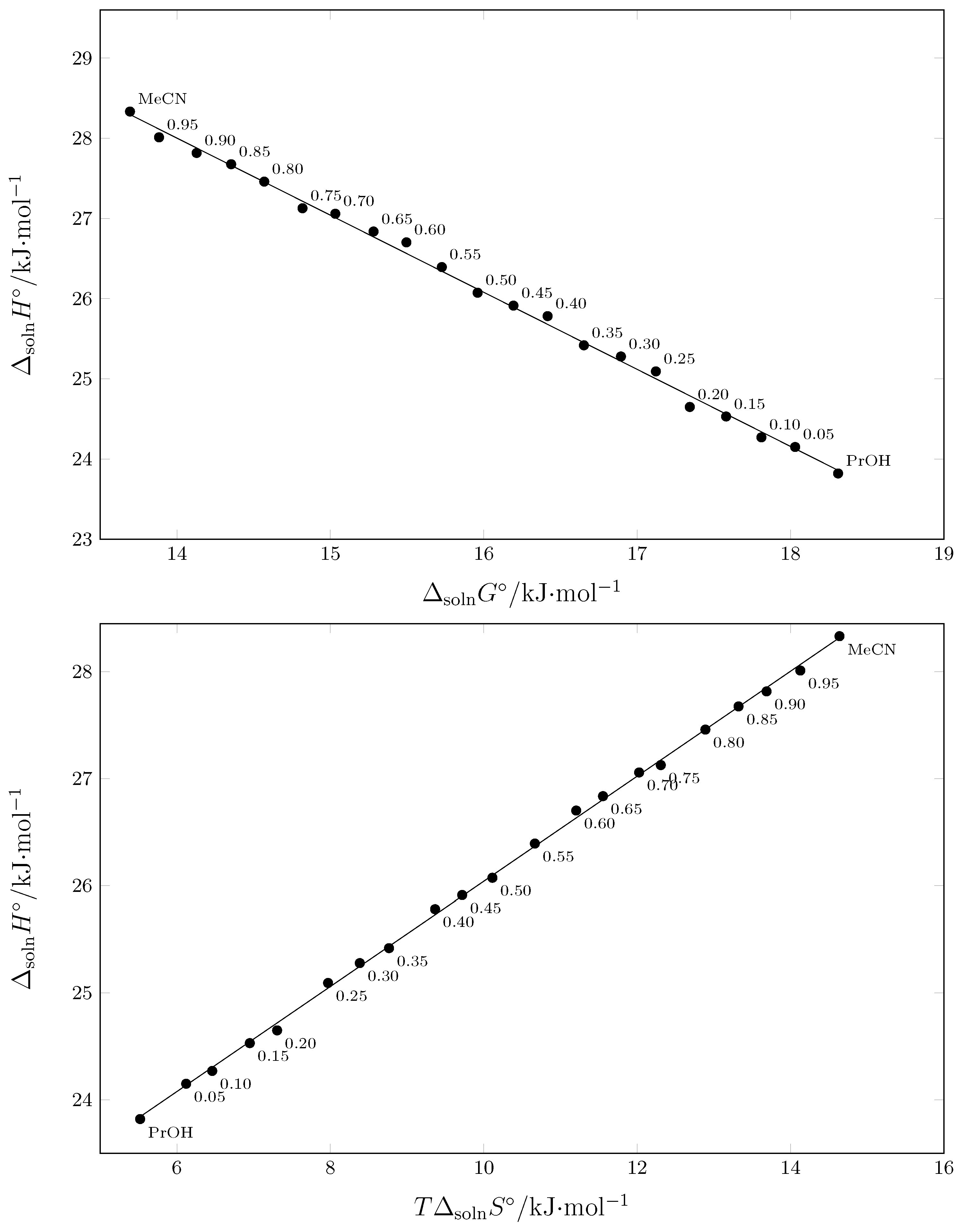
2.6. Enthalpy–Entropy Compensation (EEC) Analysis
3. Materials and Methods
3.1. Reagents
3.2. Solubility Determination
- Saturation: First, approximately 10 mL of each of the cosolvent mixtures (in this case, {MeCN (1) + 1-PrOH (2)} mixtures) is added to a 15 mL amber glass bottle. Small amounts of drug are then added until two phases (liquid/solid) are obtained. This process is performed at room temperature.
- Thermodynamic equilibrium: Once the solvents or cosolvent mixtures are saturated, the samples are placed in a circulating bath (Medingen K-22/T100, Medingen, Germany), where they are kept at a constant temperature (study temperatures: 278.15–318.15 K) for at least 48 h. During the first 36 h, the samples are shaken continuously to ensure the presence of two phases (solid–solution). After 24 h, the concentration of the solution is determined every 4 h until a constant concentration is obtained to ensure thermodynamic equilibrium between the solid phase and the solution. The sample is then allowed to rest for at least 12 h [58]. Since it is necessary to evaluate the solid phase at equilibrium in order to assess possible changes in the crystalline structure of the SMT that may affect solubility, the samples are kept at a temperature 5 degrees above the study temperature for the first 8 h to ensure a saturated solution and to obtain crystals by precipitation with decreasing temperature, necessary for step 5 of the shake flask method.
- Filtration: To ensure that the solution was free of solid particles at the time of dilution to determine the concentration of each sample, each sample was filtered through a 0.45 μm membrane (Millipore Corp. Swinnex-13, Burlington, MA, USA). To minimize concentration changes due to temperature changes at the time of filtration, syringes and filters are brought to the study temperature.
- Quantification: The quantification of SMT is performed by UV/Vis spectrophotometry (UV/Vis EMC-11- UV spectrophotometer, Duisburg, Germany). A calibration curve is developed in absolute ethanol due to the good solubility of the drug in this solvent, which guarantees the respect of the Lambert-Beer law; all the dilutions necessary for the quantification of SMT are made in absolute ethanol to avoid possible precipitations. Since the dilutions required for quantification are in most cases greater than 1:100, the effect of the solvents MeCN and 1-PrOH on the linearity or wavelength of maximum absorbance is negligible.
- Evaluation of the solid phase: To evaluate possible polymorphic changes or decomposition of SMR, the solid phases in equilibrium with the saturated solutions are analyzed by DSC (DSC 204 F1 Phoenix, Dresden, Germany). Sample mass: approximately 10.0 mg; calibration samples: indium and tin as standards; nitrogen flow: 10 mL·min−1; heating ramp: 10 K·min−1.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davis, K.J.; Athira, K. Chapter 24: Infectious Abortive Diseases. In Elements of Reproduction and Reproductive Diseases of Goats; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2024; pp. 279–296. [Google Scholar] [CrossRef]
- Ndlovu, K.; Mwanza, M.; Nleya, N.; Ngoma, L. Detection and quantification of antibiotic residues in goat milk in Mahikeng Local Municipality. J. S. Afr. Vet. Assoc. 2024, 95, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Kuppusamy, S.; Kim, S.Y.; Kim, S.C.; Kim, H.T.; Lee, Y.B. Occurrence of sulfonamide class of antibiotics resistance in Korean paddy soils under long-term fertilization practices. J. Soils Sediments 2017, 17, 1618–1625. [Google Scholar] [CrossRef]
- Cheng, G.; Xu, Y.; Zhu, X.; Xie, S.; Wang, L.; Huang, L.; Hao, H.; Liu, Z.; Pan, Y.; Chen, D.; et al. The antibacterial activities of aditoprim and its efficacy in the treatment of swine streptococcosis. Sci. Rep. 2017, 7, 41370. [Google Scholar] [CrossRef] [PubMed]
- Aswal, V.K.; Chatterjee, S.; Bhattacharyya, J. In vitro solubilization of antibiotic drug sulfamethazine: An investigation on drug–micelle aggregate formation by spectroscopic and scattering techniques. J. Surfactants Deterg. 2022, 25, 331–339. [Google Scholar] [CrossRef]
- Wang, H.; Dang, D.; Zhu, L.; Pan, M.; Zhu, J.; Lu, W.; Lu, S.; Zhao, J. Effects of varied sulfamethazine dosage and exposure durations on offspring mice. Microorganisms 2024, 12, 381. [Google Scholar] [CrossRef]
- NORMAN Network. Emerging Substances. 2024. Available online: https://www.norman-network.com/nds/susdat/susdatSearchShow.php (accessed on 3 August 2024).
- Akinwamide, S.O.; Bossuyt, S.; Akinribide, O.J.; Falodun, O.E.; Borode, A.O.; Olubambi, P.A. Chapter 7—Mitigating environmental challenges in manufacturing industries via electrochemical processes toward climate sustainability. In Smart Nanomaterials for Environmental Applications; Ayeleru, O.O., Idris, A.O., Pandey, S., Olubambi, P.A., Eds.; Micro and Nano Technologies; Elsevier: Amsterdam, The Netherlands, 2024; pp. 165–187. [Google Scholar] [CrossRef]
- Delgado, D.R. LaTeX Code of the Chemical Structure of Some Drugs; Universidad Cooperativa de Colombia: Arauca, Colombia, 2024. [Google Scholar] [CrossRef]
- Rubino, J.T.; Yalkowsky, S.H. Cosolvency and cosolvent polarity. Pharm. Res. 1987, 4, 220–230. [Google Scholar] [CrossRef]
- Rubino, J.T. Cosolvents and Cosolvency. In Encyclopedia of Pharmaceutical Science and Technology; CRC Press: Boca Raton, FL, USA, 2013; pp. 711–722. [Google Scholar] [CrossRef]
- Yu, Q.; Li, J.; Liu, C.; Yang, H. Solubility correlation by model with partial molar volume. Can. J. Chem. Eng. 2023, 101, 4151–4159. [Google Scholar] [CrossRef]
- McConvey, I.F.; Woods, D.; Lewis, M.; Gan, Q.; Nancarrow, P. The importance of acetonitrile in the pharmaceutical industry and opportunities for its recovery from waste. Org. Process Res. Dev. 2012, 16, 612–624. [Google Scholar] [CrossRef]
- Muniz-Miranda, F.; Pedone, A.; Menziani, M.C. Blueshift of the C-N stretching vibration of acetonitrile in solution: Computational and experimental study. J. Comput. Chem. 2024, 45, 2352–2359. [Google Scholar] [CrossRef]
- Desai, A.M.; Andreae, M.; Mullen, D.G.; Banaszak Holl, M.M.; Baker, J.R., Jr. Acetonitrile shortage: Use of isopropanol as an alternative elution system for ultra/high performance liquid chromatography. Anal. Methods 2011, 3, 56–58. [Google Scholar] [CrossRef]
- Yan, Z.; Lee, G.D.Z.; Deng, J.; Luo, G. Process intensification of heterogeneous dehydrochlorination of β-chlorohydrins by using n-propanol as co-extractant. Chem. Eng. Process.- Intensif. 2024, 203, 109906. [Google Scholar] [CrossRef]
- World Health Organization. 1-Propanol; World Health Organization: Geneva, Switzerland, 1990. [Google Scholar]
- Fu, C.; Xie, S. Salts and 1-propanol induced aqueous two-phase systems: Phase separation and application. J. Chem. Technol. Biotechnol. 2019, 94, 2372–2381. [Google Scholar] [CrossRef]
- Khalili, F.; Dabagh, F.; Zarghampour, A.; Hemmati, S.; Jouyban, A.; Hanaee, J.; Rahimpour, E. Solubility and thermodynamics properties of salicylic acid in binary mixtures 1-propanol and propylene glycol/ethylene glycol monomethyl ether at different temperatures. Ann. Pharm. FrançAises 2024, 82, 1013–1024. [Google Scholar] [CrossRef] [PubMed]
- Delgado, D.R.; Bahamón-Hernandez, O.; Cerquera, N.E.; Ortiz, C.P.; Martínez, F.; Rahimpour, E.; Jouyban, A.; Acree, W.E. Solubility of sulfadiazine in (acetonitrile + methanol) mixtures: Determination, correlation, dissolution thermodynamics and preferential solvation. J. Mol. Liq. 2021, 322, 114979. [Google Scholar] [CrossRef]
- Cárdenas-Torres, R.E.; Ortiz, C.P.; Acree, W.E.; Jouyban, A.; Martínez, F.; Delgado, D.R. Thermodynamic study and preferential solvation of sulfamerazine in acetonitrile + methanol cosolvent mixtures at different temperatures. J. Mol. Liq. 2022, 349, 118172. [Google Scholar] [CrossRef]
- Ortiz, C.P.; Cardenas-Torres, R.E.; Martínez, F.; Delgado, D.R. Solubility of sulfamethazine in the binary mixture of acetonitrile + methanol from 278.15 to 318.15 K: Measurement, dissolution thermodynamics, preferential solvation, and correlation. Molecules 2021, 26, 7588. [Google Scholar] [CrossRef]
- Delgado, D.R.; Ortiz, C.P.; Martínez, F.; Jouyban, A. Equilibrium solubility of sulfadiazine in (acetonitrile+ ethanol) mixtures: Determination, correlation, dissolution thermodynamics, and preferential solvation. Int. J. Thermophys. 2024, 45, 129. [Google Scholar] [CrossRef]
- Trujillo-Trujillo, C.F.; Angarita-Reina, F.; Herrera, M.; Ortiz, C.P.; Cardenas-Torres, R.E.; Martinez, F.; Delgado, D.R. Thermodynamic analysis of the solubility of sulfadiazine in (acetonitrile 1-propanol) cosolvent mixtures from 278.15 K to 318.15 K. Liquids 2023, 3, 7–18. [Google Scholar] [CrossRef]
- Ortiz, C.P.; Cardenas-Torres, R.E.; Herrera, M.; Delgado, D.R. Numerical analysis of sulfamerazine solubility in acetonitrile + 1-Propanol cosolvent mixtures at different temperatures. Sustainability 2023, 15, 6596. [Google Scholar] [CrossRef]
- Delgado, D.R.; Martínez, F. Solubility and solution thermodynamics of sulfamerazine and sulfamethazine in some ethanol+water mixtures. Fluid Phase Equilibria 2013, 360, 88–96. [Google Scholar] [CrossRef]
- Delgado, D.R.; Martínez, F. Solubility and solution thermodynamics of some sulfonamides in 1-propanol + water mixtures. J. Solut. Chem. 2014, 43, 836–852. [Google Scholar] [CrossRef]
- Delgado, D.R.; Martínez, F. Solubility and preferential solvation of sulfadiazine in methanol + water mixtures at several temperatures. Fluid Phase Equilibria 2014, 379, 128–138. [Google Scholar] [CrossRef]
- Delgado, D.R.; Martínez, F. Solution thermodynamics of sulfadiazine in some ethanol + water mixtures. J. Mol. Liq. 2013, 187, 99–105. [Google Scholar] [CrossRef]
- Delgado, D.R.; Martínez, F. Solution thermodynamics and preferential solvation of sulfamerazine in methanol + water mixtures. J. Solut. Chem. 2015, 44, 360–377. [Google Scholar] [CrossRef]
- Delgado, D.R.; Almanza, O.A.; Martínez, F.; Peña, M.A.; Jouyban, A.; Acree, W.E. Solution thermodynamics and preferential solvation of sulfamethazine in (methanol + water) mixtures. J. Chem. Thermodyn. 2016, 97, 264–276. [Google Scholar] [CrossRef]
- Sophian, L.; Piper, D.; Schneller, G. The Sulfapyrimidines: Sulfadiazine, Sulfamerazine, Sulfamethazine; Literary Licensing, LLC.: Whitefish, MT, USA, 2012. [Google Scholar]
- Moradi, H.; Bahmanyar, H.; Azizpour, H. Molecular simulation of liquid–liquid extraction of acetic acid and acetone from water in the presence of nanoparticles based on prediction of solubility parameters. Heliyon 2024, 10, e38086. [Google Scholar] [CrossRef]
- Barton, A.F.M. Handbook of Solubility Parameters and Other Cohesion Parameters, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Sun, R.; He, H.; Wan, Y.; Wang, Y.; Li, L.; Sha, J.; Jiang, G.; Li, Y.; Li, T.; Ren, B. Solubility of melatonin in ethyl acetate + (N,N-dimethylformamide, 2-methoxyethanol, 2-ethoxyethanol and methanol): Determination, correlation, thermodynamic properties and Hansen solubility parameter at saturation. J. Chem. Thermodyn. 2021, 156, 106372. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Corazza, M.L.; Voll, F.A. Modeling and experimental measurement of NaBr solubility in water, methanol, ethanol, 1-propanol, and its mixtures at different temperatures. Digit. Chem. Eng. 2023, 6, 100067. [Google Scholar] [CrossRef]
- Li, J.; Masso, J.J.; Guertin, J.A. Prediction of drug solubility in an acrylate adhesive based on the drug–polymer interaction parameter and drug solubility in acetonitrile. J. Control. Release 2002, 83, 211–221. [Google Scholar] [CrossRef]
- Martínez, F.; Gómez, A. Thermodynamic study of the solubility of some sulfonamides in octanol, water, and the mutually saturated solvents. J. Solut. Chem. 2001, 30, 909–923. [Google Scholar] [CrossRef]
- Kristl, A.; Vesnaver, G. Thermodynamic investigation of the effect of octanol–water mutual miscibility on the partitioning and solubility of some guanine derivatives. J. Chem. Soc. Faraday Trans. 1995, 91, 995–998. [Google Scholar] [CrossRef]
- Marcus, Y. The Properties of Solvents, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of va not Hoff and Arrhenius data. J. Phys. Chem. 1976, 80, 2335–2341. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistical effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Bevington, P.; Robinson, D. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
- Carstensen, J. Modeling and Data Treatment in the Pharmaceutical Sciences; Taylor & Francis: Abingdon, UK, 1996. [Google Scholar]
- Mortimer, R. Mathematics for Physical Chemistry; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Perlovich, G.L.; Kurkov, S.V.; Kinchin, A.N.; Bauer-Brandl, A. Thermodynamics of solutions III: Comparison of the solvation of (+)-naproxen with other NSAIDs. Eur. J. Pharm. Biopharm. 2004, 57, 411–420. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, J.H. Solubility. XII. Regular solutions. J. Am. Chem. Soc. 1929, 51, 66–80. [Google Scholar] [CrossRef]
- Hildebrand, J.H.; Prausnitz, J.M.; Scott, R.L. Regular and Related Solutions: The Solubility of Gases, Liquids, and Solids; Van Nostrand Reinhold: London, UK, 1970. [Google Scholar]
- Peccati, F.; Jiménez-Osés, G. Enthalpy–entropy compensation in biomolecular recognition: A computational perspective. ACS Omega 2021, 6, 11122–11130. [Google Scholar] [CrossRef]
- Lee, B. Enthalpy-entropy compensation in the thermodynamics of hydrophobicity. Biophys. Chem. 1994, 51, 271–278. [Google Scholar] [CrossRef]
- Ahiadorme, D.; Crich, D. Entropy-Enthalpy Compensation in the Methyl 5-Thio-α-D-galactopyranoside–Jacalin Interaction. Carbohydr. Res. 2024, 547, 109305. [Google Scholar] [CrossRef]
- Bustamante, P.; Romero, S.; Peña, A.; Escalera, B.; Reillo, A. Enthalpy-entropy compensation for the solubility of drugs in solvent mixtures: Paracetamol, acetanilide, and nalidixic acid in dioxane–water. J. Pharm. Sci. 1998, 87, 1590–1596. [Google Scholar] [CrossRef]
- Bustamante, C.; Bustamante, P. Nonlinear enthalpy–entropy compensation for the solubility of phenacetin in dioxane–water solvent mixtures. J. Pharm. Sci. 1996, 85, 1109–1111. [Google Scholar] [CrossRef]
- Ryde, U. A fundamental view of enthalpy–entropy compensation. Med. Chem. Commun. 2014, 5, 1324–1336. [Google Scholar] [CrossRef]
- Higuchi, T.; Connors, K. Advances in Analytical Chemistry and Instrumentation; Interscience Publishers, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Dittert, L.W.; Higuchi, T.; Reese, D.R. Phase solubility technique in studying the formation of complex salts of triamterene. J. Pharm. Sci. 1964, 53, 1325–1328. [Google Scholar] [CrossRef] [PubMed]
- Mader, W.J.; Higuchi, T. Phase solubility analysis. CRC Crit. Rev. Anal. Chem. 1970, 1, 193–215. [Google Scholar] [CrossRef]
- Delgado, D.R.; Rodríguez, G.A.; Martínez, J.A.; Rojas, J.H.; Martínez, F. Validación de una metodología analítica empleando espectrofotometría ultravioleta para el estudio de la solubilidad de algunas sulfonamidas en mezclas cosolventes alcohol + agua. Rev. Colomb. Quim. 2013, 42, 31–40. [Google Scholar]
 : 0.05; ■: 0.10;
: 0.05; ■: 0.10;  : 0.15; △: 0.20;
: 0.15; △: 0.20;  : 0.25; ▲: 0.30;
: 0.25; ▲: 0.30;  : 0.55; ◊: 0.20;
: 0.55; ◊: 0.20;  : 0.25; ⧫: 0.30;
: 0.25; ⧫: 0.30;  : 0.55; ∘: 0.60;
: 0.55; ∘: 0.60;  : 0.65; •: 0.70;
: 0.65; •: 0.70;  : 0.75; ★: 0.80;
: 0.75; ★: 0.80;  : 0.85; ⊗: 0.90;
: 0.85; ⊗: 0.90;  : 0.95; ⊕: 1.00.
: 0.95; ⊕: 1.00.
 : 0.05; ■: 0.10;
: 0.05; ■: 0.10;  : 0.15; △: 0.20;
: 0.15; △: 0.20;  : 0.25; ▲: 0.30;
: 0.25; ▲: 0.30;  : 0.55; ◊: 0.20;
: 0.55; ◊: 0.20;  : 0.25; ⧫: 0.30;
: 0.25; ⧫: 0.30;  : 0.55; ∘: 0.60;
: 0.55; ∘: 0.60;  : 0.65; •: 0.70;
: 0.65; •: 0.70;  : 0.75; ★: 0.80;
: 0.75; ★: 0.80;  : 0.85; ⊗: 0.90;
: 0.85; ⊗: 0.90;  : 0.95; ⊕: 1.00.
: 0.95; ⊕: 1.00.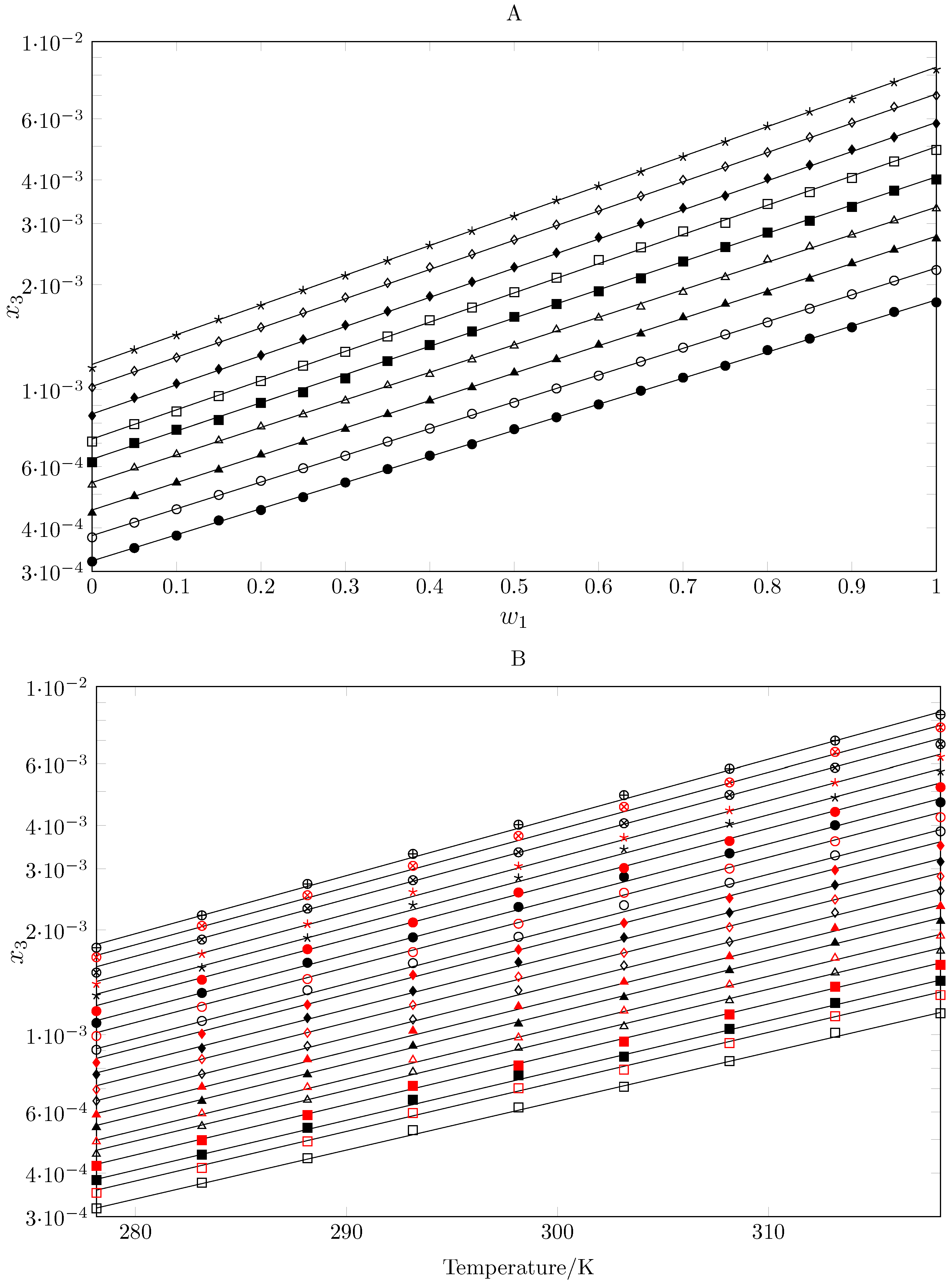
 : 0.05; •: 0.10;
: 0.05; •: 0.10;  : 0.15; ∘: 0.20
: 0.15; ∘: 0.20  : 0.25; ▲: 0.30;
: 0.25; ▲: 0.30;  : 0.35; △: 0.40;
: 0.35; △: 0.40;  : 0.45; □: 0.50;
: 0.45; □: 0.50;  : 0.55; ■: 0.60;
: 0.55; ■: 0.60;  : 0.65; ◊: 0.70;
: 0.65; ◊: 0.70;  : 0.75; ⧫: 0.80;
: 0.75; ⧫: 0.80;  : 0.85; ⊗: 0.90;
: 0.85; ⊗: 0.90;  : 0.95; ⊕: 1.00 (neat MeCN).
: 0.95; ⊕: 1.00 (neat MeCN).
 : 0.05; •: 0.10;
: 0.05; •: 0.10;  : 0.15; ∘: 0.20
: 0.15; ∘: 0.20  : 0.25; ▲: 0.30;
: 0.25; ▲: 0.30;  : 0.35; △: 0.40;
: 0.35; △: 0.40;  : 0.45; □: 0.50;
: 0.45; □: 0.50;  : 0.55; ■: 0.60;
: 0.55; ■: 0.60;  : 0.65; ◊: 0.70;
: 0.65; ◊: 0.70;  : 0.75; ⧫: 0.80;
: 0.75; ⧫: 0.80;  : 0.85; ⊗: 0.90;
: 0.85; ⊗: 0.90;  : 0.95; ⊕: 1.00 (neat MeCN).
: 0.95; ⊕: 1.00 (neat MeCN).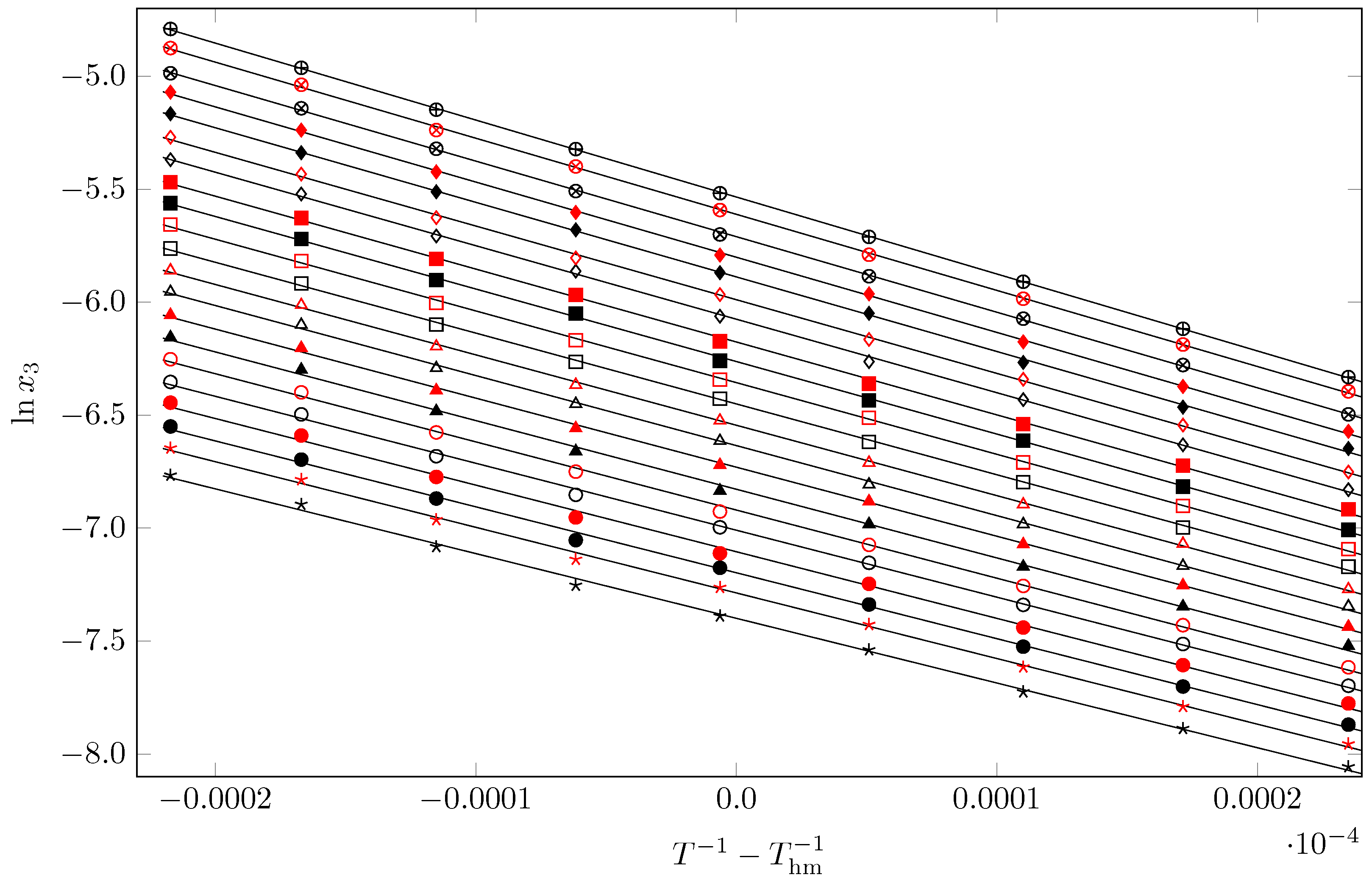
| w1 a | (kJ·mol−1) b | (kJ·mol−1) b | (J·mol−1·K−1) b | (kJ·mol−1) b | ||
|---|---|---|---|---|---|---|
| 0.00 | 18.31 | 23.82 | 18.54 | 5.52 | 0.81 | 0.19 |
| 0.05 | 18.03 | 24.15 | 20.58 | 6.12 | 0.80 | 0.20 |
| 0.10 | 17.81 | 24.27 | 21.70 | 6.46 | 0.79 | 0.21 |
| 0.15 | 17.58 | 24.53 | 23.34 | 6.95 | 0.78 | 0.22 |
| 0.20 | 17.34 | 24.65 | 24.55 | 7.31 | 0.77 | 0.23 |
| 0.25 | 17.12 | 25.09 | 26.78 | 7.97 | 0.76 | 0.24 |
| 0.30 | 16.89 | 25.28 | 28.17 | 8.38 | 0.75 | 0.25 |
| 0.35 | 16.65 | 25.42 | 29.45 | 8.77 | 0.74 | 0.26 |
| 0.40 | 16.42 | 25.78 | 31.47 | 9.37 | 0.73 | 0.27 |
| 0.45 | 16.19 | 25.91 | 32.66 | 9.72 | 0.73 | 0.27 |
| 0.50 | 15.96 | 26.07 | 33.98 | 10.11 | 0.72 | 0.28 |
| 0.55 | 15.73 | 26.39 | 35.84 | 10.67 | 0.71 | 0.29 |
| 0.60 | 15.50 | 26.70 | 37.65 | 11.21 | 0.70 | 0.30 |
| 0.65 | 15.28 | 26.84 | 38.83 | 11.55 | 0.70 | 0.30 |
| 0.70 | 15.03 | 27.06 | 40.41 | 12.03 | 0.69 | 0.31 |
| 0.75 | 14.82 | 27.13 | 41.36 | 12.31 | 0.69 | 0.31 |
| 0.80 | 14.57 | 27.46 | 43.31 | 12.89 | 0.68 | 0.32 |
| 0.85 | 14.35 | 27.68 | 44.77 | 13.32 | 0.68 | 0.33 |
| 0.90 | 14.13 | 27.82 | 46.00 | 13.69 | 0.67 | 0.33 |
| 0.95 | 13.88 | 28.01 | 47.47 | 14.13 | 0.67 | 0.34 |
| 1.00 | 13.69 | 28.33 | 49.19 | 14.64 | 0.66 | 0.34 |
| Ideal | 9.89 | 21.50 | 39.02 | 11.61 | 0.649 | 0.351 |
| a | (kJ·mol−1) b | (kJ·mol−1) b | (J·mol−1·K−1) b | (kJ·mol−1) b |
|---|---|---|---|---|
| 0.00 | 8.42 | 2.33 | −20.48 | −6.09 |
| 0.05 | 8.14 | 2.66 | −18.44 | −5.49 |
| 0.10 | 7.92 | 2.77 | −17.32 | −5.15 |
| 0.15 | 7.69 | 3.03 | −15.68 | −4.67 |
| 0.20 | 7.46 | 3.15 | −14.47 | −4.31 |
| 0.25 | 7.24 | 3.60 | −12.24 | −3.64 |
| 0.30 | 7.01 | 3.78 | −10.85 | −3.23 |
| 0.35 | 6.77 | 3.92 | −9.57 | −2.85 |
| 0.40 | 6.53 | 4.28 | −7.55 | −2.25 |
| 0.45 | 6.31 | 4.42 | −6.36 | −1.89 |
| 0.50 | 6.07 | 4.58 | −5.04 | −1.5 |
| 0.55 | 5.84 | 4.90 | −3.18 | −0.95 |
| 0.60 | 5.61 | 5.20 | −1.36 | −0.41 |
| 0.65 | 5.40 | 5.34 | −0.19 | −0.06 |
| 0.70 | 5.15 | 5.56 | 1.39 | 0.41 |
| 0.75 | 4.93 | 5.63 | 2.34 | 0.70 |
| 0.80 | 4.68 | 5.96 | 4.29 | 1.28 |
| 0.85 | 4.47 | 6.18 | 5.75 | 1.71 |
| 0.90 | 4.24 | 6.32 | 6.98 | 2.08 |
| 0.95 | 4.00 | 6.51 | 8.45 | 2.52 |
| 1.00c | 3.81 | 6.83 | 10.17 | 3.03 |
| Chemical Name | CAS a | Purity in Mass Fraction | Analytic Technique b |
|---|---|---|---|
| SMT c | 127-79-7 | >0.990 | HPLC |
| EtOH c | 64-17-5 | 0.998 | GC |
| 1-PrOH d | 71-23-8 | 0.998 | GC |
| MeCN d | 75-05-8 | 0.998 | GC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, D.R.; Castro-Camacho, J.K.; Ortiz, C.P.; Caviedes-Rubio, D.I.; Martinez, F. Dissolution Thermodynamics of the Solubility of Sulfamethazine in (Acetonitrile + 1-Propanol) Mixtures. Pharmaceuticals 2024, 17, 1594. https://doi.org/10.3390/ph17121594
Delgado DR, Castro-Camacho JK, Ortiz CP, Caviedes-Rubio DI, Martinez F. Dissolution Thermodynamics of the Solubility of Sulfamethazine in (Acetonitrile + 1-Propanol) Mixtures. Pharmaceuticals. 2024; 17(12):1594. https://doi.org/10.3390/ph17121594
Chicago/Turabian StyleDelgado, Daniel Ricardo, Jennifer Katiusca Castro-Camacho, Claudia Patricia Ortiz, Diego Ivan Caviedes-Rubio, and Fleming Martinez. 2024. "Dissolution Thermodynamics of the Solubility of Sulfamethazine in (Acetonitrile + 1-Propanol) Mixtures" Pharmaceuticals 17, no. 12: 1594. https://doi.org/10.3390/ph17121594
APA StyleDelgado, D. R., Castro-Camacho, J. K., Ortiz, C. P., Caviedes-Rubio, D. I., & Martinez, F. (2024). Dissolution Thermodynamics of the Solubility of Sulfamethazine in (Acetonitrile + 1-Propanol) Mixtures. Pharmaceuticals, 17(12), 1594. https://doi.org/10.3390/ph17121594








