Numerical and Experimental Analysis of Drug Inhalation in Realistic Human Upper Airway Model
Abstract
1. Introduction
2. Results and Discussion
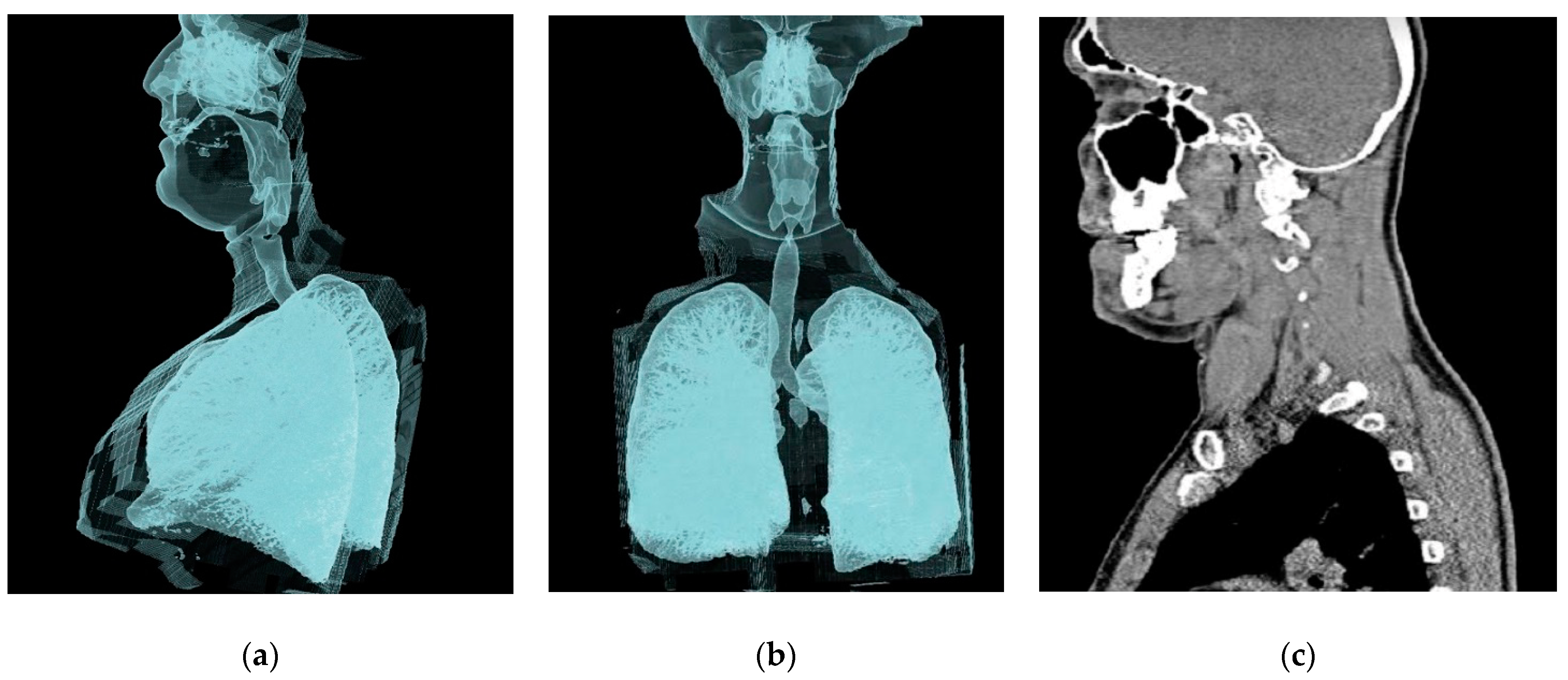
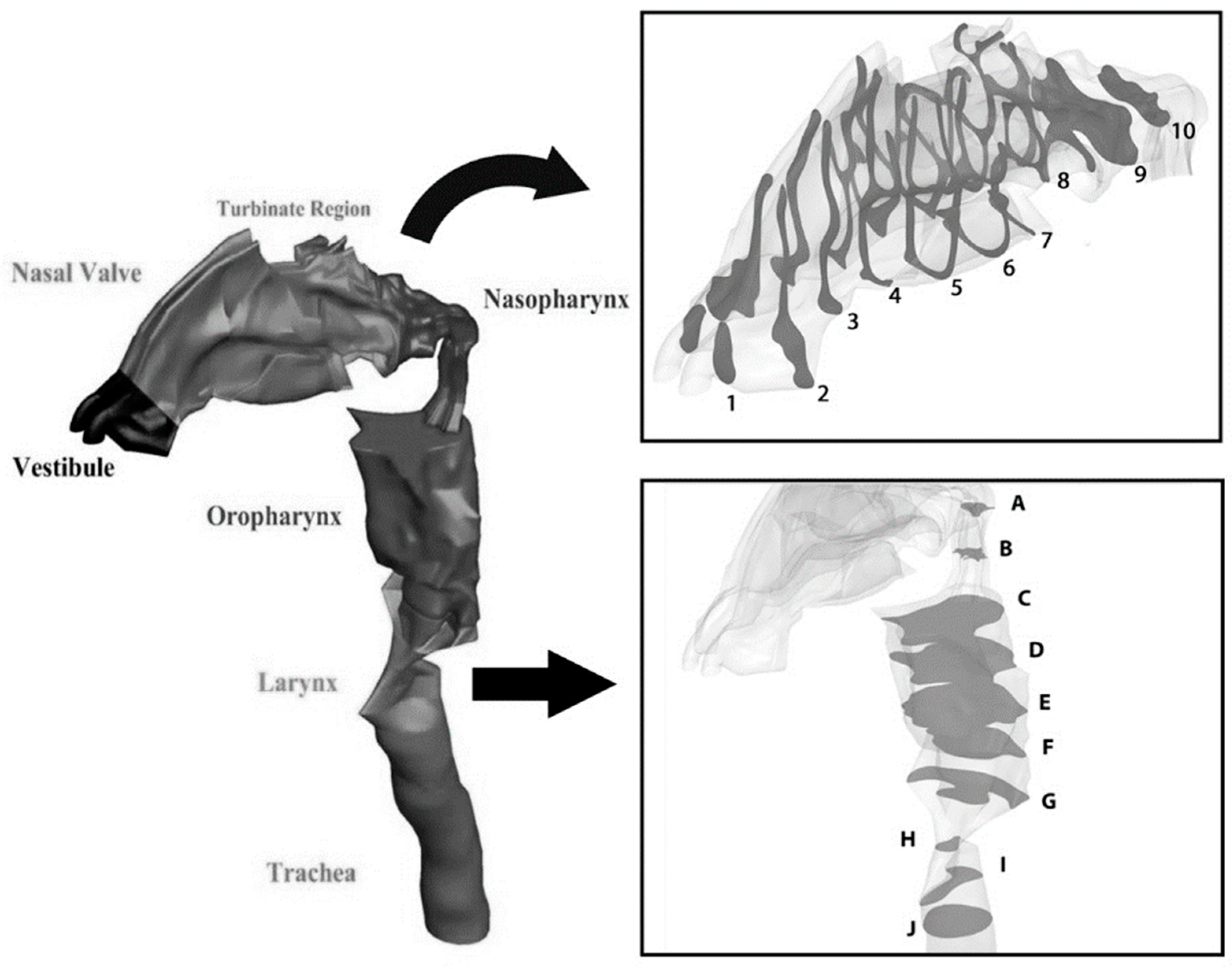
2.1. Geometry of the Model
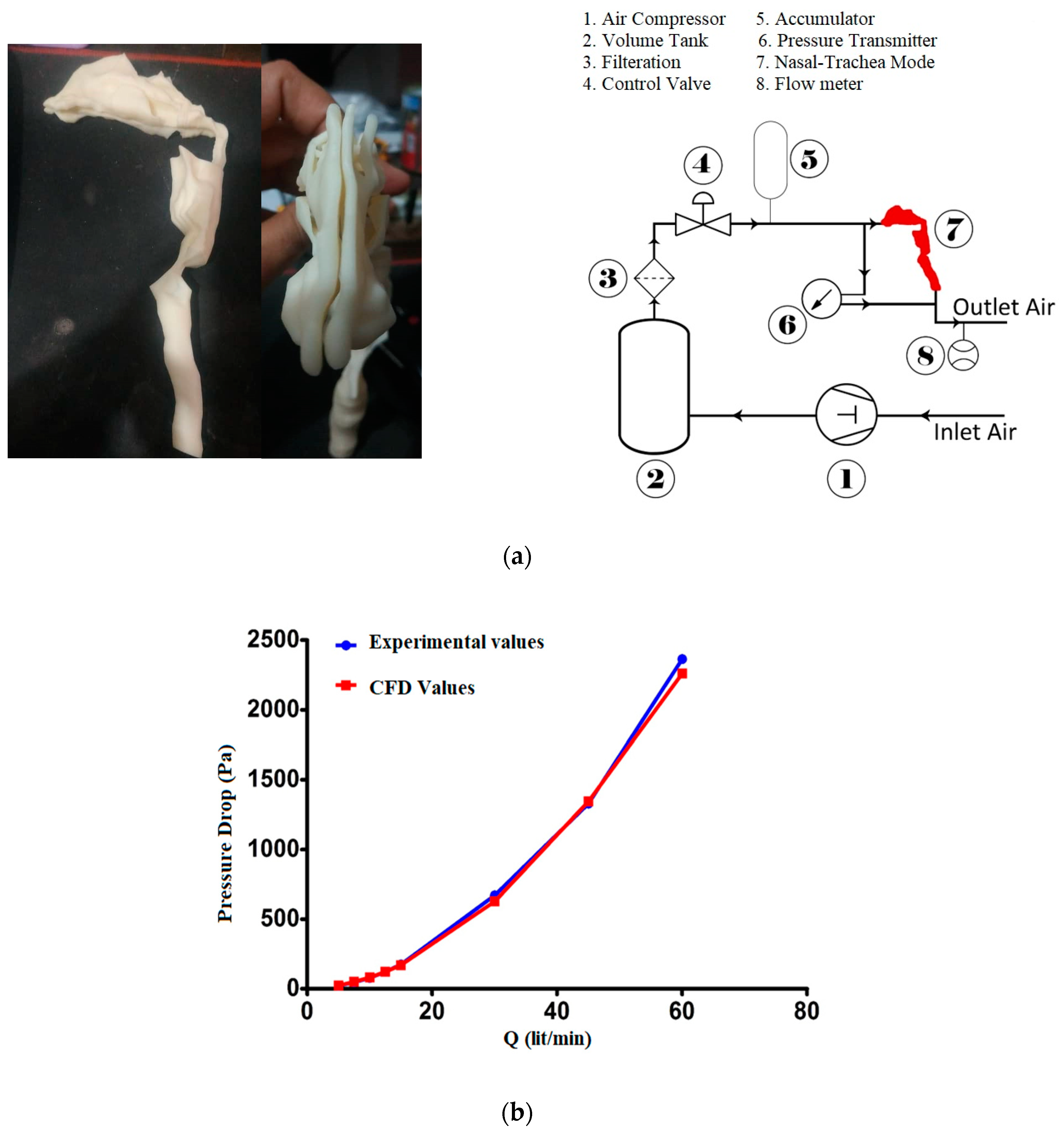
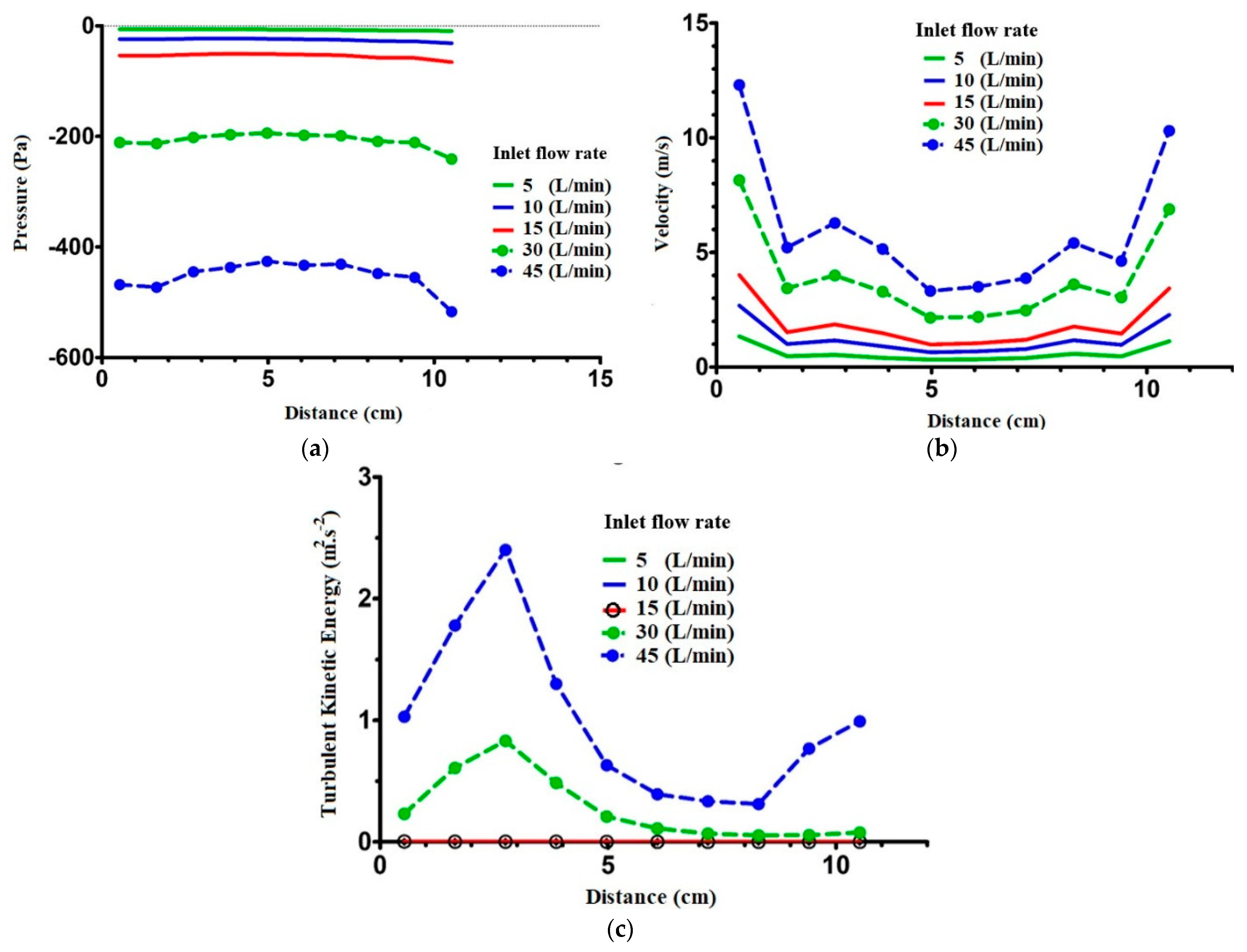
2.2. Validation
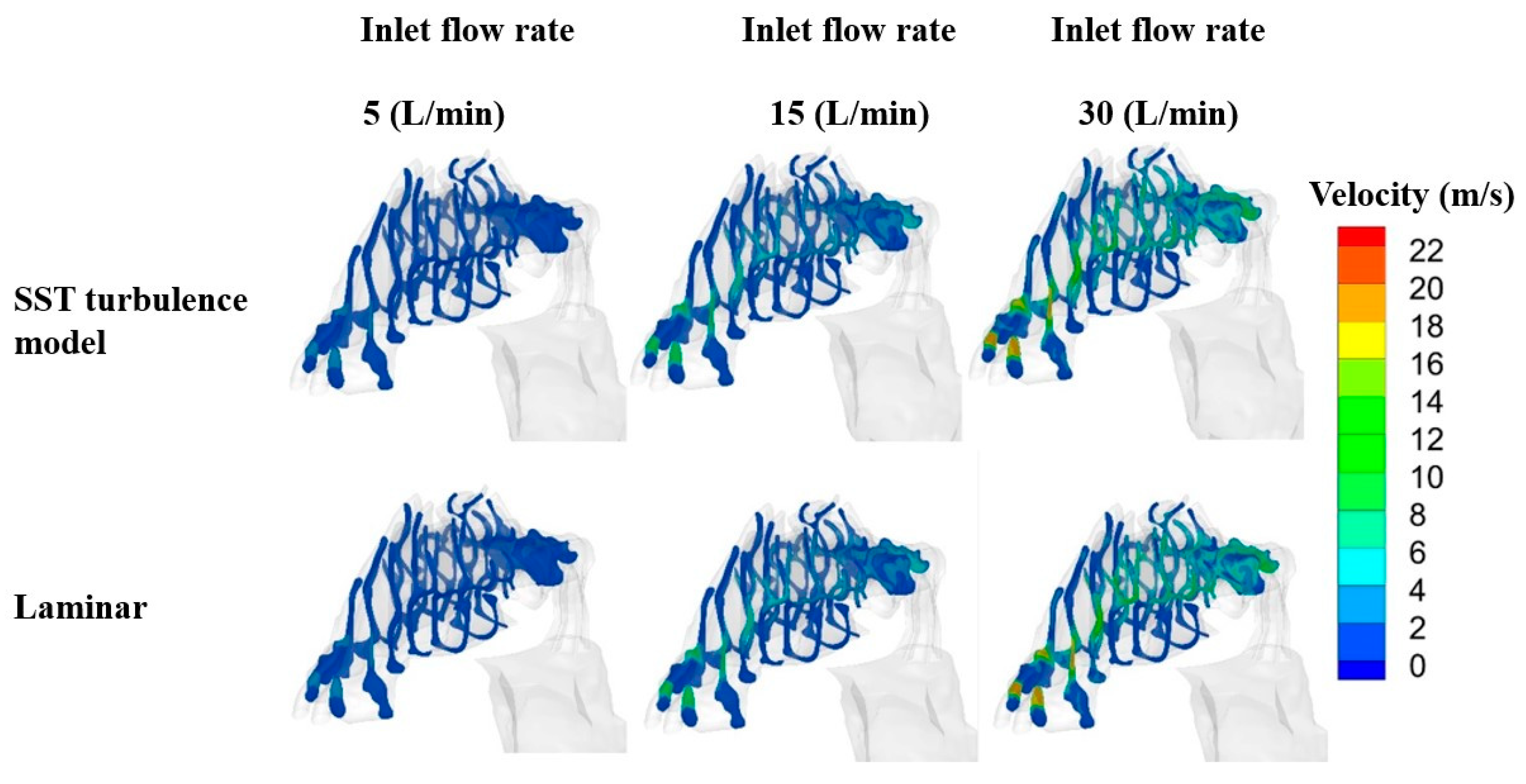
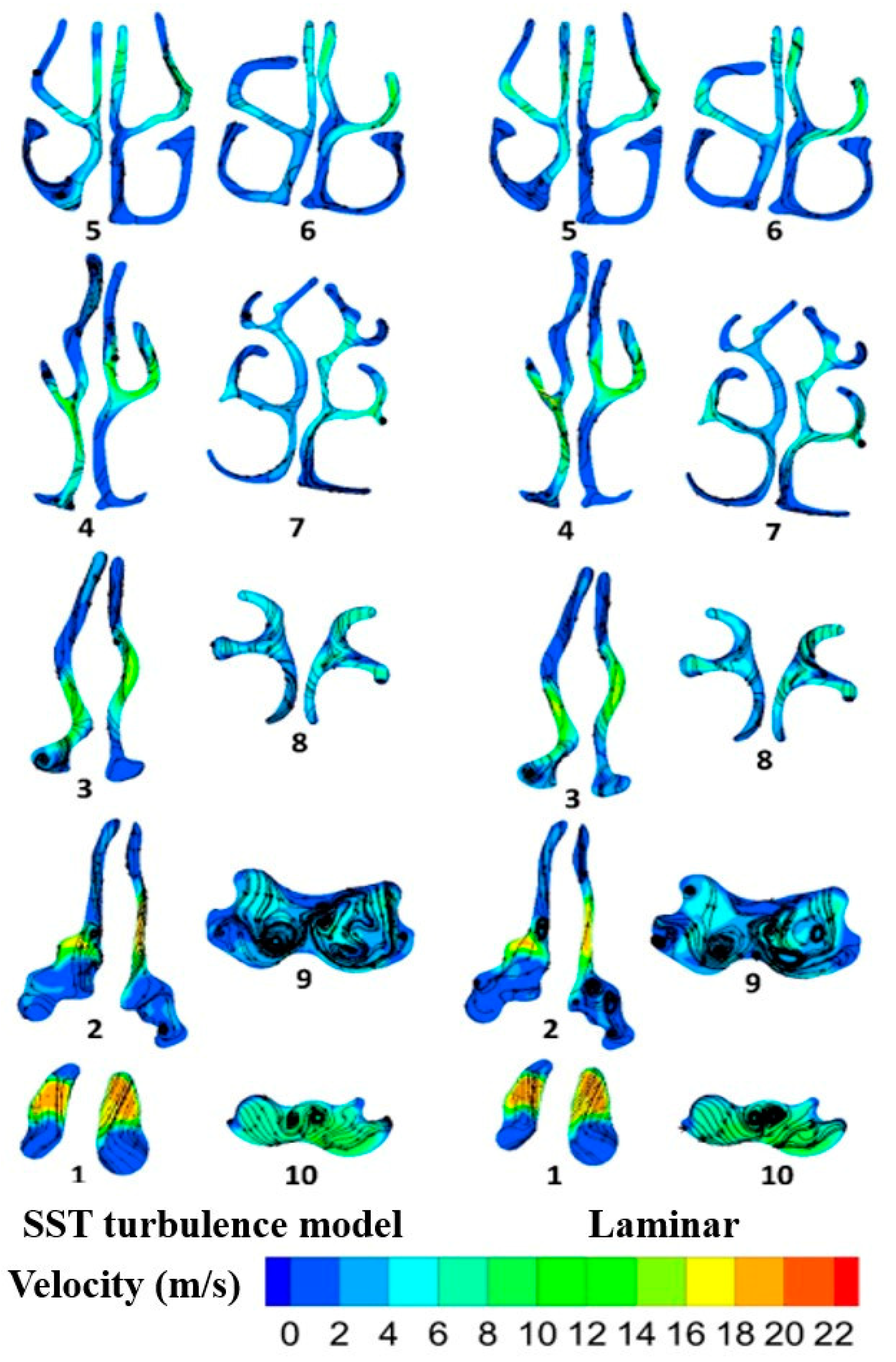
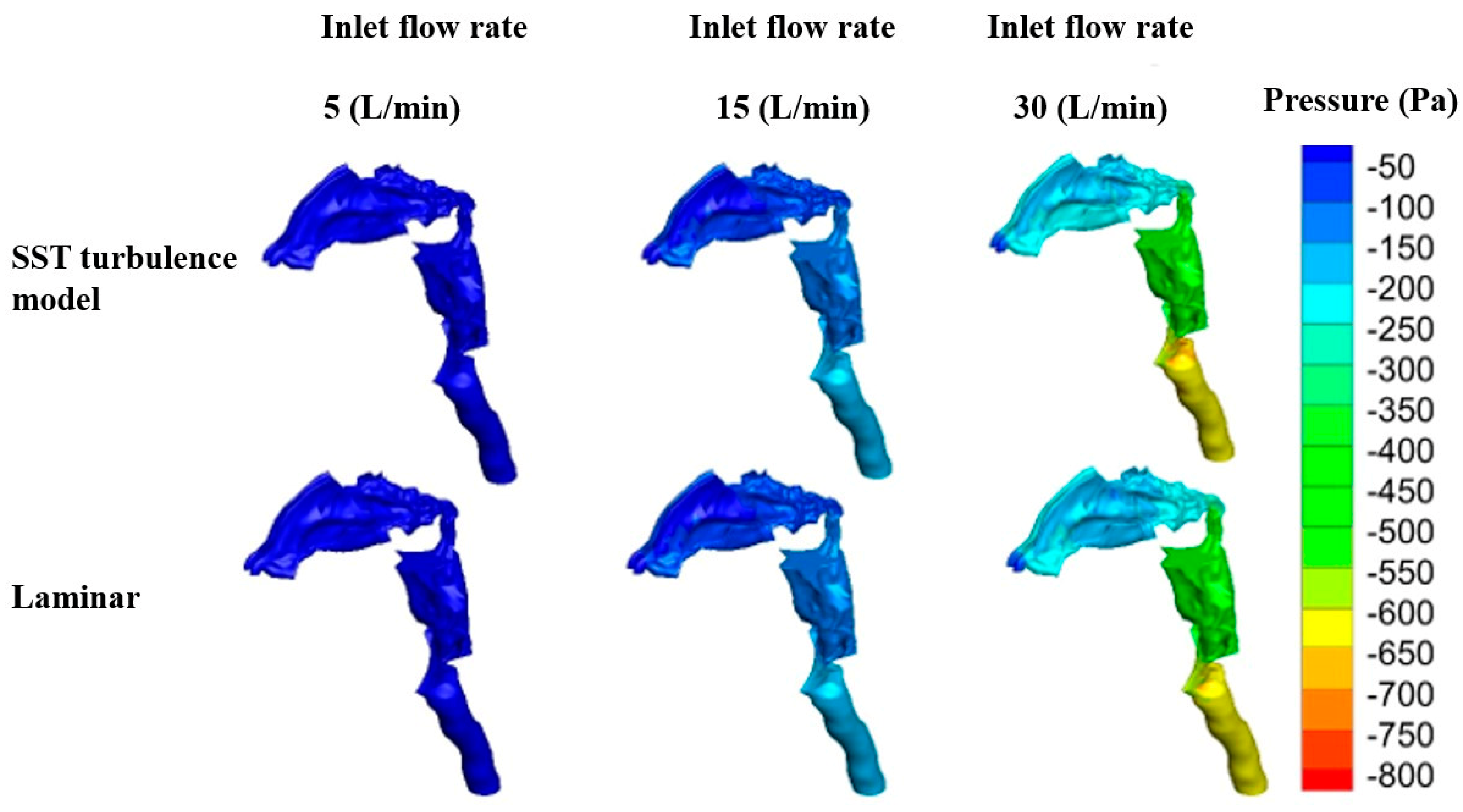
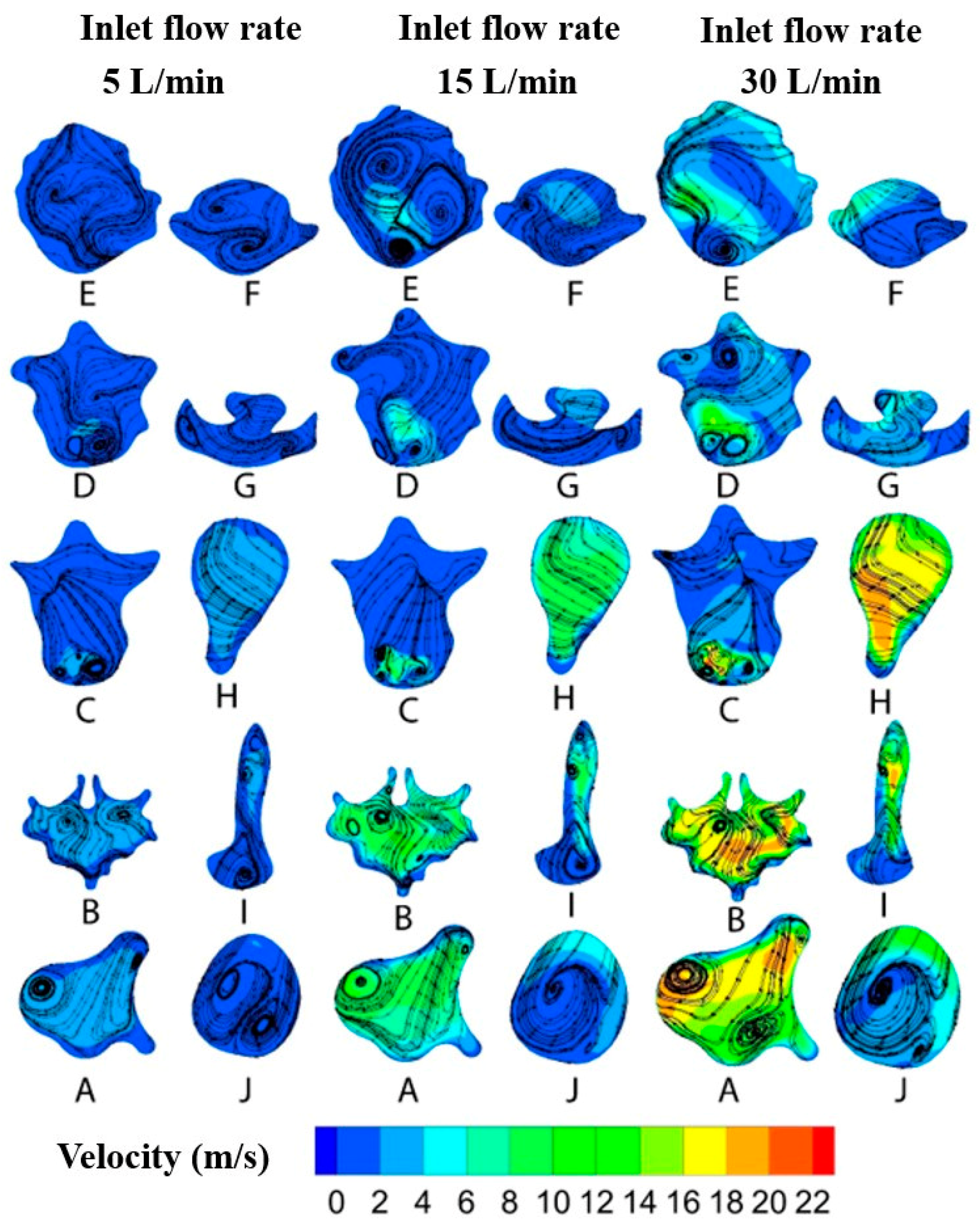
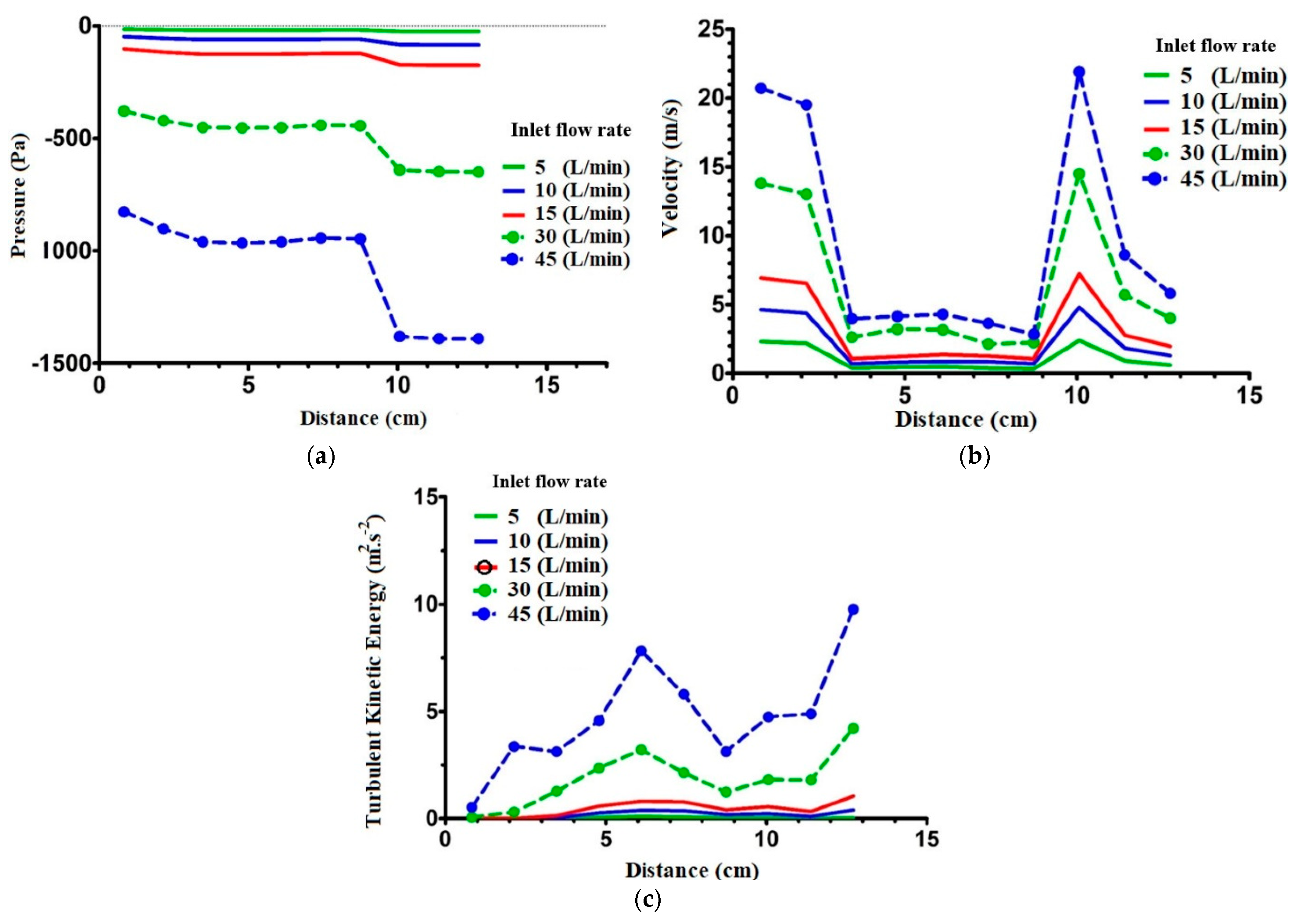
2.3. Flow Field Study
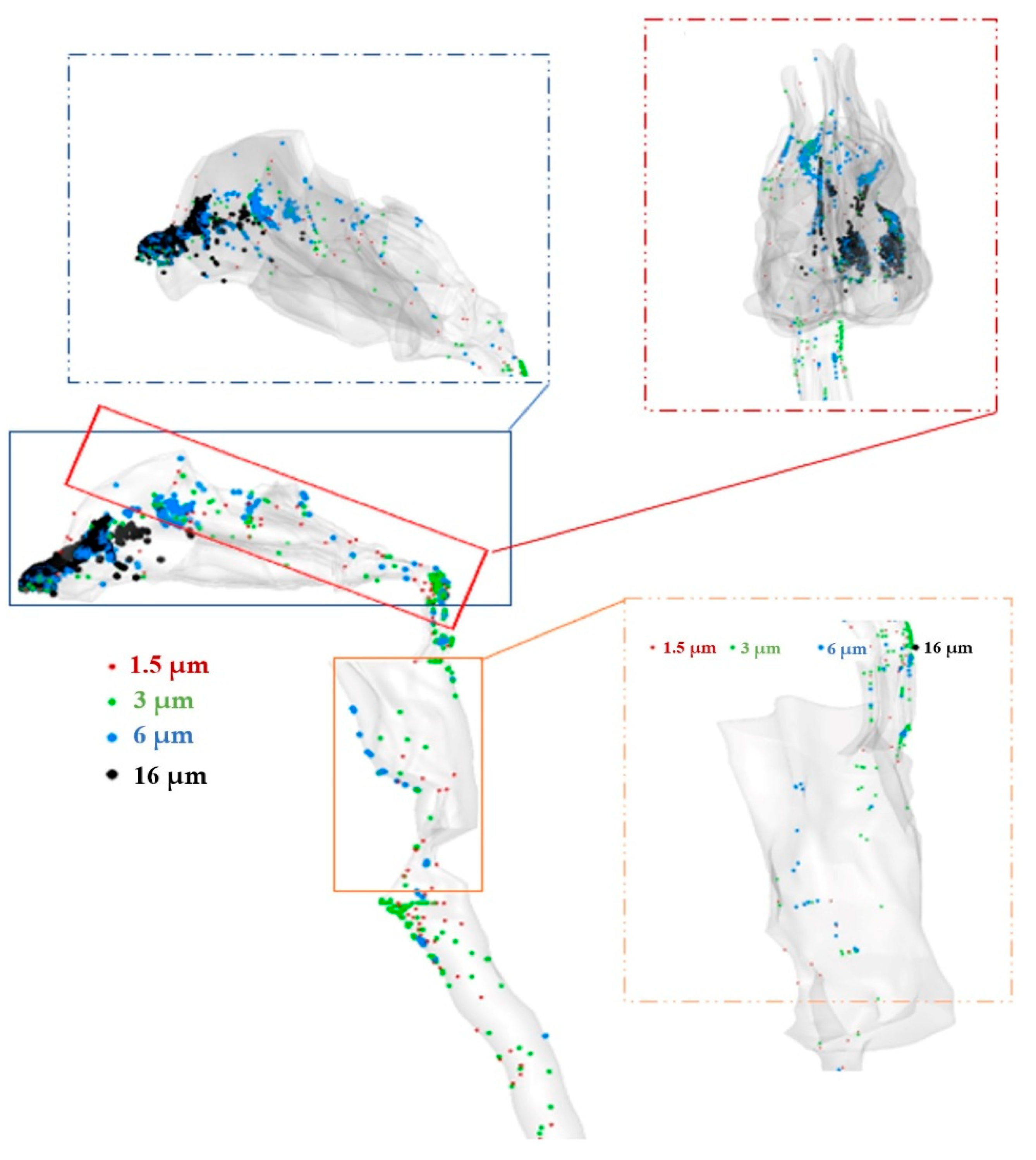
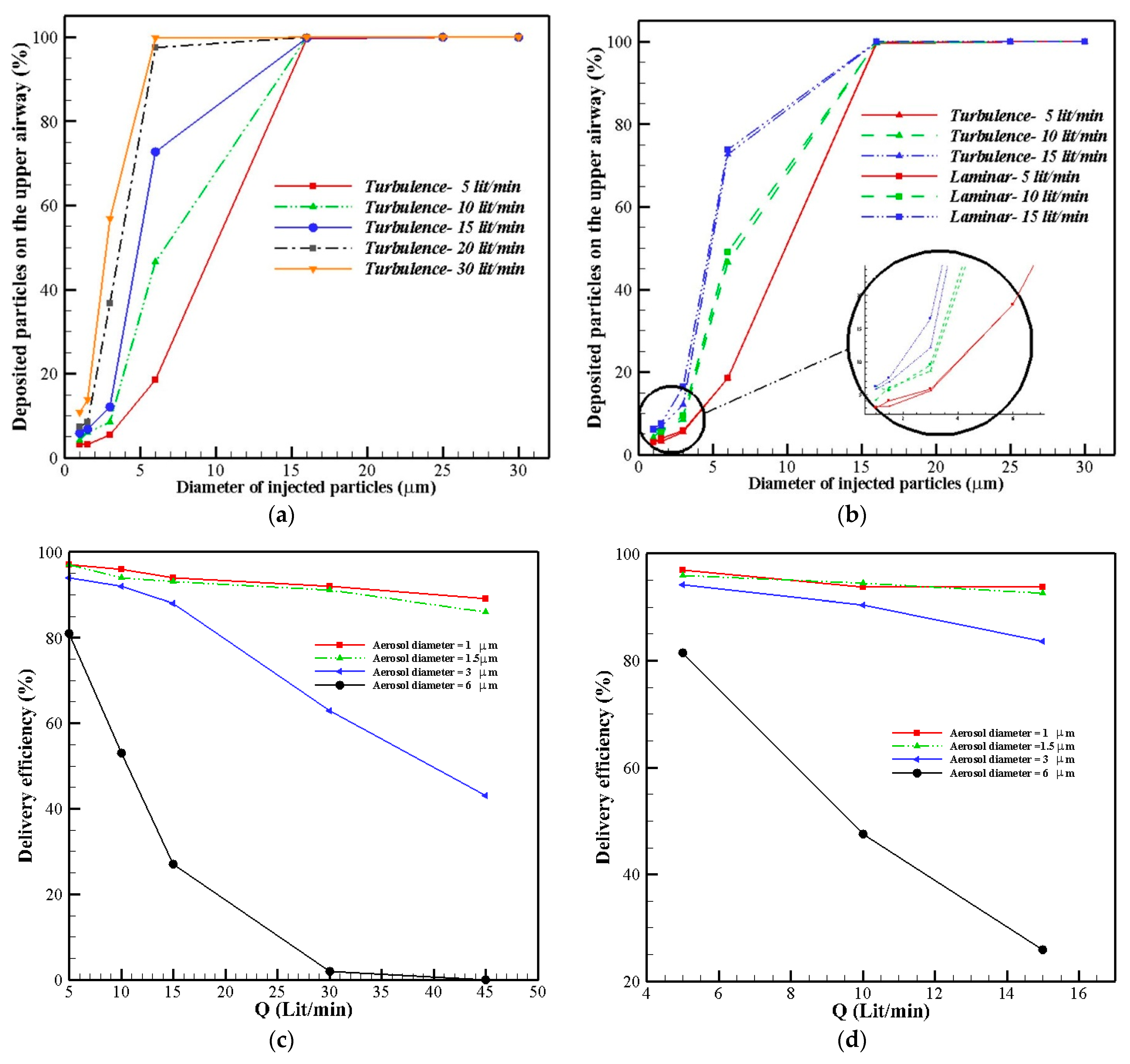
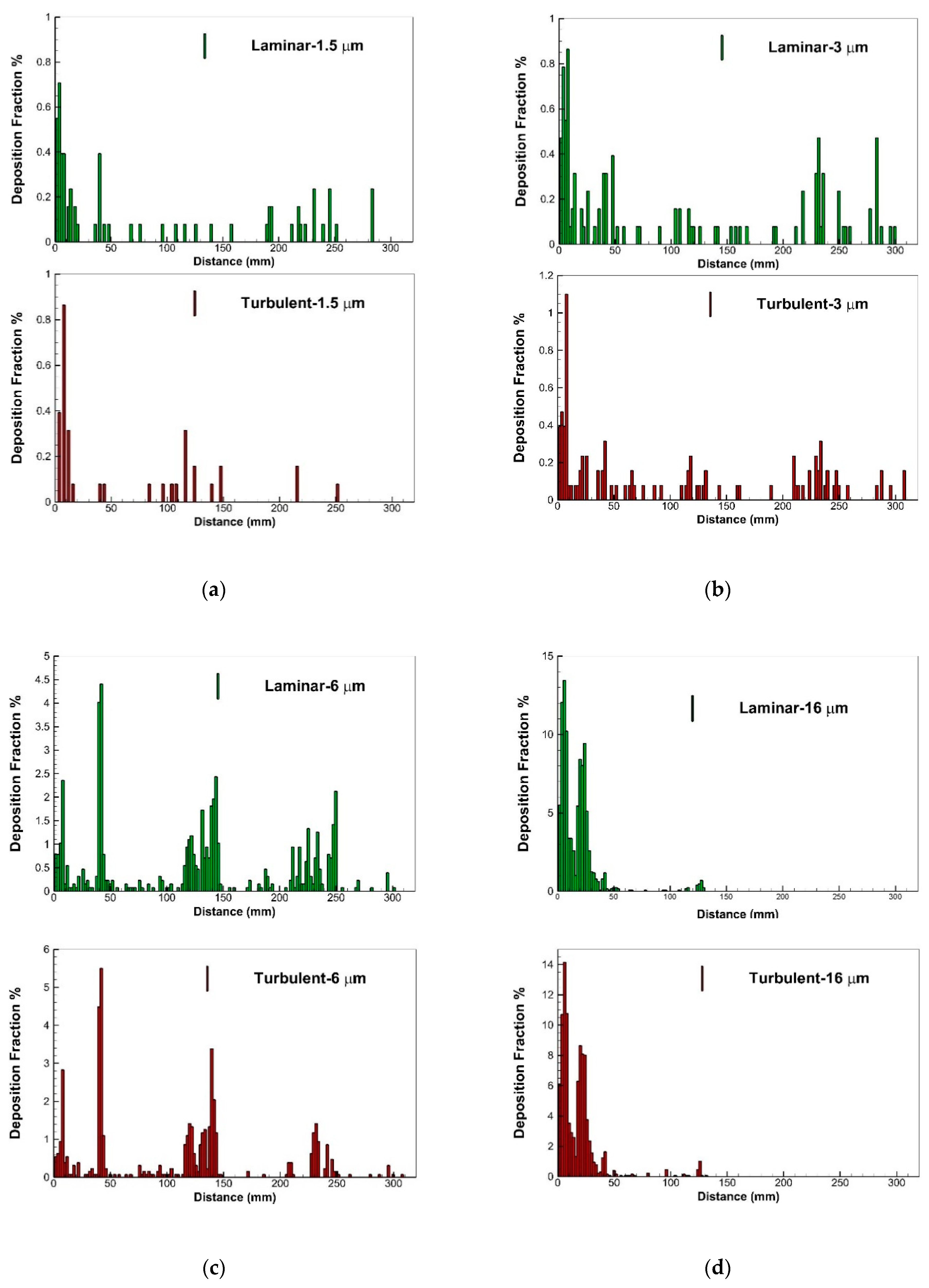
2.4. Aerosol Delivery
3. Materials and Methods
3.1. Governing Equations
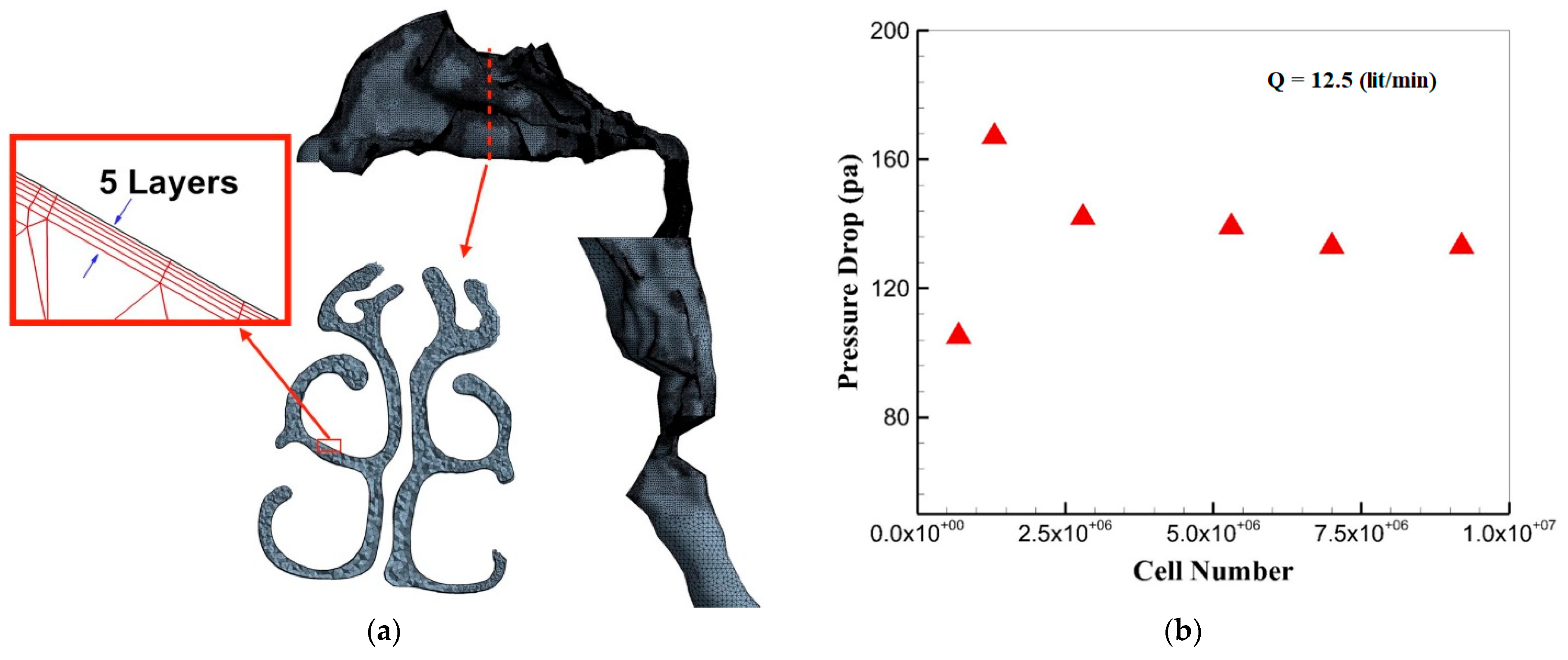
3.2. Grid Generation and Independency
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, Q.; Bates, A.J.; Cetto, R.; Doorly, D.J. The Effect of Decongestion on Nasal Airway Patency and Airflow. Sci. Rep. 2021, 11, 14410. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Dong, J.; Tian, L.; Inthavong, K.; Tu, J. Detailed Computational Analysis of Flow Dynamics in an Extended Respiratory Airway Model. Clin. Biomech. 2019, 61, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Barnes, P.J.; Blasi, F.; Ward, B.; Reeves, E.; Rabe, K.F. Respiratory Diseases in the World: One Voice “United for Lung Health”. Eur. Respir. J. 2014, 43, 3–5. [Google Scholar] [CrossRef] [PubMed]
- Hogg, J.C.; Paré, P.D.; Hackett, T.-L. The Contribution of Small Airway Obstruction to the Pathogenesis of Chronic Obstructive Pulmonary Disease. Physiol. Rev. 2017, 97, 529–552. [Google Scholar] [CrossRef]
- Abdollahi, H.; Babamiri, A.; Ahookhosh, K.; Farnoud, A.; Nabaei, M. Effects of Inhalation Flow Rate on Particle Deposition and Flow Structure in a Model of Tracheobronchial Airway. In Proceedings of the 2021 28th National and 6th International Iranian Conference on Biomedical Engineering (ICBME), IEEE, Tehran, Iran, 25 November 2021; pp. 101–106. [Google Scholar]
- Ahmadi, M.; Zuber, M.; Abdul Khader, S.M. Airflow Simulation inside the Nasal Cavity. Mapta J. Mech. Ind. Eng. 2020, 4, 21–25. [Google Scholar] [CrossRef]
- Taheri, M.H.; Pourmehran, O.; Sarafraz, M.M.; Ahookhosh, K.; Farnoud, A.; Cui, X. Effect of Swirling Flow and Particle-Release Pattern on Drug Delivery to Human Tracheobronchial Airways. Biomech. Model. Mechanobiol. 2021, 20, 2451–2469. [Google Scholar] [CrossRef]
- Ahookhosh, K.; Saidi, M.; Mohammadpourfard, M.; Aminfar, H.; Hamishehkar, H.; Farnoud, A.; Schmid, O. Flow Structure and Particle Deposition Analyses for Optimization of a Pressurized Metered Dose Inhaler (PMDI) in a Model of Tracheobronchial Airway. Eur. J. Pharm. Sci. 2021, 164, 105911. [Google Scholar] [CrossRef]
- Hahn, I.; Scherer, P.W.; Mozell, M.M. Velocity Profiles Measured for Airflow through a Large-Scale Model of the Human Nasal Cavity. J. Appl. Physiol. 1993, 75, 2273–2287. [Google Scholar] [CrossRef]
- Farnoud, A.; Tofighian, H.; Baumann, I.; Garcia, G.J.M.; Schmid, O.; Gutheil, E.; Rashidi, M.M. Large Eddy Simulations of Airflow and Particle Deposition in Pulsating Bi-Directional Nasal Drug Delivery. Phys. Fluids 2020, 32, 101905. [Google Scholar] [CrossRef]
- Farnoud, A.; Baumann, I.; Rashidi, M.M.; Schmid, O.; Gutheil, E. Simulation of Patient-Specific Bi-Directional Pulsating Nasal Aerosol Dispersion and Deposition with Clockwise 45° and 90° Nosepieces. Comput. Biol. Med. 2020, 123, 103816. [Google Scholar] [CrossRef]
- Farnoud, A.; Tofighian, H.; Baumann, I.; Martin, A.R.; Rashidi, M.M.; Menden, M.P.; Schmid, O. Pulsatile Bi-Directional Aerosol Flow Affects Aerosol Delivery to the Intranasal Olfactory Region: A Patient-Specific Computational Study. Front. Pharmacol. 2021, 12, 2902. [Google Scholar] [CrossRef] [PubMed]
- Inthavong, K.; Ma, J.; Shang, Y.; Dong, J.; Chetty, A.S.R.; Tu, J.; Frank-Ito, D. Geometry and Airflow Dynamics Analysis in the Nasal Cavity during Inhalation. Clin. Biomech. 2019, 66, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Tian, L.; Fan, Y.; Dong, J.; Inthavong, K.; Tu, J. Effect of Morphology on Nanoparticle Transport and Deposition in Human Upper Tracheobronchial Airways. J. Comput. Multiph. Flows 2018, 10, 83–96. [Google Scholar] [CrossRef]
- Zhao, K. Effect of Anatomy on Human Nasal Air Flow and Odorant Transport Patterns: Implications for Olfaction. Chem. Senses 2004, 29, 365–379. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Dalton, P.; Yang, G.C.; Scherer, P.W. Numerical Modeling of Turbulent and Laminar Airflow and Odorant Transport during Sniffing in the Human and Rat Nose. Chem. Senses 2006, 31, 107–118. [Google Scholar] [CrossRef]
- Lindemann, J.; Rettinger, G.; Kröger, R.; Sommer, F. Numerical Simulation of Airflow Patterns in Nose Models with Differently Localized Septal Perforations. Laryngoscope 2013, 123, 2085–2089. [Google Scholar] [CrossRef]
- Brüning, J.; Hildebrandt, T.; Heppt, W.; Schmidt, N.; Lamecker, H.; Szengel, A.; Amiridze, N.; Ramm, H.; Bindernagel, M.; Zachow, S.; et al. Characterization of the Airflow within an Average Geometry of the Healthy Human Nasal Cavity. Sci. Rep. 2020, 10, 3755. [Google Scholar] [CrossRef]
- Li, C.; Jiang, J.; Dong, H.; Zhao, K. Computational Modeling and Validation of Human Nasal Airflow under Various Breathing Conditions. J. Biomech. 2017, 64, 59–68. [Google Scholar] [CrossRef]
- Inthavong, K.; Ge, Q.; Se, C.M.K.; Yang, W.; Tu, J.Y. Simulation of Sprayed Particle Deposition in a Human Nasal Cavity Including a Nasal Spray Device. J. Aerosol Sci. 2011, 42, 100–113. [Google Scholar] [CrossRef]
- Lee, K.B.; Jeon, Y.S.; Chung, S.-K.; Kim, S.K. Effects of Partial Middle Turbinectomy with Varying Resection Volume and Location on Nasal Functions and Airflow Characteristics by CFD. Comput. Biol. Med. 2016, 77, 214–221. [Google Scholar] [CrossRef]
- Burgos, M.A.; Sanmiguel-Rojas, E.; del Pino, C.; Sevilla-García, M.A.; Esteban-Ortega, F. New CFD Tools to Evaluate Nasal Airflow. Eur. Arch. Oto-Rhino-Laryngol. 2017, 274, 3121–3128. [Google Scholar] [CrossRef] [PubMed]
- Balakin, B.V.; Farbu, E.; Kosinski, P. Aerodynamic Evaluation of the Empty Nose Syndrome by Means of Computational Fluid Dynamics. Comput. Methods Biomech. Biomed. Engin. 2017, 20, 1554–1561. [Google Scholar] [CrossRef]
- Shrestha, K.; Van Strien, J.; Shang, Y.; Fletcher, D.F.; Petersen, P.; Vreugde, S.; Wormald, P.J.; Singh, N.; Inthavong, K. Effect of Breathing Profiles on Nebuliser Drug Delivery Targeting the Paranasal Sinuses in a Post-Operative Nasal Cavity. J. Aerosol Sci. 2022, 161, 105913. [Google Scholar] [CrossRef]
- Pourmehran, O.; Gorji, T.B.; Gorji-Bandpy, M. Magnetic Drug Targeting through a Realistic Model of Human Tracheobronchial Airways Using Computational Fluid and Particle Dynamics. Biomech. Model. Mechanobiol. 2016, 15, 1355–1374. [Google Scholar] [CrossRef] [PubMed]
- Pourmehran, O.; Cazzolato, B.; Tian, Z.; Arjomandi, M. Acoustically-Driven Drug Delivery to Maxillary Sinuses: Aero-Acoustic Analysis. Eur. J. Pharm. Sci. 2020, 151, 105398. [Google Scholar] [CrossRef] [PubMed]
- Pourmehran, O.; Arjomandi, M.; Cazzolato, B.; Tian, Z.; Vreugde, S.; Javadiyan, S.; Psaltis, A.J.; Wormald, P.-J. Acoustic Drug Delivery to the Maxillary Sinus. Int. J. Pharm. 2021, 606, 120927. [Google Scholar] [CrossRef] [PubMed]
- Pourmehran, O.; Arjomandi, M.; Cazzolato, B.; Ghanadi, F.; Tian, Z. The Impact of Geometrical Parameters on Acoustically Driven Drug Delivery to Maxillary Sinuses. Biomech. Model. Mechanobiol. 2020, 19, 557–575. [Google Scholar] [CrossRef]
- Biglarian, M.; MomeniLarimi, M.; Firoozabadi, B.; Inthavong, K.; Farnoud, A. Targeted Drug Delivery with Polydisperse Particle Transport and Deposition in Patient-Specific Upper Airway during Inhalation and Exhalation. Respir. Physiol. Neurobiol. 2023, 308, 103986. [Google Scholar] [CrossRef] [PubMed]
- Pui, D.Y.H.; Romay-Novas, F.; Liu, B.Y.H. Experimental Study of Particle Deposition in Bends of Circular Cross Section. Aerosol Sci. Technol. 1987, 7, 301–315. [Google Scholar] [CrossRef]
- Inthavong, K. A Unifying Correlation for Laminar Particle Deposition in 90-Degree Pipe Bends. Powder Technol. 2019, 345, 99–110. [Google Scholar] [CrossRef]
- Pilou, M.; Tsangaris, S.; Neofytou, P.; Housiadas, C.; Drossinos, Y. Inertial Particle Deposition in a 90° Laminar Flow Bend: An Eulerian Fluid Particle Approach. Aerosol Sci. Technol. 2011, 45, 1376–1387. [Google Scholar] [CrossRef]
- Thune, E.L.; Kosinski, P.; Balakin, B.V.; Alyaev, S. A Numerical Study of Flow Field and Particle Deposition in Nasal Channels with Deviant Geometry. Eng. Appl. Comput. Fluid Mech. 2021, 15, 180–193. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Tong, J.C.K.; Abraham, J.P. Fluid Flow in a System with Separate Laminar and Turbulent Zones. Numer. Heat Transf. Part A Appl. 2008, 53, 341–353. [Google Scholar] [CrossRef]
- Abolhassantash, M.; Tavakol, M.M.; Abouali, O.; Yaghoubi, M.; Ahmadi, G. Deposition Fraction of Ellipsoidal Fibers in the Human Nasal Cavity- Influence of Non-Creeping Formulation of Hydrodynamic Forces and Torques. Int. J. Multiph. Flow 2020, 126, 103238. [Google Scholar] [CrossRef]
- Hörschler, I.; Meinke, M.; Schröder, W. Numerical Simulation of the Flow Field in a Model of the Nasal Cavity. Comput. Fluids 2003, 32, 39–45. [Google Scholar] [CrossRef]
- Se, C.M.K.; Inthavong, K.; Tu, J. Unsteady Particle Deposition in a Human Nasal Cavity during Inhalation. J. Comput. Multiph. Flows 2010, 2, 207–218. [Google Scholar] [CrossRef]
- O’Neill, G.; Tolley, N.S. The Complexities of Nasal Airflow: Theory and Practice. J. Appl. Physiol. 2019, 127, 1215–1223. [Google Scholar] [CrossRef] [PubMed]
- Lönnermark, A.; Ingason, H. The Effect of Cross-Sectional Area and Air Velocity on the Conditions in a Tunnel during a Fire. 2007. Available online: https://www.diva-portal.org/smash/get/diva2:962400/FULLTEXT01.pdf (accessed on 29 December 2022).
- Nomura, T.; Ushio, M.; Kondo, K.; Kikuchi, S. Effects of Nasal Septum Perforation Repair on Nasal Airflow: An Analysis Using Computational Fluid Dynamics on Preoperative and Postoperative Three-Dimensional Models. Auris Nasus Larynx 2018, 45, 1020–1026. [Google Scholar] [CrossRef]
- Wang, Y.; Elghobashi, S. On Locating the Obstruction in the Upper Airway via Numerical Simulation. Respir. Physiol. Neurobiol. 2014, 193, 1–10. [Google Scholar] [CrossRef]
- Ghoneima, A.; AlBarakati, S.; Jiang, F.; Kula, K.; Wasfy, T. Computational Fluid Dynamics Analysis of the Upper Airway after Rapid Maxillary Expansion: A Case Report. Prog. Orthod. 2015, 16, 10. [Google Scholar] [CrossRef]
- Calmet, H.; Houzeaux, G.; Vázquez, M.; Eguzkitza, B.; Gambaruto, A.M.; Bates, A.J.; Doorly, D.J. Flow Features and Micro-Particle Deposition in a Human Respiratory System during Sniffing. J. Aerosol Sci. 2018, 123, 171–184. [Google Scholar] [CrossRef]
- Babamiri, A.; Ahookhosh, K.; Abdollahi, H.; Taheri, M.H.; Cui, X.; Nabaei, M.; Farnoud, A. Effect of Laryngeal Jet on Dry Powder Inhaler Aerosol Deposition: A Numerical Simulation. Comput. Methods Biomech. Biomed. Engin. 2022, 1–16. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momeni Larimi, M.; Babamiri, A.; Biglarian, M.; Ramiar, A.; Tabe, R.; Inthavong, K.; Farnoud, A. Numerical and Experimental Analysis of Drug Inhalation in Realistic Human Upper Airway Model. Pharmaceuticals 2023, 16, 406. https://doi.org/10.3390/ph16030406
Momeni Larimi M, Babamiri A, Biglarian M, Ramiar A, Tabe R, Inthavong K, Farnoud A. Numerical and Experimental Analysis of Drug Inhalation in Realistic Human Upper Airway Model. Pharmaceuticals. 2023; 16(3):406. https://doi.org/10.3390/ph16030406
Chicago/Turabian StyleMomeni Larimi, Morsal, Arash Babamiri, Mohit Biglarian, Abas Ramiar, Reza Tabe, Kiao Inthavong, and Ali Farnoud. 2023. "Numerical and Experimental Analysis of Drug Inhalation in Realistic Human Upper Airway Model" Pharmaceuticals 16, no. 3: 406. https://doi.org/10.3390/ph16030406
APA StyleMomeni Larimi, M., Babamiri, A., Biglarian, M., Ramiar, A., Tabe, R., Inthavong, K., & Farnoud, A. (2023). Numerical and Experimental Analysis of Drug Inhalation in Realistic Human Upper Airway Model. Pharmaceuticals, 16(3), 406. https://doi.org/10.3390/ph16030406






