The IQA Energy Partition in a Drug Design Setting: A Hepatitis C Virus RNA-Dependent RNA Polymerase (NS5B) Case Study
Abstract
1. Introduction
2. Systems
2.1. Overall Context
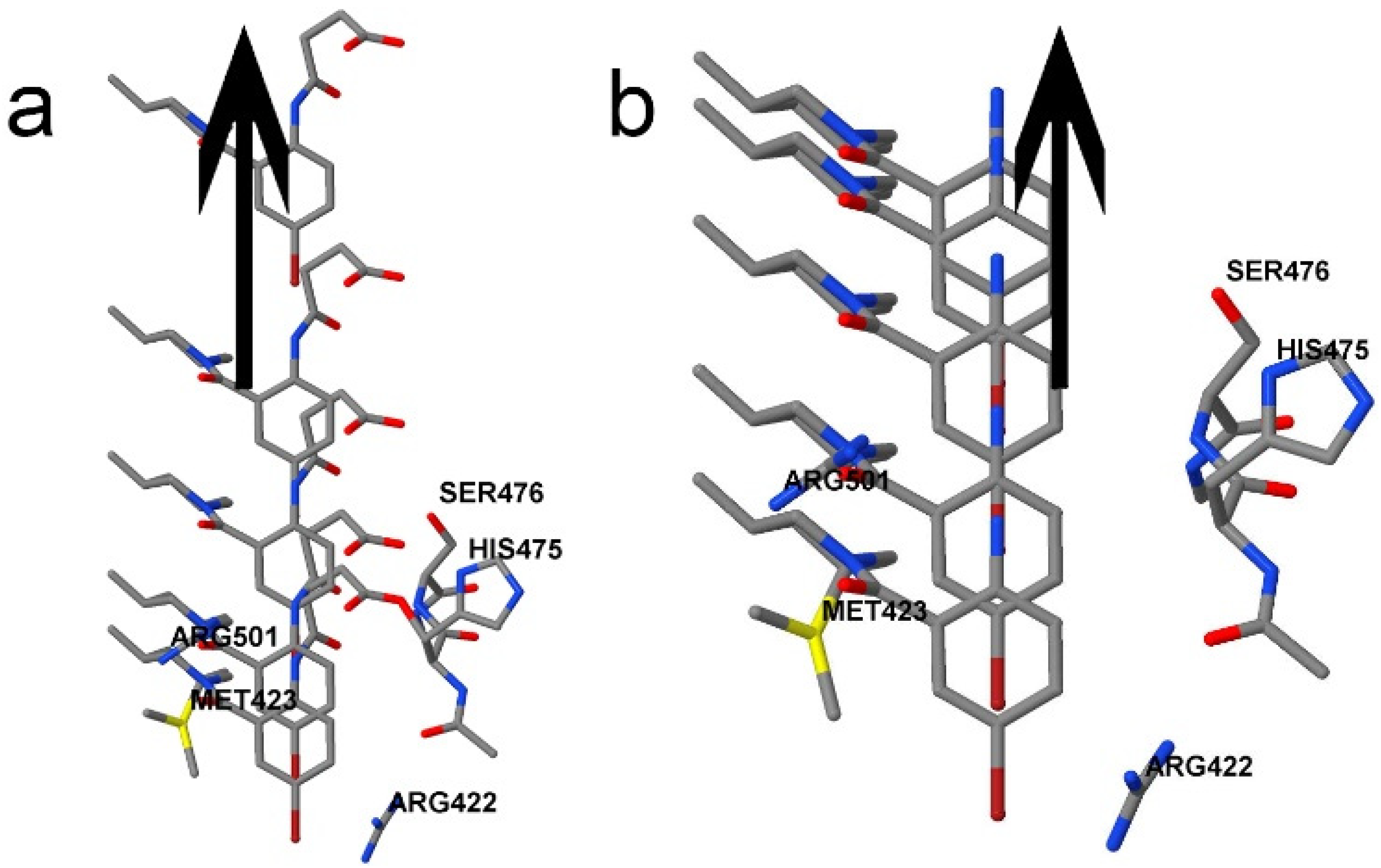
2.2. System Details
3. Methodology and Computational Details
3.1. Theoretical and Computational Background
3.1.1. Interacting Quantum Atoms
3.1.2. The Relative Energy Gradient (REG) Method
3.2. Computational Details
4. Results
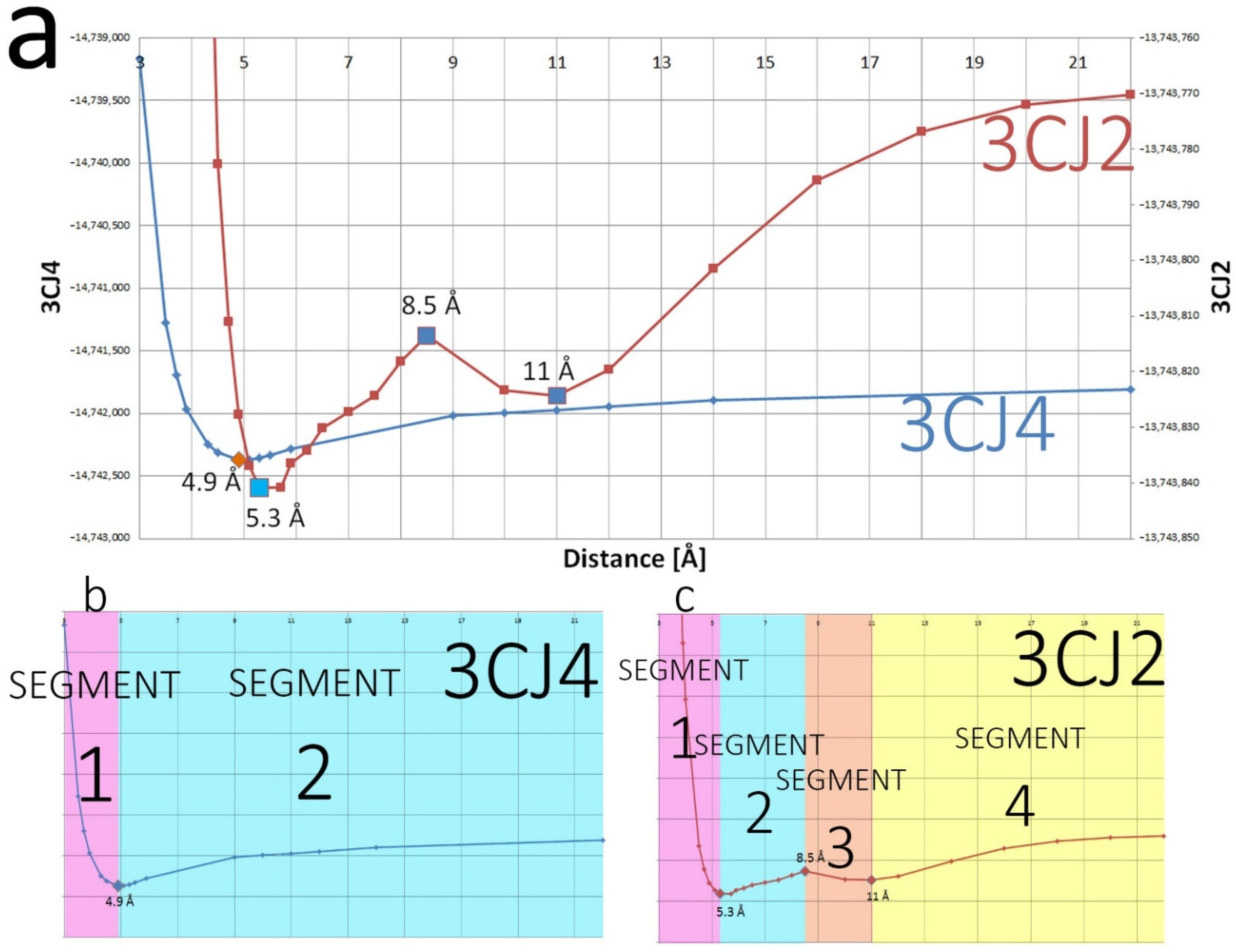
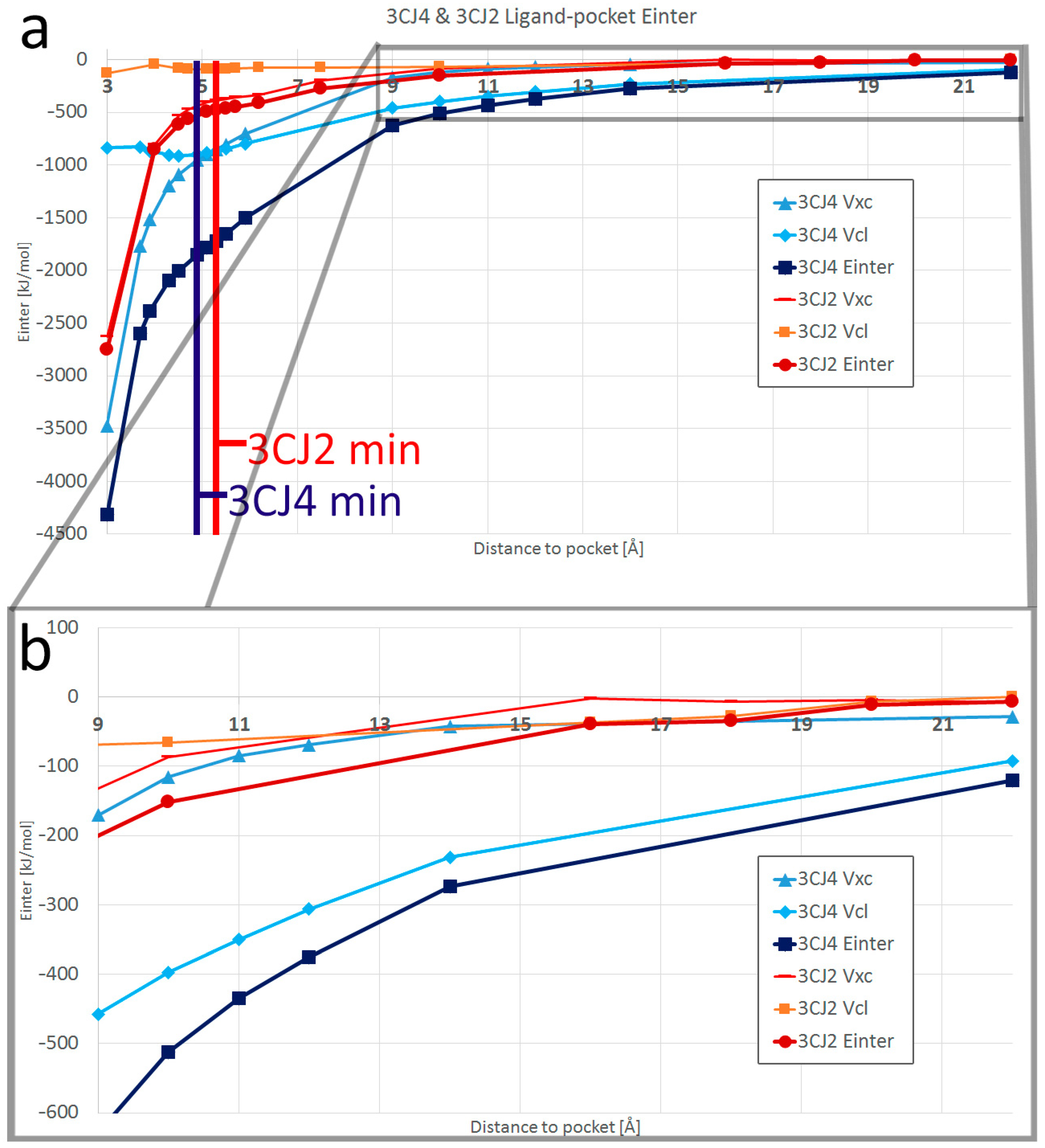
4.1. The PES of the Total System
4.2. Relative Energy Gradient (REG) Method
4.2.1. Generalities
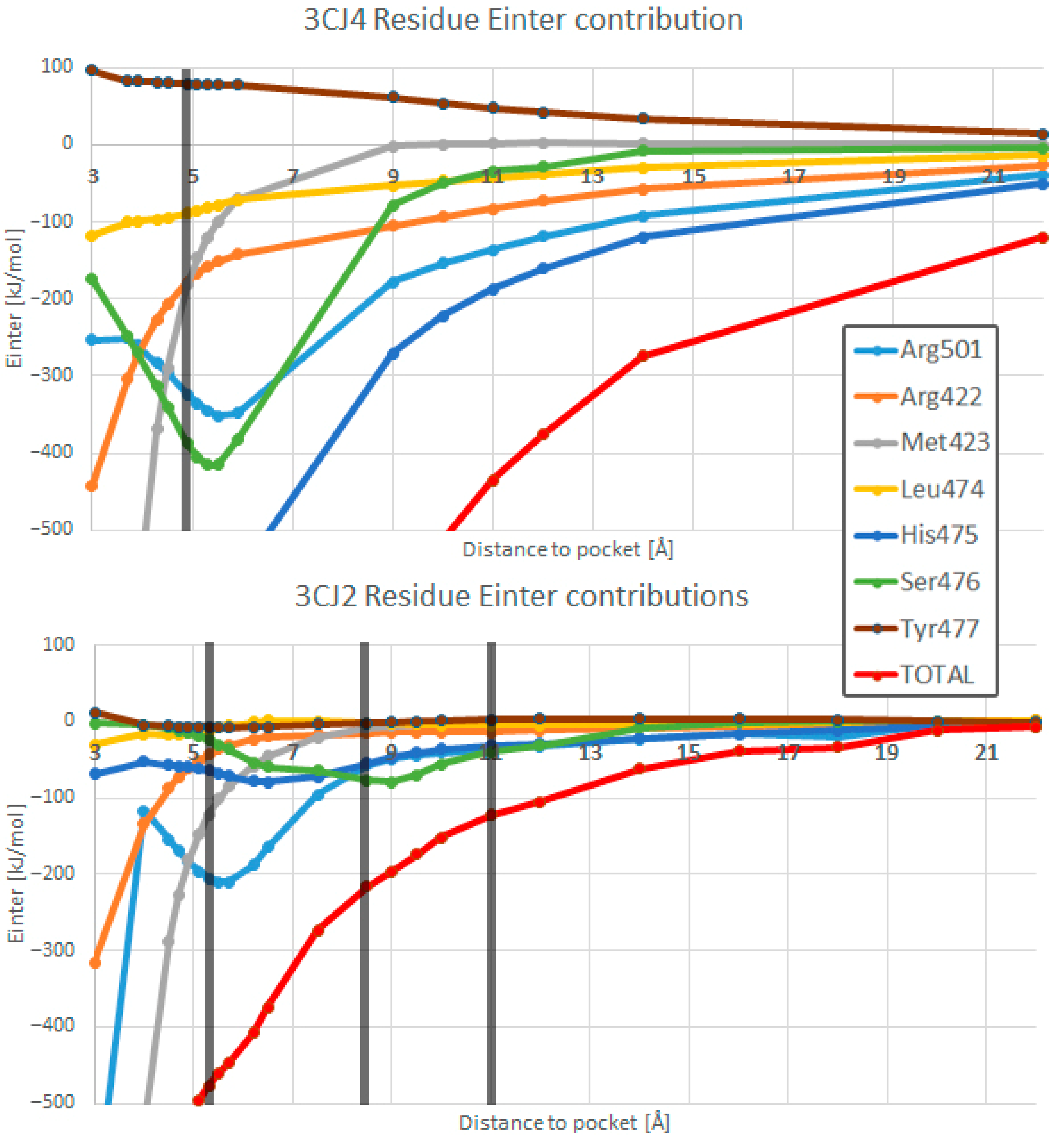
4.2.2. The 3CJ4 System
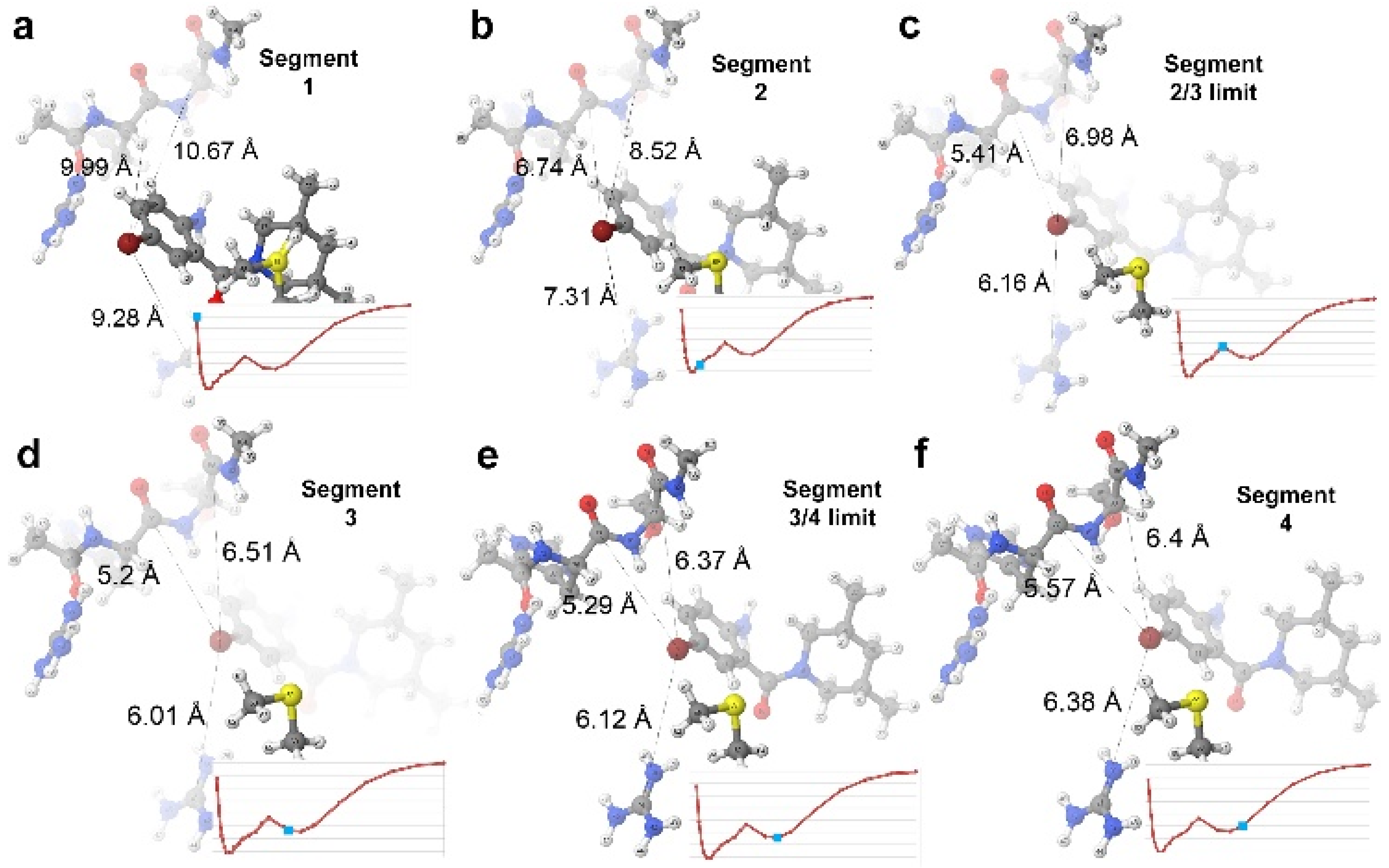
4.2.3. The 3CJ2 System
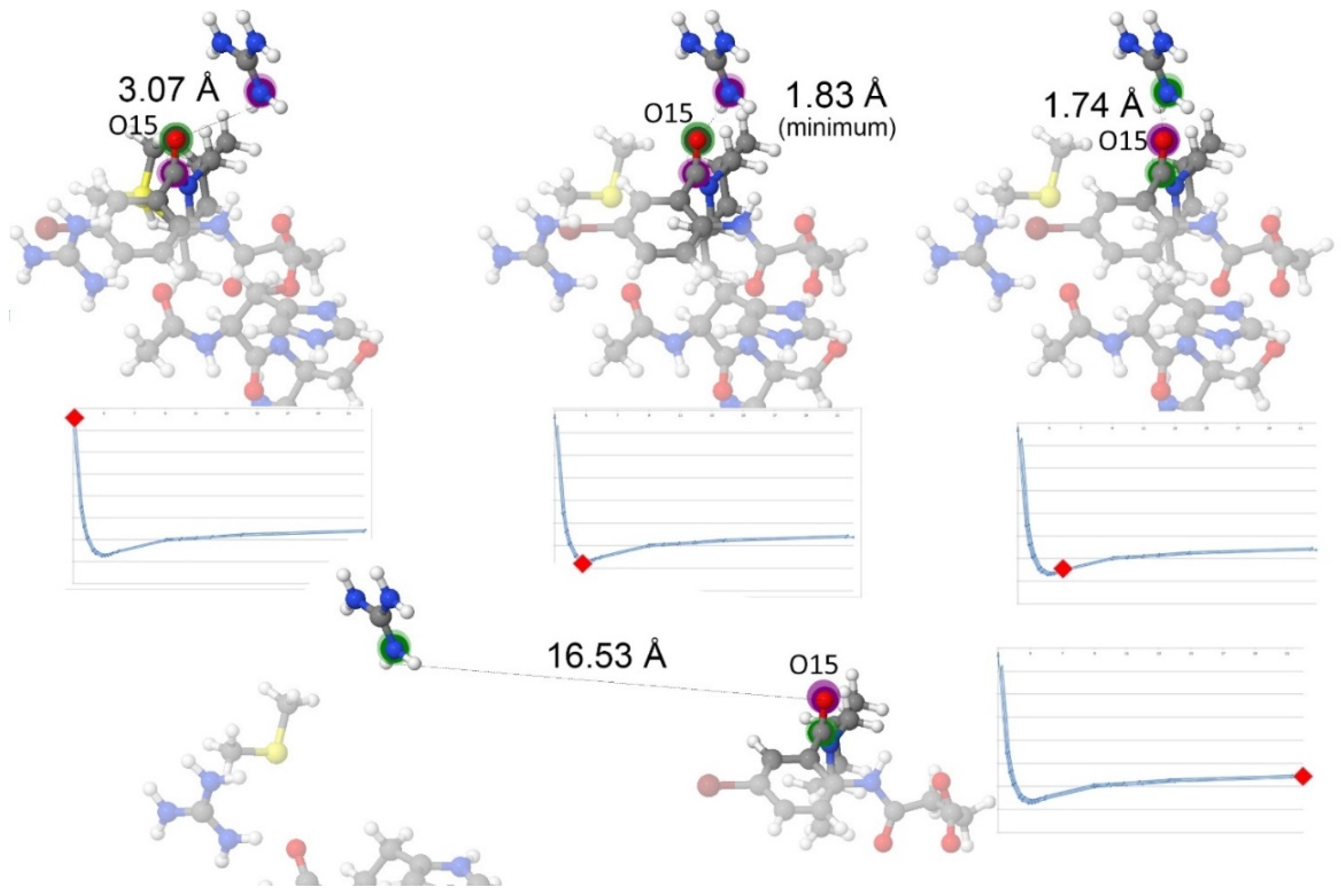
4.3. Interacting Quantum Fragments Analysis
5. Discussion
6. Conclusions
- The changes in IQA energies along the progressive snapshots of a system where a coordinate of interest is changed (in this case, ligand–pocket distance) can explain and find the pharmacophore of a drug candidate from the interaction IQA data of a drug candidate (ligand) and protein pocket. The REG-IQA ranking determines which IQA terms can be used as a subset for explaining the full energetic behaviour of the system.
- It was observed from the two types of REG ranking (A-A′ and A-B) that the full atomic contributions ranking (A-A′) is a better first approach when looking at atomic contributions, as it only contains as many terms as the number of atoms in the system, i.e., it is a summary of the whole A-B ranking. In this ranking, an atom either has a contribution in favour of the whole system energetic profile or against it. The A-B interactions are more detailed but are not an appropriate first way of looking at a system this size or larger, as an atom can have contributions both in favour of and against the system’s energetic behaviour. We suggest A-B interaction energies to be considered only as a second step, for particularly important pairs of atoms whose energies are of interest and to find out which type of IQA energy is responsible for the importance of certain atoms.
- Hydrogen bonds are very strong when compared with other electrostatic interactions. This work confirmed that new hydrogen bonds in improved drug candidates can mask other important interactions in the PES.
- The addition of more electrostatic interactions, coming from the addition of a polar group in the drug design process, shifted the overall optimal position of the distance between the drug candidate and the pocket by 0.4 Å, as the global minimum will occur at the optimal distance considering all hydrogen bonds at the same time.
- A neighbour effect was observed, in which an atom loses stability when it donates a proton or when its covalently bonded neighbour becomes a hydrogen acceptor. The energy rises when its covalent neighbour becomes involved in a hydrogen bond. This effect can only be observed in the full atomic contributions (A-A′) REG ranking, which summarises hundreds of IQA pairwise (A-B) terms. However, only by looking at the pairwise A-B ranking is it possible to observe that Vcl is the type of IQA energy responsible for this effect.
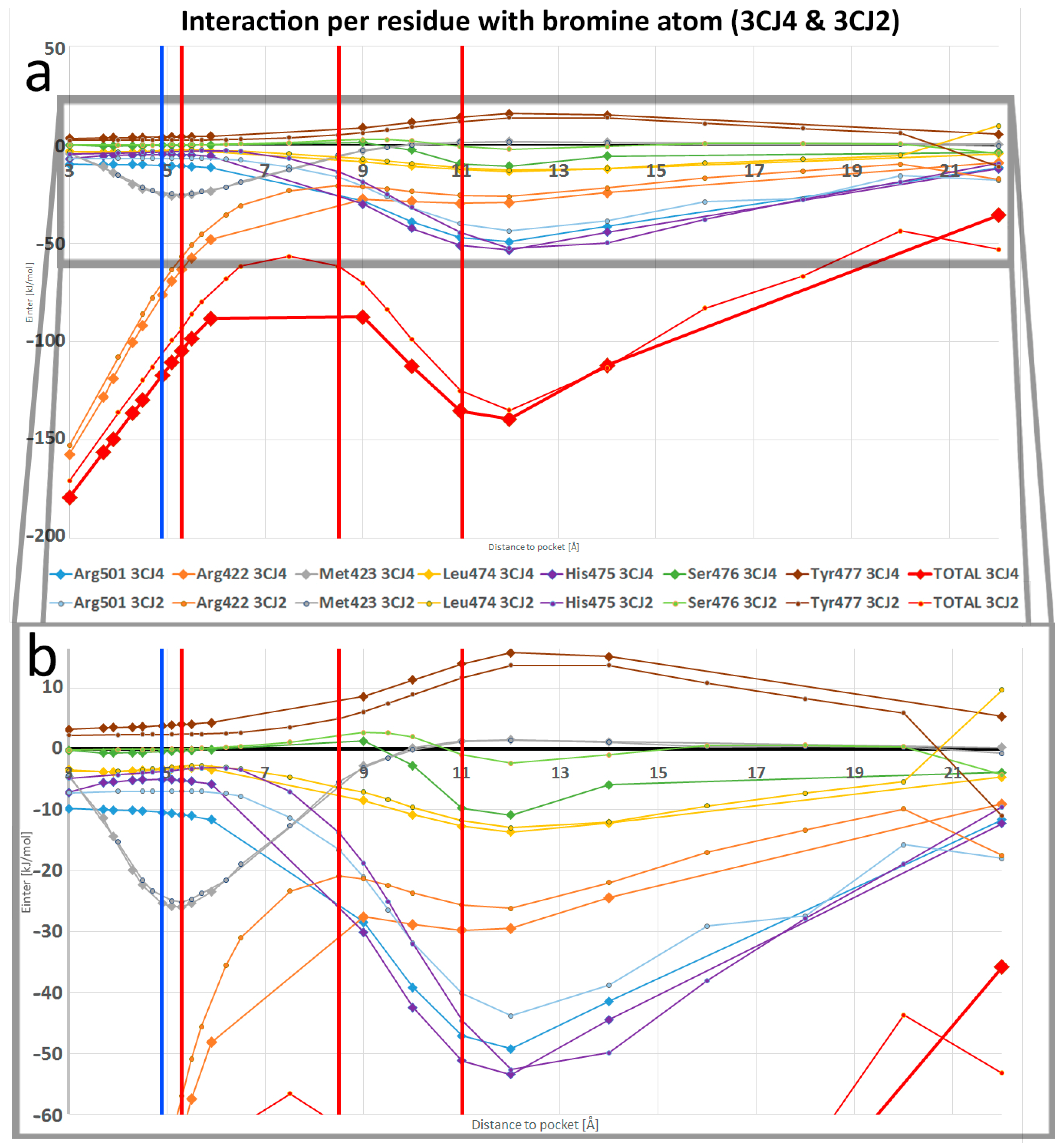
- The REG-IQA method reveals the importance of the self-energies in the system’s stabilisation when the ligand and the pocket approach each other too closely. A ranking of only the bromine A-B interactions reveals the importance of self-energy when a bromine atom is far enough and Eself is more negative. This means that the heavy atom “would rather be by itself”.
- The REG method allows the analysis of even a small increase in stability caused by the electrostatic attraction of positive residues interacting with the bromine atom of the ligand when it moves away from the allosteric site, and for us pinpoint that this behaviour comes mainly from electrostatics (Vcl) and sterics (Eself). Maybe the importance of electrostatics was to be expected considering the partial charge of the atom, but the importance of Eself is a novel finding.
- The IQF analysis obtains the ligand–pocket interaction energy in the IQA framework. At short range, the interaction has a predominantly covalent component until the separation of the global minimum, beyond which the contribution by Vxc wanes and the electrostatics (Vcl) take the predominant role in the waning interaction.
- IQF confirms that the interaction between the ligand bromine atom and the pocket is largely similar across the two different systems, which supports the very concept of fragment-based drug design. The interactions of the moieties of earlier stages of a drug candidate are maintained as new moieties are added to improve them.
- An IQA study allows for a thorough assessment of the enthalpic component in drug design, which is more difficult to optimise than the entropic contribution. A polar group in the drug candidate may help to bind it strongly to the pocket, but the surrounding solvent will also interact with this polar group and the entropic penalties coming from desolvation can decrease the binding. As drug candidates are currently being optimised both enthalpically and entropically, the importance of hydrophobic, poorly soluble drug candidates and a better description of the non-polar interactions makes IQA and QCT important newcomers to the field of drug design, which can contribute to the identification of more efficient drug candidates.
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Popelier, P.L.A.; Kosov, D.S. Atom-atom partitioning of intramolecular and intermolecular Coulomb energy. J. Chem. Phys. 2001, 114, 6539. [Google Scholar] [CrossRef]
- Salvador, P.; Duran, M.; Mayer, I. One- and two-center energy components in the atoms in molecules theory. J. Chem. Phys. 2001, 115, 1153. [Google Scholar] [CrossRef]
- Blanco, M.A.; Martín Pendás, A.; Francisco, E. Interacting quantum atoms: A correlated energy decomposition scheme based on the quantum theory of atoms in molecules. J. Chem. Theory Comput. 2005, 1, 1096. [Google Scholar] [CrossRef]
- Antonysamy, S.S.; Aubol, B.; Blaney, J.; Browner, M.F.; Giannetti, A.M.; Harris, S.F.; Hebert, N.; Hendle, J.; Hopkins, S.; Jefferson, E.; et al. Fragment-based discovery of hepatitis C virus NS5b RNA polymerase inhibitors. Bioorg. Med. Chem. Lett. 2008, 18, 2990. [Google Scholar] [CrossRef] [PubMed]
- Popelier, P.L.A. The Chemical Bond—100 Years Old and Getting Stronger; Mingos, M., Ed.; Springer: Cham, Switzerland, 2016; p. 71. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Guevara-Vela, J.M.; Francisco, E.; Rocha-Rinza, T.; Martín Pendás, A. Interacting Quantum Atoms—A Review. Molecules 2020, 25, 4028. [Google Scholar] [CrossRef] [PubMed]
- Symons, B.C.B.; Williamson, D.J.; Brooks, C.M.; Wilson, A.L.; Popelier, P.L.A. Does the Intra-Atomic Deformation Energy of Interacting Quantum Atoms Represent Steric Energy? Chem. Open 2019, 8, 560. [Google Scholar]
- García-Revilla, M.A.; Cortés-Guzmán, F.; Rocha-Rinza, T.; Hernández-Trujillo, J. Latin American contributions to quantum chemical topology. Int. J. Quantum Chem. 2019, 119, e25789. [Google Scholar] [CrossRef]
- Badri, Z.; Foroutan-Nejad, C.; Kozelka, J.; Marek, R. On the non-classical contribution in lone-pair–π interaction. PCCP 2015, 17, 26183. [Google Scholar] [CrossRef]
- Maxwell, P.; Popelier, P.L.A. Transferable atoms: An intra-atomic perspective through the study of homogeneous oligopeptides. Mol. Phys. 2016, 114, 1304. [Google Scholar] [CrossRef]
- Guevara-Vela, J.M.; Romero-Montalvo, E.; Costales, A.; Martín Pendás, A.; Rocha-Rinza, T. The nature of resonance-assisted hydrogen bonds: A quantum chemical topology perspective. PCCP 2016, 18, 26383. [Google Scholar] [CrossRef]
- Eskandari, K.; Lesani, M. Does Fluorine Participate in Halogen Bonding? Chem. Eur. J. 2015, 21, 4739. [Google Scholar] [CrossRef]
- Romero-Montalvo, E.; Guevara-Vela, J.M.; Vallejo Narváez, W.E.; Costales, A.; Martín Pendás, Á.; Hernández-Rodríguez, M.; Rocha-Rinza, T. The bifunctional catalytic role of water clusters in the formation of acid rain. Chem. Commun. 2017, 53, 3516. [Google Scholar] [CrossRef]
- Castor-Villegas, V.M.; Guevara-Vela, J.M.; Vallejo Narváez, W.E.; Martín Pendás, Á.; Rocha-Rinza, T.; Fernández-Alarcón, A. On the strength of hydrogen bonding within water clusters on the coordination limit. J. Comput. Chem. 2020, 41, 2266. [Google Scholar] [CrossRef] [PubMed]
- Holguín-Gallego, F.J.; Chávez-Calvillo, R.; García-Revilla, M.; Francisco, E.; Martín Pendás, Á.; Rocha-Rinza, T. Electron correlation in the interacting quantum atoms partition via coupled-cluster lagrangian densities. J. Comput. Chem. 2016, 37, 1753. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Voet, A.; Zhang, K.Y. Fragment based drug design: From experimental to computational approaches. Curr. Med. Chem. 2012, 19, 5128. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Archundia, M.; Bello, M.; Correa-Basurto, J. Design of Drugs by Filtering Through ADMET, Physicochemical and Ligand-Target Flexibility Properties. Methods Mol. Biol. 2018, 1824, 403. [Google Scholar]
- Martínez-Mayorga, K.; Madariaga-Mazon, A.; Medina-Franco, J.L.; Maggiora, G. The impact of chemoinformatics on drug discovery in the pharmaceutical industry. Expert Opin. Drug Discov. 2020, 15, 293. [Google Scholar] [CrossRef]
- Bancet, A.; Raingeval, C.; Lomberget, T.; Le Borgne, M.; Guichou, J.-F.; Krimm, I. Fragment Linking Strategies for Structure-Based Drug Design. J. Med. Chem. 2020, 63, 11420. [Google Scholar] [CrossRef]
- Li, Q. Application of Fragment-Based Drug Discovery to Versatile Targets. Front. Mol. Biosci. 2020, 7, 180. [Google Scholar] [CrossRef]
- Robertson, A.J.; Wilson, A.L.; Burn, M.J.; Cliff, M.J.; Popelier, P.L.A.; Waltho, J.P. The Relationship between Enzyme conformational Change, Proton Transfer, and Phosphoryl Transfer in β-Phosphoglucomutase. ACS Catal. 2021, 11, 12840. [Google Scholar] [CrossRef]
- Thacker, J.C.R.; Popelier, P.L.A. The ANANKE relative energy gradient (REG) method to automate IQA analysis over configurational change. Theor. Chem. Acc. 2017, 136, 86. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.T.; Huang, K.J.; Tseng, C.K.; Chen, K.J.; Wang, H.M.; Lee, J.C. Efficient in silico assay of inhibitors of hepatitis C Virus RNA-dependent RNA polymerase by structure-based virtual screening and in vitro evaluation. Assay Drug Dev. Technol. 2011, 9, 290. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Johnson, K.A. Thumb Site 2 Inhibitors of Hepatitis C Viral RNA-dependent RNA Polymerase Allosterically Block the Transition from Initiation to Elongation. J. Biol. Chem. 2016, 291, 10067. [Google Scholar] [CrossRef]
- Koch, U.; Narjes, F. Recent progress in the development of inhibitors of the hepatitis C virus RNA-dependent RNA polymerase. Curr. Top. Med. Chem. 2007, 7, 1302. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Dorsch, W.; Lauffer, D.J.; Bilimoria, D.; Chauret, N.; Court, J.J.; Das, S.K.; Denis, F.; Mani, N.; Nanthakumar, S.; et al. Discovery of Novel Allosteric HCV NS5B Inhibitors. 2. Lactam-Containing Thiophene Carboxylates. ACS Med. Chem. Lett. 2017, 8, 251. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Zhou, E.; Ren, C.; Wang, J.; Wang, Y. Small molecule NS5B RdRp non-nucleoside inhibitors for the treatment of HCV infection: A medicinal chemistry perspective. Eur. J. Med. Chem. 2022, 240, 114595. [Google Scholar] [CrossRef] [PubMed]
- Deredge, D.; Li, J.; Johnson, K.A.; Wintrode, P.L. Hydrogen/Deuterium Exchange Kinetics Demonstrate Long Range Allosteric Effects of Thumb Site 2 Inhibitors of Hepatitis C Viral RNA-dependent RNA Polymerase. J. Biol. Chem. 2016, 291, 10078. [Google Scholar] [CrossRef]
- Barreca, M.L.; Iraci, N.; Manfroni, G.; Cecchetti, V. Allosteric inhibition of the hepatitis C virus NS5B polymerase: In silico strategies for drug discovery and development. Future Med. Chem. 2011, 3, 1027. [Google Scholar] [CrossRef] [PubMed]
- Love, R.A.; Parge, H.E.; Yu, X.; Hickey, M.J.; Diehl, W.; Gao, J.; Wriggers, H.; Ekker, A.; Wang, L.; Thomson, J.A.; et al. Crystallographic identification of a noncompetitive inhibitor binding site on the hepatitis C virus NS5B RNA polymerase enzyme. J. Virol. 2003, 77, 7575. [Google Scholar] [CrossRef]
- Hajduk, P.J.; Greer, J. A decade of fragment-based drug design: Strategic advances and lessons learned. Nat. Rev. Drug Discov. 2007, 6, 211. [Google Scholar] [CrossRef]
- Chan, L.; Das, S.K.; Reddy, T.J.; Poisson, C.; Proulx, M.; Pereira, O.; Courchesne, M.; Roy, C.; Wang, W.; Siddiqui, A.; et al. Discovery of thiophene-2-carboxylic acids as potent inhibitors of HCV NS5B polymerase and HCV subgenomic RNA replication. Part 1: Sulfonamides. Bioorg. Med. Chem. Lett. 2004, 14, 793. [Google Scholar] [CrossRef] [PubMed]
- Golub, A.G.; Gurukumar, K.R.; Basu, A.; Bdzhola, V.G.; Bilokin, Y.; Yarmoluk, S.M.; Lee, J.-C.; Talele, T.T.; Nichols, D.B.; Kaushik-Basu, N. Discovery of new scaffolds for rational design of HCV NS5B polymerase inhibitors. Eur. J. Med. Chem. 2012, 58, 258. [Google Scholar] [CrossRef] [PubMed]
- O’Farrell, D.; Trowbridge, R.; Rowlands, D.; Jäger, J. Substrate Complexes of Hepatitis C Virus RNA Polymerase (HC-J4): Structural Evidence for Nucleotide Import and De-novo Initiation. J. Mol. Biol. 2003, 326, 1025. [Google Scholar] [CrossRef]
- Boyce, S.E.; Tirunagari, N.; Niedziela-Majka, A.; Perry, J.; Wong, M.; Kan, E.; Lagpacan, L.; Barauskas, O.; Hung, M.; Fenaux, M.; et al. Structural and Regulatory Elements of HCV NS5B Polymerase–β-Loop and C-Terminal Tail–Are Required for Activity of Allosteric Thumb Site II Inhibitors. PLoS ONE 2014, 9, e84808. [Google Scholar]
- The PyMOL Molecular Graphics System; Version 2.2.3; Schrödinger, LLC.: New York, NY, USA, 2015.
- Abdurakhmanov, E.; Solbak, S.O.; Danielson, U.H. Biophysical Mode-of-Action and Selectivity Analysis of Allosteric Inhibitors of Hepatitis C Virus (HCV) Polymerase. Viruses 2017, 9, 151. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, P.; Martín Pendás, A.; Popelier, P.L.A. Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory. Phys. Chem. Chem. Phys. 2016, 18, 20986. [Google Scholar] [CrossRef]
- Guevara-Vela, J.M.; Romero-Montalvo, E.; Gómez, V.A.M.; Chávez-Calvillo, R.; García-Revilla, M.; Francisco, E.; Martín Pendás, Á.; Rocha-Rinza, T. Hydrogen bond cooperativity and anticooperativity within the water hexamer. PCCP 2016, 18, 19557. [Google Scholar] [CrossRef]
- Orangi, N.; Eskandari, K.; Thacker, J.C.R.; Popelier, P.L.A. Directionality of Halogen Bonds: An Interacting Quantum Atoms (IQA) and Relative Energy Gradient (REG) Study. Chem. Phys. Chem. 2019, 20, 1922. [Google Scholar] [CrossRef]
- Martín Pendás, A.; Blanco, M.A.; Francisco, E. Chemical fragments in real space: Definitions, properties, and energetic decompositions. J. Comput. Chem. 2007, 28, 161. [Google Scholar] [CrossRef]
- Martín Pendás, A.; Francisco, E.; Blanco, M.A. Charge transfer, chemical potentials, and the nature of functional groups: Answers from quantum chemical topology. Faraday Discuss. 2007, 135, 423. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll; Version 16.01.09; TK Gristmill Software: Overland Park, KS, USA, 2016. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Polestshuk, P.M. Accurate integration over atomic regions bounded by zero-flux surfaces. J. Comput. Chem. 2013, 34, 206. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Pu, J.; Lynch, B.J.; Truhlar, D.G. Tests of second-generation and third-generation density functionals for thermochemical kinetics. Phys. Chem. Chem. Phys. 2004, 6, 673. [Google Scholar] [CrossRef]
- Hanson, R.M. Jmol–a paradigm shift in crystallographic visualization. J. Appl. Crystallogr. 2010, 43, 1250. [Google Scholar] [CrossRef]
- Vallejo Narváez, W.E.; Jiménez, E.I.; Romero-Montalvo, E.; Sauza-de la Vega, A.; Quiroz-García, B.; Hernández-Rodríguez, M.; Rocha-Rinza, T. Acidity and basicity interplay in amide and imide self-association. Chem. Sci. 2018, 9, 4402. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Ng, K.K.; Cherney, M.M.; Chan, L.; Yannopoulos, C.G.; Bedard, J.; Morin, N.; Nguyen-Ba, N.; Alaoui-Ismaili, M.H.; Bethell, R.C.; et al. Non-nucleoside analogue inhibitors bind to an allosteric site on HCV NS5B polymerase. Crystal structures and mechanism of inhibition. J. Biol. Chem. 2003, 278, 9489. [Google Scholar] [CrossRef]
- Freire, E. Do enthalpy and entropy distinguish first in class from best in class? Drug Discov. Today 2008, 13, 861. [Google Scholar] [CrossRef]
- Krimmer, S.G.; Klebe, G. Thermodynamics of protein–ligand interactions as a reference for computational analysis: How to assess accuracy, reliability and relevance of experimental data. J. Comput. Aided Mol. Des. 2015, 29, 867. [Google Scholar] [CrossRef]
- Popelier, P.L.A. Non-covalent interactions from a Quantum Chemical Topology perspective. J. Mol. Model. 2022, 28, 276. [Google Scholar] [CrossRef]
- Phipps, M.J.S.; Fox, T.; Tautermann, C.S.; Skylaris, C.-K. Energy decomposition analysis approaches and their evaluation on prototypical protein–drug interaction patterns. Chem. Soc. Rev. 2015, 44, 3177. [Google Scholar] [CrossRef]
- Thapa, B.; Raghavachari, K. Energy Decomposition Analysis of Protein–Ligand Interactions Using Molecules-in-Molecules Fragmentation-Based Method. J. Chem. Inf. Model 2019, 59, 3474. [Google Scholar] [CrossRef]
- Phipps, M.J.S.; Fox, T.; Tautermann, C.S.; Skylaris, C.K. Energy Decomposition Analysis Based on Absolutely Localized Molecular Orbitals for Large-Scale Density Functional Theory Calculations in Drug Design. J. Chem. Theory Comput. 2016, 12, 3135. [Google Scholar] [CrossRef] [PubMed]
- Zapata-Acevedo, C.A.; Guevara-Vela, J.M.; Popelier, P.L.A.; Rocha-Rinza, T.R. Binding Energy Partition of Promising IRAK-4 Inhibitor (Zimlovisertib) for the Treatment of COVID-19 Pneumonia. Chem. Phys. Chem. 2022. Epub ahead of print. [Google Scholar] [CrossRef] [PubMed]
- López, R.; Díaz, N.; Francisco, E.; Martín Pendás, A.; Suárez, D. QM/MM Energy Decomposition Using the Interacting Quantum Atoms Approach. J. Chem. Inf. Model 2022, 62, 1510. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.U.D. Descriptors and their selection methods in QSAR analysis: Paradigm for drug design. Drug Discov. Today 2016, 21, 1291. [Google Scholar]



| PDB ID | Ligand Diagram | IC50 (μM) | Kd (μM) |
|---|---|---|---|
| 3CJ2 | 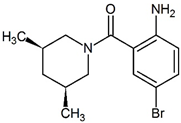 | 17 | 14 |
| 3CJ4 | 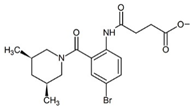 | 1 | 0.31 |
| IQA Energy Term | Location | Partial Charge | REG Value | Pearson Correlation Coefficient |
|---|---|---|---|---|
| H91 | His475 sidechain, interacting directly with the acid moiety of the ligand | Positive | 0.164 | 0.997 |
| S69 | Met423, interacting directly with the ligand piperidine | Neutral | 0.144 | 0.999 |
| O47 | Ligand acid moiety, interacting directly with His475 sidechain | Negative | 0.100 | 0.998 |
| H74 | Met423, interacting directly with the ligand piperidine | Neutral | 0.095 | 0.989 |
| H30 | Ligand piperidine, interacting directly with Met423 | Neutral | 0.083 | 0.995 |
| C89 | His475 sidechain, interacting directly with the acid moiety of the ligand | Neutral | 0.075 | 0.975 |
| H21 | Ligand piperidine, interacting directly with Met423 | Neutral | 0.061 | 0.944 |
| […] | […] | […] | […] | […] |
| N93 | His475 imidazole | Negative | −0.008 | −0.638 |
| O46 | Ligand acid moiety | Negative | −0.008 | −0.858 |
| C61 | Arg422 central carbon | Positive | −0.011 | −0.958 |
| C81 | His475 main chain | Positive | −0.015 | −0.912 |
| H94 | His475 imidazole | Positive | −0.018 | −0.991 |
| IQA Energy Term (A_B) | Location of A and of B, Separated by a Comma | Partial Charge | REG Value | Pearson Correlation Coefficient |
|---|---|---|---|---|
| Vcl_Pair_C45_H91 | Ligand (C45), His475 (H91) | Positive, neutral | 0.327 | 0.995 |
| Eself_O47 | Ligand | Negative | 0.275 | 0.999 |
| Eself_S69 | Met423 | Neutral | 0.225 | 0.996 |
| Vxc_Pair_C89_H91 | His475, His475 | Neutral, neutral | 0.149 | 0.999 |
| Eself_H91 | His475 | Neutral | 0.143 | 0.989 |
| […] | […] | […] | […] | |
| Vxc_Pair_O47_H91 | Ligand (O47), His475 | Negative, neutral | −0.121 | −0.990 |
| Vcl_Pair_O46_H91 | Ligand (O46), His475 | Negative, neutral | −0.152 | −0.987 |
| Vcl_Pair_O47_H91 | Ligand (O47), His475 | Negative, neutral | −0.298 | −0.996 |
| IQA Energy Term | Location | Partial Charge | REG Value | Pearson Correlation Coefficient |
|---|---|---|---|---|
| O47 | Ligand acid moiety (hydrogen acceptor) | Negative | 0.800 | 0.997 |
| O46 | Ligand acid moiety (hydrogen acceptor) | Negative | 0.498 | 0.998 |
| O15 | Ligand tertiary amide (hydrogen acceptor) | Negative | 0.493 | 0.990 |
| O38 | Ligand secondary amide (hydrogen acceptor) | Negative | 0.422 | 0.999 |
| N8 | Ligand secondary amide | Negative | 0.335 | 0.990 |
| N16 | Ligand piperidine | Negative | 0.237 | 0.961 |
| […] | […] | […] | […] | […] |
| N48 | Arg501 (hydrogen donor) | Negative | −0.138 | −0.957 |
| N93 | His475 imidazole (hydrogen donor) | Negative | −0.159 | −0.886 |
| O108 | Ser476 hydroxyl (hydrogen donor) | Negative | −0.176 | −0.863 |
| N101 | Ser476 main chain (hydrogen donor) | Negative | −0.220 | −0.997 |
| C14 | Ligand tertiary amide (neighbour of hydrogen acceptor) | Positive | −0.375 | −0.968 |
| C10 | Ligand secondary amide (neighbour of hydrogen acceptor) | Positive | −0.422 | −0.994 |
| C45 | Ligand acid moiety (neighbour of hydrogen acceptor) | Positive | −0.555 | −0.962 |
| IQA Energy Term (A_B) | Location of A and of B, Separated by a Comma | Partial Charge | REG Value | Pearson Correlation Coefficient |
|---|---|---|---|---|
| Vcl_Pair_c45_n93 | Ligand acid moiety (C45), His475 imidazole (N93) | Positive, negative | 1.313 | 0.997 |
| Vcl_Pair_o47_h109 | Ligand acid moiety (O47), Ser476 (H109) | Negative, positive | 1.276 | 0.990 |
| Vcl_Pair_c45_o108 | Ligand acid moiety(C45), Ser476 (O108) | Positive, negative | 1.250 | 0.987 |
| Vcl_Pair_o47_h94 | Ligand acid moiety (O47), His475 imidazole (H94) | Negative, positive | 1.194 | 0.989 |
| Vcl_Pair_o15_c51 | Ligand tertiary amide (O15), Arg501 (C51) | Negative, positive | 1.151 | 0.981 |
| Vcl_Pair_c45_n101 | Ligand acid moiety (C45), Ser476 main chain (N101) | Positive, negative | 1.033 | 0.997 |
| Vcl_Pair_o47_c87 | Ligand acid moiety (O47), His475 main chain (C87) | Negative, positive | 0.962 | 0.992 |
| Vcl_Pair_c10_n101 | Ligand secondary amide (C10), Ser476 main chain (N101) | Positive, negative | 0.962 | 0.992 |
| Vcl_Pair_o38_c87 | Ligand secondary amide (O38), His475 main chain (C87) | Negative, positive | 0.868 | 0.995 |
| Vcl_Pair_c14_n48 | Ligand tertiary amide (C14), Arg501 (N48) | Positive, negative | 0.867 | 0.970 |
| Vcl_Pair_o47_c95 | Ligand acid moiety (O47), His475 imidazole (C95) | Negative, positive | 0.853 | 0.994 |
| Vcl_Pair_o15_h49 | Ligand tertiary amide (O15), Arg501 (H49) | Negative, positive | 0.846 | 0.988 |
| […] | […] | […] | […] | |
| Vcl_Pair_c45_h94 | Ligand acid moiety (C45), His475 imidazole (H94) | Positive, positive | 1.013 | −0.995 |
| Vcl_Pair_c45_h109 | Ligand acid moiety (C45), Ser476 (H109) | Positive, positive | 1.045 | 0.992 |
| Vcl_Pair_o38_n101 | Ligand secondary amide (O38), Ser476 main chain (N101) | Negative, negative | 1.057 | −0.997 |
| Vcl_Pair_o47_n101 | Ligand acid moiety (O47), Ser476 main chain (N101) | Negative, negative | 1.071 | −0.997 |
| Vcl_Pair_o15_n48 | Ligand tertiary amide (O15), Arg501 (N48) | Negative, negative | 1.150 | −0.984 |
| Vcl_Pair_o47_o108 | Ligand acid moiety (O47), Ser476 (O108) | Negative, negative | 1.430 | −0.992 |
| Vcl_Pair_o47_n93 | Ligand acid moiety (O47), His475 imidazole (N93) | Negative, negative | 1.449 | −0.998 |
| Segment 2 | Segment 4 | ||||||
|---|---|---|---|---|---|---|---|
| IQA Energy Term | Location | Partial Charge | REG Value | IQA Energy Term | Location | Partial Charge | REG Value |
| O15 | Ligand tertiary amide (hydrogen acceptor) | Negative | 4.238 | O15 | Ligand tertiary amide (hydrogen acceptor) | Negative | 4.399 |
| C41 | Arg501 | Positive | 2.326 | N8 | Ligand amino group (secondary amide in 3CJ4) | Negative | 4.100 |
| N8 | Ligand amino group (secondary amide in 3CJ4) | Negative | 1.811 | H4 | Ligand bromo-aryl | Neutral | 3.943 |
| H40 | Arg501 | Positive | 1.513 | N16 | Ligand piperidine | Negative | 2.981 |
| N16 | Ligand piperidine | Negative | 1.257 | C41 | Arg501 | Positive | 0.860 |
| H6 | Ligand bromo-aryl | Neutral | 1.046 | C2 | Ligand bromo-aryl | Positive | 0.701 |
| H44 | Arg501 | Positive | 0.657 | O98 | Ser476 sidechain | Negative | 0.408 |
| H47 | Arg501 | Positive | 0.643 | C51 | Arg422 | Positive | 0.355 |
| H46 | Arg501 | Positive | 0.580 | C71 | Leu474 | Positive | 0.350 |
| […] | […] | […] | […] | […] | […] | […] | […] |
| C11 | Ligand bromo-aryl | Neutral | −0.682 | N38 | Arg501 (hydrogen donor) | Negative | −0.915 |
| N38 | Arg501 (hydrogen donor) | Negative | −0.732 | C35 | Ligand dimethyl piperidine | Positive | −0.946 |
| H12 | Ligand bromo-aryl | Neutral | −0.793 | C17 | Ligand dimethyl piperidine | Positive | −1.004 |
| N45 | Arg501 | Negative | −0.988 | H9 | Ligand primary amine | Positive | −1.688 |
| N42 | Arg501 | Negative | −1.030 | H10 | Ligand primary amine | Positive | −1.779 |
| H39 | Arg501 | Positive | −1.307 | C7 | Ligand primary amine | Positive | −1.795 |
| H4 | Ligand bromo-aryl | Neutral | −1.607 | Br1 | Ligand bromo-aryl | Negative | −2.539 |
| C14 | Ligand tertiary amide (neighbour of hydrogen acceptor) | Positive | −2.263 | C14 | Ligand tertiary amide (neighbour of hydrogen acceptor) | Positive | −4.595 |
| IQA Energy Term | Location | Partial Charge | REG Value | Pearson Correlation Coefficient |
|---|---|---|---|---|
| C14 | Ligand, tertiary amide (neighbour to Hydrogen acceptor) | Positive | 4.404 | 0.948 |
| Br1 | Ligand, bromo-aryl moiety | Negative | 4.335 | 0.954 |
| N38 | Arg501 (hydrogen donor) | Negative | 1.701 | 0.978 |
| H10 | Ligand, primary amine | Positive | 1.571 | 0.940 |
| C7 | Ligand, bromo-aryl moiety (bonded to amino group) | Positive | 1.502 | 0.935 |
| H9 | Ligand, primary amine | Positive | 1.398 | 0.936 |
| H4 | Ligand, bromo-aryl moiety | Positive | 1.136 | 0.723 |
| C17 | Ligand, dimethylpiperidine | - | 0.931 | 0.946 |
| C35 | Ligand, dimethylpiperidine | - | 0.909 | 0.948 |
| […] | […] | […] | […] | […] |
| C41 | Arg501 | Positive | −1.529 | −0.983 |
| H6 | Ligand, bromo-aryl moiety | - | −2.502 | −0.997 |
| N16 | Ligand, dimethylpiperidine | Negative | −2.822 | −0.947 |
| N8 | Ligand, amino group bonded to bromo-aryl moiety | Negative | −4.048 | −0.951 |
| O15 | Ligand, tertiary amide (hydrogen acceptor) | Negative | −5.477 | −0.964 |
| IQA Energy Term (A_B) | Location of A and of B, Separated by a Comma | Partial Charge | REG Value | Pearson Correlation Coefficient |
|---|---|---|---|---|
| Vcl_Pair_br1_c77 | Ligand, His475 | Negative, positive | 2.995 | 0.959 |
| Vcl_Pair_br1_c41 | Ligand, Arg501 | Negative, positive | 2.924 | 0.960 |
| Vcl_Pair_br1_c100 | Ligand, Ser476 | Negative, positive | 2.299 | 0.942 |
| Eself_br1 | Ligand | Negative | 2.247 | 0.952 |
| Vcl_Pair_br1_c14 | Ligand (both) | Negative, positive | 1.739 | 0.947 |
| Vcl_Pair_br1_h92 | Ligand, Ser476 | Negative, positive | 1.655 | 0.930 |
| Vcl_Pair_br1_c85 | Ligand, His475 | Negative, positive | 1.587 | 0.935 |
| […] | […] | […] | […] | |
| Vcl_Pair_br1_o78 | Ligand, His475 | Negative, negative | −1.730 | −0.956 |
| Vcl_Pair_br1_o98 | Ligand, Ser476 | Negative, negative | −1.841 | −0.909 |
| Vcl_Pair_br1_n102 | Ligand, Ser476 | Negative, negative | −1.927 | −0.948 |
| Vcl_Pair_br1_n83 | Ligand, His475 | Negative, negative | −2.304 | −0.933 |
| Vcl_Pair_br1_n38 | Ligand, Arg501 | Negative, negative | −2.863 | −0.961 |
| Vcl_Pair_br1_n91 | Ligand, Ser476 | Negative, negative | −3.438 | −0.949 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapata-Acevedo, C.A.; Popelier, P.L.A. The IQA Energy Partition in a Drug Design Setting: A Hepatitis C Virus RNA-Dependent RNA Polymerase (NS5B) Case Study. Pharmaceuticals 2022, 15, 1237. https://doi.org/10.3390/ph15101237
Zapata-Acevedo CA, Popelier PLA. The IQA Energy Partition in a Drug Design Setting: A Hepatitis C Virus RNA-Dependent RNA Polymerase (NS5B) Case Study. Pharmaceuticals. 2022; 15(10):1237. https://doi.org/10.3390/ph15101237
Chicago/Turabian StyleZapata-Acevedo, César A., and Paul L. A. Popelier. 2022. "The IQA Energy Partition in a Drug Design Setting: A Hepatitis C Virus RNA-Dependent RNA Polymerase (NS5B) Case Study" Pharmaceuticals 15, no. 10: 1237. https://doi.org/10.3390/ph15101237
APA StyleZapata-Acevedo, C. A., & Popelier, P. L. A. (2022). The IQA Energy Partition in a Drug Design Setting: A Hepatitis C Virus RNA-Dependent RNA Polymerase (NS5B) Case Study. Pharmaceuticals, 15(10), 1237. https://doi.org/10.3390/ph15101237






