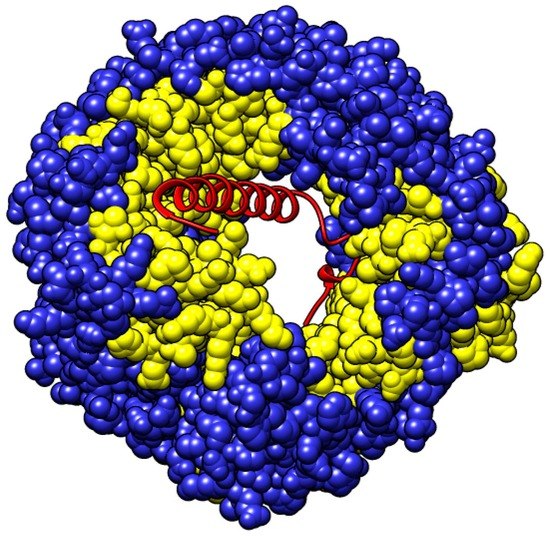
Heterodimer Binding Scaffolds Recognition via the Analysis of Kinetically Hot Residues
Abstract
1. Introduction
2. Materials and Methods
2.1. GNM Code
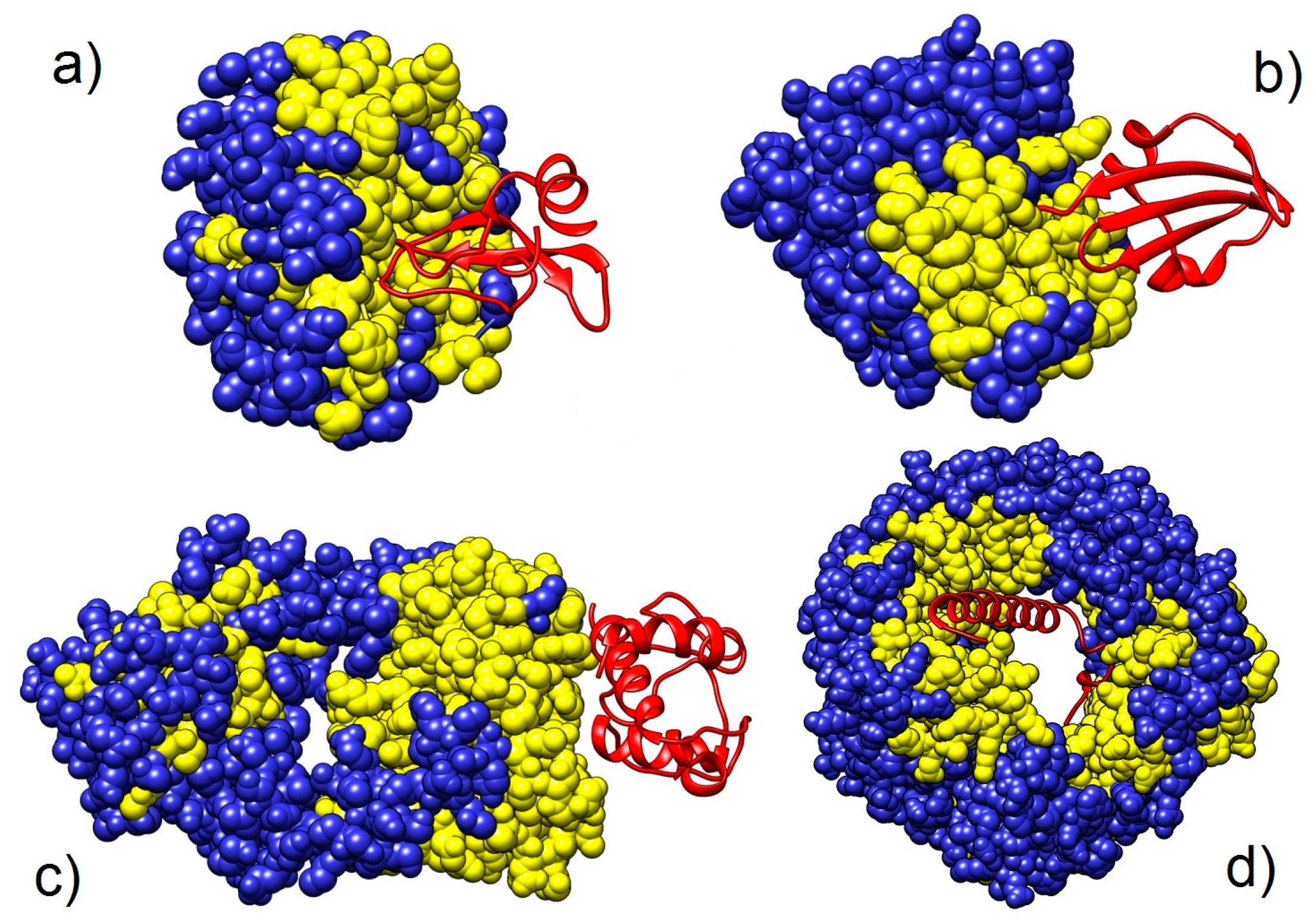
2.2. Targets
2.3. Training Set
2.4. Testing Sets
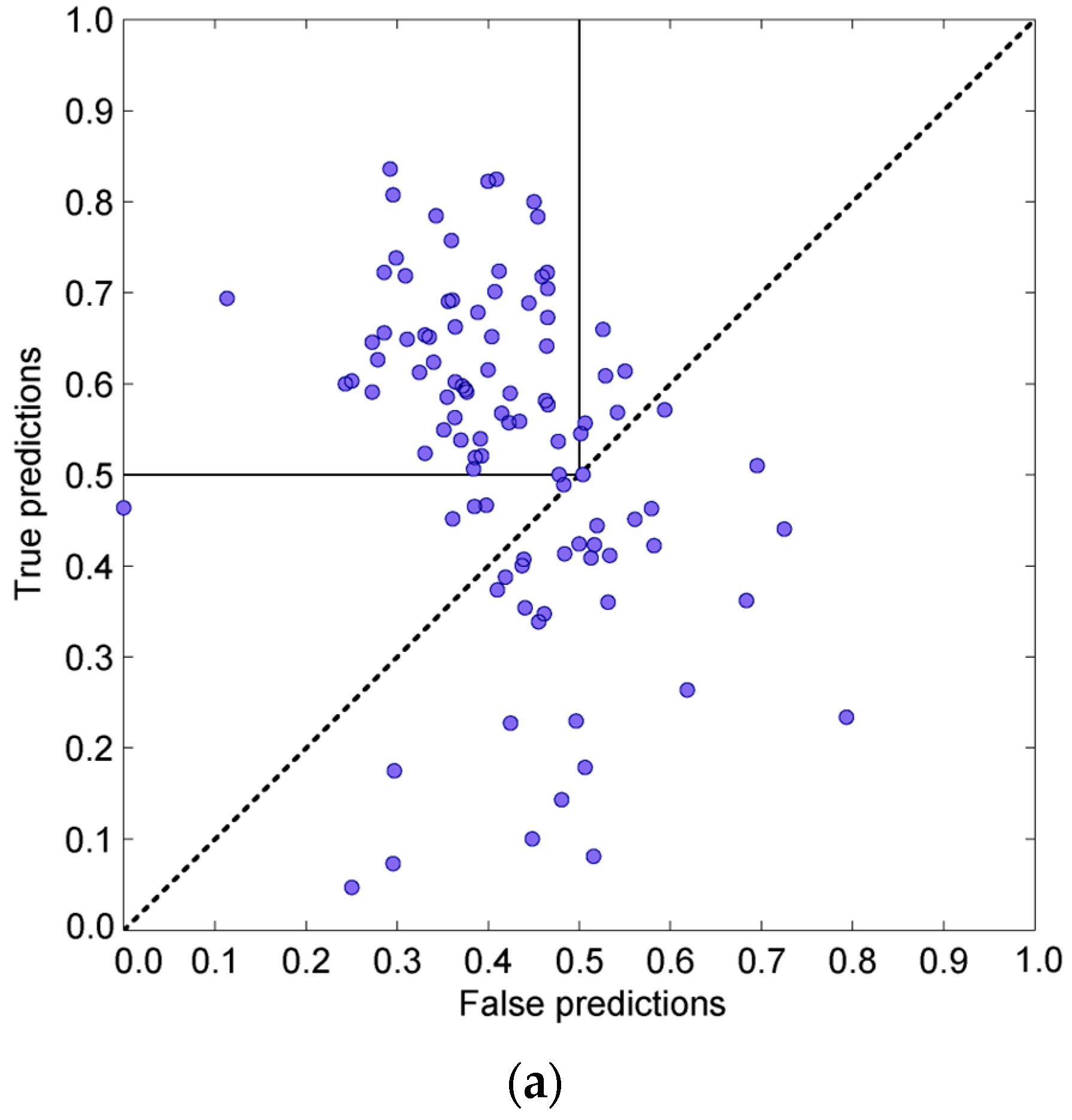
3. Results and Discussion
3.1. Simplest 1D Prediction (Sequential Neighbors Influence only) Based on 5 Fastest Modes
3.2. First Attempt to Improve the Prediction
3.2.1. Prediction Based on the Fast Modes That Corresponds to Top 10% of the Eigenvalues
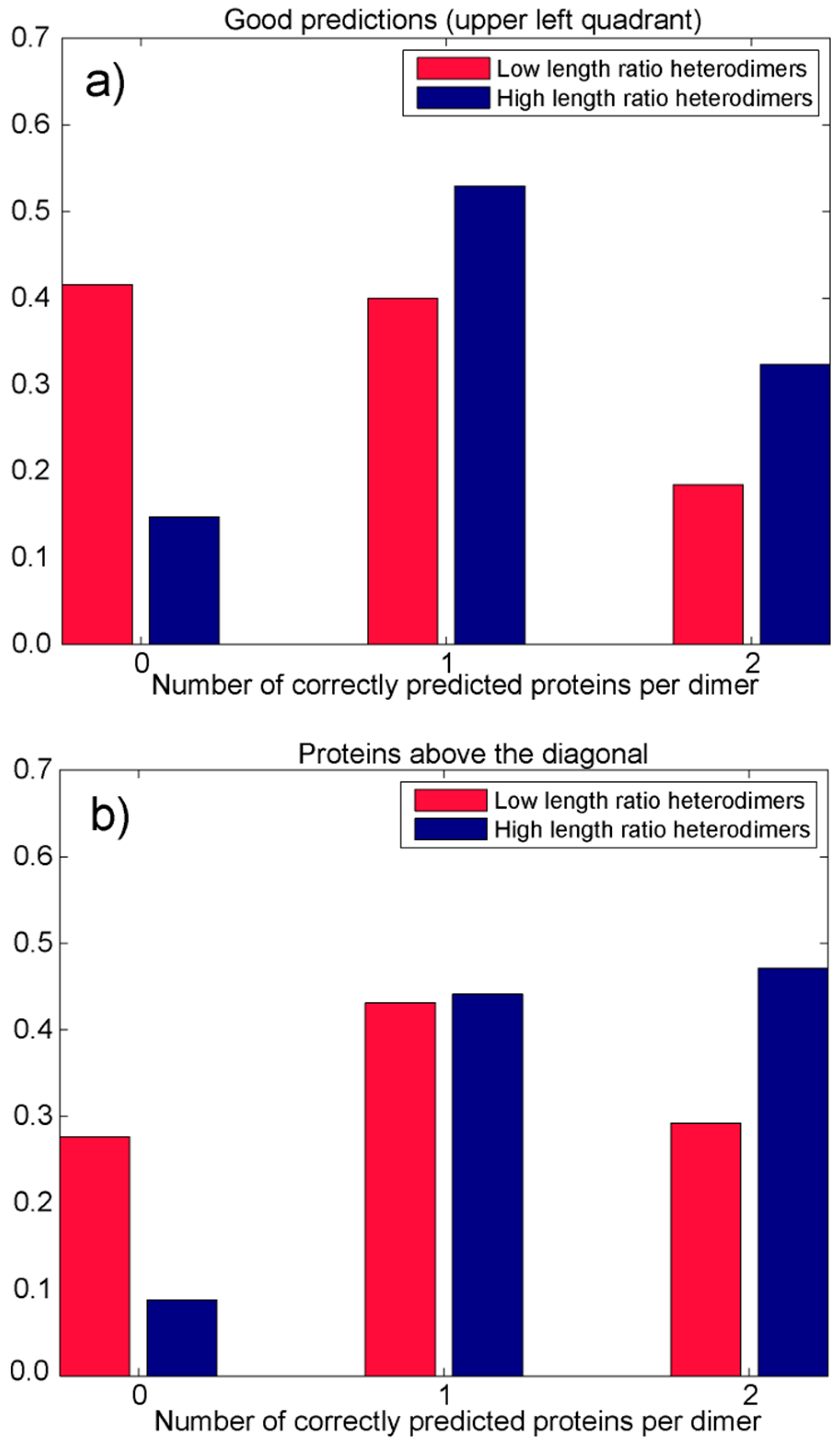
3.2.2. Analysis of Heterodimers with Very Different Sequence Lengths
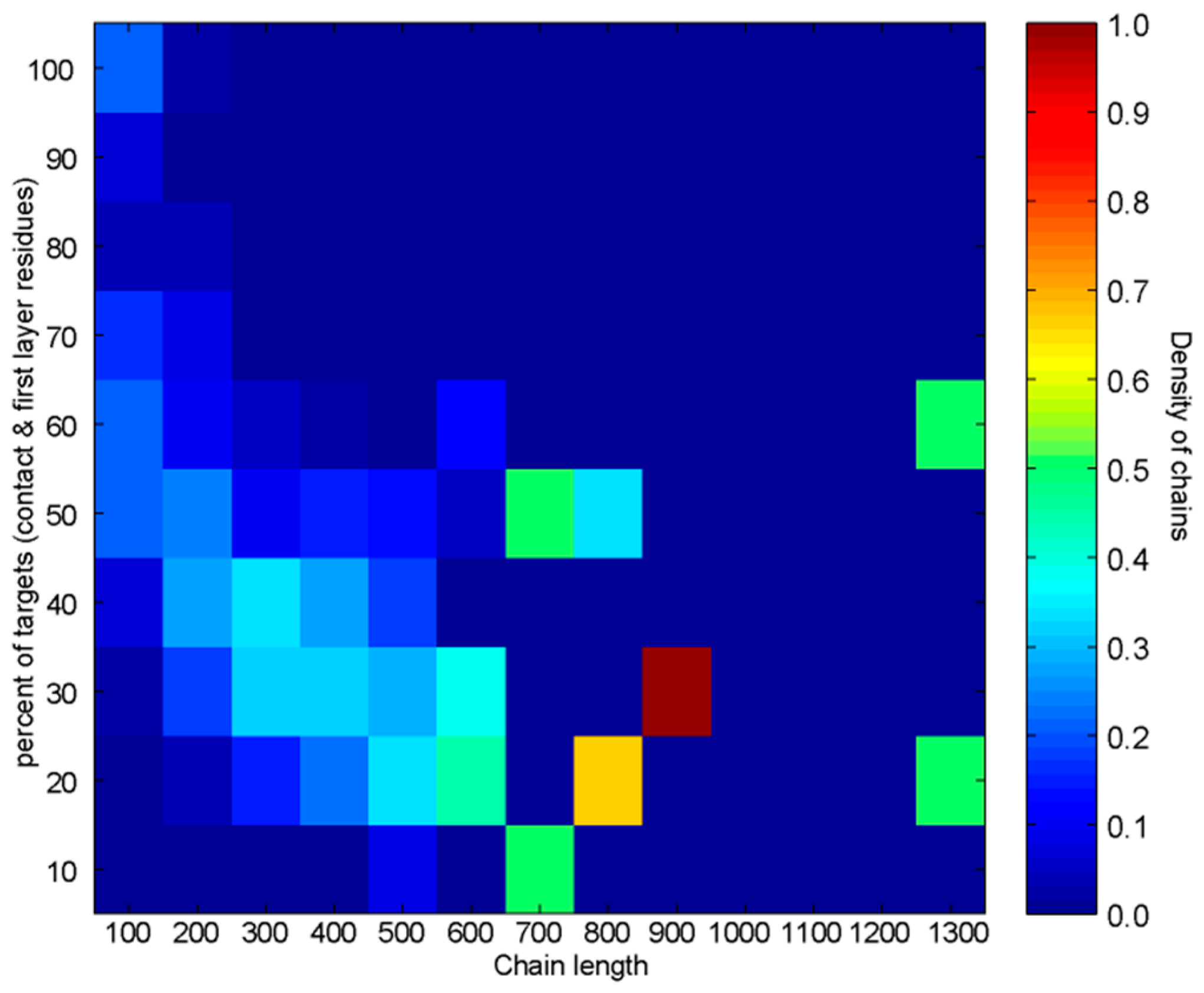
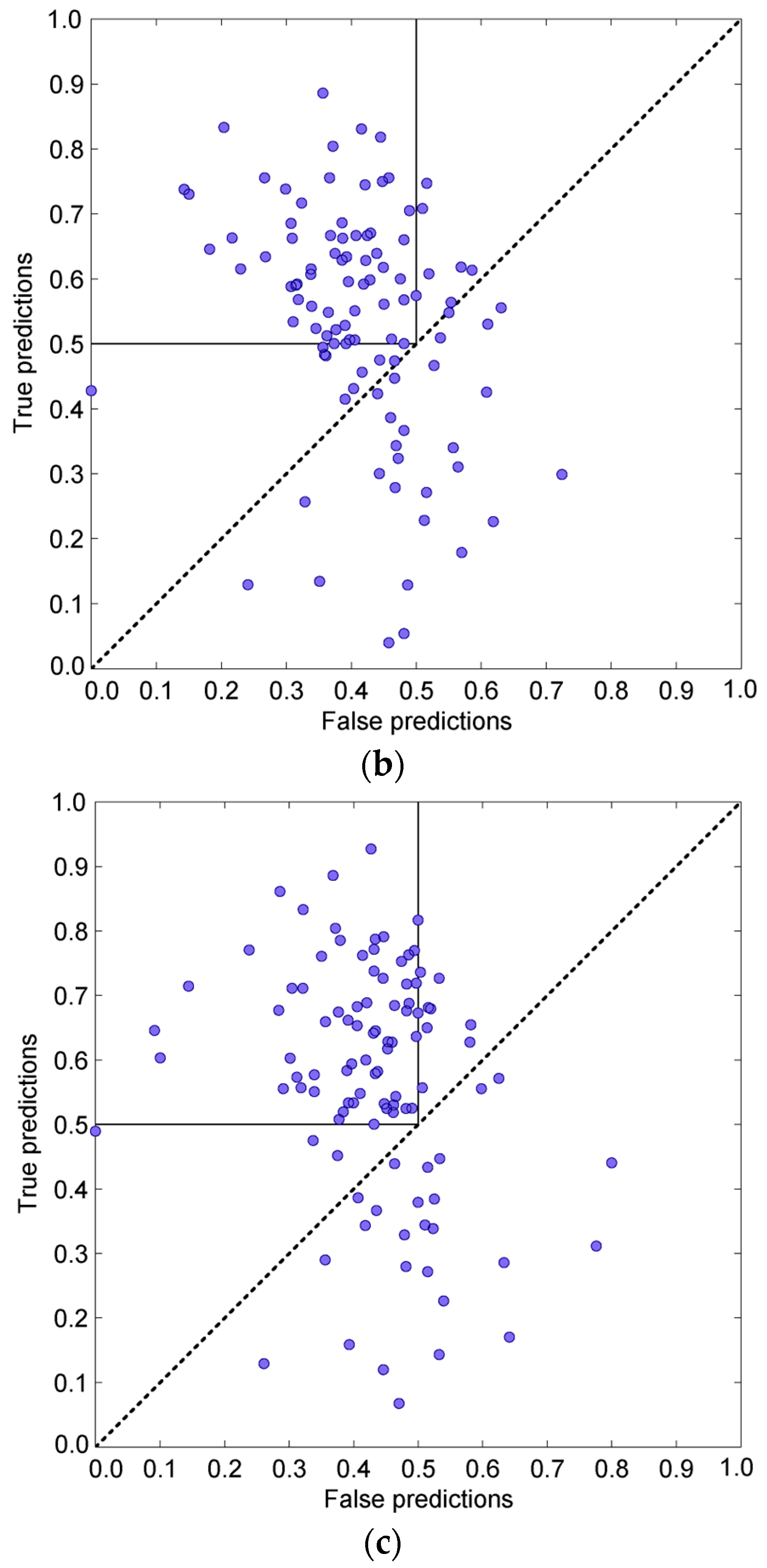
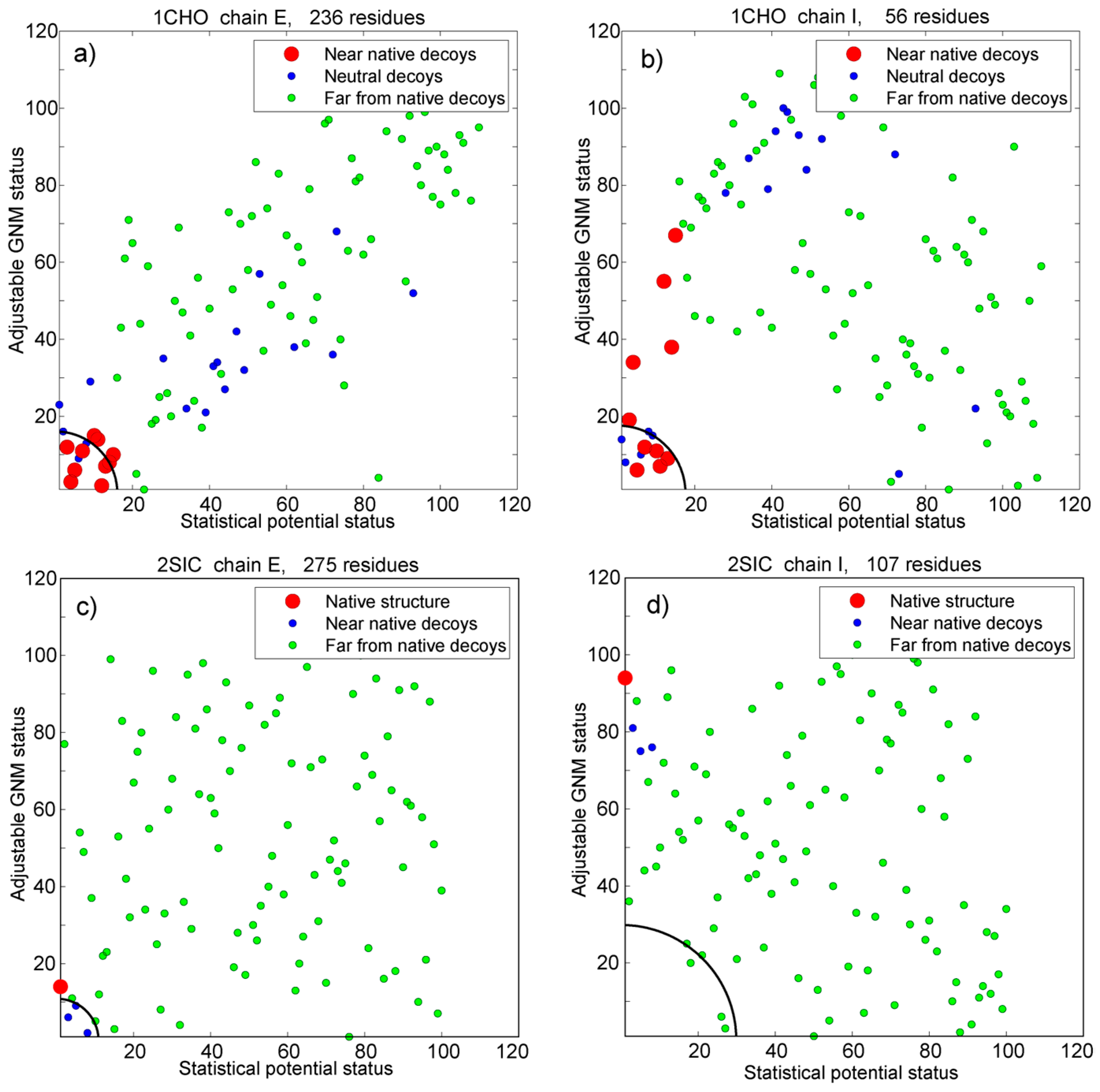
3.3. Prediction Based on the Adjustable Number of Modes
- –
- If the overall percentage of predictions is too large for that protein’s sequence length class (for example, if the percentage of predictions is larger than 60% of the total number of residues), the number of fast modes should be reduced by one, and the whole prediction procedure should be repeated (Equation (1)).
- –
- If the percentage of predictions is too small for the protein’s sequence length class (e.g., less than 20% of all residues), the number of fast modes should be increased by one, and the whole prediction procedure should be repeated (Equation (1)).
- –
- The procedure should be repeated until the percentage of predictions does not fit between the maximum and minimum amount of predictions for a given sequence length.
3.3.1. One-Dimensional Linear Prediction
3.3.2. 3D Spatial Prediction—Variable Influence of Hot Residues
3.3.3. Combining the Sequential and Spatial Approaches
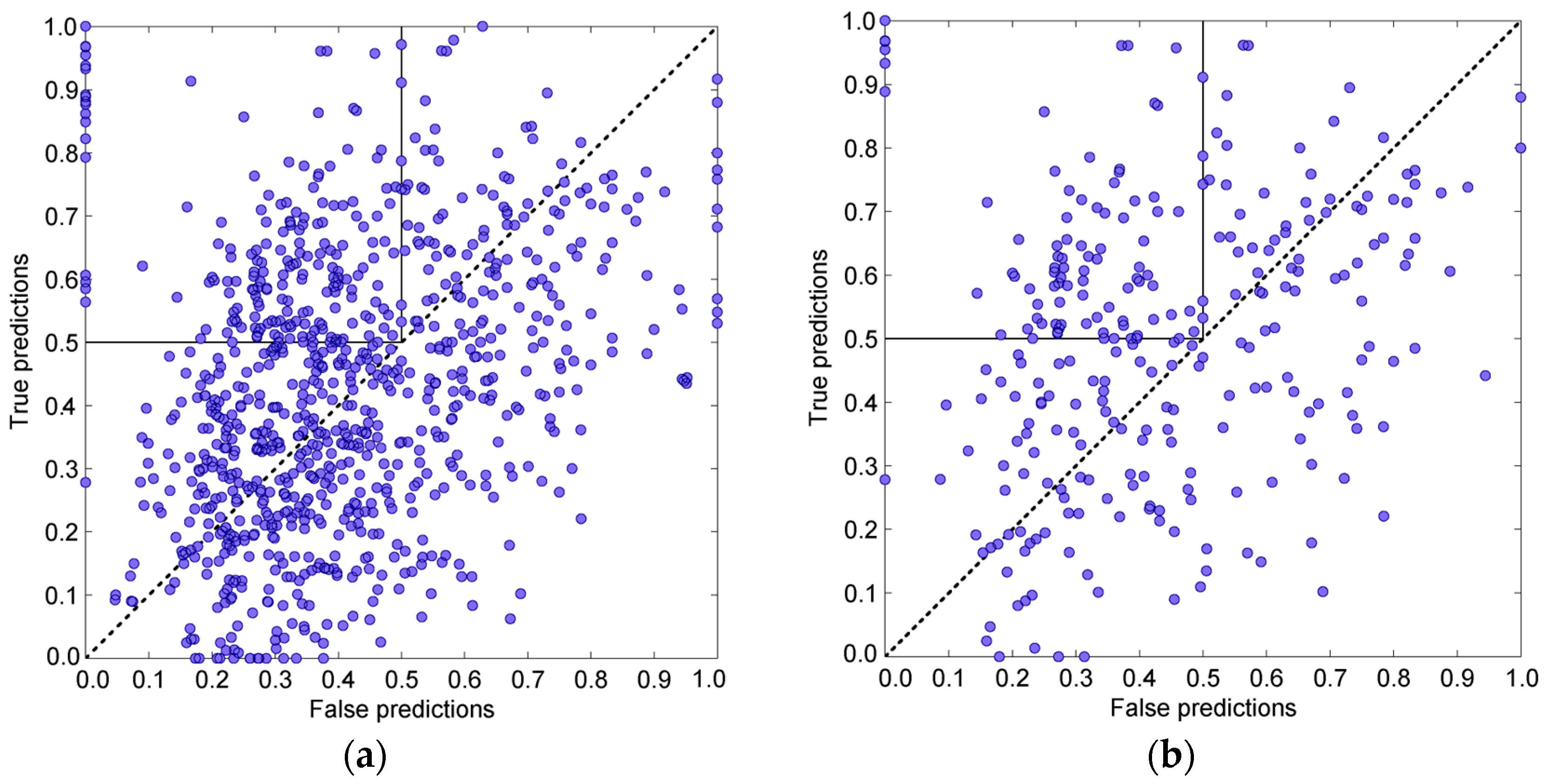
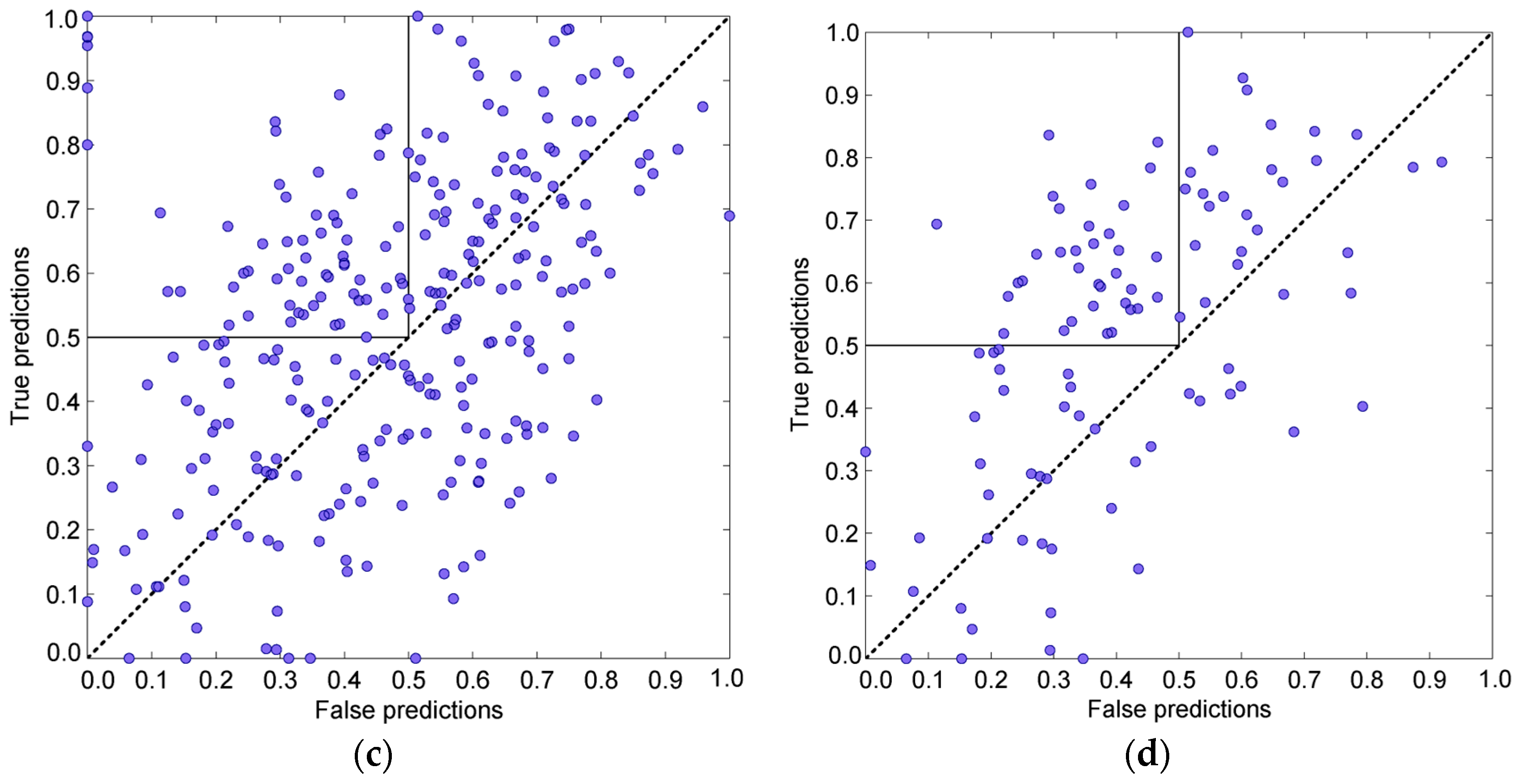
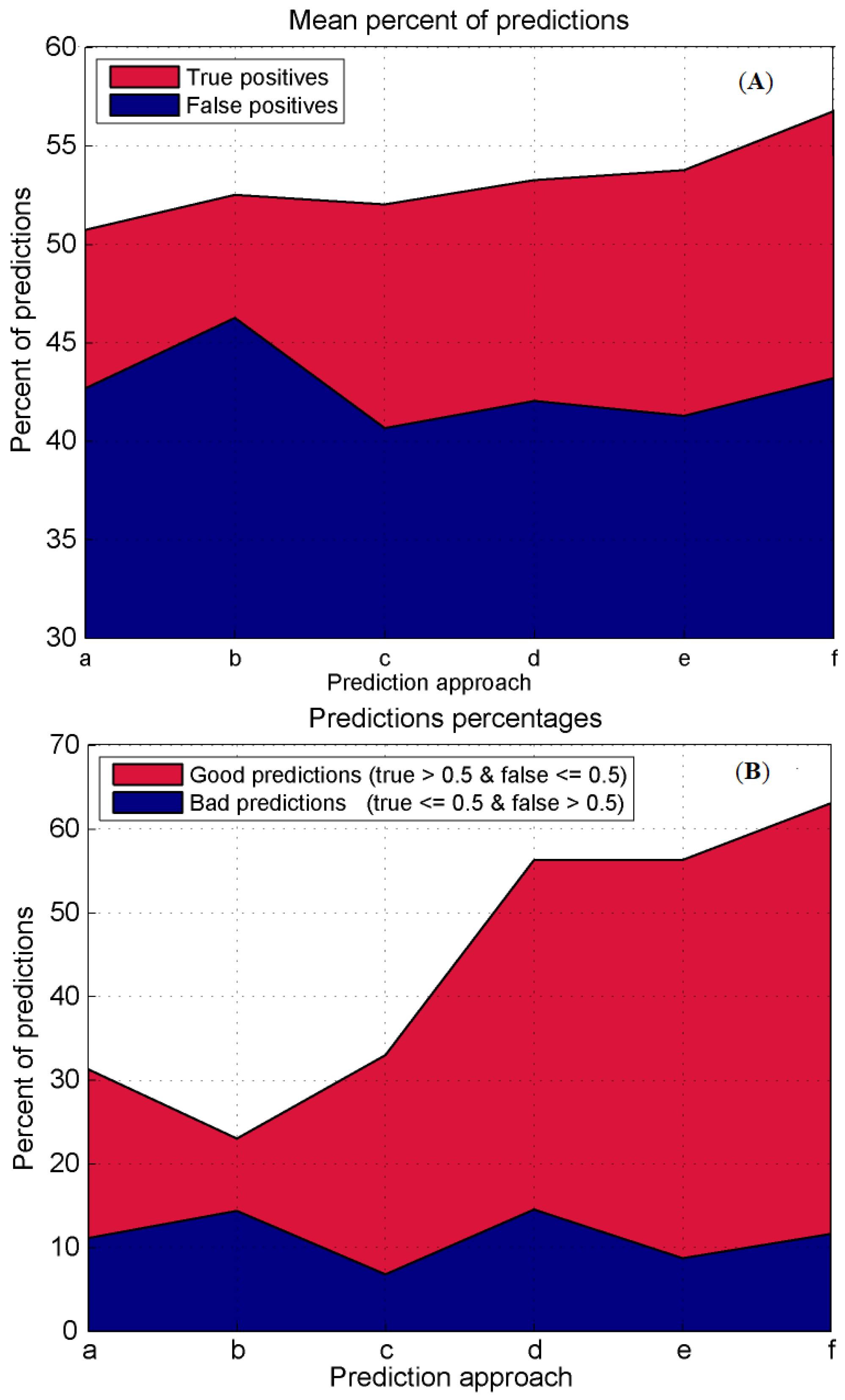
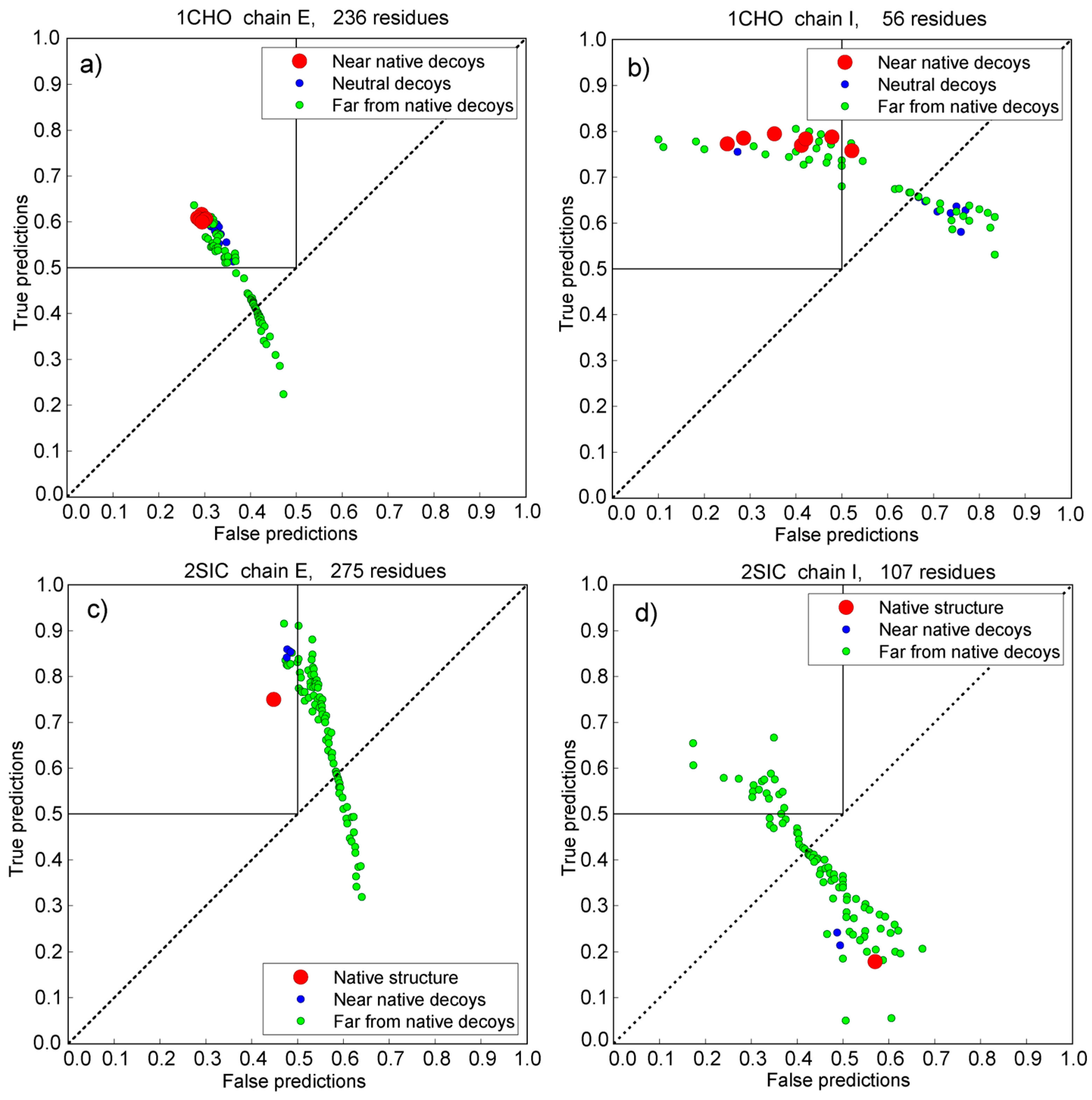
3.4. Prediction Algorithms Comparison
3.5. Vakser and Sternberg Decoy Sets
4. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Mardis, E.R. The impact of next-generation sequencing technology on genetics. Trends Genet. 2008, 24, 133–141. [Google Scholar] [CrossRef] [PubMed]
- Quail, M.A.; Smith, M.; Coupland, P.; Otto, T.D.; Harris, S.R.; Connor, T.R.; Bertoni, A.; Swerdlow, H.P.; Gu, Y. A tale of three next generation sequencing platforms: Comparison of Ion Torrent, Pacific Biosciences and Illumina MiSeq sequencers. BMC Genom. 2012, 13, 341. [Google Scholar] [CrossRef] [PubMed]
- Pabinger, S.; Dander, A.; Fischer, M.; Snajder, R.; Sperk, M.; Efremova, M.; Krabichler, B.; Speicher, M.R.; Zschocke, J.; Trajanoski, Z. A survey of tools for variant analysis of next-generation genome sequencing data. Brief. Bioinform. 2014, 15, 256–278. [Google Scholar] [CrossRef] [PubMed]
- The UniProt Consortium. UniProt: A hub for protein information. Nucleic Acids Res. 2015, 43, D204–D212. [Google Scholar]
- Uhlén, M.; Faqerberg, L.; Hallstrom, B.M.; Lindskog, C.; Oksvold, P.; Mardinoqlu, A.; Sivertsson, A.; Kampf, C.; Sjostedt, E.; Asplund, A.; et al. Tissue-based map of the human proteome. Science 2015, 347, 1260419. [Google Scholar] [CrossRef] [PubMed]
- Kola, I.; Landis, J. Can the pharmaceutical industry reduce attrition rates? Nat. Rev. Drug Discov. 2004, 3, 711–716. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, L.; Kirk, R. High drug attrition rates-where are we going wrong? Nat. Rev. Clin. Oncol. 2011, 8, 189–190. [Google Scholar] [CrossRef] [PubMed]
- Abad-Zapatero, C.; Perišić, O.; Wass, J.; Bento, A.P.; Overington, J.; Al-Lazikani, B.; Johnson, M.E. Ligand efficiency indices for an effective mapping of chemico-biological space: The concept of an atlas-like representation. Drug Discov. Today 2010, 15, 804–811. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, N.; Langlois, R.E.; Zhao, G.; Lu, H. Kernel-based machine learning protocol for predicting DNA-binding proteins. Nucleic Acid Res. 2005, 30, 6486–6493. [Google Scholar] [CrossRef] [PubMed]
- Langlois, R.E.; Carson, M.B.; Bhardwaj, N.; Lu, H. Learning to Translate Sequence and Structure to Function: Identifying DNA Binding and Membrane Binding Proteins. Ann. Biomed. Eng. 2007, 35, 1043–1052. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, N.; Stahelin, R.V.; Zhao, G.; Cho, W.; Lu, H. MeTaDoR: A comprehensive resource for membrane targeting domains and their host proteins. Bioinformatics 2007, 23, 3110–3112. [Google Scholar] [CrossRef] [PubMed]
- Carson, M.B.; Langlois, R.; Lu, H. NAPS: A residue-level nucleic acid-binding prediction server. Nucleic Acid Res. 2010, 38, W431–W435. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, N.; Gerstein, M.; Lu, H. Genome-wide sequence-based prediction of peripheral proteins using a novel semi-supervised learning technique. BMC Bioinform. 2010, 11, S6. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. Atomistic Description of the Folding of a Dimeric Protein. J. Phys. Chem. B 2013, 117, 12935–12942. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Klepeis, J.L.; Shaw, D.E. Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014, 24, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, B.A.; Panchenko, A.R. Deciphering Protein-Protein Interactions. Part I. Experimental Techniques and Databases. PLoS Comput. Biol. 2007, 3. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, B.A.; Panchenko, A.R. Deciphering Protein-Protein Interactions. Part II. Computational Methods to Predict Protein and Domain Interaction Partners. PLoS Comput. Biol. 2007, 3. [Google Scholar] [CrossRef] [PubMed]
- Moal, I.H.; Moretti, R.; Baker, D.; Fernandez-Recio, J. Scoring functions for protein-protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 862–867. [Google Scholar] [CrossRef] [PubMed]
- Baaden, M.; Marrink, S.J. Coarse-grain modelling of protein-protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 878–886. [Google Scholar] [CrossRef] [PubMed]
- Wodak, S.J.; Vlasblom, J.; Turinsky, A.L.; Pu, S. Protein-protein interaction networks: The puzzling riches. Curr. Opin. Struct. Biol. 2013, 23, 941–953. [Google Scholar] [CrossRef] [PubMed]
- Mosca, R.; Pons, T.; Céol, A.; Valencia, A.; Aloy, P. Towards a detailed atlas of protein-protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 929–940. [Google Scholar] [CrossRef] [PubMed]
- Neuvirth, H.; Raz, R.; Schreiber, G. ProMate: A Structure Based Prediction Program to Identify the Location of Protein-Protein Binding Sites. J. Mol. Biol. 2004, 338, 181–199. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhou, HX. Prediction of interface residues in protein-protein complexes by a consensus neural network method: Test against NMR data. Proteins Struct. Funct. Bioinform. 2005, 61, 21–35. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Zhang, C.; Liu, S.; Zhou, Y. Protein binding site prediction using an empirical scoring function. Nucleic Acid Res. 2006, 34, 3698–3707. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.C.; Petrey, D.; Norel, R.; Honig, B.H. Protein interface conservation across structure space. Proc. Natl. Acad. Sci. USA 2010, 107, 10896–10901. [Google Scholar] [CrossRef] [PubMed]
- Saccà, C.; Teso, S.; Diligenti, M.; Passerini, A. Improved multi-level protein-protein interaction prediction with semantic-based regularization. BMC Bioinform. 2014, 15, 103. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.C.; Petrey, D.; Deng, L.; Qiang, L.; Shi, Y.; Thu, C.A.; Bisikirska, B.; Lefebvre, C.; Accili, D.; Hunter, T.; et al. Structure-based prediction of protein-protein interactions on a genome-wide scale. Nature 2012, 490, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, N.; Lu, H. Co-expression among constituents of a motif in the protein-protein interaction network. J. Bioinform. Comput. Biol. 2009, 7, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Rader, A.J. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 2005, 15, 586–592. [Google Scholar] [CrossRef] [PubMed]
- Basdevant, N.; Borgis, D.; Ha-Duong, T. Modeling Protein-Protein Recognition in Solution Using the Coarse-Grained Force Field SCORPION. J. Chem. Theory Comput. 2012, 9, 803–813. [Google Scholar] [CrossRef] [PubMed]
- Ravikumar, K.M.; Huang, W.; Yang, S. Coarse-Grained Simulations of Protein-Protein Association: An Energy Landscape Perspective. Biophys. J. 2012, 103, 837–845. [Google Scholar] [CrossRef] [PubMed]
- Zacharias, M. Combining coarse-grained nonbonded and atomistic bonded interactions for protein modeling. Proteins Struct. Funct. Bioinform. 2013, 81, 81–92. [Google Scholar] [CrossRef] [PubMed]
- Solernou, A.; Fernandez-Recio, J. pyDockCG: New Coarse-Grained Potential for Protein-Protein Docking. J. Phys. Chem. B 2011, 115, 6032–6039. [Google Scholar] [CrossRef] [PubMed]
- Ołdziej, S.; Czaplewski, C.; Liwo, A.; Chinchio, M.; Nanias, M.; Vila, J.A.; Khalili, M.; Jagielska, Y.A.A.A.; Makowski, M.; Schafroth, H.D.; et al. Physics-based protein-structure prediction using a hierarchical protocol based on the UNRES force field: Assessment in two blind tests. Proc. Natl. Acad. Sci. USA 2005, 102, 7547–7552. [Google Scholar] [CrossRef] [PubMed]
- Frembgen-Kesner, T.; Elcock, A.H. Absolute Protein-Protein Association Rate Constants from Flexible, Coarse-Grained Brownian Dynamics Simulations: The Role of Intermolecular Hydrodynamic Interactions in Barnase-Barstar Association. Biophys. J. 2010, 99, L75–L77. [Google Scholar] [CrossRef] [PubMed]
- Min, J.-L.; Xiao, X.; Chou, K.-C. iEzy-Drug: A Web Server for Identifying the Interaction between Enzymes and Drugs in Cellular Networking. BioMed Res. Int. (BMRI) 2013, 2013, 701317. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Min, J.-L.; Wang, P.; Chou, K.-C. iGPCR-Drug: A Web Server for Predicting Interaction between GPCRs and Drugs in Cellular Networking. PLoS ONE 2013, 8, e72234. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Min, J.-L.; Wang, P.; Chou, K.-C. Predict Drug-Protein Interaction in Cellular Networking. Curr. Top. Med. Chem. 2013, 13, 1707–1712. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.-N.; Xiao, X.; Min, J.-L.; Chou, K.-C. iNR-Drug: Predicting the Interaction of Drugs with Nuclear Receptors in Cellular Networking. Int. J. Mol. Sci. (IJMS) 2014, 15, 4915–4937. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Min, J.-L.; Lin, W.-Z.; Liu, Z.; Cheng, X.; Chou, K.-C. iDrug-Target: Predicting the interactions between drug compounds and target proteins in cellular networking via benchmark dataset optimization approach. J. Biomol. Struct. Dyn. 2015, 33, 2221–2233. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.; Liu, Z.; Xiao, X.; Liu, B.; Chou, K.-C. iPPI-Esml: An ensemble classifier for identifying the interactions of proteins by incorporating their physicochemical properties and wavelet transforms into PseAAC. J. Theor. Biol. 2015, 377, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.; Liu, Z.; Xiao, X.; Liu, B.; Chou, K.-C. Identification of protein-protein binding sites by incorporating the physicochemical properties and stationary wavelet transforms into pseudo amino acid composition. J. Biomol. Struct. Dyn. 2016, 34, 1946–1961. [Google Scholar] [CrossRef] [PubMed]
- Mullard, A. Protein-protein interaction inhibitors get into the groove. Nat. Rev. Drug Discov. 2012, 11, 173–175. [Google Scholar] [CrossRef] [PubMed]
- Morelli, X.; Bourgeas, R.; Roche, P. Chemical and structural lessons from recent successes in protein-protein interaction inhibition (2P2I). Curr. Opin. Chem. Biol. 2011, 15, 475–481. [Google Scholar] [CrossRef] [PubMed]
- Basse, M.J.; Betzi, S.; Bourgeas, R.; Bouzidi, S.; Chetrit, B.; Hamon, V.; Morelli, X.; Roche, P. 2P2Idb: A structural database dedicated to orthosteric modulation of protein-protein interactions. Nucleic Acids Res. 2013, 41, D824–D827. [Google Scholar] [CrossRef] [PubMed]
- Porta-Pardo, E.; Hrabe, T.; Godzik, A. Cancer3D: Understanding cancer mutations through protein structures. Nucleic Acids Res. 2014, 43, D968–D973. [Google Scholar] [CrossRef] [PubMed]
- James, H.M.; Guth, E. Theory of the Increase in Rigidity of Rubber during Cure. J. Chem. Phys. 1947, 15, 669–683. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical thermodynamics of random networks. Proc. R. Soc. A 1976, 351, 351–380. [Google Scholar] [CrossRef]
- Karplus, M.; Kushick, J. Method for estimating the configurational entropy of macromolecules. Macromolecules 1981, 14, 325–332. [Google Scholar] [CrossRef]
- Levy, R.M.; Karplus, M.; Kushick, J.; Perahia, D. Evaluation of the configurational entropy for proteins: Application to molecular dynamics simulations of an α-helix. Macromolecules 1984, 17, 1370–1374. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Theory of Rubber Elasticity. Polym. J. 1985, 17, 1–12. [Google Scholar] [CrossRef]
- Tirion, M.M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1995, 77, 1905–1908. [Google Scholar] [CrossRef] [PubMed]
- Haliloglu, T.; Bahar, I.; Erman, B. Gaussian Dynamics of Folded Proteins. Phys. Rev. Lett. 1997, 79, 3090–3093. [Google Scholar] [CrossRef]
- Bahar, I.; Atilgan, A.R.; Erman, B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997, 2, 173–181. [Google Scholar] [CrossRef]
- Bahar, I.; Atilgan, A.R.; Demirel, M.C.; Erman, B. Vibrational Dynamics of Folded Proteins. Phys. Rev. Lett. 1998, 80, 2733–2736. [Google Scholar] [CrossRef]
- Demirel, M.C.; Atiligan, A.R.; Jernigan, R.L.; Erman, B.; Bahar, I. Identification of kinetically hot residues in proteins. Protein Sci. 1998, 7, 2522–2532. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Erman, B.; Jernigan, R.L.; Atilgan, A.R.; Covell, D.G. Collective motions in HIV-1 reverse transcriptase: Examination of flexibility and enzyme function. J. Mol. Biol. 1999, 285, 1023–1037. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Eyal, E.; Chennubhotla, C.; Jee, J.; Gronenborn, A.M.; Bahar, I. Insights into Equilibrium Dynamics of Proteins from Comparison of NMR and X-Ray Data with Computational Predictions. Structure 2007, 15, 741–749. [Google Scholar] [CrossRef] [PubMed]
- Haliloglu, T.; Keskin, O.; Ma, B.; Nussinov, R. How Similar Are Protein Folding and Protein Binding Nuclei? Examination of Vibrational Motions of Energy Hot Spots and Conserved Residues. Biophys. J. 2005, 88, 1552–1559. [Google Scholar] [CrossRef] [PubMed]
- Perišić, O. Contact and first layer residues prediction in protein dimers using the Gaussian Network model with adjustable number of fast modes. arXiv, 2013; arXiv:1312.7376v1. [Google Scholar]
- Perišić, O. Heterodimer binding scaffolds recognition via the analysis of kinetically hot residues. arXiv, 2016; arXiv:1609.06556. [Google Scholar]
- Bogan, A.A.; Thorn, K.S. Anatomy of hot spots in protein interfaces. J. Mol. Biol. 1998, 280, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Moreira, I.S.; Fernandes, P.A.; Ramos, M.J. Hot spots-A review of the protein-protein interface determinant amino-acid residues. Proteins Struct. Funct. Bioinform. 2007, 68, 803–812. [Google Scholar] [CrossRef] [PubMed]
- Tuncbag, N.; Gursoy, A.; Keskin, O. Identification of computational hot spots in protein interfaces: Combining solvent accessibility and inter-residue potentials improves the accuracy. Bioinformatics 2009, 25, 1513–1520. [Google Scholar] [CrossRef] [PubMed]
- Lise, S.; Archambeau, C.; Pontil, M.; Jones, D.T. Prediction of hot spot residues at protein-protein interfaces by combining machine learning and energy-based methods. BMC Bioinform. 2009, 10, 365. [Google Scholar] [CrossRef] [PubMed]
- Lise, S.; Buchan, D.; Pontil, M.; Jones, D.T. Predictions of Hot Spot Residues at Protein-Protein Interfaces Using Support Vector Machines. PLoS ONE 2011, 6, e16774. [Google Scholar] [CrossRef] [PubMed]
- Kozakov, D.; Hall, D.R.; Chuang, G.-Y.; Cencic, R.; Brenke, R.; Grove, L.E.; Beglov, D.; Pelletier, J.; Whitty, A.; Vajda, S. Structural conservation of druggable hot spots in protein-protein interfaces. Proc. Natl. Acad. Sci. USA 2011, 108, 13528–13533. [Google Scholar] [CrossRef] [PubMed]
- Tuncbag, N.; Gursoy, A.; Nussinov, R.; Keskin, O. Predicting protein-protein interactions on a proteome scale by matching evolutionary and structural similarities at interfaces using PRISM. Nat. Protoc. 2011, 6, 1341–1354. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Guan, J.; Wei, X.; Yi, Y.; Zhang, Q.C.; Zhou, S. Boosting Prediction Performance of Protein-Protein Interaction Hot Spots by Using Structural Neighborhood Properties. J. Comput. Biol. 2013, 20, 878–891. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Tang, H.; Ye, J.; Lin, H.; Chou, K.-C. iRNA-PseU: Identifying RNA pseudouridine sites. Mol. Ther. Nucleic Acids 2016, 5, e332. [Google Scholar] [PubMed]
- Chenga, X.; Xiaoa, X.; Chou, K.-C. pLoc-mVirus: Predict subcellular localization of multi-location virus proteins via incorporating the optimal GO information into general PseAAC. Gene 2017, 628, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Feng, P.; Ding, H.; Yang, H.; Chen, W.; Lin, H.; Chou, K.-C. iRNA-PseColl: Identifying the Occurrence Sites of Different RNA Modifications by Incorporating Collective Effects of Nucleotides into PseKNC. Mol. Ther. Nucleic Acids 2017, 7, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Xiao, X.; Chou, K.-C. pLoc-mPlant: Predict subcellular localization of multi-location plant proteins by incorporating the optimal GO information into general PseAAC. Mol. BioSyst. 2017, 13, 1722–1727. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Wang, S.; Long, R.; Chou, K.-C. iRSpot-EL: Identify recombination spots with an ensemble learning approach. Bioinformatics 2017, 33, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Cheng, X.; Su, S.; Mao, Q.; Chou, K.-C. pLoc-mGpos: Incorporate Key Gene Ontology Information into General PseAAC for Predicting Subcellular Localization of Gram-Positive Bacterial Proteins. Nat. Sci. 2017, 9, 330–349. [Google Scholar] [CrossRef]
- Qiu, W.-R.; Sun, B.-Q.; Xiao, X.; Xua, Z.-C.; Jia, J.-H.; Chou, K.-C. iKcr-PseEns: Identify lysine crotonylation sites in histone proteins with pseudo components and ensemble classifier. Genomics 2017. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Xiao, X.; Chou, K.-C. pLoc-mGneg: Predict subcellular localization of Gram-negative bacterial proteins by deep gene ontology learning via general PseAAC. Genomics 2017. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Zhao, S.-G.; Lin, W.-Z.; Xiao, X.; Chou, K.-C. pLoc-mAnimal: Predict subcellular localization of animal proteins with both single and multiple sites. Bioinformatics 2017, 33, 3524–3531. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Xiao, X.; Chou, K.-C. pLoc-mEuk: Predict subcellular localization of multi-label eukaryotic proteins by extracting the key GO information into general PseAAC. Genomics 2018, 110, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Ehsan, A.; Mahmood, K.; Khan, Y.D.; Khan, S.A.; Chou, K.-C. A Novel Modeling in Mathematical Biology for Classification of Signal Peptides. Sci. Rep. 2018, 8, 1039. [Google Scholar] [CrossRef] [PubMed]
- Feng, P.; Yang, H.; Ding, H.; Lin, H.; Chen, W.; Chou, K.-C. iDNA6mA-PseKNC: Identifying DNA N6-methyladenosine sites by incorporating nucleotide physicochemical properties into PseKNC. Genomics 2018. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Yang, F.; Huang, D.S.; Chou, K.-C. iPromoter-2L: A two-layer predictor for identifying promoters and their types by multi-window-based PseKNC. Bioinformatics 2018, 34, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Li, F.; Takemoto, K.; Haffari, G.; Akutsu, T.; Chou, K.-C.; Webb, G.I. PREvaIL, an integrative approach for inferring catalytic residues using sequence, structural, and network features in a machine-learning framework. J. Theor. Biol. 2018, 443, 125–137. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Xiao, X.; Chou, K.-C. pLoc-mHum: Predict subcellular localization of multi-location human proteins via general PseAAC to winnow out the crucial GO information. Bioinformatics 2018. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.-C. Some remarks on protein attribute prediction and pseudo amino acid composition (50th Anniversary Year Review). J. Theor. Biol. 2011, 273, 236–247. [Google Scholar] [CrossRef] [PubMed]
- Sternberg Decoy Sets. Available online: http://www.sbg.bio.ic.ac.uk/docking/ (accessed on 8 March 2018).
- Liu, S.; Gao, Y.; Vakser, I.A. DOCKGROUND protein-protein docking decoy set. Bioinformatics 2008, 24, 2634–2635. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Skolnick, J. Development of Unified Statistical Potentials Describing Protein-Protein Interactions. Biophys. J. 2003, 84, 1895–1901. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Weisstein, E.W. Singular Value Decomposition at mathworld.wolfram.com. Available online: http://mathworld.wolfram.com/SingularValueDecomposition.html (accessed on 8 March 2018).
- Smith, T.F.; Waterman, M.S. Identification of Common Molecular Subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef]
- Abagyan, R.A.; Batalov, S. Do Aligned Sequences Share the Same Fold? J. Mol. Biol. 1997, 273, 355–368. [Google Scholar] [CrossRef] [PubMed]
- Wood, T.C.; Pearson, W.R. Evolution of Protein Sequences and Structures. J. Mol. Biol. 1999, 291, 977–995. [Google Scholar] [CrossRef] [PubMed]
- Gan, H.H.; Perlow, R.A.; Roy, S.; Ko, J.; Wu, M.; Huang, J.; Yan, S.; Nicoletta, A.; Vafai, J.; Sun, D.; et al. Analysis of Protein Sequence/Structure Similarity Relationships. Biophys. J. 2002, 83, 2781–2791. [Google Scholar] [PubMed]
- Eswar, N.; Marti-Renom, M.A.; Webb, B.; Madhusudhan, M.S.; Eramian, D.; Shen, M.; Pieper, U.; Sali, A. Comparative Protein Structure Modeling With MODELLER. Curr. Protoc. Bioinform. 2006. [Google Scholar] [CrossRef]
- Martin, J.; Lavery, R. Arbitrary protein-protein docking targets biologically relevant interfaces. BMC Biophys. 2012, 5, 7. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.-C.; Shen, H.-B. Recent advances in developing web-servers for predicting protein attributes. Nat. Sci. 2009, 1, 63–92. [Google Scholar] [CrossRef]
- Lin, H.; Deng, E.-Z.; Ding, H.; Chen, W.; Chou, K.-C. iPro54-PseKNC: A sequence-based predictor for identifying sigma-54 promoters in prokaryote with pseudo k-tuple nucleotide composition. Nucleic Acids Res. 2014, 42, 12961–12972. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Yang, F.; Chou, K.-C. 2L-piRNA: A Two-Layer Ensemble Classifier for Identifying Piwi-Interacting RNAs and Their Function. Mol. Ther. Nucleic Acids 2017, 7, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Long, R.; Chou, K.-C. iDHS-EL: Identifying DNase I hypersensitive sites by fusing three different modes of pseudo nucleotide composition into an ensemble learning framework. Bioinformatics 2016, 32, 2411–2418. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Fang, L.; Long, R.; Lan, X.; Chou, K.-C. iEnhancer-2L: A two-layer predictor for identifying enhancers and their strength by pseudo k-tuple nucleotide composition. Bioinformatics 2016, 32, 362–369. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.-C. Impacts of Bioinformatics to Medicinal Chemistry. Med. Chem. 2015, 11, 218–234. [Google Scholar] [CrossRef] [PubMed]
- Kastritis, P.L.; Bonvin, A.M.J.J. Molecular origins of binding affinity: Seeking the Archimedean point. Curr. Opin. Struct. Biol. 2013, 23, 868–877. [Google Scholar] [CrossRef] [PubMed]
- London, N.; Raveh, B.; Schueler-Furman, O. Peptide docking and structure-based characterization of peptide binding: From knowledge to know-how. Curr. Opin. Struct. Biol. 2013, 23, 894–902. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perišić, O. Heterodimer Binding Scaffolds Recognition via the Analysis of Kinetically Hot Residues. Pharmaceuticals 2018, 11, 29. https://doi.org/10.3390/ph11010029
Perišić O. Heterodimer Binding Scaffolds Recognition via the Analysis of Kinetically Hot Residues. Pharmaceuticals. 2018; 11(1):29. https://doi.org/10.3390/ph11010029
Chicago/Turabian StylePerišić, Ognjen. 2018. "Heterodimer Binding Scaffolds Recognition via the Analysis of Kinetically Hot Residues" Pharmaceuticals 11, no. 1: 29. https://doi.org/10.3390/ph11010029
APA StylePerišić, O. (2018). Heterodimer Binding Scaffolds Recognition via the Analysis of Kinetically Hot Residues. Pharmaceuticals, 11(1), 29. https://doi.org/10.3390/ph11010029