TDLAS-Based Rapid and Accurate Measurement of Near-Ambient Temperature Using Near-Infrared Vibrational Water Vapor Transitions
Abstract
1. Introduction
2. Experimental Apparatus and Methods
2.1. Fundamental Spectroscopy
2.2. Experimental Details and Data Analysis
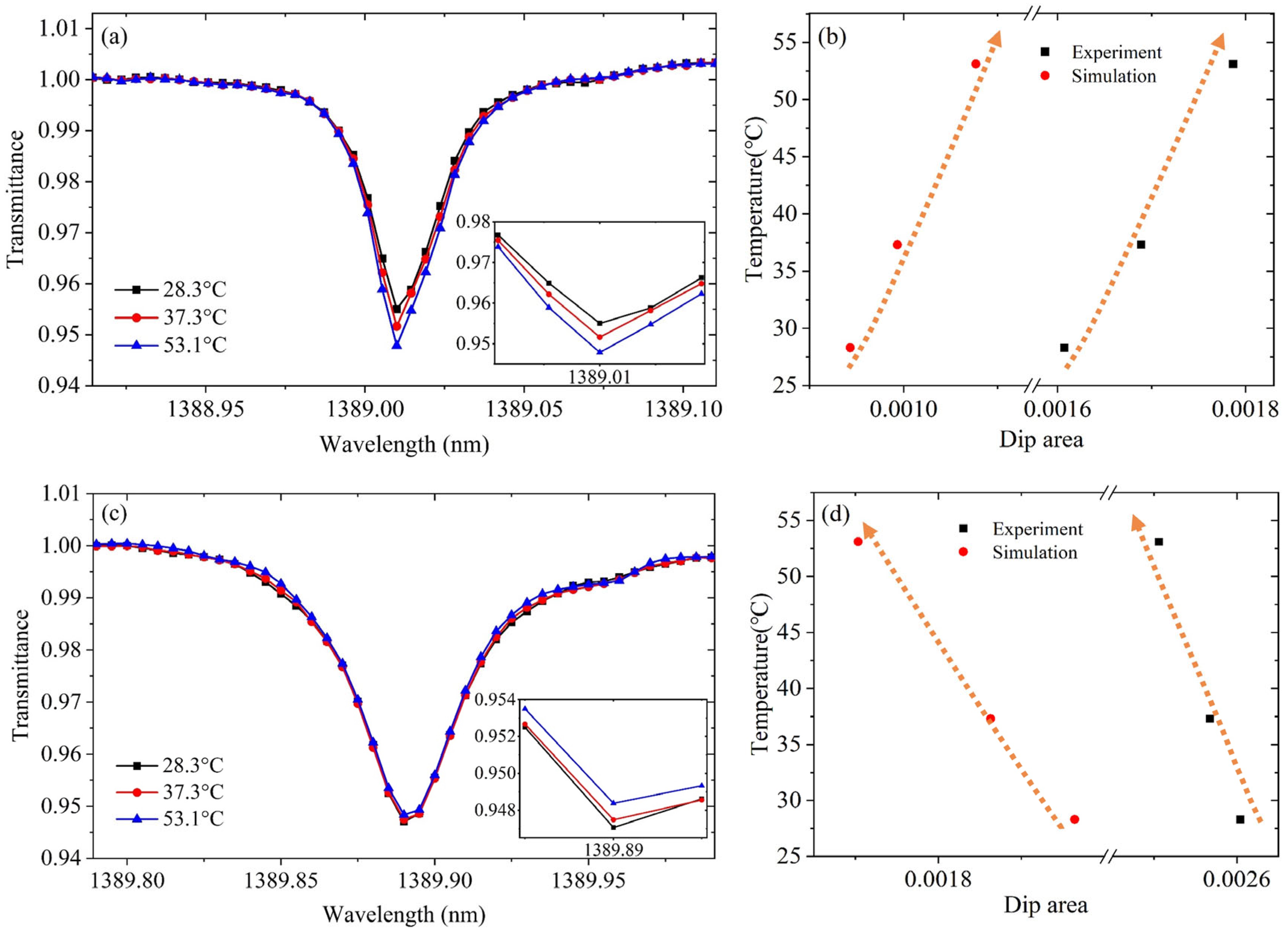
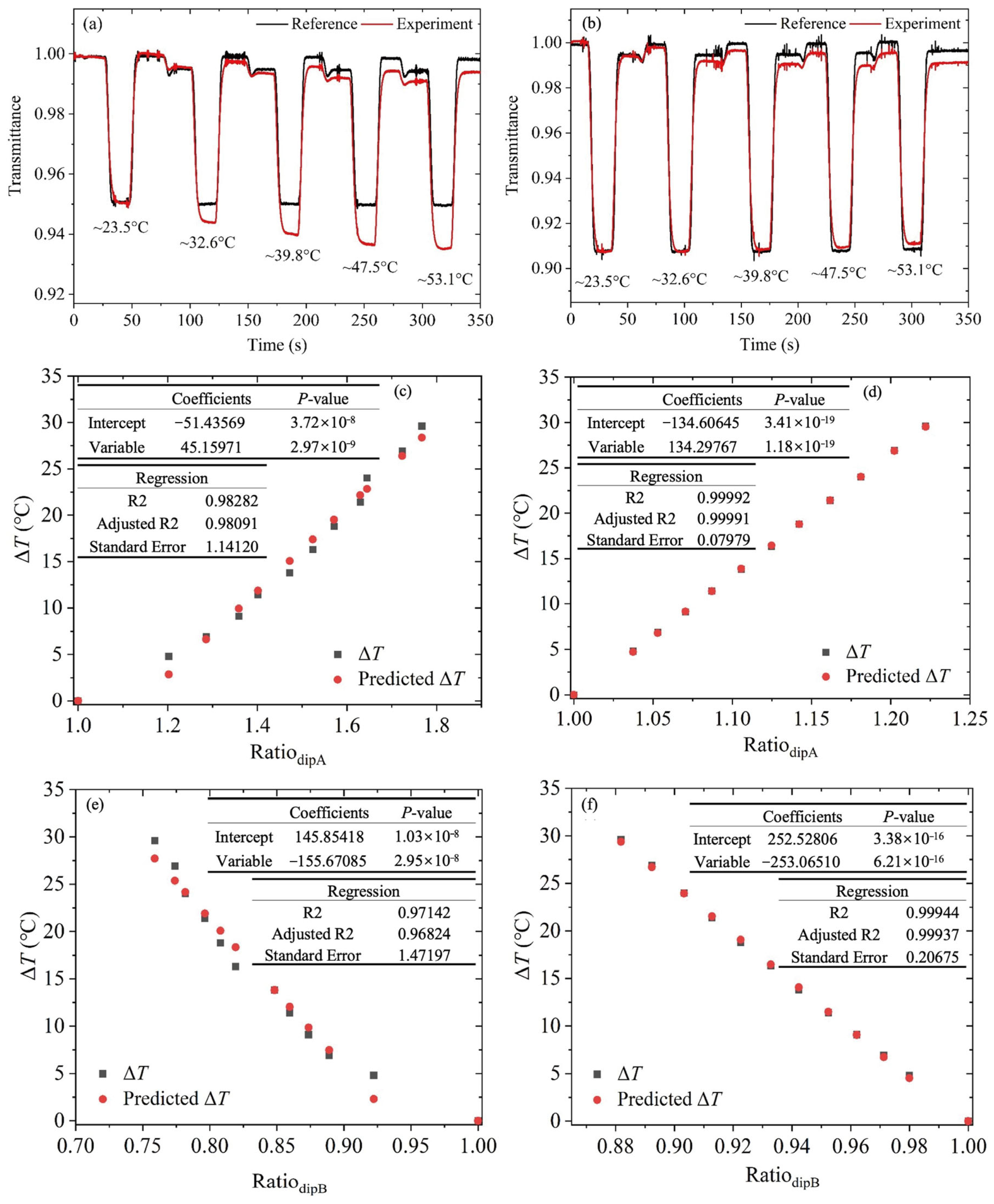
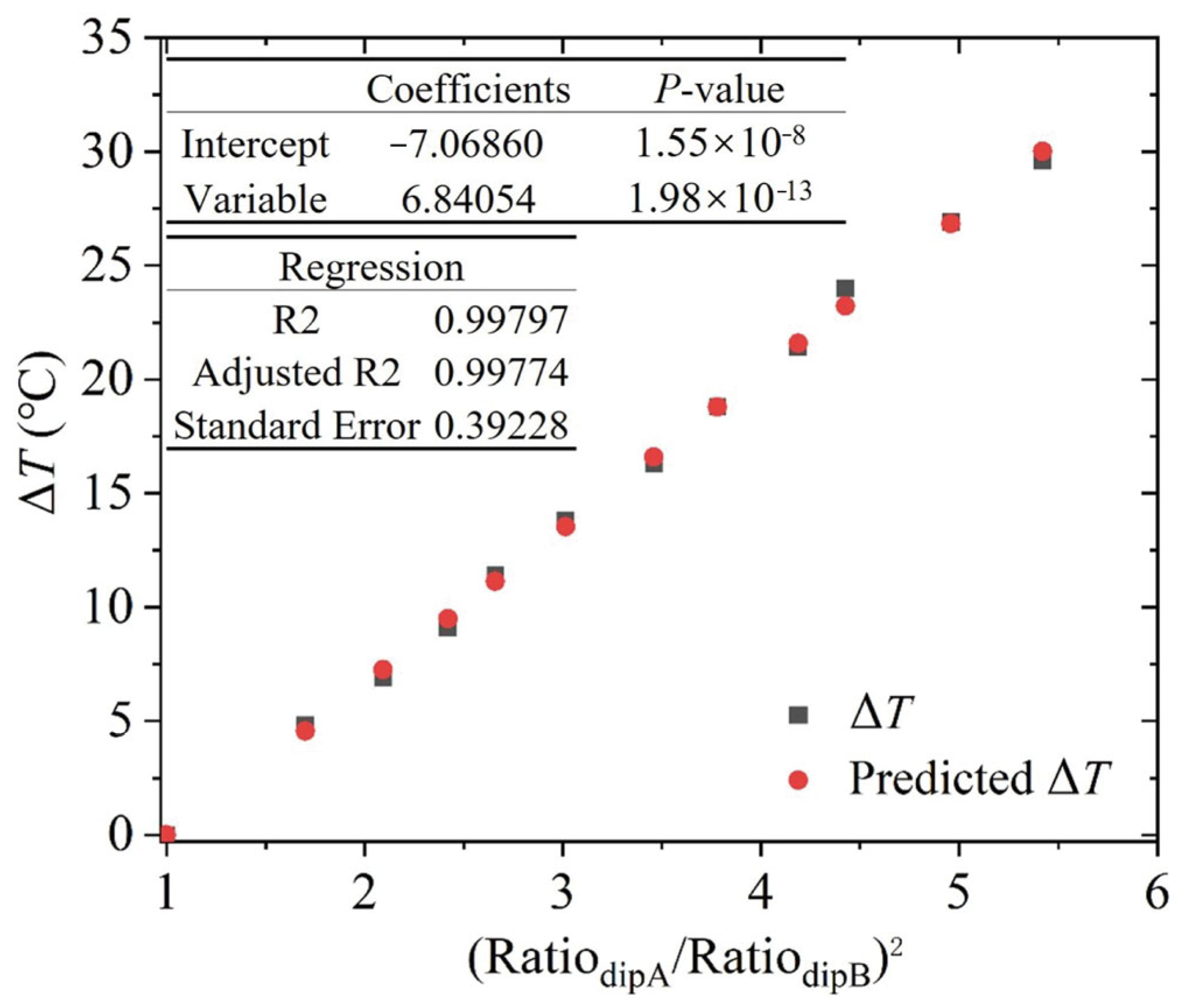
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ngo, T.T.; Huang, J.H.; Wang, C.C. The BFGS Method for Estimating the Interface Temperature and Convection Coefficient in Ultrasonic Welding. Int. Commun. Heat Mass Transf. 2015, 69, 66–75. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Longtin, J.P.; Attinger, D. Interfacial Temperature Measurements, High-Speed Visualization and Finite-Element Simulations of Droplet Impact and Evaporation on a Solid Surface. Int. J. Heat Mass Transf. 2010, 53, 3733–3744. [Google Scholar] [CrossRef]
- Basu, S.; Lambe, D.E.; Kumar, R. Water Vapor and Carbon Dioxide Species Measurements in Narrow Channels. Int. J. Heat Mass Transf. 2010, 53, 703–714. [Google Scholar] [CrossRef]
- Ye, Y.; Wan, S.; Li, S.; Peng, Y.; He, X.; Qin, M. Fabrication and Characterization of a MEMS Thermal Convective Accelerometer on Silicon-in-Glass Substrate. IEEE Sens. J. 2024, 24, 9619–9625. [Google Scholar] [CrossRef]
- Kasparkova, V.; Halabalová, V.; Simek, L.; Ruzicka, J.; Janca, J. Separation of Bacteria in Temperature Gradient: Micro-Thermal Focusing Field-Flow Fractionation. J. Biochem. Biophys. Methods 2007, 70, 685–687. [Google Scholar] [CrossRef]
- Braun, D.; Libchaber, A. Trapping of DNA by Thermophoretic Depletion and Convection. Phys. Rev. Lett. 2002, 89, 188103. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Yousefi, T.; Saghir, M.Z. Accurate Measurement of Temperature and Concentration Distribution of a Mixture in a Rectangular Parallelepiped Enclosure. Int. Commun. Heat Mass Transf. 2016, 76, 225–236. [Google Scholar] [CrossRef]
- Park, H.; Park, J.; Jung, S.Y. Measurements of Velocity and Temperature Fields in Natural Convective Flows. Int. J. Heat Mass Transf. 2019, 139, 293–302. [Google Scholar] [CrossRef]
- AlWaaly, A.A.; Dobson, P.S.; Paul, M.C.; Steinmann, P. Thermocouple Heating Impact on the Temperature Measurement of Small Volume of Water in a Cooling System. Appl. Therm. Eng. 2017, 127, 650–661. [Google Scholar] [CrossRef]
- Modliński, N.; Madejski, P.; Janda, T.; Szczepanek, K.; Kordylewski, W. A Validation of Computational Fluid Dynamics Temperature Distribution Prediction in a Pulverized Coal Boiler with Acoustic Temperature Measurement. Energy 2015, 92, 77–86. [Google Scholar] [CrossRef]
- Lee, J.; Bong, C.; Sun, H.; Jeong, J.; Bak, M.S. Thermometry of Combustion Gases Using Light Emission and Acoustic Wave from Laser-Induced Sparks. J. Phys. Appl. Phys. 2019, 52, 315201. [Google Scholar] [CrossRef]
- Kampmann, S.; Leipertz, A.; Döbbeling, K.; Haumann, J.; Sattelmayer, T. Two-Dimensional Temperature Measurements in a Technical Combustor with Laser Rayleigh Scattering. Appl. Opt. 1993, 32, 6167–6172. [Google Scholar] [CrossRef] [PubMed]
- Grib, S.W.; Jiang, N.; Hsu, P.S.; Danehy, P.M.; Roy, S. Rayleigh-Scattering-Based Two-Dimensional Temperature Measurement at 100-kHz Frequency in a Reacting Flow. Opt. Express 2019, 27, 27902–27916. [Google Scholar] [CrossRef] [PubMed]
- Eckbreth, A.C.; Hall, R.J. CARS Thermometry in a Sooting Flame. Combust. Flame 1979, 36, 87–98. [Google Scholar] [CrossRef]
- Vestin, F.; Sedarsky, D.; Collin, R.; Alden, M.; Linne, M.; Bengtsson, P. Rotational Coherent Anti-Stokes Raman Spectroscopy (CARS) Applied to Thermometry in High-Pressure Hydrocarbon Flames. Combust. Flame 2008, 154, 143–152. [Google Scholar] [CrossRef]
- Goldenstein, C.S.; Spearrin, R.M.; Jeffries, J.B.; Hanson, R.K. Infrared Laser-Absorption Sensing for Combustion Gases. Prog. Energy Combust. Sci. 2017, 60, 132–176. [Google Scholar] [CrossRef]
- Bolshov, M.A.; Kuritsyn, Y.A.; Liger, V.V.; Mironenko, V.R.; Leonov, S.B.; Yarantsev, D.A. Measurements of the Temperature and Water Vapor Concentration in a Hot Zone by Tunable Diode Laser Absorption Spectrometry. Appl. Phys. B 2010, 100, 397–407. [Google Scholar] [CrossRef]
- Rieker, G.B.; Li, H.; Liu, X.; Jeffries, J.B.; Hanson, R.K.; Allen, M.G.; Wehe, S.D.; Mulhall, P.A.; Kindle, H.S. A Diode Laser Sensor for Rapid, Sensitive Measurements of Gas Temperature and Water Vapour Concentration at High Temperatures and Pressures. Meas. Sci. Technol. 2007, 18, 1195–1204. [Google Scholar] [CrossRef]
- Peng, W.Y.; Cassady, S.J.; Strand, C.L.; Goldenstein, C.S.; Spearrin, R.M.; Brophy, C.M.; Jeffries, J.B.; Hanson, R.K. Single-Ended Mid-Infrared Laser-Absorption Sensor for Time-Resolved Measurements of Water Concentration and Temperature within the Annulus of a Rotating Detonation Engine. Proc. Combust. Inst. 2019, 37, 1435–1443. [Google Scholar] [CrossRef]
- Ren, W.; Farooq, A.; Davidson, D.F.; Hanson, R.K. CO Concentration and Temperature Sensor for Combustion Gases Using Quantum-Cascade Laser Absorption near 4.7 mm. Appl. Phys. B 2012, 107, 849–860. [Google Scholar] [CrossRef]
- Bolshov, M.A.; Kuritsyn, Y.A.; Romanovskii, Y.V. Tunable Diode Laser Spectroscopy as a Technique for Combustion Diagnostics. Spectrochim. Acta Part B At. Spectrosc. 2015, 106, 45–66. [Google Scholar] [CrossRef]
- Goldenstein, C.S.; Schultz, I.A.; Spearrin, R.M.; Jeffries, J.B.; Hanson, R.K. Scanned-Wavelength-Modulation Spectroscopy near 2.5 mm for H2O and Temperature in a Hydrocarbon-Fueled Scramjet Combustor. Appl. Phys. B 2014, 116, 717–727. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Huang, Y.; Wang, Y.; Liu, X. Reconstruction and Simulation of Temperature and CO2 Concentration in an Axisymmetric Flame Based on TDLAS. Optik 2018, 170, 166–177. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, G.; Liu, X.; Gao, G.; Cai, T. A TDLAS Sensor for Simultaneous Measurement of Temperature and C2H4 Concentration Using a Differential Absorption Scheme at High Temperature. Front. Phys. 2020, 8, 44. [Google Scholar] [CrossRef]
- Chang, E.; Streicher, J.W.; Krish, A.; Hanson, R.K. AIAA High-Temperature Infrared-Based Diagnostic for Nitric Oxide Using Tunable Diode Laser Absorption Spectroscopy; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2022. [Google Scholar]
- Zhou, X.; Liu, X.; Jeffries, J.B.; Hanson, R.K. Development of a Sensor for Temperature and Water Concentration in Combustion Gases Using a Single Tunable Diode Laser. Meas. Sci. Technol. 2003, 14, 1459–1468. [Google Scholar] [CrossRef]
- Li, H.; Farooq, A.; Jeffries, J.B.; Hanson, R.K. Near-Infrared Diode Laser Absorption Sensor for Rapid Measurements of Temperature and Water Vapor in a Shock Tube. Appl. Phys. B 2007, 89, 407–416. [Google Scholar] [CrossRef]
- Liu, X.; Jeffries, J.B.; Hanson, R.K. Measurements of Spectral Parameters of Water-Vapour Transitions near 1388 and 1345 nm for Accurate Simulation of High-Pressure Absorption Spectra. Meas. Sci. Technol. 2007, 18, 1185–1194. [Google Scholar] [CrossRef]
- Rieker, G.B.; Li, H.; Liu, X.; Liu, J.T.C.; Jeffries, J.B.; Hanson, R.K.; Allen, M.G.; Wehe, S.D.; Mulhall, P.A.; Kindle, H.S.; et al. Rapid Measurements of Temperature and H2O Concentration in IC Engines with a Spark Plug-Mounted Diode Laser Sensor. Proc. Combust. Inst. 2007, 31, 3041–3049. [Google Scholar] [CrossRef]
- Ngo, N.H.; Ibrahim, N.; Landsheere, X.; Tran, H.; Chelin, P.; Schwell, M.; Hartmann, J.M. Intensities and Shapes of H2O Lines in the Near-Infrared by Tunable Diode Laser Spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 870–877. [Google Scholar] [CrossRef]
- Kee, Y.Y.; Asako, Y.; Ken, T.L.; Sidik, N.A.C. Uncertainty of Temperature Measured by Thermocouple. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 68, 54–62. [Google Scholar] [CrossRef]
- Mallet, A.; Tsenkova, R.; Muncan, J.; Charnier, C.; Latrille, E.; Bendoula, R.; Steyer, J.P.; Roger, J.M. Relating Near-Infrared Light Path-Length Modifications to the Water Content of Scattering Media in Near-Infrared Spectroscopy: Toward a New Bouguer-Beer-Lambert Law. Anal. Chem. 2021, 93, 6817–6823. [Google Scholar] [CrossRef] [PubMed]
- Gamache, R.R.; Roller, C.; Lopes, E.; Gordon, I.E.; Rothman, L.S.; Polyansky, O.L.; Zobov, N.E.; Kyuberis, A.A.; Tennyson, J.; Yurchenko, S.N.; et al. Total Internal Partition Sums for 166 Isotopologues of 51 Molecules Important in Planetary Atmospheres: Application to HITRAN2016 and Beyond. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 70–87. [Google Scholar] [CrossRef]
- Sur, R.; Sun, K.; Jeffries, J.B.; Hanson, R.K. Multi-Species Laser Absorption Sensors for in Situ Monitoring of Syngas Composition. Appl. Phys. B 2014, 115, 9–24. [Google Scholar] [CrossRef]
- Silver, J.A. Frequency-Modulation Spectroscopy for Trace Species Detection: Theory and Comparison among Experimental Methods. Appl. Opt. 1992, 31, 707–717. [Google Scholar] [CrossRef]
- Ye, Y.; Wan, S.; Li, S.; He, X. Mechanical Wind Sensor Based on Additive Manufacturing Technology. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- An, X.; Kraetschmer, T.; Takami, K.; Sanders, S.T.; Ma, L.; Cai, W.; Li, X.; Roy, S.; Gord, J.R. Validation of Temperature Imaging by H2O Absorption Spectroscopy Using Hyperspectral Tomography in Controlled Experiments. Appl. Opt. 2011, 50, A29–A37. [Google Scholar] [CrossRef]
- Li, H.; Farooq, A.; Jeffries, J.B.; Hanson, R.K. Diode Laser Measurements of Temperature-Dependent Collisional-Narrowing and Broadening Parameters of Ar-Perturbed H2O Transitions at 1391.7 and 1397.8 nm. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 132–143. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, E.R.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Vasilenko, I.A.; Naumenko, O.V. Expert Assessment of the Accuracy of Determining the Intensities of Vibrational-Rotational Lines of Water Vapor in the HITRAN Database in the Range 2500–6500 cm−1. Atmos. Ocean. Opt. 2024, 37, 461–468. [Google Scholar] [CrossRef]
- Ducreux, E.; Grouiez, B.; Robert, S.; Lepere, M.; Vispoel, B.; Gamache, R.R.; Regalia, L. Measurements of H2O Broadened by CO2 Line-Shape Parameters: Beyond the Voigt Profile. J. Quant. Spectrosc. Radiat. Transf. 2024, 323, 109026. [Google Scholar] [CrossRef]
- Humlicek, J. Optimized Computation of the Voigt and Complex Probability Functions. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 437–444. [Google Scholar] [CrossRef]


| 1 (cm−1) | λ (nm) | Vibration Modes | (cm−1) | 2 (cm−2/(molec/cm3)) | (cm−1/atm) | |
|---|---|---|---|---|---|---|
| 7194.81 | 1389.89 | 0.69 | 95.20 | 3.07 × 10−21 | 0.10 | |
| 7199.38 | 1389.01 | 0.62 | 888.60 | 8.96 × 10−22 | 0.06 |
| T (°C) | Q(T) | Q(T)/Q(T0) | T (°C) | Q(T) | Q(T)/Q(T0) |
|---|---|---|---|---|---|
| 0 | 154.72066 | 0.88599 | 5 | 159.00232 | 0.91051 |
| 10 | 163.32625 | 0.93527 | 15 | 167.69207 | 0.96027 |
| 20 | 172.09942 | 0.98551 | 25 | 176.54793 | 1.01098 |
| 30 | 181.03724 | 1.03669 | 35 | 185.56697 | 1.06263 |
| 40 | 190.13676 | 1.0888 | 45 | 194.74624 | 1.11519 |
| 50 | 199.39505 | 1.14181 | 55 | 204.08282 | 1.16866 |
| 60 | 208.80918 | 1.19572 |
| RA | RA2 | RA, RA2 | RB | RB2 | RB, RB2 | ||
|---|---|---|---|---|---|---|---|
| Standard Error | 1.14120 | 0.75644 | 0.56913 | 1.47197 | 1.68444 | 0.69683 | |
| p-value | P1 | 2.97 × 10−9 | 7.32 × 10−11 | 7.20 × 10−4 | 2.95 × 10−8 | 9.98 × 10−8 | 4.70 × 10−4 |
| P2 | / | / | 2.28 × 10−2 | / | / | 1.56 × 10−4 | |
| RA, RB 1 | RA/RB | RB/RA | (RA/RB)2 | (RB/RA)2 | RA/RB, (RA/RB)2 | ||
| Standard Error | 1.20965 | 0.75223 | 2.11287 | 0.39228 | 2.79582 | 0.41298 | |
| p-value | P1 | 9.22 × 10−1 | 6.96 × 10−11 | 7.74 × 10−7 | 1.98 × 10−13 | 9.81 × 10−6 | 1.59 × 10−3 |
| P2 | 4.98 × 10−2 | / | / | / | / | 7.38 × 10−1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Gao, J. TDLAS-Based Rapid and Accurate Measurement of Near-Ambient Temperature Using Near-Infrared Vibrational Water Vapor Transitions. Sensors 2025, 25, 2839. https://doi.org/10.3390/s25092839
Zhang J, Gao J. TDLAS-Based Rapid and Accurate Measurement of Near-Ambient Temperature Using Near-Infrared Vibrational Water Vapor Transitions. Sensors. 2025; 25(9):2839. https://doi.org/10.3390/s25092839
Chicago/Turabian StyleZhang, Jiaao, and Jiao Gao. 2025. "TDLAS-Based Rapid and Accurate Measurement of Near-Ambient Temperature Using Near-Infrared Vibrational Water Vapor Transitions" Sensors 25, no. 9: 2839. https://doi.org/10.3390/s25092839
APA StyleZhang, J., & Gao, J. (2025). TDLAS-Based Rapid and Accurate Measurement of Near-Ambient Temperature Using Near-Infrared Vibrational Water Vapor Transitions. Sensors, 25(9), 2839. https://doi.org/10.3390/s25092839







