A Novel Inductive Displacement Sensor Based on Dual-Excitation and Single-Sensing Coils for Core Displacement Measurement
Abstract
1. Introduction
- (1)
- A novel inductive displacement sensor with a segmented multi-group coil structure is proposed, which utilizes the optim linear range of the sensing coil’s voltage of to measure the core displacement; the stroke range can be easily increased.
- (2)
- Mathematical and finite element simulation models are established to systematically investigate the influence of sensor coil structure, number of turns, and excitation frequency on output characteristics through theoretical analysis and simulation studies.
- (3)
- A sensor prototype is built to test its performance. The experimental results demonstrate that the measurement accuracy of the designed sensor is less than 1.5 mm and linearity error is 0.35%. The measurement accuracy is greatly improved compared to the other inductive displacement sensors used in nuclear reactors.
2. Design of Sensor
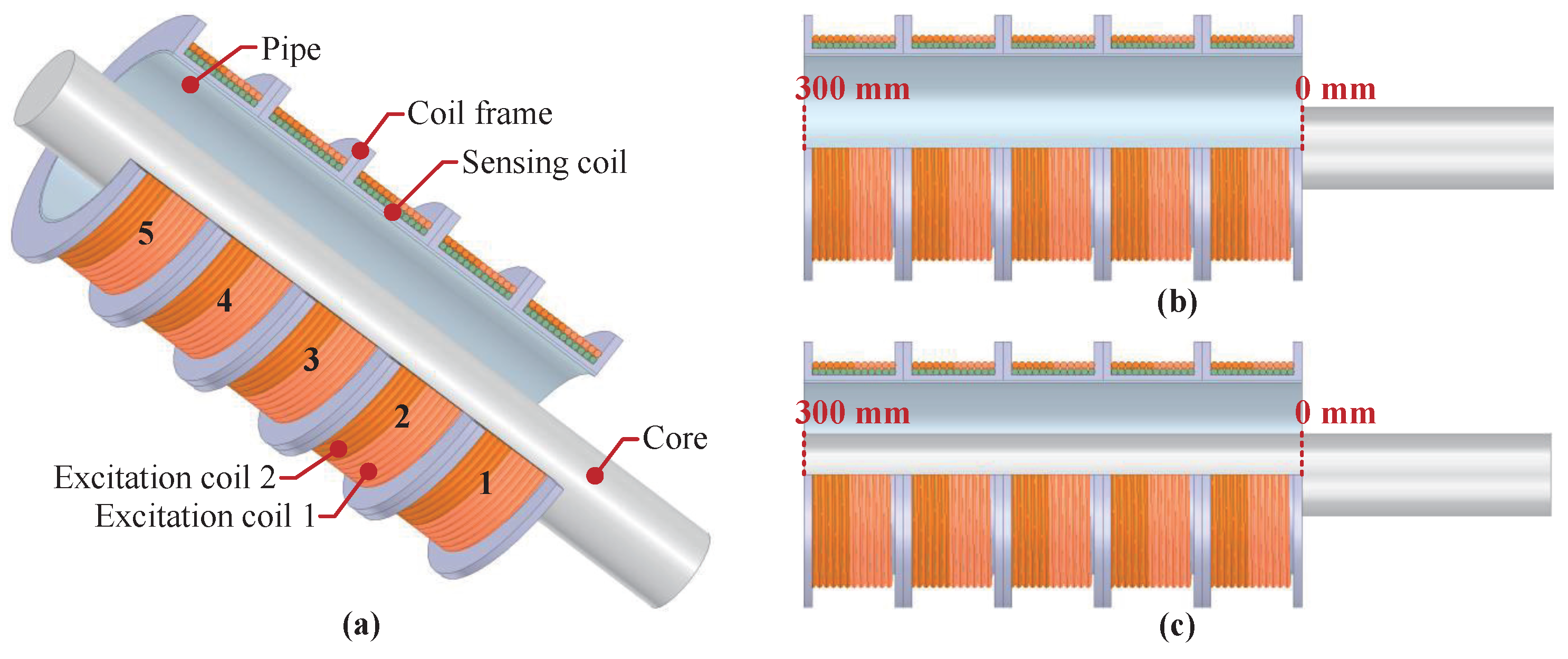
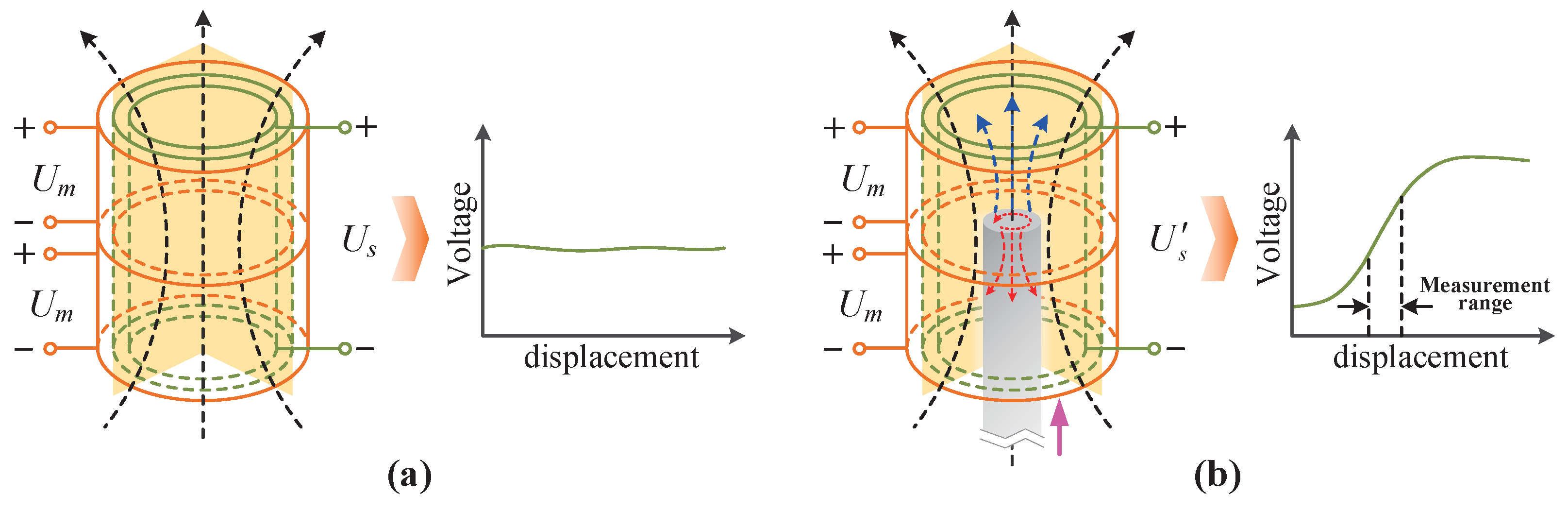
2.1. Structure and Measurement Principle of Sensor
2.2. Mathematical Model of Sensor
- (1)
- External excitation source: excitation frequency and excitation voltage amplitude ;
- (2)
- Sensor structure: coil equivalent resistance , equivalent inductance , number of turns of the excitation coil , and the sensing coil .
3. Finite Element Analysis
3.1. Excitation Coil Structure Analysis
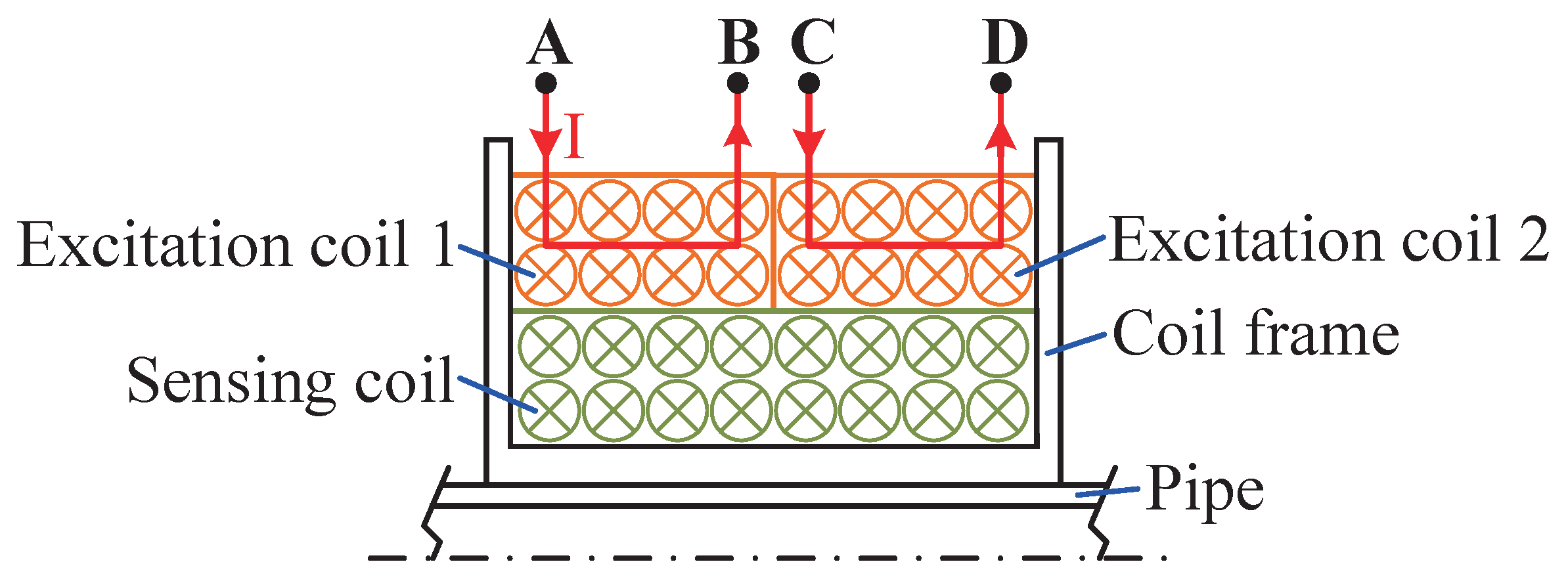
3.1.1. Series and Parallel Structure Analysis
3.1.2. Analysis of Asymmetry in Excitation Coils
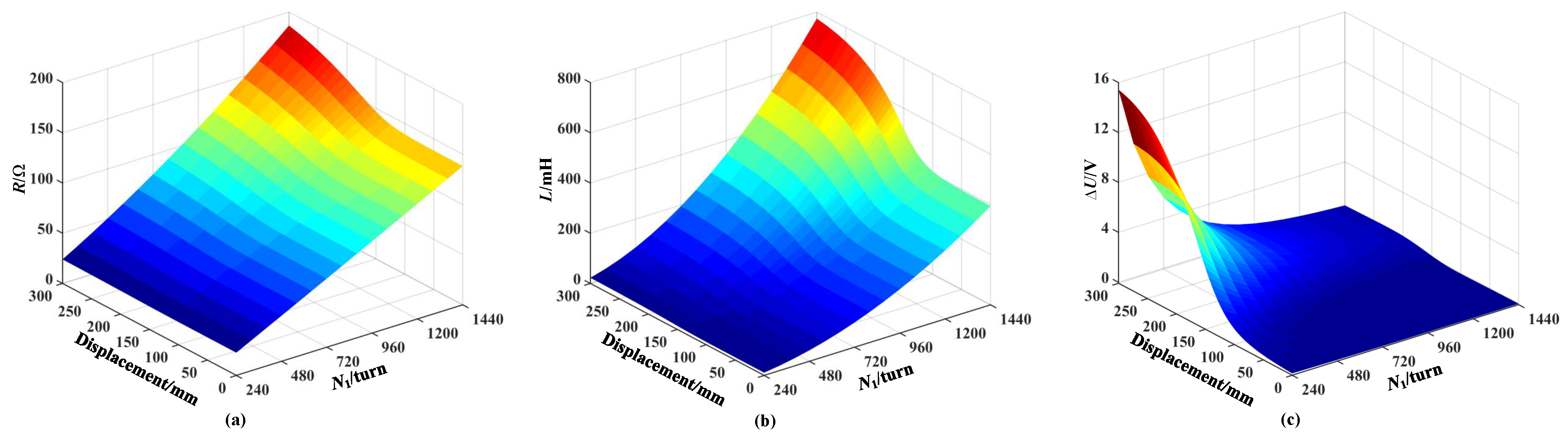
3.2. Influence of the Number of Turns of the Excitation Coil on Sensor Performance
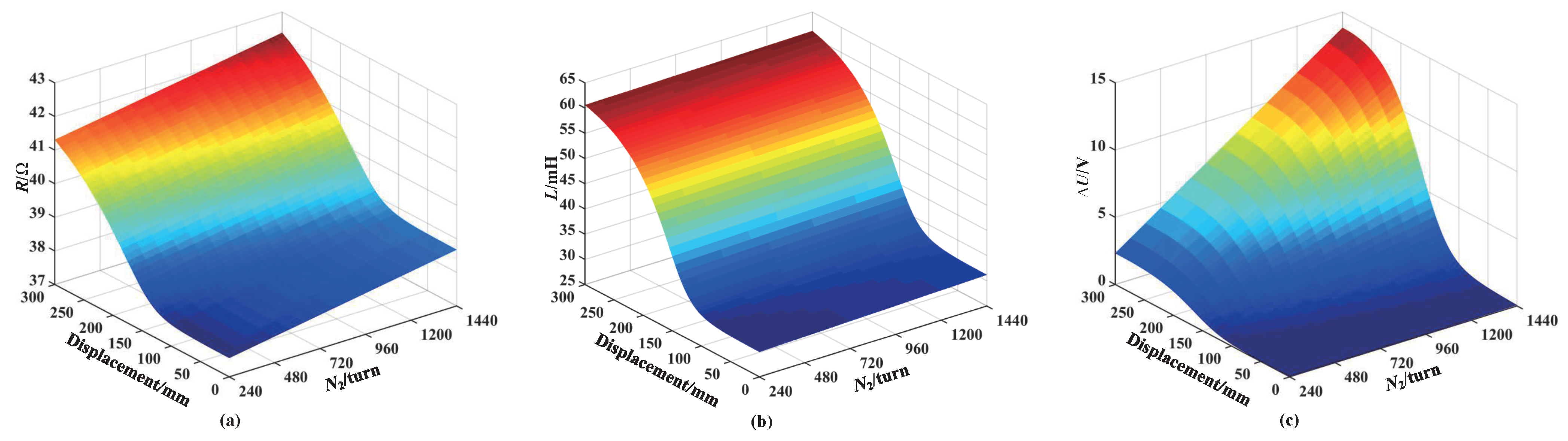
3.3. Influence of the Number of Turns of the Sensing Coil on Sensor Performance
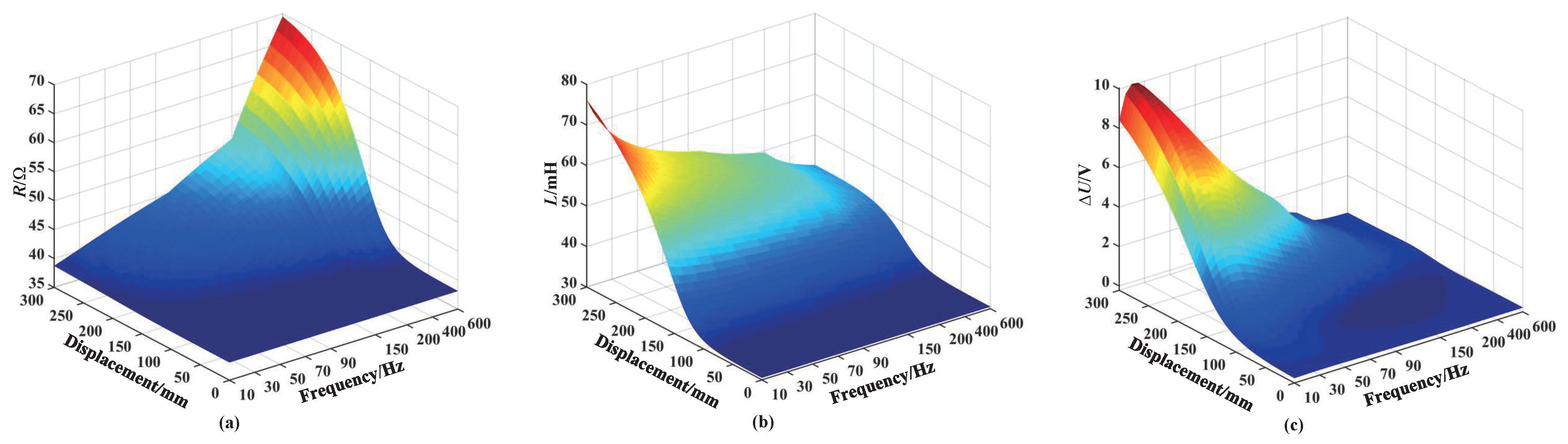
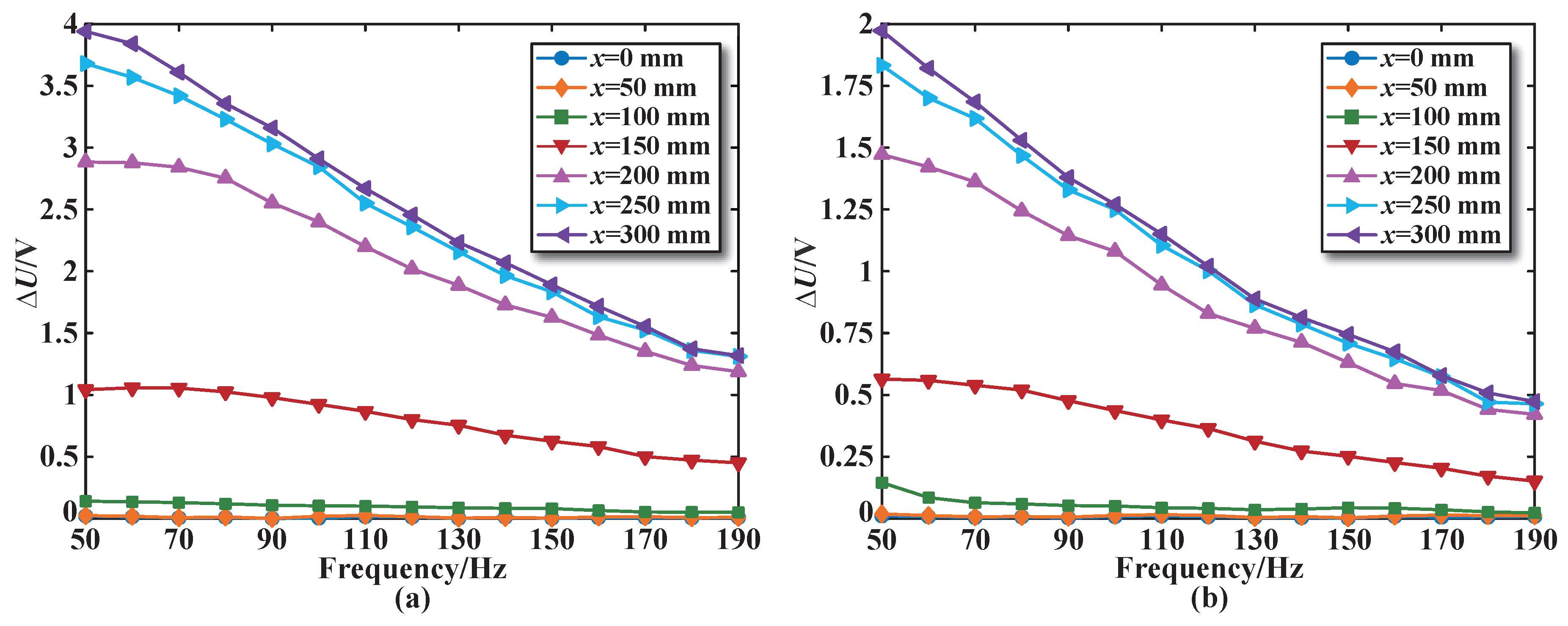
3.4. Influence of the Excitation Frequency on Sensor Performance
4. Experimental Verification
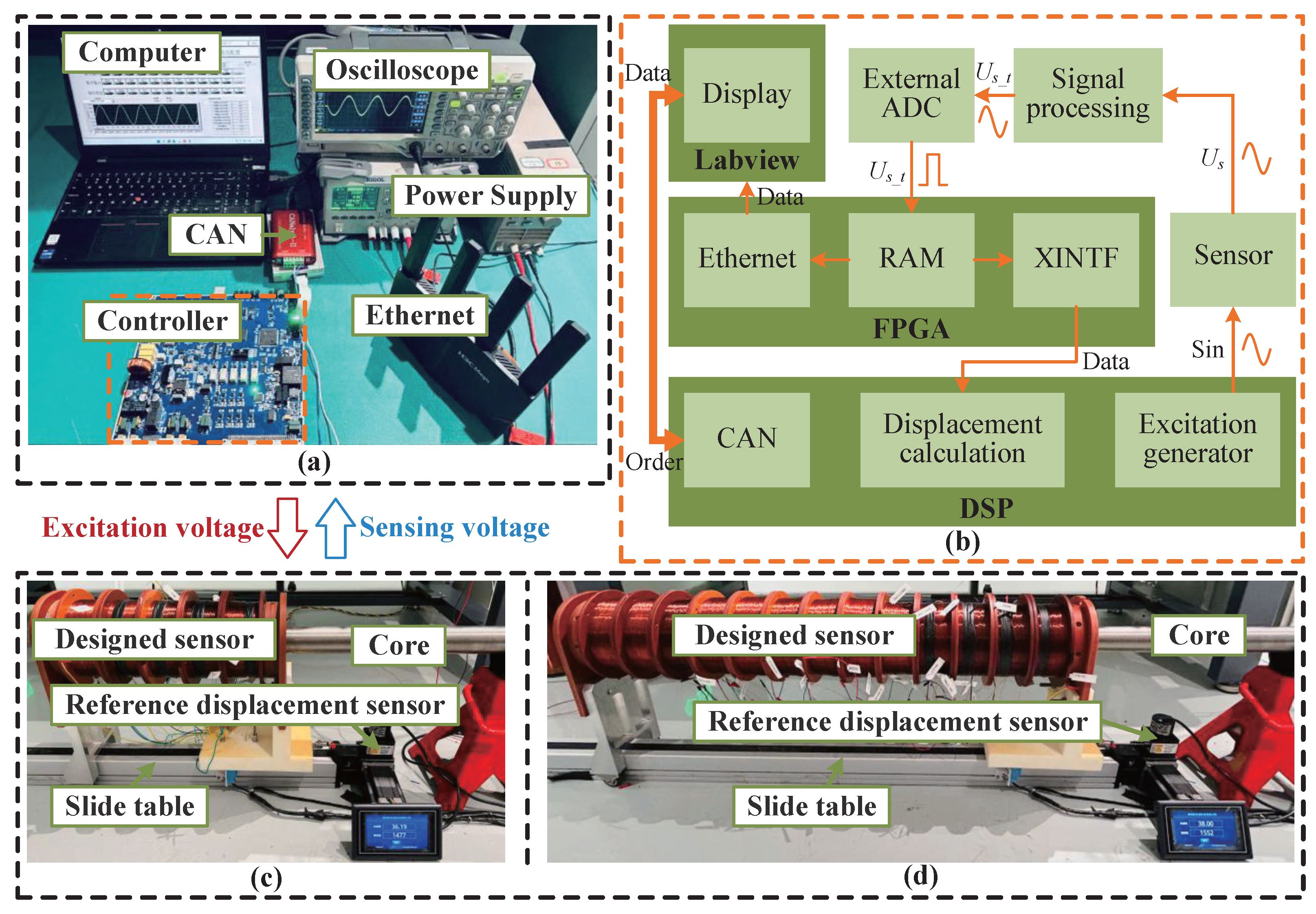
4.1. Measurement Setup
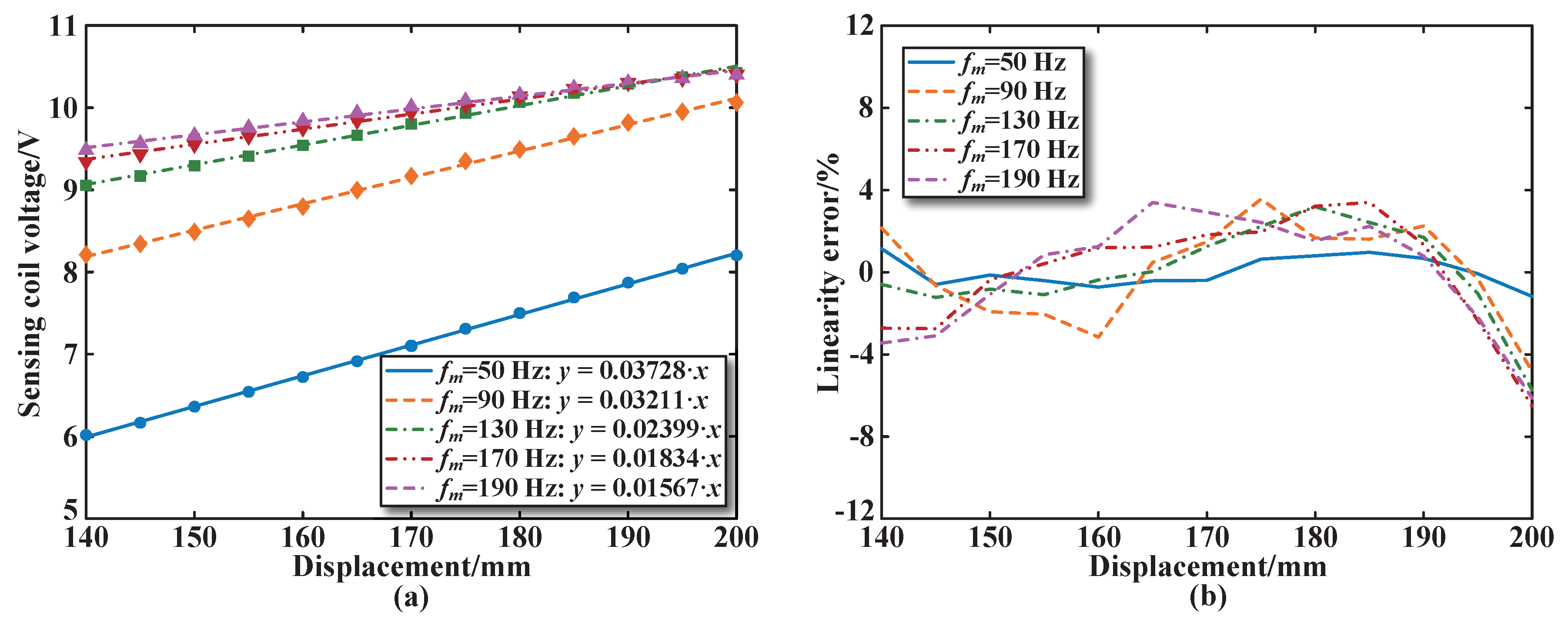
4.2. Static Characteristics Test
4.3. Dynamic Characteristics Test
4.4. Performance Test
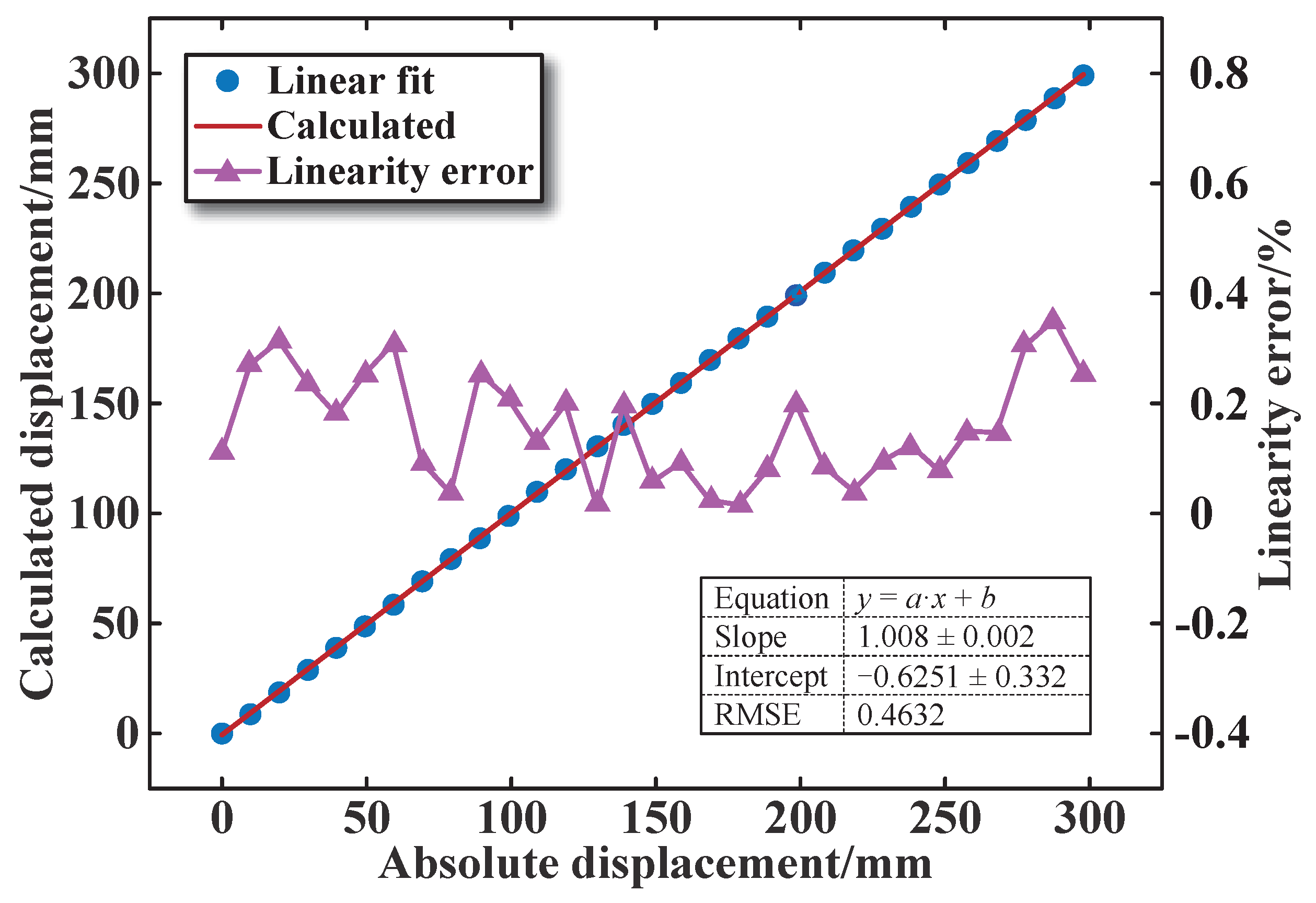
4.4.1. Accuracy Test
4.4.2. Repeatability Tests
5. Conclusions
- (1)
- The coil structure and parameters are closely related to sensor output. For excitation coils with the same number of turns, the parallel structure enables a sensor output voltage increment that is approximately twice that of the series structure. For the sensing coil, the larger the number of turns, the greater the coil inductance and resistance, resulting in a larger sensing coil voltage increment, thereby improving sensor sensitivity.
- (2)
- The excitation frequency has a great influence on the displacement measurement performance of the sensor. The excitation frequency and the output of the sensor show a nonlinear relationship. Within the range of 35 Hz–55 Hz, the sensing coil voltage increment is large. In order to facilitate the design of a single-phase inverter excitation circuit, the excitation frequency is selected as 50 Hz in this paper.
- (3)
- After the experimental performance tests, the designed sensor is shown to have stable core displacement measurement performance, with a linearity error of 0.35% within the full 300 mm stroke. It can perform high-precision measurements of <1.5 mm, which meets the actual use requirements of a nuclear reactor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, G.; Liu, Q.; Wang, J.; Dong, L.; Bo, H. Dynamic characteristics of the capacitance control rod position measurement sensor system in NHR-200. Ann. Nucl. Energy 2020, 138, 107215. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, H.; Liu, Q. Review on sensors to measure control rod position for nuclear reactor. Ann. Nucl. Energy 2020, 144, 107485. [Google Scholar] [CrossRef]
- Hu, P.; Chang, D.; Tan, J.; Yang, R.; Yang, H.; Fu, H. Displacement measuring grating interferometer: A review. Front. Inform. Technol. Electron. 2019, 20, 631–654. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, W.; Zhao, F.; Fang, Y.; Zhang, Z.; Ren, X.; Yin, L.; Shi, Y.; Chen, B.; Liu, H. A novel peak positioning method for nanometer displacement measurement by optical linear encoder. Measurement 2025, 242, 115888. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Liu, C.; Cai, G.; Wang, W. survey on the grating based optical position encoder. Opt. Laser Technol. 2021, 143, 107352. [Google Scholar] [CrossRef]
- He, Q.; Fan, S.; Chen, N.; Tan, R.; Chen, F.; Fan, D. Analysis of inductive displacement sensors with large range and nanoscale resolution. Appl. Sci. 2021, 11, 10134. [Google Scholar] [CrossRef]
- Li, W.; Hu, J.; Su, Z.; Wang, D. Analysis and design of axial inductive displacement sensor. Measurement 2022, 187, 110159. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, W.; Lu, L. Study on gray code control rod position indicator. Nucl. Eng. Des. 1998, 186, 429–436. [Google Scholar]
- Lei, Q. Comparison of CPR1000 and AP1000 rod position indication systems. Nucl. Power Eng. 2009, 30, 45–48. [Google Scholar]
- Casey, D.; Danny, D.; Gregory, W. Control Rod Position Indication Systems and Methods for Nuclear Power Plants. U.S. Patent 8824617B2, 2 September 2014. [Google Scholar]
- Paul, B. Control Rod Position Indicator. U.S. Patent 10269460B2, 23 April 2019. [Google Scholar]
- Mandal, H.; Bera, S.; Saha, S.; Sadhu, P.; Beara, S. Study of a modified LVDT type displacement transducer with unlimited range. IEEE Sens. J. 2018, 18, 9501–9514. [Google Scholar] [CrossRef]
- Raj, M.; Meera, V.; Janani, P. Comparative study and transient analysis of winding shapes in linear variable differential transformer. In Proceedings of the 2014 IEEE 2nd International Conference on Electrical Energy Systems, Chennai, India, 7–9 January 2014; pp. 132–134. [Google Scholar]
- Reinholz, D.; Reinholz, B.; Seethaler, R. Design and validation of a variable reluctance differential solenoid transducer with an ironless stator. IEEE Sens. J. 2022, 22, 21585–21591. [Google Scholar] [CrossRef]
- Reinholz, B.; Seethaler, R. Design and validation of a variable reluctance differential solenoid transducer. IEEE Sens. J. 2019, 19, 11063–11071. [Google Scholar] [CrossRef]
- Ripka, P.; Mirzaei, M.; Chirtsov, A.; Vyhnanek, J. Transformer position sensor for a pneumatic cylinder. Sens. Actuators A Phys. 2019, 294, 91–101. [Google Scholar] [CrossRef]
- Mirzaei, M.; Ripka, P.; Chirtsov, A.; Grim, V. Temperature stability of the transformer position transducer for pneumatic cylinder. J. Magn. Magn. Mater. 2020, 503, 166636. [Google Scholar] [CrossRef]
- Veeraian, P.; Gandhi, U.; Mangalanathan, U. Fractional order linear variable differential transformer: Design and analysis. AEU-Int. J. Electron. Commun. 2017, 79, 141–150. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, K.; Lei, H.; Li, B. An accurate modeling and design method of inductive displacement sensor. Measurement 2023, 219, 113253. [Google Scholar] [CrossRef]
- Ford, R.; Weissbach, R.; Loker, D. A novel DSP-based LVDT signal conditioner. IEEE Trans. Instrum. Meas. 2001, 50, 768–774. [Google Scholar] [CrossRef]
- Flammini, A.; Marioli, D.; Sisinni, E.; Taroni, A. Least mean square method for LVDT signal processing. IEEE Trans. Instrum. Meas. 2007, 27, 2294–2300. [Google Scholar] [CrossRef]
- Rerkratn, A.; Tongcharoen, J.; Petchmaneelumka, W.; Riewruja, V. Linear-range extension for linear variable differential transformer using hyperbolic sine function. Sensors 2022, 22, 3674. [Google Scholar] [CrossRef]
- Thongdit, P.; Angkeaw, K. Enhancing the linearity range of LVDT using hyperbolic sine function. In Proceedings of the 2022 International Symposium on Intelligent Signal Processing and Communication Systems, Penang, Malaysia, 1–5 November 2022. [Google Scholar]
- Mishra, S.; Panda, G.; Das, D. A novel method of extending the linearity range of linear variable differential transformer using artificial neural network. IEEE Trans. Instrum. Meas. 2010, 59, 947–953. [Google Scholar] [CrossRef]
- Li, M.; Gong, Q.; Wu, W.; Hai, H.; Ma, C.; CHe, C. Nonlinear correction of LVDT sensor based on ACO-BP neural network. J. Phys. Conf. Ser. 2020, 1678, 012084. [Google Scholar] [CrossRef]
- Santhosh, K.; Roy, B. Online implementation of an adaptive calibration technique for displacement measurement using lvdt. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications, Melbourne, Australia, 19–21 June 2013. [Google Scholar]
- Mocitan, B.; Gliga, M. Optimization of an Inductive Displacement Transducer. Sensors 2023, 23, 8152. [Google Scholar] [CrossRef] [PubMed]
- Petchmaneelumka, W.; Songsuwankit, K.; Tongcharoen, J.; Riewruja, V. Linear-range extension for linear variable differential transformer using binomial series. Sens. Mater. 2020, 32, 475. [Google Scholar] [CrossRef]
- Nehra, B.; Sreekantan, A. Evaluation of simple linearizing circuit topologies for LVDT. IEEE Sens. Lett. 2023, 7, 1–4. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Y.; Li, N.; Qian, Z.; Liu, D.; Qian, Z.; Zhang, C. A New inductive debris sensor based on dual-excitation coils and dual-sensing coils for online debris monitoring. Sensors 2021, 21, 7556. [Google Scholar] [CrossRef]
- Shen, X.; Han, Q.; Wang, Y.; Wu, B.; Zhu, R. Research on detection performance of four-coil inductive debris sensor. IEEE Sens. J. 2023, 23, 223–227. [Google Scholar] [CrossRef]
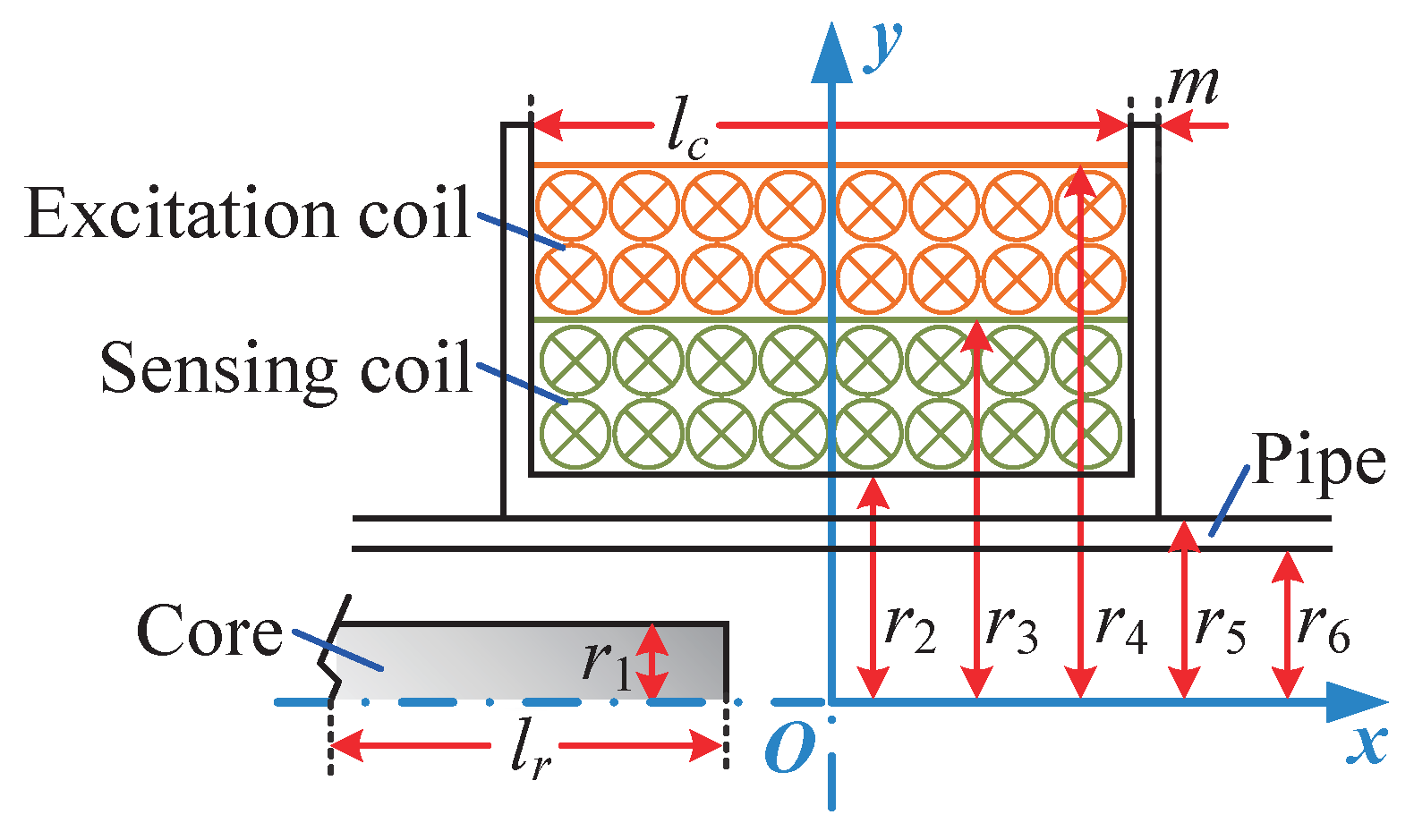

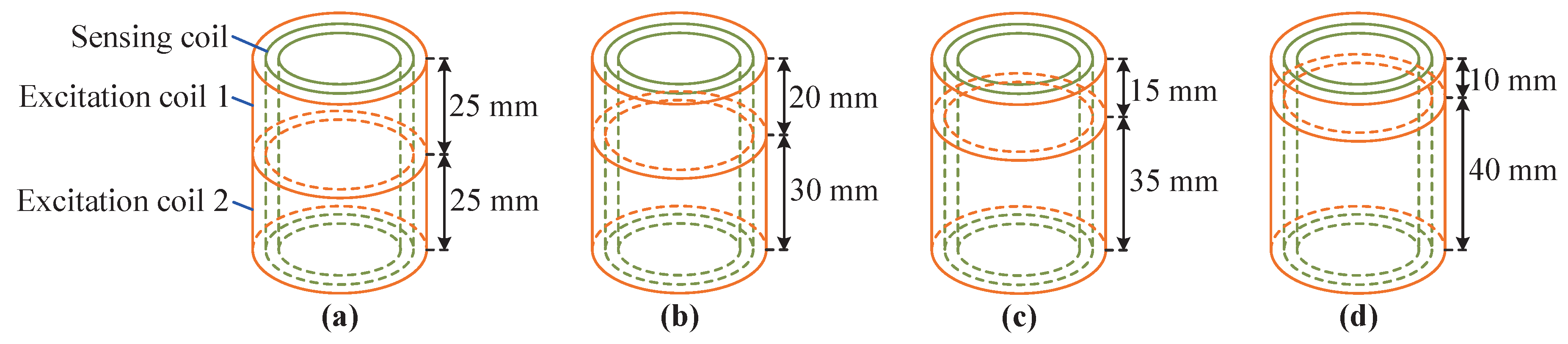




| Parts | Parameters | Value |
|---|---|---|
| Excitation soure | Amplitude () | 10 V |
| Frequency () | 50 Hz | |
| Sensing coil | Number of turns for the sensing coil () | 800 |
| Length () | 50 mm | |
| Inner radius () | 60 mm | |
| Outer radius () | 61.2 mm | |
| Excitation coils 1 and 2 | Number of turns for the excitation coil () | 400 |
| Length () | 25 mm | |
| Inner radius () | 61.2 mm | |
| Outer radius () | 62.4 mm | |
| Coil frame | Coil spacing (m) | 5 mm |
| Inner radius () | 57 mm | |
| Outer radius () | 60 mm | |
| Pipe | Inner radius () | 55.5 mm |
| Outer radius () | 57 mm | |
| Core | Length () | 1000 mm |
| Radius () | 25 mm |
| Operating Range | Linearity Error | Sensitivity |
|---|---|---|
| [10 mm, 70 mm] | 1.38% | 0.0639 V/mm |
| [15 mm, 75 mm] | 0.82% | 0.0671 V/mm |
| [20 mm, 80 mm] | 0.47% | 0.0682 V/mm |
| [25 mm, 85 mm] | 0.77% | 0.0674 V/mm |
| [30 mm, 90 mm] | 1.17% | 0.0647 V/mm |
| [35 mm, 95 mm] | 1.39% | 0.0618 V/mm |
| [40 mm, 100 mm] | 1.48% | 0.0582 V/mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Xu, Q.; Miao, Y.; Zhang, W.; Wang, C.; Li, M.; Tang, S. A Novel Inductive Displacement Sensor Based on Dual-Excitation and Single-Sensing Coils for Core Displacement Measurement. Sensors 2025, 25, 2827. https://doi.org/10.3390/s25092827
Gao L, Xu Q, Miao Y, Zhang W, Wang C, Li M, Tang S. A Novel Inductive Displacement Sensor Based on Dual-Excitation and Single-Sensing Coils for Core Displacement Measurement. Sensors. 2025; 25(9):2827. https://doi.org/10.3390/s25092827
Chicago/Turabian StyleGao, Longjiang, Qiwei Xu, Yiru Miao, Wei Zhang, Chunlei Wang, Mengshu Li, and Shihan Tang. 2025. "A Novel Inductive Displacement Sensor Based on Dual-Excitation and Single-Sensing Coils for Core Displacement Measurement" Sensors 25, no. 9: 2827. https://doi.org/10.3390/s25092827
APA StyleGao, L., Xu, Q., Miao, Y., Zhang, W., Wang, C., Li, M., & Tang, S. (2025). A Novel Inductive Displacement Sensor Based on Dual-Excitation and Single-Sensing Coils for Core Displacement Measurement. Sensors, 25(9), 2827. https://doi.org/10.3390/s25092827






