Harmonic Distortion Measurements for Non-Destructive Evaluation of Steel Strips
Abstract
1. Introduction
2. The Harmonic Distortion Measurement
2.1. Formal Statement of the Characterisation Problem
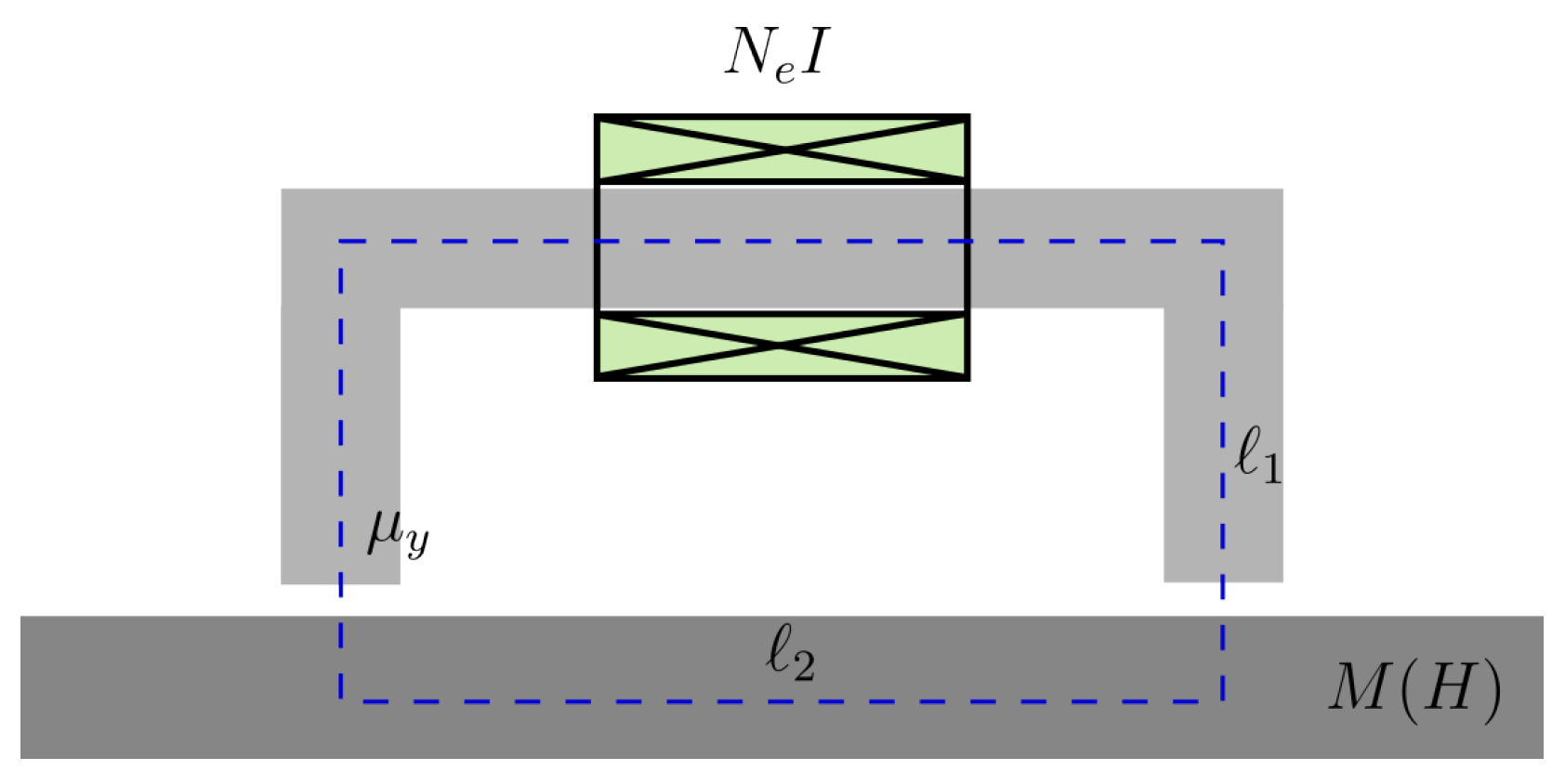
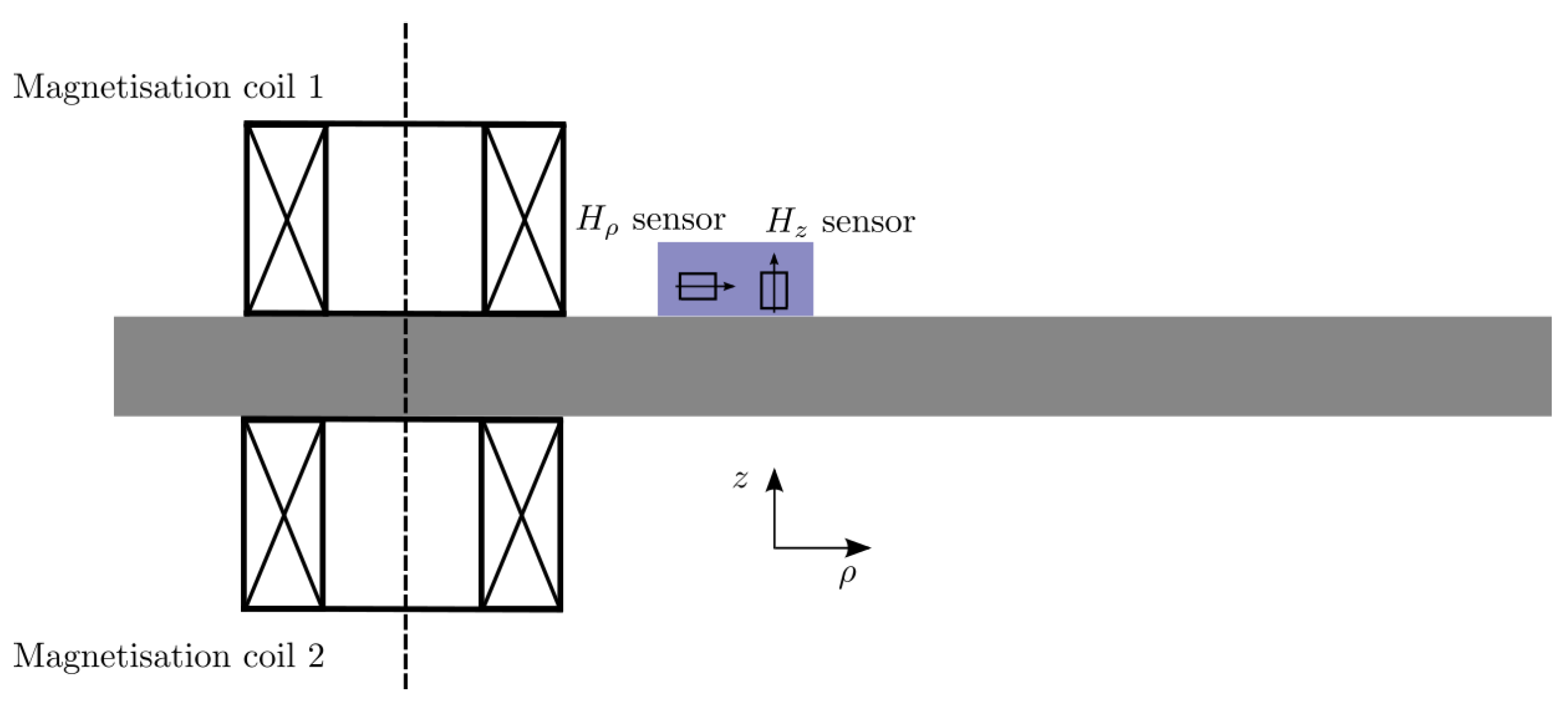
2.2. Measurement Principle, Basic Setups and Experimental Observables
2.3. Industrial Realisations: 3MA, HACOM, and PropertyMon Systems
3. Magnetic Properties
3.1. Parametric Models for the Description of Magnetic Hysteresis
3.2. Spectral Analysis of the Hysteresis Operator
3.3. The Harmonic Distortion Identifier K
4. Measurement Processing and Inversion
4.1. Semi-Analytical Approximations for the Inverse Operator
4.2. Direct Extraction of the Coercive Field from the Magnetic Field
4.3. Numerical and Statistical Analysis of Forward and Inverse Operator
5. Numerical Example
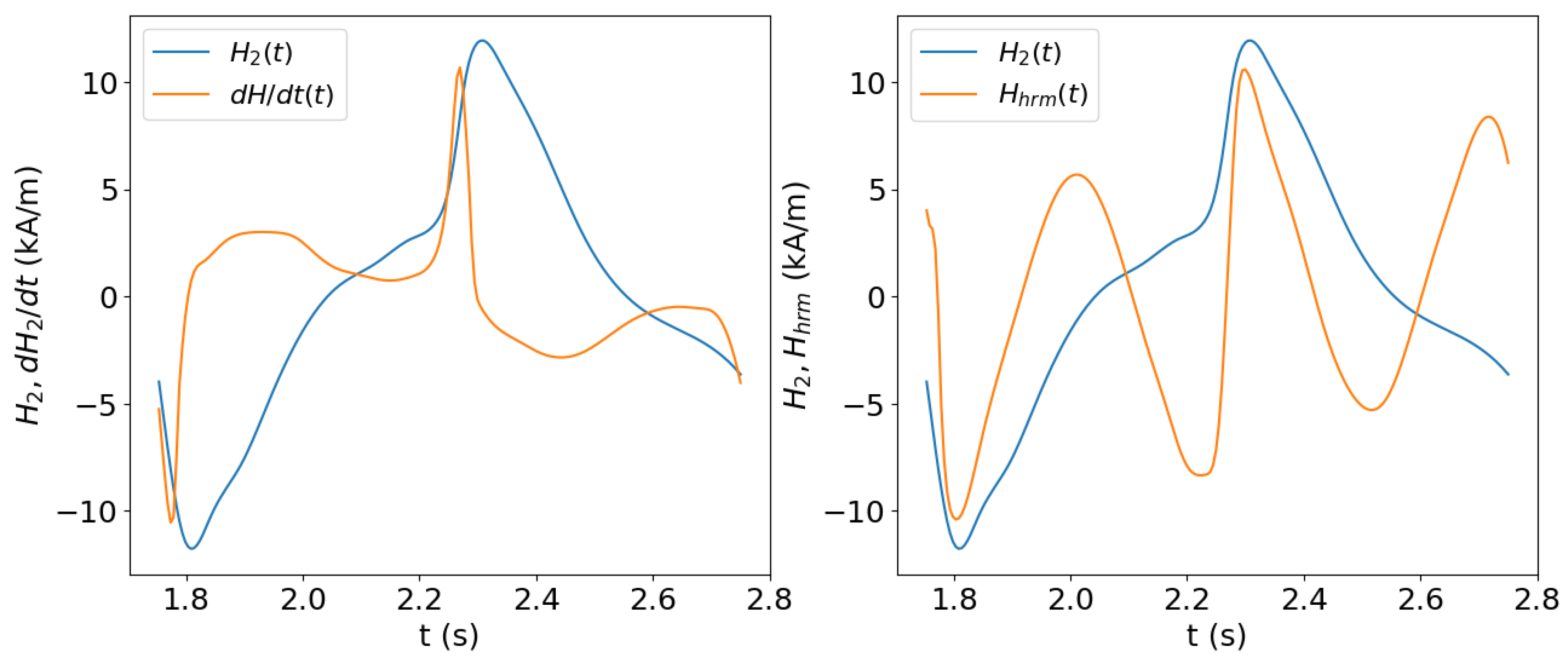
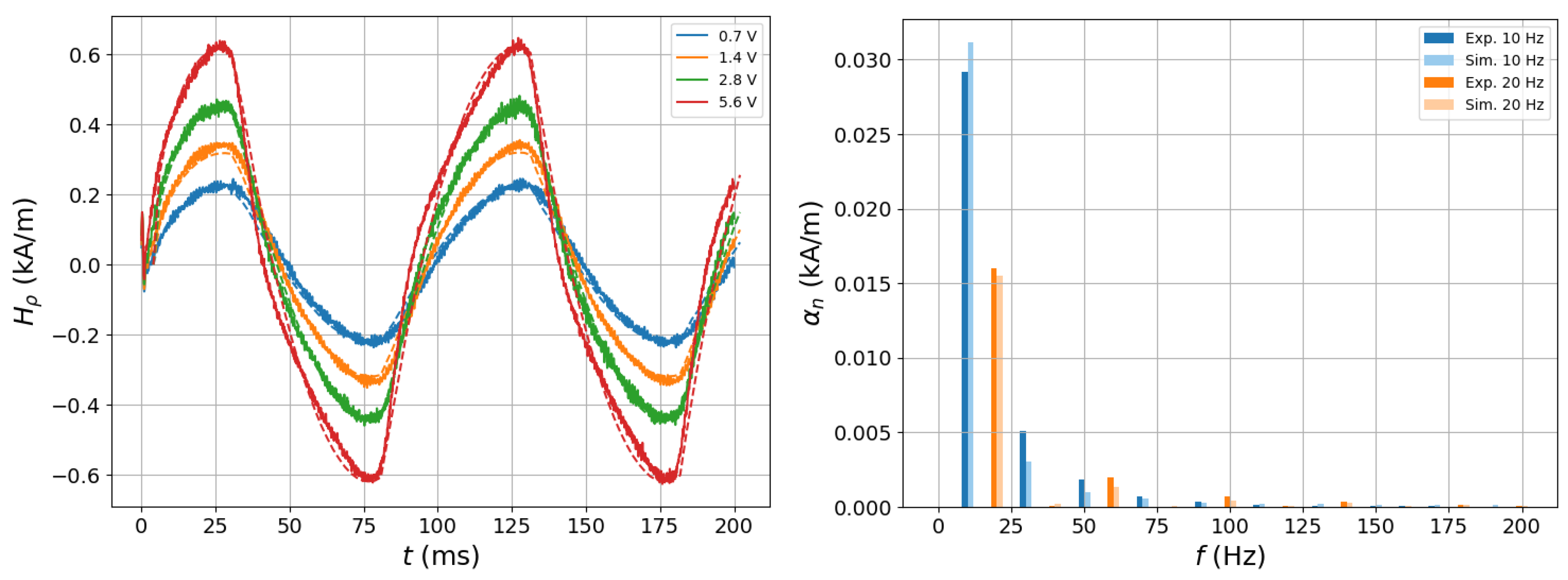
5.1. Harmonic Distortion Measurements in an Open-Circuit Configuration
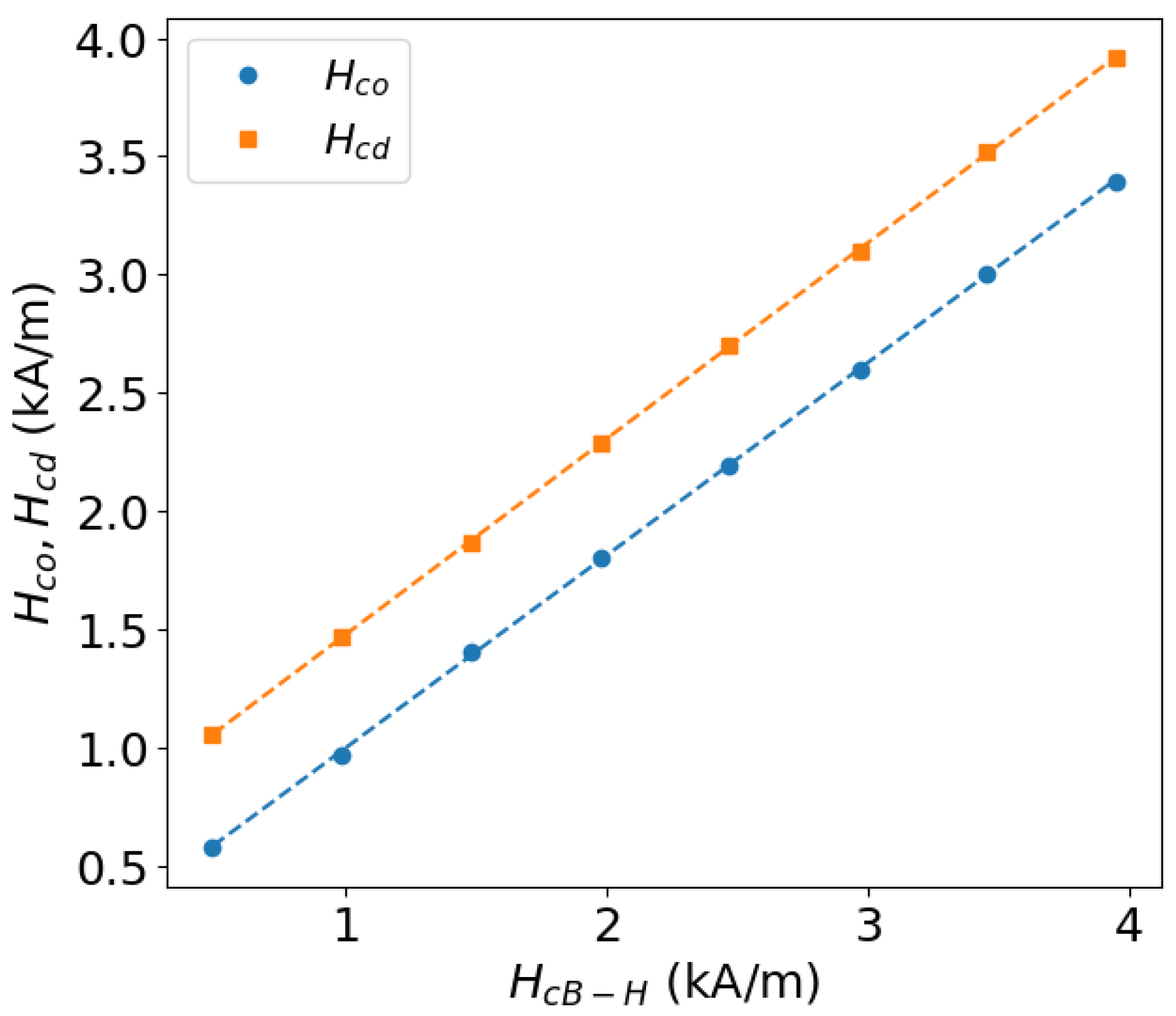
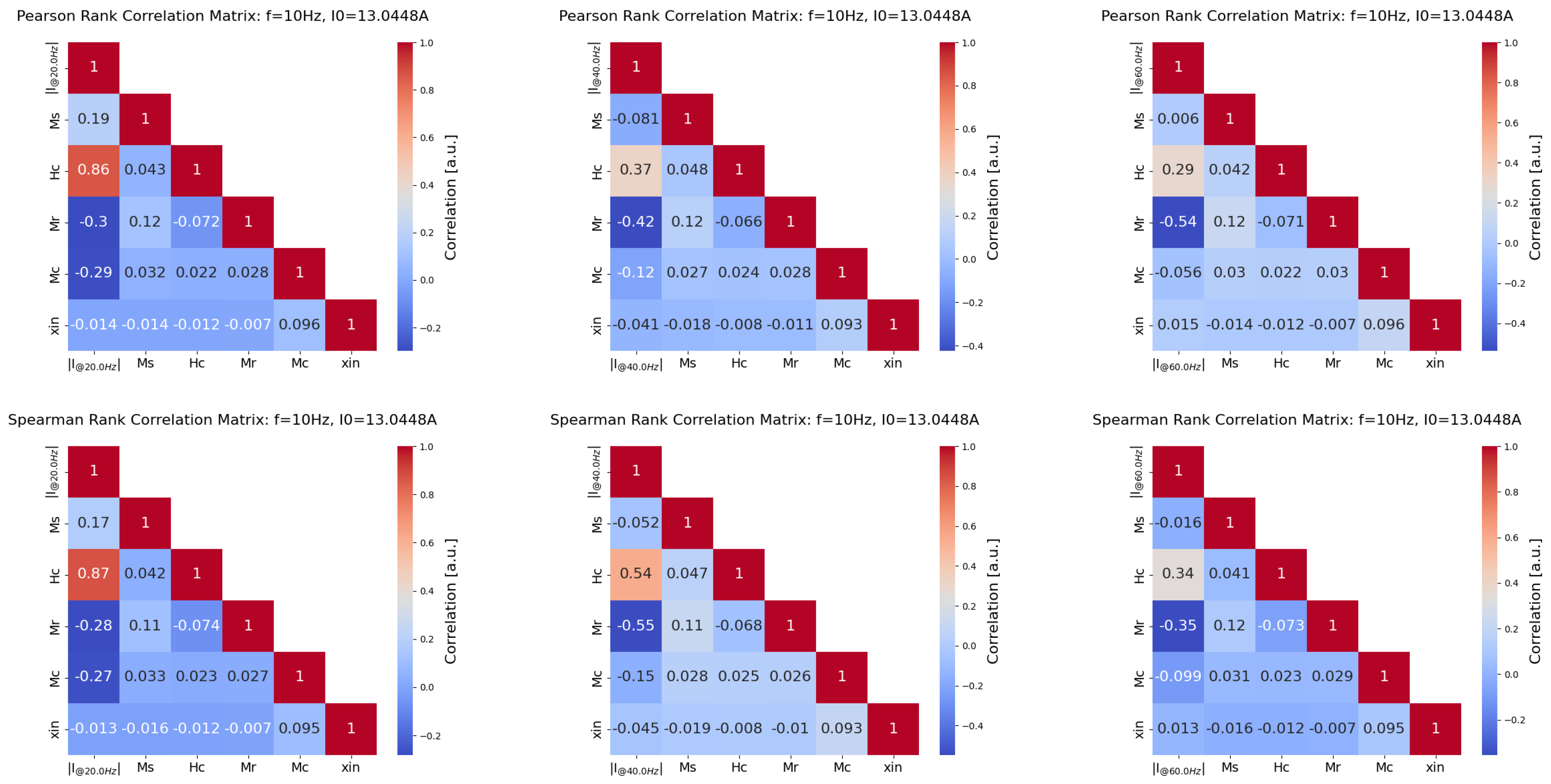
5.2. Correlation with Hysteresis Parameters
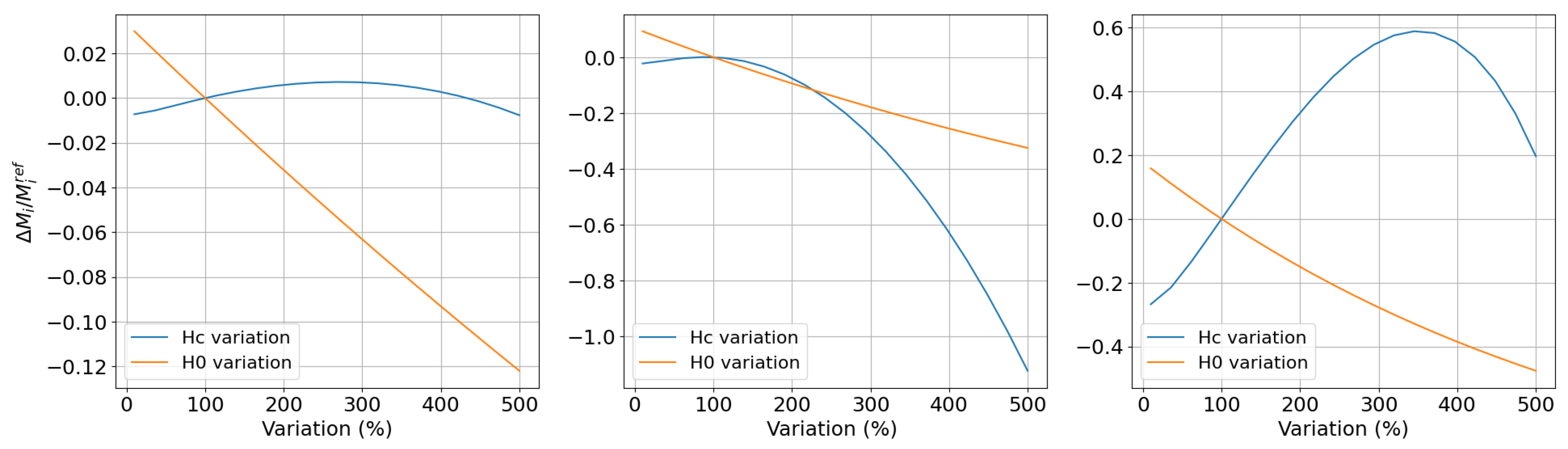
5.3. Sensitivity Analysis of Hysteresis Parameters Based on Harmonic Distortion Measurements
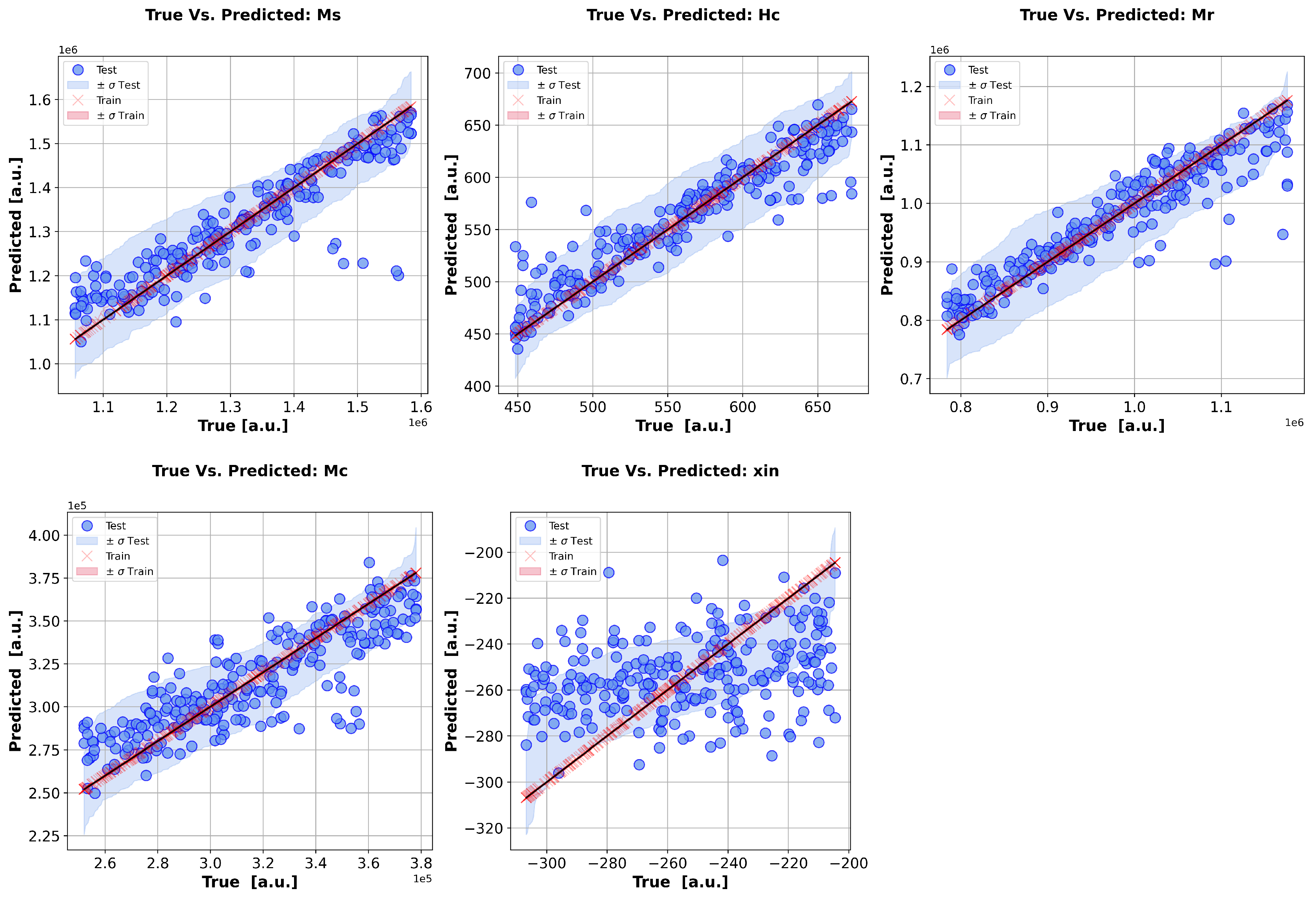
5.4. Prediction of the Material Parameters via Direct Inversion of Operator
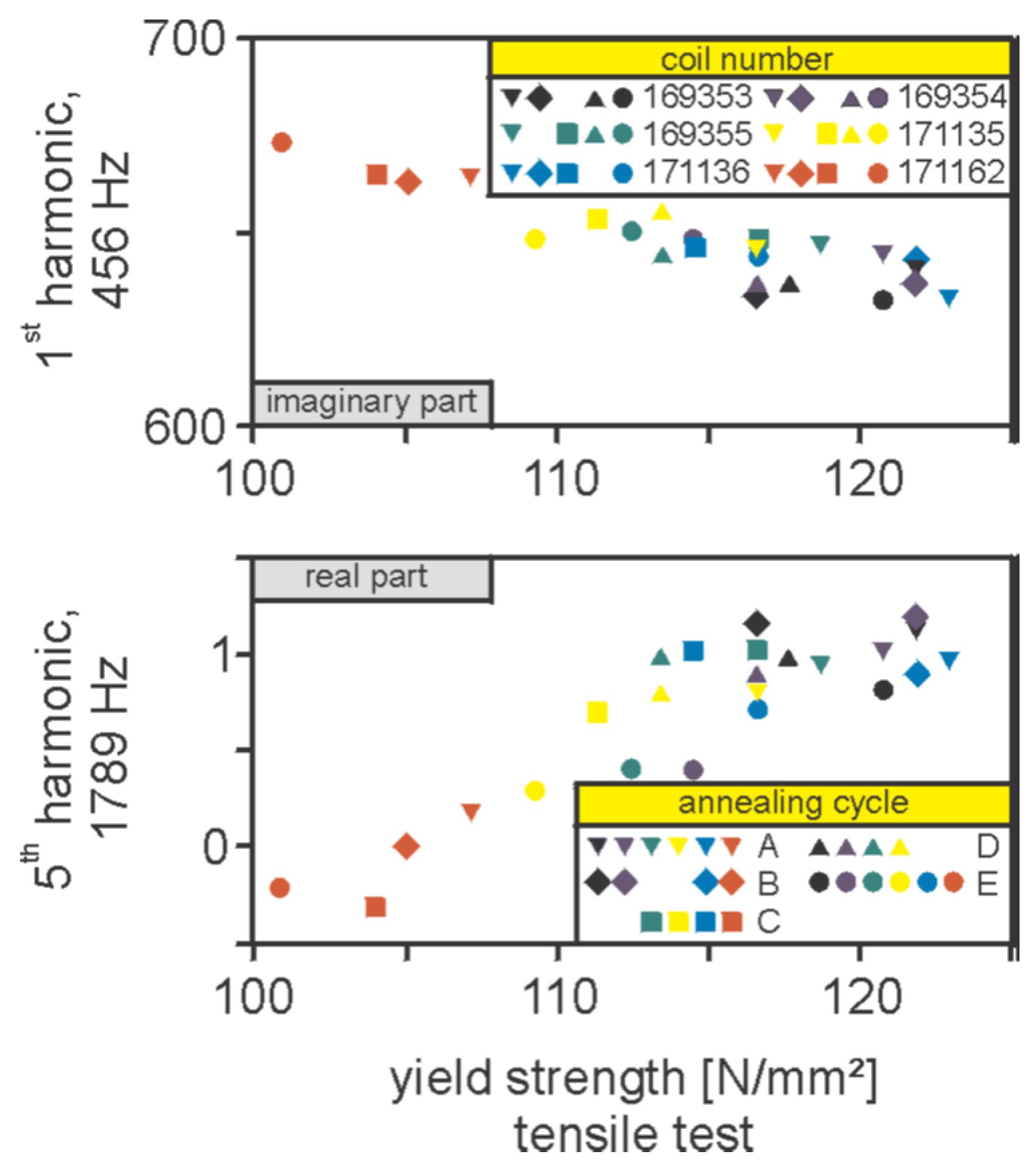
6. Correlation with the Microstructure and the Mechanical Properties
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Ponomarev Model
- We assume that a polycrystalline steel with a uniaxial excitation can be coarsely approximated by an Ising system;
- We accept that (A1) is generally valid for the entire region of interest and not only around the coercive field.
Appendix B. Spectral Decomposition of the Ponomarev Expression
References
- Ktena, A.; Hasicic, M.; Landgraf, F.J.; Moudilou, E.; Angelopoulos, S.; Hristoforou, E. On the use of differential permeability and magnetic Barkhausen Noise Measurements for Magnetic NDT Applications. J. Magn. Magn. Mater. 2022, 546, 168898. [Google Scholar] [CrossRef]
- Vourna, P.; Ktena, A.; Tsarabaris, P.; Hristoforou, E. Magnetic Residual Stress Monitoring Technique for Ferromagnetic Steels. Metals 2018, 8, 592. [Google Scholar] [CrossRef]
- Hristoforou, E.; Vourna, P.; Ktena, A. On the Universality of the Dependence of Magnetic Parameters on Residual Stresses in Steels. IEEE Trans. Magn. 2016, 51, 6201106. [Google Scholar] [CrossRef]
- Gupta, B.; Uchimoto, T.; Ducharne, B.; Sebald, G.; Miyazaki, T. Magnetic incremental permeability non-destructive evaluation of 12 Cr-Mo-V-W steel creep test samples with varied ageing levels and thermal treatments. NDT E Int. 2019, 104, 42–50. [Google Scholar] [CrossRef]
- Gupta, B.; Ducharne, B.; Sebald, G.; Uchimoto, T. Physical interpretation of the microstructure for aged 12 Cr-Mo-V-W steel creep test samples based on simulation of magnetic incremental permeability. J. Magn. Magn. Mater. 2019, 489, 165250. [Google Scholar] [CrossRef]
- Matsumoto, T.; Uchimoto, T.; Takagi, T.; Dobmann, G.; Ducharne, B.; Oozono, S.; Yuya, H. Investigation of electromagnetic nondestructive evaluation of residual strain in low carbon steels using the eddy current magnetic signature (EC-MS) method. J. Magn. Magn. Mater. 2019, 479, 212–221. [Google Scholar] [CrossRef]
- Zhang, S.; Ducharne, B.; Uchimoto, T.; A Kita, Y.T.D. Simulation tool for the Eddy current magnetic signature (EC-MS) nondestructive method. J. Magn. Magn. Mater. 2020, 513, 167221. [Google Scholar] [CrossRef]
- Bach, G.; Goebbels, K.; Theiner, W. Characterization of hardening depth by Barkhausen noise measurement. Mater. Eval. 1988, 46, 1576–1580. [Google Scholar] [CrossRef]
- Saquet, O.; Tapuleasa, D.; Chicois, J. Use of Barkhausen noise for determination of surface hardened depth. Nondestr. Test. Eval. 1998, 14, 277–292. [Google Scholar] [CrossRef]
- Moorthy, V.; Shaw, B.A.; Day, S. Evaluation of applied and residual stresses in case-carburised En36 steel subjected to bending using the magnetic Barkhausen emission technique. Acta Mater. 2004, 52, 1927–1936. [Google Scholar] [CrossRef]
- Kleber, X.; Hug, A.; Merlin, J.; Soler, M. Ferrite-martensite steels characterization using magnetic Barkhausen noise measurements. ISIJ Int. 2004, 44, 1033–1039. [Google Scholar] [CrossRef]
- Bahadur, A.; Mitra, A.; Kumar, R.; Sagar, P. Evaluation and correlation of residual stress measurement in steel. J. Nondestr. Eval. 2007, 26, 47–55. [Google Scholar] [CrossRef]
- Davut, K.; Gur, H. Monitoring the microstructural changes during tempering of quenched SAE 5140 steel by magnetic Barkhausen noise. J. Nondestr. Eval. 2007, 26, 107–113. [Google Scholar] [CrossRef]
- Vourna, P.; Ktena, A.; Tsakiridis, P.; Hristoforou, E. A novel approach of accurately evaluating residual stress and microstructure of welded electrical steels. NDT E Int. 2015, 71, 33–42. [Google Scholar] [CrossRef]
- Lasaosa, A.; Gurruchaga, K.; Arizti, F.; Martínez-de-Guerenu, A. Induction Hardened Layer Characterization and Grinding Burn Detection by Magnetic Barkhausen Noise Analysis. J. Nondestr. Eval. 2017, 36. [Google Scholar] [CrossRef]
- Martínez-de-Guerenu, A.; Arizti, F.; Díaz-Fuentes, M.; Gutiérrez, I. Recovery during annealing in a cold rolled low carbon steel. Part I: Kinetics and microstructural characterization. Acta Mater. 2004, 52, 3657–3664. [Google Scholar] [CrossRef]
- Martínez-de-Guerenu, A.; Arizti, F.; Gutiérrez, I. Recovery during annealing in a cold rolled low carbon steel. Part II: Modelling the kinetics. Acta Mater. 2004, 52, 3665–3670. [Google Scholar] [CrossRef]
- Martínez-de-Guerenu, A.; Gurruchaga, K.; Arizti, F. Use of magnetic techniques for characterisation of the microstructure evolution during the annealing of low carbon steels. In Proceedings of the 9th European Conference on Non-Destructive Testing (ECNDT), Berlin, Germany, 25–29 September 2006; pp. 1–11. [Google Scholar]
- Dobmann, G.; Altpeter, I.; Bernd Wolter, R.K. Industrial Applications of 3MA—Micromagnetic Multiparameter Microstructure and Stress Analysis. In Proceedings of the 5th International Conference Structural Integrity of Welded Structure, Timisora, Romania, 20–21 November 2007. [Google Scholar]
- Dobmann, G.; Altpeter, I.; Wolter, B.; Kern, R. Industrial applications of 3MA - Micromagnetic Multiparameter Microstructure and Stress Analysis. In Proceedings of the Electromagnetic Nondestructive Evaluation (XI); Studies in Applied Electromagnetics and Mechanics; Tamburrino, A., Melikhov, Y., Chen, Z., Udpa, L., Eds.; IOS Press: Amsterdam, Netherlands, 2008; Volume 31, pp. 18–25. [Google Scholar] [CrossRef]
- Dobmann, G. Physical Basics and Industrial Applications of 3MA—Micromagnetic Multiparameter Microstructure And Stress Analysis. In Proceedings of the 10th European Conference on Non-Destructive Testing, Moscow, Russia, 7–11 June 2010. [Google Scholar]
- The 3MA System Is Commercialised by Fraunhofer Institute for Nondestructive Testing; IZFP: Saarbrücken, Germany; Available online: https://www.izfp.fraunhofer.de (accessed on 9 February 2025).
- The PropertyMon System Is Commercially Available From Primetals, Linz, Austia. Available online: https://www.primetals.com (accessed on 9 February 2025).
- The IMPOC System Is Commercialised by EMG Automation, Wenden, Germany. Available online: https://www.emg.elexis.group (accessed on 9 February 2025).
- European Communities; Kroos, J.; Stolzenberg, M.; Evertz, T. Combined Measuring System for an Improved Non-Destructive Determination of the Mechanical/Technological Material Properties of Steel Sheet; Publications Office: Luxembourg, 2005. [Google Scholar]
- European Communities; Stolzenberg, M.; Schmidt, R.; Casajus, A.; Kebe, T.; Falkenstrom, M.; Martinez de Guerenu, A.; Link, N.; Ploegaert, H.; Van den Berg, F.; et al. Online Material Characterisation at Strip Production (OMC); Publications Office: Luxembourg, 2013. [Google Scholar] [CrossRef]
- Skarlatos, A.; Reboud, C.; Svaton, T.; de Guerenu, A.M.; Kebe, T.; van den Berg, F. Modelling the IMPOC response for different steel strips. In Proceedings of the 19th World Conference on Nondestructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Van den Berg, F.D.; Kok, P.J.J.; Yang, H.; Aarnts, M.P.; Meilland, P.; Kebe, T.; Stolzenberg, M.; Krix, D.; Zhu, W.; Peyton, A.J.; et al. Product Uniformity Control—A Research Collaboration of European Steel Industries to Non-Destructive Evaluation of Microstructure and Mechanical Properties. In Electromagnetic Nondestructive Evaluation (XXII); IOS Press: Amsterdam, Netherlands, 2018; Volume 43, Studies in Applied Electromagnetics and Mechanics; pp. 120–129. [Google Scholar] [CrossRef]
- Skarlatos, A.; Reboud, C.; Kebe, T.; van den Berg, F.; Schmidt, R. Simulation of IMPOC ystem for online monitoring of steel mechanical properties. In Proceedings of the 12th European Conference on Nondestructive Testing, Gothenburg, Sweden, 11–15 June 2018. [Google Scholar]
- European Communities; Van den Berg, F.; Kok, P.; Yang, H.; Aarnts, M.; Fintelman, D.; Meilland, P.; Kebe, T.; Stolzenberg, M.; Krix, D.; et al. Product Uniformity Control (PUC); Publications Office: Luxembourg, 2020. [Google Scholar] [CrossRef]
- van den Berg, F.; Aarnts, M.; Yang, H.; Melzer, S.; Fintelman, D.; Ennis, B.; Gillgren, L.; Jorge-Badiola, D.; Martínez-De-Guerenu, A.; Davis, C.; et al. How the EU project “Online Microstructure Analytics” advances inline sensing of microstructure during steel manufacturing. In Proceedings of the European Conference on Non-Destructive Testing (ECNDT), Lisbon, Portugal, 3–7 July 2023. [Google Scholar]
- O’Dwyer, J.; O’Donnell, T. Choosing the relaxation parameter for the solution of nonlinear magnetic field problems by the Newton-Raphson method. IEEE Trans. Magn. 1995, 31, 1484–1487. [Google Scholar] [CrossRef]
- Drobny, S.; Weiland, T. Numerical calculation of nonlinear transient field problems with the Newton-Raphson method. IEEE Trans. Magn. 2000, 36, 809–812. [Google Scholar] [CrossRef]
- Munteanu, I.; Drobny, S.; Weiland, T.; Ioan, D. Triangle search method for nonlinear electromagnetic field computation. COMPEL 2001, 20, 417–430. [Google Scholar] [CrossRef]
- Gyselinck, J.; Dular, P.; Geuzaine, C.; Legros, W. Harmonic-balance finite-element modeling of electromagnetic devices: A novel approach. IEEE Trans. Magn. 2002, 38, 521–524. [Google Scholar] [CrossRef]
- Yuan, J.; Clemens, M.; De Gersem, H.; Weiland, T. Solution of transient hysteretic magnetic field problems with hybrid newton-polarization methods. IEEE Trans. Magn. 2005, 41, 1720–1723. [Google Scholar] [CrossRef]
- Bíró, O.; Preis, K. An efficient time domain method for nonlinear periodic eddy current problems. IEEE Trans. Magn. 2006, 42, 695–698. [Google Scholar] [CrossRef]
- Circ, I.R.; Hantila, F. An efficient harmonic method for solving nonlinear time-periodic eddy-current problems. IEEE Trans. Magn. 2007, 43, 1185–1188. [Google Scholar] [CrossRef]
- Bíró, O.; Koczka, G.; Preis, K. Fast time-domain finite element analysis of 3-D nonlinear time-periodic eddy current problems with T, Φ-Φ formulation. IEEE Trans. Magn. 2011, 47, 1170–1173. [Google Scholar] [CrossRef]
- Skarlatos, A.; Theodoulidis, T. A modal approach for the solution of the non-linear induction problem in ferromagnetic Media. IEEE Trans. Magn. 2016, 55, 7000211. [Google Scholar] [CrossRef]
- Sabariego, R.V.; Gyselinck, J. Eddy-Current-Effect Homogenization of Windings in Harmonic-Balance Finite-Element Models. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Sabariego, R.V.; Niyomsatian, K.; Gyselinck, J. Eddy-Current-Effect Homogenization of Windings in Harmonic-Balance Finite-Element Models Coupled to Nonlinear Circuits. IEEE Trans. Magn. 2018, 54, 7206304. [Google Scholar] [CrossRef]
- Skarlatos, A.; Theodoulidis, T. Study of the non-linear eddy-current response in a ferromagnetic plate: Theoretical analysis for the 2D case. NDT E Int. 2018, 93, 150–156. [Google Scholar] [CrossRef]
- Scolaro, E.; Alberti, L.; Sabariego, R.V.; Gyselinck, J. Harmonic balance applied to a 2D nonlinear finite-element magnetic model with motion and circuit coupling. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3275. [Google Scholar] [CrossRef]
- Tumanski, S. Handbook of Magnetic Measurements; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Mayergoyz, I. Mathematical Models of Hysteresis and Their Applications, 1st ed.; Elsevier Science Inc.: New York, NY, USA, 2003. [Google Scholar]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Appl. Phys. 1984, 55, 2115–2120. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Hauser, H. Energetic model of ferromagnetic hysteresis. J. Appl. Phys. 1994, 75, 2584–2597. [Google Scholar] [CrossRef]
- Mel’gui, M.A. Formulas for describing nonlinear and hysteretic properties of ferromagnets. Defektoskopiya 1987, 11, 3–10, (Translated from Rusian). [Google Scholar]
- Bergqvist, A. Magnetic vector hysteresis model with dry friction-like pinning. IEEE Trans. Magn. 1997, 233, 342–347. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism; Wiley-IEEE Press: New York, NY, USA, 1993. [Google Scholar]
- Skarlatos, A.; Ducharne, B. Combination of hysteresis models for accuracy improvement and stabilized electromagnetic calculations. J. Magn. Magn. Mater. 2024, 592, 171747. [Google Scholar] [CrossRef]
- Ponomarev, Y.F. Harmonic analysis of the magnetization of ferromagnets remagnetized by an alternating field, with magnetic hysteresis taken into account. I. Method of describing magnetic hysteresis loops. Defektoskopiya 1985, 11, 61–67, (Translated from Rusian). [Google Scholar]
- Skarlatos, A.; Martínez-de Guerenu, A.; Badiola, D.J.; Lelidis, I. Interpretation of the magnetic susceptibility behaviour of soft carbon steels based on the scaling theory of second order phase transitions for systems with supercritical disorder. J. Magn. Magn. Mater. 2022, 555, 169265. [Google Scholar] [CrossRef]
- Theodoulidis, T.P.; Kriezis, E.E. Eddy Current Canonical Problems (with Applications to Nondestructive Evaluation); Tech Science Press: Forsyth, GA, USA, 2006. [Google Scholar]
- Pitsch, H. Die Entwicklung und Erprobung der Oberwellenanalyse im Zeitsignal der Magnetischen Tangenzialfeldstärke als neues Modul des 3MA-Ansatzes (Mikromagnetische Multiparameter Mikrostruktur- und Spannungsanalyse). Ph.D. Thesis, Universität des Saarlandes Darmstadt, Saarland, Germany, 1989. [Google Scholar]
- Dobmann, G.; Pitsch, H. Magnetic Tangential Field-Strengt-Inspection, a Further NDT-Tool for 3MA. In Nondestructive Characterization of Materials: Proceedings of the 3rd International Symposium Saarbrücken, FRG, Saarbrücken, Germany, 3–6 October 1988; Springer: Berlin/Heidelberg, Germany, 1989; pp. 636–643. [Google Scholar]
- Fillon, G.; Lord, M.; Buissère, J.F. Coercivity measurement from analysis of the tangential magnetic field. In Nondestructive Characterisation of Materials IV; Ruud, C.O., Bussiere, J.F., Robert, E., Green, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 230–323. [Google Scholar]
- Durin, G.; Zapperi, S. The Barkhausen effect. In The Science of Hysteresis, 1st ed.; Bertotti, G., Mayergoyz, I.D., Eds.; Academic Press: Cambridge, MA, USA, 2006; Volume II, Chapter 3; pp. 181–267. [Google Scholar]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Skarlatos, A.; Poulakis, N. Experimental and theoretical study of the harmonic distortion in a ferromagnetic plate excited by a pair of air-cored coils. NDT E Int. 2024, 145, 103136. [Google Scholar] [CrossRef]
- van den Heuvel, E.; Zhan, Z. Myths About Linear and Monotonic Associations: Pearson’s r, Spearman’s ρ, and Kendall’s τ. Am. Stat. 2022, 76, 44–52. [Google Scholar] [CrossRef]
- Skarlatos, A.; Miorelli, R.; Reboud, C.; van den Berg, F. Magnetic characterisation of steel strips using transient field measurements: Global sensitivity analysis and regression from a machine-learning perspective. Inverse Probl. 2024, 40, 045012. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Willey & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Mikheev, M.N.; Gorkunov, E.S. Relationship of magnetic properties to the structural condition of a substabce—The physical basis of magnetic structure analysis (review). Sov. J. Nondestruct. Test. 1974, 17, 579–592. [Google Scholar]
- Mager, A. Über den Einfluß der Korngrße auf die Koerzitivkraff. Ann. D Phys. 1952, 11, 15–16. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. The influence of grain size and impurities on the magnetic properties of the soft magnetic alloy 47.5% NiFe. IEEE Trans. Magn. 1974, 10, 172–174. [Google Scholar] [CrossRef]
- Degauque, J.; Astie, B.; Porteseil, J.; Vergne, R. Influence of the grain size on the magnetic and magnetomechanical properties of high-purity iron. J. Magn. Magn. Mater. 1982, 26, 261–263. [Google Scholar] [CrossRef]
- Sablik, M.J. Modeling the effect of grain size and dislocation density on hysteretic magnetic properties in steels. J. Appl. Phys. 2001, 89, 5610–5613. [Google Scholar] [CrossRef]
- Dupré, L.; Sablik, M.J.; Keer, R.V.; Melkebeek, J. Modelling of microstructural effects on magnetic hysteresis properties. J. Phys. D Appl. Phys. 2002, 35, 2086–2090. [Google Scholar] [CrossRef]
- Kersten, M. Grundlagen Einer Theorie der Ferromagnetischen Hysterese und der Koerzitivkraft; Verlag von S. Hirzel: Leipzig, Germany, 1944. [Google Scholar]
- Kneller, E. Ferromagnetismus; Springer: Berlin/Heidelberg, Germany, 1962. [Google Scholar]
- Zhou, L.; Davis, C.; Kok, P.; van den Berg, F. Magnetic NDT for steel microstructure characterisation—Modelling the effect of second phase distribution on magnetic relative permeabilty. In Proceedings of the 19th World Conference on Non-Destructive Testing (WCNDT 2016), Munich, Germany, 13–17 June 2016. [Google Scholar]

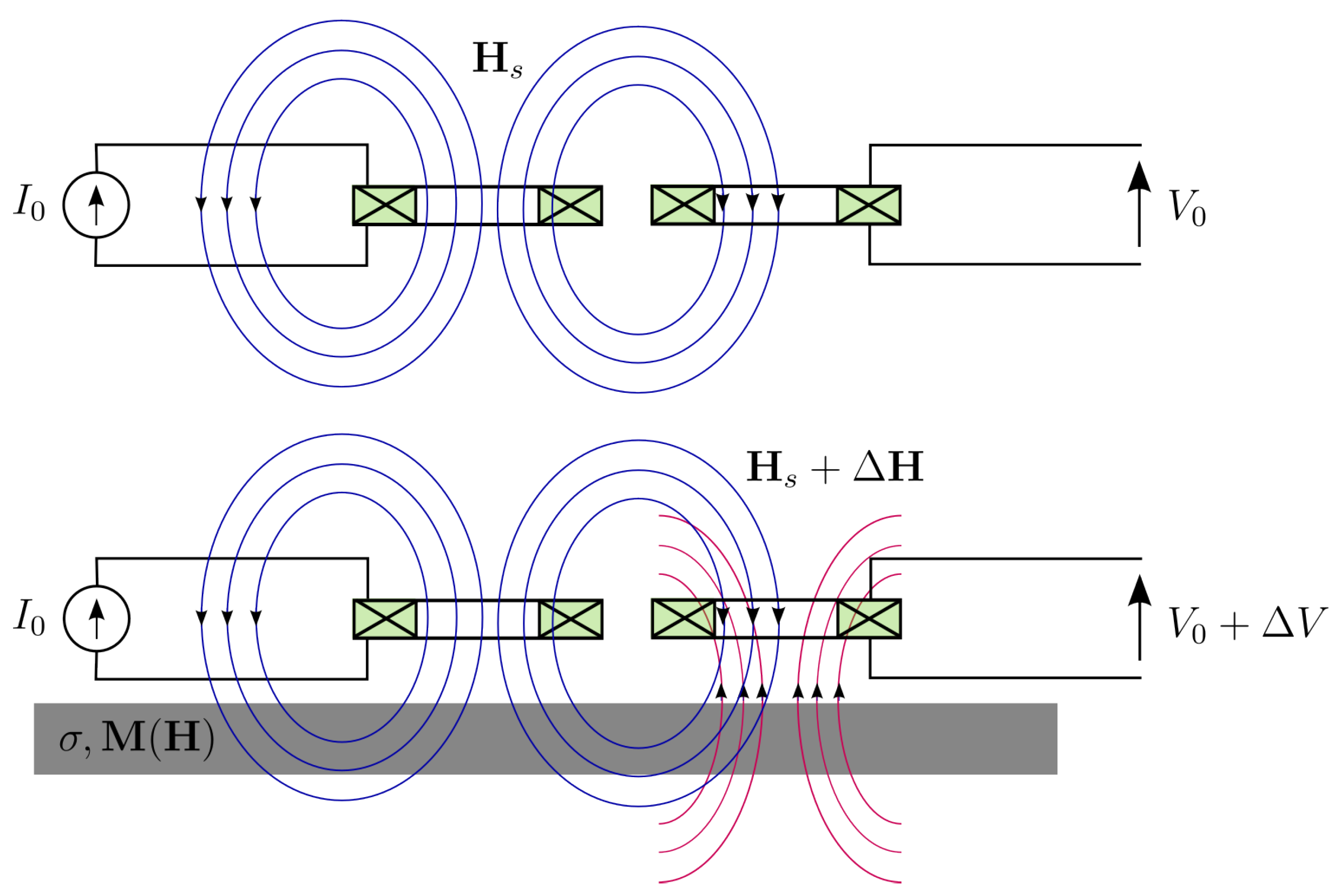
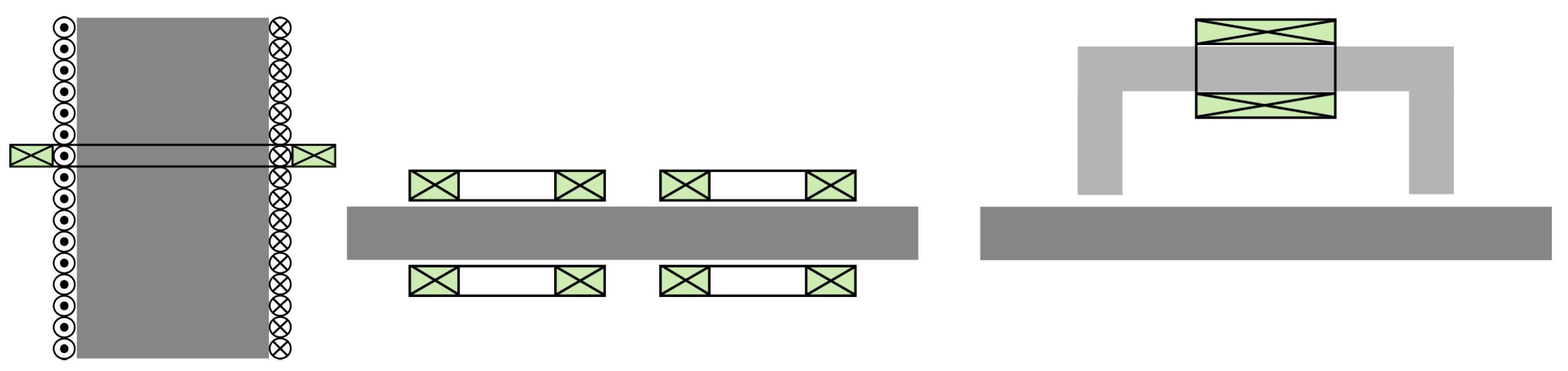

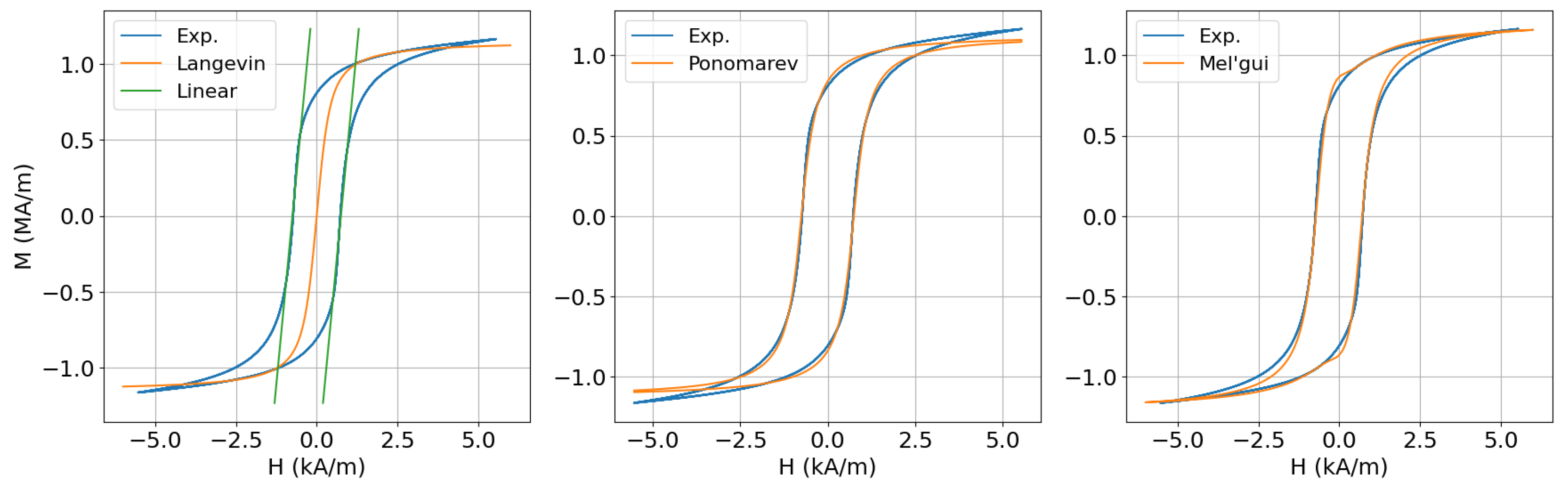
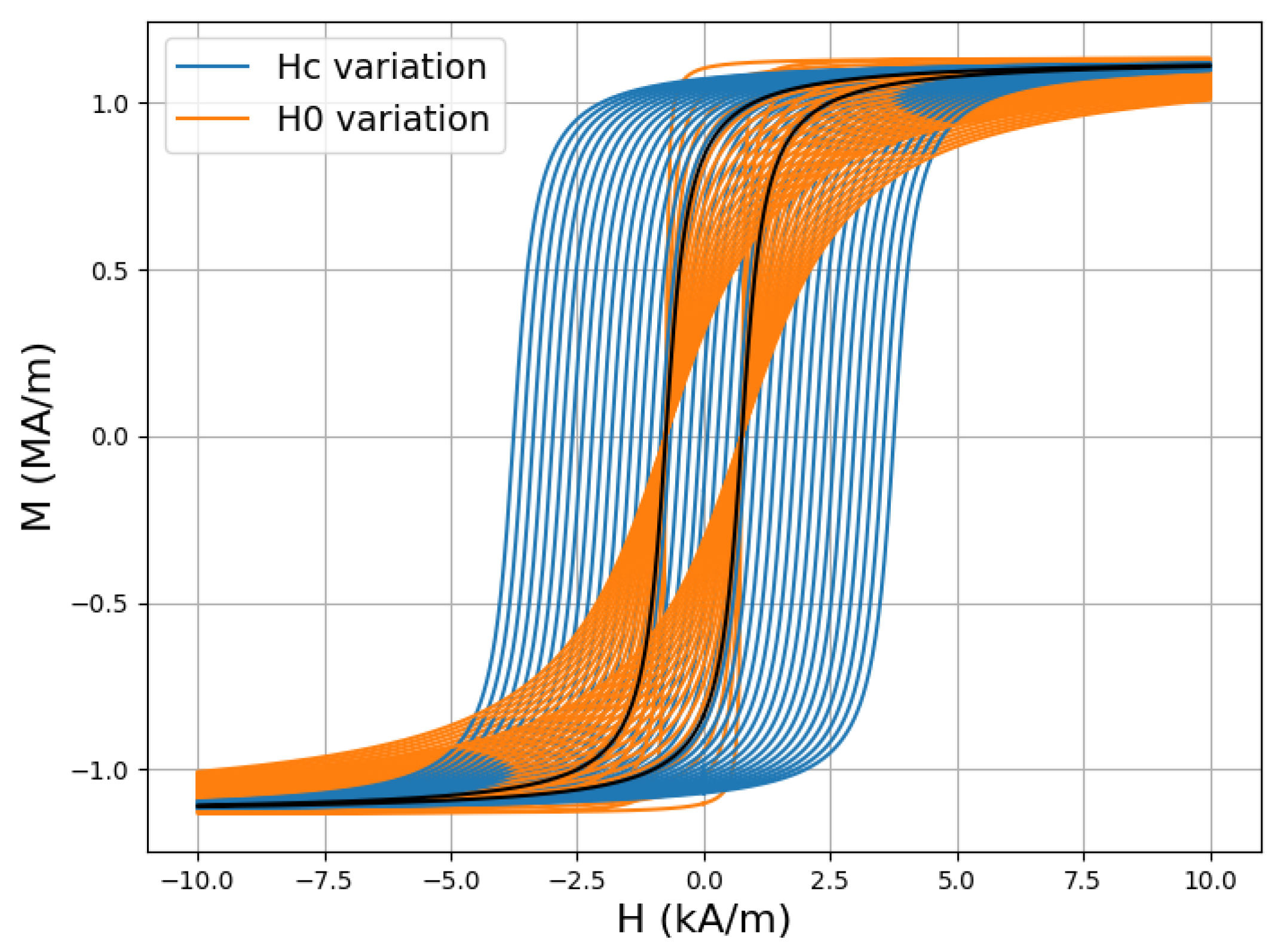

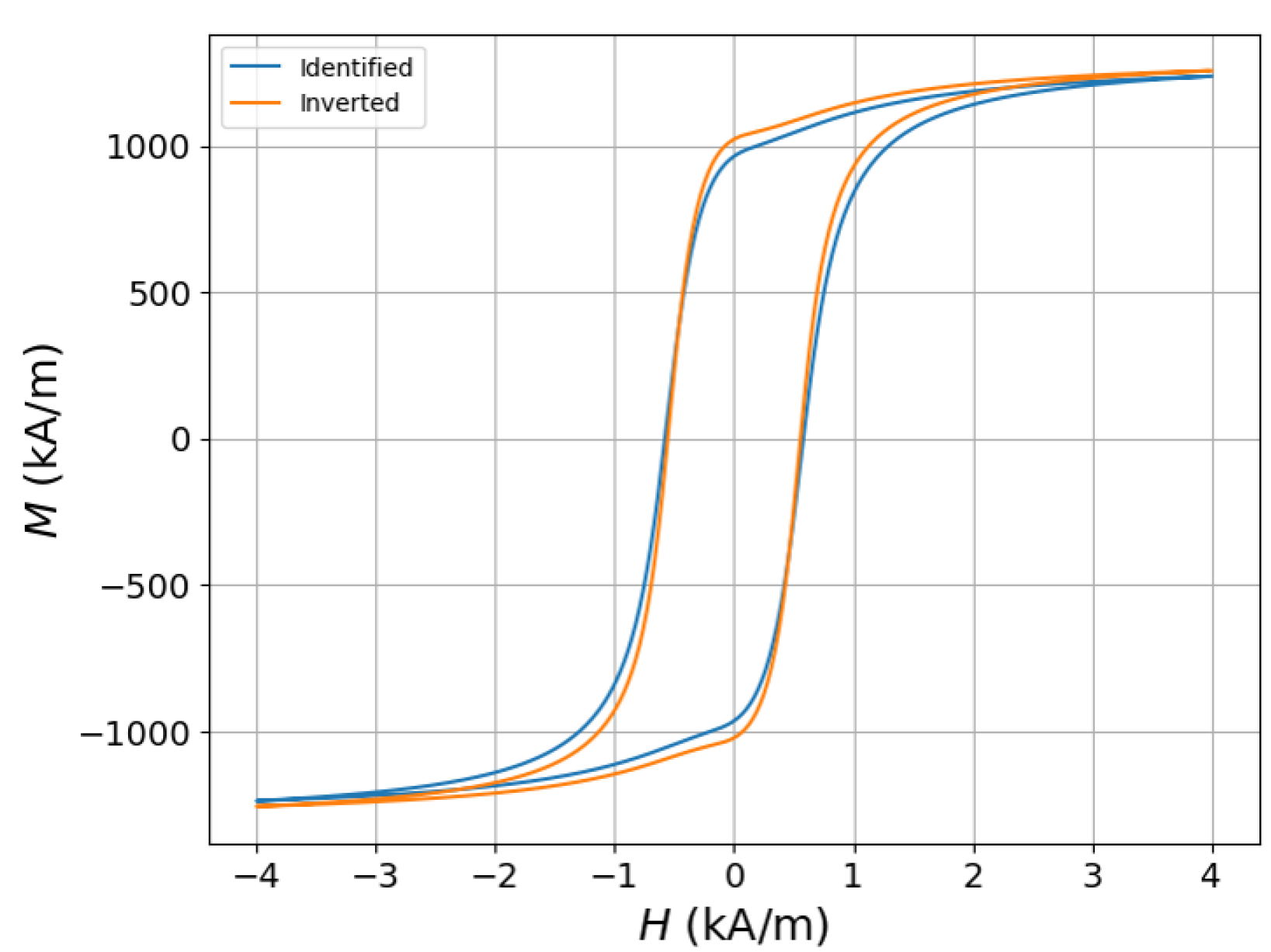

| Model | Parameters | Domain of Description |
|---|---|---|
| Langevin | high-field | |
| Backlash | close to | |
| Ponomarev | irreversible | |
| Mel’gui | irreversible, reversible |
| Parameter | Value |
|---|---|
| 721.694 kA/m | |
| 0.751 kA/m | |
| 0.326 kA/m |
| Mel’gui Model Parameters | Intervals | Sampling Strategy |
|---|---|---|
| MA/m | Uniform | |
| A/m | Uniform | |
| MA/m | Uniform | |
| MA/m | Uniform | |
| Uniform |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skarlatos, A.; Miorelli, R. Harmonic Distortion Measurements for Non-Destructive Evaluation of Steel Strips. Sensors 2025, 25, 2769. https://doi.org/10.3390/s25092769
Skarlatos A, Miorelli R. Harmonic Distortion Measurements for Non-Destructive Evaluation of Steel Strips. Sensors. 2025; 25(9):2769. https://doi.org/10.3390/s25092769
Chicago/Turabian StyleSkarlatos, Anastassios, and Roberto Miorelli. 2025. "Harmonic Distortion Measurements for Non-Destructive Evaluation of Steel Strips" Sensors 25, no. 9: 2769. https://doi.org/10.3390/s25092769
APA StyleSkarlatos, A., & Miorelli, R. (2025). Harmonic Distortion Measurements for Non-Destructive Evaluation of Steel Strips. Sensors, 25(9), 2769. https://doi.org/10.3390/s25092769






