Small Defects Detection of Galvanized Strip Steel via Schatten-p Norm-Based Low-Rank Tensor Decomposition
Abstract
Highlights
- Compared with the deep learning method for surface defect detection, the proposed SLRTD-based detection method is simpler and more effective in a galvanized strip steel production line.
- The proposed SLRTD-based detection method of surface defect can be applied for other industrial products, such as glass, fabric, LCD, and AMOLED.
Abstract
1. Introduction
- We propose an SLRTD method by digging out inter-patch correlation-ships of surface defect images of galvanized strip steel. The separated defect foreground target information with sparse outliers is embedded in the background of low-rank representation.
- To achieve an accurate estimation of non-defect background rank, we incorporate weighted Schatten -norm regularization for the background component, allowing for better noise removal while preserving edges, ultimately leading to improved detection results. Concurrently, a nonlinear reweighting strategy and tensor singular value decomposition (t-SVD) are adopted to help the model more delicately balance the low-rank and sparse components throughout the iterative process, which elevates the separation accuracy between the defect target and non-defect background.
- According to the alternating direction method of multipliers (ADMM), we solve the sparse and low-rank decomposition problem. Experiment results demonstrate the feasibility and effectiveness of the proposed SLRTD method.
2. Related Works
2.1. Filtering-Based Methods
2.2. Data-Driven-Based Methods
2.3. Tensor Decomposition-Based Methods
3. Methodology
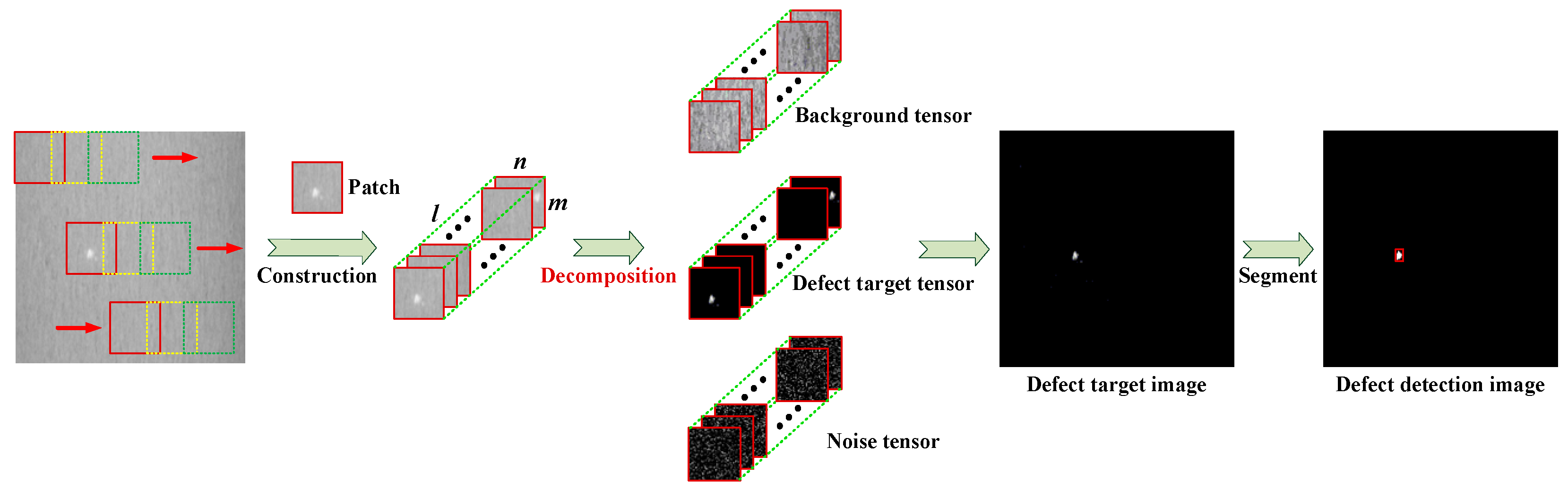
3.1. Construction of Tensor Model for Defect Image
| Algorithm 1: Solving Equation (11) |
| Input: ,
Output: step 1: Conduct FFT operation: step 2: Conduct SVD operation on each frontal slice of for do , Compute for do end for , end for for do end for step 3: Compute |
3.2. Model Solution
| Algorithm 2: Solving Equation (7) by ADMM |
| Input: Original defect image sequence tensor
,
,
Output: , , Initialize: , , , , , , While: not converged, do step 1: Update by Equation (11) step 2: Update by Equation (15) step 3: Update by Equation (16) step 4: Update by Equation (19) step 5: Update by Equation (20) step 6: Check the convergence condition step 7: Update end While |
3.3. Model Analysis
3.3.1. Computational Complexity
3.3.2. Convergence of Algorithm
4. Experiment
4.1. Experimental Setup
4.1.1. Data Collection and Preprocessing
4.1.2. Evaluation Metrics
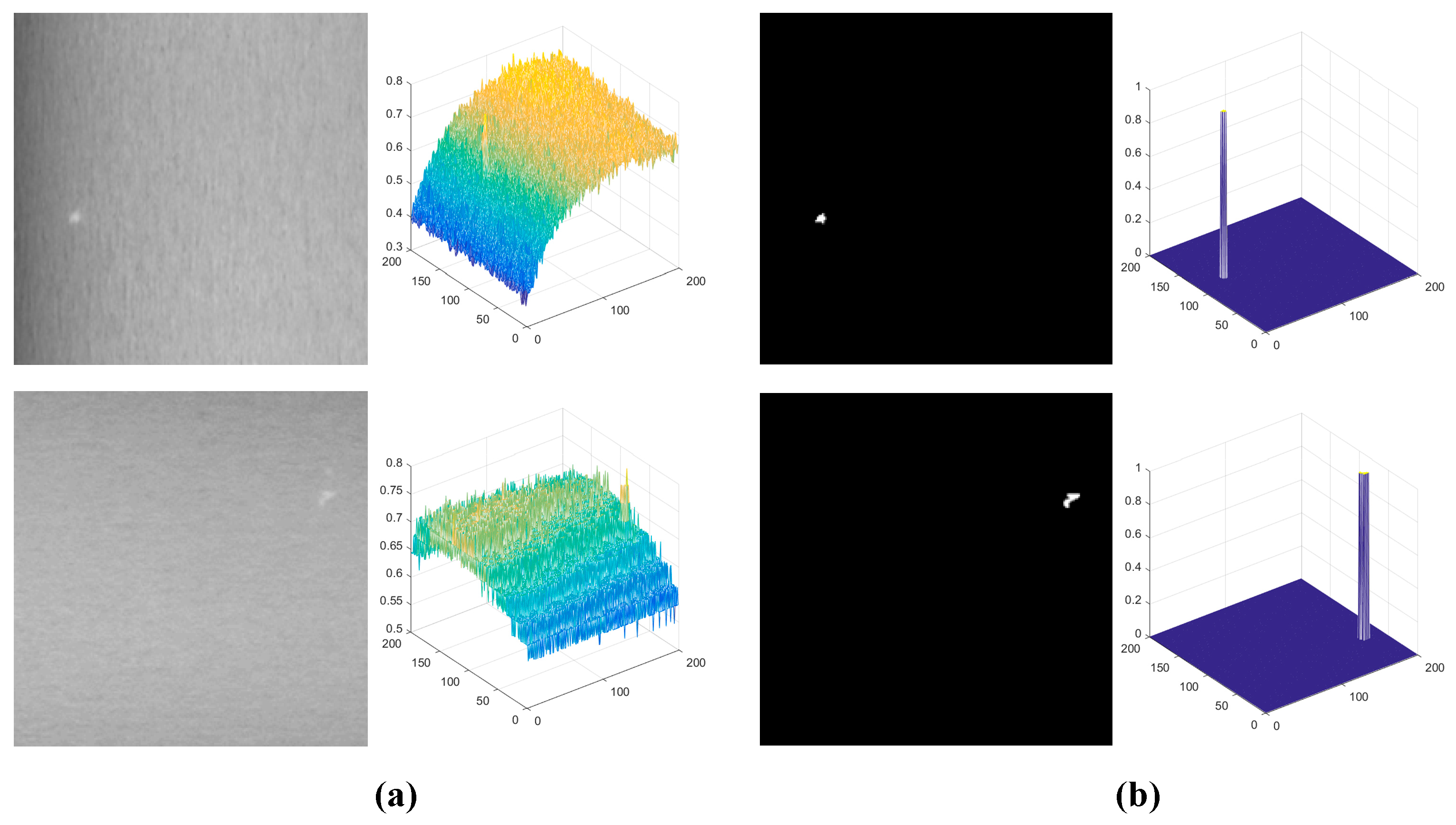
4.2. Validation of the Proposed SLRTD Method
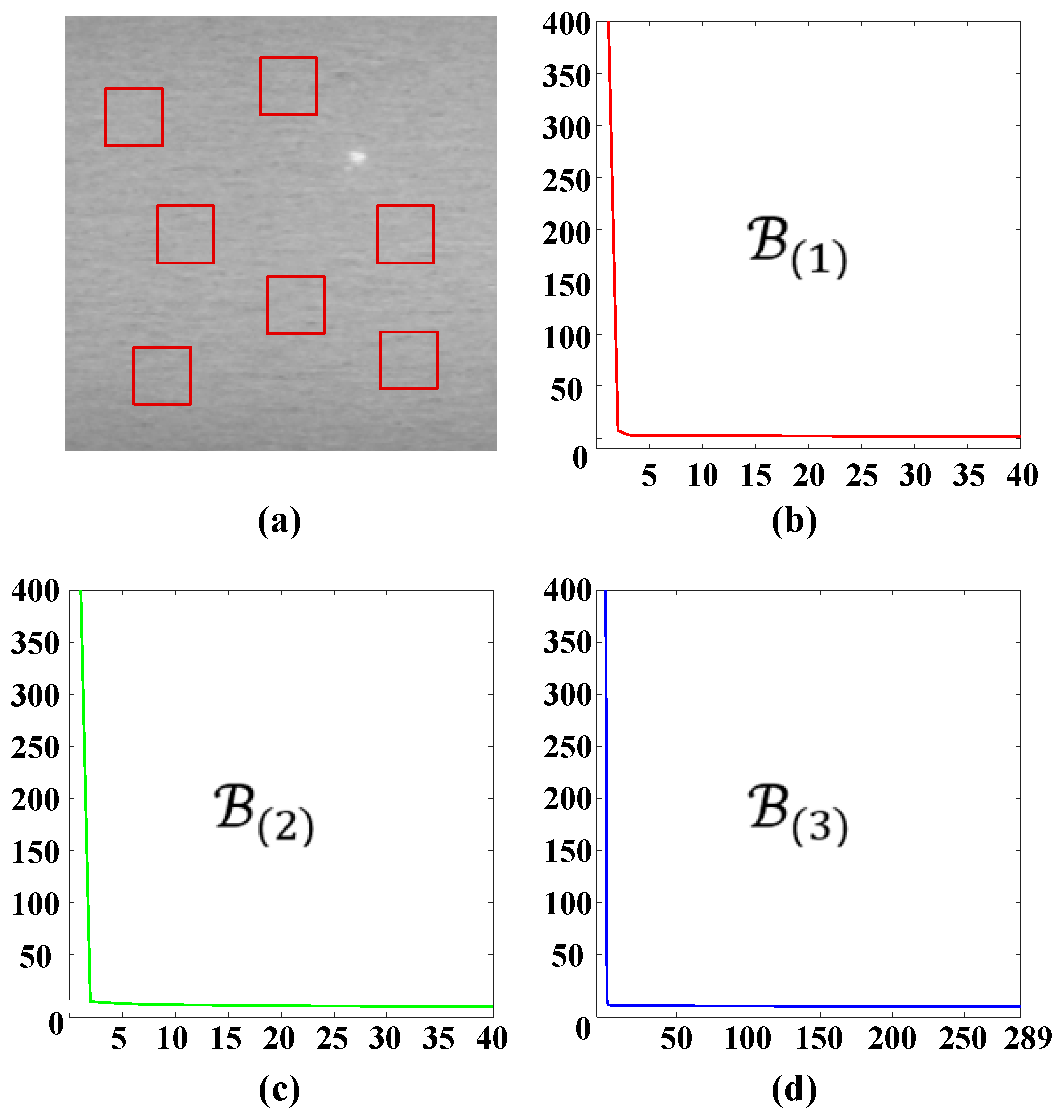
4.2.1. Parameter Analysis
- Patch size
- b.
- Step size
- c.
- Value of Schatten-
4.2.2. Robustness to Noise
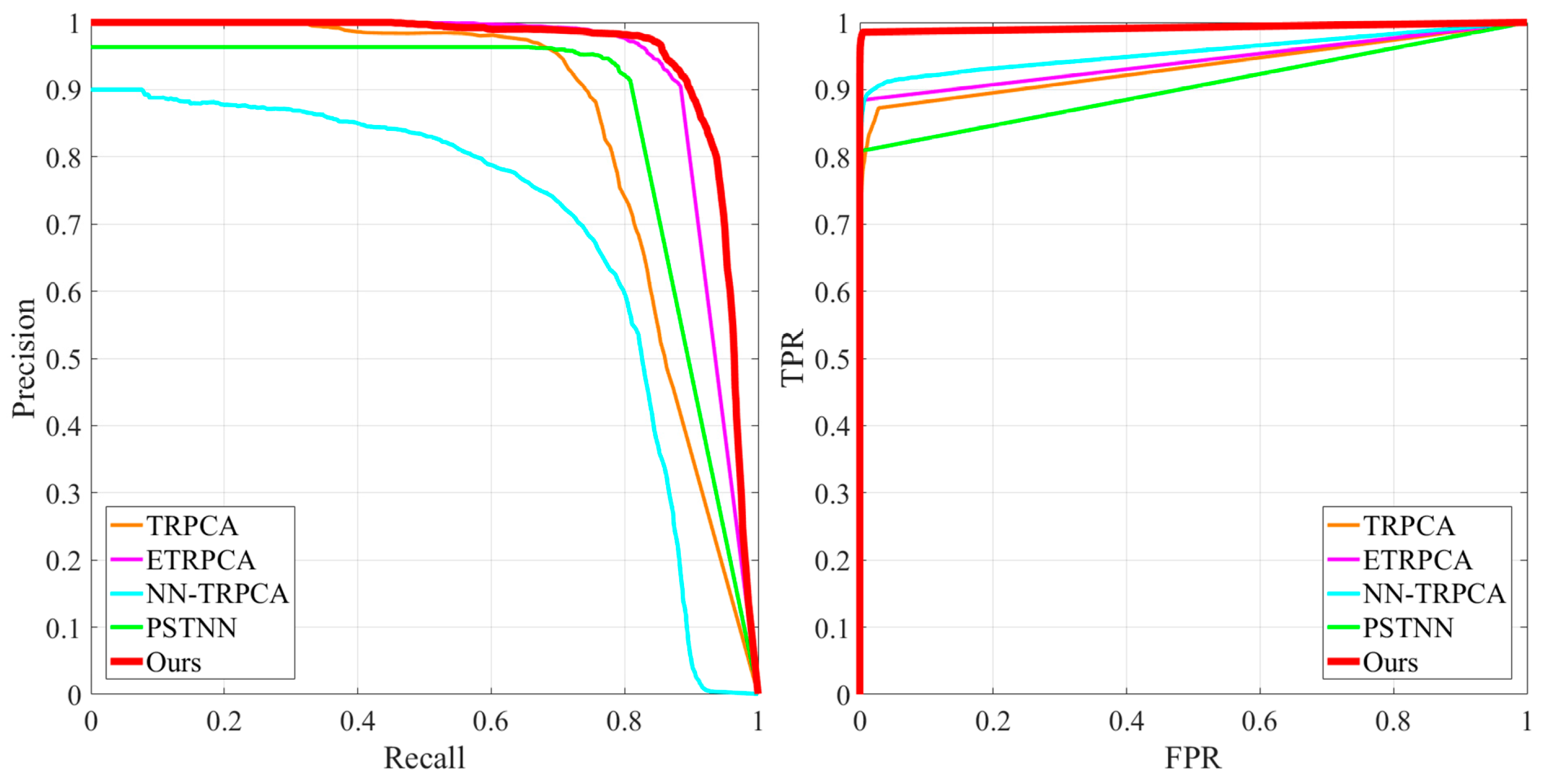
4.3. Comparison with the State-of-the-Art Methods
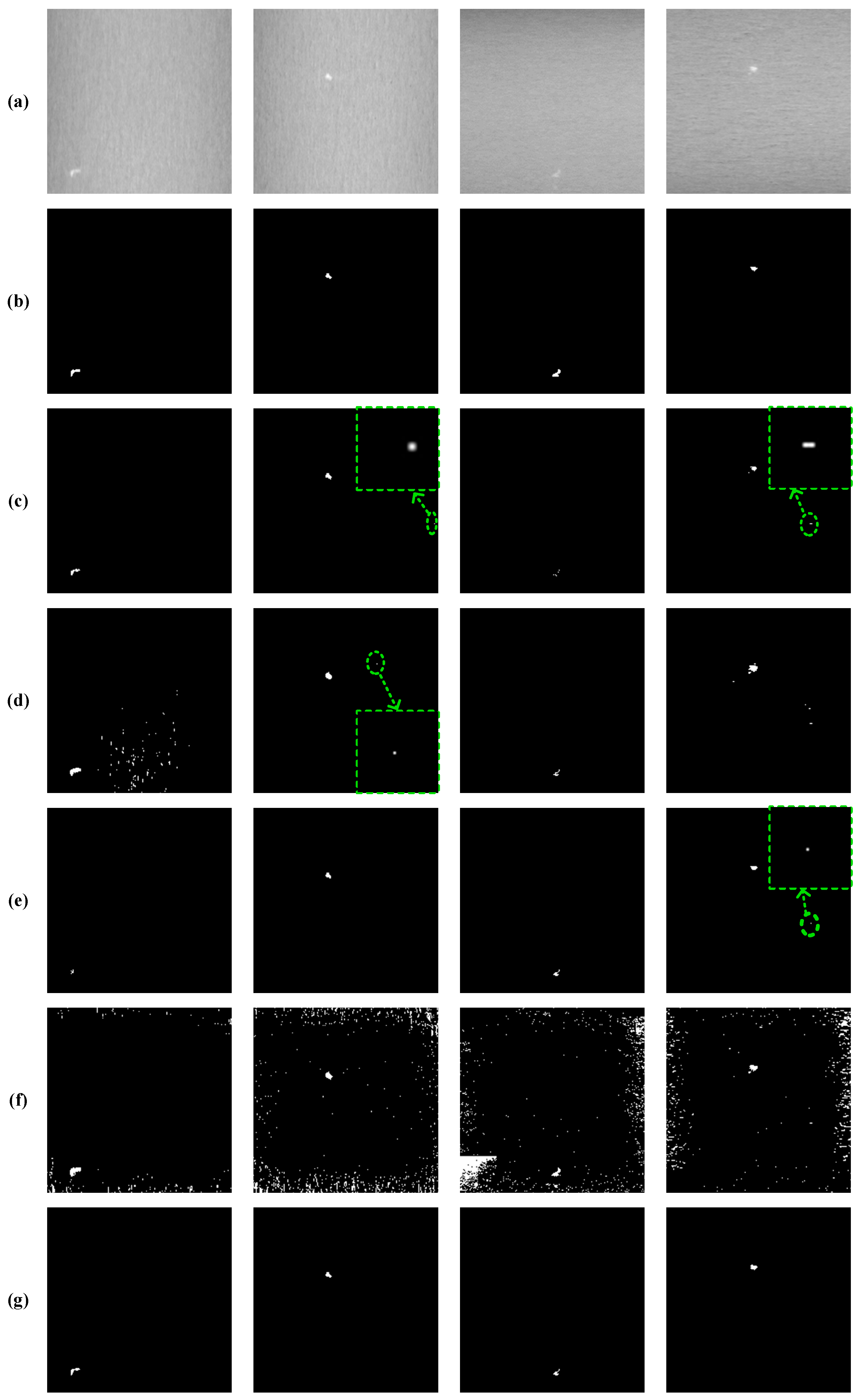
4.3.1. Qualitative Comparison
4.3.2. Quantitative Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diers, J.; Pigorsch, C. A survey of methods for automated quality control based on images. Int. J. Comput. Vision 2023, 131, 2553–2581. [Google Scholar] [CrossRef]
- Zhu, J.P.; He, G.H.; Zhou, P. MFNet: A novel multilevel feature fusion network with multibranch structure for surface defect detection. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Cheng, G.; Yuan, X.; Yao, X.W.; Yan, K.B.; Zeng, Q.H.; Xie, X.X.; Han, J.W. Towards large-scale small object detection: Survey and benchmarks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13467–13488. [Google Scholar] [CrossRef]
- Li, J.; Wu, R.; Zhang, S.; Chen, Y.L.; Dong, Z.C. FASCNet: An edge-computational defect detection model for industrial parts. IEEE Internet. Things. 2023, 11, 6622–6637. [Google Scholar] [CrossRef]
- Luo, Q.W.; Chen, Y.W.; Su, J.J.; Yang, C.H.; Silvén, O.; Liu, L. Prior-guided YOLOX for tiny roll mark detection on strip steel. IEEE Sens. J. 2024, 24, 15575–15587. [Google Scholar] [CrossRef]
- Ameri, R.; Hsu, C.C.; Band, S.S. A systematic review of deep learning approaches for surface defect detection in industrial applications. Eng. Appl. Artif. Intel. 2023, 130, 107717. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M.; Hill, R.; Allen, P. A comprehensive review of convolutional neural networks for defect detection in industrial applications. IEEE Access 2024, 12, 94250–94295. [Google Scholar] [CrossRef]
- Zou, Z.X.; Chen, K.Y.; Shi, Z.W.; Guo, Y.H.; Ye, J.P. Object detection in 20 years: A survey. Proc. IEEE 2023, 111, 257–276. [Google Scholar] [CrossRef]
- Jha, S.B.; Babiceanu, R.F. Deep CNN-based visual defect detection: Survey of current literature. Comput. Ind. 2023, 14, 103911. [Google Scholar] [CrossRef]
- Liu, G.H.; Chu, M.X.; Gong, R.F.; Zheng, Z.H. Global attention module and cascade fusion network for steel surface defect detection. Pattern Recogn. 2024, 158, 110979. [Google Scholar] [CrossRef]
- Zare, A.; Ozdemir, A.; Iwen, M.A.; Aviyente, S. Extension of PCA to higher order data structures: An introduction to tensors, tensor decompositions, and tensor PCA. Proc. IEEE 2018, 106, 1341–1358. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.G.; An, W. Infrared dim and small target detection via multiple subspace learning and spatial-temporal patch-tensor model. IEEE T. Geosci. Remote. 2020, 59, 3737–3752. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, M. Low-rank tensor recovery via non-convex regularization, structured factorization and spatio-temporal characteristics. Pattern Recogn. 2023, 137, 109343. [Google Scholar] [CrossRef]
- Wang, M.H.; Hong, D.F.; Han, Z.; Li, J.X.; Yao, J.; Gao, L.R.; Zhang, B.; Chanussot, J. Tensor decompositions for hyperspectral data processing in remote sensing: A comprehensive review. IEEE Geosci. Remote Sens. Mag. 2023, 11, 26–72. [Google Scholar] [CrossRef]
- Luo, Y.; Li, X.R.; Chen, S.H. 5-D spatial-temporal information-based infrared small target detection in complex environments. Pattern Recogn. 2024, 158, 111003. [Google Scholar] [CrossRef]
- Zeng, N.Y.; Wu, P.S.; Wang, Z.D.; Li, H.; Liu, W.; Liu, X.H. A small-sized object detection oriented multi-scale feature fusion approach with application to defect detection. IEEE Trans. Instrum. Meas. 2022, 71, 3507014. [Google Scholar] [CrossRef]
- Wen, X.; Shan, J.; He, Y.; Song, K. Steel surface defect recognition: A survey. Coatings 2023, 13, 17. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Xie, Q.; Wu, Y.; Yu, Z.; Wang, J. Tiny defect detection in high-resolution aero-engine blade images via a coarse-to-fine framework. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Li, M.; Miao, D.Q.; Pedrycz, W.; Wang, Z.G.; Jiang, M.H. Construction of a feature enhancement network for small object detection. Pattern Recogn. 2023, 143, 109801. [Google Scholar] [CrossRef]
- Hou, X.Q.; Liu, M.Q.; Zhang, S.L.; Wei, P.; Chen, B.D. CANet: Contextual information and spatial attention based network for detecting small defects in manufacturing industry. Pattern Recogn. 2023, 140, 109558. [Google Scholar] [CrossRef]
- Yang, B.Y.; Liu, Z.Y.; Duan, G.F.; Tan, J.R. Residual shape adaptive dense-nested Unet: Redesign the long lateral skip connections for metal surface tiny defect inspection. Pattern Recogn. 2023, 147, 110073. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.Q. Reweighted infrared patch-tensor model with both nonlocal and local priors for single-frame small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Lu, C.Y.; Feng, J.S.; Chen, Y.D.; Liu, W.; Lin, Z.C.; Yan, S.C. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.D.; Peng, Z.M. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Gao, Q.X.; Zhang, P.; Xia, W.; Xie, D.Y.; Gao, X.B.; Tao, D.C. Enhanced tensor RPCA and its application. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 2133–2140. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, X.; Liu, X.Z.; Zhou, Z.X. Logarithmic norm regularized low-rank factorization for matrix and tensor completion. IEEE Trans. Image Process. 2021, 30, 3434–3449. [Google Scholar] [CrossRef]
- Luo, Y.; Li, X.R.; Yan, Y.F.; Xia, C.Q. Spatial-temporal tensor representation learning with priors for infrared small target detection. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9598–9620. [Google Scholar] [CrossRef]
- Wang, H.L.; Peng, J.J.; Qin, W.J.; Wang, J.J.; Meng, D.Y. Guaranteed tensor recovery fused low-rankness and smoothness. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10990–11007. [Google Scholar] [CrossRef]
- Geng, X.Y.; Guo, Q.; Hui, S.X.; Yang, M.; Zhang, C.M. Tensor robust PCA with nonconvex and nonlocal regularization. Comput. Vis. Image Und. 2024, 243, 104007. [Google Scholar] [CrossRef]
- Huang, Z.X.; Zhao, E.W.; Zheng, W.; Peng, X.D.; Niu, W.L.; Yang, Z. Infrared small target detection via two-stage feature complementary improved tensor low-rank sparse decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 17690–17709. [Google Scholar] [CrossRef]
- Liu, C.T.; Wang, H. Research on infrared dim and small target detection algorithm based on low-rank tensor recovery. J. Syst. Eng. Electron. 2023, 34, 861–872. [Google Scholar] [CrossRef]
- Guo, J.; Wu, Y.Q.; Dai, Y.M. Small target detection based on reweighted infrared patch-image model. IET Image Process. 2018, 12, 70–79. [Google Scholar] [CrossRef]
- Xie, Y.; Gu, S.H.; Liu, Y.; Zuo, W.M.; Zhang, W.S.; Zhang, L. Weighted Schatten p-norm minimization for image denoising and background subtraction. IEEE Trans. Image Process. 2016, 25, 4842–4857. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.G.; Li, M.; An, W. Infrared small target detection via spatial-temporal infrared patch-tensor model and weighted Schatten p-norm minimization. Infrared Phys. Techn. 2019, 102, 103050. [Google Scholar] [CrossRef]
- Zuo, W.M.; Meng, D.Y.; Zhang, L.; Feng, X.C.; Zhang, D. A generalized iterated shrinkage algorithm for non-convex sparse coding. In Proceedings of the 2013 IEEE International Conference on Computer Vision 2013, Sydney, NSW, Australia, 1–8 December 2013; IEEE: Piscataway, NJ, USA, 2014; pp. 217–224. [Google Scholar] [CrossRef]
- Xie, D.Y.; Yang, M.; Gao, Q.X.; Song, W. Non-convex tensorial multi-view clustering by integrating l1-based sliced-Laplacian regularization and l2,p-sparsity. Pattern Recognit. 2024, 154, 110605. [Google Scholar] [CrossRef]




| Patch | Step | AUC | MAE |
|---|---|---|---|
| 20 × 20 | 10 | 0.9341 | 0.0009 |
| 20 | 0.9712 | 0.0030 | |
| 30 × 30 | 10 | 0.9501 | 0.0007 |
| 20 | 0.9728 | 0.0019 | |
| 30 | 0.9775 | 0.0046 | |
| 40 × 40 | 10 | 0.9560 | 0.0005 |
| 20 | 0.9737 | 0.0017 | |
| 30 | 0.9769 | 0.0034 | |
| 40 | 0.9762 | 0.0034 | |
| 50 × 50 | 10 | 0.9589 | 0.0006 |
| 20 | 0.9732 | 0.0014 | |
| 30 | 0.9760 | 0.0021 | |
| 40 | 0.9744 | 0.0018 | |
| 50 | 0.9731 | 0.0015 |
| p | AUC | MAE |
|---|---|---|
| 0.1 | 0.9994 | 0.0613 |
| 0.2 | 0.9895 | 0.0263 |
| 0.3 | 0.9887 | 0.0105 |
| 0.4 | 0.9769 | 0.0042 |
| 0.5 | 0.9737 | 0.0018 |
| 0.6 | 0.9658 | 0.0009 |
| 0.7 | 0.9560 | 0.0005 |
| 0.8 | 0.9415 | 0.0005 |
| 0.9 | 0.9326 | 0.0005 |
| 1 | 0.9255 | 0.0005 |
| SNR | No Noise | 36 dB | 32 dB | 28 dB | |
|---|---|---|---|---|---|
| Index | |||||
| AUC | 0.9560 | 0.9386 | 0.9058 | 0.8272 | |
| MAE | 0.005 | 0.1610 | 0.1731 | 0.1939 | |
| Method | TRPCA | ETRPCA | NN-TRPCA | PSTNN | Ours | |
|---|---|---|---|---|---|---|
| Index | ||||||
| AUC | 0.9352 | 0.9259 | 0.9427 | 0.8925 | 0.9560 | |
| 0.5407 | 0.6569 | 0.6730 | 0.4028 | 0.8364 | ||
| MAE | 0.0160 | 0.0004 | 0.0071 | 0.0003 | 0.0005 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Yan, X.; Liu, H.; Gong, C. Small Defects Detection of Galvanized Strip Steel via Schatten-p Norm-Based Low-Rank Tensor Decomposition. Sensors 2025, 25, 2606. https://doi.org/10.3390/s25082606
Zhou S, Yan X, Liu H, Gong C. Small Defects Detection of Galvanized Strip Steel via Schatten-p Norm-Based Low-Rank Tensor Decomposition. Sensors. 2025; 25(8):2606. https://doi.org/10.3390/s25082606
Chicago/Turabian StyleZhou, Shiyang, Xuguo Yan, Huaiguang Liu, and Caiyun Gong. 2025. "Small Defects Detection of Galvanized Strip Steel via Schatten-p Norm-Based Low-Rank Tensor Decomposition" Sensors 25, no. 8: 2606. https://doi.org/10.3390/s25082606
APA StyleZhou, S., Yan, X., Liu, H., & Gong, C. (2025). Small Defects Detection of Galvanized Strip Steel via Schatten-p Norm-Based Low-Rank Tensor Decomposition. Sensors, 25(8), 2606. https://doi.org/10.3390/s25082606





