Capturing Free Surface Dynamics of Flows over a Stepped Spillway Using a Depth Camera
Abstract
1. Introduction
2. Materials and Methods
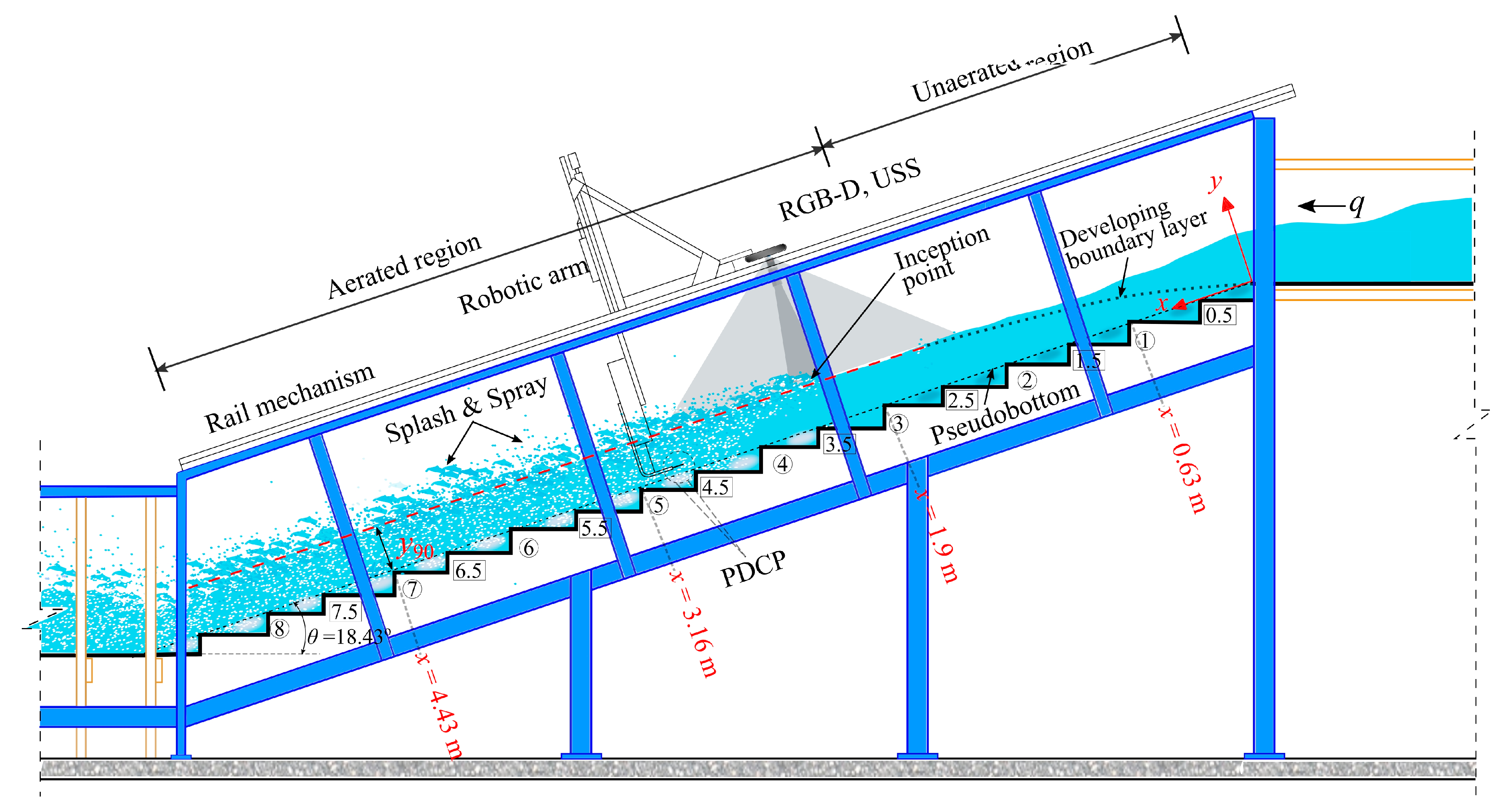
2.1. Experimental Set-Up
2.2. Intel® RealSenseTM RGB-D Camera Overview and Working Principle
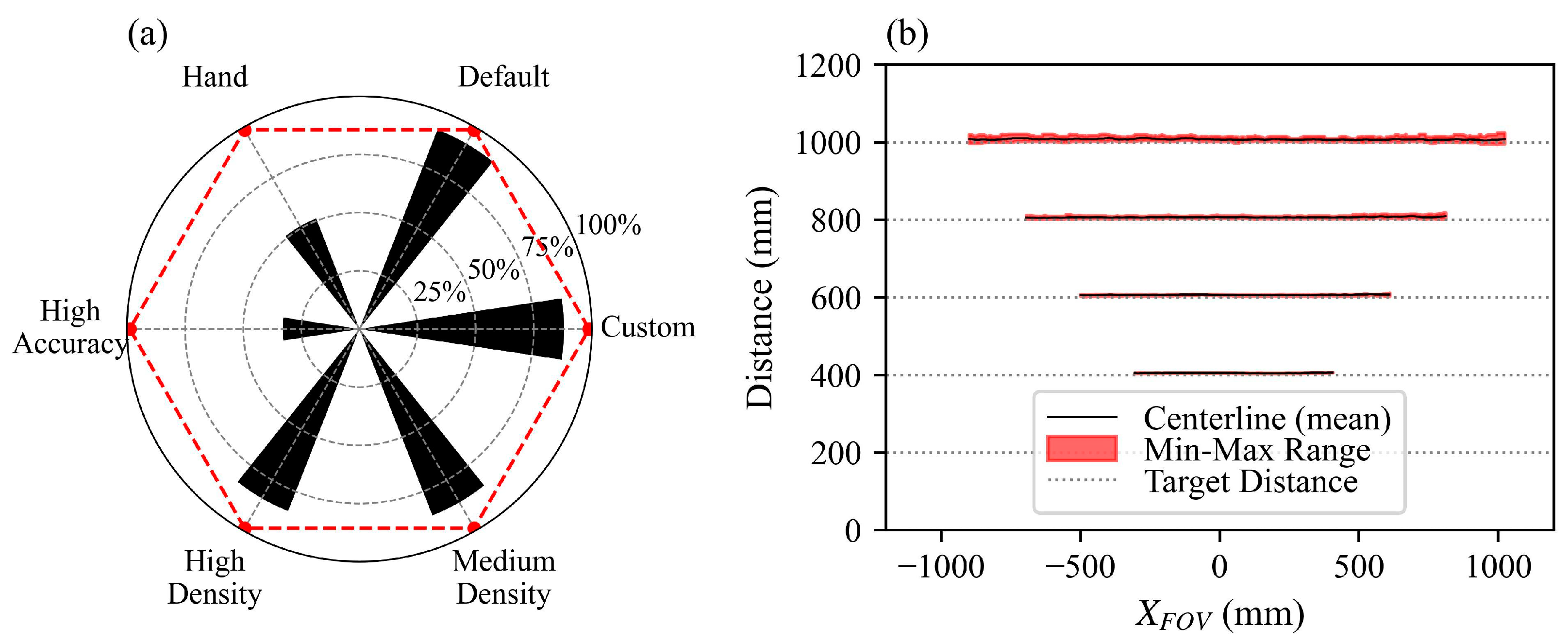
2.3. Camera Settings
2.4. RGB-D Data Acquisition and Post-Processing
2.4.1. Conversion from Pixel Coordinates to Global 3D Coordinate System
2.4.2. Post Processing and Data Filtering
3. Results
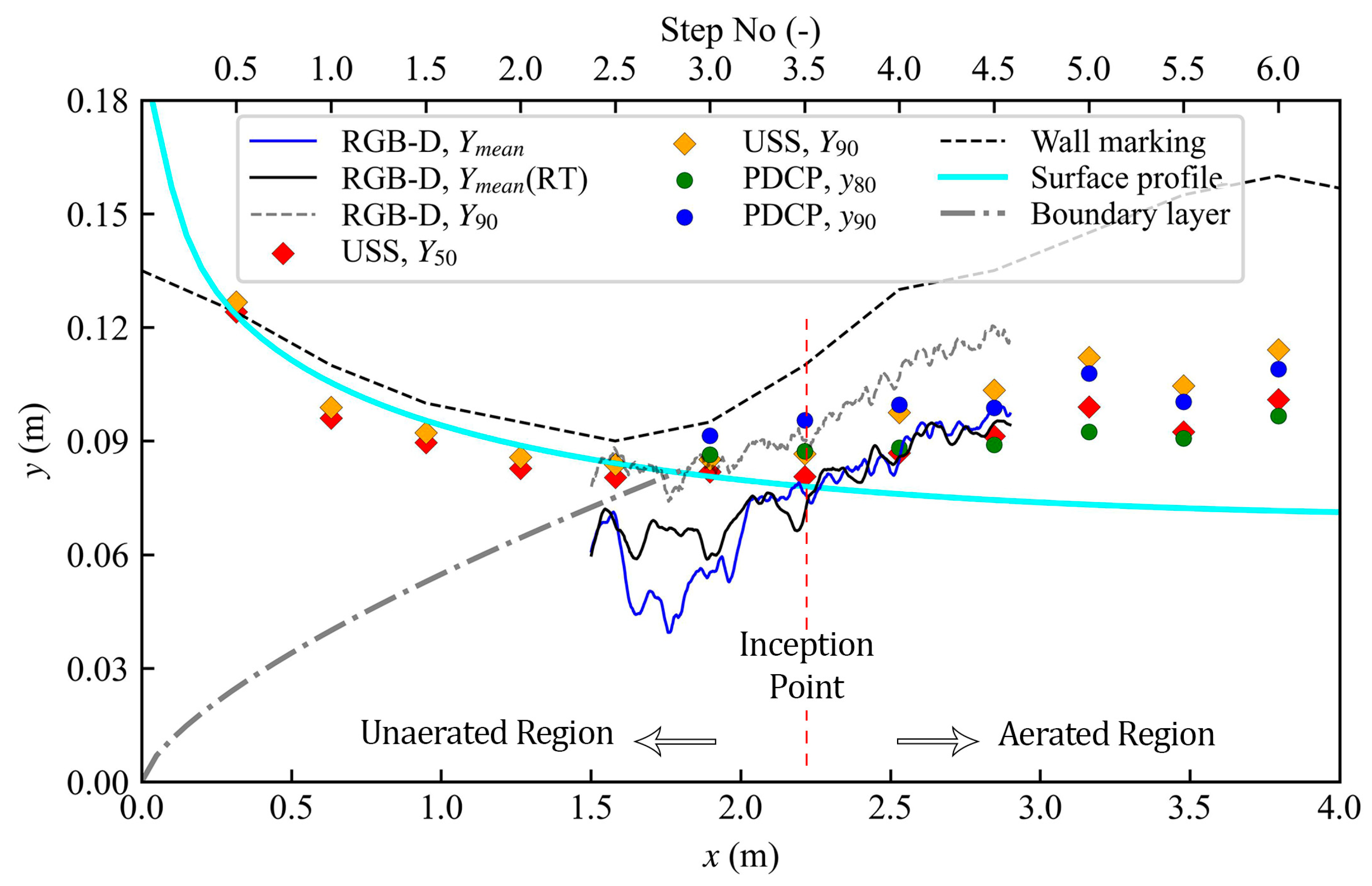
3.1. Water Surface Observations
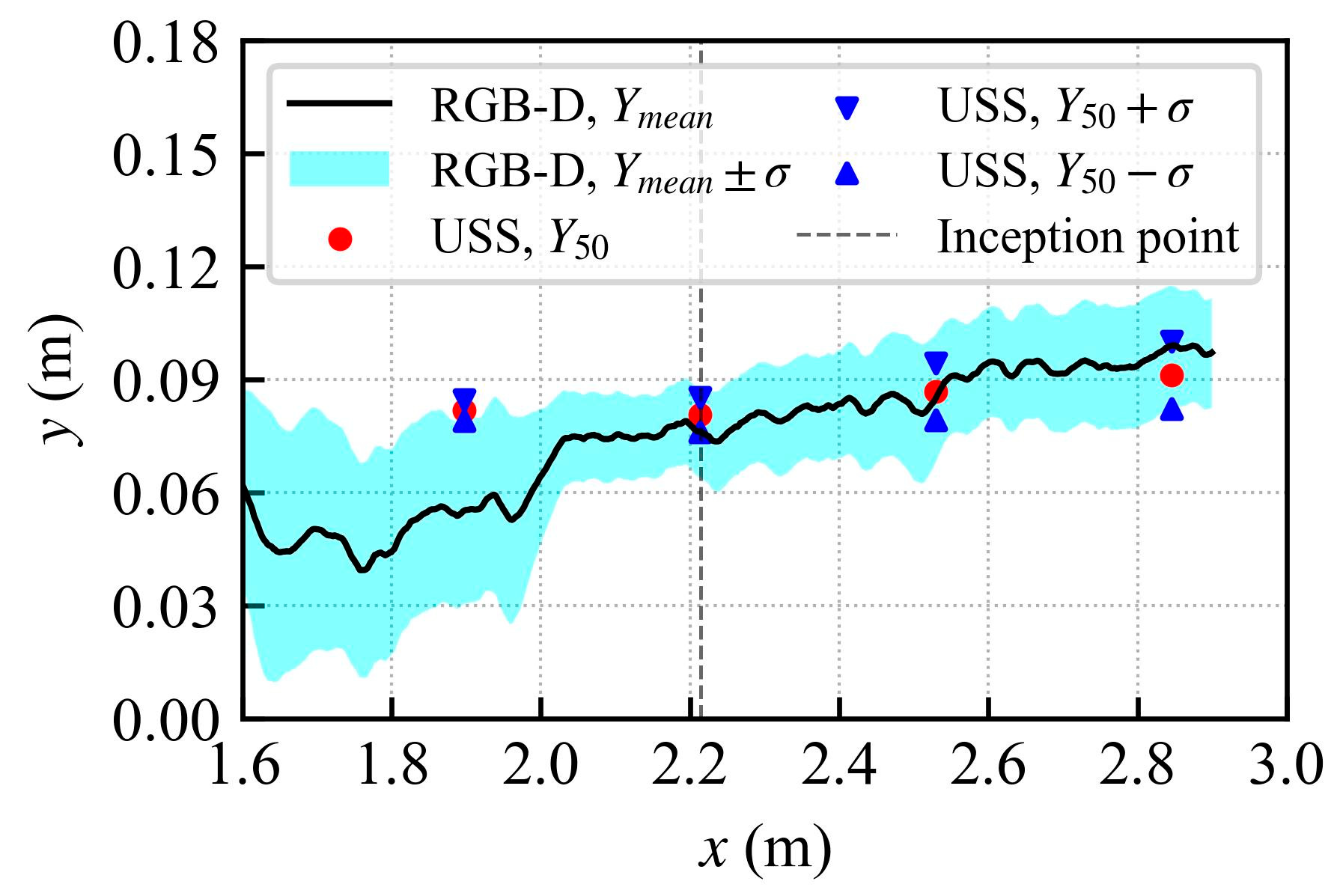
3.2. Water Surface Profiles
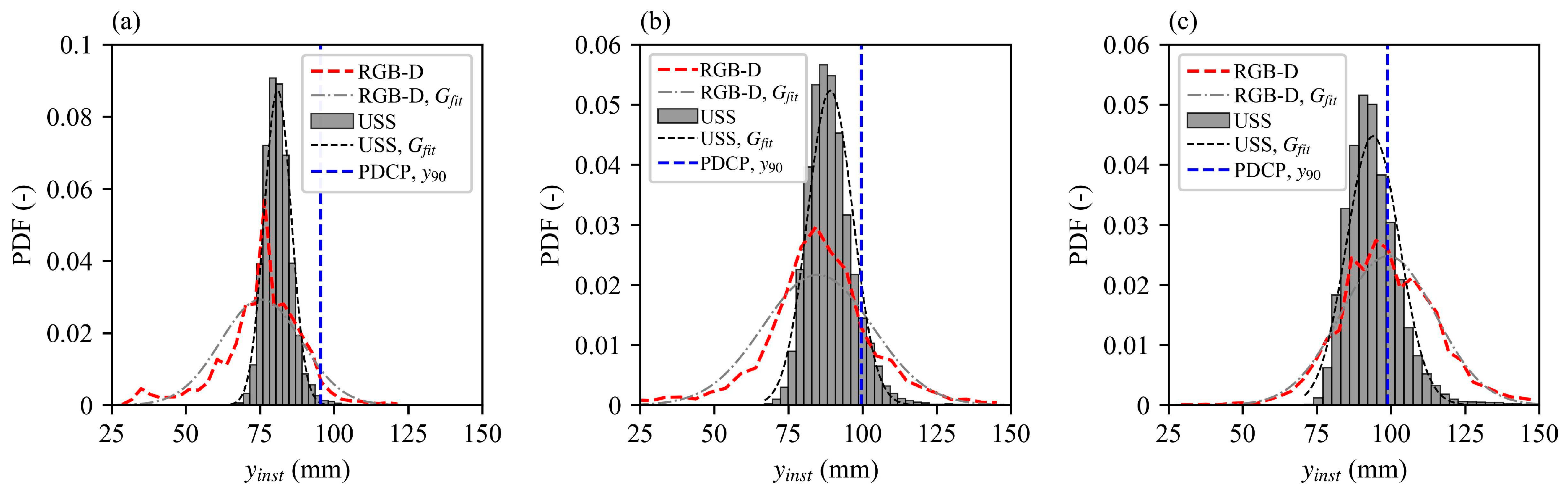
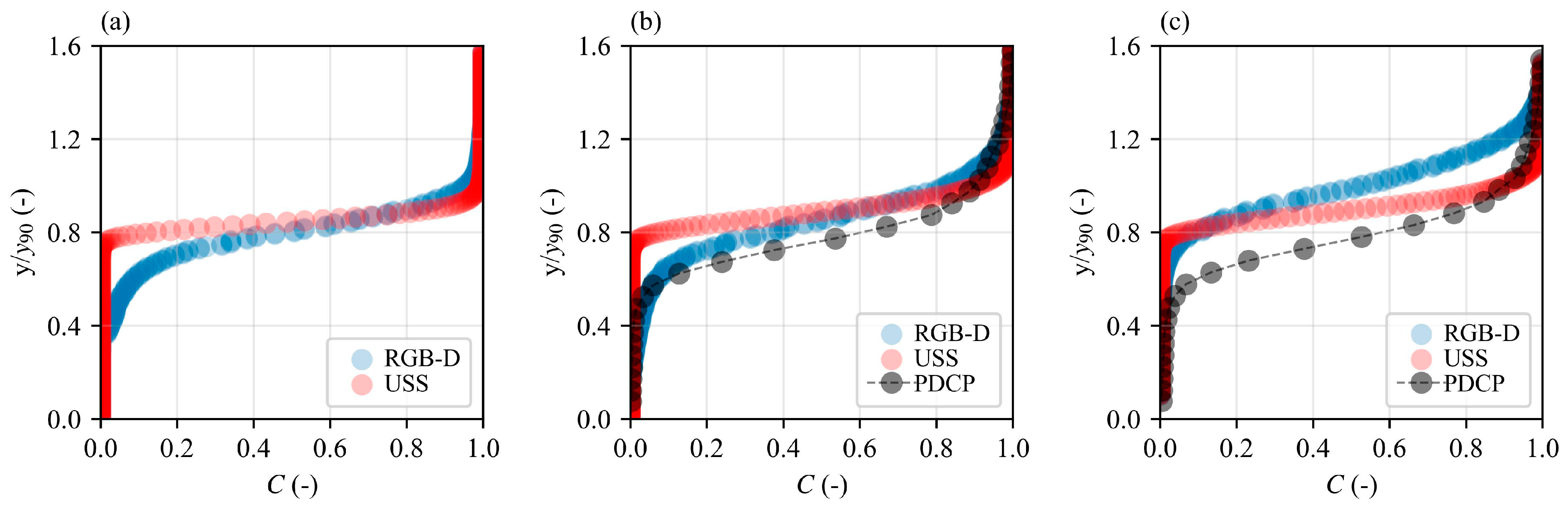
3.3. Water Surface Fluctuations
3.4. Air Concentrations and Interface Frequencies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valero, D.; Felder, S.; Kramer, M.; Wang, H.; Carrillo, J.M.; Pfister, M.; Bung, D.B. Air–water flows. J. Hydraul. Res. 2024, 62, 319–339. [Google Scholar] [CrossRef]
- Killen, J.M. The Surface Characteristics of Self Aerated Flow in Steep Channels. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1968. [Google Scholar]
- KC, M.R.; Crookston, B.; Flake, K.; Felder, S. Enhancing flow aeration on an embankment sloped stepped spillway using a labyrinth weir. J. Hydraul. Res. 2025, 63, 32–47. [Google Scholar] [CrossRef]
- Rak, G.; Hočevar, M.; Kolbl Repinc, S.; Novak, L.; Bizjan, B. A review on methods for measurement of free water surface. Sensors 2023, 23, 1842. [Google Scholar] [CrossRef] [PubMed]
- Mouaze, D.; Murzyn, F.; Chaplin, J.R. Free surface length scale estimation in hydraulic jumps. J. Fluids Eng. 2005, 127, 1191–1193. [Google Scholar] [CrossRef]
- Murzyn, F.; Mouazé, D.; Chaplin, J.R. Air–water interface dynamic and free surface features in hydraulic jumps. J. Hydraul. Res. 2007, 45, 679–685. [Google Scholar] [CrossRef]
- Hager, W.H. Classical hydraulic jump: Free surface profile. Can. J. Civ. Eng. 1993, 20, 536–539. [Google Scholar] [CrossRef]
- Weber, L.J.; Schumate, E.D.; Mawer, N. Experiments on flow at a 90° open-channel junction. J. Hydraul. Eng. 2001, 127, 340–350. [Google Scholar] [CrossRef]
- Meireles, I.; Matos, J. Skimming flow in the nonaerated region of stepped spillways over embankment dams. J. Hydraul. Eng. 2009, 135, 685–689. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C.; Hanson, G.J. Simplistic design methods for moderate-sloped stepped chutes. J. Hydraul. Eng. 2014, 140, 04014062. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Two-Phase Flow Characteristics of Stepped Spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Felder, S. Air-Water Flow Properties on Stepped Spillways for Embankment Dams: Aeration, Energy Dissipation and Turbulence on Uniform, Non-Uniform and Pooled Stepped Chutes. Ph.D. Thesis, School of Civil Engineering, The University of Queensland, St Lucia, QLD, Australia, 2013. [Google Scholar]
- Bung, D.B. Developing flow in skimming flow regime on embankment stepped spillways. J. Hydraul. Res. 2011, 49, 639–648. [Google Scholar] [CrossRef]
- Herringe, R.A.; Davis, M.R. Detection of instantaneous phase changes in gas-liquid mixtures. J. Phys. E Sci. Instrum. 1974, 7, 807. [Google Scholar] [CrossRef]
- Kramer, M.; Valero, D.; Chanson, H.; Bung, D.B. Towards reliable turbulence estimations with phase-detection probes: An adaptive window cross-correlation technique. Exp Fluids 2018, 60, 2. [Google Scholar] [CrossRef]
- Kramer, M.; Bung, D.B. Improving the measurement of air–water flow properties using remote distance sensing technology. J. Hydraul. Eng. 2025, 151, 04024051. [Google Scholar] [CrossRef]
- Cui, H.; Felder, S.; Kramer, M. Non-intrusive measurements of air-water flow properties in supercritical flows down grass-lined spillways. In Proceedings of the 9th IAHR International Symposium on Hydraulic Structures—9th ISHS, IIT Roorkee, Roorkee, India, 24–27 October 2022. [Google Scholar]
- Zhang, G.; Valero, D.; Bung, D.B.; Chanson, H. On the estimation of free-surface turbulence using ultrasonic sensors. Flow Meas. Instrum. 2018, 60, 171–184. [Google Scholar] [CrossRef]
- Li, R.; Splinter, K.D.; Felder, S. LIDAR Scanning as an Advanced Technology in Physical Hydraulic Modelling: The Stilling Basin Example. Remote Sens. 2021, 13, 3599. [Google Scholar] [CrossRef]
- Isidoro, J.M.G.P.; Martins, R.; Carvalho, R.F.; de Lima, J.L.M.P. A high-Frequency low-cost technique for Measuring small-scale water level fluctuations using computer vision. Measurement 2021, 180, 109477. [Google Scholar] [CrossRef]
- Ferreira, E.; Chandler, J.; Wackrow, R.; Shiono, K. Automated extraction of free surface topography using SFM-MVS photogrammetry. Flow Meas. Instrum. 2017, 54, 243–249. [Google Scholar] [CrossRef]
- Bung, D.B. Non-intrusive detection of air–water surface roughness in self-aerated chute flows. J. Hydraul. Res. 2013, 51, 322–329. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Application of local optical flow methods to high-velocity free-surface flows: Validation and application to stepped chutes. Exp. Therm. Fluid Sci. 2018, 90, 186–199. [Google Scholar] [CrossRef]
- Kramer, M.; Chanson, H. Free-surface instabilities in high-velocity air-water flows down stepped chutes. In Proceedings of the International Symposium on Hydraulic Structures, Aachen, Germany, 15–18 May 2018. [Google Scholar]
- Steinke, R.; Bung, D.B. 4D Particle tracking velocimetry of an undular hydraulic jump. J. Hydraul. Res. 2024, 62, 488–501. [Google Scholar] [CrossRef]
- Montano, L.; Li, R.; Felder, S. Continuous measurements of time-varying Free-surface profiles in aerated hydraulic jumps with a LiDAR. Exp. Therm. Fluid Sci. 2018, 93, 379–397. [Google Scholar] [CrossRef]
- Nina, Y.A.; Shi, R.; Wüthrich, D.; Chanson, H. Intrusive and non-intrusive two-phase air-water measurements on stepped spillways: A physical study. Exp. Therm. Fluid Sci. 2022, 131, 110545. [Google Scholar] [CrossRef]
- Pavlovčič, U.; Rak, G.; Hočevar, M.; Jezeršek, M. Ranging of turbulent water surfaces using a laser triangulation principle in a laboratory environment. J. Hydraul. Eng. 2020, 146, 04020052. [Google Scholar] [CrossRef]
- Kramer, M.; Felder, S. Remote sensing of aerated flows at large dams: Proof of concept. Remote Sens. 2021, 13, 2836. [Google Scholar] [CrossRef]
- Pleterski, Ž.; Hočevar, M.; Bizjan, B.; Kolbl Repinc, S.; Rak, G. Measurements of complex free water surface topography using a photogrammetric method. Remote Sens. 2023, 15, 4774. [Google Scholar] [CrossRef]
- Bung, D.B.; Crookston, B.M.; Valero, D. Turbulent free-surface monitoring with an RGB-D sensor: The hydraulic jump case. J. Hydraul. Res. 2021, 59, 779–790. [Google Scholar] [CrossRef]
- Microsoft. Introducing the Intel® RealSenseTM Depth Camera D455. Available online: https://www.intelrealsense.com/depth-camera-d455/ (accessed on 12 January 2025).
- Hunt, S.L.; Kadavy, K.C. Energy dissipation on flat-sloped stepped spillways: Part 1. Upstream of the inception point. Trans. ASABE 2010, 53, 103–109. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C. Inception point for embankment dam stepped spillways. J. Hydraul. Eng. 2013, 139, 60–64. [Google Scholar] [CrossRef]
- Meireles, I.C.; Bombardelli, F.A.; Matos, J. Air entrainment onset in skimming flows on steep stepped spillways: An analysis. J. Hydraul. Res. 2014, 52, 375–385. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C. Estimated splash and training wall height requirements for stepped chutes applied to embankment dams. J. Hydraul. Eng. 2017, 143, 06017018. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Hydraulic design of stepped spillways. J. Hydraul. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Cain, P.; Wood, I.R. Measurements of self-aerated flow on a spillway. J. Hydraul. Div. 1981, 107, 1425–1444. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Phase-detection probe measurements in high-velocity free-surface flows including a discussion of key sampling parameters. Exp. Therm. Fluid Sci. 2015, 61, 66–78. [Google Scholar] [CrossRef]
- Microsoft. Intel® RealSenseTM Computer Vision Solutions. Available online: https://www.intelrealsense.com/ (accessed on 27 October 2024).
- Carfagni, M.; Furferi, R.; Governi, L.; Santarelli, C.; Servi, M.; Uccheddu, F.; Volpe, Y. Metrological and critical characterization of the Intel D415 stereo depth camera. Sensors 2019, 19, 489. [Google Scholar] [CrossRef]
- Ahn, J.Y.; Kim, D.W.; Lee, Y.H.; Kim, W.; Hong, J.K.; Shim, Y.; Kim, J.H.; Eune, J.; Kim, S.-W. MOYA: Interactive AI toy for children to develop their language skills. In Proceedings of the 9th Augmented Human International Conference, Seoul, Republic of Korea, 7–9 February 2018; pp. 1–2. [Google Scholar]
- Bayer, J.; Faigl, J. On autonomous spatial exploration with small hexapod walking robot using tracking camera Intel Realsense T265. In Proceedings of the 2019 European Conference on Mobile Robots (ECMR), Prague, Czech Republic, 4–6 September 2019; pp. 1–6. [Google Scholar]
- Nebiker, S.; Meyer, J.; Blaser, S.; Ammann, M.; Rhyner, S. Outdoor mobile mapping and AI-based 3D object detection with low-cost RGB-D cameras: The use case of on-street parking statistics. Remote Sens. 2021, 13, 3099. [Google Scholar] [CrossRef]
- Anwar, Q.; Hanif, M.; Shimotoku, D.; Kobayashi, H.H. Driver awareness collision/proximity detection system for heavy vehicles based on deep neural network. J. Phys. Conf. Ser. 2022, 2330, 012001. [Google Scholar] [CrossRef]
- Microsoft. Release Intel® RealSenseTM SDK 2.0 Beta (v2.56.3) IntelRealSense/Librealsense. Available online: https://github.com/IntelRealSense/librealsense/releases/tag/v2.56.3 (accessed on 19 January 2025).
- Grunnet-Jepsen, A.; Sweetser, J.N.; Woodfill, J. Best-Known-Methods for Tuning Intel® RealSenseTM D400 Depth Cameras for Best Performance. 10; Intel: Santa Clara, CA, USA, 2024. [Google Scholar]
- Grunnet-Jepsen, A.; Sweestser, J.; Khuong, T.; Dorodnicov, S.; Tong, D.; Mulla, O. Intel® RealSenseTM Self-Calibration for D400 Series Depth Cameras; White Paper; Intel: Santa Clara, CA, USA, 2021. [Google Scholar]
- Valero, D.; Chanson, H.; Bung, D.B. Robust estimators for free surface turbulence characterization: A stepped spillway application. Flow Meas. Instrum. 2020, 76, 101809. [Google Scholar] [CrossRef]
- Chanson, H. The hydraulics of stepped chutes and spillways. Can. J. Civ. Eng. 2002, 29, 634. [Google Scholar] [CrossRef]
- Megh Raj, K.C.; Brian, C. A laboratory study on the energy dissipation of a bevel-faced stepped spillway for embankment dam applications. In Proceedings of the 10th International Symposium on Hydraulic Structures (ISHS 2024), ETH Zurich, Zurich, Switzerland, 17–19 June 2024; pp. 530–537. [Google Scholar]
- Valero, D. On the Fluid Mechanics of Self-Aeration in Open Channel Flows. Ph.D. Dissertation, Universite de Liege, Liège, Belgium, 2018. [Google Scholar]
- Fu, L.; Gao, F.; Wu, J.; Li, R.; Karkee, M.; Zhang, Q. Application of consumer RGB-D cameras for fruit detection and localization in field: A critical review. Comput. Electron. Agric. 2020, 177, 105687. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Air–water flows and free-surface profiles on a non-uniform stepped chute. J. Hydraul. Res. 2014, 52, 253–263. [Google Scholar] [CrossRef]
- Zhang, G.; Chanson, H. Hydraulics of the developing flow region of stepped spillways. I: Physical modeling and boundary layer development. J. Hydraul. Eng. 2016, 142, 04016015. [Google Scholar] [CrossRef]
- Wang, H. Turbulence and Air Entrainment in Hydraulic Jumps. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2014. [Google Scholar]
- Kramer, M.; Valero, D. Linking turbulent waves and bubble diffusion in self-aerated open-channel flows: Two-state air concentration. J. Fluid Mech. 2023, 966, A37. [Google Scholar] [CrossRef]






| Reference | Non-Intrusive Methods Used | Application Area |
|---|---|---|
| Kramer and Bung (2024) [16] | Laser point sensor | Hydraulic jump and stepped spillway |
| Cui et al. (2022) [17] | USS | Grass lined spillway surface |
| Bung (2013) [22] | USS/ High speed camera | Stepped spillway/Smooth invert chute |
| Nina et al. (2022) [27] | High speed camera | Stepped spillway |
| Pacloccic et al. (2020) [28] | High speed camera/LiDAR | Channel confluence |
| Kramer and Felder (2021) [29] | High speed camera | Stepped spillway |
| Montano et al. (2018) [26] | LiDAR | Hydraulic jump |
| Pleterski et al. (2023) [30] | RGB camera array | Supercritical junction flow |
| Steinke and Bung (2024) [25] | USS/RGB-D Camera/4D PTV | Undular hydraulic jump |
| Bung et al. (2021) [31] | RGB-D camera | Hydraulic jump |
| Features | Specifications |
|---|---|
| Nominal Dimensions (width × height × depth) | 124 mm × 26 mm × 29 mm |
| Depth Field of View | HFoV: 87° ± 3°, VFoV: 58° ± 1°, DFoV: 95° ± 3° |
| Depth Frame Rate | 90 fps (maximum) |
| RGB Field of View | HFoV: 90° ± 1°, VFoV: 65° ± 1°, DFoV: 98° ± 3° |
| RGB Frame Rate | 60 fps (maximum) |
| Infrared Projector Field of View | HFoV: 90°, VFoV: 63°, DFoV: 99° |
| Ideal Range | 0.6 m to 6 m |
| RGB Resolution (maximum) | 1920 × 1080 |
| Depth Resolution (maximum) | 1280 × 720 |
| Baseline Distance | 95 mm |
| Depth Technology | Stereoscopic |
| RGB sensor Technology | Global Shutter |
| Depth Accuracy | <2% at 4 m |
| Parameter | Range/Value | Description/Notes |
|---|---|---|
| Visual presets | Custom, Default, Hand, High accuracy, High density, Medium density | A custom preset was selected based on better fill rates and resulting depth map |
| Sampling frequency (fRGB) | 30–90 Hz | Higher frame rates capture rapid free-surface fluctuations. Adopted: 90 Hz |
| Image resolution | Multiple, e.g., 848 × 100, 848 × 480, 1280 × 720, 1280 × 800, etc. | Selected 848 × 480 pixels to balance field of view and spatial resolution. |
| Laser power | 250 mW (range: 0–360 mW) | Higher power improved depth detection in aerated regions; set per Bung et al. [31] and Carfagni et al. [41] |
| Depth unit | 1 mm | Defines internal quantization scale of depth |
| Depth exposure | 33,000 μs (range: 10,000–40,000 μs) | Adjusted to optimize depth sensing for lighting conditions used in this study |
| Image gain | Minimum set to 16 (range: 0–64) | Helps balance brightness in challenging lighting or high exposure scenarios |
| S. No. | Location | Type | Shape | Rating | Light Color |
|---|---|---|---|---|---|
| L1 | ~0.8 m above weir crest | LED | 1-m Linear (2 rows) | 500 W | White |
| L2 | ~1 m above step edge 3.5 | LED | 10″ Ring | 10 W | White |
| L3 | ~2.4 m above step edge 6 | LED | 1-m Linear (2 rows) | 500 W | White |
| L4 | Underneath steps | LED | 1 m Linear (2 rows) | 500 W | White |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
K C, M.R.; Crookston, B.M.; Bung, D.B. Capturing Free Surface Dynamics of Flows over a Stepped Spillway Using a Depth Camera. Sensors 2025, 25, 2525. https://doi.org/10.3390/s25082525
K C MR, Crookston BM, Bung DB. Capturing Free Surface Dynamics of Flows over a Stepped Spillway Using a Depth Camera. Sensors. 2025; 25(8):2525. https://doi.org/10.3390/s25082525
Chicago/Turabian StyleK C, Megh Raj, Brian M. Crookston, and Daniel B. Bung. 2025. "Capturing Free Surface Dynamics of Flows over a Stepped Spillway Using a Depth Camera" Sensors 25, no. 8: 2525. https://doi.org/10.3390/s25082525
APA StyleK C, M. R., Crookston, B. M., & Bung, D. B. (2025). Capturing Free Surface Dynamics of Flows over a Stepped Spillway Using a Depth Camera. Sensors, 25(8), 2525. https://doi.org/10.3390/s25082525











