Research on the Assembly of Square Parts on Circular Production Lines Using Admittance Control for Six-DOF Robots
Abstract
1. Introduction
2. Complex Part Assembly Situation
Typical Failure Analysis of Square Hole Assembly
3. Hole Search Strategies Analysis
3.1. Archimedes Spiral Hole Search
3.2. Working Principle of the Vertical Hole Search Strategy
- (1)
- Force Feedback Perception:
- (2)
- Force/Displacement Model:
- (3)
- Vertical Adjustment and Search:
- (4)
- Error Reduction:
3.3. Vertical Hole Search Strategy
4. Admittance Control and Its Theoretical Foundation
4.1. Theoretical Foundation of Admittance Control
4.2. Admittance Parameter Analysis of Admittance Control
5. Square Hole Compliance Assembly Experiment
5.1. Hardware of the Control System
5.2. Sensor Gravity Compensation Experiment
5.3. Robot Communication Section
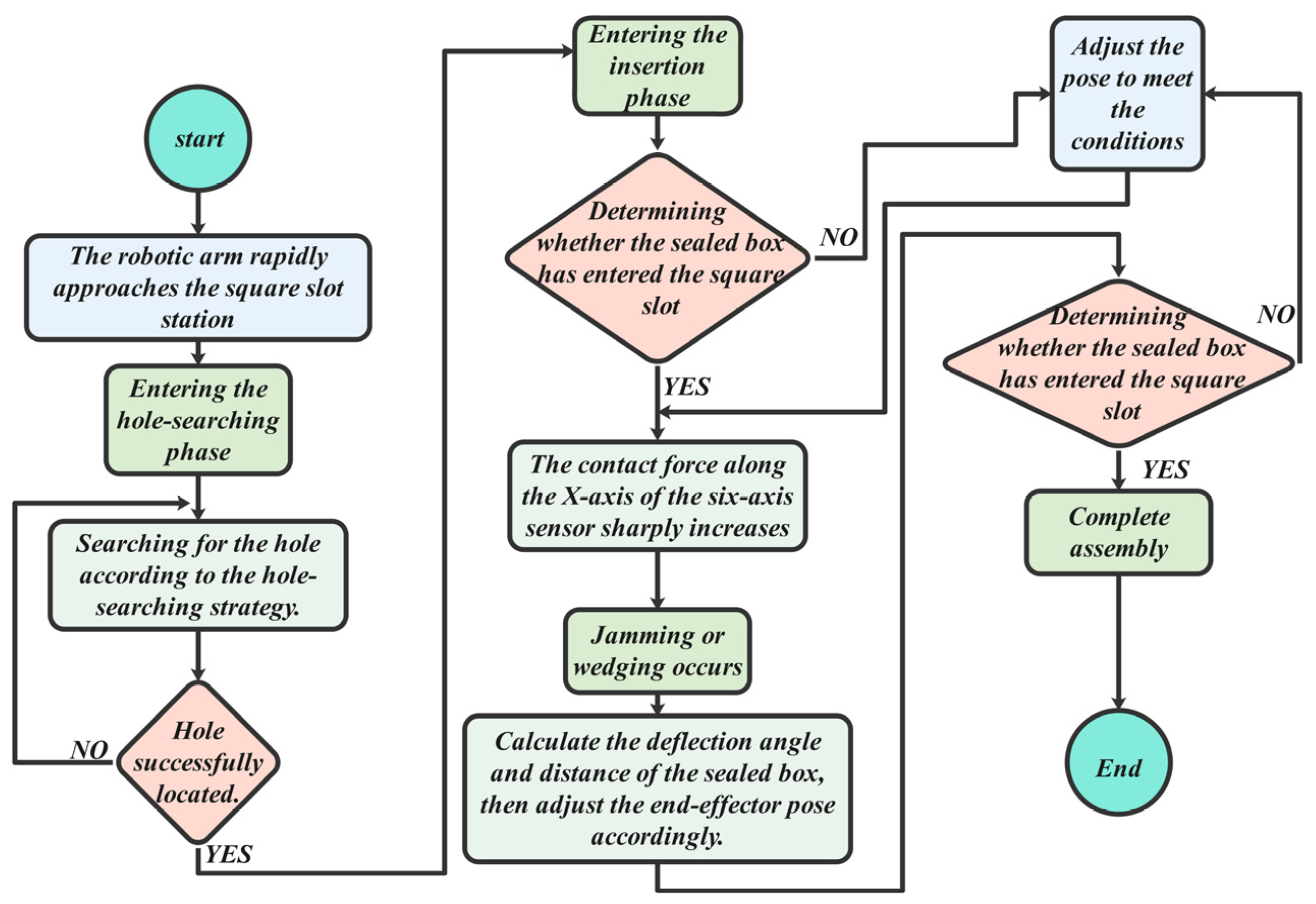
5.4. Compliant Assembly Process
6. Discussion
7. Conclusions
- (1)
- Through system analysis, the effects of the three parameters—, , and —on the system’s characteristics were analyzed, and the adjustment rules were summarized. These rules were then applied in the experiment. Admittance parameters affect the system’s stability to varying degrees. Based on the actual assembly process requirements and through the comparison of the three simulations, it was found that, when other parameters remain unchanged, the system’s step response speed slows down as increases, while the steady-state error remains largely unchanged. The damping parameter influences the system’s stability; as decreases, the system becomes more stable. The stiffness parameter is dependent on the sensitivity required for external force control, with a smaller value being preferred for more stringent force requirements.
- (2)
- To demonstrate the advantages of the improved vertical hole searching strategy proposed in this paper, 10 experimental trials were conducted to test the average hole search contact adjustment time and calculate the success rate. A detailed statistical analysis was then performed, and a t-test confirmed that the improved vertical hole searching strategy significantly outperformed the Archimedean spiral hole searching strategy in both hole search adjustment time and success rate (p < 0.05). Therefore, the advantages of the improved vertical search strategy are confirmed. Compared to the traditional Archimedes spiral hole search strategy, the average search adjustment time was increased by 5.8 s, improving efficiency by 46.4%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Y.; Ning, H.; Rangarajan, E.; Merali, A.; Geale, A.; Lindenroth, L.; Xu, Z.; Wang, W.; Kruse, P.; Morris, S.; et al. Design of a Cost-Effective Ultrasound Force Sensor and Force Control System for Robotic Extra-Body Ultrasound Imaging. Sensors 2025, 25, 468. [Google Scholar] [CrossRef]
- Nievas, N.; Pagès-Bernaus, A.; Bonada, F.; Echeverria, L.; Domingo, X. Reinforcement Learning for Autonomous Process Control in Industry4.0: Advantages and challenges. Appl. Artif. Intell. 2024, 38, 2383101. [Google Scholar] [CrossRef]
- Zahedi, F.; Chang, D.; Lee, H. User-adaptive Variable Damping Control Using Bayesian Optimization to Enhance Physical Human-robot Interaction. IEEE Robot. Autom. Lett. 2022, 7, 2724–2731. [Google Scholar] [CrossRef]
- Okochi, T.; Sakai, M.; Morita, Y. Direct Teaching/Playback Method for the Contact Task of a Six-DOF Manipulator Using a Parallel-Wire-Type Teaching Device with a Remote Center Compliance Device. In Proceedings of the 23rd International Conference on Control, Automation and Systems (ICCS), Yeosu, Republic of Korea, 17–20 October 2023; pp. 1554–1558. [Google Scholar] [CrossRef]
- Su, J.; Liu, C.; Li, R. Robot Precision Assembly Combining With Passive and Active Compliant Motions. IEEE Trans. Ind. Electron. 2022, 8, 8157–8167. [Google Scholar] [CrossRef]
- Whitney, D.E. Historical Perspective and State of the Art in Robot Force Control. J. Robot. Res. 1987, 6, 120–132. [Google Scholar] [CrossRef]
- Yin, Y.; Zhu, J.; Wei, Z. Force Control of Robot: An Overview. J. Nanjing Univ. Aeronaut. Astronaut. 1997, 2, 220–230. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFD9697&filename=NJHK702.019 (accessed on 13 January 1997).
- Sturges, R.H.; Laowattana, S. Design Fan Orthogonal Compliance for Polygonal Peg Insertion. ASMEJ Mech. Des. 1996, 118, 106–114. [Google Scholar] [CrossRef]
- Cutkosky, M.R.; Wright, P.K. Active Control of a Compliant Wrist in Manufacturing Tasks. J. Eng. Ind. 1986, 108, 36–43. [Google Scholar] [CrossRef]
- Lee, S.; Won, S.; Choi, S. Development of a New Variable Remote Center Complain for Assembly Robots. Adv. Robot. 2000, 14, 241–255. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Z.; Kong, L.; Wang, H. Analysis and Validation of a Flexible Planar Two Degrees-of-Freedom Parallel Manipulator with Structural Passive Compliance. J. Mech. Robot. Trans. ASME 2020, 12, 011011. [Google Scholar] [CrossRef]
- Deng, X.; Li, B.; Chen, Z. A Kind of Plane Compliant Grippers. China Mech. Eng. 1994, 6, 48–49. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFD9495&filename=ZGJX406.021 (accessed on 10 June 1994).
- Yuan, S.; Zhang, H. Development of Error-Absorbtion Compliant Robot Hand and Its Design. J. Beijing Univ. Technol. 1998, 24, 33–38. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFD9899&filename=BJGD801.005 (accessed on 22 January 1997).
- Xu, D.; Mo, H.; Yi, J.; Huang, L.; Yin, L. Hybrid compliant control with variable-stiffness wrist for assembly and grinding application. Robot. Auton. Syst. 2024, 180, 104756. [Google Scholar] [CrossRef]
- Kumar, N.; Rani, M. Neural network-based hybrid force/position control of constrained reconfigurable manipulators. Neurocomputing 2021, 420, 1–14. [Google Scholar] [CrossRef]
- Dehghan, S.A.M.; Koofigar, H.R.; Sadeghian, H.; Ekramian, M. Observer-based adaptive force–position control for nonlinear bilateral teleoperation with time delay. Control Eng. Pract. 2021, 107, 104679. [Google Scholar] [CrossRef]
- Baspinar, C. Robust Position/Force Control of Constrained Compliant Joint Robots With Constraint Uncertainties. J. Intell. Robot. Syst. 2020, 100, 945–954. [Google Scholar] [CrossRef]
- Peng, F.; Wen, H.; Zhang, C.; Xu, B.; Li, J.; Su, H. Adaptive Robust Force Position Control for Flexible Active Prosthetic Knee Using Gait Trajectory. Appl. Sci. 2020, 10, 2755. [Google Scholar] [CrossRef]
- Lai, J.; Lu, B.; Chu, H.K. Variable-Stiffness Control of a Dual-Segment Soft Robot Using Depth Vision. IEEE ASME Trans. Mechatron. 2022, 27, 1034–1045. [Google Scholar] [CrossRef]
- Zhang, C.; Mu, C.; Wang, Y.; Li, J.; Liu, Z. Collision Detection for Six-DOF Serial Robots Force/Position Hybrid Control Based on Continuous Friction Model. Meas. Control 2023, 56, 571–582. [Google Scholar] [CrossRef]
- Xing, H.; Ding, L.; Chen, J.; Gao, H.; Deng, Z. Robotic Valve Turning with a Wheeled Mobile Manipulator via Hybrid Passive/Active Compliance. Sensors 2024, 24, 7249. [Google Scholar] [CrossRef]
- Han, M.; Lian, W.; Liu, J.; Yang, D.; Li, T. Hybrid force-position coordinated control of a parallel mechanism with the number of redundant actuators equal to its DOF. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 11081–11096. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, W.; Ling, J.; Xiao, X.; Tan, K.K.; Lee, T.H. Adaptive robust impedance control for an ear surgical device with soft interaction. IEEE-ASME Trans. Mechatron. 2022, 27, 1784–1795. [Google Scholar] [CrossRef]
- Park, H.; Park, J.; Lee, D.-H.; Park, J.-H.; Baeg, M.-H.; Bae, J.-H. Compliance-based robotic peg-in-hole assembly strategy without force feedback. IEEE Trans. Ind. Electron. 2017, 64, 6299–6309. [Google Scholar] [CrossRef]
- Roveda, L.; Pedrocchi, N.; Vicentini, F.; Tosatti, L.M. An interaction controller formulation to systematically avoid force overshoots through impedance shaping method with compliant robot base. Mechatronics 2016, 39, 42–53. [Google Scholar] [CrossRef]
- Inoue, T.; De Magistris, G.; Munawar, A.; Yokoya, T.; Tachibana, R. Deep reinforcement learning for high precision assembly tasks. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; pp. 819–825. Available online: https://www.engineeringvillage.com/app/doc/?docid=cpx_3a288d0d17f89d38a06M5c851017816328&usageOrigin=share (accessed on 14 August 2017).
- Xu, J.; Hou, Z.; Wang, W.; Xu, B.; Zhang, K.; Chen, K. Feedback Deep Deterministic Policy Gradient With Fuzzy Reward for Robotic Multiple Peg-in-Hole Assembly Tasks. IEEE Trans. Ind. Inform. 2019, 15, 1658–1667. [Google Scholar] [CrossRef]
- Ren, T.; Dong, Y.; Wu, D.; Chen, K. Learning-based variable compliance control for robotic assembly Learning-Based Variable Compliance Control for Robotic Assembly. J. Mech. Robot. Trans. ASME 2018, 10, 061008. [Google Scholar] [CrossRef]
- Kaspar, M.; Munoz, O.; Juan, D.; Bock, J. Sim2Real Transfer for Reinforcement Learning without Dynamics Randomization. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 4383–4388. Available online: https://www.engineeringvillage.com/app/doc/?docid=cpx_M4242fe0917f8a612cdbM6f631017816328&usageOrigin=share (accessed on 19 February 2020).
- Ahn, K.-H.; Na, M.; Song, J.-B. Robotic assembly strategy via reinforcement learning based on force and visual information. Robot. Auton. Syst. 2023, 164, 104399. [Google Scholar] [CrossRef]
- Xu, G.; Lin, X.; Zhong, Y.; Shi, D. CAD model based Multi sensor vision system. Robot 1991, 13, 7–14. [Google Scholar] [CrossRef]
- Song, H.-C.; Kim, Y.-L.; Song, J.-B. Guidance algorithm for complex-shape peg-in-hole strategy based on geometrical information and force control. Adv. Robot. 2016, 30, 552–563. [Google Scholar] [CrossRef]
- Zhan, D.; Li, P.; Qiu, X.; Li, S. Simulation and Experimental Study on Axial Force Adaptive Control in CFRP Hole-making Process. Mech. Sci. Technol. Aerosp. Eng. 2024, 43, 474–482. [Google Scholar] [CrossRef]
- Zeng, Q.; Hu, Y.; Meng, Z.; Wan, L. Research on Velocity Feedforward Control and Precise Damping Technology of a Hydraulic Support Face Guard System Based on Displacement Feedback. Machines 2024, 12, 676. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.; Cheng, G.; Zhang, P.; Jia, X. Trajectory tracking control of upper limb rehabilitation robot based on optimal discrete sliding mode control. Meas. Control 2023, 56, 1142–1155. [Google Scholar] [CrossRef]
- Pires, J.; Norberto, Z.; Carlos, Y. From CAD design to robot models and simulation tools. Test-case example using the Kassow 810 collaborative robot. Ind. Robot. Int. J. Robot. Res. Appl. 2021, 48, 856–876. [Google Scholar] [CrossRef]
- Park, H.; Bae, J.H.; Park, J.H.; Baeg, M.H.; Park, J. Intuitive pegin-hole assembly strategy with a compliant manipulator. In Proceedings of the 2013 44th IEEE International Symposium on Robotics, ISR 2013, Seoul, Republic of Korea, 24–26 October 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Kim, Y.-L.; Song, H.-C.; Song, J.-B. Hole detection algorithm for chamferless square pegin-hole based on shape recognition using F/T sensor. Int. J. Precis. Eng. Manuf. 2014, 15, 425–432. [Google Scholar] [CrossRef]






















| 1 kg Pick-and-Place Cycle Performance Parameters | |
|---|---|
| Maximum TCP Acceleration | 35 m/s·s |
| Acceleration Time from 0 to 1 m/s | 0.06 s |
| Repetition Accuracy | 0.025 mm |
| Axis Movement | Working Range | Maximum Axis Speed |
|---|---|---|
| Axis 1 (Rotation) | +170° to −170° | 288 °/s |
| Axis 2 (Arm) | +135° to −100° | 240 °/s |
| Axis 3 (Arm) | +70° to −200° | 300 °/s |
| Axis 4 (Wrist) | +270° to −270° | 400 °/s |
| Axis 5 (Bend) | +130° to −130° | 405 °/s |
| Axis 6 (Twist) | +400° to −400° | 600 °/s |
| Mechanical Characteristics | |
|---|---|
| Weight | 800 g |
| Dimensions | Φ125 mm × 67.5 mm |
| Overload Capacity | 300% FS |
| Zero Drift | 0.2% FS/10 °C |
| Sensitivity Drift | 0.1% FS/30 min |
| Search Strategy | Average Search Time (s) | Success Rate (%) | Standard Deviation | Confidence Interval (95%) | p-Value |
|---|---|---|---|---|---|
| The improved vertical search strategy | 15.7 | 95 | 0.5 | [15.2, 16.2] | p < 0.05 |
| Archimedes spiral search strategy | 21.5 | 85 | 1.2 | [20.3, 22.7] |
| Parameter | Simulation Result | Experiment Result | Difference Analysis |
|---|---|---|---|
| Contact Force Adjustment Range (N) | 4.75 | 6.62 | The contact force increases significantly in the experiment due to slight mechanical friction and blockage, leading to a higher contact force. |
| Impedance Parameter Adjustment Rules ( , ) | Consistent trends | Consistent trends | No difference in the adjustment pattern, but since the actual robot is not exactly the same as the simulation, experimental parameters are set based on the simulation’s pattern. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Z.; Chen, J.; Li, H.; Xiang, W.; Chang, D.; Liu, Z. Research on the Assembly of Square Parts on Circular Production Lines Using Admittance Control for Six-DOF Robots. Sensors 2025, 25, 1138. https://doi.org/10.3390/s25041138
Chai Z, Chen J, Li H, Xiang W, Chang D, Liu Z. Research on the Assembly of Square Parts on Circular Production Lines Using Admittance Control for Six-DOF Robots. Sensors. 2025; 25(4):1138. https://doi.org/10.3390/s25041138
Chicago/Turabian StyleChai, Zhiyuan, Junhua Chen, Hao Li, Wenping Xiang, Dongdong Chang, and Zewen Liu. 2025. "Research on the Assembly of Square Parts on Circular Production Lines Using Admittance Control for Six-DOF Robots" Sensors 25, no. 4: 1138. https://doi.org/10.3390/s25041138
APA StyleChai, Z., Chen, J., Li, H., Xiang, W., Chang, D., & Liu, Z. (2025). Research on the Assembly of Square Parts on Circular Production Lines Using Admittance Control for Six-DOF Robots. Sensors, 25(4), 1138. https://doi.org/10.3390/s25041138






