Scene-Adaptive Loader Trajectory Planning and Tracking Control
Abstract
1. Introduction
- (1)
- To address the unique scenarios of loader operations, an improved Hybrid A* planning algorithm based on dynamic grid maps is proposed, enhancing the adaptability of trajectory planning.
- (2)
- To improve loader tracking performance, a hierarchical trajectory tracking control scheme is employed. Firstly, in the upper-layer control, a fuzzy fractional-order PID controller with preview control incorporating curvature speed adaptation is selected. Secondly, to mitigate the impact of the unique articulated steering structure on tracking, a PD controller based on a nonlinear extended state observer (NLESO) is utilized in the lower-layer control.
- (3)
- The application of the proposed planning and control scheme to actual vehicles has been supported by a large number of experimental results, which thoroughly demonstrate the effectiveness of this strategy.
2. Kinematic Modeling and Problem Statement
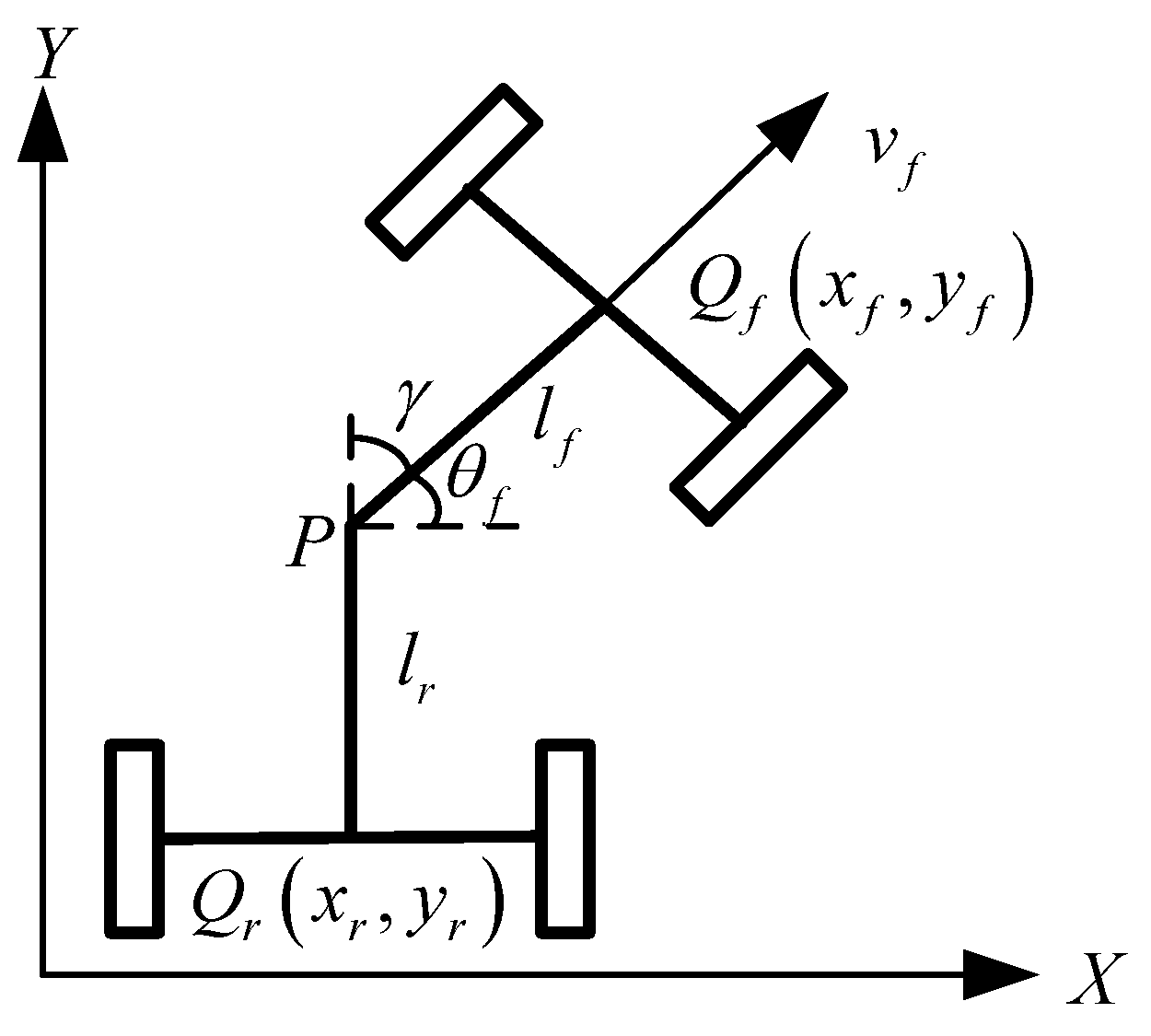
2.1. Kinematic Modeling
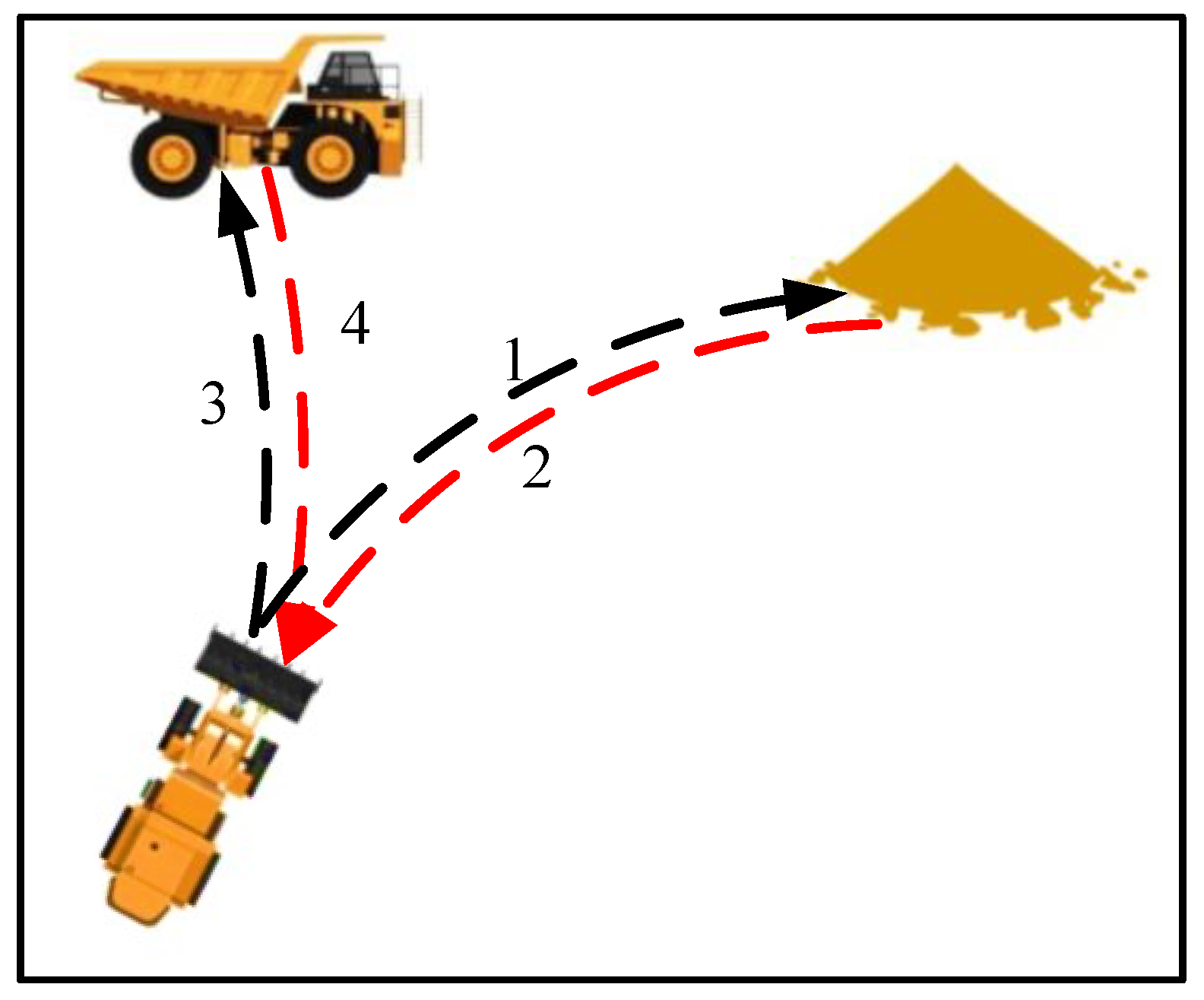
2.2. Problem Statement
3. Trajectory Planner
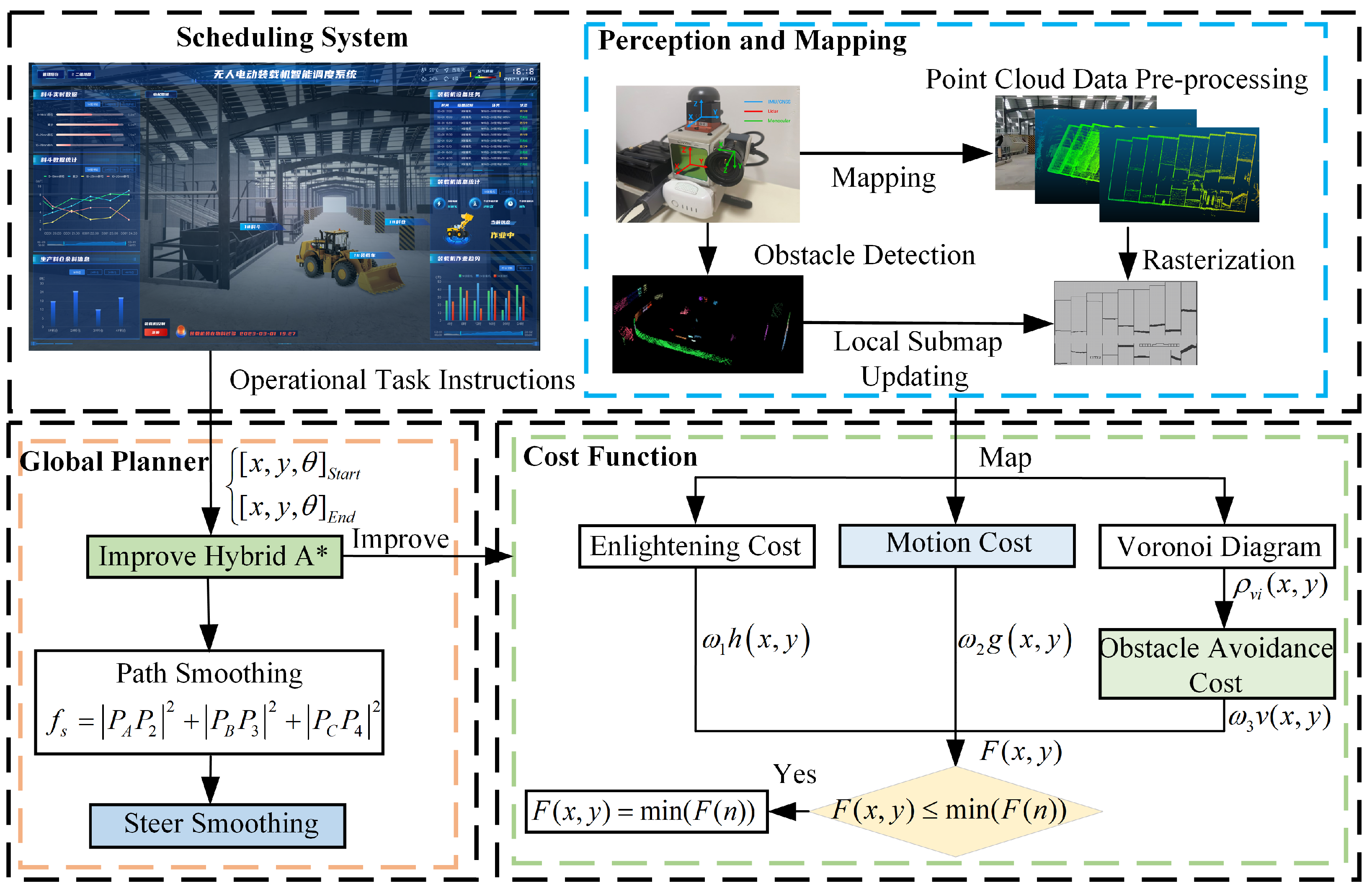
3.1. Path Planning Based on Improved Hybrid A* Algorithm
3.1.1. Collision Avoidance
3.1.2. Cost Function
3.2. Path Post-Processing
3.2.1. Smoothing Process
3.2.2. Path Connection at Turning Points
4. Trajectory Tracking and Control
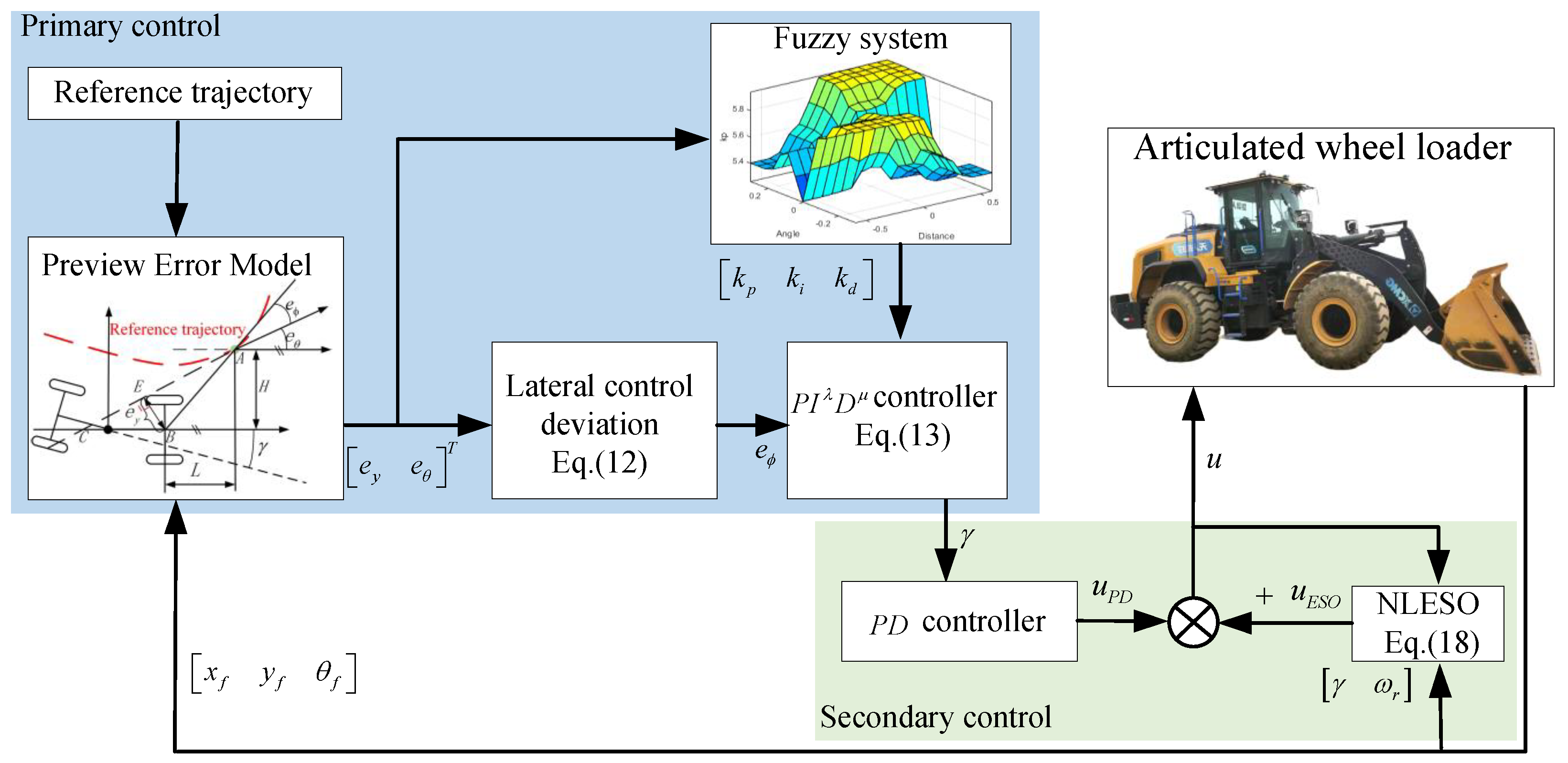
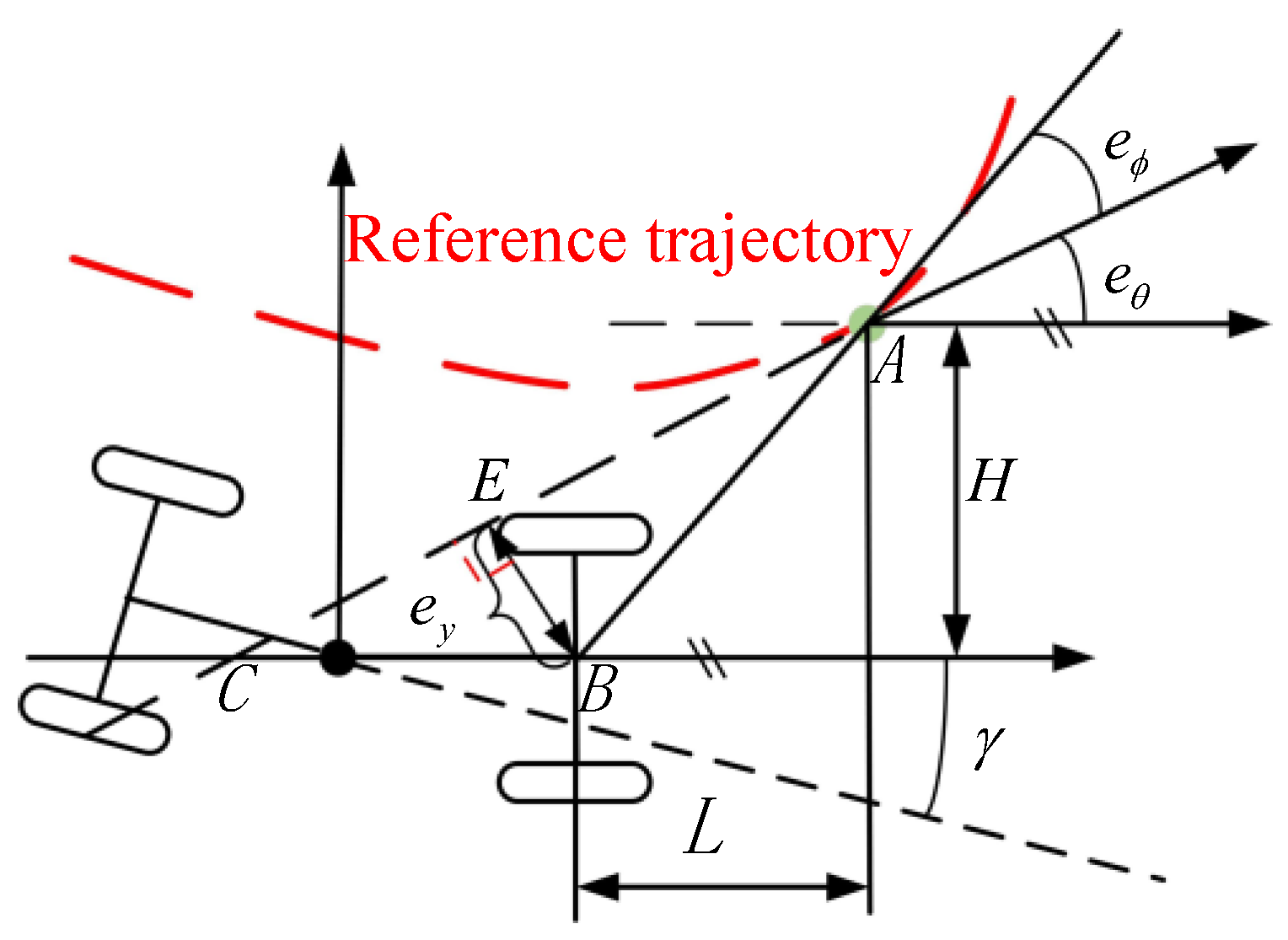
4.1. Preview Error Model
4.2. Lateral Control Deviation
4.3. Fuzzy Fractional-Order PID Controller
4.3.1. Fractional-Order PID Controller
4.3.2. Fuzzy Rules
4.4. Extended State Observer
5. Results and Discussion
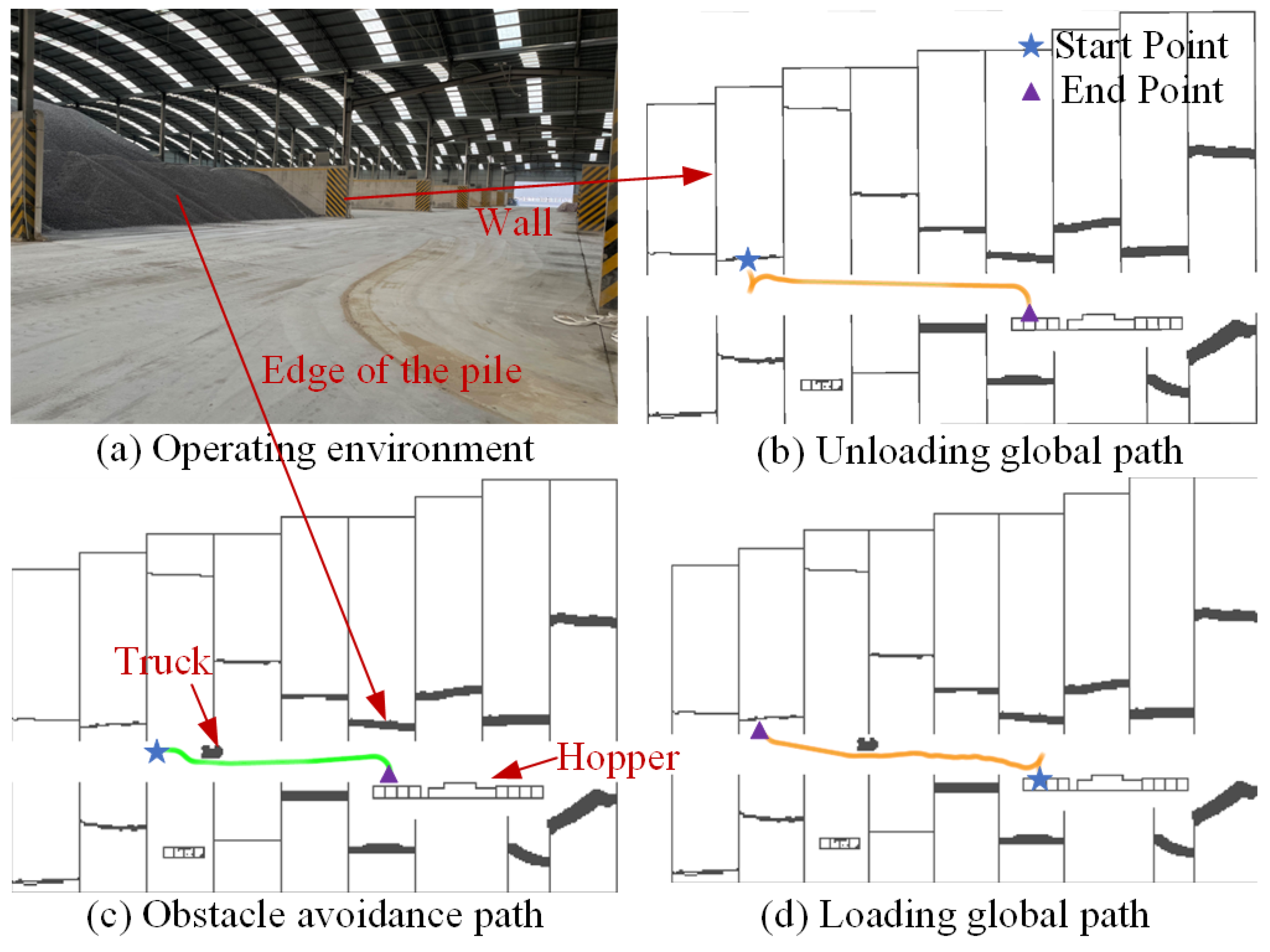
5.1. Planning Performance
5.2. Steering Performance
5.3. Trajectory Tracking Performance
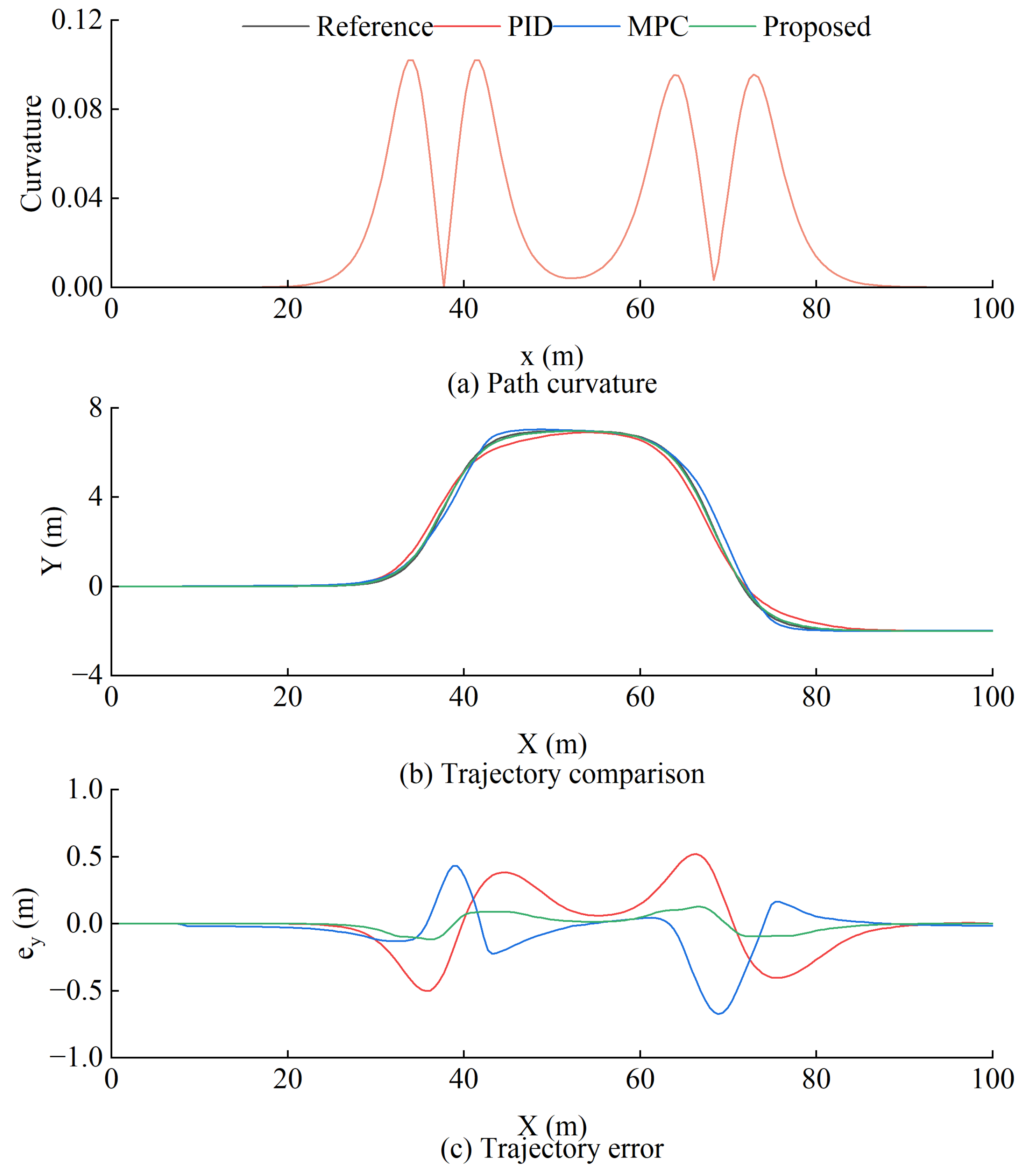
5.3.1. Simulation Results
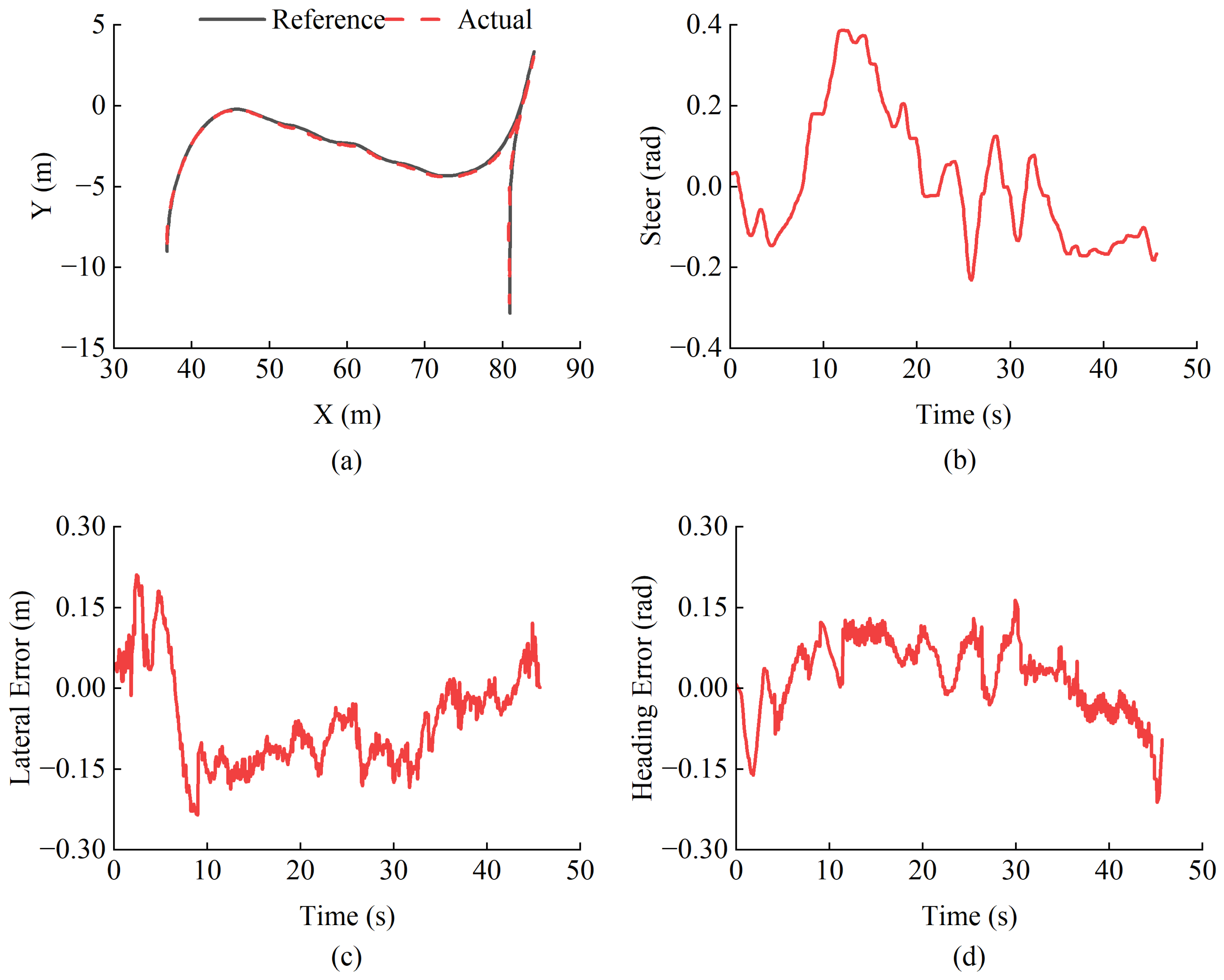
5.3.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Takita, Y.; Ohkawa, S.; Date, H. High Stability Lateral Guided Method for Articulated Vehicle Based on Sensor Steering Mechanism. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 24–26 October 2012; Volume 1, pp. 351–356. [Google Scholar]
- Dadhich, S.; Bodin, U.; Andersson, U. Key challenges in automation of earth-moving machines. Autom. Constr. 2016, 68, 212–222. [Google Scholar] [CrossRef]
- Ghabcheloo, R.; Hyvönen, M.; Uusisalo, J.; Karhu, O.; Järä, J.; Huhtala, K. Autonomous motion control of a wheel loader. In Proceedings of the Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2009; Volume 48937, pp. 427–434. [Google Scholar]
- Yossawee, W.; Tsubouchi, T.; Kurisu, M.; Sarata, S. A semi-optimal path generation scheme for a frame articulated steering-type vehicle. Adv. Robot. 2006, 20, 867–896. [Google Scholar] [CrossRef]
- Alshaer, B.; Darabseh, T.; Alhanouti, M. Path planning, modeling and simulation of an autonomous articulated heavy construction machine performing a loading cycle. Appl. Math. Model. 2013, 37, 5315–5325. [Google Scholar] [CrossRef]
- Choi, J.-w.; Huhtala, K. Constrained global path optimization for articulated steering vehicles. IEEE Trans. Veh. Technol. 2015, 65, 1868–1879. [Google Scholar] [CrossRef]
- Chen, X.; Yang, C.; Hu, H.; Gao, Y.; Zhu, Q.; Shao, G. A Hybrid DWA-MPC Framework for Coordinated Path Planning and Collision Avoidance in Articulated Steering Vehicles. Machines 2024, 12, 939. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T.; Kominiak, D.; Nyberg, R. Design and experimental evaluation of a novel sliding mode controller for an articulated vehicle. Robot. Auton. Syst. 2018, 103, 213–221. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. Effect of kinematic parameters on MPC based on-line motion planning for an articulated vehicle. Robot. Auton. Syst. 2015, 70, 16–24. [Google Scholar] [CrossRef]
- Bai, G.; Liu, L.; Meng, Y.; Luo, W.; Gu, Q.; Ma, B. Path tracking of mining vehicles based on nonlinear model predictive control. Appl. Sci. 2019, 9, 1372. [Google Scholar] [CrossRef]
- Chen, X.; Yang, C.; Cheng, J.; Hu, H.; Shao, G.; Gao, Y.; Zhu, Q. A novel iterative learning-model predictive control algorithm for accurate path tracking of articulated steering vehicles. IEEE Robot. Autom. Lett. 2024, 9, 7373–7380. [Google Scholar] [CrossRef]
- Qiang, W.; Yu, W.; Xu, Q.; Xie, H. Study on Robust Path-Tracking Control for an Unmanned Articulated Road Roller Under Low-Adhesion Conditions. Electronics 2025, 14, 383. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, J.; Hu, H.; Shao, G.; Gao, Y.; Zhu, Q. A Novel Fuzzy Logic Switched MPC for Efficient Path Tracking of Articulated Steering Vehicles. Robotics 2024, 13, 134. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, C.; Li, S.; Wang, Z.; Zhang, Y. Pre-work for the birth of driver-less scraper (Lhd) in the underground mine: The path tracking control based on an lqr controller and algorithms comparison. Sensors 2021, 21, 7839. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Ren, Z.; Yao, Z.; Tan, X. Synchronized path planning and tracking for front and rear axles in articulated wheel loaders. Autom. Constr. 2024, 165, 105538. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Guastafsson, T. Kinematic modeling and simulation studies of a LHD vehicle under slip angles. In Computational Intelligence and Bioinformatics/755: Modelling, Identification, and Simulation; ACTA Press: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Kawabe, T.; Takei, T.; Imanishi, E. Path planning to expedite the complete transfer of distributed gravel piles with an automated wheel loader. Adv. Robot. 2021, 35, 1418–1437. [Google Scholar] [CrossRef]
- Penin, B.; Giordano, P.R.; Chaumette, F. Vision-based reactive planning for aggressive target tracking while avoiding collisions and occlusions. IEEE Robot. Autom. Lett. 2018, 3, 3725–3732. [Google Scholar] [CrossRef]
- Ren, Z.; Rathinam, S.; Likhachev, M.; Choset, H. Multi-objective safe-interval path planning with dynamic obstacles. IEEE Robot. Autom. Lett. 2022, 7, 8154–8161. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, J.; Luo, W.; Zhao, Y.; Tang, R.; Mei, K.; Wang, P. A Shortest Distance Priority UAV Path Planning Algorithm for Precision Agriculture. Sensors 2024, 24, 7514. [Google Scholar] [CrossRef] [PubMed]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Gao, P.; Xu, P.; Cheng, H.; Zhou, X.; Zhu, D. Hybrid Path Planning for Unmanned Surface Vehicles in Inland Rivers Based on Collision Avoidance Regulations. Sensors 2023, 23, 8326. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.; Tan, B.Y.; Garg, N.P.; Li, L.; Sidarta, A.; Ang, W.T. An intention prediction based shared control system for point-to-point navigation of a robotic wheelchair. IEEE Robot. Autom. Lett. 2022, 7, 8893–8900. [Google Scholar] [CrossRef]
- Li, X.; Wang, G.; Yao, Z.; Qu, J. Dynamic model and validation of an articulated steering wheel loader on slopes and over obstacles. Veh. Syst. Dyn. 2013, 51, 1305–1323. [Google Scholar] [CrossRef]
- Liu, S.; Hou, Z.; Tian, T.; Deng, Z.; Li, Z. A novel dual successive projection-based model-free adaptive control method and application to an autonomous car. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3444–3457. [Google Scholar] [CrossRef]
- Sotelo, M.A. Lateral control strategy for autonomous steering of Ackerman-like vehicles. Robot. Auton. Syst. 2003, 45, 223–233. [Google Scholar] [CrossRef]
- Yuan, X.; Huang, G.; Shi, K. Improved adaptive path following control system for autonomous vehicle in different velocities. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3247–3256. [Google Scholar] [CrossRef]
- Tian, T.; Lv, J.; Tang, J. Stability comparison of different controllers for hydraulic turbine fractional order interval parameter time-delay system. Syst. Sci. Control Eng. 2023, 11, 2221309. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, J.; Wang, Z.; Zhang, J.; Liu, J. Research on Electric Oil–Pneumatic Active Suspension Based on Fractional-Order PID Position Control. Sensors 2024, 24, 1644. [Google Scholar] [CrossRef] [PubMed]
- Haggag, S.; Alstrom, D.; Cetinkunt, S.; Egelja, A. Modeling, control, and validation of an electro-hydraulic steer-by-wire system for articulated vehicle applications. IEEE/ASME Trans. Mechatron. 2005, 10, 688–692. [Google Scholar] [CrossRef]






| Output Parameters | Range | Input Parameters | Range |
|---|---|---|---|
| [5.20, 6.00] | [−0.6, 0.6] | ||
| [0.36, 0.42] | [−0.3, 0.3] | ||
| [0.60, 0.65] |
| NB | NS | Z | PS | PB | ||
| NB | ||||||
| NS | ||||||
| Z | ||||||
| PS | ||||||
| PB | ||||||
| Module | Parameter Settings |
|---|---|
| Path planning | |
| Path tracking |
| ME | MAE | RMSE | ||
|---|---|---|---|---|
| PD | 7.11 | 2.67 | 0.29 | |
| Unload | PD with NLESO | 6.24 | 2.37 | 0.22 |
| PD | 10.2 | 5.64 | 0.43 | |
| Load | PD with NLESO | 6.26 | 2.22 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Dong, W.; Zheng, T.; Wang, Y.; Li, X. Scene-Adaptive Loader Trajectory Planning and Tracking Control. Sensors 2025, 25, 1135. https://doi.org/10.3390/s25041135
Li Y, Dong W, Zheng T, Wang Y, Li X. Scene-Adaptive Loader Trajectory Planning and Tracking Control. Sensors. 2025; 25(4):1135. https://doi.org/10.3390/s25041135
Chicago/Turabian StyleLi, Yingnan, Wenwen Dong, Tianhao Zheng, Yakun Wang, and Xuefei Li. 2025. "Scene-Adaptive Loader Trajectory Planning and Tracking Control" Sensors 25, no. 4: 1135. https://doi.org/10.3390/s25041135
APA StyleLi, Y., Dong, W., Zheng, T., Wang, Y., & Li, X. (2025). Scene-Adaptive Loader Trajectory Planning and Tracking Control. Sensors, 25(4), 1135. https://doi.org/10.3390/s25041135






