MR-FuSN: A Multi-Resolution Selective Fusion Approach for Bearing Fault Diagnosis
Abstract
1. Introduction
- A feature extraction module is designed, combining residual convolution, multi-resolution, and attention mechanisms, effectively extracting key features at different scales and improving the detection accuracy of bearing fault diagnosis.
- An adaptive dual-kernel channel-focusing module is developed that dynamically adjusts processing strategies based on the characteristics of the input data, thereby enhancing the model’s adaptability and diagnostic efficiency in complex data environments.
- The model was validated using two bearing datasets and compared to other diagnostic methods, thereby demonstrating its advantages in terms of accuracy and noise resistance. These results confirm the effectiveness and potential value of the proposed model for practical applications.
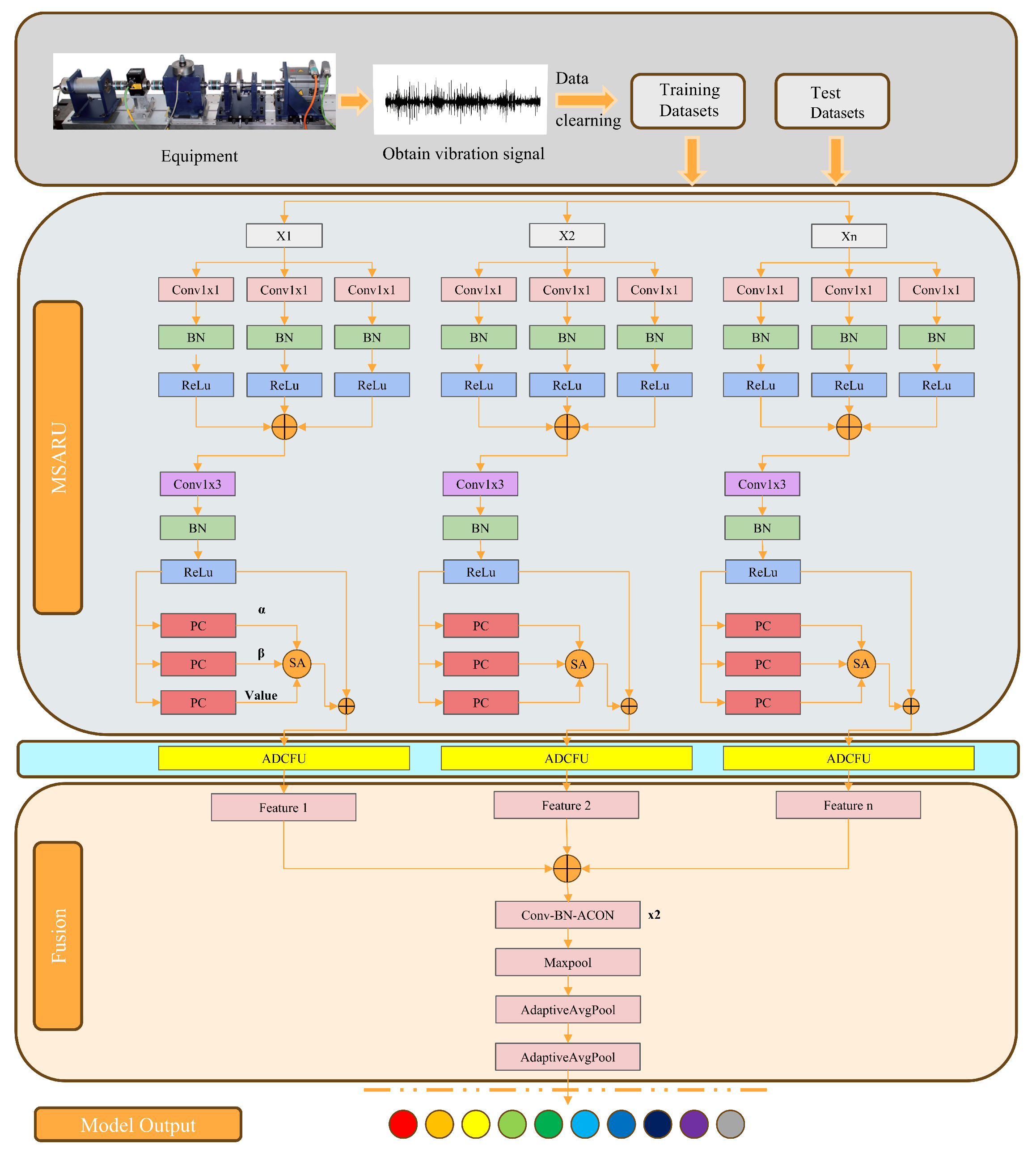
2. Principle and Model Framework
2.1. Multi-Level Spatial Attention Residual Unit
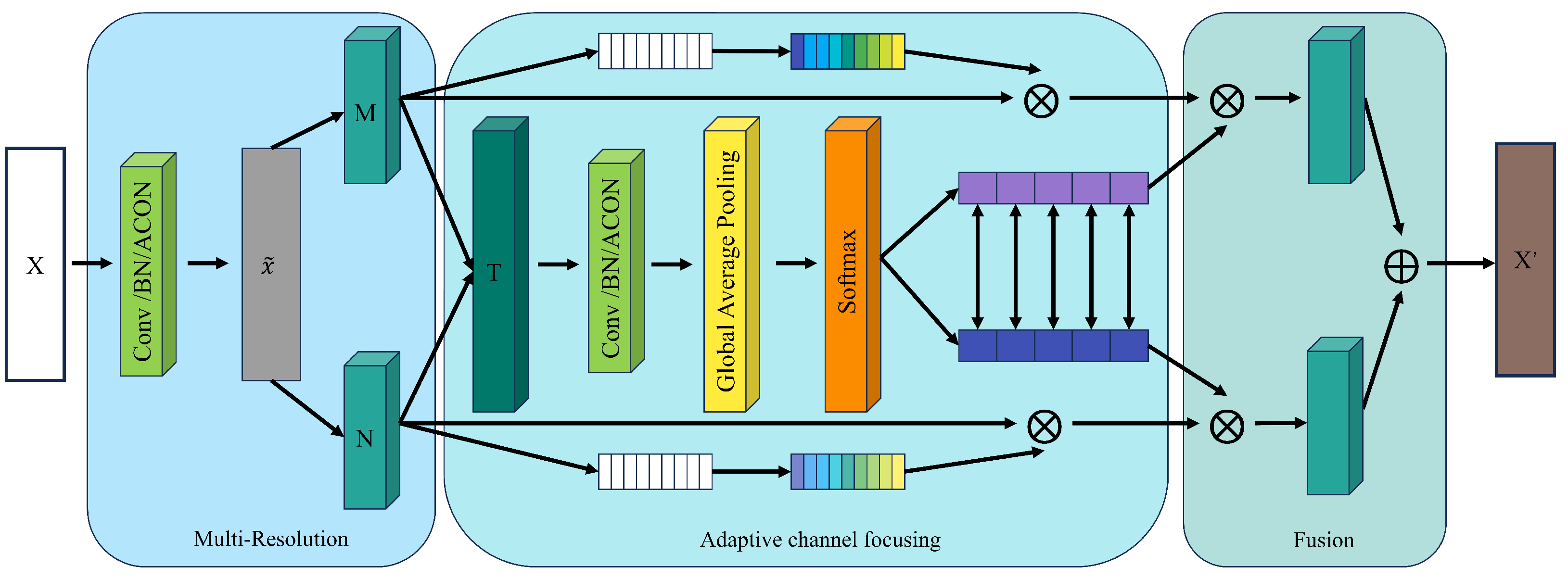
2.2. Adaptive Dual-Core Channel-Focusing Unit
2.3. Multi-Resolution Fusion Strategy
3. Fault Diagnosis Process Based on the MR-FuSN Model
4. Experimental Verification
4.1. Description of Experimental Datasets
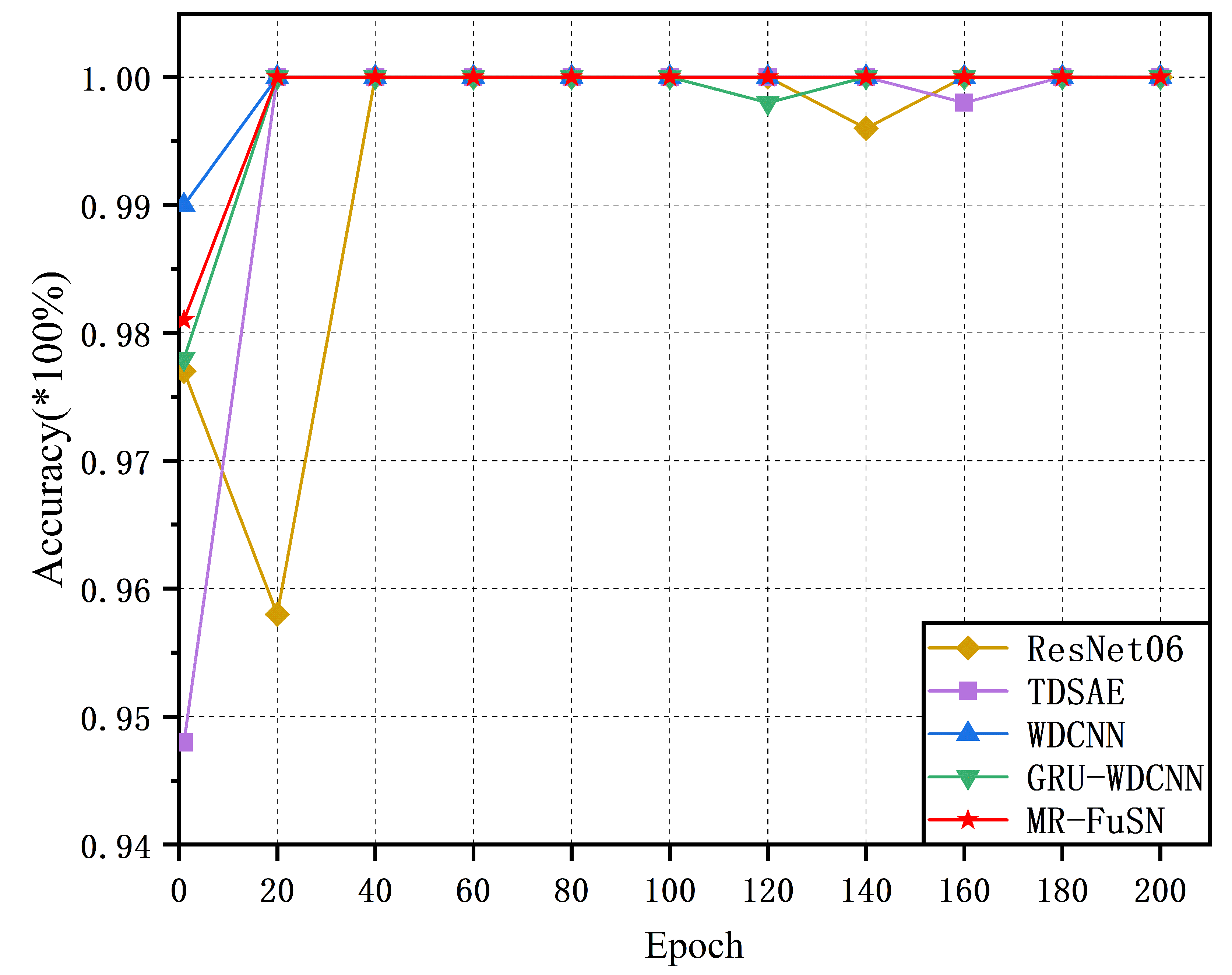
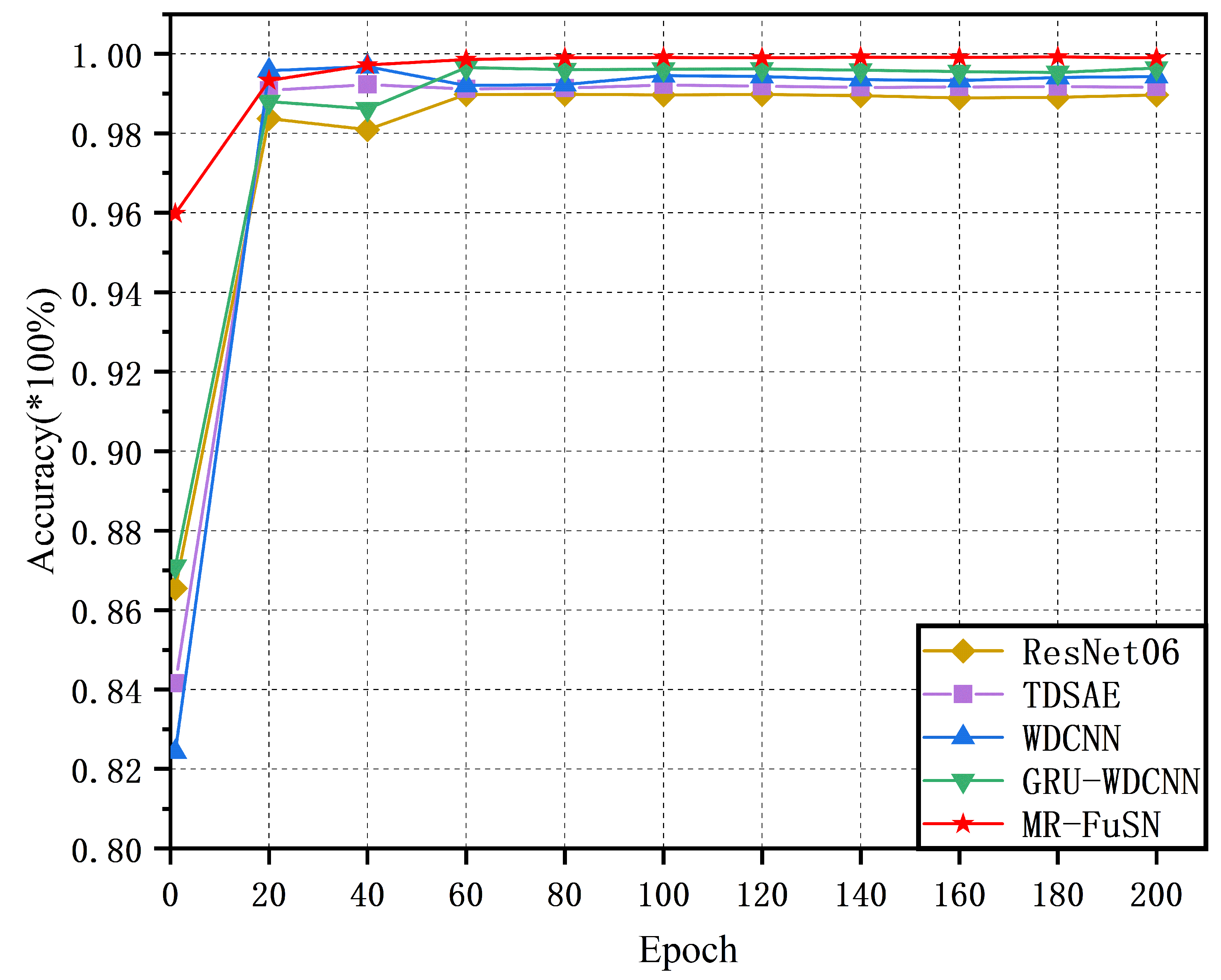
4.2. Accuracy Comparison with Other Methods
4.3. Noise Interference Experiment
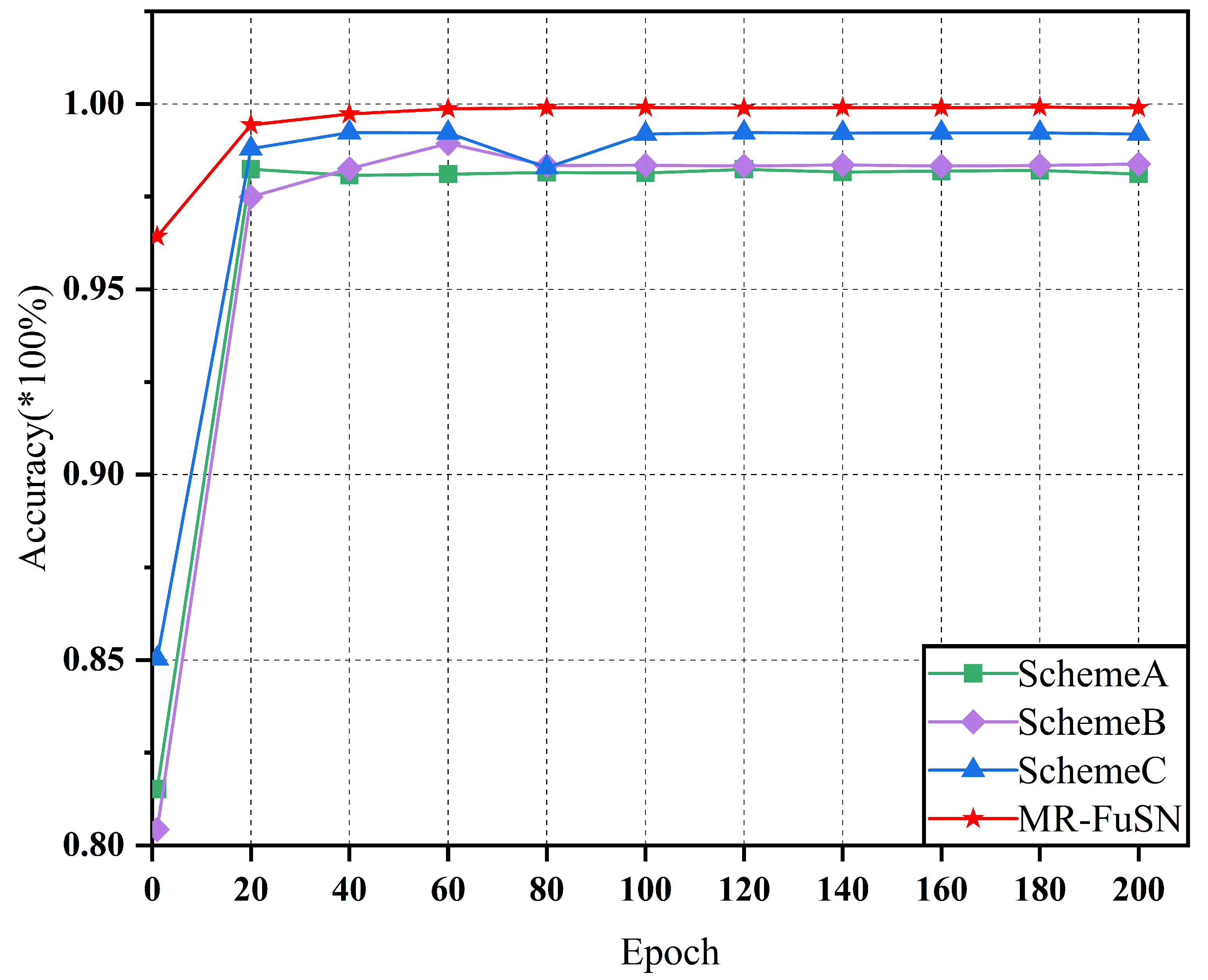
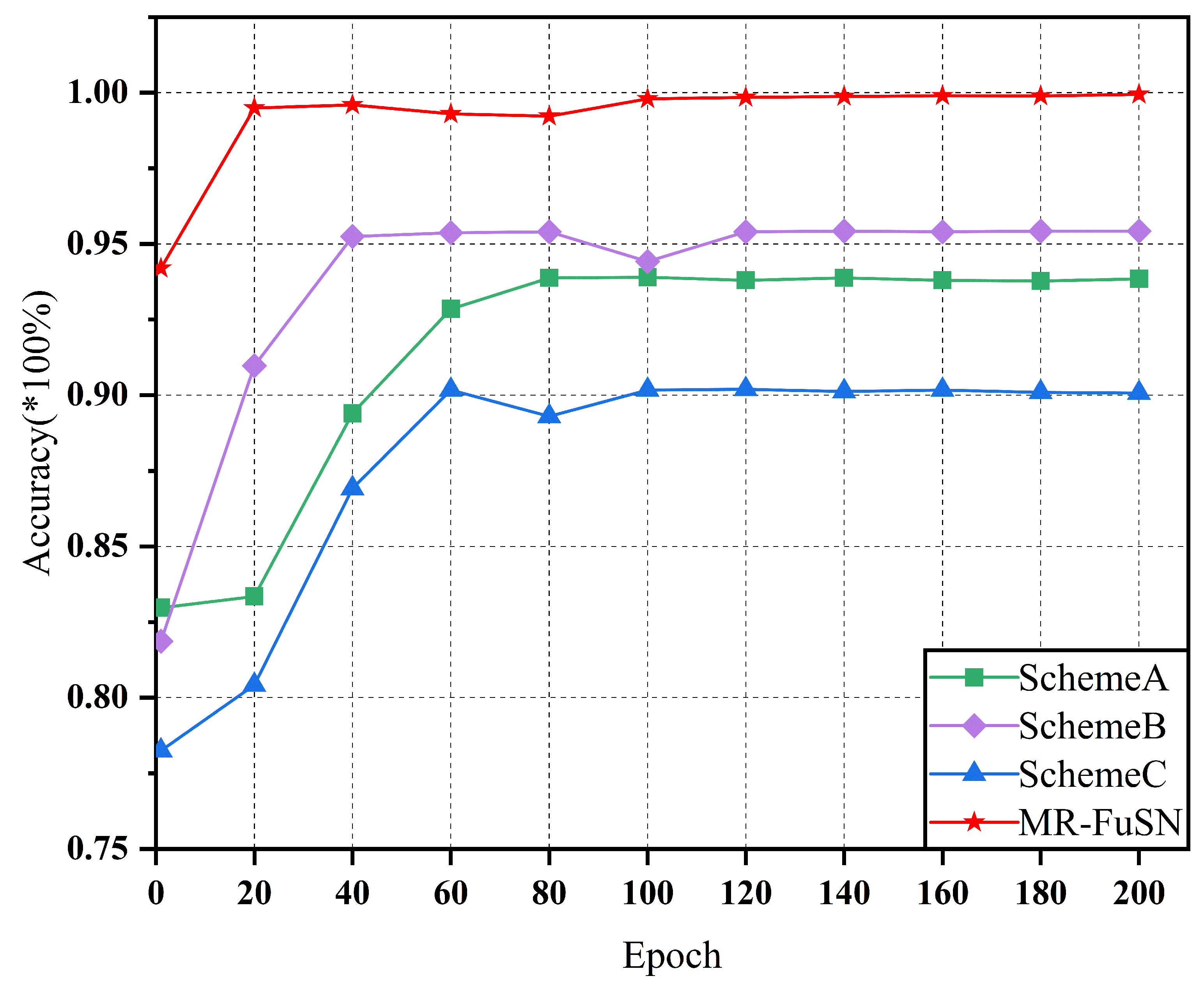
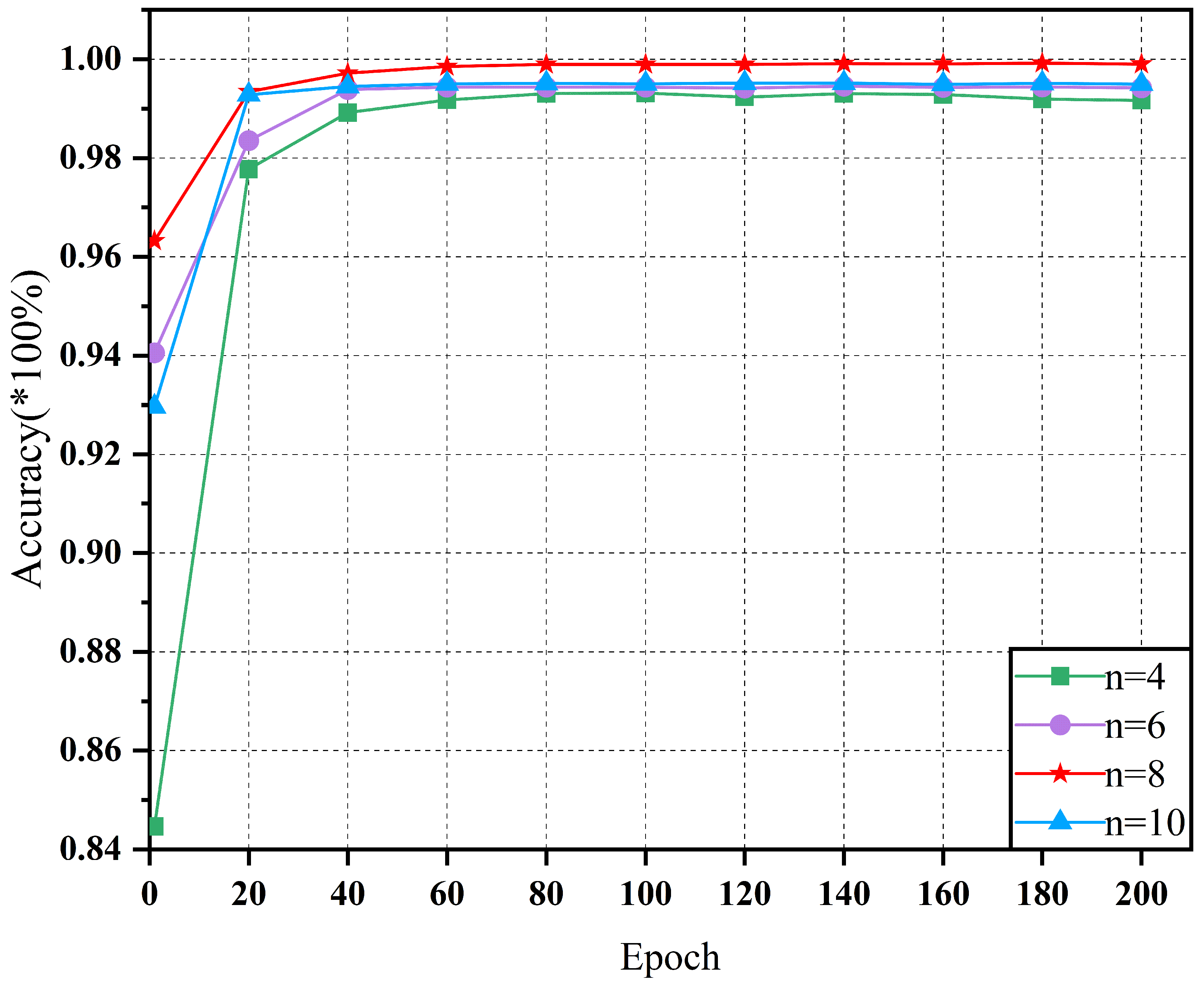
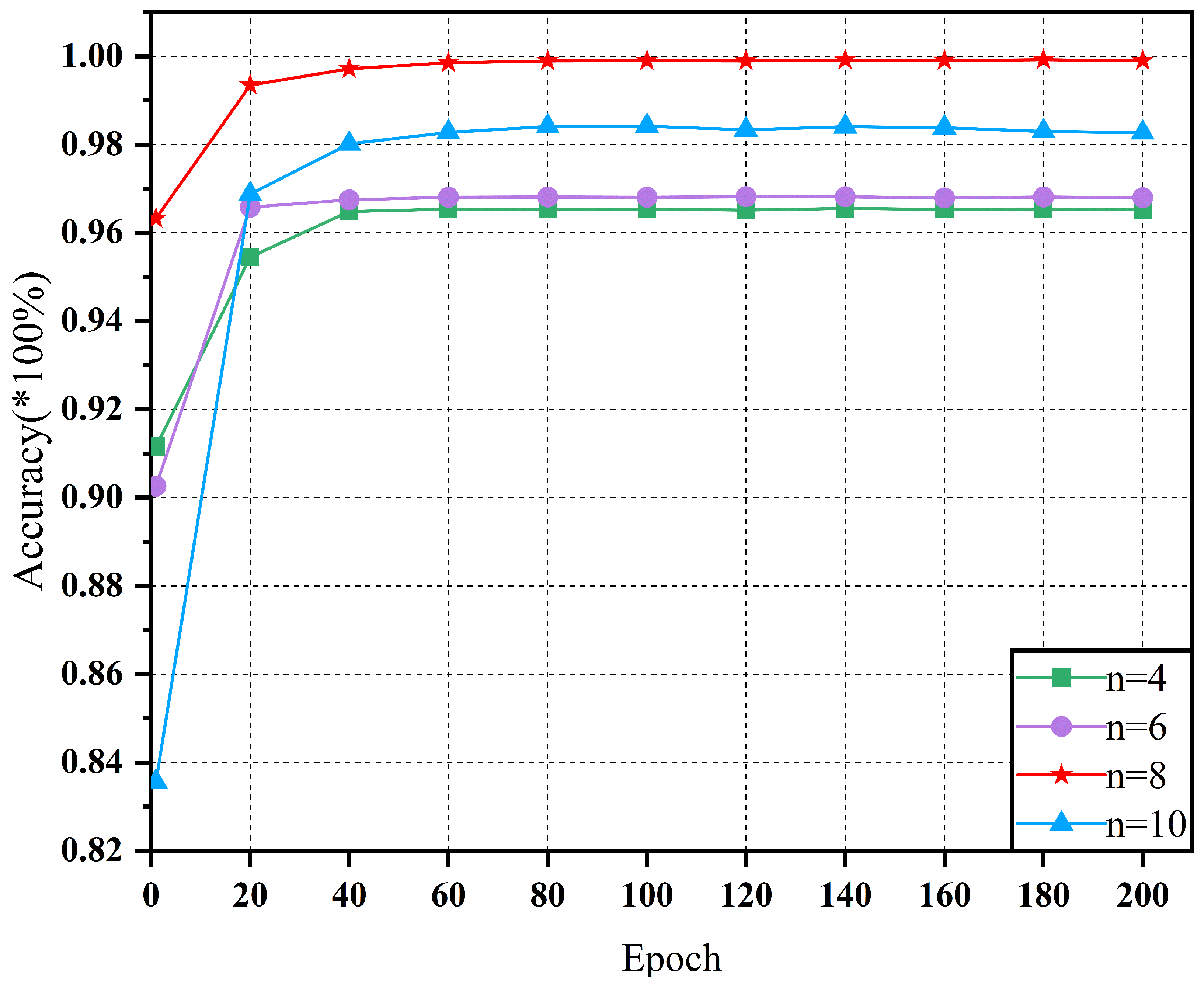
4.4. Ablation Experiment
4.4.1. Comparison of Different Network Architectures
4.4.2. Network Width Parameter Selection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Izagirre, U.; Andonegui, I.; Landa-Torres, I.; Zurutuza, U. A practical and synchronized data acquisition network architecture for industrial robot predictive maintenance in manufacturing assembly lines. Robot. Comput.-Integr. Manuf. 2022, 74, 102287. [Google Scholar] [CrossRef]
- Zhao, M.; Jia, X. A novel strategy for signal denoising using reweighted SVD and its applications to weak fault feature enhancement of rotating machinery. Mech. Syst. Signal Process. 2017, 94, 129–147. [Google Scholar] [CrossRef]
- Chen, C.; Liu, C.; Wang, T.; Zhang, A.; Wu, W.; Cheng, L. Compound fault diagnosis for industrial robots based on dual-transformer networks. J. Manuf. Syst. 2023, 66, 163–178. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, D.; Zhang, W.-a. MSWR-LRCN: A new deep learning approach to remaining useful life estimation of bearings. Control Eng. Pract. 2022, 118, 104969. [Google Scholar] [CrossRef]
- Song, Q.; Jiang, X.; Du, G.; Liu, J.; Zhu, Z. Smart multichannel mode extraction for enhanced bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 189, 110107. [Google Scholar] [CrossRef]
- Wang, S.; Tian, J.; Liang, P.; Xu, X.; Yu, Z.; Liu, S.; Zhang, D. Single and simultaneous fault diagnosis of gearbox via wavelet transform and improved deep residual network under imbalanced data. Eng. Appl. Artif. Intell. 2024, 133, 108146. [Google Scholar] [CrossRef]
- Rai, V.; Mohanty, A. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.; Cheng, J. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. J. Sound Vib. 2006, 294, 269–277. [Google Scholar]
- He, F.; Ye, Q. A bearing fault diagnosis method based on wavelet packet transform and convolutional neural network optimized by simulated annealing algorithm. Sensors 2022, 22, 1410. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Tang, Y. Singularity analysis using continuous wavelet transform for bearing fault diagnosis. Mech. Syst. Signal Process. 2002, 16, 1025–1041. [Google Scholar] [CrossRef]
- Qin, Y.; Mao, Y.; Tang, B.; Wang, Y.; Chen, H. M-band flexible wavelet transform and its application to the fault diagnosis of planetary gear transmission systems. Mech. Syst. Signal Process. 2019, 134, 106298. [Google Scholar] [CrossRef]
- Kumar, A.; Vashishtha, G.; Gandhi, C.; Tang, H.; Xiang, J. Sparse transfer learning for identifying rotor and gear defects in the mechanical machinery. Measurement 2021, 179, 109494. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Li, J.; Huang, R.; He, G.; Liao, Y.; Wang, Z.; Li, W. A two-stage transfer adversarial network for intelligent fault diagnosis of rotating machinery with multiple new faults. IEEE/ASME Trans. Mechatron. 2020, 26, 1591–1601. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. A novel adaptive convolutional neural network for fault diagnosis of hydraulic piston pump with acoustic images. Adv. Eng. Inform. 2022, 52, 101554. [Google Scholar] [CrossRef]
- Yu, S.; Wang, M.; Pang, S.; Song, L.; Qiao, S. Intelligent fault diagnosis and visual interpretability of rotating machinery based on residual neural network. Measurement 2022, 196, 111228. [Google Scholar] [CrossRef]
- Wu, C.; Jiang, P.; Ding, C.; Feng, F.; Chen, T. Intelligent fault diagnosis of rotating machinery based on one-dimensional convolutional neural network. Comput. Ind. 2019, 108, 53–61. [Google Scholar] [CrossRef]
- Zhang, J.; Yi, S.; Liang, G.; Hongli, G.; Xin, H.; Hongliang, S. A new bearing fault diagnosis method based on modified convolutional neural networks. Chin. J. Aeronaut. 2020, 33, 439–447. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Wu, J.; Chen, Z.; Xu, X. Rolling bearing fault diagnosis based on wavelet packet transform and convolutional neural network. Appl. Sci. 2020, 10, 770. [Google Scholar] [CrossRef]
- Jia, X.; Xiao, B.; Zhao, Z.; Ma, L.; Wang, N. Bearing fault diagnosis method based on CNN-LightGBM. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1043, 022066. [Google Scholar] [CrossRef]
- Hao, X.; Zheng, Y.; Lu, L.; Pan, H. Research on intelligent fault diagnosis of rolling bearing based on improved deep residual network. Appl. Sci. 2021, 11, 10889. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Chen, Y.; Jin, Y.; Bai, G. Selective kernel convolution deep residual network based on channel-spatial attention mechanism and feature fusion for mechanical fault diagnosis. ISA Trans. 2023, 133, 369–383. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Yi, C.; Yan, L.; Song, X.; Xu, D.; Huang, C.; Zhou, L.; Lin, J. Multi-objective sparsity maximum mode de-composition: A new method for rotating machine fault diagnosis on high-speed train axle box. IEEE Trans. Veh. Technol. 2023, 72, 12744–12756. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70, 1–35. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, X.; Sun, B.; Zhai, J.; Liu, Z. Multireceptive field denoising residual convolutional networks for fault diagnosis. IEEE Trans. Ind. Electron. 2021, 69, 11686–11696. [Google Scholar] [CrossRef]
- Yu, S.; Pang, S.; Ning, J.; Wang, M.; Song, L. ANC-Net: A novel multi-scale active noise cancellation network for rotating machinery fault diagnosis based on discrete wavelet transform. Expert Syst. Appl. 2025, 265, 125937. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Guo, J.; He, Q.; Gu, F. DNOCNet: A Novel End-to-End Network for Induction Motor Drive Systems Fault Diagnosis Under Speed Fluctuation Condition. IEEE Trans. Ind. Inform. 2024, 20, 8284–8293. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Cui, L.; Tian, X.; Wei, Q.; Liu, Y. A self-attention based contrastive learning method for bearing fault diagnosis. Expert Syst. Appl. 2024, 238, 121645. [Google Scholar] [CrossRef]
- Han, J.; Yang, W.; Wang, Y.; Chen, L.; Luo, Z. Remote Sensing Teacher: Cross-Domain Detection Transformer with Learnable Frequency-Enhanced Feature Alignment in Remote Sensing Imagery. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5619814. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Wang, J.; Zheng, X.; Liu, B. LiConvFormer: A lightweight fault diagnosis framework using separable multiscale convolution and broadcast self-attention. Expert Syst. Appl. 2024, 237, 121338. [Google Scholar] [CrossRef]
- Yao, Y.; Gui, G.; Yang, S.; Zhang, S. A recursive multi-head self-attention learning for acoustic-based gear fault diagnosis in real-industrial noise condition. Eng. Appl. Artif. Intell. 2024, 133, 108240. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Noman, K.; Li, Z.; Feng, K.; Liu, Z.; Deng, Z. Multivariate multiscale dispersion Lempel–Ziv complexity for fault diagnosis of machinery with multiple channels. Inf. Fusion 2024, 104, 102152. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, H.; Yao, R.; Mu, M.; Yang, Q. Rolling bearing intelligent fault diagnosis towards variable speed and imbalanced samples using multiscale dynamic supervised contrast learning. Reliab. Eng. Syst. Saf. 2024, 243, 109805. [Google Scholar] [CrossRef]
- Guo, B.; Qiao, Z.; Zhang, N.; Wang, Y.; Wu, F.; Peng, Q. Attention-based ConvNeXt with a parallel multiscale dilated convolution residual module for fault diagnosis of rotating machinery. Expert Syst. Appl. 2024, 249, 123764. [Google Scholar] [CrossRef]
- Gong, B.; An, A.; Shi, Y.; Zhang, X. Fast fault detection method for photovoltaic arrays with adaptive deep multiscale feature enhancement. Appl. Energy 2024, 353, 122071. [Google Scholar] [CrossRef]
- Song, X.; Cong, Y.; Song, Y.; Chen, Y.; Liang, P. A bearing fault diagnosis model based on CNN with wide convolution kernels. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 4041–4056. [Google Scholar] [CrossRef]
- Shenfield, A.; Howarth, M. A novel deep learning model for the detection and identification of rolling element-bearing faults. Sensors 2020, 20, 5112. [Google Scholar] [CrossRef]
- Imambi, S.; Prakash, K.B.; Kanagachidambaresan, G. PyTorch; Springer: Berlin/Heidelberg, Germany, 2021; pp. 87–104. [Google Scholar]


| Class Label | Fault Diameters | Number of Samples | Fault Types |
|---|---|---|---|
| 0 | 0 | 400 | Normal |
| 1 | 0.007 | 400 | IF |
| 2 | 0.007 | 400 | BF |
| 3 | 0.007 | 400 | OF |
| 4 | 0.014 | 400 | IF |
| 5 | 0.014 | 400 | BF |
| 6 | 0.014 | 400 | OF |
| 7 | 0.021 | 400 | IF |
| 8 | 0.021 | 400 | BF |
| 9 | 0.021 | 400 | OF |
| Class Label | Bearing Code | Number of Samples | Fault Types |
|---|---|---|---|
| 0 | K003 | 400 | Normal |
| 1 | KA04 | 400 | OR |
| 2 | KA16 | 400 | OR |
| 3 | KI04 | 400 | IR |
| 4 | KI16 | 400 | IR |
| 5 | KI18 | 400 | IR |
| 6 | KA01 | 400 | OR |
| 7 | KA05 | 400 | OR |
| 8 | KI01 | 400 | IR |
| 9 | KI05 | 400 | IR |
| Model | (Train) | (Test) | (Train) | (Test) |
|---|---|---|---|---|
| MR-FuSN | ||||
| ResNet | ||||
| TDSAE | ||||
| WDCNN | ||||
| GRU-WDCNN |
| Model | SNR = −5 dB | SNR = 0 dB | SNR = 10 dB | SNR = −5 dB | SNR = 0 dB | SNR = 10 dB |
|---|---|---|---|---|---|---|
| () | () | () | () | () | () | |
| MR-FuSN | 99.33% | 99.97% | 100.00% | 98.45% | 99.85% | 99.98% |
| ±1.24% | ±0.12% | ±0.01% | ±1.18% | ±0.15% | ±0.02% | |
| ResNet | 49.49% | 66.75% | 99.10% | 48.12% | 62.34% | 97.89% |
| ±7.52% | ±5.25% | ±2.00% | ±6.33% | ±4.78% | ±1.45% | |
| TDSMAE | 50.36% | 68.77% | 99.47% | 52.11% | 65.23% | 98.56% |
| ±3.91% | ±1.67% | ±0.55% | ±4.02% | ±2.89% | ±0.67% | |
| WDCNN | 80.71% | 90.58% | 99.81% | 78.92% | 88.45% | 99.45% |
| ±3.42% | ±0.32% | ±0.27% | ±3.15% | ±1.12% | ±0.25% | |
| GRU- | 87.90% | 92.33% | 100.00% | 85.67% | 90.12% | 99.92% |
| WDCNN | ±1.62% | ±0.42% | ±0.02% | ±2.01% | ±0.98% | ±0.03% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, L.; Tang, S.; Wang, M.; Qiao, S.; Yu, S.; Liu, W.; Li, J. MR-FuSN: A Multi-Resolution Selective Fusion Approach for Bearing Fault Diagnosis. Sensors 2025, 25, 1134. https://doi.org/10.3390/s25041134
Sha L, Tang S, Wang M, Qiao S, Yu S, Liu W, Li J. MR-FuSN: A Multi-Resolution Selective Fusion Approach for Bearing Fault Diagnosis. Sensors. 2025; 25(4):1134. https://doi.org/10.3390/s25041134
Chicago/Turabian StyleSha, Lin, Shikai Tang, Min Wang, Sibo Qiao, Shihang Yu, Weixia Liu, and Jiaqi Li. 2025. "MR-FuSN: A Multi-Resolution Selective Fusion Approach for Bearing Fault Diagnosis" Sensors 25, no. 4: 1134. https://doi.org/10.3390/s25041134
APA StyleSha, L., Tang, S., Wang, M., Qiao, S., Yu, S., Liu, W., & Li, J. (2025). MR-FuSN: A Multi-Resolution Selective Fusion Approach for Bearing Fault Diagnosis. Sensors, 25(4), 1134. https://doi.org/10.3390/s25041134









