Wearable and Thermal Drift-Compensated Monitoring System Based on Fiber Bragg Grating Sensors for a 3D-Printed Foot Prosthesis
Abstract
1. Introduction
2. Materials and Methods
2.1. Working Principle of Fiber Brag Grating Sensors
2.2. Optoeletronic Unit: Redondo Optics Miniature MOFIS
- a broadband light source in the C-band 1550 nm window;
- four individual high-sensitive detection channels;
- a switching technology to acquire multiple fibers in sequential mode.
- Light Source. MOFISTM employs a Superluminescent Light Emitting Diode (SLED) for light emission. SLEDs are semiconductor devices emitting broadband light through electrical current injection, representing a hybrid technology between LEDs and laser diodes.
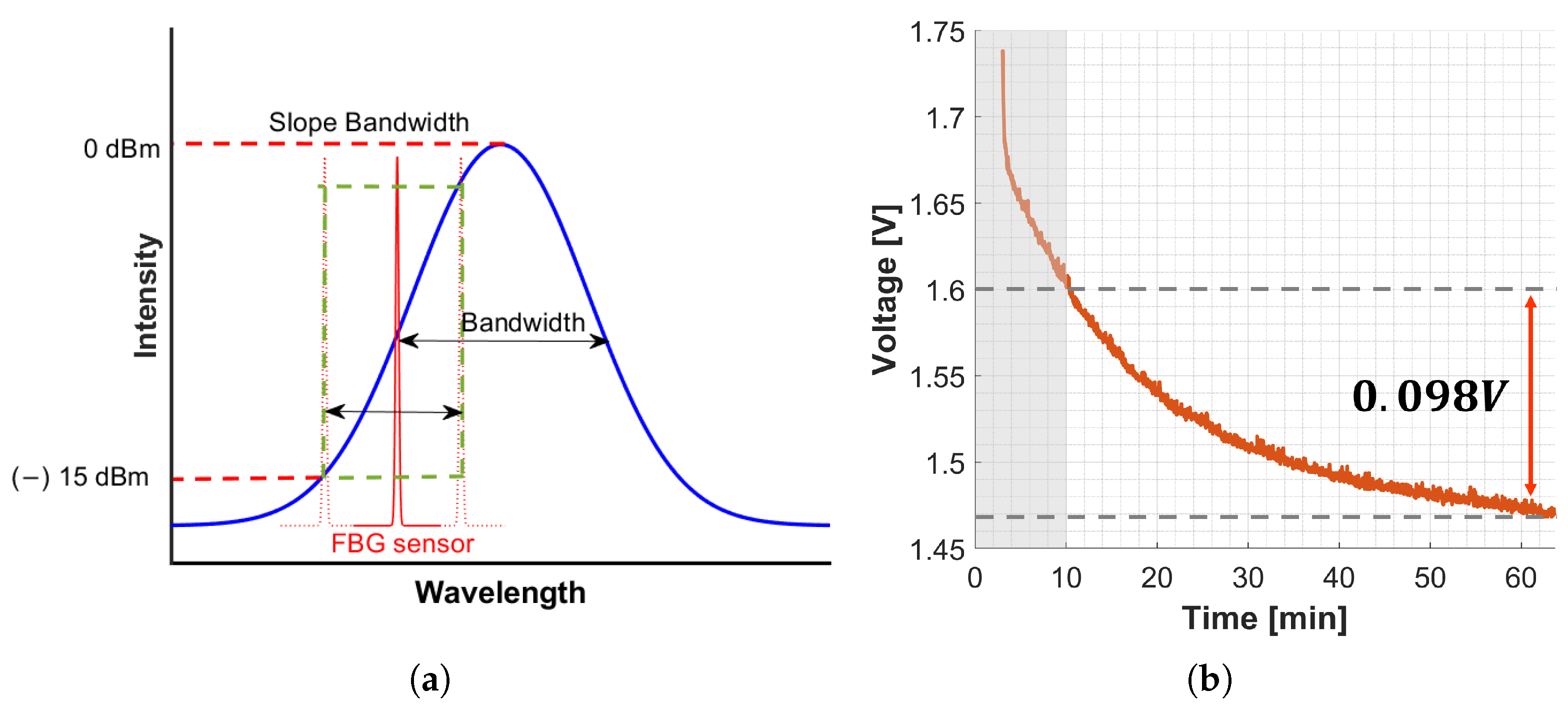
- Monitoring Mode. MOFISTM monitoring mode is based on Wavelength Division Multiplexing (WDM), a technology that multiplexes several optical carrier signals onto a single optical fiber using different wavelengths of laser light [29,30]. WDM enables the sharing of an optical fiber among many different signals simultaneously. The WDM operating principle for an array of FBGs works as follows: the SLED light is sent along the fiber and each FBG reflects a particular wavelength . Then, the reflected spectrum is analyzed via WDM Gaussian demodulators. The demodulators output a voltage value that depends on the wavelength returned. Figure 1a shows the working principle of the WDM demodulator integrated into the optoelectronic unit under study. The provided software implements a Gaussian model to fit the intensity to wavelength response of the WDM demodulator. The mathematical equation describing the model is provided in (4):where V is the measured voltage and is the Bragg wavelength corresponding to the measured voltage. The model is defined by the optical filter central wavelength and the optical filter standard deviation c, related to the full-width-half-maximum of the filter.
2.3. Compensation Algorithm
- is the informative contribution of the measured voltage. is the measured voltage share due to the wavelength shift caused by strain or temperature variation.
- is the voltage offset due to electronics, it is constant and measured before plugging in the fiber.
- is the measured voltage share caused by light source instability.
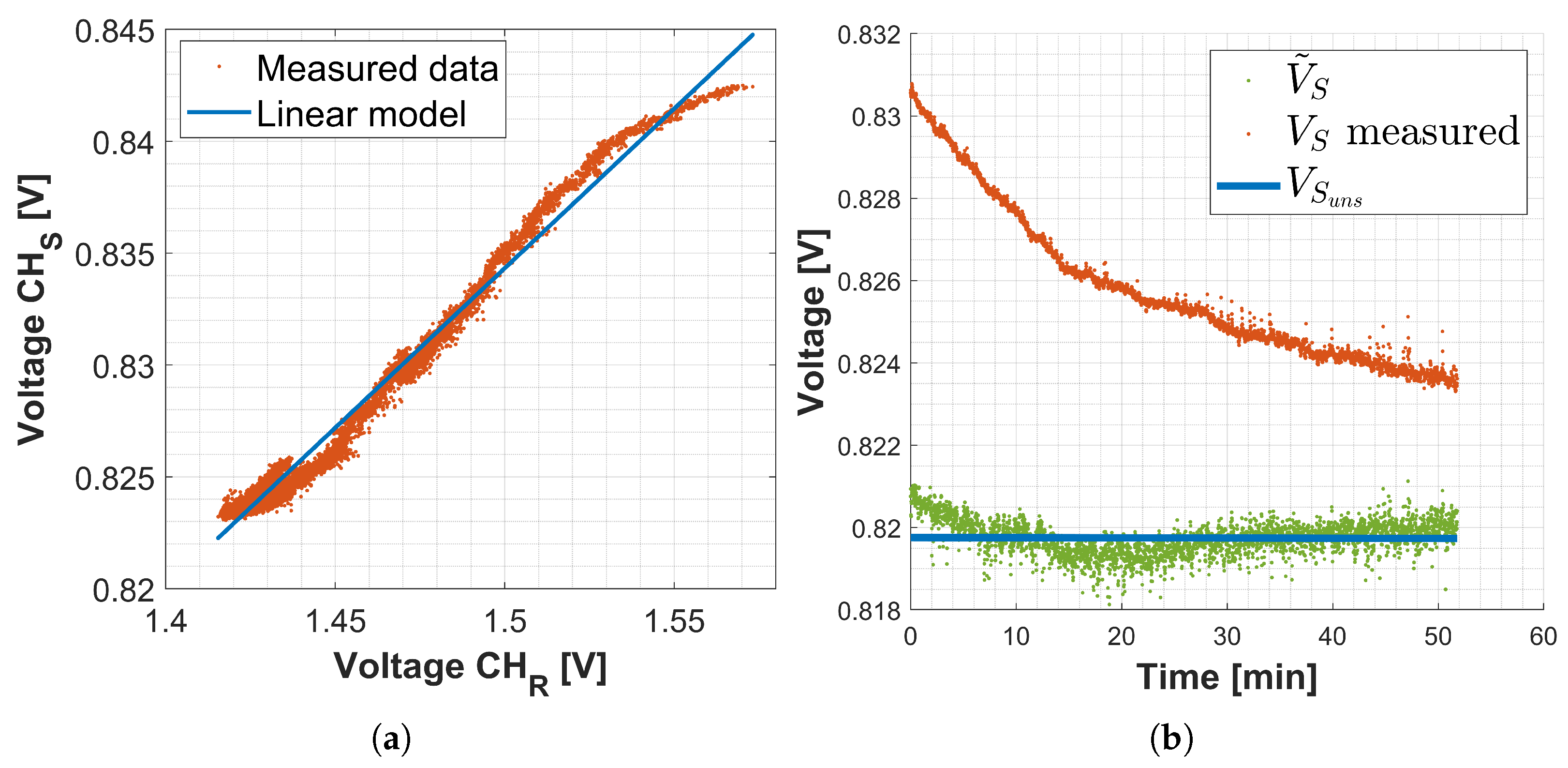
- Hp1: the drift voltage share in the detection channel adopted as the sensor is directly proportional to that of the detection channel adopted as a reference, as shown in (6a). Hp1 is a fundamental assumption for the proposed method. Its validity was experimentally verified by calculating the Pearson correlation coefficient on the signals acquired from the reference and sensing FBGs under resting conditions, Section 2.5.1. The Pearson coefficient was calculated with the standard formula reported in (6b):where is the covariance between and ; whereas and are the standard deviation of and , respectively.
- Hp2: there is no drift at the initial instant, so the voltage share due to drift is null at t = 0 for both detection channels:
2.4. Sensors Positioning Identification
2.5. Tests
2.5.1. Parameter Identification and Algorithm Validation
- was measured 10 min later the MOFIS was switched on.
- Optical fibers were plugged in after the measurement.
- The test started 15 min after the fiber was plugged in.
- No temperature variation or strain were applied to the FBGs.
- Tests were performed on different days to be consistent.
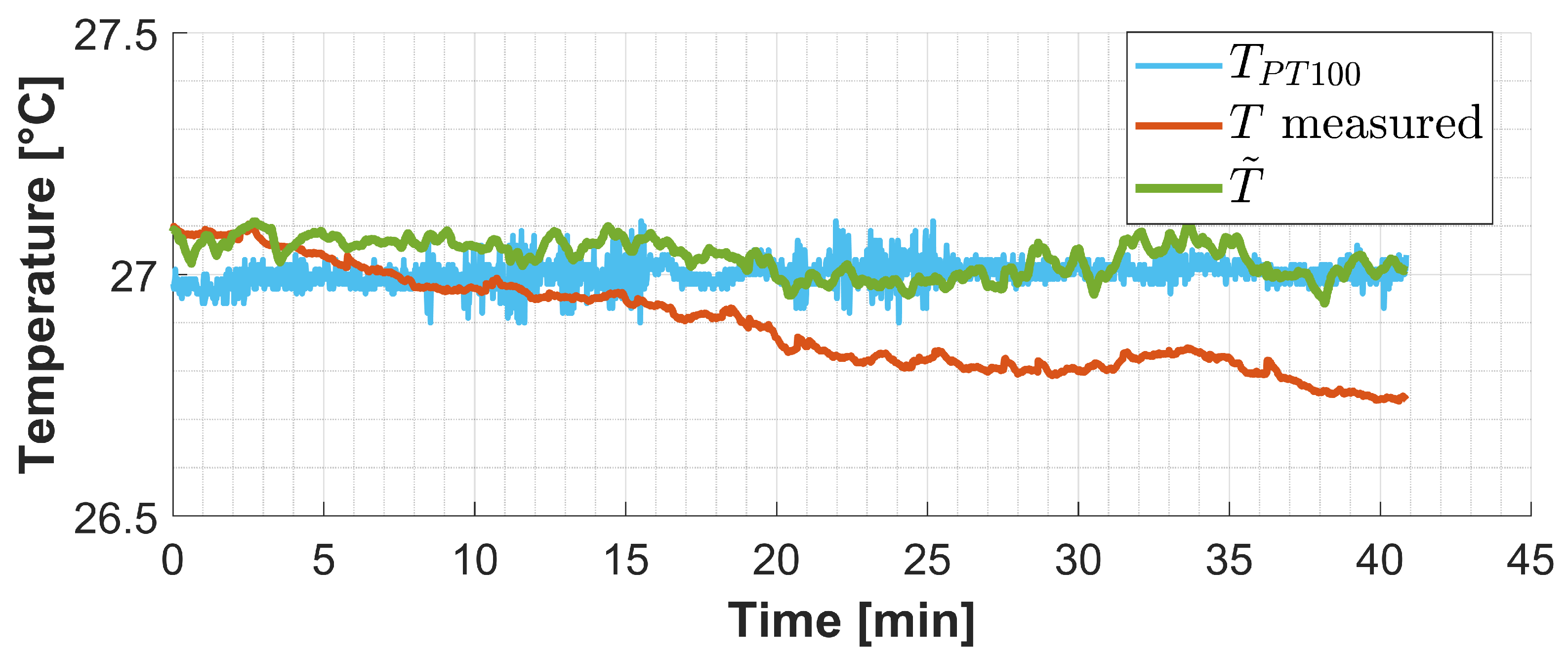
2.5.2. Temperature Test
- was measured 10 min after the MOFIS was turned on.
- Optical fibers were plugged in after measurement.
- The test started 15 min after the fiber was plugged in, and once the target temperature in the thermal chamber has been reached.
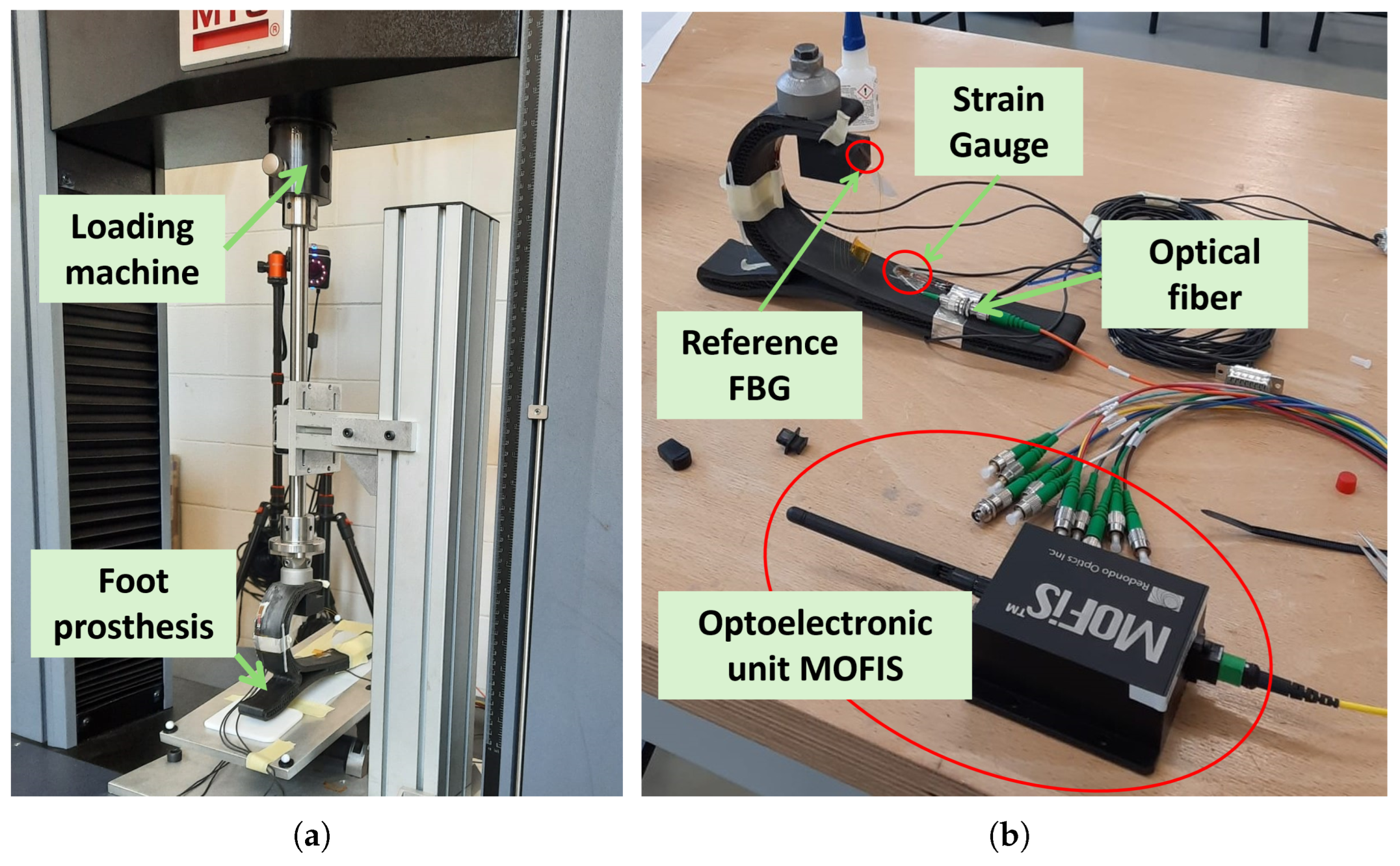
2.5.3. Mechanical Tests
- the foot prosthesis;
- the FBG-based monitoring system composed of the fiber with the sensing and the reference FBGs, the optoelectronic unit MOFISTM, a processing unit;
- the strain gauges, the signal amplifier SCOUT55, a processing unit;
- the MTS compression machine provided by a platform to allow prosthesis inclination during the tests.
3. Experimental Results and Discussion
3.1. Compensation Variable Identification and Hypothesis Verification
3.2. Algorithm Validation
Temperature Test
- Root Mean Square Error (RMSE);
- Mean Absolute Error (MAE);
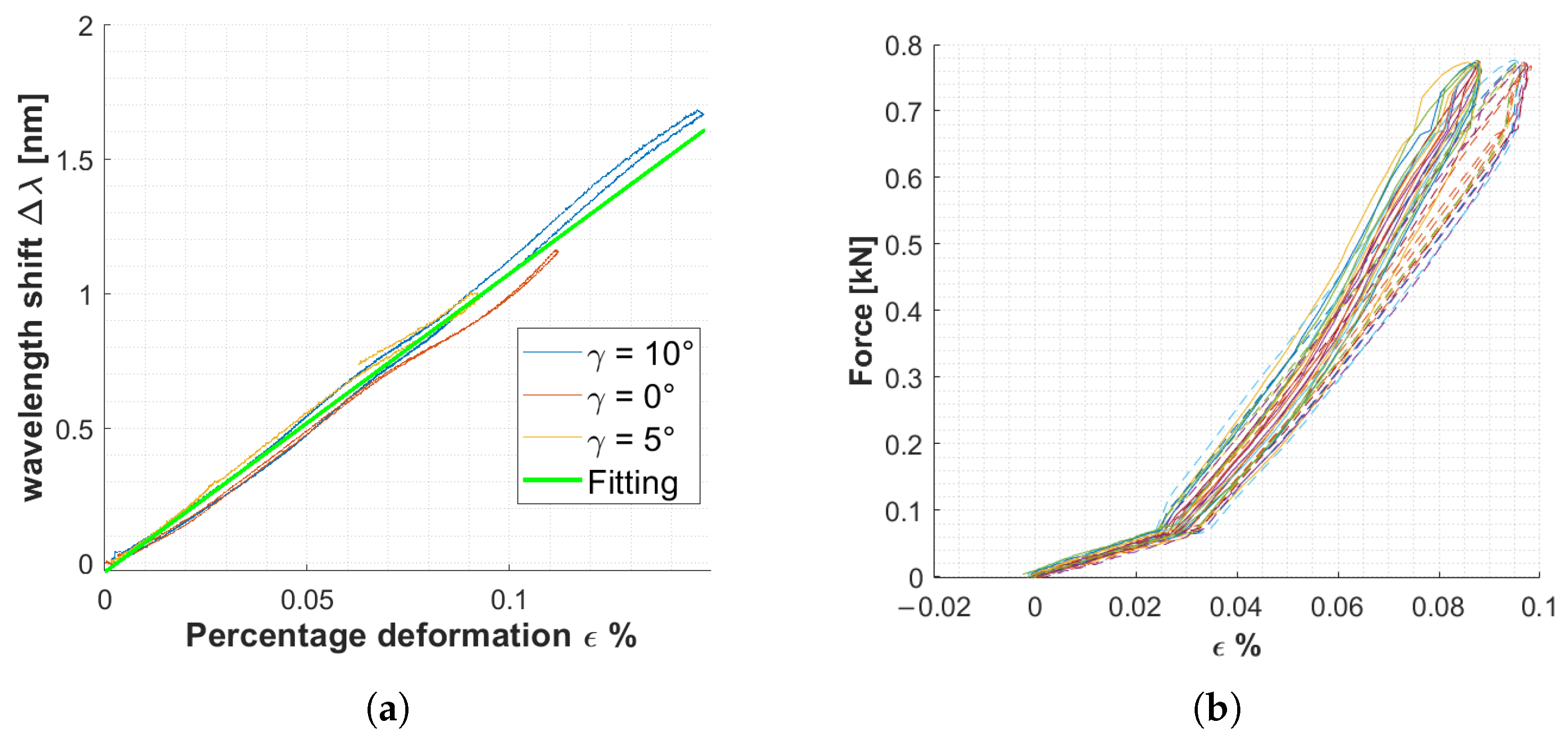
3.3. Mechanical Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McDonald, C.L.; Westcott-McCoy, S.; Weaver, M.R.; Haagsma, J.; Kartin, D. Global prevalence of traumatic non-fatal limb amputation. Prosthet. Orthot. Int. 2021, 45, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Yuan, B.; Hu, D.; Gu, S.; Xiao, S.; Song, F. The global burden of traumatic amputation in 204 countries and territories. Front. Public Health 2023, 11, 1258853. [Google Scholar] [CrossRef] [PubMed]
- Chadwell, A.; Diment, L.; Micó-Amigo, M.; Morgado Ramírez, D.Z.; Dickinson, A.; Granat, M.; Kenney, L.; Kheng, S.; Sobuh, M.; Ssekitoleko, R.; et al. Technology for monitoring everyday prosthesis use: A systematic review. J. Neuroeng. Rehabil. 2020, 17, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Hafner, B.J.; Sanders, J.E. Considerations for development of sensing and monitoring tools to facilitate treatment and care of persons with lower limb loss. J. Rehabil. Res. Dev. 2014, 51, 1. [Google Scholar] [CrossRef]
- Moreno-Gomez, A.; Perez-Ramirez, C.A.; Dominguez-Gonzalez, A.; Valtierra-Rodriguez, M.; Chavez-Alegria, O.; Amezquita-Sanchez, J.P. Sensors used in structural health monitoring. Arch. Comput. Methods Eng. 2018, 25, 901–918. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg Grating Sensors toward Structural Health Monitoring in Composite Materials: Challenges and Solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef]
- Glisic, B.; Inaudi, D. Fibre Optic Methods for Structural Health Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Paloschi, D.; Polimadei, A.; Korganbayev, S.; Orsetti, V.; Mazzotta, C.; Cigada, A.; Caponero, M.A.; Saccomandi, P. Three-Dimensional-Printed Sensing Samples Embedding Fiber Bragg Gratings: Metrological Evaluation of Different Sample Materials and Fiber Coatings. IEEE Trans. Instrum. Meas. 2023, 72, 9506210. [Google Scholar] [CrossRef]
- Rohan, R.; Venkadeshwaran, K.; Ranjan, P. Recent advancements of fiber Bragg grating sensors in biomedical application: A review. J. Opt. 2024, 53, 282–293. [Google Scholar] [CrossRef]
- Al-Fakih, E.A.; Abu Osman, N.A.; Mahamd Adikan, F.R.; Eshraghi, A.; Jahanshahi, P. Development and Validation of Fiber Bragg Grating Sensing Pad for Interface Pressure Measurements Within Prosthetic Sockets. IEEE Sens. J. 2016, 16, 965–974. [Google Scholar] [CrossRef]
- Al-Fakih, E.A.; Osman, N.A.A.; Eshraghi, A.; Adikan, F.R.M. The Capability of Fiber Bragg Grating Sensors to Measure Amputees’ Trans-Tibial Stump/Socket Interface Pressures. Sensors 2013, 13, 10348–10357. [Google Scholar] [CrossRef] [PubMed]
- Galvão, J.R.; Zamarreño, C.R.; Martelli, C.; Cardozo Da Silva, J.C.; Arregui, F.J.; Matías, I.R. Mapping in Carbon-Fiber Prosthesis Using Optical Fiber Sensors. IEEE Sens. J. 2017, 17, 3–4. [Google Scholar] [CrossRef]
- Butt, A.M.; Qureshi, K.K. Smart Lower Limb Prostheses with a Fiber Optic Sensing Sole: A Multicomponent Design Approach. Sens. Mater. 2019, 31, 2965–2979. [Google Scholar] [CrossRef]
- Lavarda, M.D.; Gomes, D.F.; Paes, T.; de Sousa, R.O.; Dreyer, U.J.; da Silva, J.C.C.; Martelli, C. Smart Foot Based on FBG Integrated in Composite Material and Adaptive Fuzzy Controller. IEEE Sens. Lett. 2023, 7, 5001004. [Google Scholar] [CrossRef]
- Pant, S.; Umesh, S.; Asokan, S. Knee Angle Measurement Device Using Fiber Bragg Grating Sensor. IEEE Sens. J. 2018, 18, 10034–10040. [Google Scholar] [CrossRef]
- R. Diaz, C.A.; Leal-Junior, A.G.; M. Avellar, L.; C. Antunes, P.F.; Pontes, M.J.; Marques, C.A.; Frizera, A.; N. Ribeiro, M.R. Perrogator: A Portable Energy-Efficient Interrogator for Dynamic Monitoring of Wavelength-Based Sensors in Wearable Applications. Sensors 2019, 19, 2962. [Google Scholar] [CrossRef]
- Ogawa, K.; Koyama, S.; Haseda, Y.; Fujita, K.; Ishizawa, H.; Fujimoto, K. Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter. Sensors 2019, 19, 3222. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, E.A.; Esterkin, Y.; Kempen, C.; Sun, Z. Multi-channel monolithic integrated optic fiber Bragg grating sensor interrogator. Photonic Sens. 2011, 1, 281–288. [Google Scholar] [CrossRef][Green Version]
- Friedemann, M.; Voigt, S.; Werner, M.L.; Hecker, R.; Mehner, J. Drift analysis and stabilization of a Fiber Bragg Grating interrogation device. In Proceedings of the 2020 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 8–9 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Sheng, W.; Dang, H.; Peng, G.D. Hysteresis and temperature drift compensation for FBG demodulation by utilizing adaptive weight least square support vector regression. Opt. Express 2021, 29, 40547–40558. [Google Scholar] [CrossRef]
- Lin, H.; Sheng, W. Research on Temperature Drift Error Correction of Tunable Filter Based on CNN-LSTM. In Proceedings of the 2023 4th International Conference on Advanced Electrical and Energy Systems (AEES), Shanghai, China, 1–3 December 2023; pp. 87–91. [Google Scholar] [CrossRef]
- Yang, Z.; Yao, G.; Li, Y. A novel wavelength calibration method for Fiber Bragg Grating sensor system. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 83–85. [Google Scholar] [CrossRef]
- Petermann, I. Fibre Bragg Gratings: Characterization, Realization and Simulation. Ph.D. Thesis, KTH, Stockholm, Sweden, 2007. [Google Scholar]
- Fernández-Ruiz, M.R.; Carballar, A. Fiber Bragg Grating-Based Optical Signal Processing: Review and Survey. Appl. Sci. 2021, 11, 8189. [Google Scholar] [CrossRef]
- Chen, J.; Liu, B.; Zhang, H. Review of fiber Bragg grating sensor technology. Front. Optoelectron. 2011, 4, 204. [Google Scholar] [CrossRef]
- Hill, K.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Korganbayev, S.; Orrico, A.; Bianchi, L.; Paloschi, D.; Wolf, A.; Dostovalov, A.; Saccomandi, P. PID Controlling Approach Based on FBG Array Measurements for Laser Ablation of Pancreatic Tissues. IEEE Trans. Instrum. Meas. 2021, 70, 7006409. [Google Scholar] [CrossRef]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355. [Google Scholar] [CrossRef]
- Ozcelik, D.; Parks, J.W.; Wall, T.A.; Stott, M.A.; Parks, H.C.J.W.; Hawkins, A.R.; Schmidt, H. Optofluidic wavelength division multiplexing for single-virus detection. Proc. Natl. Acad. Sci. USA 2015, 112, 12933–12937. [Google Scholar] [CrossRef]
- Chae, C.J.; Oh, N.H. WDM/TDM PON system employing a wavelength-selective filter and a continuous-wave shared light source. IEEE Photonics Technol. Lett. 1998, 10, 1325–1327. [Google Scholar] [CrossRef]
- Manual-MOFIS-M400-100X; Redondo Optics: Redondo Beach, CA, USA, 2019.
- Castro-Caicedo, A.; Nieto-Callejas, M.; Torres, P.; Lain, R.; Suarez-Burgoa, L. Manufacturing and reliability of a fiber Bragg grating strain sensor designed for uniaxial compression test of rocks. Dyna 2019, 86, 234–242. [Google Scholar] [CrossRef]
- Martulli, L.M.; Luppino, G.; Rollo, G.; Kostovic, M.; Romanò, J.; Garavaglia, L.; Sorrentino, A.; Pittaccio, S.; Saccomandi, P.; Tarabini, M.; et al. Finite element simulation of the full stance-phase in the design process of a 3d-printed composite foot prosthesis. In Proceedings of the 11th International Conference on Composites Testing and Model Identification, Girona, Spain, 31 May–2 June 2023. [Google Scholar]
- ISO TS 16955:2016; BSI Standards Publication Prosthetics—Quantification of Physical Parameters of Ankle-Foot Devices and Foot Units. International Organization for Standardization: Geneva, Switzerland, 2016.
- ISO 22675:2016; BSI Standards Publication Prosthetics—Testing of Ankle-Foot Devices and Foot Units—Requirements and Test Methods. International Organization for Standardization: Geneva, Switzerland, 2016.
- Arya, V.; Sherrer, D.; Wang, A.; Claus, R.; Jones, M. Application of thin-film optical filters to the temperature compensation of optical fiber grating-based devices. IEEE Trans. Instrum. Meas. 1997, 46, 1173–1177. [Google Scholar] [CrossRef]
- Todd, M.D.; Johnson, G.A.; Althouse, B.L. A novel Bragg grating sensor interrogation system utilizing a scanning filter, a Mach-Zehnder interferometer and a 3 × 3 coupler. Meas. Sci. Technol. 2001, 12, 771. [Google Scholar] [CrossRef]
- Chehura, E.; Ye, C.C.; Tatam, R.P. In-line laser Doppler velocimeter using fibre-optic Bragg grating interferometric filters. Meas. Sci. Technol. 2003, 14, 724. [Google Scholar] [CrossRef]
- Li, Y.; Lu, B.; Ren, L.; Chen, H.; Qiu, Y.; Mao, B.; Zhou, P.; Zhao, C.; Dong, X. A highly precise FBG sensor interrogation system with wavemeter calibration. Opt. Fiber Technol. 2019, 48, 207–212. [Google Scholar] [CrossRef]
- Alvarez-Botero, G.; Baron, F.E.; Cano, C.C.; Sosa, O.; Varon, M. Optical sensing using fiber bragg gratings: Fundamentals and applications. IEEE Instrum. Meas. Mag. 2017, 20, 33–38. [Google Scholar] [CrossRef]
- Lin, Y.B.; Chang, K.C.; Chern, J.C.; Wang, L. Packaging methods of fiber-Bragg grating sensors in civil structure applications. IEEE Sens. J. 2005, 5, 419–424. [Google Scholar] [CrossRef]
- Cheng, C.C.; Lo, Y.L.; Li, W.Y.; Kuo, C.T.; Cheng, H.C. Estimations of fiber Bragg grating parameters and strain gauge factor using optical spectrum and strain distribution information. Appl. Opt. 2007, 46, 4555–4562. [Google Scholar] [CrossRef]
- González-Gallego, M.; Terroba Ramírez, F.; Martínez-Vicente, J.L.; González del Val, M.; López-Cela, J.J.; Frövel, M. Fiber Bragg Gratings Sensor Strain–Optic Behavior with Different Polymeric Coatings Subjected to Transverse Strain. Polymers 2024, 16, 1223. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hsieh, C.; Lin, C. Strain measurement for composite tubes using embedded, fiber Bragg grating sensor. Sens. Actuators Phys. 2011, 167, 63–69. [Google Scholar] [CrossRef]



| Monitoring Mode | WDM Multiplexing |
| Sensing Channels | Four FBG transducers on a single fiber cable network |
| Wavelength Range | 60 nm @ 1550 nm C-Band |
| Sensor Dynamic Range | 2000 per each FBG sensor |
| Sensor Accuracy | ≤0.1 |
| Sampling Rate | ≤250 Hz to 20 kHz |
| Data Communication | Wireless (UDP protocol) |
| Power Consumption | ≤1250 mW @ 3.7 Vdc (Max.) |
| Power Supply | Li-Battery 3.7 V @ 6 W/h—Rechargeable |
| Weight | <250 g |
| FBG1 | FBG2 | |
|---|---|---|
| Wavelength () | 1529 nm | nm |
| Bandwidth | nm | nm |
| SLSR | dB | 21 dB |
| Reflectivity | 51.35% | 49.88% |
| FBG length | 5 mm | 5 mm |
| Fiber type | Polymide A2 | Polymide A2 |
| Recoating | Polymide | Polymide |
| Tilt Angle | Load | Speed [mm/s] |
|---|---|---|
| 0 | 1100 | 5 |
| 5 | 660 | 20 |
| 10 | 660 | 36 |
| RMSE [°C] | MAE [°C] | |
|---|---|---|
| 0.06 | 0.05 | |
| T uncompensated | 0.15 | 0.13 |
| Improvement | 50% | 60% |
| Metric | MOFISTM Compensation Algorithm | Literature |
|---|---|---|
| Error % on full scale | 0.18% | 0.5% [37] |
| MAE | 1.9 pm | 1.81 pm [21] |
| Absolute error | 0.03 °C | 0.05 °C [22] |
| RMSE | MAE | |
|---|---|---|
| 0.0093 | 0.0058 | |
| 0.0071 | 0.0066 | |
| 0.0080 | 0.0055 | |
| Mean values | 0.0081 | 0.0059 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Chicca, S.; Rollo, G.; Sorrentino, A.; Gruppioni, E.; Tarabini, M.; Saccomandi, P. Wearable and Thermal Drift-Compensated Monitoring System Based on Fiber Bragg Grating Sensors for a 3D-Printed Foot Prosthesis. Sensors 2025, 25, 885. https://doi.org/10.3390/s25030885
Del Chicca S, Rollo G, Sorrentino A, Gruppioni E, Tarabini M, Saccomandi P. Wearable and Thermal Drift-Compensated Monitoring System Based on Fiber Bragg Grating Sensors for a 3D-Printed Foot Prosthesis. Sensors. 2025; 25(3):885. https://doi.org/10.3390/s25030885
Chicago/Turabian StyleDel Chicca, Sara, Gennaro Rollo, Andrea Sorrentino, Emanuele Gruppioni, Marco Tarabini, and Paola Saccomandi. 2025. "Wearable and Thermal Drift-Compensated Monitoring System Based on Fiber Bragg Grating Sensors for a 3D-Printed Foot Prosthesis" Sensors 25, no. 3: 885. https://doi.org/10.3390/s25030885
APA StyleDel Chicca, S., Rollo, G., Sorrentino, A., Gruppioni, E., Tarabini, M., & Saccomandi, P. (2025). Wearable and Thermal Drift-Compensated Monitoring System Based on Fiber Bragg Grating Sensors for a 3D-Printed Foot Prosthesis. Sensors, 25(3), 885. https://doi.org/10.3390/s25030885









