4D Pointwise Terrestrial Laser Scanning Calibration: Radiometric Calibration of Point Clouds
Highlights
- A novel framework for the pointwise radiometric calibration of terrestrial laser scanning (TLS) is presented, which is a combination of the LiDAR range equation, texture-dependent LiDAR cross-section determination, and a neural network technique.
- This method significantly enhances the radiometric resolution of TLS on color targets, with accuracy improvements of 31–49% across different color patches and precision improvements of approximately 97% within the same color patch for four TLS devices.
- TLS intensity attributes can be identified as a standardized fourth dimension in addition to the 3D spatial point clouds for more reliable reflectivity-based analysis.
- This framework demonstrates the potential path towards more robust 4D TLS calibration, where standard radiometric values from various target geometries (target materials, roughness, albedo, and edgy and tilted surfaces) are strictly required.
Abstract
1. Introduction
1.1. Problem Background
1.2. Significance and Purposes
2. Related Works
3. TLS Background
3.1. TLS Deliverables
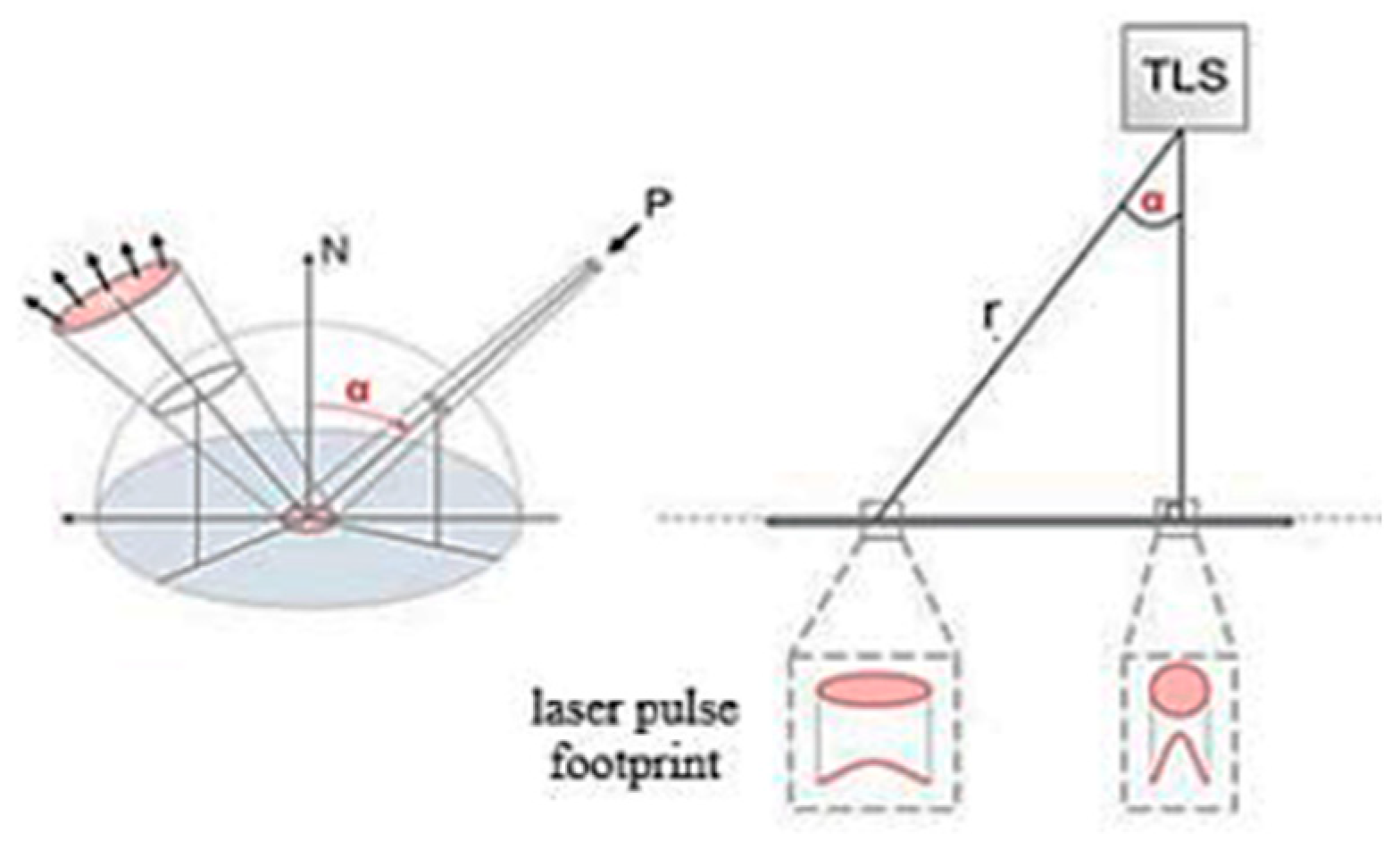
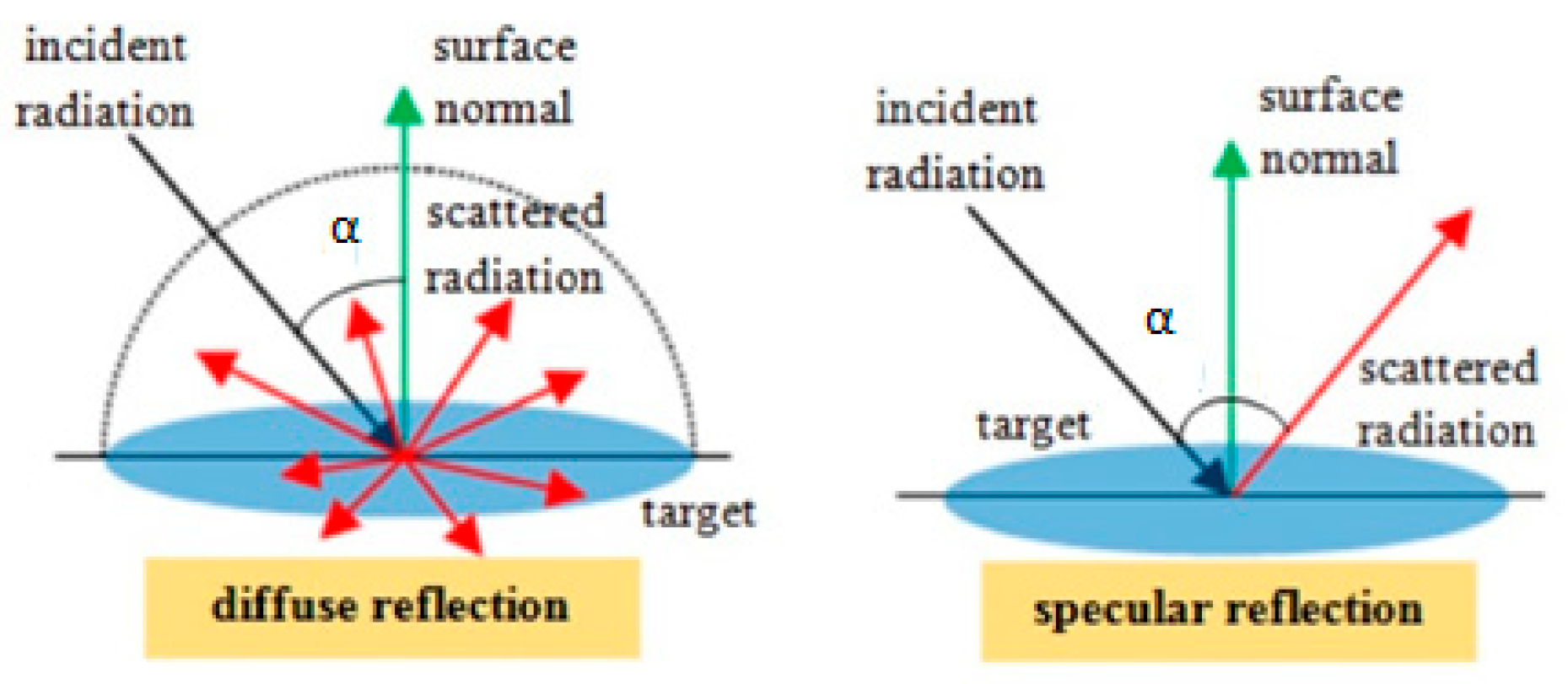
3.2. Object- and Surface-Related Issues
4. Methods
- The parameters, such as range, incidence angle, and color-dependent reflectivity obtained from the LiDAR range equation, are integrated into a feature matrix, and the output variable is determined as the intensity values.
- The dataset is randomly divided into training (80%) and testing (20%) subsets to enable the independent evaluation of neural network performance (i.e., weightings on spatial parameters for a single point observation).
- A feed-forward neural network with two hidden layers (each containing 10 neurons) is trained using the Levenberg–Marquardt (trainlm) optimization algorithm. The hidden layers use the hyperbolic tangent sigmoid (tansig) activation function, while the output layer employs a linear (purelin) function suitable for regression. As an example, training is performed with a learning rate of , a maximum of epochs, and an early stopping criterion based on validation error. Finally, the objective function minimizes the mean squared error between predicted intensity and color-dependent intensity using the LiDAR range equation (i.e., those were formerly validated through the intrinsic reflectance coefficient).
- During the validation process, the point reflectivity (i.e., intensity) from a presumed color patch is compared against the reference reflectivity (i.e., intensity derived from neutral colors) within each dataset. This comparison provides a quantitative assessment of the improvements achieved by both the data-driven method and the physical, laser-based approach (Section 7).
5. Data Experiment
5.1. Laser Study
5.2. Data Collection Steps
6. Results
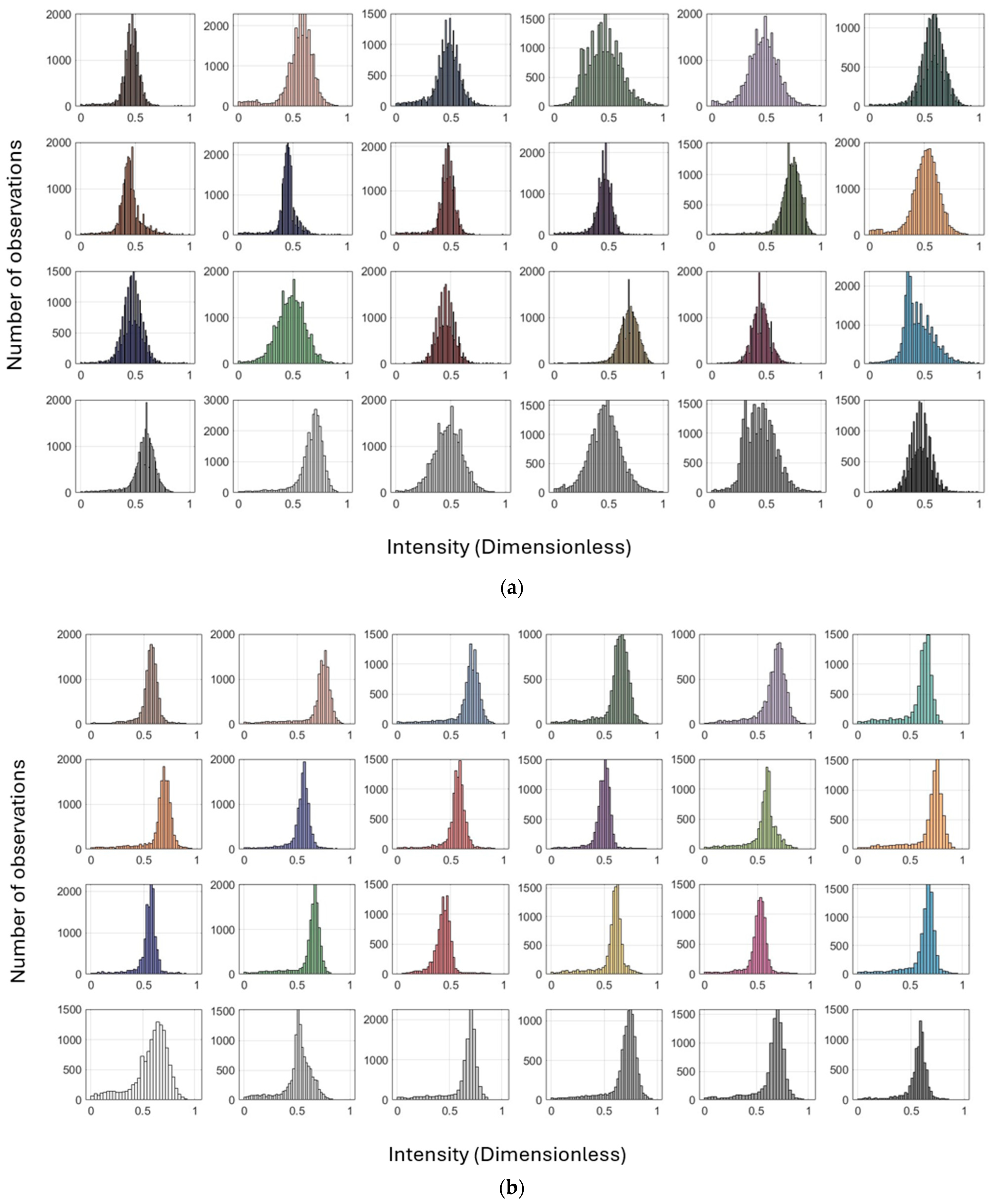
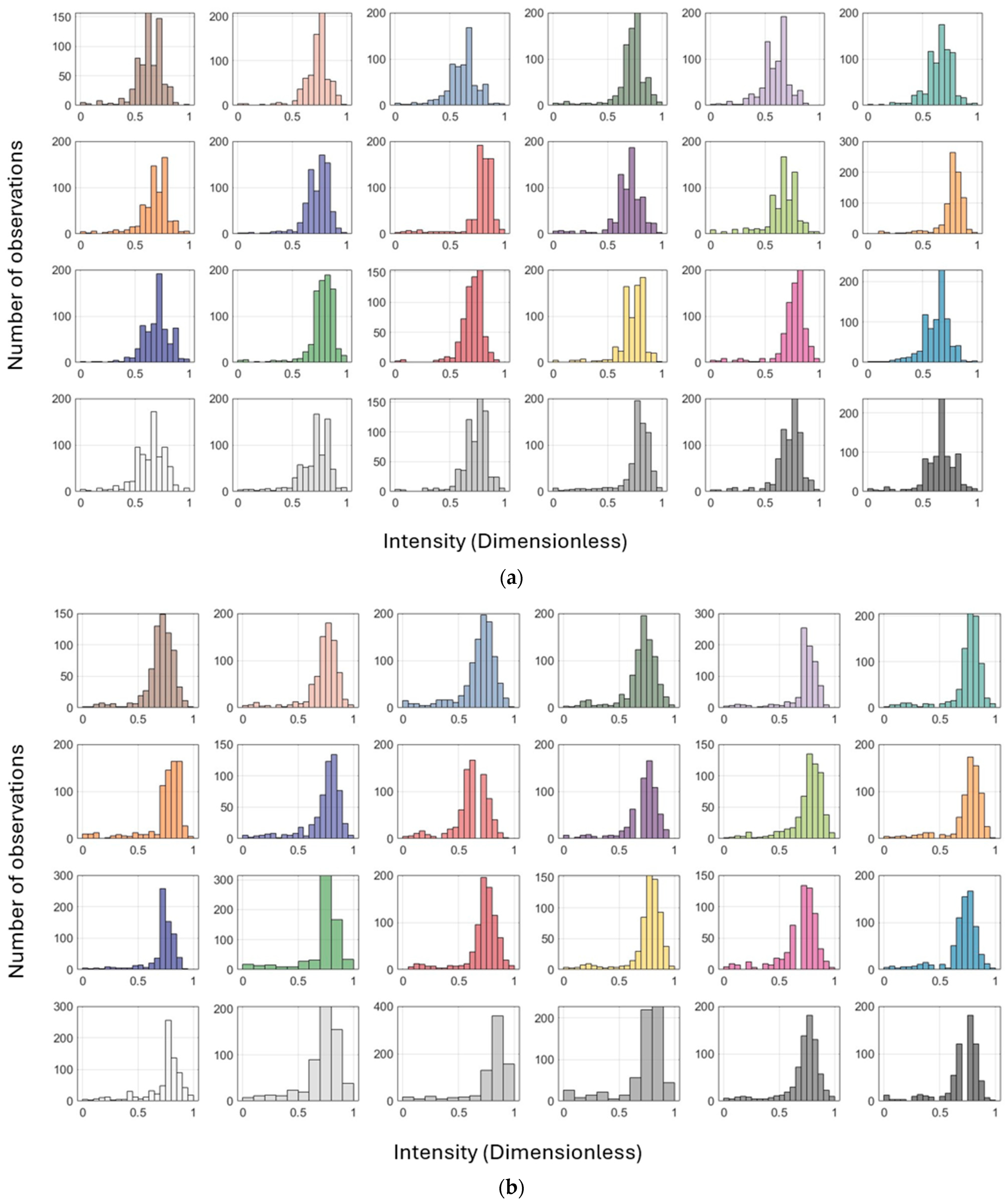
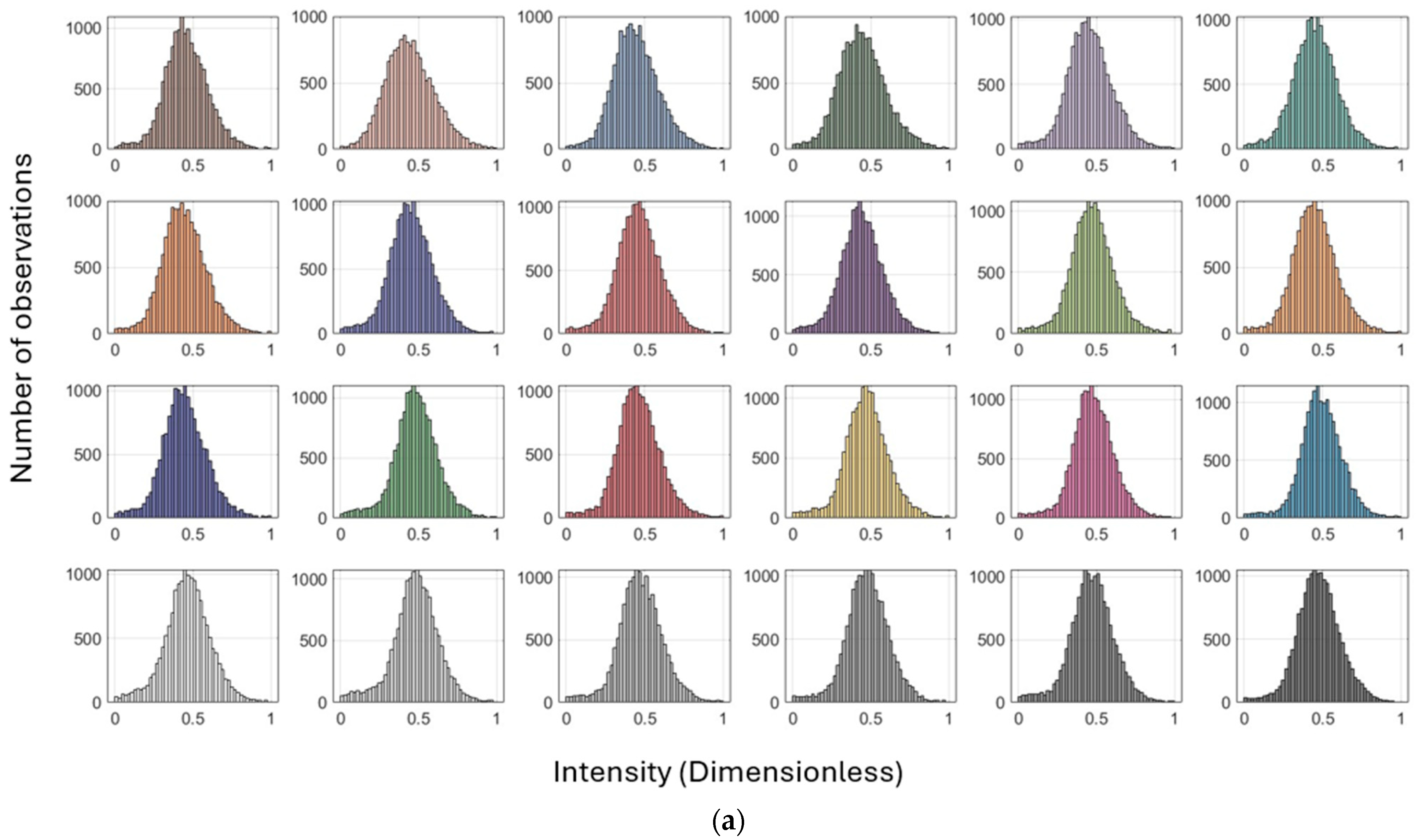
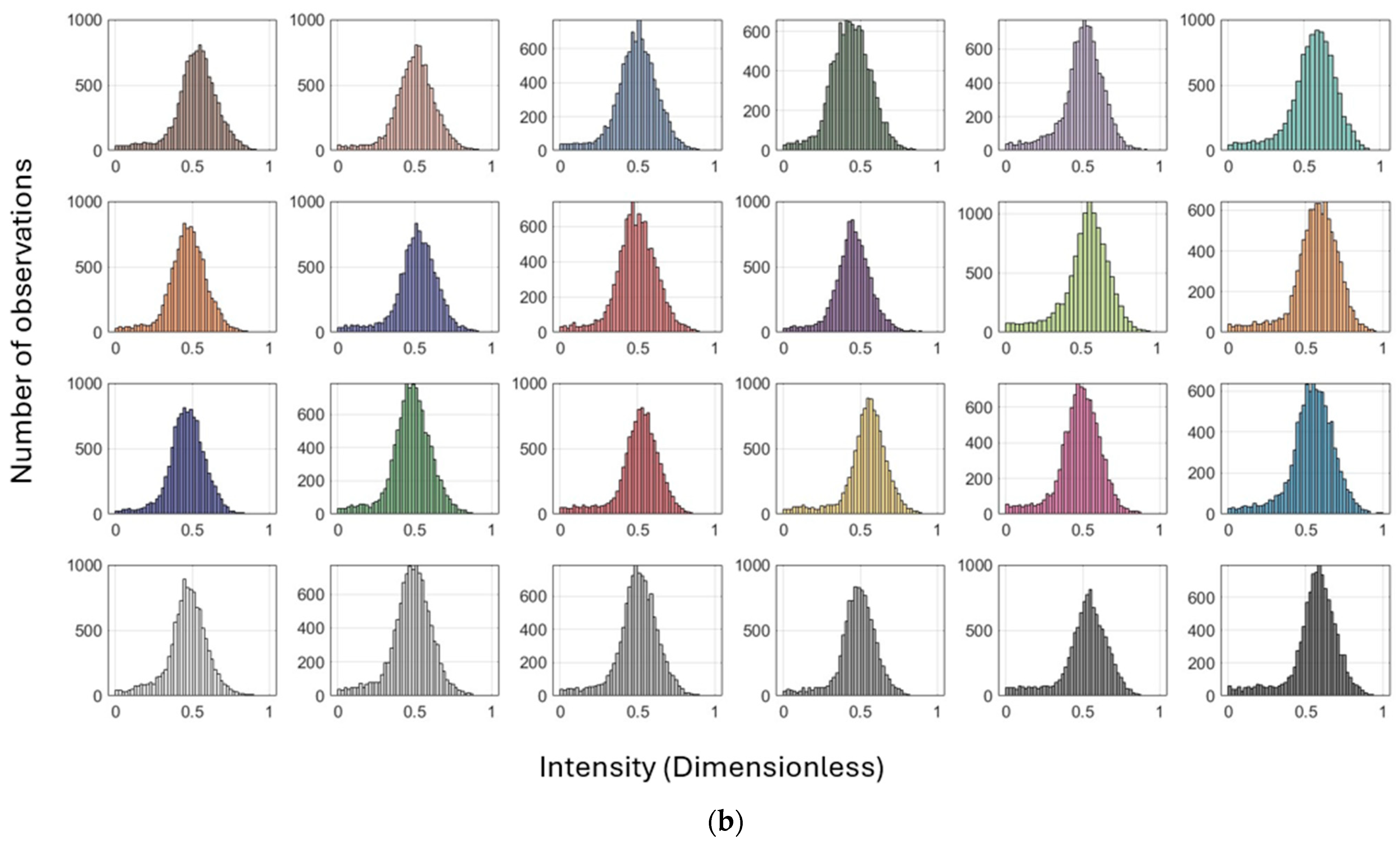
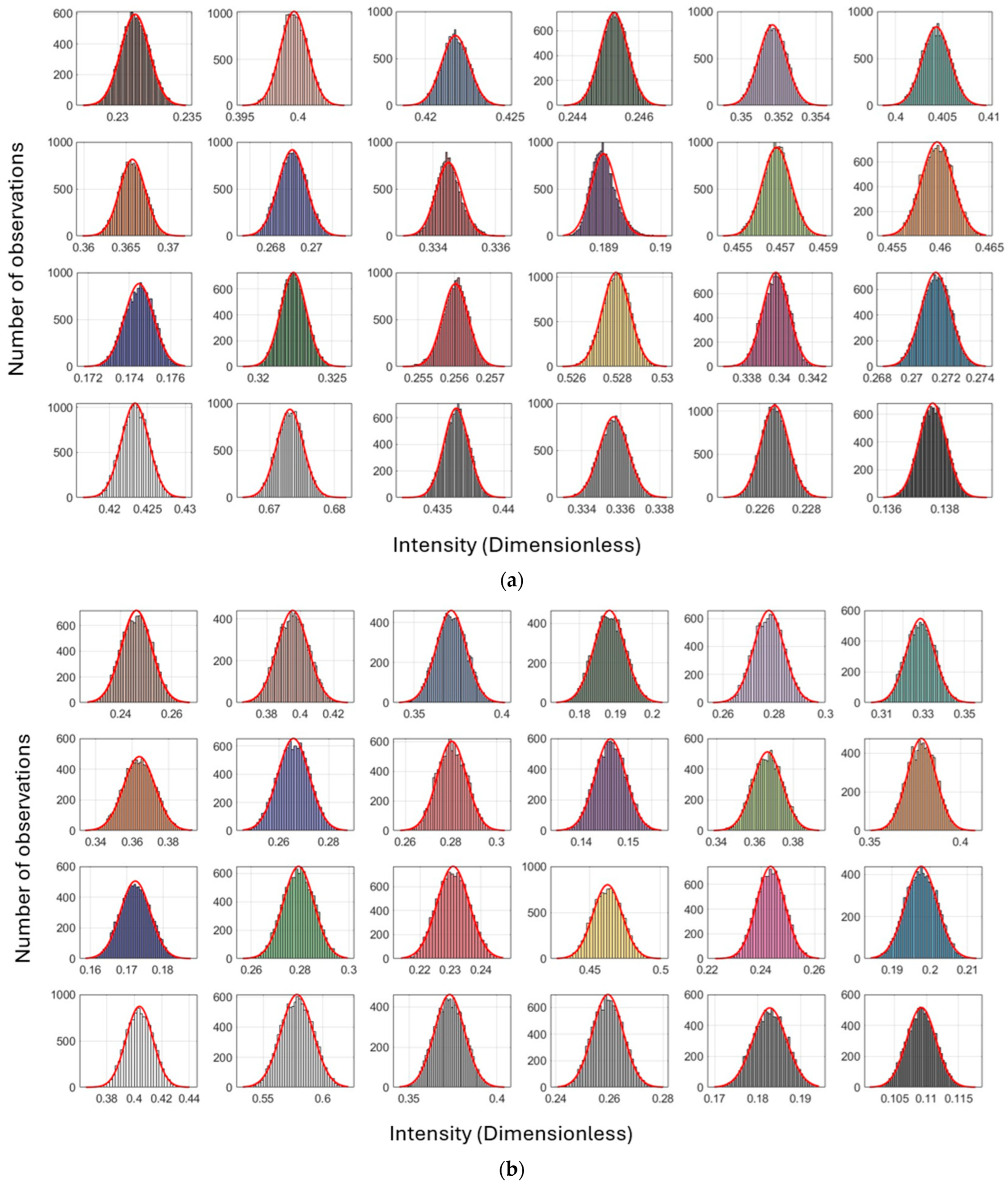
6.1. Pre-Processing Stages
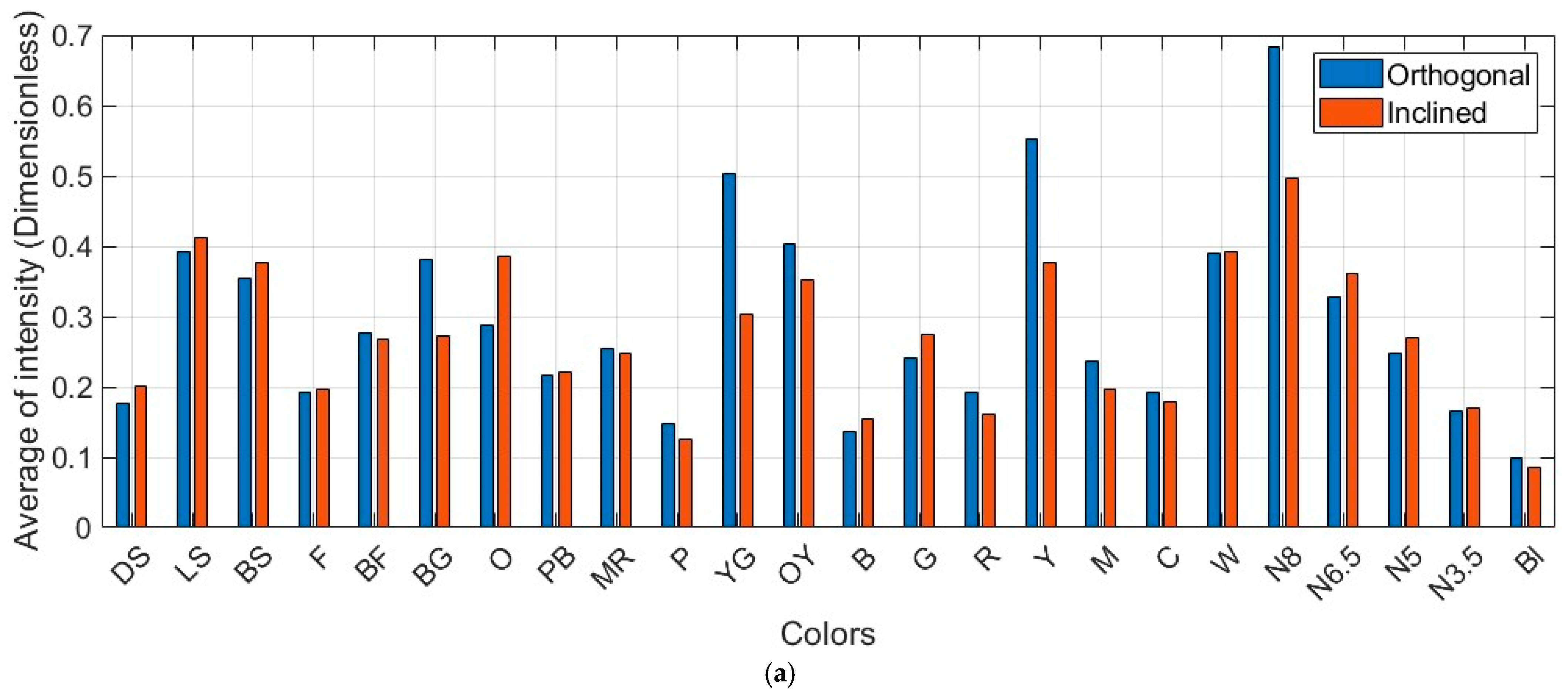
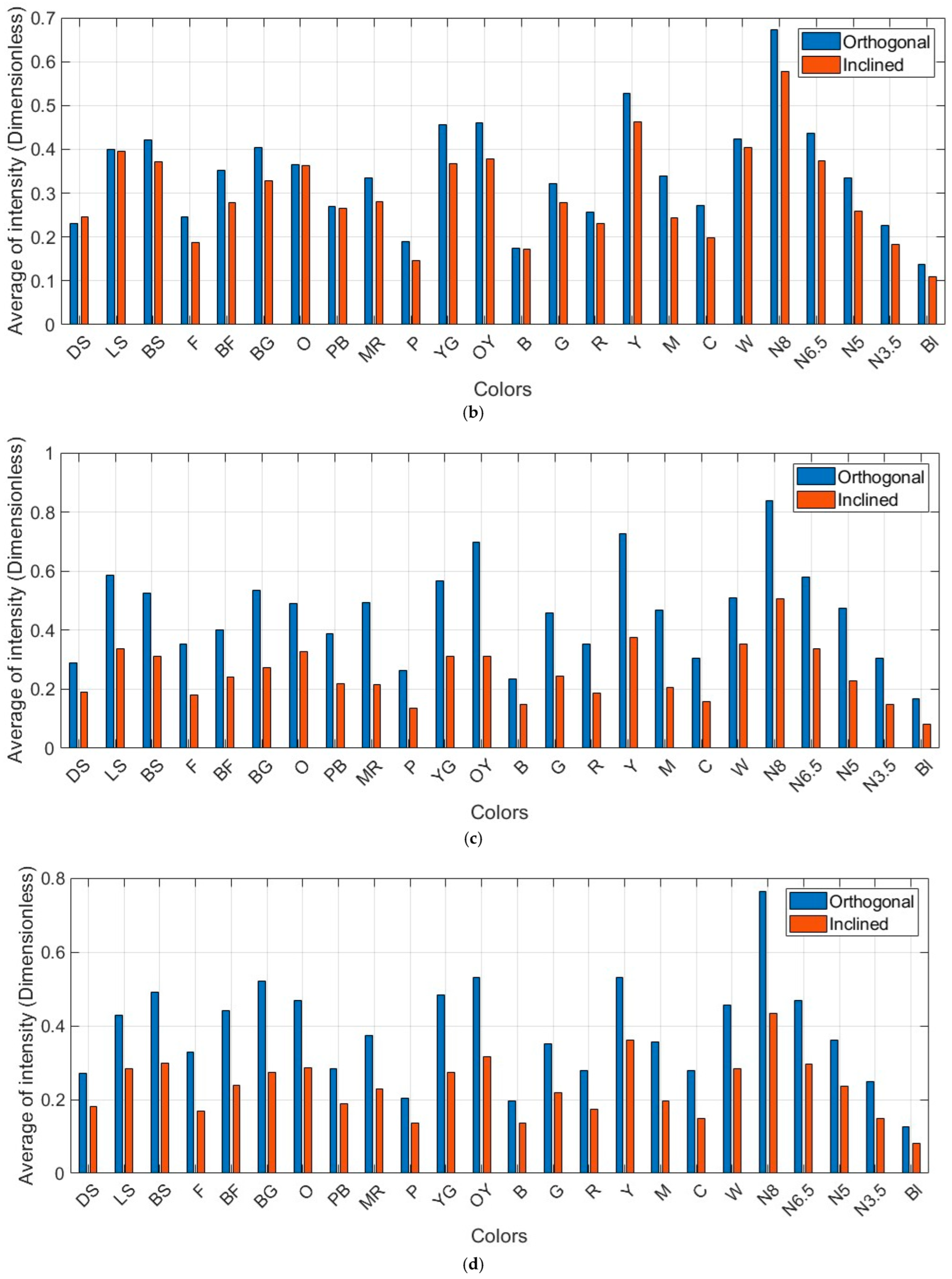
6.1.1. Radiometric Comparison: Intensity vs. RGB Across Scanners
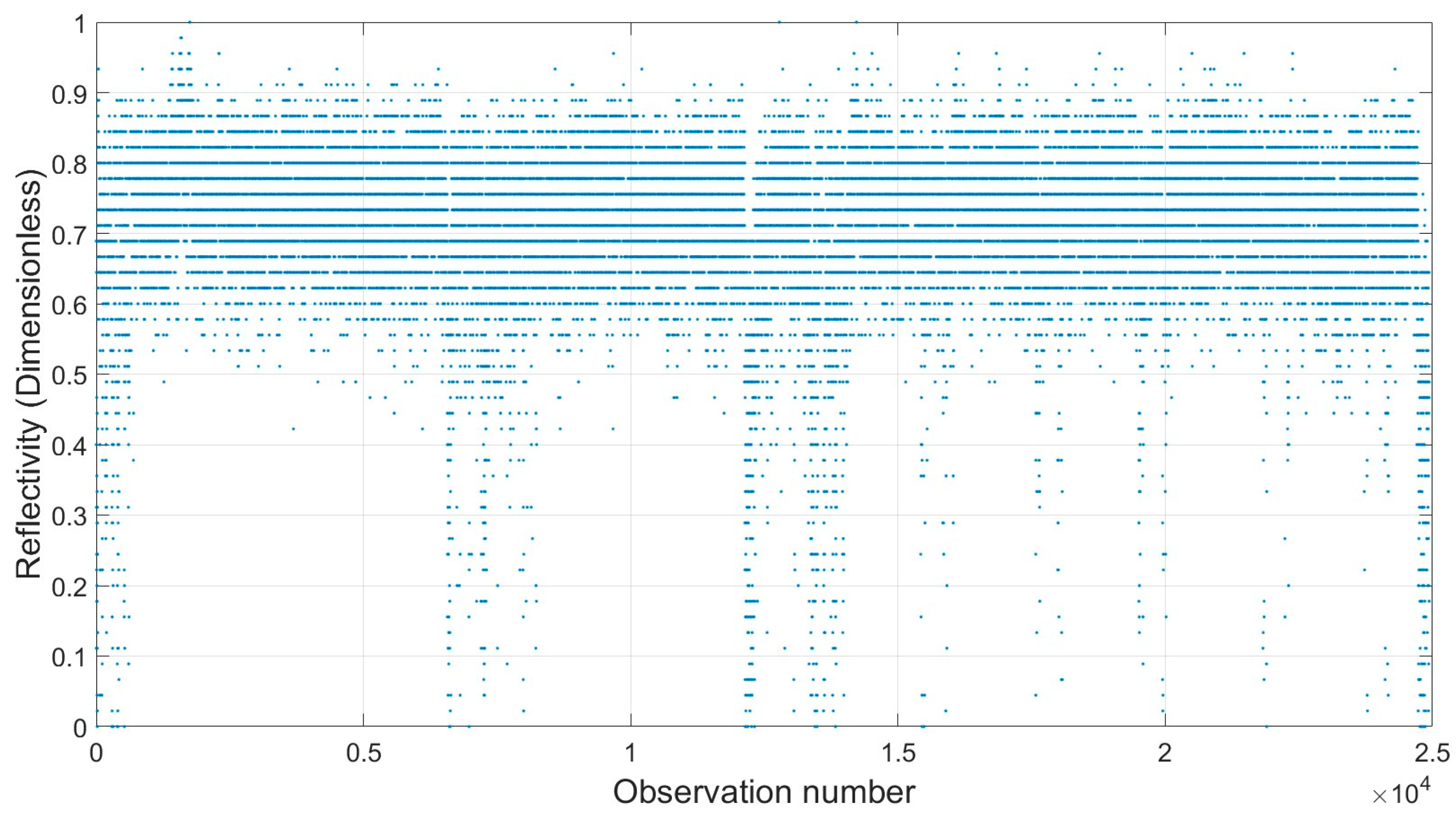
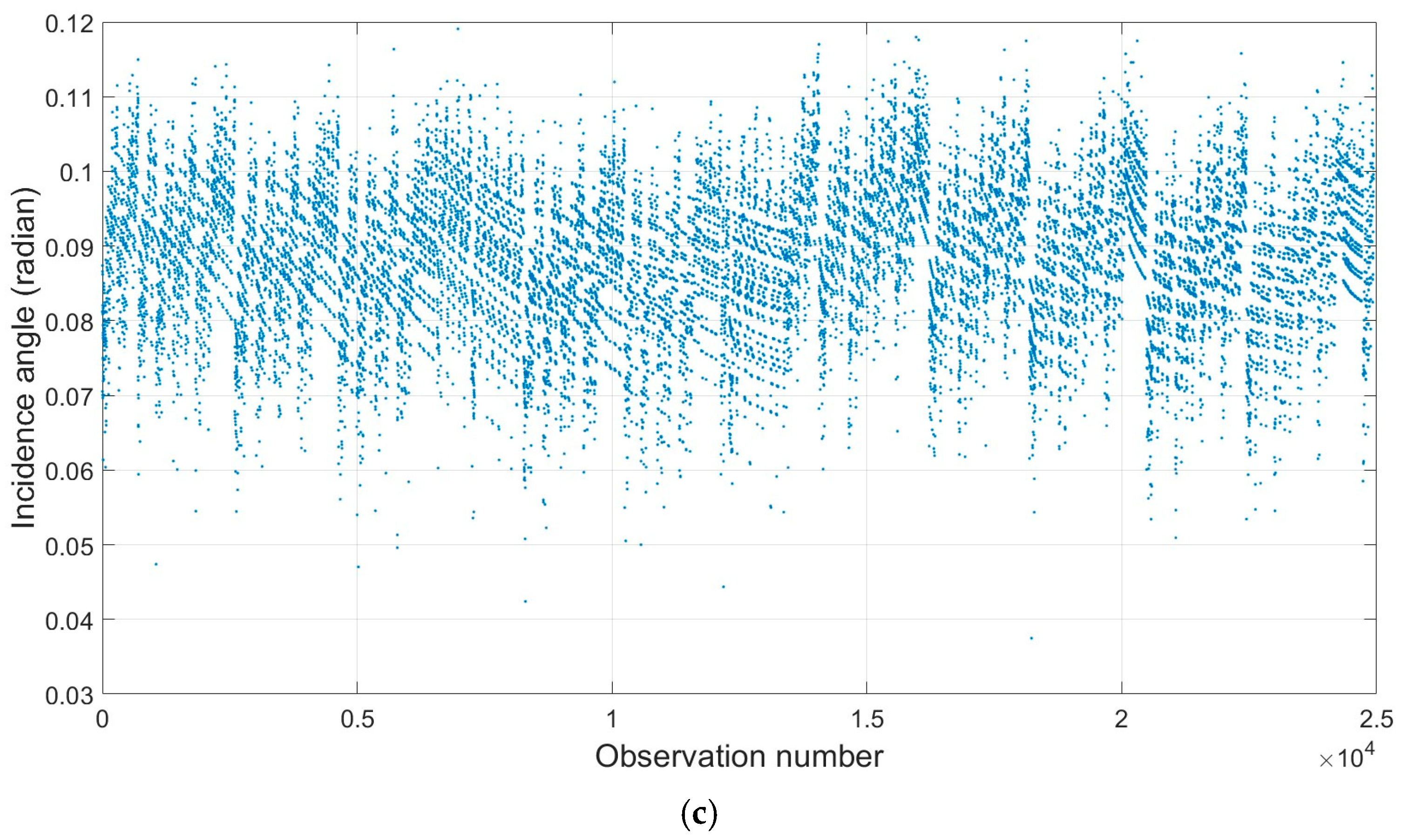
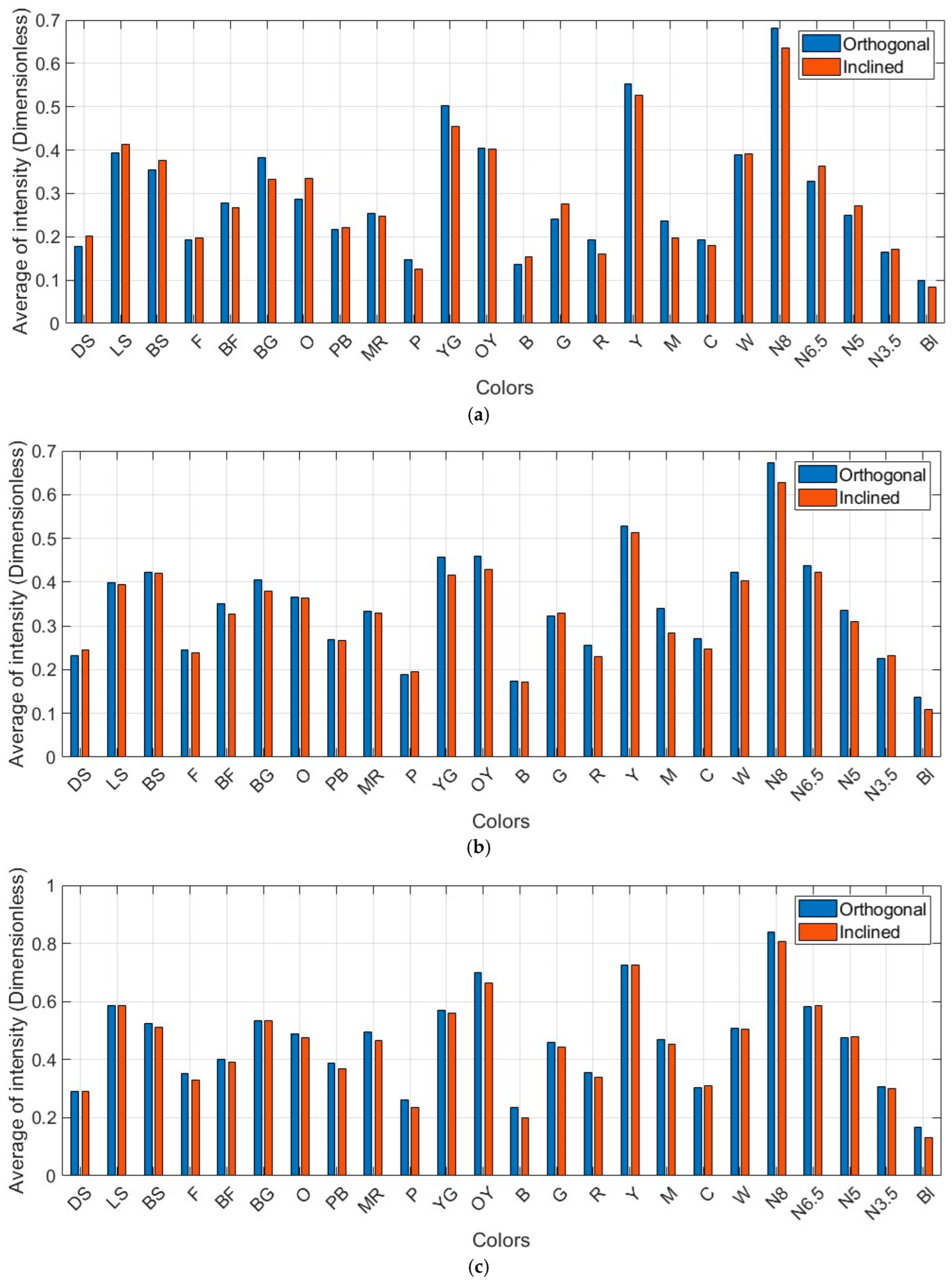
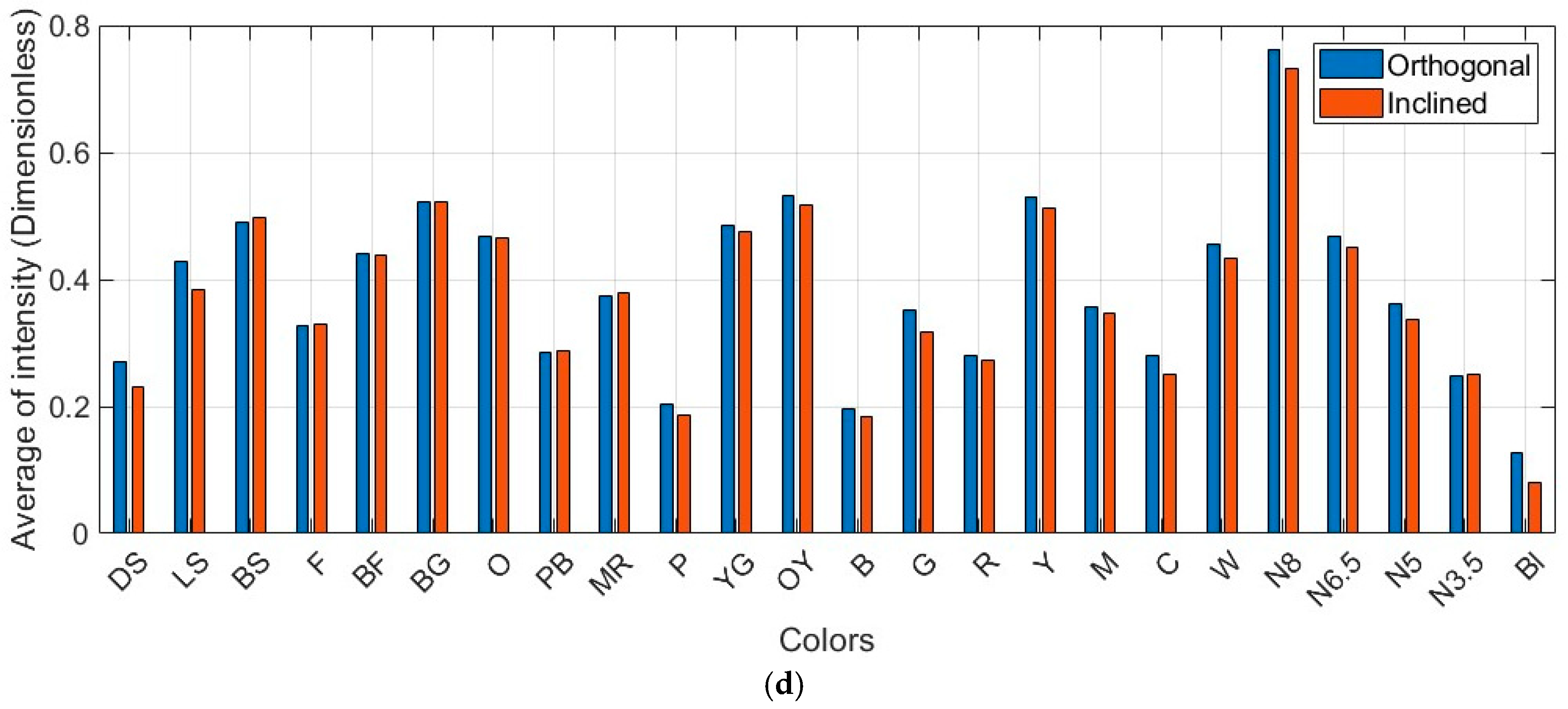
6.1.2. Reflectivity and Geometric Effects
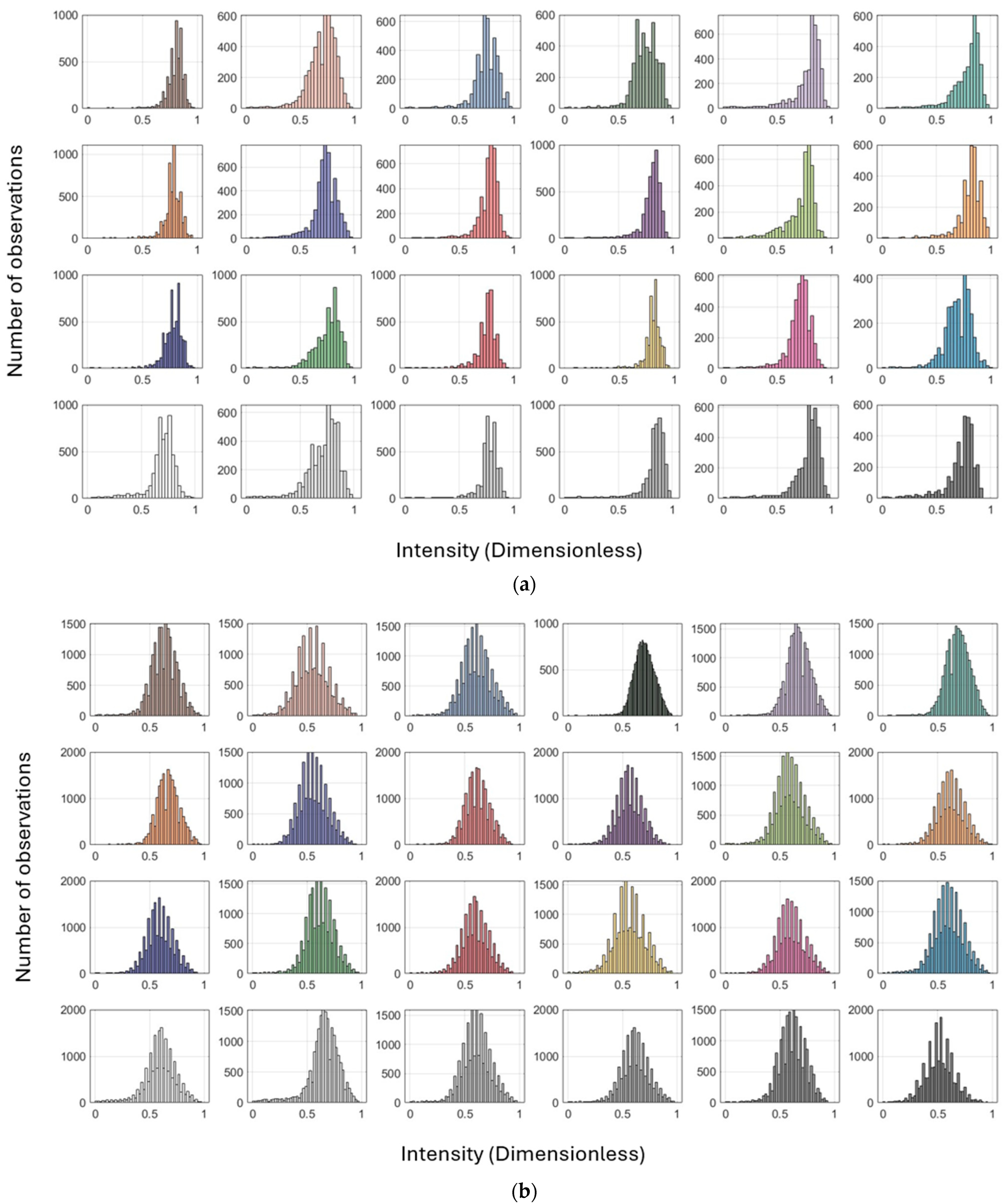
6.2. Pointwise Radiometric Calibration Using LiDAR Range Equation
- (1)
- At the receiver (i.e., TLS) location, the area of the receiver relative to the effective average area illuminated by the reflection from the target
- (2)
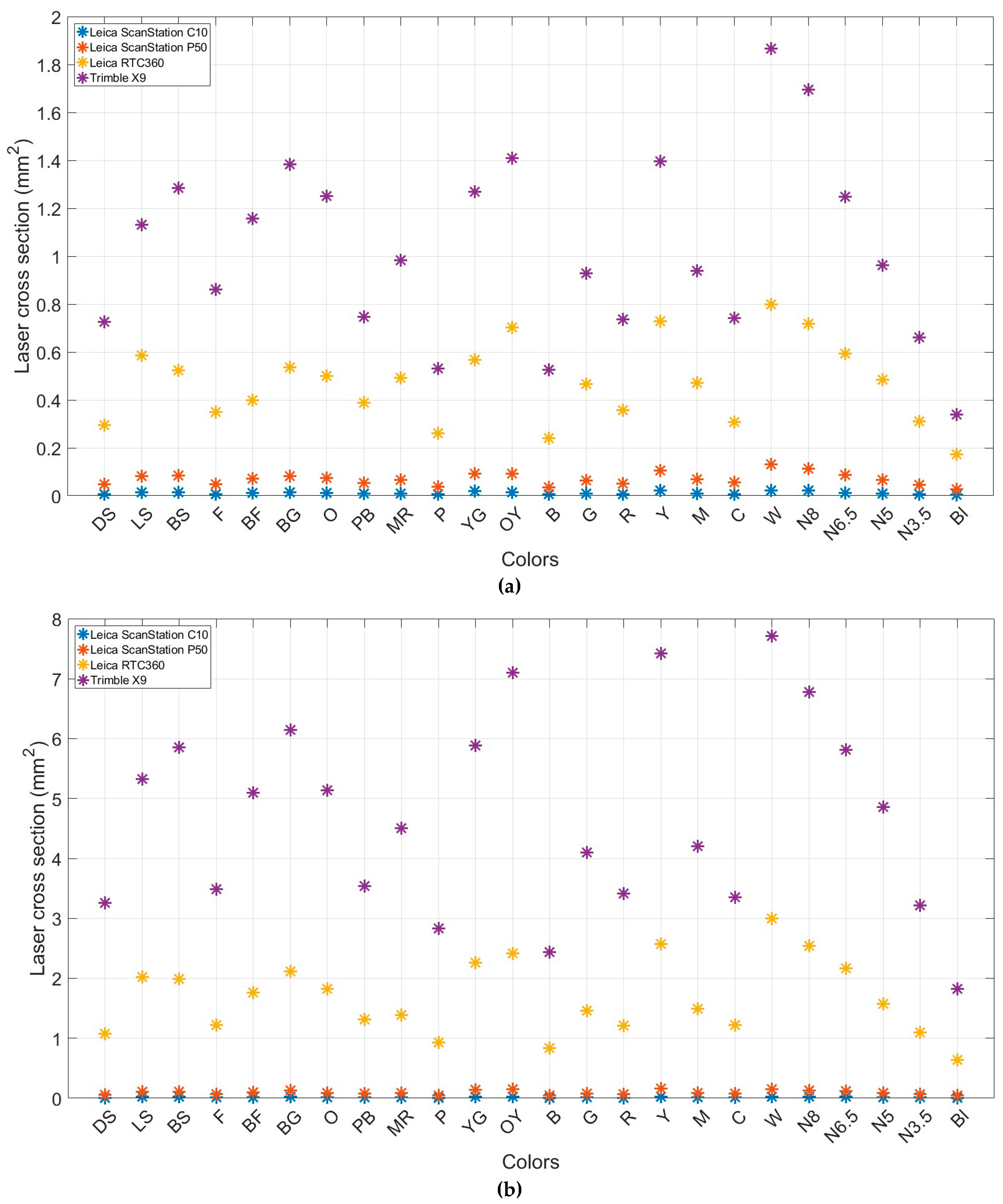
- At the target location, the area of the LiDAR cross-section relative to the illumination area (i.e., particular attention must be drawn to determining the non-physical area of cross-section).
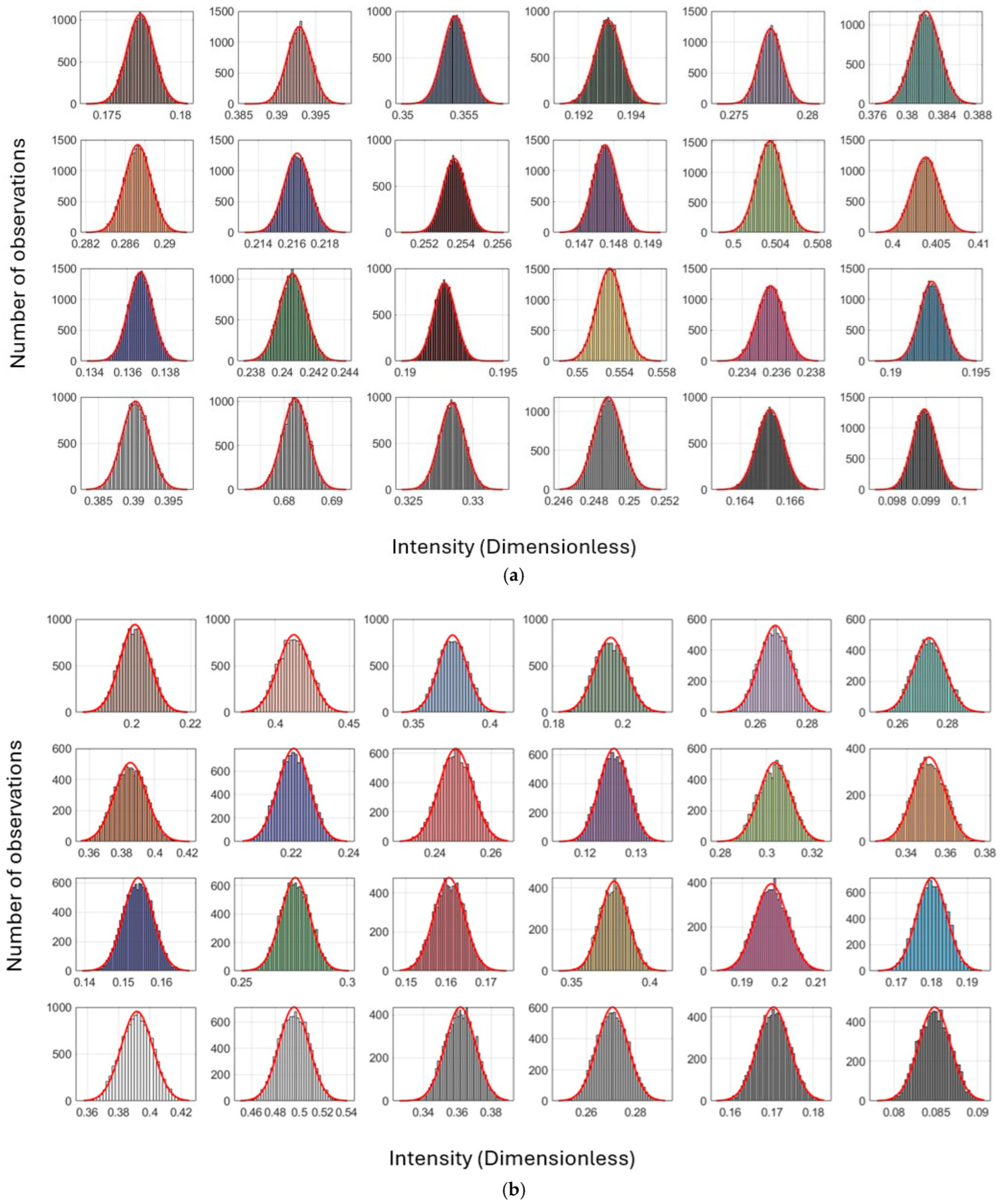
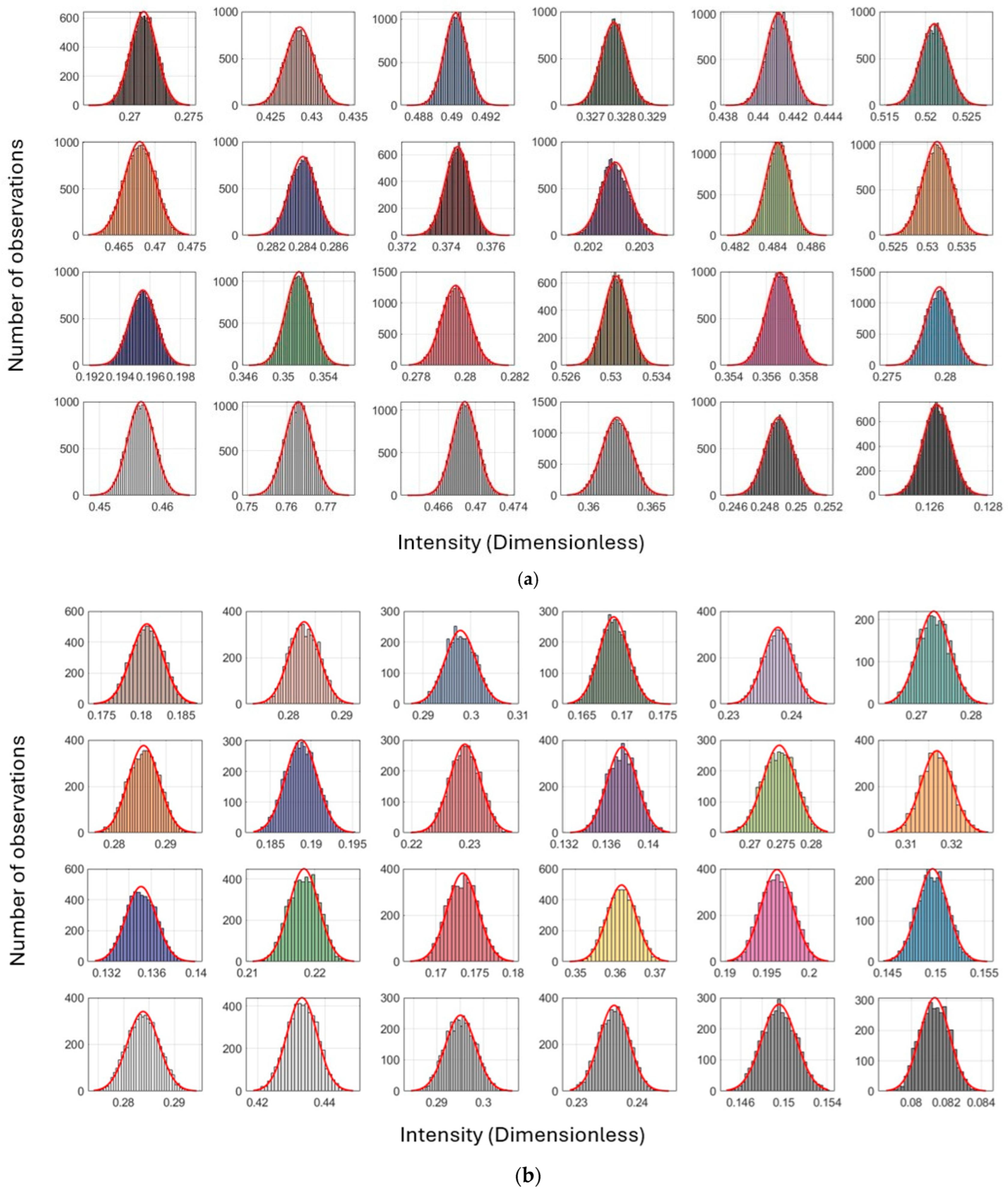
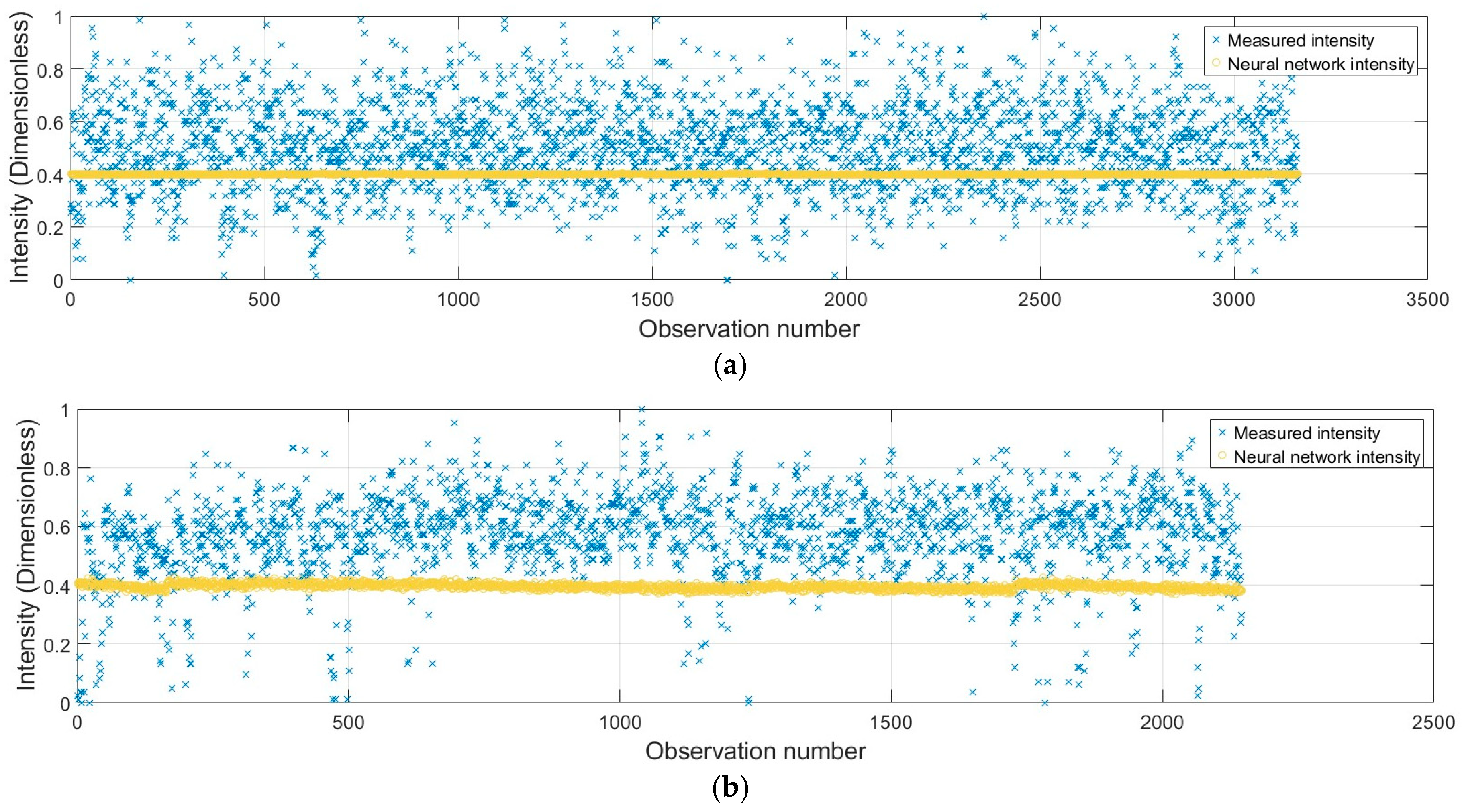
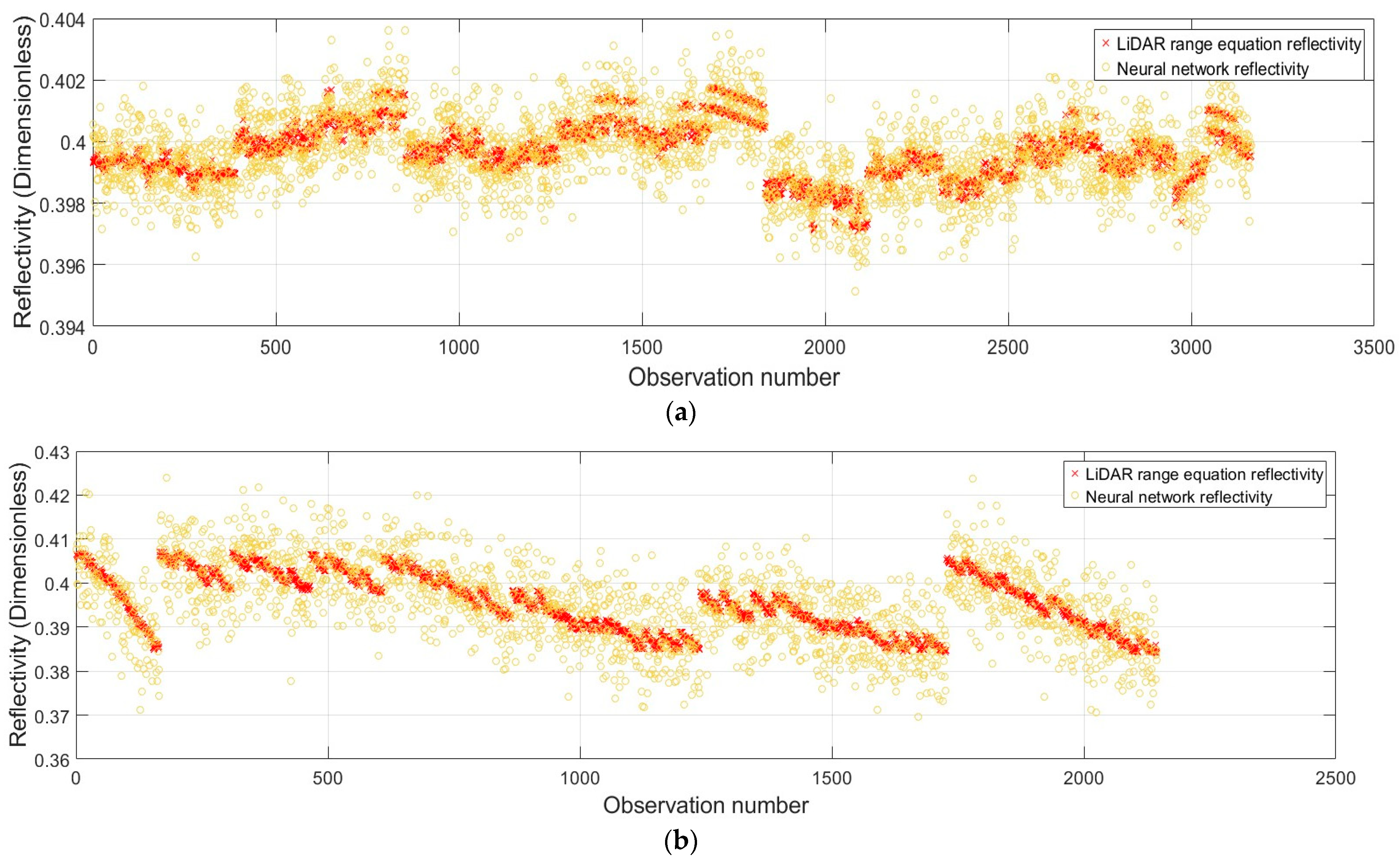
6.3. Pointwise Radiometric Calibration Using a Neural Network
7. Discussions on Reflectivity (Intensity)
8. Conclusions and Future Investigations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Perceptual Intensity Equation
Appendix B. Pre-Processing Steps
Appendix C. Pointwise Radiometric Calibration Using the LiDAR Range Equation
Appendix D. Pointwise Radiometric Calibration Using a Neural Network

References
- Mcmanamon, P.F. Field Guide to Lidar; SPIE Library: Bellingham, WA USA, 2015. [Google Scholar]
- National Research Council (NRC). Laser Radar: Progress and Opportunities in Active Electro-Optical Sensing; The National Academies Press: Washington, DC, USA, 2014. [Google Scholar]
- Reshetyuk, Y. Self-Calibration and Direct Georeferencing in Terrestrial Laser Scanning. Ph.D. Thesis, KTH University, Stockholm, Sweden, 2009. [Google Scholar]
- Soudarissanane, S.; Ree, J.V.; Bucksch, A.; Lindenbergh, R. Error Budget of Terrestrial Laser Scanning: Influence of the Incidence Angle on the Scan Quality. In Proc. of the 10. Anwendungsbezogener Workshop zur Erfassung, Modellierung, Verarbeitung und; Gesellschaft zur Forderung Angewandter Informatik: Berlin, Germany, 2006. [Google Scholar]
- Soudarissanane, S.; Lindenbergh, R.; Gorte, B. Reducing the errors in terrestrial laser scanning by optimizing the measurement set-up. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008. [Google Scholar]
- Sabzali, M.; Pilgrim, L. Hybrid Atmospheric Modeling of Refractive Index Gradients in Long-Range TLS-Based Deformation Monitoring. Remote Sens. 2025, 17, 3513. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X. Intensity data correction based on incidence angle and distance for terrestrial laser scanner. J. Appl. Remote Sens. 2015, 9, 094094. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Jaakkola, A.; Kaasalainen, M.; Krooks, A.; Kukko, A. Analysis of Incidence Angle and Distance Effects on Terrestrial Laser Scanner Intensity: Search for Correction Methods. Remote Sens. 2011, 3, 2207–2221. [Google Scholar] [CrossRef]
- Soudarissananae, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Incidence Angle Influence on the Quality of Terrestrial Laser Scanning Points. In Proceedings of the Laser Scanning 2009, Paris, France, 1–2 September 2009. Bretar, F., Pierrot-Deseillignay, M., Vosselman, G., Eds. [Google Scholar]
- Krooks, A.; Kaasalainen, S.; Hakala, T.K.H. Correction of intensity incidence angle effect in terrestrial laser scanning. In Proceedings of the ISPRS Workshop Laser Scanning, Antalya, Turkey, 11–13 November 2013. [Google Scholar]
- Soudarissanane, S.; Lindenbergh, R.C. Optimizing terrestrial laser scanning measurement set-ups. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Calgary, AB, Canada, 29–31 August 2011. [Google Scholar]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogram. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Pfeifer, N.; Dorininger, P.; Haring, A.; Fan, H. Investigating terrestrial laser scanning intensity data: Quality and functional relations. In Proceedings of the International Conference on Optical 3-D Measurement Techniques VIII, Zurich, Switzerland, 9–12 July 2007; pp. 328–337. Available online: http://hdl.handle.net/20.500.12708/42100 (accessed on 15 September 2025).
- Voisin, S.; Foufou, S.; Truchetet, F.; Paage, D. Abidi Sttudy of ambient light influence for three-dimensional scanners based on structured light. Opt. Eng. 2007, 46, 030502. [Google Scholar] [CrossRef]
- Clark, J.; Robson, S. Accuracy of measurements made with a Cyrax 2500 Laser Scanner against surfaces of known color. Surv. Rev. 2004, 37, 626–638. [Google Scholar] [CrossRef]
- Bolkas, D.; Martinez, A. Effect of target color and scanning geometry on terrestrial LiDAR point-cloud noise and plane fitting. J. Appl. Geod. 2017, 12, 109–127. [Google Scholar] [CrossRef]
- Yaman, A.; Yilmaz, H.M. The effects of object surface colors on terrestrial laser scanners. Int. J. Eng. Geosci. 2017, 2, 68–74. [Google Scholar] [CrossRef]
- Stal, C.; De Maeyer, P.; De Ryck, M.; De Wulf, A.; Goossens, R.; Nutten, T. Comparison of Geometric and Radiometric Information from Photogrammetry and Color-Enriched Laser Scanning. In Proceedings of the FIG Working Week 2011: Bridging the Gap Between Cultures, Murrakech, Morocco, 18–22 May 2011. [Google Scholar]
- Wujanz, D. Intensity calibration method for 3D laser scanner. J. N. Z. Institute Surv. 2009, 299, 7–13. [Google Scholar]
- Julin, A.; Kurkela, M.; Rantanen, T.; Virtanen, J.P.; Maksimainen, M.; Kukko, A.; Kaartinen, H.; Vaaja, M.T.; Hyyppa, J.; Hyyppa, H. Evaluating the Quality of TLS Point Cloud Colorization. Remote Sens. 2020, 12, 2748. [Google Scholar] [CrossRef]
- Wang, Z.; Varga, M.; Medic, T.; Wieser, A. Assessing the alignment between geometry and colors in TLS colored point clouds. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Science, Cairo, Egypt, 2–7 September 2023. [Google Scholar]
- Balaguer-Puig, M.; Molada-Tebar, A.; Marques-Mateu, A.; Lerma, J.L. Characterization of Intensity Values on Terrestrial Laser Scanning for Recording Enhancement. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Science, Ottawa, ON, Canada, 28 August–1 September 2017. [Google Scholar]
- Sabzali, M.; Pilgrim, L. New Parametrization of Bundle Block Adjustment for Self-Calibration of Terrestrial Laser Scanner (TLS). Photogrammetric Rec. 2025, 40, 40009. [Google Scholar]
- Lichti, D.D.; Harvey, B.R. The effects of reflecting surface material properties on time-of-flight laser scanner measurements. In Proceedings of the Symposium on Geospatial theory, Processing and Applications, Ottawa, ON, Canada, 8–12 July 2002. [Google Scholar]
- Tonietto, L.; Gonzaga, L.J.; Veronez, M.R.; Kazmierczak, C.D.S.; Arnold, D.C.C.; Costa, C.A.D. New Method for Evaluating Surface Roughness Parameters Acquired by Laser Scanning. Nature 2019, 9, 15038. [Google Scholar] [CrossRef] [PubMed]
- Berger, A.B. State of the art in surface reconstruction from point clouds. Eurographics Star Rep. 2014, 1, 161–185. [Google Scholar]
- Mah, J.; Samson, C.; McKinnon, S.D.; Tibodeau, D. 3D laser imaging for surface roughness analysis. Int. J. Rock Mech. Min. Sci. 2013, 58, 111–117. [Google Scholar] [CrossRef]
- Moreau, N.; Roudet, C.; Gentil, C. Study and Comparison of Surface Roughness Measurements. In Journées du Groupe de Travail en, Lyon, 2014. Available online: https://hal.science/file/index/docid/1068988/filename/articleGTMG2014_Moreau_09_03_soir.pdf (accessed on 15 September 2025).
- Silva, B.B.D.; Braga, A.C.; Braga, C.C.; Olivera, L.M.M.D.; Montenegro, S.M.G.L.; Junior, B.B. Procedure for calculation of the albedo with OLI-Landsat 8 images: Application to Brazilian semi-arid. Rev. Bras. Eng. Agric. Ambient. 2016, 20, 3–8. [Google Scholar] [CrossRef]
- Maar, H.; Zogg, H.M. WFD-Wave Form Digitizer Technology White Paper. Leica Geosystem, 2021. Available online: https://naic.nrao.edu/arecibo/phil/hardware/theodolites/leicaDoc/Leica%20Nova%20Documentation/White%20Paper/WFD%20Technology/Leica_Nova_MS50_WFD-Wave_Form_Digitizer_Technology_en.pdf (accessed on 15 September 2025).
- Tan, K.; Cheng, X.; Cheng, X. Modeling hemispherical reflectance for natural surfaces based on terrestrial laser scanning backscattered intensity data. Opt. Soc. Am. 2016, 24, 22971–22988. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.; Zhang, W.; Shen, F.; Cheng, X. Investigation of TLS Intensity Data and Distance Measurement Errors from Target Specular Reflections. J. Remote Sens. 2018, 10, 1077. [Google Scholar] [CrossRef]
- Mcmanamon, P.F. LiDAR Technologies and Systems; SPIE Press Book: Bellingham, WA, USA, 2019. [Google Scholar]
- Jenn, D. Radar and Laser Cross Section Engineering; American Institute of Aeronautics and Astronomy: Reston, VA, USA, 2019. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rishi, S. The Guide to the Expression of Uncertainty in Measurement (GUM)—The New Approach; IOP Publishing Ltd.: Bristol, UK, 2024. [Google Scholar]
- Houghton, T. Harnessing Multiscale Non-imaging Optics for Automotive Flash LiDAR and Heterogenous Semiconductor Integration. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2020. [Google Scholar]
- Freeman, O.J.; Williamson, C.A. Visualizing the trade-offs between laser eye protection and laser eye dazzle. J. Laser Appl. 2020, 32, 012008. [Google Scholar] [CrossRef]
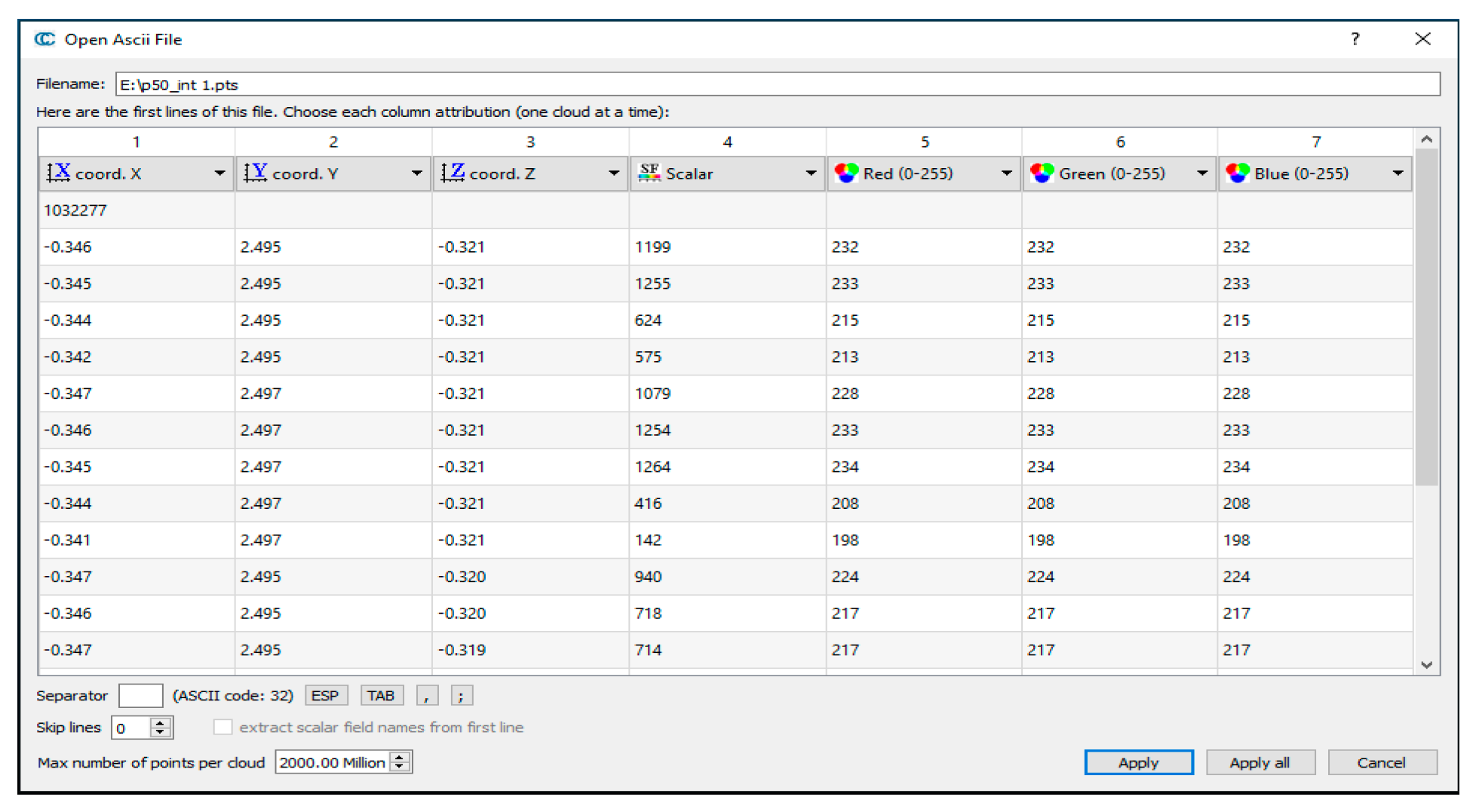



| Specifications | TLSs | |||
|---|---|---|---|---|
| Leica ScanStation P50 1 | Leica ScanStation C10 2 | Leica RTC360 3 | Trimble X9 4 | |
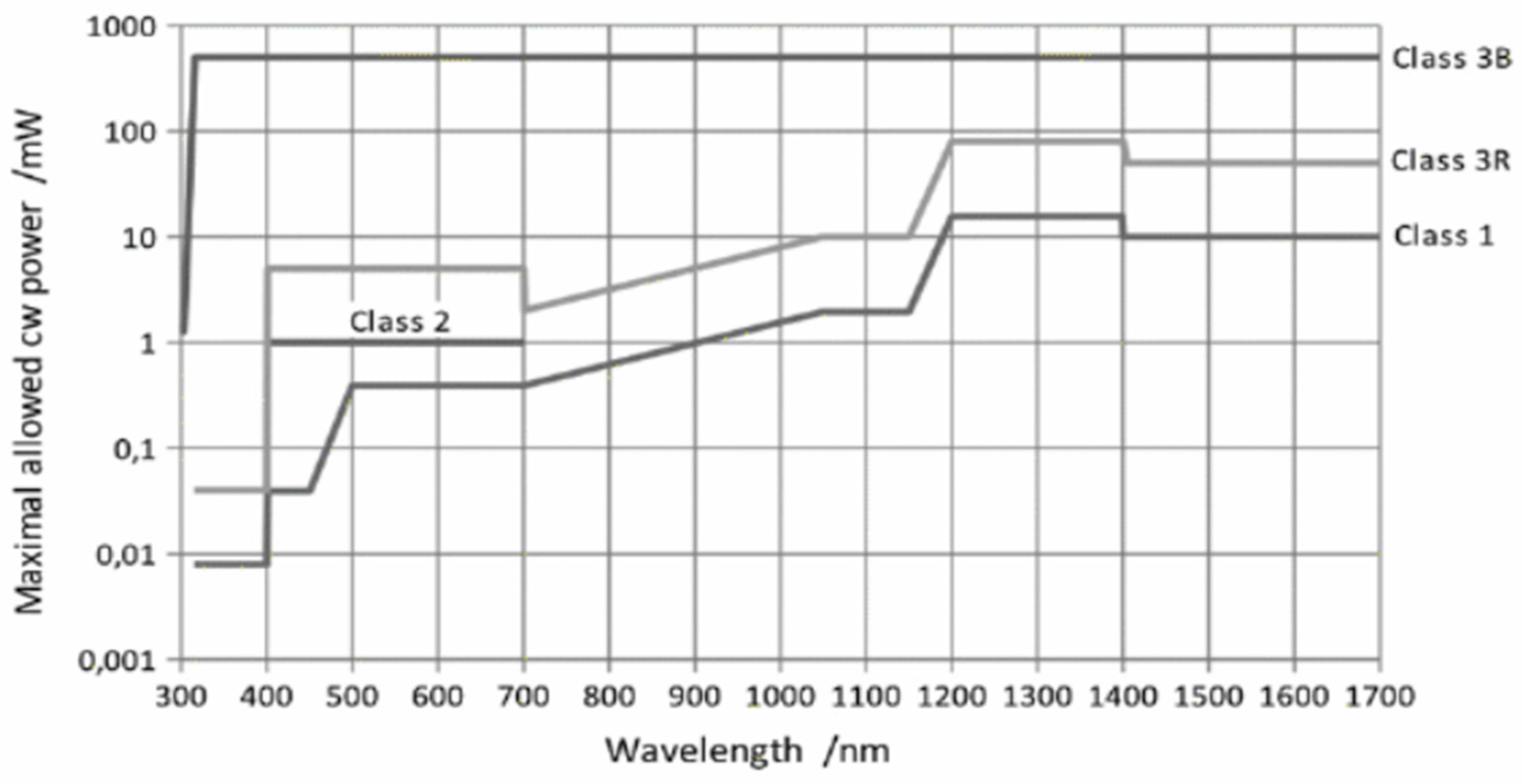
| Laser class | ||||
| Wavelength | ||||
| Initial beam diameter | (FWHM) | |||
| Spot size * | (FWHH-based); (Gaussian-based) | |||
| Beam divergence | (FWHM, full angle) | (full angle) | ||
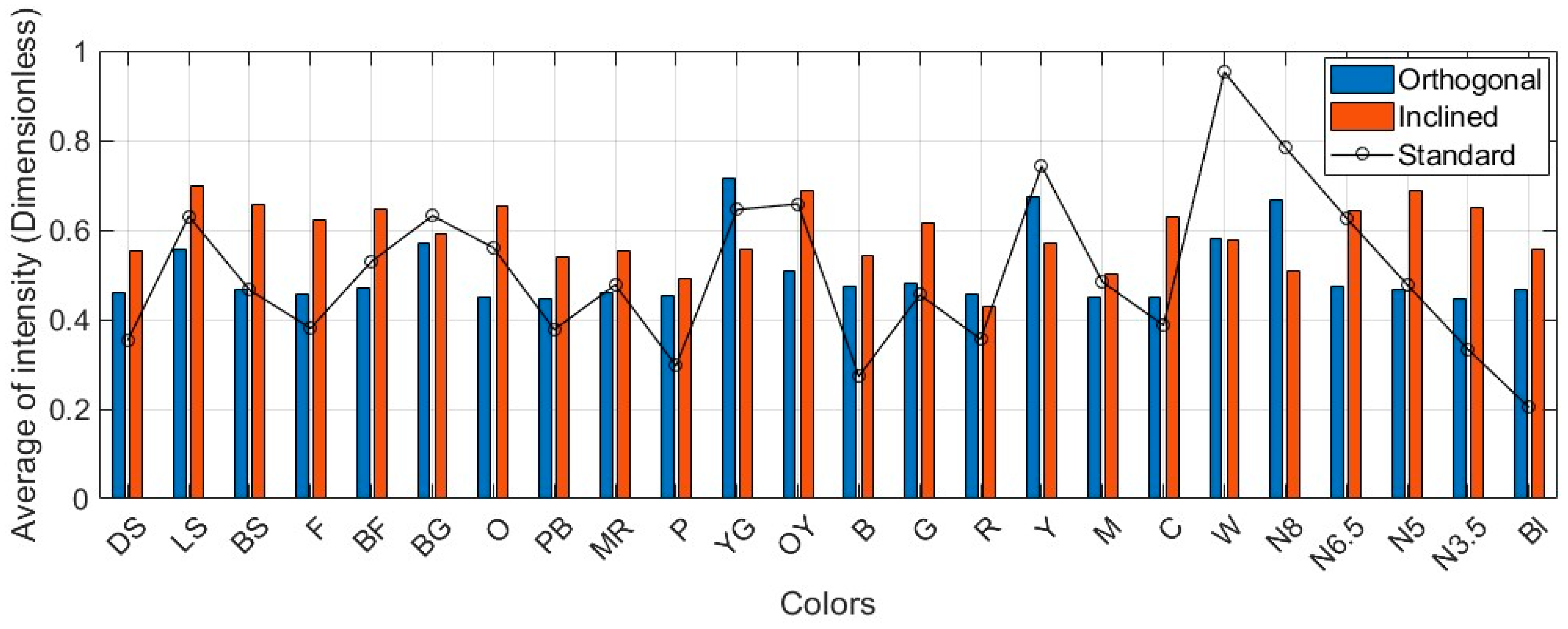
| Standard Intensity Values | |||||
|---|---|---|---|---|---|
| Dark skin (DS) | Light skin (LS) | Blue sky (BS) | Foliage (F) | Blue flower (BF) | Bluish green (BG) |
| 0.35 | 0.63 | 0.65 | 0.38 | 0.53 | 0.62 |
| Orange (O) | Purplish blue (PB) | Moderate red (MR) | Purple (P) | Yellow green (YG) | Orange yellow (OY) |
| 0.57 | 0.41 | 0.49 | 0.29 | 0.66 | 0.70 |
| Blue (B) | Green (G) | Red (R) | Yellow (Y) | Magenta (M) | Cyan (C) |
| 0.27 | 0.46 | 0.38 | 0.76 | 0.48 | 0.38 |
| White (W) | Neutral 8 (N8) | Neutral 6.5 (N6.5) | Neutral 5 (N5) | Neutral 3.5 (N3.5) | Black (Bl) |
| 0.95 | 0.79 | 0.63 | 0.48 | 0.33 | 0.20 |
| TLSs | |||
|---|---|---|---|
| Leica ScanStation P50 | Leica ScanStation C10 | Leica RTC360 | Trimble X9 |
| Scanning Conditions | Standard Deviation | TLSs | |||
|---|---|---|---|---|---|
| Leica ScanStation P50 | Leica ScanStation C10 | Leica RTC360 | Trimble X9 | ||
| Orthogonal | Measured intensity | 0.179 | 0.134 | 0.168 | 0.176 |
| Computed intensity from RGB | 0.178 | 0.132 | 0.167 | 0.176 | |
| Inclined | Measured intensity | 0.181 | 0.179 | 0.187 | 0.189 |
| Computed intensity from RGB | 0.182 | 0.173 | 0.189 | 0.189 | |
| TLSs | Leica ScanStation P50 | Leica ScanStation C10 | Leica RTC360 | Trimble X9 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SC 1/NP | O | NP | I | NP | O | NP | I | NP | O | NP | I | NP | O | NP | I | NP |
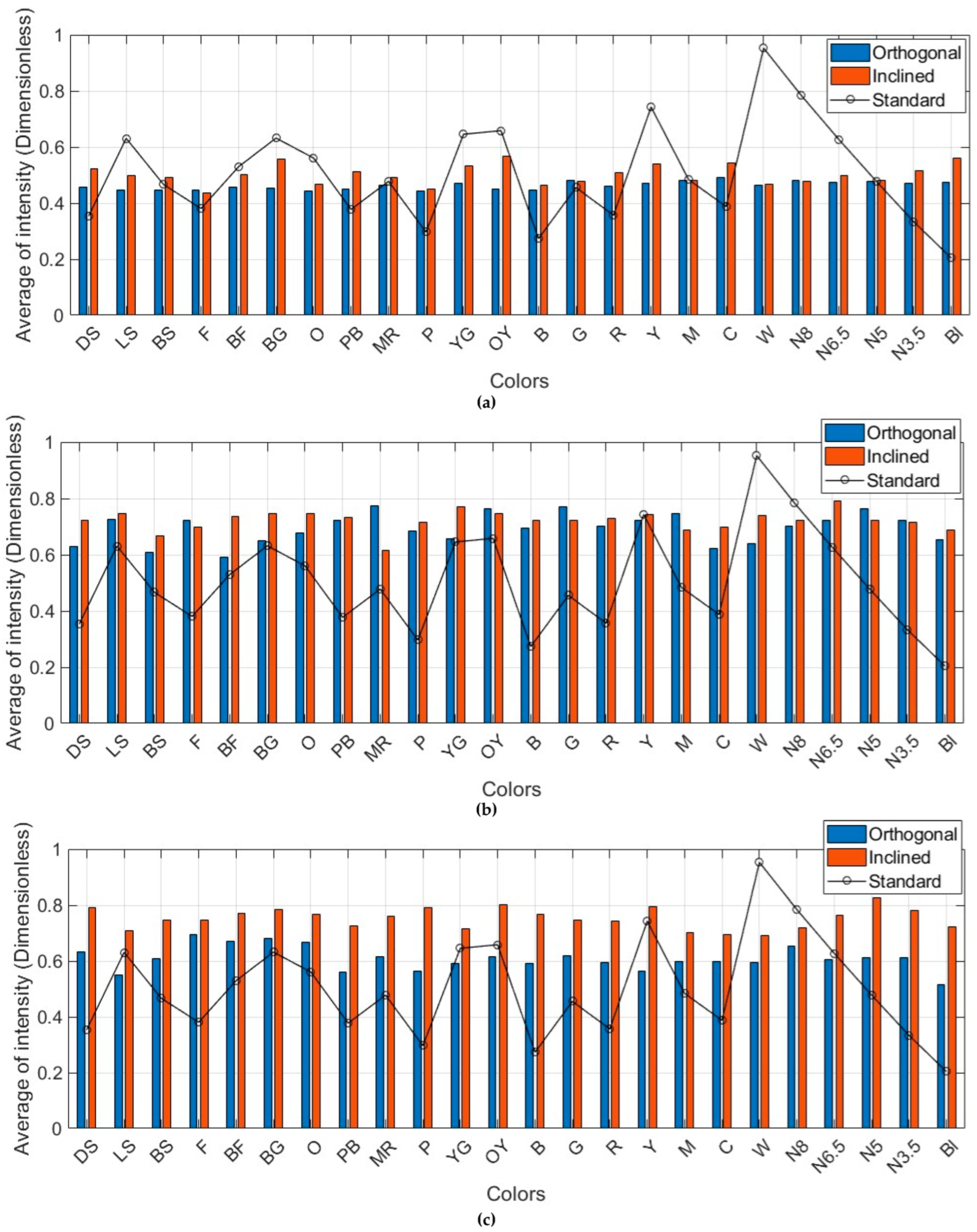
| DS | 0.458 | 16,328 | 0.523 | 11,227 | 0.459 | 25,591 | 0.554 | 12,461 | 0.630 | 0.137 | 0.724 | 681 | 0.632 | 18,976 | 0.791 | 5425 |
| LS | 0.446 | 15,816 | 0.499 | 10,723 | 0.558 | 25,900 | 0.700 | 11,654 | 0.726 | 0.128 | 0.747 | 763 | 0.550 | 18,923 | 0.709 | 5262 |
| BS | 0.447 | 16,148 | 0.492 | 10,328 | 0.467 | 26,096 | 0.656 | 10,116 | 0.609 | 0.146 | 0.668 | 988 | 0.607 | 19,181 | 0.745 | 4042 |
| F | 0.447 | 16,285 | 0.437 | 10,419 | 0.457 | 24,021 | 0.624 | 9656 | 0.721 | 0.145 | 0.698 | 840 | 0.694 | 19,381 | 0.745 | 4457 |
| BF | 0.458 | 16,548 | 0.500 | 10,258 | 0.470 | 24,969 | 0.647 | 8895 | 0.591 | 0.132 | 0.735 | 814 | 0.669 | 19,298 | 0.772 | 4049 |
| BG | 0.452 | 16,422 | 0.558 | 9907 | 0.570 | 24,557 | 0.593 | 7943 | 0.651 | 0.128 | 0.748 | 796 | 0.682 | 19,083 | 0.785 | 3386 |
| O | 0.444 | 16,271 | 0.468 | 10,988 | 0.451 | 25,168 | 0.655 | 13,098 | 0.677 | 0.147 | 0.747 | 729 | 0.669 | 18,803 | 0.768 | 5880 |
| PB | 0.451 | 16,560 | 0.513 | 10,941 | 0.448 | 26,204 | 0.541 | 11,434 | 0.724 | 0.123 | 0.732 | 561 | 0.559 | 18,868 | 0.725 | 5128 |
| MR | 0.464 | 16,823 | 0.490 | 10,242 | 0.461 | 26,274 | 0.554 | 9754 | 0.773 | 0.164 | 0.616 | 755 | 0.615 | 19,363 | 0.761 | 3981 |
| P | 0.442 | 16,952 | 0.451 | 10,323 | 0.452 | 26,233 | 0.490 | 9753 | 0.684 | 0.152 | 0.714 | 628 | 0.563 | 19,362 | 0.791 | 4632 |
| YG | 0.471 | 16,750 | 0.534 | 10,454 | 0.716 | 25,253 | 0.559 | 9259 | 0.657 | 0.155 | 0.770 | 593 | 0.590 | 19,225 | 0.715 | 3992 |
| OY | 0.452 | 16,288 | 0.568 | 9899 | 0.510 | 25,230 | 0.690 | 7782 | 0.764 | 0.129 | 0.745 | 679 | 0.615 | 18,989 | 0.803 | 3222 |
| B | 0.446 | 16,440 | 0.463 | 10,927 | 0.475 | 24,375 | 0.543 | 12,840 | 0.695 | 0.126 | 0.722 | 699 | 0.592 | 18,791 | 0.767 | 5761 |
| G | 0.481 | 16,702 | 0.478 | 10,826 | 0.481 | 24,354 | 0.617 | 11,926 | 0.770 | 0.132 | 0.721 | 641 | 0.619 | 19,131 | 0.748 | 5275 |
| R | 0.462 | 16,605 | 0.508 | 10,635 | 0.457 | 25,515 | 0.430 | 9544 | 0.703 | 0.125 | 0.728 | 801 | 0.595 | 19,214 | 0.742 | 3996 |
| Y | 0.472 | 16,850 | 0.539 | 10,877 | 0.673 | 24,938 | 0.571 | 10,088 | 0.723 | 0.129 | 0.744 | 632 | 0.564 | 19,192 | 0.795 | 4704 |
| M | 0.479 | 16,596 | 0.481 | 10,361 | 0.450 | 24,659 | 0.503 | 9151 | 0.748 | 0.145 | 0.686 | 585 | 0.599 | 19,252 | 0.702 | 4008 |
| C | 0.491 | 16,557 | 0.542 | 9781 | 0.450 | 24,724 | 0.630 | 7927 | 0.623 | 0.131 | 0.697 | 705 | 0.597 | 18,979 | 0.696 | 3151 |
| W | 0.465 | 16,595 | 0.466 | 11,176 | 0.580 | 24,589 | 0.579 | 12,668 | 0.640 | 0.148 | 0.739 | 757 | 0.596 | 18,539 | 0.690 | 5571 |
| N8 | 0.480 | 16,798 | 0.479 | 10,932 | 0.667 | 24,921 | 0.509 | 11,808 | 0.703 | 0.152 | 0.721 | 574 | 0.654 | 19,015 | 0.719 | 5255 |
| N6.5 | 0.473 | 16,659 | 0.499 | 10,467 | 0.474 | 24,264 | 0.643 | 10,298 | 0.723 | 0.136 | 0.790 | 756 | 0.605 | 19,192 | 0.763 | 4155 |
| N5 | 0.477 | 16,705 | 0.481 | 10,475 | 0.466 | 24,543 | 0.689 | 10,031 | 0.762 | 0.164 | 0.724 | 640 | 0.612 | 19,140 | 0.825 | 4731 |
| N3.5 | 0.470 | 16,682 | 0.515 | 10,594 | 0.445 | 24,674 | 0.650 | 9130 | 0.722 | 0.138 | 0.715 | 742 | 0.612 | 19,049 | 0.780 | 3870 |
| Bl | 0.476 | 16,880 | 0.559 | 10,332 | 0.467 | 24,588 | 0.557 | 7969 | 0.655 | 0.152 | 0.688 | 620 | 0.516 | 18,833 | 0.723 | 3485 |
| TLSs | Leica ScanStation P50 | Leica ScanStation C10 | Leica RTC360 | Trimble X9 | ||||
|---|---|---|---|---|---|---|---|---|
| Scanning Conditions | Orthogonal | Inclined | Orthogonal | Inclined | Orthogonal | Inclined | Orthogonal | Inclined |
| Dark skin (DS) | 0.142 | 0.144 | 0.099 | 0.107 | 0.137 | 0.147 | 0.128 | 0.107 |
| Light skin (LS) | 0.158 | 0.137 | 0.143 | 0.161 | 0.128 | 0.172 | 0.151 | 0.132 |
| Blue sky (BS) | 0.147 | 0.141 | 0.127 | 0.154 | 0.146 | 0.168 | 0.139 | 0.129 |
| Foliage (F) | 0.155 | 0.133 | 0.152 | 0.138 | 0.145 | 0.159 | 0.109 | 0.128 |
| Blue flower (BF) | 0.149 | 0.140 | 0.141 | 0.146 | 0.132 | 0.177 | 0.119 | 0.165 |
| Bluish green (BG) | 0.144 | 0.156 | 0.121 | 0.150 | 0.128 | 0.169 | 0.119 | 0.143 |
| Orange (O) | 0.144 | 0.130 | 0.115 | 0.145 | 0.147 | 0.191 | 0.114 | 0.103 |
| Purplish blue (PB) | 0.144 | 0.143 | 0.108 | 0.108 | 0.123 | 0.172 | 0.134 | 0.130 |
| Moderate red (MR) | 0.144 | 0.139 | 0.103 | 0.113 | 0.164 | 0.161 | 0.120 | 0.117 |
| Purple (P) | 0.141 | 0.127 | 0.104 | 0.099 | 0.152 | 0.163 | 0.126 | 0.128 |
| Yellow green (YG) | 0.142 | 0.157 | 0.125 | 0.143 | 0.155 | 0.165 | 0.138 | 0.149 |
| Orange yellow (OY) | 0.145 | 0.152 | 0.135 | 0.166 | 0.129 | 0.172 | 0.135 | 0.129 |
| Blue (B) | 0.145 | 0.122 | 0.109 | 0.108 | 0.126 | 0.151 | 0.129 | 0.112 |
| Green (G) | 0.144 | 0.135 | 0.134 | 0.139 | 0.132 | 0.194 | 0.129 | 0.139 |
| Red (R) | 0.142 | 0.142 | 0.098 | 0.099 | 0.125 | 0.173 | 0.131 | 0.121 |
| Yellow (Y) | 0.143 | 0.143 | 0.116 | 0.135 | 0.129 | 0.170 | 0.146 | 0.115 |
| Magenta (M) | 0.136 | 0.140 | 0.096 | 0.114 | 0.145 | 0.179 | 0.138 | 0.120 |
| Cyan (C) | 0.137 | 0.148 | 0.137 | 0.146 | 0.131 | 0.170 | 0.141 | 0.132 |
| White (W) | 0.149 | 0.135 | 0.118 | 0.172 | 0.148 | 0.188 | 0.146 | 0.133 |
| Neutral 8 (N8) | 0.149 | 0.137 | 0.129 | 0.143 | 0.152 | 0.178 | 0.146 | 0.149 |
| Neutral 6.5 (N6.5) | 0.142 | 0.137 | 0.133 | 0.160 | 0.136 | 0.200 | 0.136 | 0.123 |
| Neutral 5 (N5) | 0.142 | 0.127 | 0.149 | 0.153 | 0.164 | 0.208 | 0.135 | 0.143 |
| Neutral 3.5 (N3.5) | 0.143 | 0.155 | 0.142 | 0.153 | 0.138 | 0.170 | 0.127 | 0.145 |
| Black (Bl) | 0.140 | 0.155 | 0.113 | 0.120 | 0.152 | 0.180 | 0.134 | 0.152 |
| Scanning Conditions | Accuracy | TLSs | |||
|---|---|---|---|---|---|
| Leica ScanStation P50 | Leica ScanStation C10 | Leica RTC360 | Trimble X9 | ||
| Orthogonal | Before | 0.178 | 0.134 | 0.187 | 0.176 |
| After | 0.093 | 0.093 | 0.096 | 0.095 | |
| Improvement | 48% | 31% | 49% | 46% | |
| Inclined | Before | 0.182 | 0.179 | 0.167 | 0.189 |
| After | 0.097 | 0.103 | 0.104 | 0.116 | |
| Improvement | 47% | 42% | 38% | 39% | |
| TLSs | Leica ScanStation P50 | Leica ScanStation C10 | Leica RTC360 | Trimble X9 | ||||
|---|---|---|---|---|---|---|---|---|
| Scanning Conditions | Orthogonal | Inclined | Orthogonal | Inclined | Orthogonal | Inclined | Orthogonal | Inclined |
| Dark skin (DS) | 0.001 | 0.006 | 0.001 | 0.005 | 0.001 | 0.003 | 0.001 | 0.002 |
| Light skin (LS) | 0.001 | 0.009 | 0.002 | 0.011 | 0.002 | 0.005 | 0.002 | 0.003 |
| Blue sky (BS) | 0.001 | 0.009 | 0.001 | 0.010 | 0.001 | 0.006 | 0.001 | 0.003 |
| Foliage (F) | 0.000 | 0.004 | 0.001 | 0.005 | 0.000 | 0.003 | 0.000 | 0.002 |
| Blue flower (BF) | 0.001 | 0.006 | 0.001 | 0.006 | 0.000 | 0.004 | 0.001 | 0.002 |
| Bluish green (BG) | 0.001 | 0.007 | 0.002 | 0.006 | 0.001 | 0.004 | 0.002 | 0.003 |
| Orange (O) | 0.001 | 0.009 | 0.001 | 0.010 | 0.002 | 0.005 | 0.002 | 0.003 |
| Purplish blue (PB) | 0.001 | 0.006 | 0.001 | 0.005 | 0.001 | 0.003 | 0.001 | 0.002 |
| Moderate red (MR) | 0.000 | 0.006 | 0.001 | 0.006 | 0.001 | 0.003 | 0.001 | 0.003 |
| Purple (P) | 0.000 | 0.003 | 0.000 | 0.003 | 0.000 | 0.002 | 0.000 | 0.001 |
| Yellow green (YG) | 0.001 | 0.008 | 0.001 | 0.007 | 0.001 | 0.005 | 0.001 | 0.003 |
| Orange yellow (OY) | 0.002 | 0.008 | 0.002 | 0.008 | 0.002 | 0.005 | 0.002 | 0.003 |
| Blue (B) | 0.001 | 0.004 | 0.001 | 0.004 | 0.001 | 0.002 | 0.001 | 0.001 |
| Green (G) | 0.001 | 0.006 | 0.001 | 0.007 | 0.002 | 0.004 | 0.001 | 0.002 |
| Red (R) | 0.000 | 0.005 | 0.001 | 0.004 | 0.001 | 0.003 | 0.001 | 0.002 |
| Yellow (Y) | 0.001 | 0.010 | 0.001 | 0.009 | 0.002 | 0.005 | 0.001 | 0.004 |
| Magenta (M) | 0.001 | 0.005 | 0.001 | 0.004 | 0.002 | 0.003 | 0.001 | 0.002 |
| Cyan (C) | 0.001 | 0.004 | 0.001 | 0.004 | 0.001 | 0.003 | 0.001 | 0.002 |
| White (W) | 0.002 | 0.010 | 0.002 | 0.010 | 0.003 | 0.005 | 0.002 | 0.003 |
| Neutral 8 (N8) | 0.002 | 0.013 | 0.003 | 0.012 | 0.004 | 0.009 | 0.003 | 0.004 |
| Neutral 6.5 (N6.5) | 0.001 | 0.009 | 0.001 | 0.009 | 0.002 | 0.005 | 0.001 | 0.003 |
| Neutral 5 (N5) | 0.001 | 0.006 | 0.001 | 0.006 | 0.002 | 0.004 | 0.001 | 0.002 |
| Neutral 3.5 (N3.5) | 0.001 | 0.004 | 0.001 | 0.004 | 0.001 | 0.002 | 0.001 | 0.002 |
| Black (Bl) | 0.000 | 0.002 | 0.000 | 0.002 | 0.001 | 0.001 | 0.000 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabzali, M.; Pilgrim, L. 4D Pointwise Terrestrial Laser Scanning Calibration: Radiometric Calibration of Point Clouds. Sensors 2025, 25, 7035. https://doi.org/10.3390/s25227035
Sabzali M, Pilgrim L. 4D Pointwise Terrestrial Laser Scanning Calibration: Radiometric Calibration of Point Clouds. Sensors. 2025; 25(22):7035. https://doi.org/10.3390/s25227035
Chicago/Turabian StyleSabzali, Mansoor, and Lloyd Pilgrim. 2025. "4D Pointwise Terrestrial Laser Scanning Calibration: Radiometric Calibration of Point Clouds" Sensors 25, no. 22: 7035. https://doi.org/10.3390/s25227035
APA StyleSabzali, M., & Pilgrim, L. (2025). 4D Pointwise Terrestrial Laser Scanning Calibration: Radiometric Calibration of Point Clouds. Sensors, 25(22), 7035. https://doi.org/10.3390/s25227035






