Intelligent Fault Diagnosis of Hydraulic Pumps Based on Multi-Source Signal Fusion and Dual-Attention Convolutional Neural Networks
Abstract
1. Introduction
2. Basic Theory
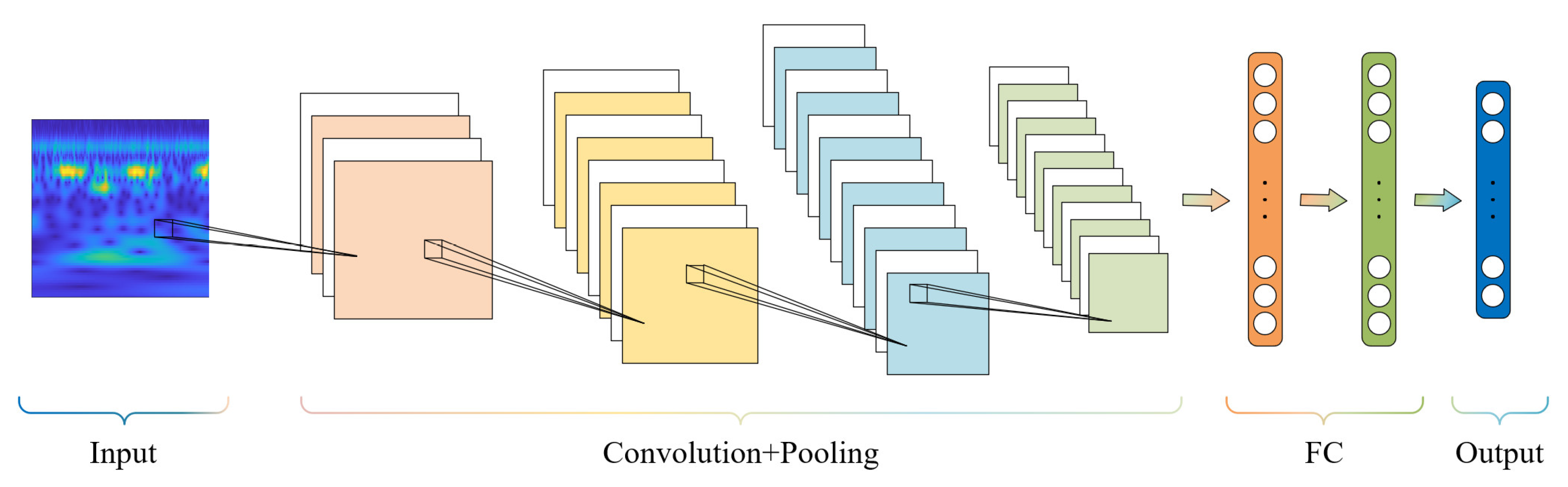
2.1. Convolutional Neural Networks
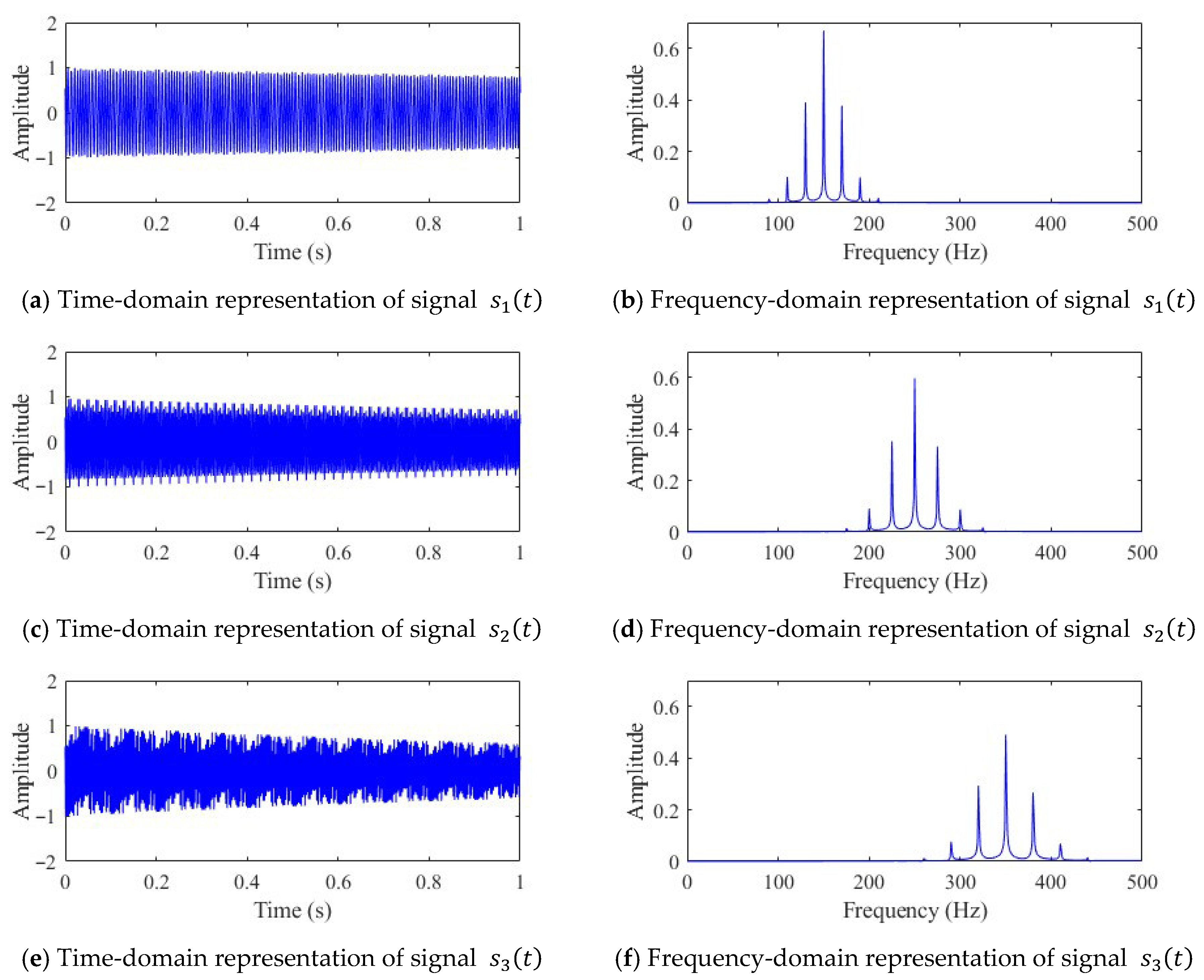
2.2. Short-Time Fourier Transform
3. Research Methodology
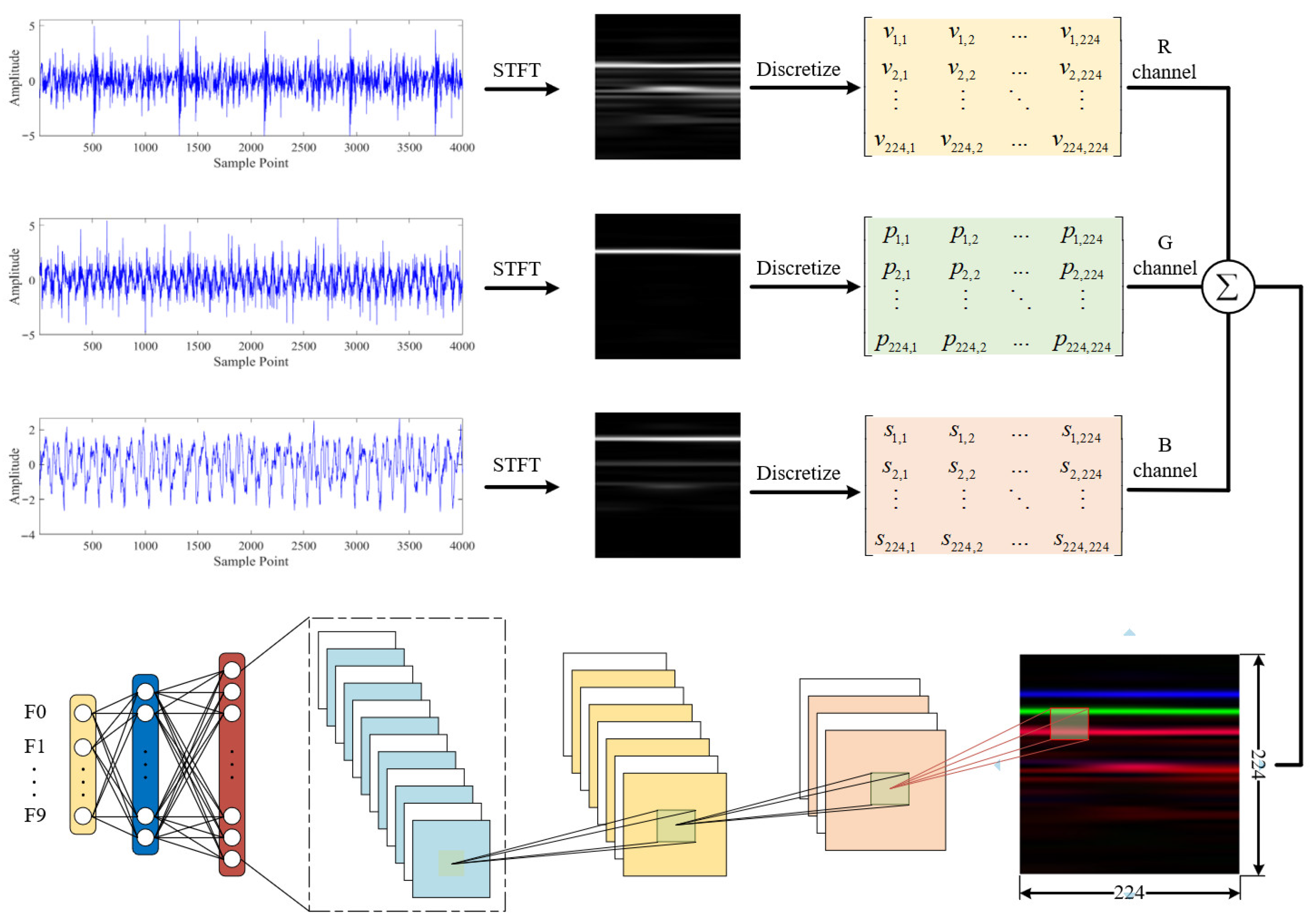
3.1. RGB Image Fusion Method for Multi-Source Signals
| Algorithm 1. RGB Image Generation Process from Multi-Channel Signals Using STFT | |
| Step | Description |
| Input: | Multi-channel signals x(t), p(t), s(t) with sampling rate fs. |
| Output: | RGB fusion images IRGB. |
| Step 1: | For each signal segment xi(t), pi(t), si(t): |
| Step 2: | Z-score Normalization Standardize each segment to have zero mean and unit variance to ensure signals are on the same scale; applied to all channels |
| Step 3: | STFT Computation Compute Short-Time Fourier Transform (STFT) for each segment and limit the frequency range to a specified upper bound. |
| Step 4: | Convert STFT magnitudes to decibels (dB) and normalize to the range [0,1]. |
| Step 5: | Resize each channel image to a fixed size. |
| Step 6: | Combine the three channel images to form an RGB image. |
| Step 7: | Save the generated RGB image as a PNG file, naming according to class and index |
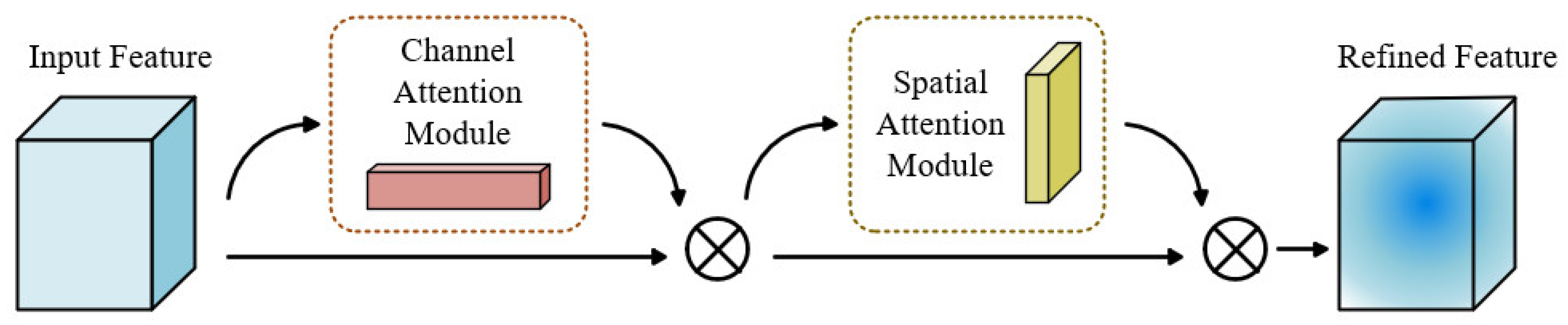
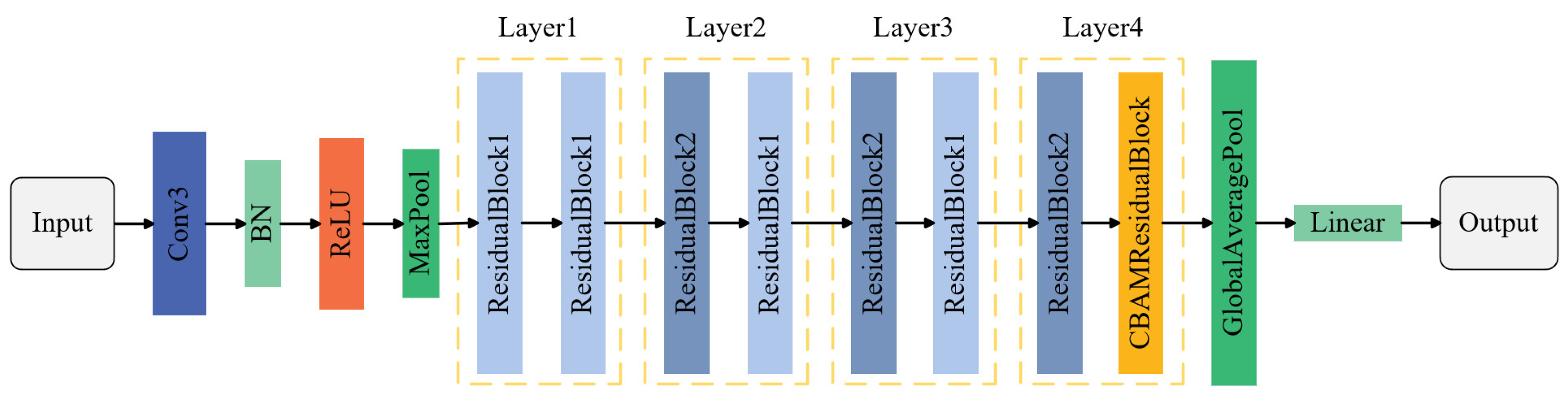
3.2. Design of the Improved ResNet-18 Network
| Algorithm 2. Algorithmic description of the construction process of CBAM-ResNet-18 network | |
| Step | Description |
| Input: | Input image size 224 × 224 × 3; kernel size k; stride s; padding p; number of filters Fi; channel and spatial attention weights from CBAM. |
| Output: | Layer graph LCBAM-ResNet18 containing all convolutional, normalization, residual, and attention connections. |
| Step 1: | Initialize an empty layer graph L←∅. |
| Step 2: | Add input stem: a. Add imageInputLayer with z-score normalization. b. Add a 7 × 7 convolution layer (64 filters, stride = 2, padding = 3). c. Apply batch normalization and ReLU activation. d. Add 3 × 3 max pooling (stride = 2). |
| Step 3: | Construct residual stages: for each residual block group Gi∈{Res2, Res3, Res4, Res5} do a. Main path (branch2): add two 3 × 3 convolution layers with batch normalization and ReLU. b. Shortcut path (branch1): if downsampling is required, add a 1 × 1 convolution (stride = 2). c. Merge: fuse the two branches via additionLayer(2) followed by ReLU activation. end for |
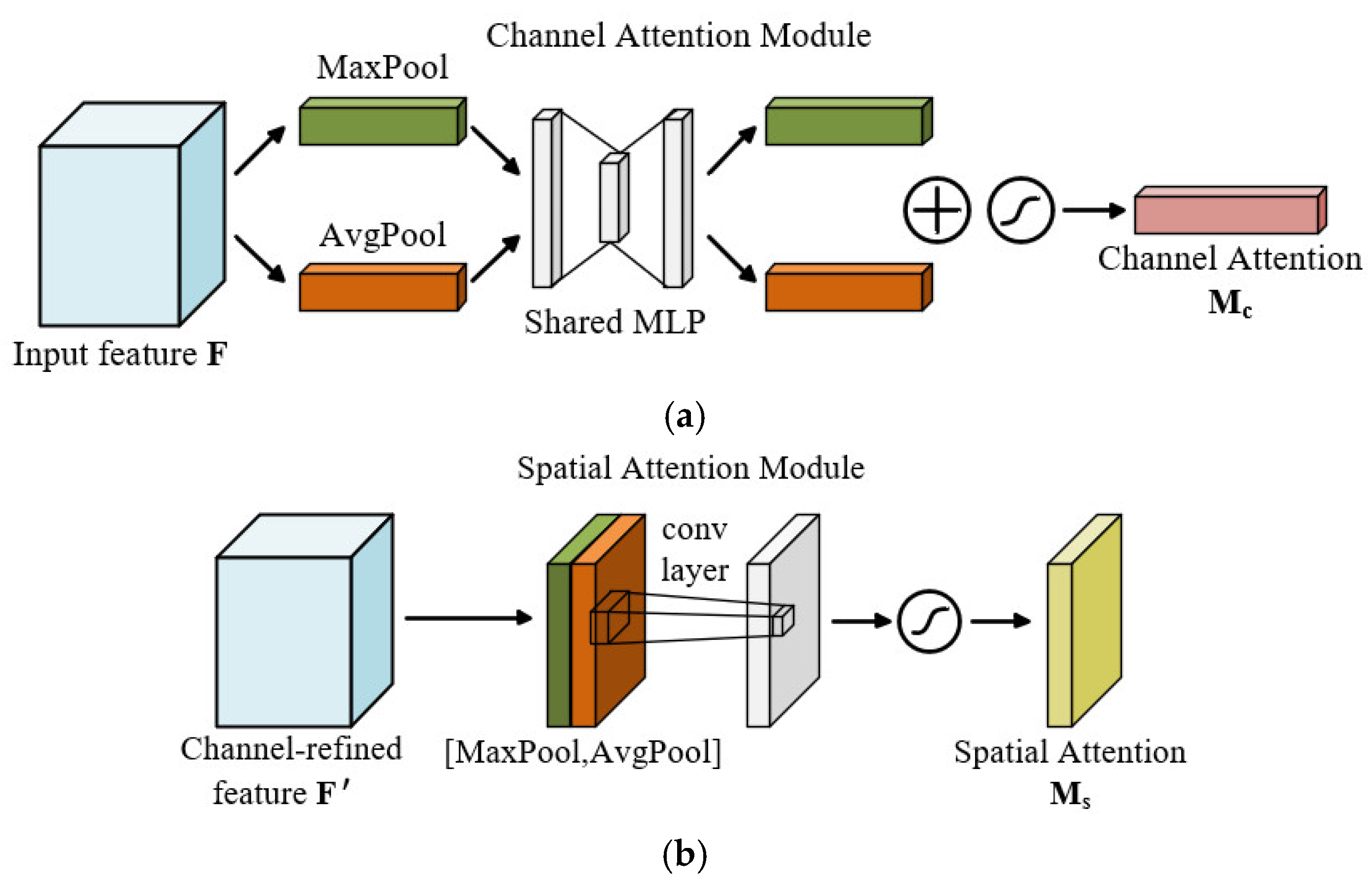
| Step 4: | Insert CBAM: a. Detach the output of the final residual block (Res5b). b. Add CBAM subnetwork with two sequential attention units: —Channel attention: global average pooling → MLP → sigmoid weighting. —Spatial attention: concatenate max/avg feature maps → convolution → sigmoid. c. Reconnect CBAM output to the main residual path. |
| Step 5: | Add classification head: a. Apply global average pooling. b. Add a fully connected layer (10 output neurons). c. Append softmax and classification layers. |
| Step 6: | Return the completed network graph LCBAM-ResNet18 |
| Notes: | The CBAM adaptively refines features via channel and spatial attention, improving discriminative capability while preserving ResNet-18’s computational efficiency. |
3.3. Fault Diagnosis Procedure
- 1.
- Data Collection: Operational data of the hydraulic pump under various operating conditions are acquired using sensors—such as vibration, pressure, and sound—placed at key locations on the pump.
- 2.
- Data Preprocessing: The raw signals are segmented into fixed-length intervals and normalized using Z-score standardization to make the amplitudes dimensionless, eliminating scale differences among different physical quantities.
- 3.
- RGB Image Construction: Each signal segment is transformed into a grayscale spectrogram using STFT and discretized into a grayscale matrix. The matrix amplitudes are then normalized to a 0–255 range. The grayscale matrices of the individual signals are assigned to the R, G, and B channels, respectively. Finally, the three matrices corresponding to the same time interval are combined to form a single RGB image.
- 4.
- Model Training: The resulting RGB images are fed into a convolutional neural network, with the dataset split into training and testing sets in appropriate proportions, to train the CNN model to recognize various fault types of the hydraulic pump.
4. Experimental Setup and Results Analysis
4.1. Dataset Description
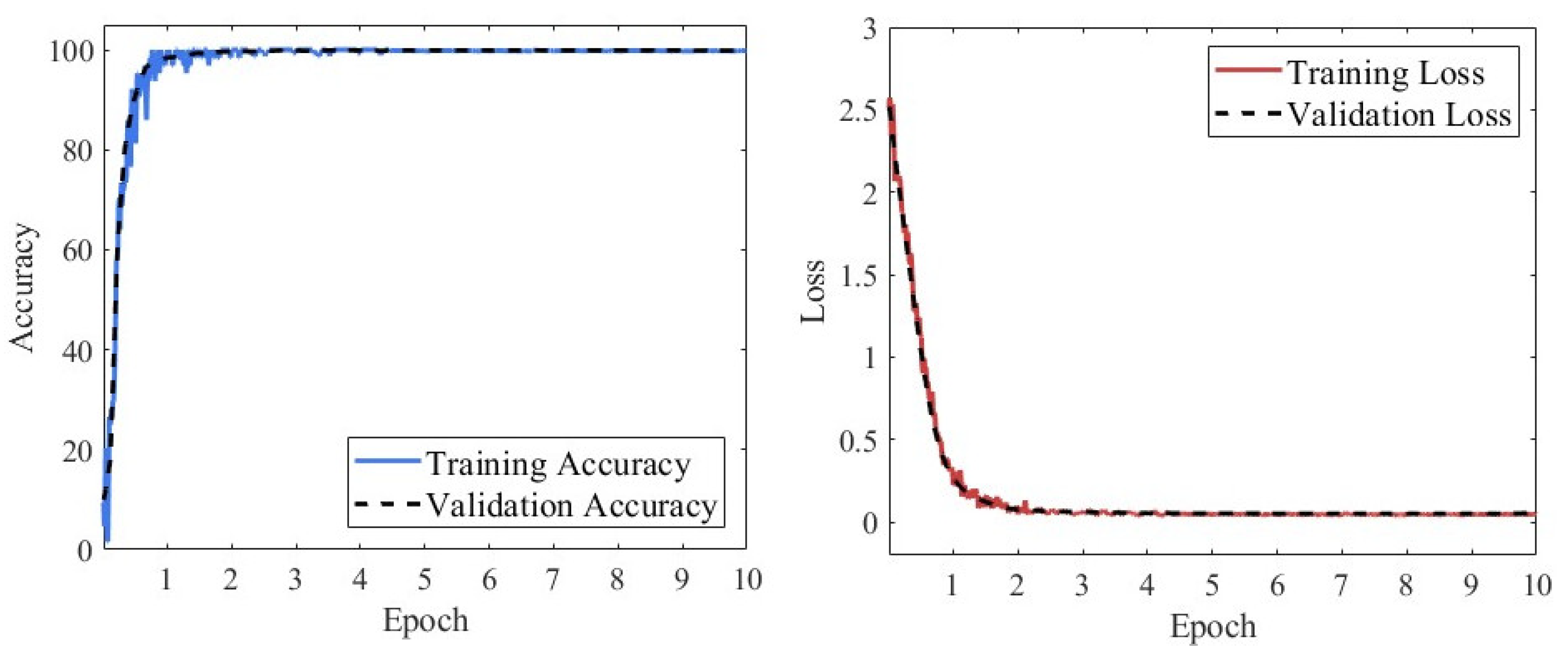
4.2. Data Preprocessing and Hyperparameter Settings
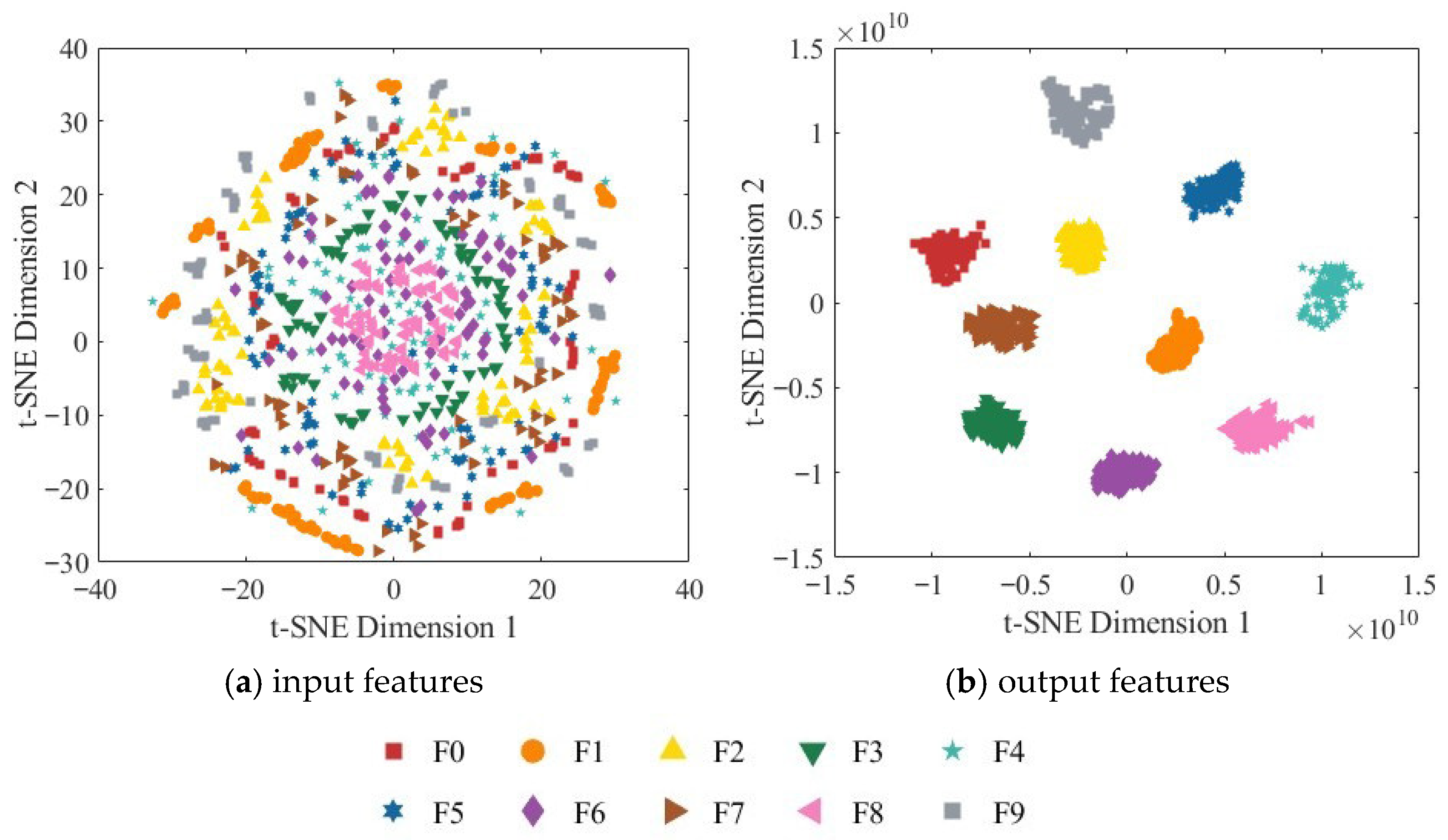
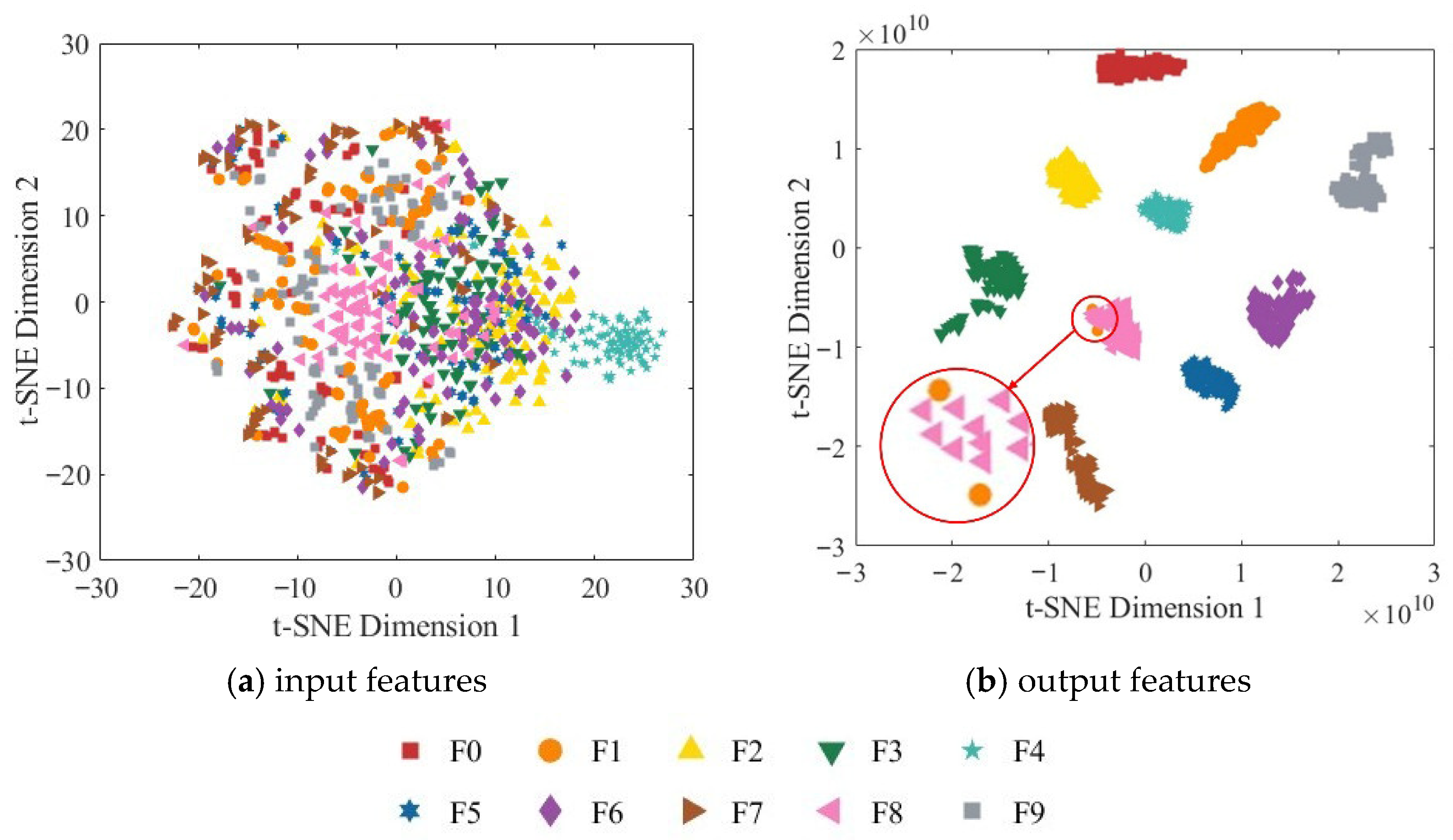
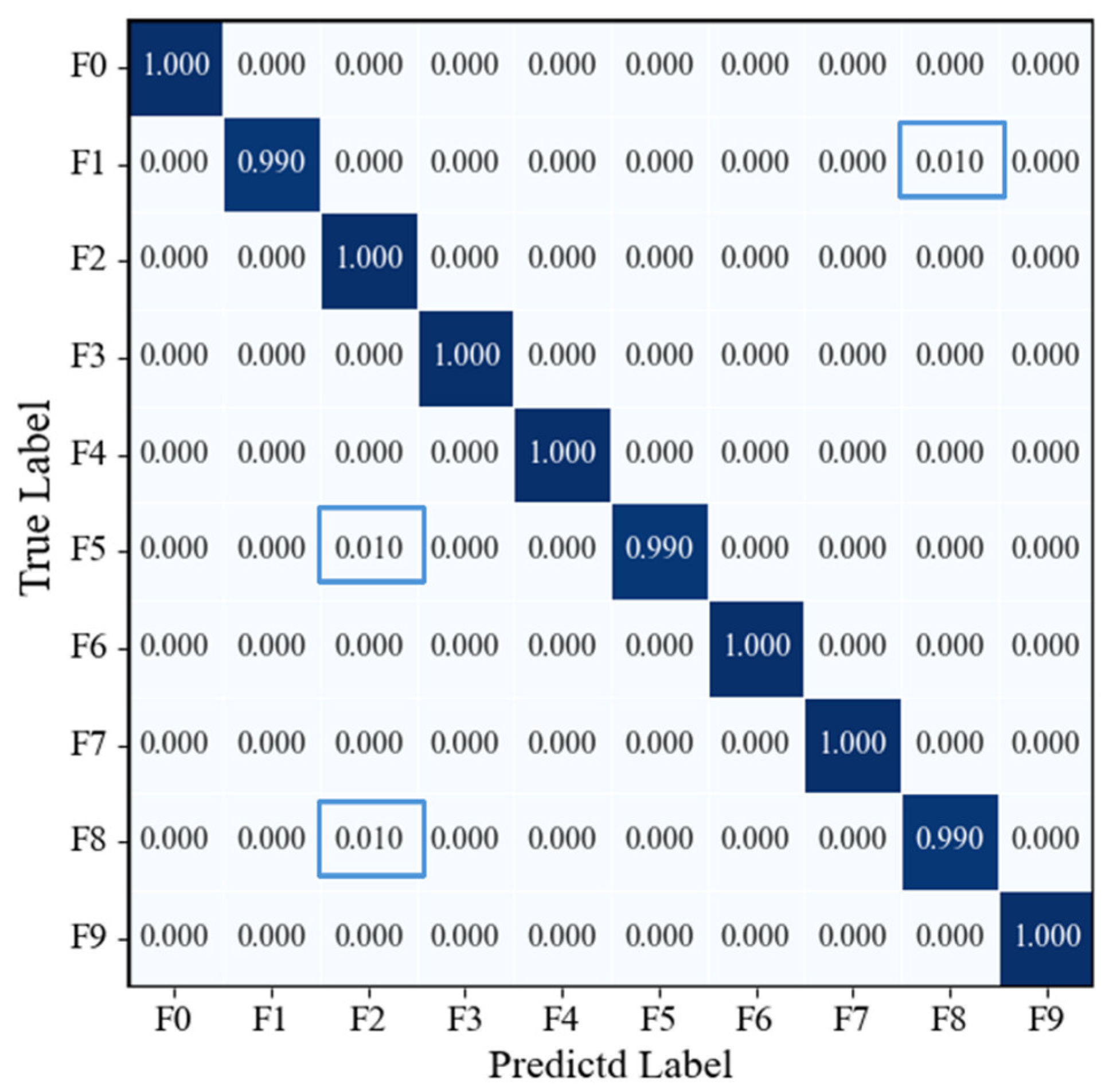
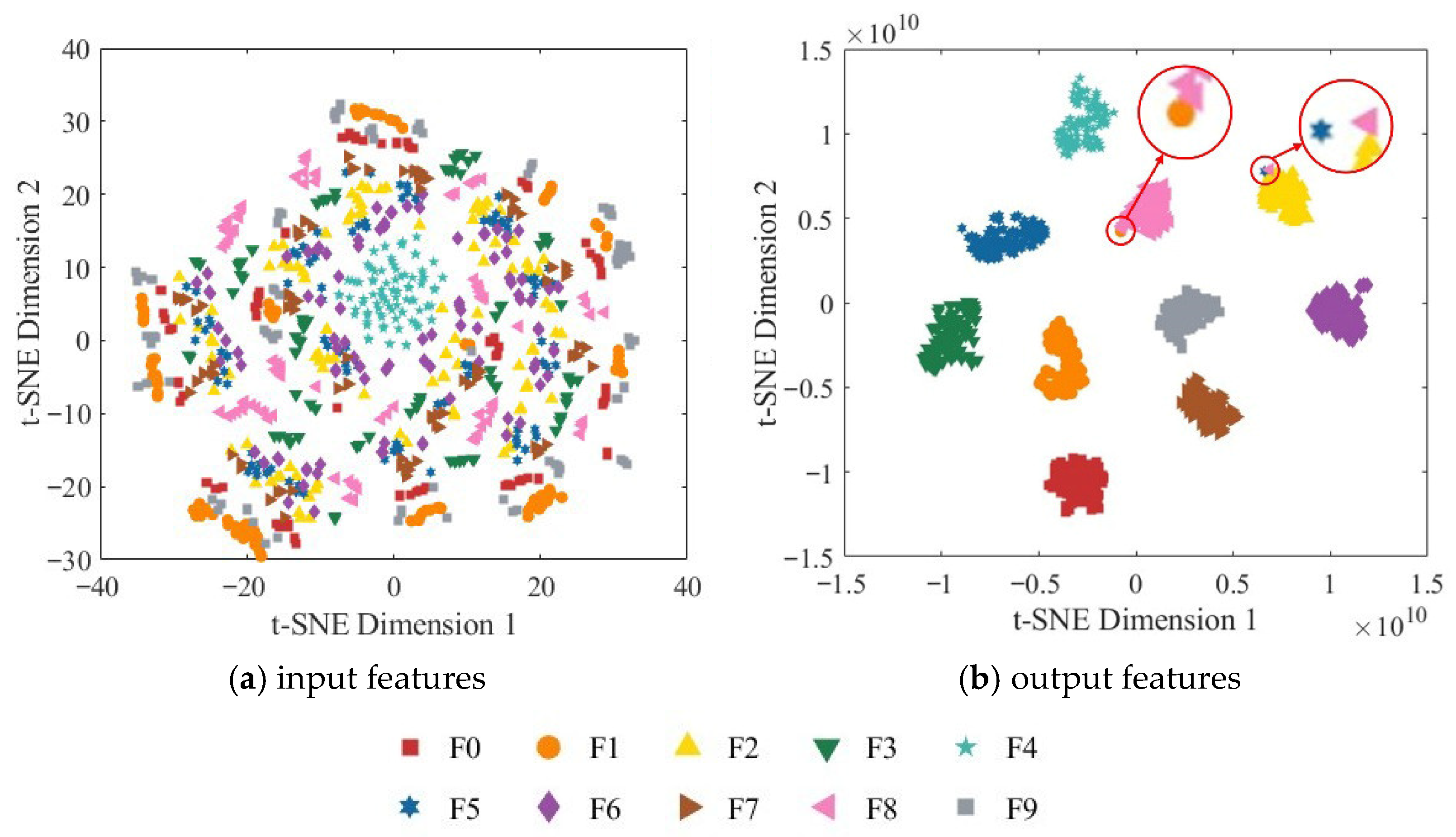
4.3. Results Analysis
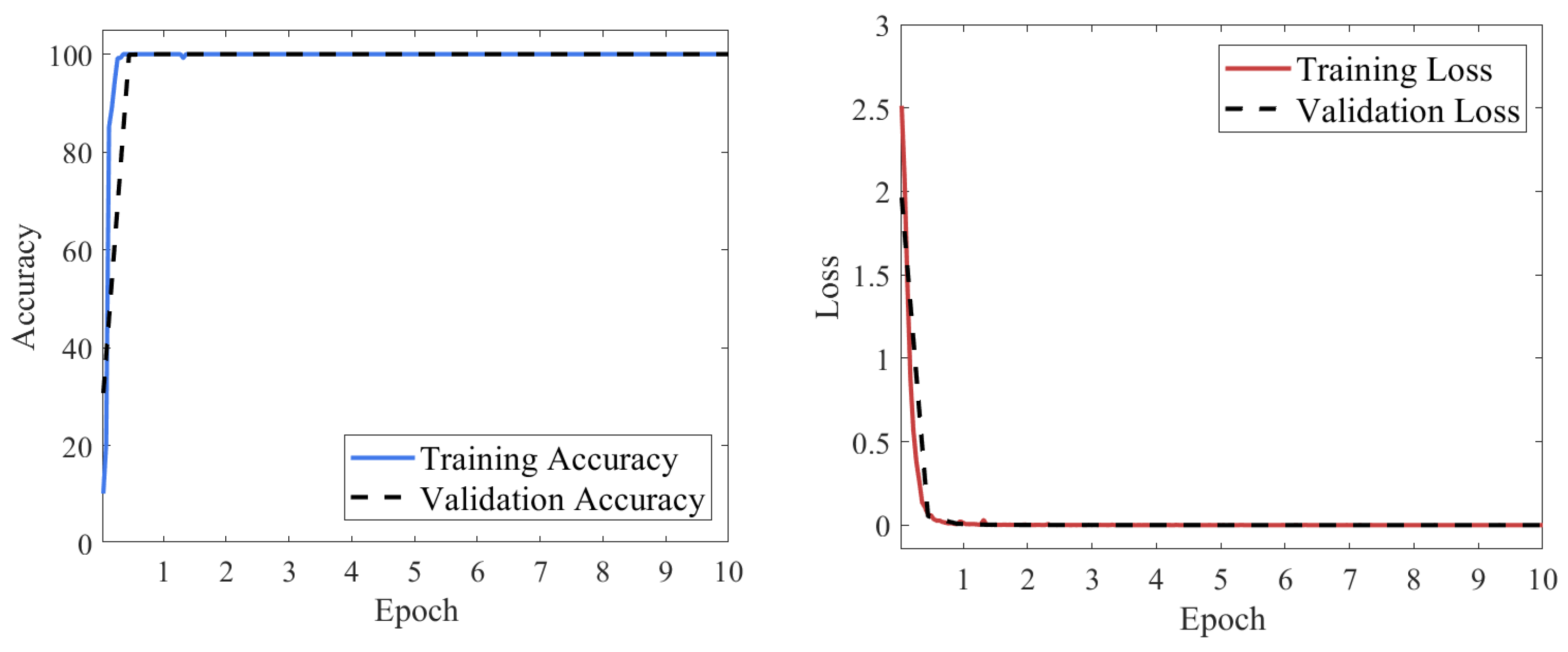
4.3.1. Hydraulic Pump Fault Diagnosis Based on RGB-CBAM-ResNet-18
4.3.2. Comparative Analysis
5. Conclusions
- (1)
- In this paper, time-frequency features of vibration, pressure, and sound signals are extracted to construct uniform-scale RGB images, enabling visualization of multi-source data fusion and adapting to the input requirements of convolutional neural networks. Experimental results demonstrate that this fusion strategy significantly improves fault identification performance compared with single-signal input.
- (2)
- Based on the ResNet-18 architecture, an improved approach incorporating a dual attention mechanism was proposed, and a novel residual module integrating both channel and spatial attention mechanisms was designed. Comparative experiments verified the network’s superior capability in feature extraction and classification performance.
- (3)
- An intelligent fault diagnosis framework integrating multi-source signal fusion with the improved residual neural network was developed to achieve automatic identification and classification of multiple hydraulic pump fault states, enhancing the intelligence of the diagnostic process and demonstrating high diagnostic accuracy and strong engineering applicability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.; Li, G.; Tang, S.; Wang, R.; Su, H.; Wang, C. Acoustic signal-based fault detection of hydraulic piston pump using a particle swarm optimization enhancement CNN. Appl. Acoust. 2022, 192, 108718. [Google Scholar] [CrossRef]
- Xia, S.; Huang, W.; Zhang, J. A novel fault diagnosis method based on nonlinear-CWT and improved YOLOv8 for axial piston pump using output pressure signal. Adv. Eng. Inform. 2025, 64, 103041. [Google Scholar] [CrossRef]
- Liu, S.; Yin, J.; Zhang, Y.; Liang, P. MLIFT: Multi-scale linear interaction fusion transformer for fault diagnosis of hydraulic pumps. Measurement 2025, 254, 117892. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Wang, R.; Tang, S.; Su, H.; Cao, K. Intelligent fault diagnosis of hydraulic piston pump combining improved LeNet-5 and PSO hyperparameter optimization. Appl. Acoust. 2021, 183, 108336. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearings using an improved multi-scale convolutional neural network with feature attention mechanism. ISA Trans. 2021, 110, 379–393. [Google Scholar] [CrossRef]
- Xiao, Q.; Li, S.; Zhou, L.; Shi, W. Improved variational mode decomposition and CNN for intelligent rotating machinery fault diagnosis. Entropy 2022, 24, 908. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Zhong, Y.; Tang, H. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Eang, C.; Lee, S. Predictive maintenance and fault detection for motor drive control systems in industrial robots using CNN-RNN-based observers. Sensors 2025, 25, 25. [Google Scholar] [CrossRef]
- Lian, C.; Zhao, Y.; Sun, T.; Dong, F.; Zhan, Z.; Xin, L. A new time series data imaging scheme for mechanical fault diagnosis. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Liang, Z.; Shao, H.; Yu, K.; Yu, W. An adaptive domain adaptation method for rolling bearings’ fault diagnosis fusing deep convolution and self-attention networks. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Kumar, A.; Gandhi, C.P.; Zhou, Y.; Kumar, R.; Xiang, J. Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images. Appl. Acoust. 2020, 167, 107399. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Wang, S.; Li, W.; Sarkodie-Gyan, T.; Feng, S. A hybrid deep-learning model for fault diagnosis of rolling bearings. Measurement 2021, 169, 108502. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Gao, R.X. A new intelligent bearing fault diagnosis method using SDP representation and SE-CNN. IEEE Trans. Instrum. Meas. 2020, 69, 2377–2389. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Shao, H.; Lin, J.; Zhang, L.; Galar, D.; Kumar, U. A novel approach of multisensory fusion to collaborative fault diagnosis in maintenance. Inf. Fusion 2021, 74, 65–76. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Liu, J.; Wu, B.; Hu, Y. Graph features dynamic fusion learning driven by multi-head attention for large rotating machinery fault diagnosis with multi-sensor data. Eng. Appl. Artif. Intell. 2023, 125, 106601. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; de Silva, C.W. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE/ASME Trans. Mechatron. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Zhong, S.; Fu, S.; Lin, L. A novel gas turbine fault diagnosis method based on transfer learning with CNN. Measurement 2019, 137, 435–453. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Vashishtha, G.; Chauhan, S.; Sehri, M.; Hebda-Sobkowicz, J.; Zimroz, R.; Dumond, P.; Kumar, R. Advancing machine fault diagnosis: A detailed examination of convolutional neural networks. Meas. Sci. Technol. 2024, 36, 22001. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J.; Zhang, Q.; Liu, K.; Li, K.; Liao, X. Identification and classification of aluminum scrap grades based on the Resnet18 model. Appl. Sci. 2022, 12, 11133. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, K.; Bai, R.; Sun, D.; Meng, Z. An enhanced convolutional neural network for bearing fault diagnosis based on time–frequency image. Measurement 2020, 157, 107667. [Google Scholar] [CrossRef]
- Zhu, Z.; Peng, G.; Chen, Y.; Gao, H. A convolutional neural network based on a capsule network with strong generalization for bearing fault diagnosis. Neurocomputing 2019, 323, 62–75. [Google Scholar] [CrossRef]
- Kibrete, F.; Engida Woldemichael, D.; Shimels Gebremedhen, H. Multi-sensor data fusion in intelligent fault diagnosis of rotating machines: A comprehensive review. Measurement 2024, 232, 114658. [Google Scholar] [CrossRef]
- Guo, J.; Yang, Y.; Li, H.; Dai, L.; Huang, B. A parallel deep neural network for intelligent fault diagnosis of drilling pumps. Eng. Appl. Artif. Intell. 2024, 133, 108071. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–19. ISBN 978-3-030-01233-5. [Google Scholar] [CrossRef]
- Jiang, K.; Xie, T.; Yan, R.; Wen, X.; Li, D.; Jiang, H.; Jiang, N.; Feng, L.; Duan, X.; Wang, J. An Attention Mechanism-Improved YOLOv7 Object Detection Algorithm for Hemp Duck Count Estimation. Agriculture 2022, 12, 1659. [Google Scholar] [CrossRef]
- Yan, S.; Wei, H.; Yang, C.; Liu, Z.; Zhang, S.; Zhao, L. Fault diagnosis of rolling bearing based on CBAM-ICNN. In Proceedings of the 2024 39th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Dalian, China, 7–9 June 2024; pp. 1420–1425. [Google Scholar] [CrossRef]
- He, C.; Yasenjiang, J.; Lv, L.; Xu, L.; Lan, Z. Gearbox fault diagnosis based on MSCNN-LSTM-CBAM-SE. Sensors 2024, 24, 4682. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, Q.; Gao, L. Deep convolutional neural networks for tea tree pest recognition and diagnosis. Symmetry 2021, 13, 2140. [Google Scholar] [CrossRef]
- Jing, L.; Wang, T.; Zhao, M.; Wang, P. An adaptive multi-sensor data fusion method based on deep convolutional neural networks for fault diagnosis of planetary gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-L.; Zhang, B.-X.; Xu, J.-H.; Chen, Z.-L.; Zheng, X.-Y.; Zhu, K.-Q.; Xie, H.; Bo, Z.; Yang, Y.-R.; Wang, X.-D. Fault diagnosis and removal for hybrid power generation systems based on an ensemble deep learning diagnostic method with self-healing strategies. Int. J. Hydrogen Energy 2025, 109, 1297–1313. [Google Scholar] [CrossRef]

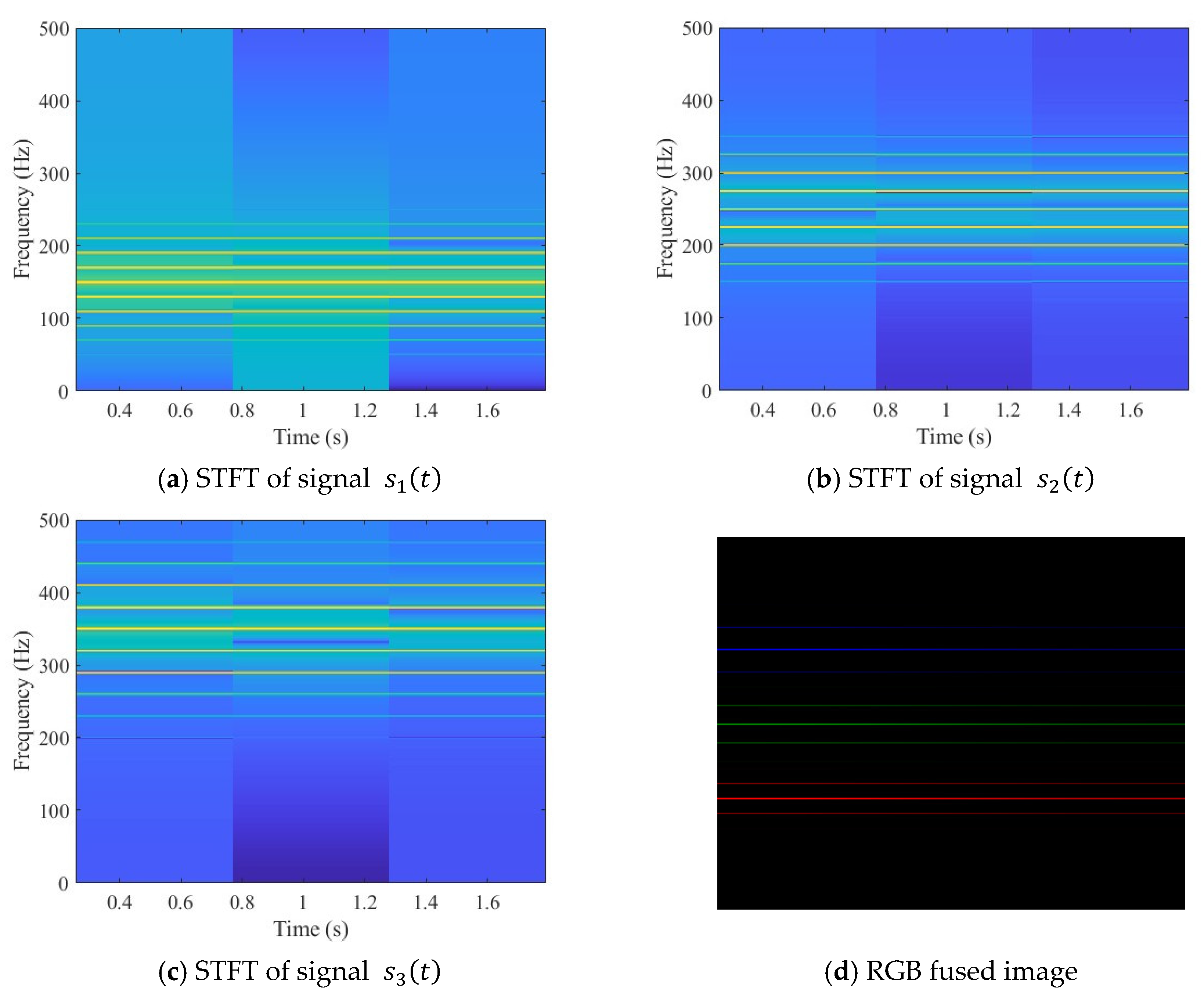












| Fusion Level | Advantages | Disadvantages |
|---|---|---|
| Data-level Fusion | Retains the most complete raw information, providing richer data support for end-to-end feature learning in deep learning models. | Requires strict time synchronization and signal normalization; sensitive to noise; high-dimensional data may increase computational and storage costs. |
| Feature-level Fusion | Balances information retention with model adaptability, enhancing the discriminative capability of feature representations. | Relies on manual feature extraction and selection; low degree of automation in the modeling process; sensitive to feature weighting and fusion strategies. |
| Decision-level Fusion | Exhibits good robustness and scalability; suitable for multi-model ensembles and cross-domain diagnostic scenarios. | Only fuses final outputs, failing to effectively utilize raw data and intermediate feature information, which may reduce diagnostic accuracy. |
| Component | Model | Specifications |
|---|---|---|
| Constant-Pressure Variable Pump | P08-B3-F-R-01 | Displacement: 8 mL/r |
| Rated Pressure: 3~21 MPa | ||
| Rated Speed: 500~2000 r/min | ||
| Drive Motor | C07-43BO | Rated Power: 5.5 kW |
| Rated Speed: 1440 r/min | ||
| Accelerometer | PCB M603C01 | Sensitivity: 100 mV/g |
| Range: ±50 g | ||
| Frequency Response: 0.5 Hz~10 kHz | ||
| Pressure Sensor | PS300-B250G1/2MA3P | Measurement Range: 0~25 MPa |
| Supply Voltage: 12~30 VDC | ||
| Output Signal: 4~20 mA | ||
| Sound Level Meter | AWA5661 | Measurement Range: 25~140 dB |
| Sensitivity: 40 mV/Pa | ||
| Frequency Range: 10 Hz~16 kHz |
| No. | Fault Type | Setting Method | Label |
|---|---|---|---|
| 1 | Normal | — | F0 |
| 2 | Loose Slipper (mild) | Use a plunger slipper assembly with a certain degree of looseness; slipper clearance: 0.24 mm | F1 |
| 3 | Loose Slipper (Severe) | Use a plunger slipper assembly with a certain degree of looseness; slipper clearance: 0.48 mm | F2 |
| 4 | Slipper Wear (mild) | Grind the slipper with 80-grit sandpaper until its mass decreases by 0.2 g and slightly uneven wear is applied | F3 |
| 5 | Slipper Wear (Severe) | Grind the slipper with 40-grit sandpaper until its mass decreases by 0.6 g and slightly uneven wear is applied | F4 |
| 6 | Plunger Wear (mild) | Grind the plunger with 180-grit sandpaper until its mass decreases by 0.15 g | F5 |
| 7 | Plunger Wear (Severe) | Grind the plunger with 100-grit sandpaper until its mass decreases by 0.45 g | F6 |
| 8 | Bearing Inner Ring Fault | Use EDM to machine a 1 mm wide × 1 mm deep groove through the inner ring raceway along the perpendicular direction | F7 |
| 9 | Bearing Outer Ring Fault | Use EDM to machine a 1 mm wide × 1 mm deep groove through the outer ring raceway along the perpendicular direction | F8 |
| 10 | Bearing Rolling Element Fault | Use EDM to machine a 1 mm diameter × 1 mm deep pit on a rolling element of the bearing | F9 |
| Model | Acc | Model File Size (M) | Params (M) | MFLOPs | Latency (ms) |
|---|---|---|---|---|---|
| RGB-CBAM-ResNet-18 | 99.97 | 39.66 | 11.27 | 2494.64 | 8.27 |
| SVM | 92.89 | 0.24 | 0.03 | 0.14 | 0.07 |
| CWT-ResNet-18 | 99.85 | 39.33 | 11.18 | 1733.89 | 5.70 |
| STFT-ResNet-18 | 99.83 | 39.27 | 11.13 | 1727.33 | 5.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Gu, X.; Zhao, Y.; Tang, E.; Jiang, X.; Song, Z.; Zeng, L. Intelligent Fault Diagnosis of Hydraulic Pumps Based on Multi-Source Signal Fusion and Dual-Attention Convolutional Neural Networks. Sensors 2025, 25, 7018. https://doi.org/10.3390/s25227018
Jiang W, Gu X, Zhao Y, Tang E, Jiang X, Song Z, Zeng L. Intelligent Fault Diagnosis of Hydraulic Pumps Based on Multi-Source Signal Fusion and Dual-Attention Convolutional Neural Networks. Sensors. 2025; 25(22):7018. https://doi.org/10.3390/s25227018
Chicago/Turabian StyleJiang, Wanlu, Xiaoyang Gu, Yonghui Zhao, Enyu Tang, Xu Jiang, Zixu Song, and Linghui Zeng. 2025. "Intelligent Fault Diagnosis of Hydraulic Pumps Based on Multi-Source Signal Fusion and Dual-Attention Convolutional Neural Networks" Sensors 25, no. 22: 7018. https://doi.org/10.3390/s25227018
APA StyleJiang, W., Gu, X., Zhao, Y., Tang, E., Jiang, X., Song, Z., & Zeng, L. (2025). Intelligent Fault Diagnosis of Hydraulic Pumps Based on Multi-Source Signal Fusion and Dual-Attention Convolutional Neural Networks. Sensors, 25(22), 7018. https://doi.org/10.3390/s25227018







