A Path-Planning Scheme for Autonomous Vehicle Navigation Integrating BJA* and Improved DWA Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. BJA* Algorithm
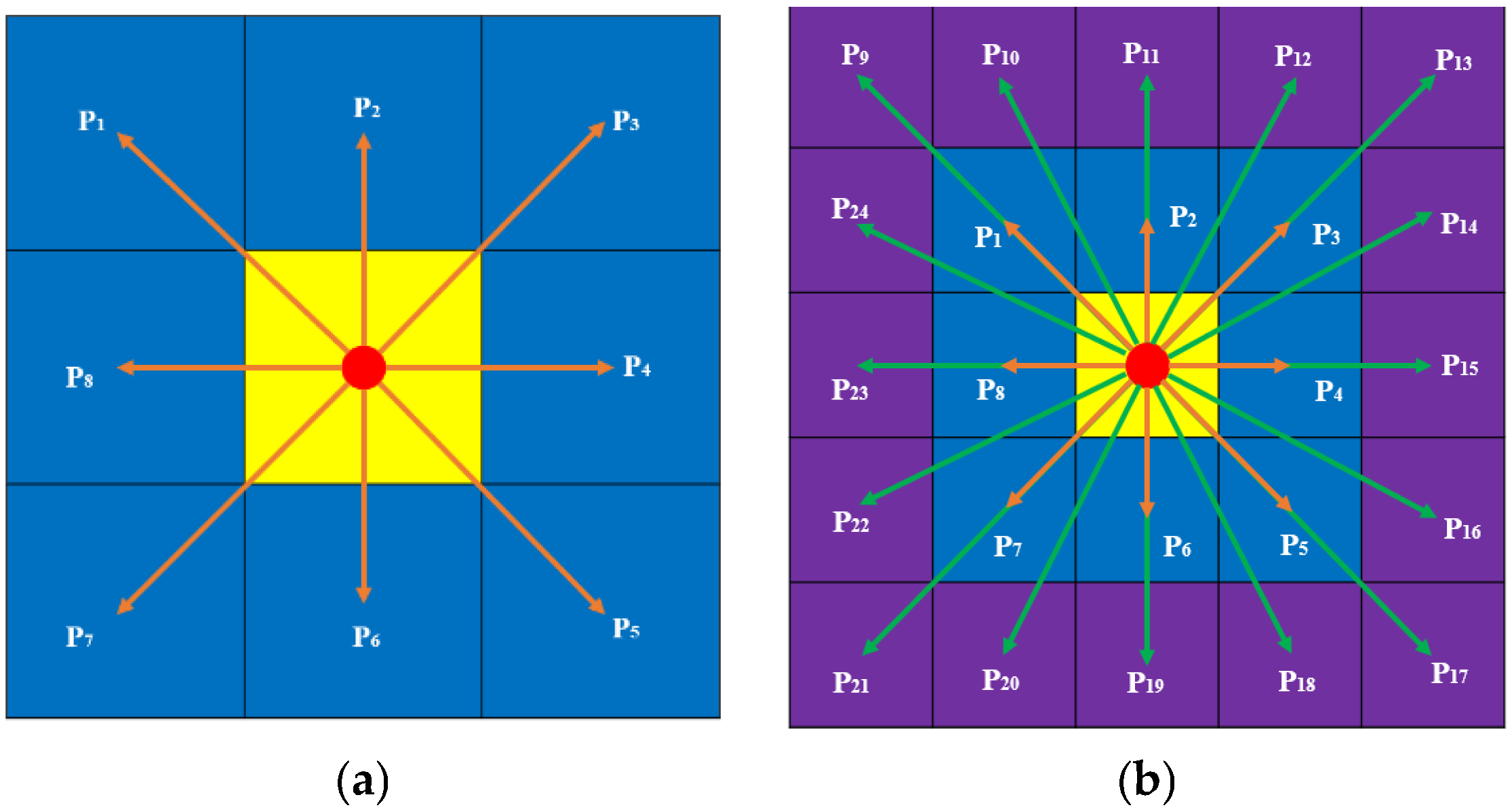
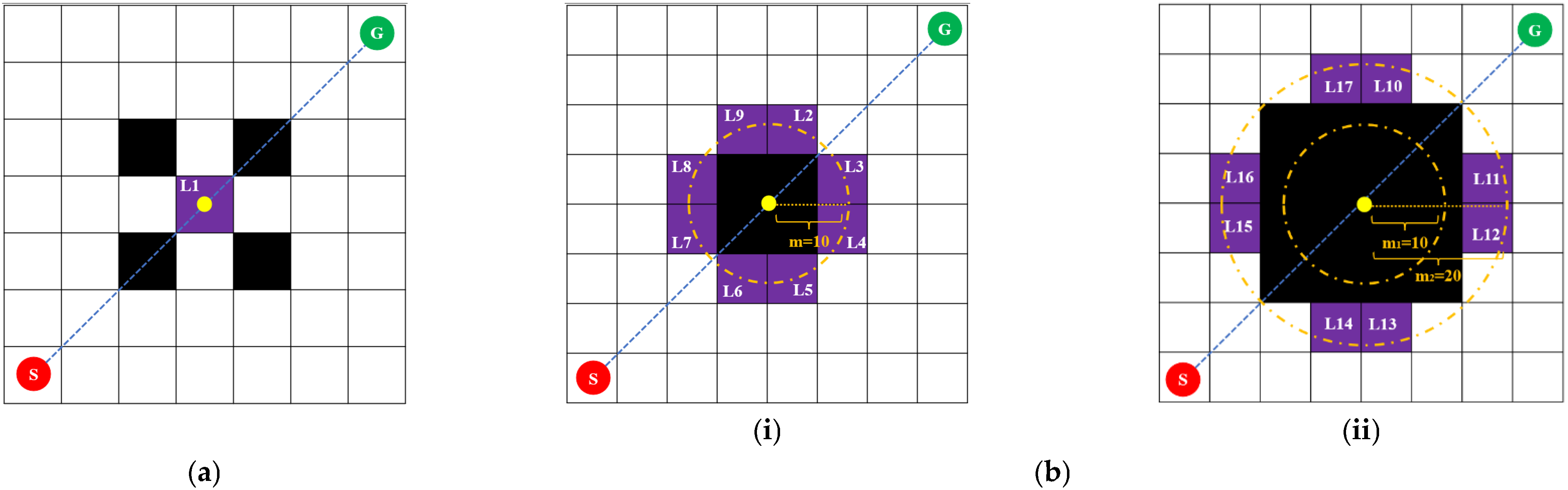
2.1.1. 24-Neighborhood Search
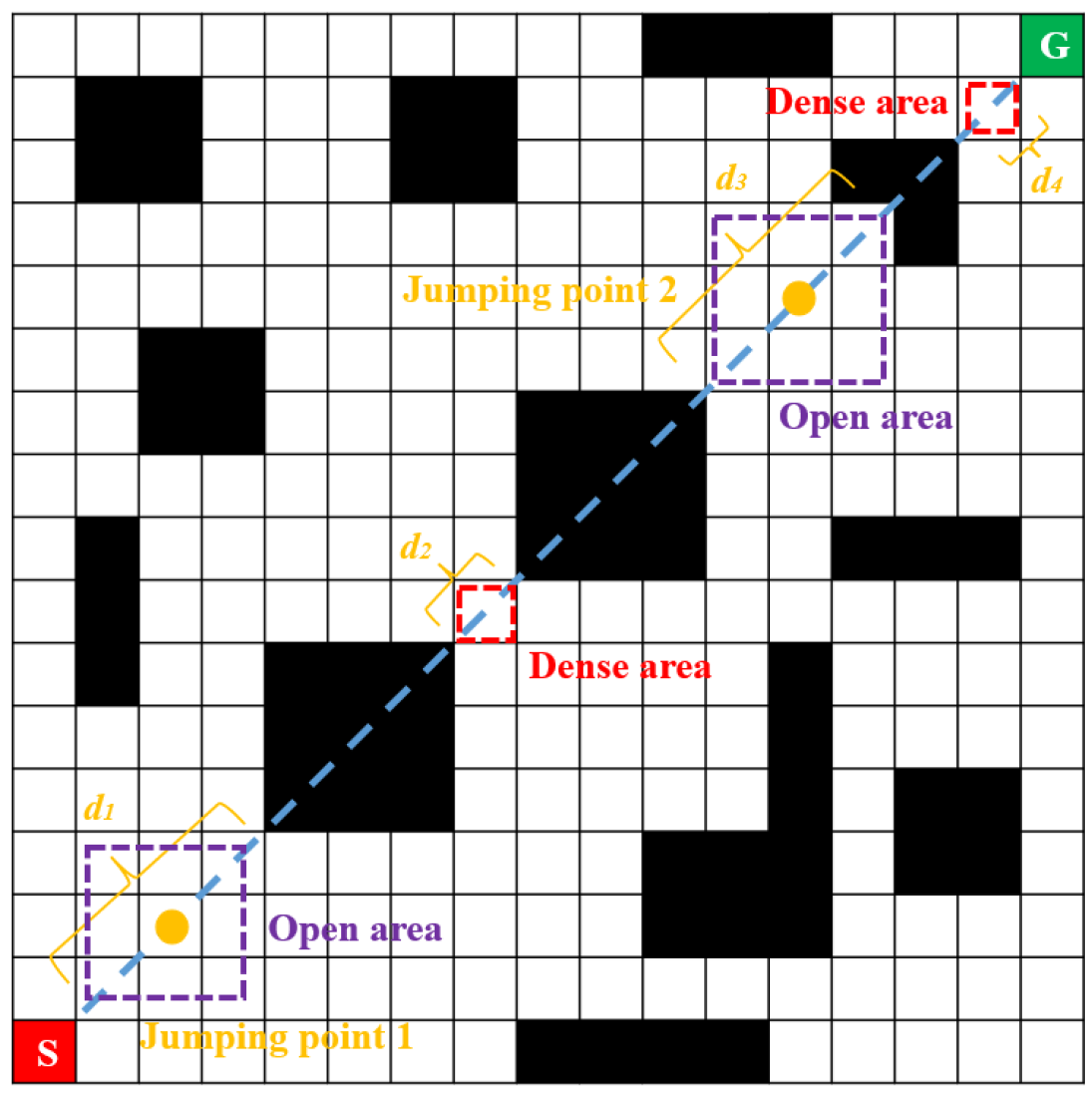
2.1.2. Jump-Point Selection
2.1.3. Determination of Meeting Nodes
2.1.4. Improvements to the Evaluation Function
2.2. DWA Algorithm
2.2.1. Bicycle Model
2.2.2. Speed and Heading-Angle Constraint
2.2.3. Correction Constraint
2.2.4. Improvement of the Evaluation Function
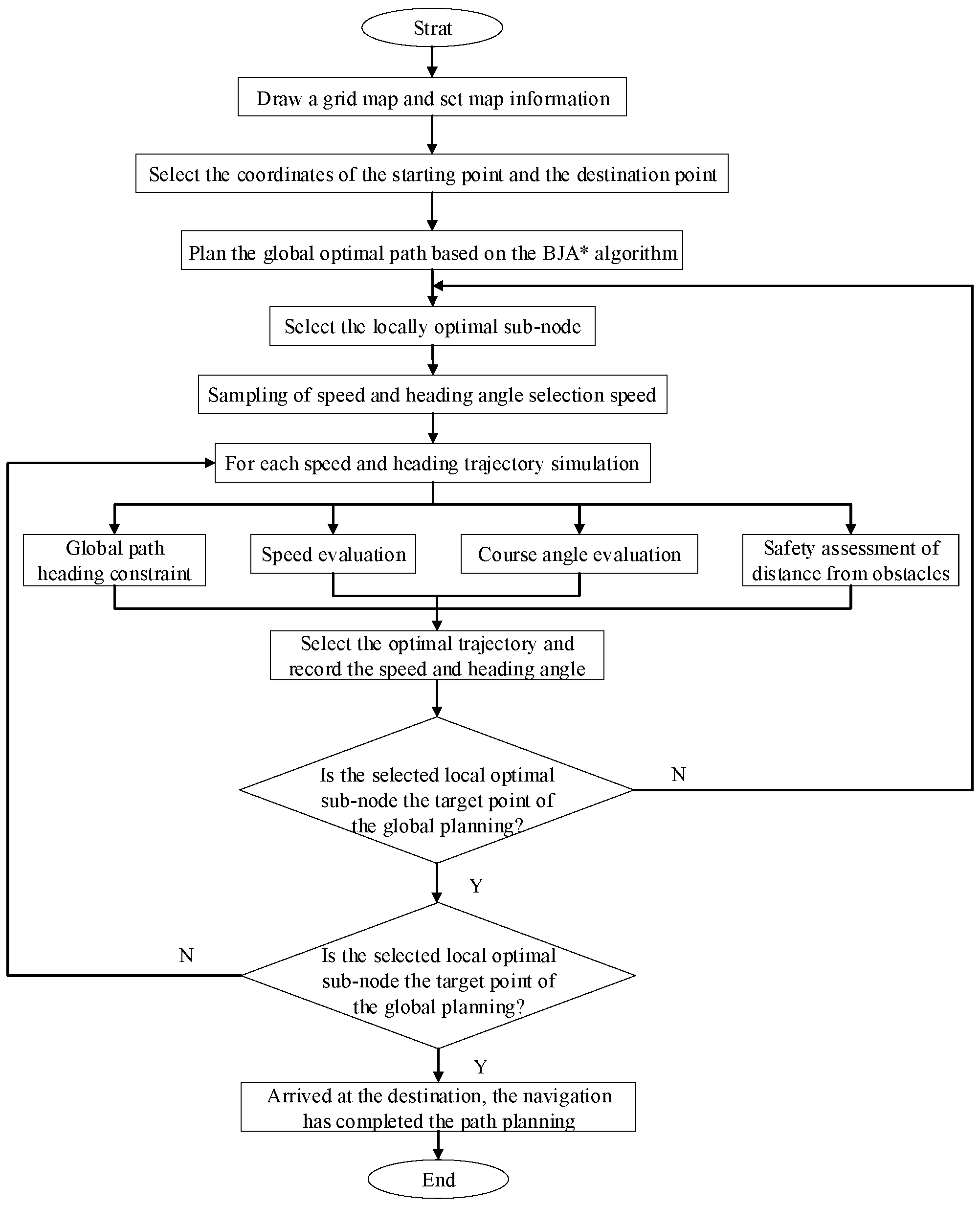
2.3. Fusion Algorithm
3. Results
3.1. Global Path-Planning Simulation Verification
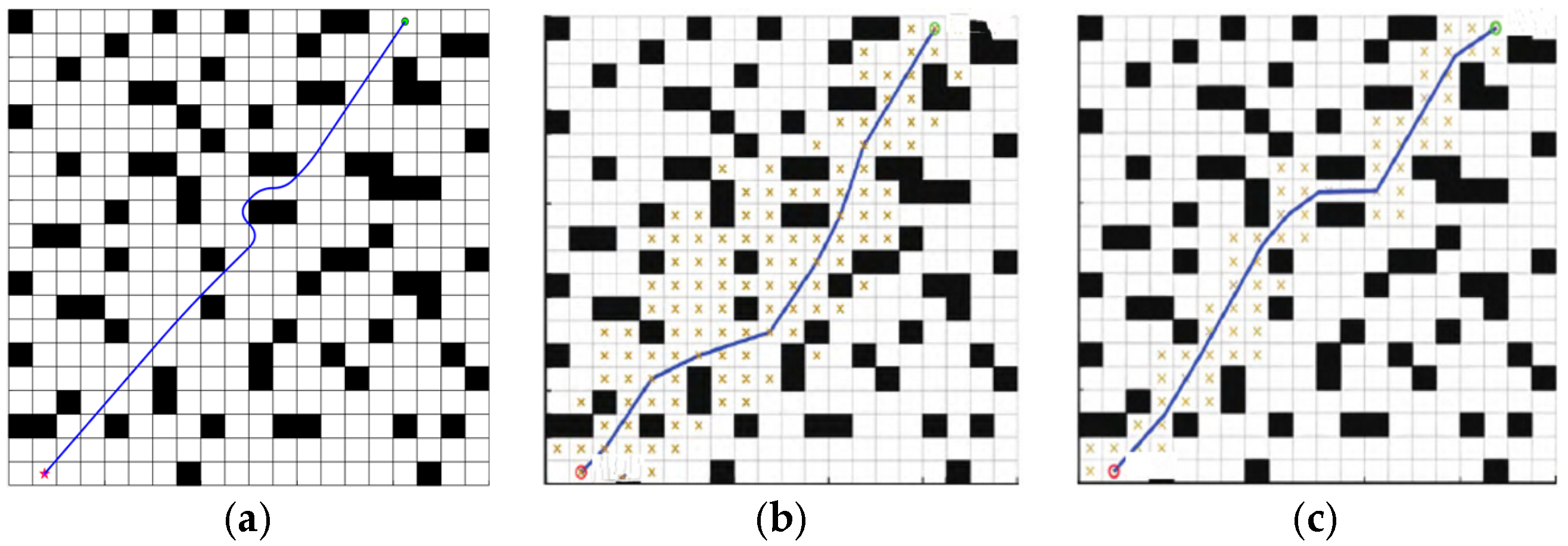
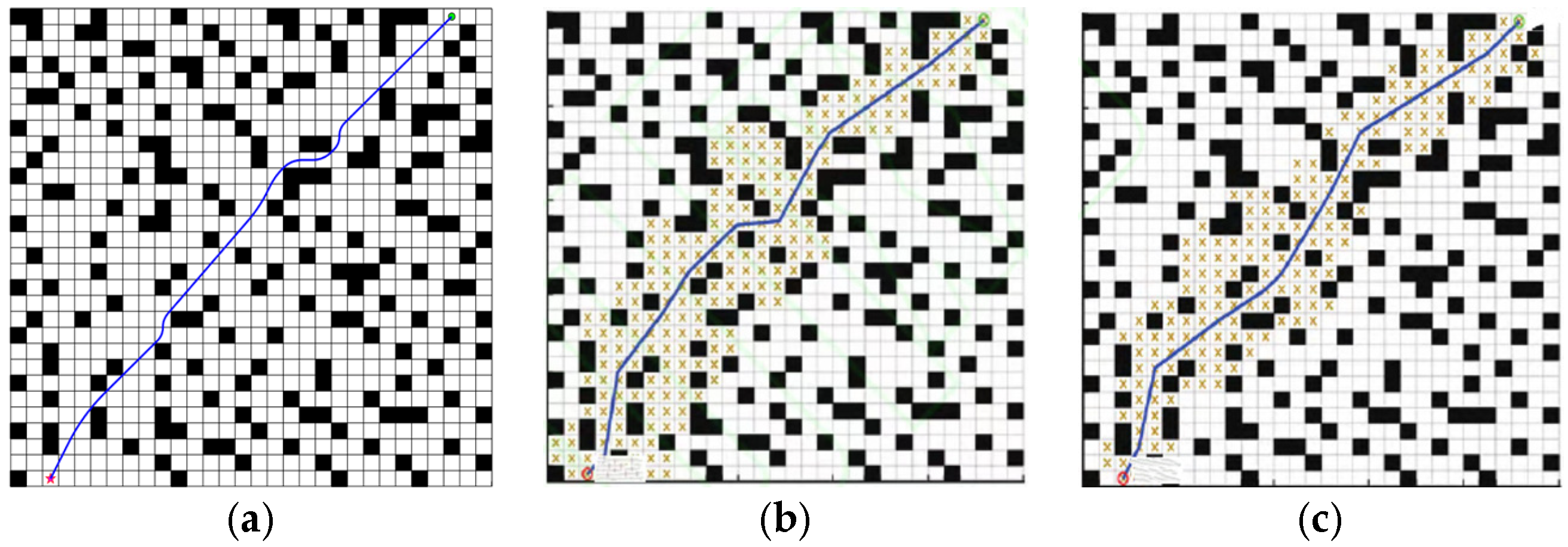
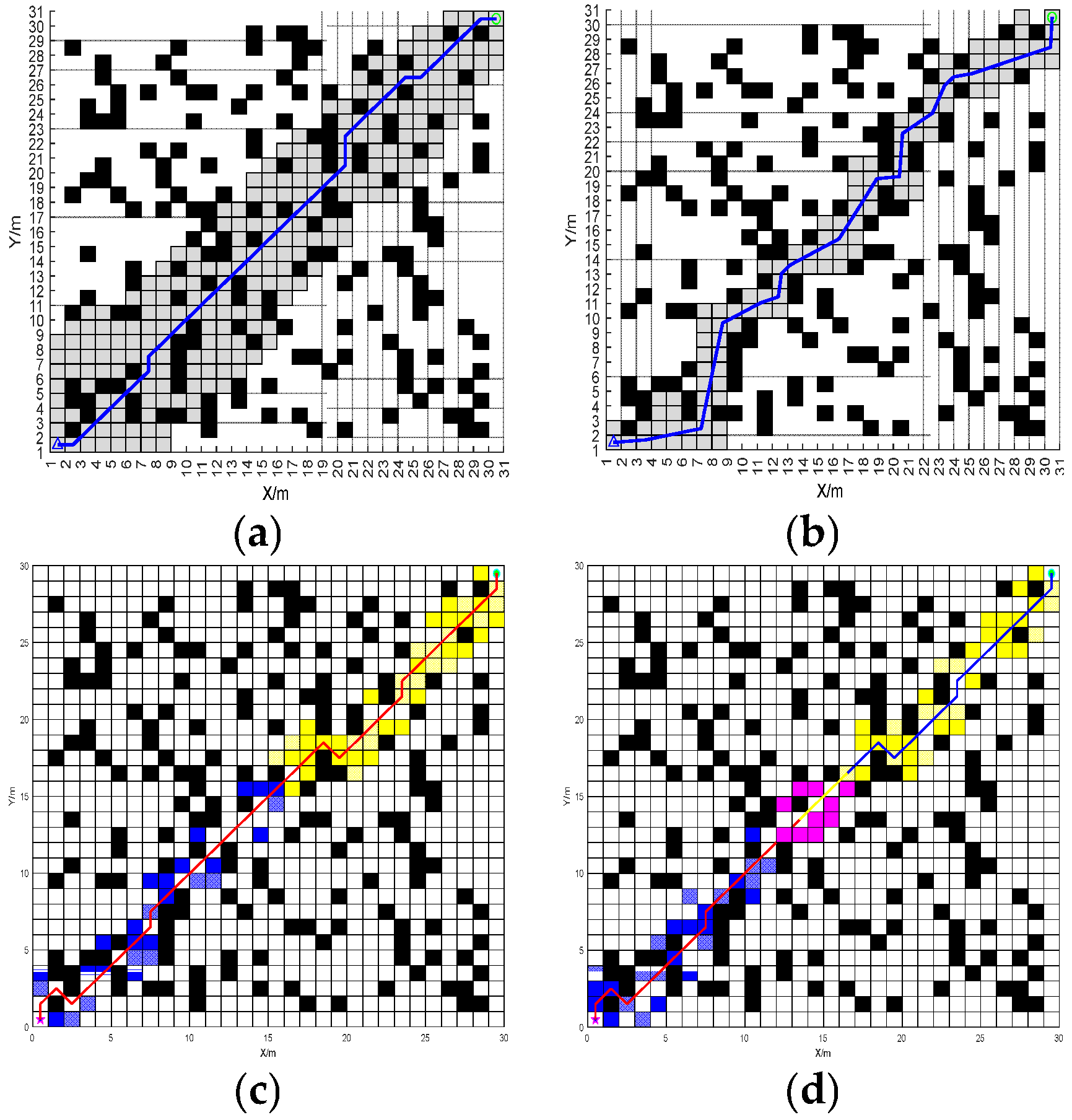
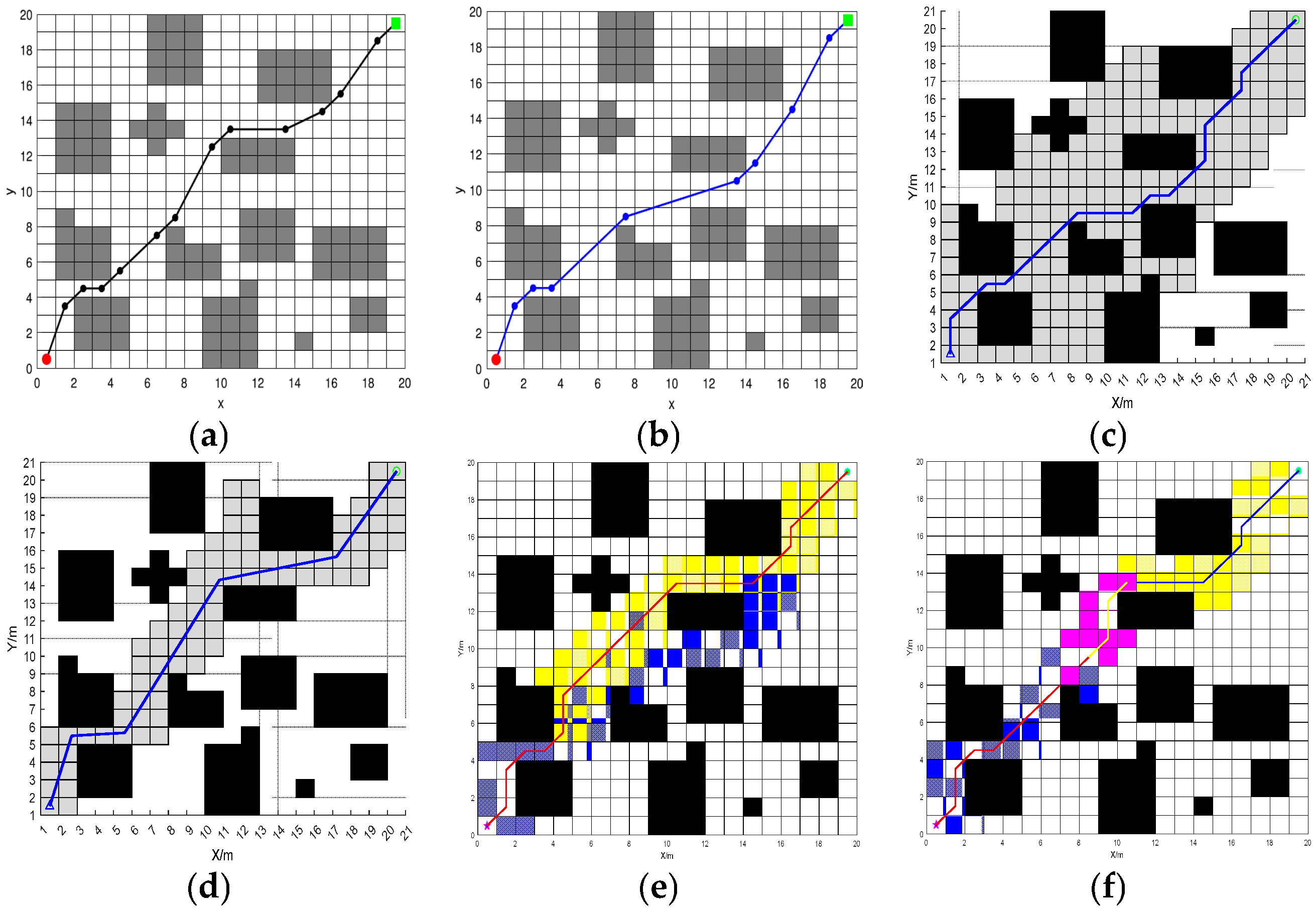
3.1.1. Comparison of BJA* Algorithm and Popular A* Improved Algorithm
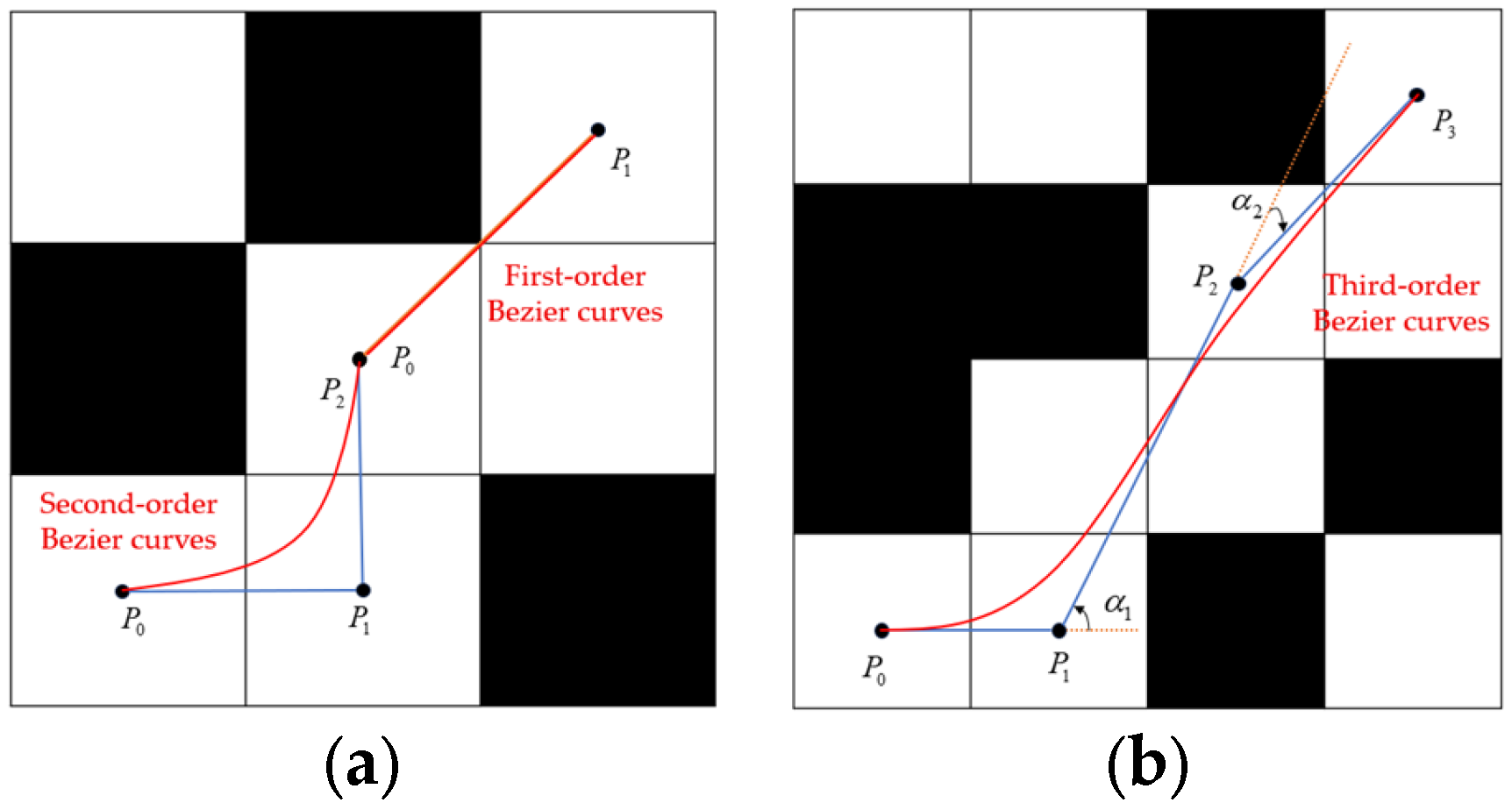
3.1.2. Path Planning Post-Processing
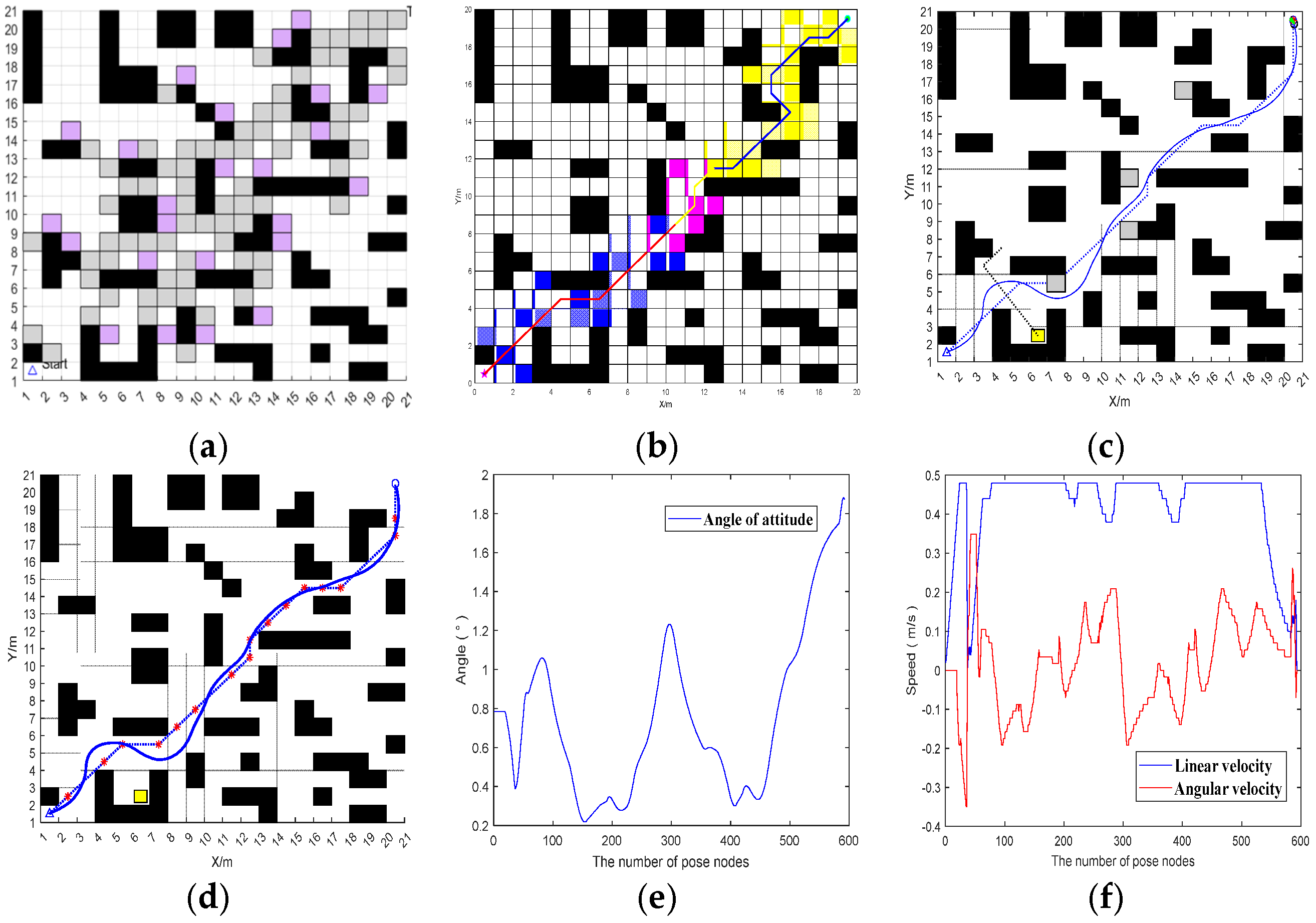
3.1.3. Ablation-Based Analysis of BJA* Algorithm
3.1.4. Statistical Test of BJA* Algorithm
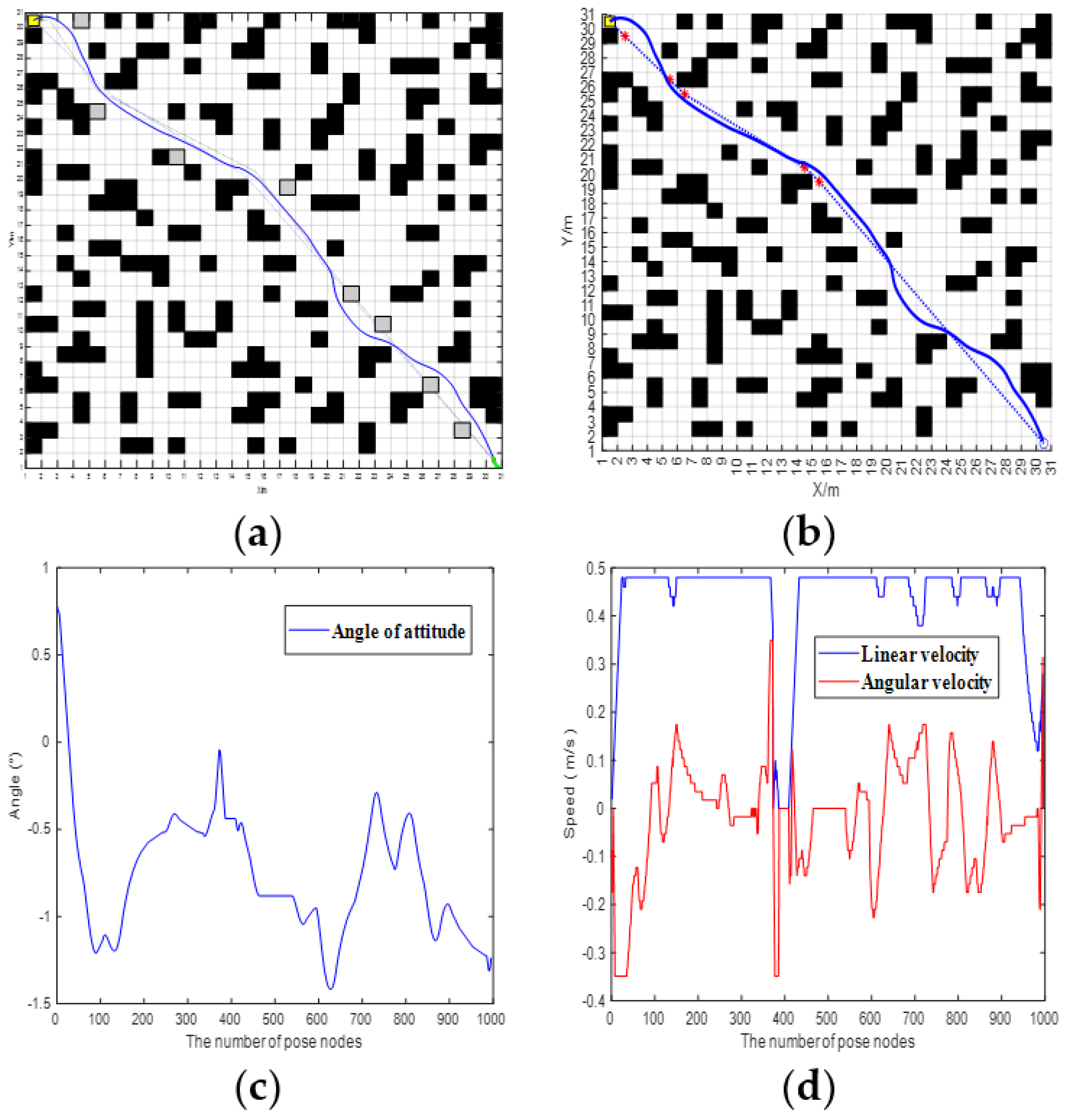
3.1.5. Comparison of BJA* Algorithm and Fusion Algorithm
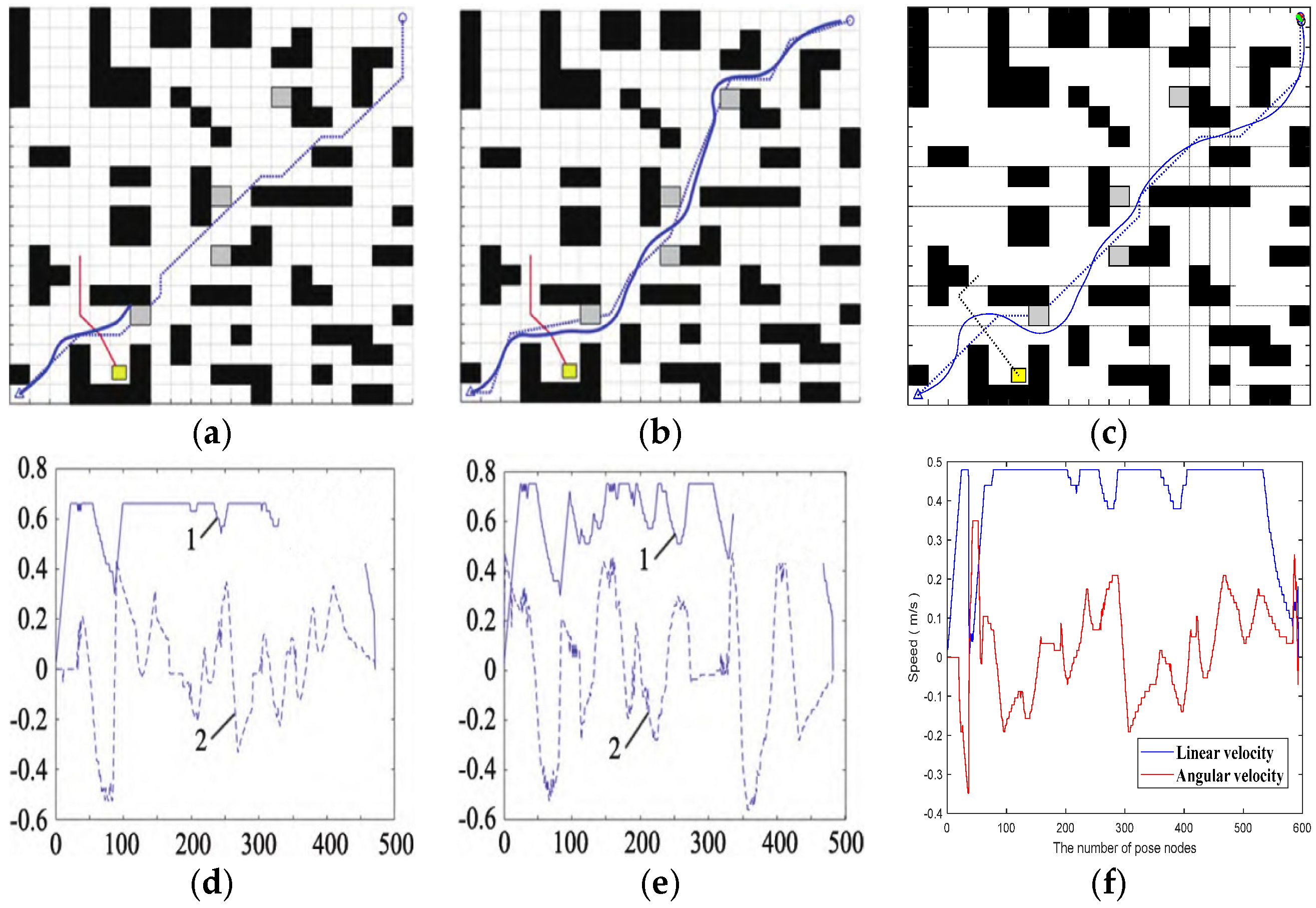
3.2. Local Obstacle-Avoidance Simulation Verification
3.2.1. Analysis of Local Obstacle Avoidance by the Fusion Algorithm
3.2.2. Comparison Test Between Fusion Algorithm and Excellent Algorithm
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, W.; Zhu, F.S. Review on Path Planning Algorithm for Robot Navigation. Comput. Eng. Appl. 2023, 59, 10–20. [Google Scholar]
- Wang, X.; Zhu, Q.X.; Zhu, Y.H. A Review of Path Planning Algorithms for Two-Dimensional Mobile Robots. Comput. Eng. Appl. 2023, 59, 51–66. [Google Scholar]
- Lamini, C.; Said, B.; Ali, E. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Gong, H.; Ni, C.; Wang, P. Smooth Path Planning Method Based on Dijkstra Algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2024, 50, 535–541. [Google Scholar]
- Chen, J.Q.; Li, M.Y.; Su, Y.S. Direction Constraints Adaptive Extended Bidirectional A* Algorithm Based on Random Two-Dimensional Map Environments. Robot. Auton. Syst. 2023, 165, 104930. [Google Scholar] [CrossRef]
- Huang, S.Q.; Wu, X.R.; Huang, G.M. Depth-Inspired Improvement of 3D A* Algorithm Based on Dynamic Field of View. Robot 2024, 46, 513–523. [Google Scholar]
- Pan, Z.D.; Zhou, Y.; Guo, W. Path Planning of Tidal Flat Track Vehicle Based on CB-RRT* Algorithm. Acta Armamentaria 2024, 45, 1117–1128. [Google Scholar]
- Wahab, A.N.M.; Nazir, A.; Khalil, A. Improved Genetic Algorithm for Mobile Robot Path Planning in Static Environments. Expert Syst. Appl. 2024, 249, 123762. [Google Scholar] [CrossRef]
- Ntakolia, C.; Lyridis, D.V. A Comparative Study on Ant Colony Optimization Algorithm Approaches for Solving Multi-objective Path Planning Problems in Case of Unmanned Surface Vehicles. Ocean. Eng. 2022, 255, 111418. [Google Scholar] [CrossRef]
- Xu, L.; Cao, M.Y.; Song, B.Y. A New Approach to Smooth Path Planning of Mobile Robot Based on Quartic Bezier Transition Curve and Improved PSO Algorithm. Neurocomputing 2022, 473, 98–106. [Google Scholar] [CrossRef]
- Wu, Z.T.; Dai, J.Y.; Jiang, B.P. Robot Path Planning Based on Artificial Potential Field with Deterministic Annealing. ISA Trans. 2023, 138, 74–87. [Google Scholar] [CrossRef]
- Liao, T.J.; Chen, F.; Wu, Y.T. Research on Path Planning with The Integration of Adaptive A* Algorithm and Improved Dynamic Window Approach. Electronics 2024, 13, 455. [Google Scholar] [CrossRef]
- Han, L.G.; Sheng, Z.; Xu, H. Path Planning Algorithm for Variable Step CDBA-RRT* Robot with Multi-Strategy Cooperative Extension. Comput. Appl. Res. 2025, 43, 1–10. [Google Scholar]
- Akopov, A.S.; Beklaryan, L.A. Evolutionary Synthesis of High-Capacity Reconfigurable Multilayer Road Networks Using a Multiagent Hybrid Clustering-Assisted Genetic Algorithm; IEEE Access: New York, NY, USA, 2025. [Google Scholar]
- Tang, G.W.; Zhang, X.D.; Hou, P.F. Multi-objective Path Planning for Agricultural Unmanned Vehicles Based on The Fusion of Improved A* and ACO Algorithm. J. Chin. Agric. Mech. 2025, 46, 255–260. [Google Scholar]
- Feng, Z.P.; Li, Z.G.; Xia, G.Q. Improved A* and Mobile Robot Path Planning Algorithm of APF Research. Comput. Eng. Appl. 2025, 61, 132–145. [Google Scholar]
- Kong, J.L.; Zhang, P.K.; Liu, X.P. Research on The Improved A* Algorithm of Two-way Search Mechanism. Comput. Eng. Appl. 2021, 57, 231–237. [Google Scholar]
- Zhang, C.C.; Fang, J.D. Path Planning of Autonomous Mobile Robot Based on Directional Weighted A* Algorithm. J. Comput. Appl. 2017, 37 (Suppl. S2), 77–81. [Google Scholar]
- Xu, X.; Zeng, J.Z.; Zhao, Y. Research on Global Path Planning Algorithm for Mobile Robots Based on Improved A*. Expert Syst. Appl. 2024, 243, 122922. [Google Scholar] [CrossRef]
- Chen, M.Y.; Qiao, G.F.; Zou, X.; Cao, J.Y.; Tian, L. Research on Path Smoothing Processing of Mobile Robots Based on Improved Bidirectional A* Algorithm. J. Syst. Simul. 2024, 1–9. [Google Scholar] [CrossRef]
- Sun, R.T.; Yuan, Q.N.; Yi, J.H. Improved Particle Swarm Algorithm and Dynamic Window Method for Dynamic Path Planning. Small Microcomput. Syst. 2023, 44, 1707–1712. [Google Scholar]
- Chang, X.X.; Hu, W.; Ji, S.D. Research on Obstacle Avoidance of Mobile Robot Based on Improved Dynamic Window Method. Comb. Mach. Tools Autom. Mach. Technol. 2021, 33–36. [Google Scholar]
- Missura, M.; Bennewitz, M. Predictive Collision Avoidance for The Dynamic Window Approach. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: New York, NY, USA, 2019; pp. 8620–8626. [Google Scholar]
- Liu, Y.M.; Huang, H.S.; Fan, Q.S. Mobile Robot Path Planning Based on Improved A* and DWA Algorithm. Comput. Integr. Manuf. Syst. 2024, 30, 158–171. [Google Scholar]
- Wu, F.L.; Guo, S.Y. Dynamic Path Planning of AGV Based on Fusion of Improved A* and Dynamic Window Approach Algorithms. Sci. Technol. Eng. 2020, 20, 12452–12459. [Google Scholar]
- Tang, N.Y. Research on Indoor Robot Path Planning Algorithm Based on ROS. Master’s Thesis, Chang’an University, Xi’an, China, 2023. [Google Scholar]
- Xia, Q. Research on Autonomous Valet Parking System with Vehicle-Yard Collaboration and Its Key Technologies. Yangtze Inf. Commun. 2022, 35, 21–23. [Google Scholar]
- Yildirim, M.Y.; Rustu, A. An Efficient Grid-Based Path Planning Approach Using Improved Artificial Bee Colony Algorithm. Knowledge-Based Systems. Knowl.-Based Syst. 2025, 318, 113528. [Google Scholar] [CrossRef]
- Tian, T.; Liang, Z.; Wei, Y.; Luo, Q.; Zhou, Y. Hybrid Whale Optimization with A Firefly Algorithm for Function Optimization and Mobile Robot Path Planning. Biomimetics 2024, 9, 39. [Google Scholar] [CrossRef]
- Zhang, J.H.; Tao, Z.S.; Peng, P. Smooth Path Planning Based on Extended Search Neighborhood A* Algorithm. J. Change Univ. Sci. Technol. 2018, 41, 124–127+146. [Google Scholar]
- Liu, Y.T.; Chao, X.Y.; Zhu, Y.C.; Nalin, Q.; Zhang, W. Research on Unmanned Vehicle Path Planning Based on Improved A* and DWA Algorithms. Automob. Technol. 2025, 1–10. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Zhang, Z.A. Fusion Improved A* Security Mobile Robot Path Planning with DWA. J. Comb. Mach. Tools Autom. Process. Technol. 2025, 37–43. [Google Scholar]







| Algorithm | Path Length (m) | Algorithm Traversal Time (s) | Number of Path Turns (Time) | |
|---|---|---|---|---|
| Map 1 | A* | 75.598 | 2.7743 | 11 |
| Floyd-A* | 71.0122 | 0.22024 | 6 | |
| BA* | 64.1838 | 0.38109 | 9 | |
| BJA* | 62.0698 | 0.16779 | 5 | |
| Map 2 | A* | 47.7696 | 1.10756 | 13 |
| Floyd-A* | 46.7656 | 1.04056 | 18 | |
| BA* | 45.0122 | 0.23349 | 10 | |
| BJA* | 44.0122 | 0.11725 | 10 | |
| Algorithm | Path Length (m) | Algorithm Traversal Time (s) | Number of Pat Turns (Time) |
|---|---|---|---|
| BJA* | 44.0122 | 0.11725 | 10 |
| Remove redundant nodes | 43.542 | 0.10286 | 8 |
| Path smoothing processing | 41.236 | 0.08561 | 5 |
| Algorithm | Path Length (m) | Algorithm Traversal Time (s) | Number of Path Turns (Time) |
|---|---|---|---|
| A* | 47.7696 | 1.10756 | 13 |
| Floyd-A* | 46.7656 | 1.04056 | 18 |
| BJA*-1 | 45.2162 | 1.11725 | 12 |
| BJA*-2 | 47.8469 | 0.19046 | 11 |
| BJA* | 44.0122 | 0.11725 | 10 |
| Algorithm | Best | Mean | Std. |
|---|---|---|---|
| A* | 30.1658 | 55.4892 | 78.965 |
| Floyd-A* | 29.5797 | 34.1859 | 6.3254 |
| [28] ABC | 29.7990 | 31.0777 | 0.6451 |
| [28] IABC | 28.464 | 28.5245 | 0.1818 |
| [29] WOA | 28.7003 | 45.4813 | 67.0978 |
| [29] PSO | 28.464 | 31.6773 | 4.6007 |
| [29] GWO | 28.8269 | 30.5589 | 2.4051 |
| [29] STOA | 29.4046 | 29.4531 | 0.1345 |
| [29] SSA | 28.8269 | 29.8522 | 0.3687 |
| [29] SOA | 28.8269 | 29.458 | 0.2247 |
| [29] FWOA | 28.464 | 29.372 | 0.5622 |
| BA* | 29.799 | 30.2543 | 0.5971 |
| BJA* | 27.8496 | 27.912 | 0.1527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, K.; Zhou, G.; Lu, H. A Path-Planning Scheme for Autonomous Vehicle Navigation Integrating BJA* and Improved DWA Algorithms. Sensors 2025, 25, 7017. https://doi.org/10.3390/s25227017
Xin K, Zhou G, Lu H. A Path-Planning Scheme for Autonomous Vehicle Navigation Integrating BJA* and Improved DWA Algorithms. Sensors. 2025; 25(22):7017. https://doi.org/10.3390/s25227017
Chicago/Turabian StyleXin, Kai, Guoxu Zhou, and Huacai Lu. 2025. "A Path-Planning Scheme for Autonomous Vehicle Navigation Integrating BJA* and Improved DWA Algorithms" Sensors 25, no. 22: 7017. https://doi.org/10.3390/s25227017
APA StyleXin, K., Zhou, G., & Lu, H. (2025). A Path-Planning Scheme for Autonomous Vehicle Navigation Integrating BJA* and Improved DWA Algorithms. Sensors, 25(22), 7017. https://doi.org/10.3390/s25227017