Enhancing Point Cloud Registration for Pipe Fittings: A Coarse-to-Fine Approach with DANIP Keypoint Detection and ICP Optimization
Abstract
1. Introduction
- An innovative 3D point cloud keypoint detection method, DANIP, is proposed, which combines a density-aware anomaly point removal mechanism with a multi-scale locally adaptive threshold detection based on normal vector inner products. This method demonstrates exceptional performance in keypoint detection accuracy, matching precision, and computational efficiency.
- We introduce a coarse-to-fine point cloud registration method based on DANIP keypoint detection and the ICP algorithm. This method effectively addresses the limitations of the ICP algorithm, which is prone to local optima, while significantly improving convergence efficiency and computational performance in the registration process.
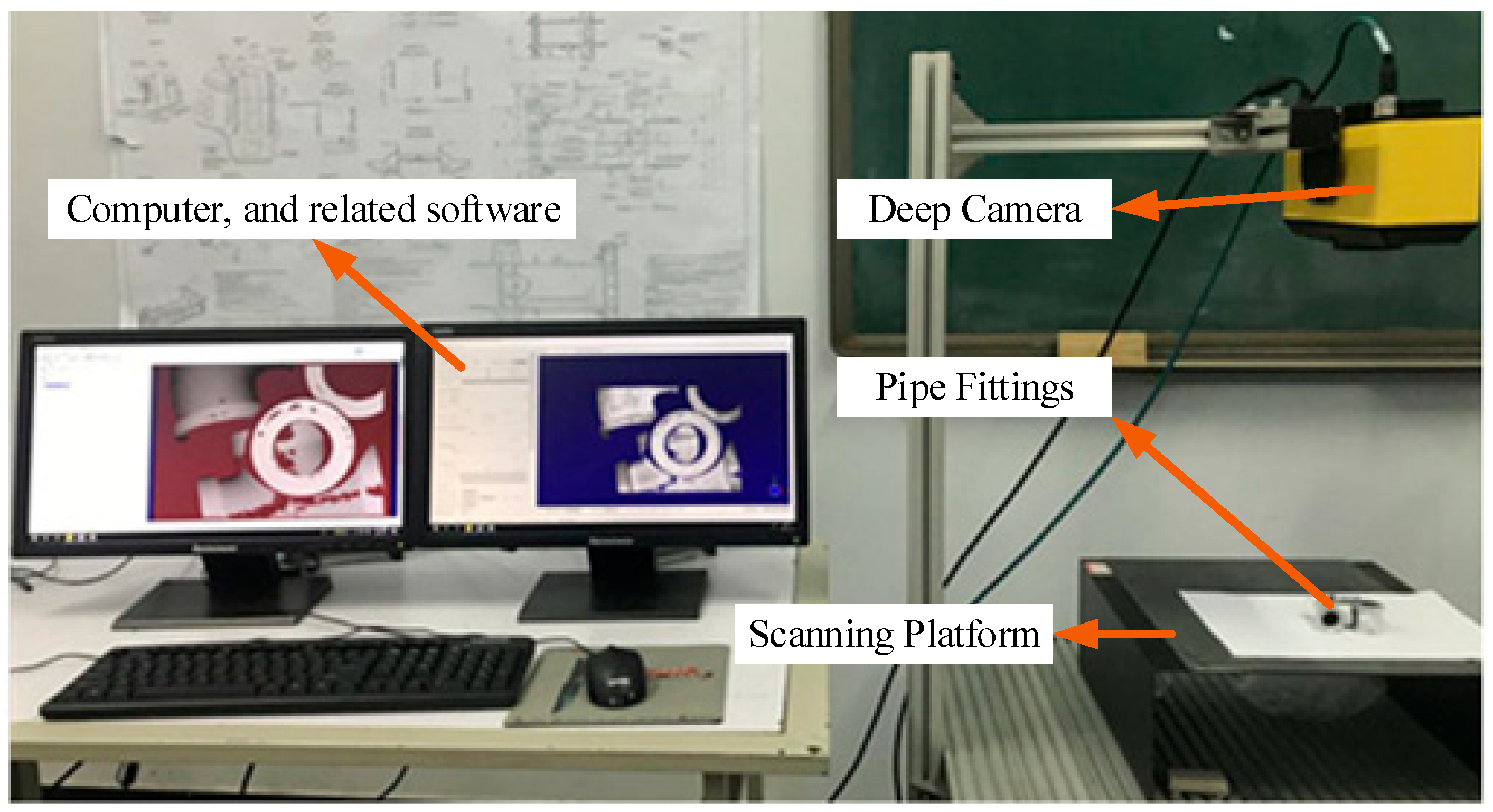
- We conduct a registration study of common pipe fittings in real-world environments to evaluate the effectiveness of the coarse-to-fine point cloud registration method based on DANIP and ICP. The proposed method achieves higher registration accuracy than mainstream algorithms, even in multi-view scenarios with severe data loss.
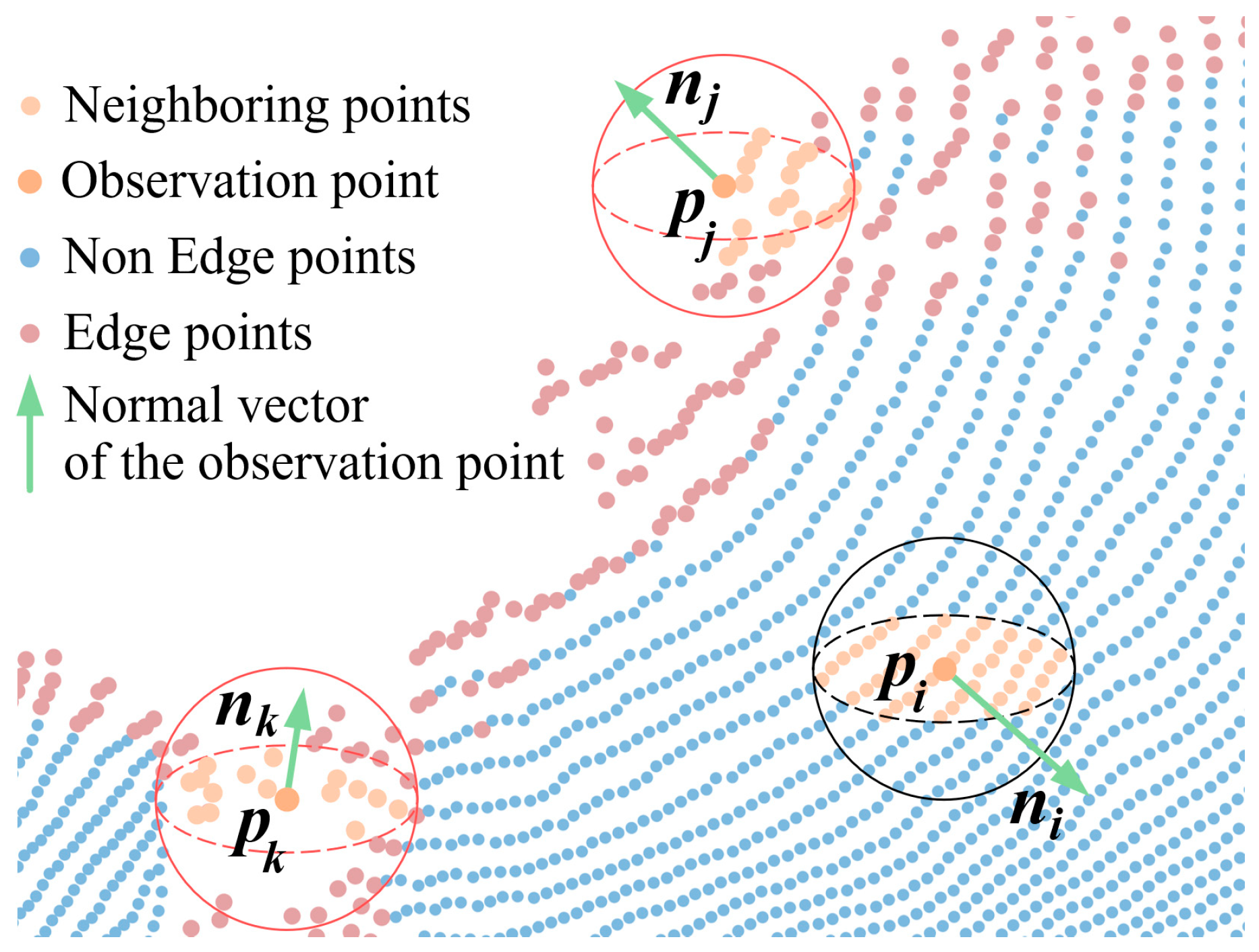
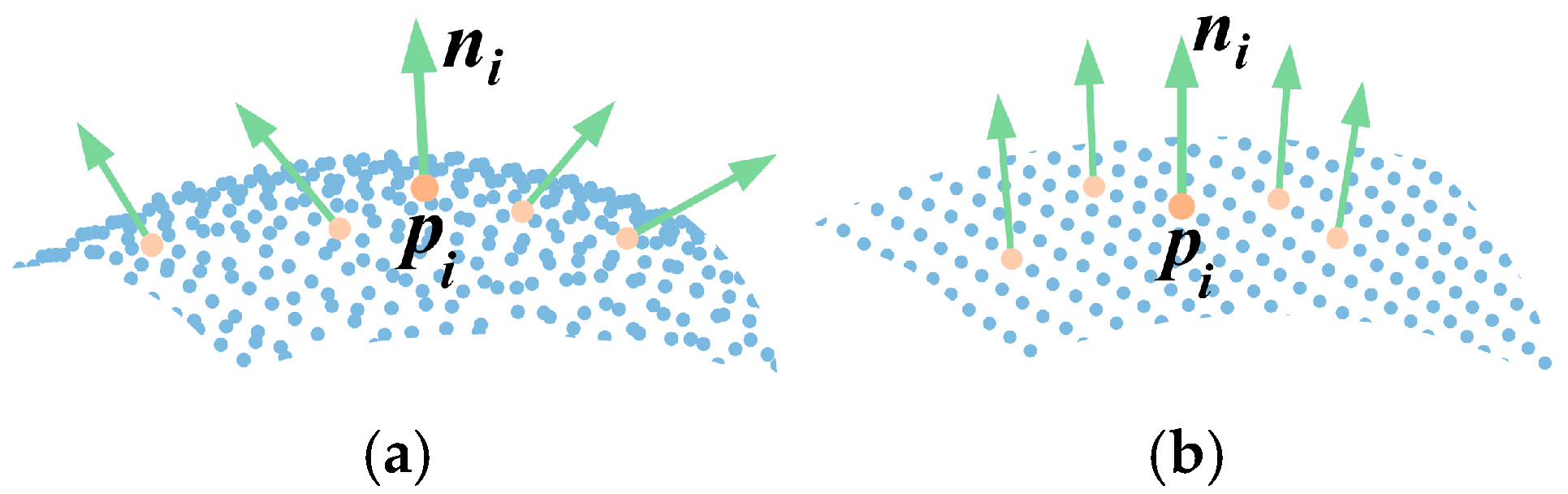
2. Density-Aware Normal Inner Product Keypoint Detection
2.1. Density-Aware Normal Inner Product
2.2. Non-Maximum Suppression
| Algorithm 1. DANIP Algorithm | |
| Input: point cloud P and number of neighboring points k Output: keypoint KP | |
| 1 | Calculate the local dynamic threshold ti based on Equation (3); |
| 2 | Use the local dynamic threshold ti to filter out edge outliers according to Equation (1); |
| 3 | Compute the normal vector nP of the point cloud P; |
| 4 | Calculate the response value tRi for dynamic multi-scale keypoint detection based on Equations (4)–(6); |
| 5 | For non-edge points, determine the candidate keypoints using Equation (7); |
| 6 | Construct the local neighborhood covariance matrix using Equations (8) and (9); |
| 7 | Determine the threshold for non-maximum suppression based on Equations (10) and (11); |
| 8 | Perform non-maximum suppression on the candidate keypoints based on Equation (11) to obtain the final keypoints KP. |
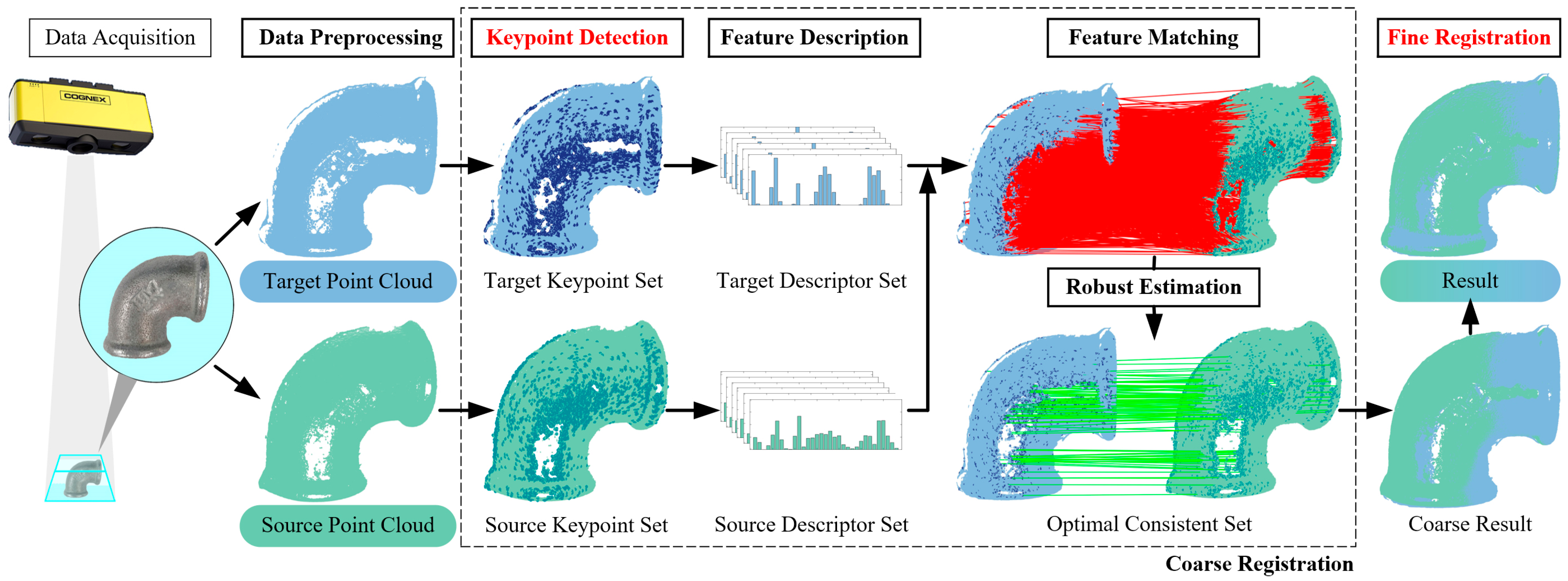
3. Coarse-to-Fine Registration Using DANIP Keypoints and ICP
3.1. Coarse Registration Based on DANIP Keypoints
3.1.1. Data Preprocessing
3.1.2. Keypoint Detection
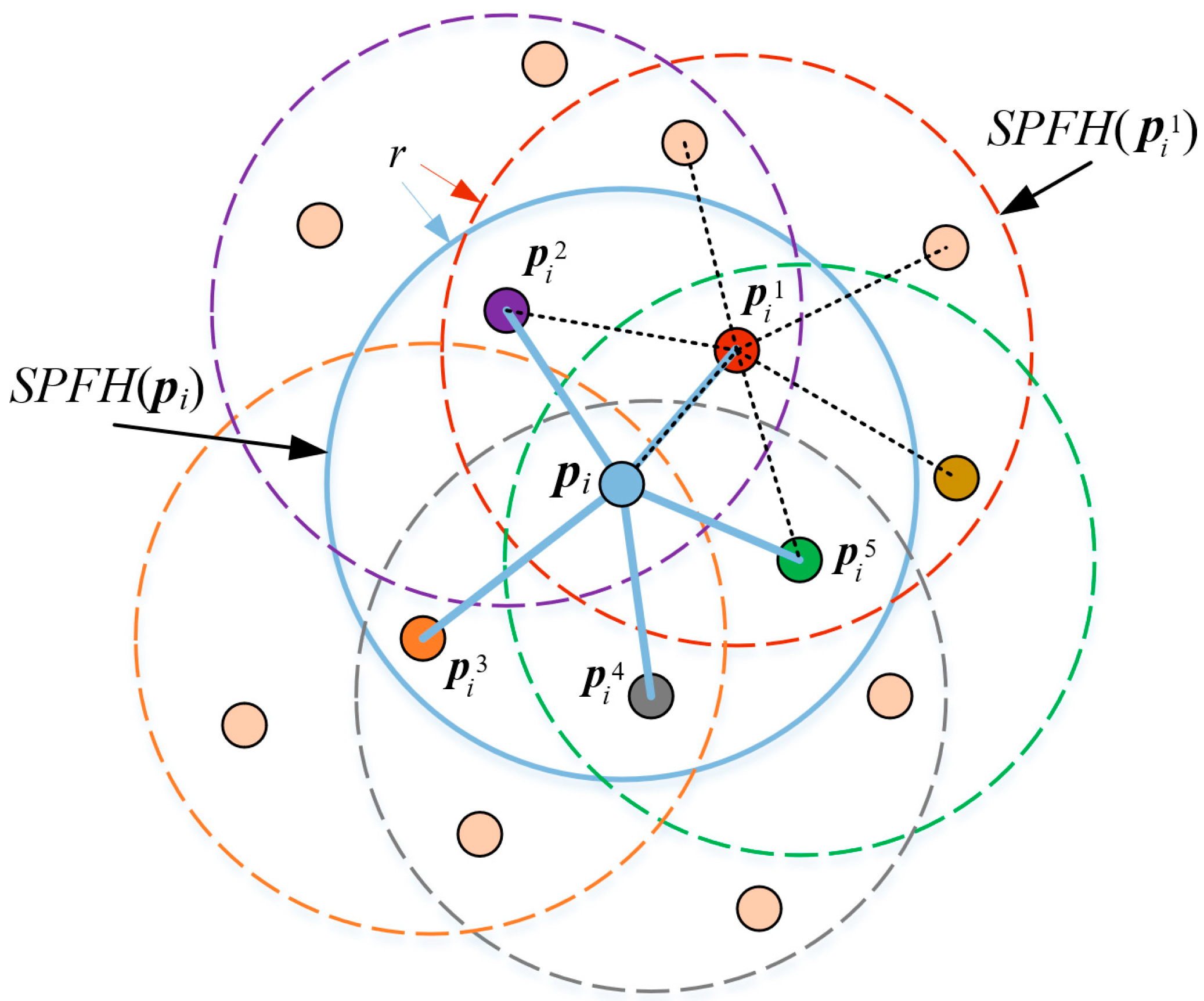
3.1.3. Feature Description
3.1.4. Feature Matching
3.1.5. Robust Estimation
3.2. Fine Registration
4. Experimental Evaluation
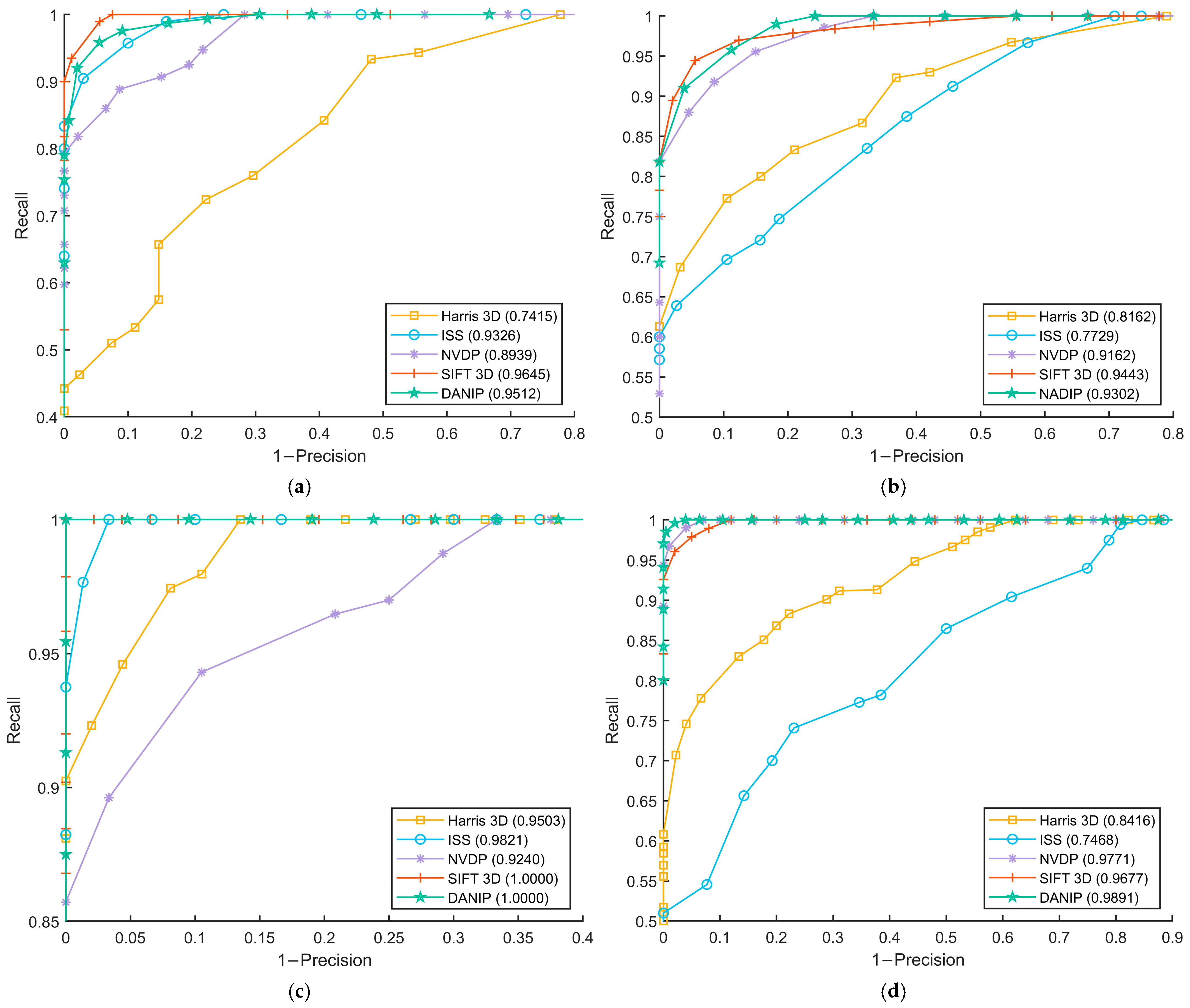
4.1. Keypoint Detection Performance
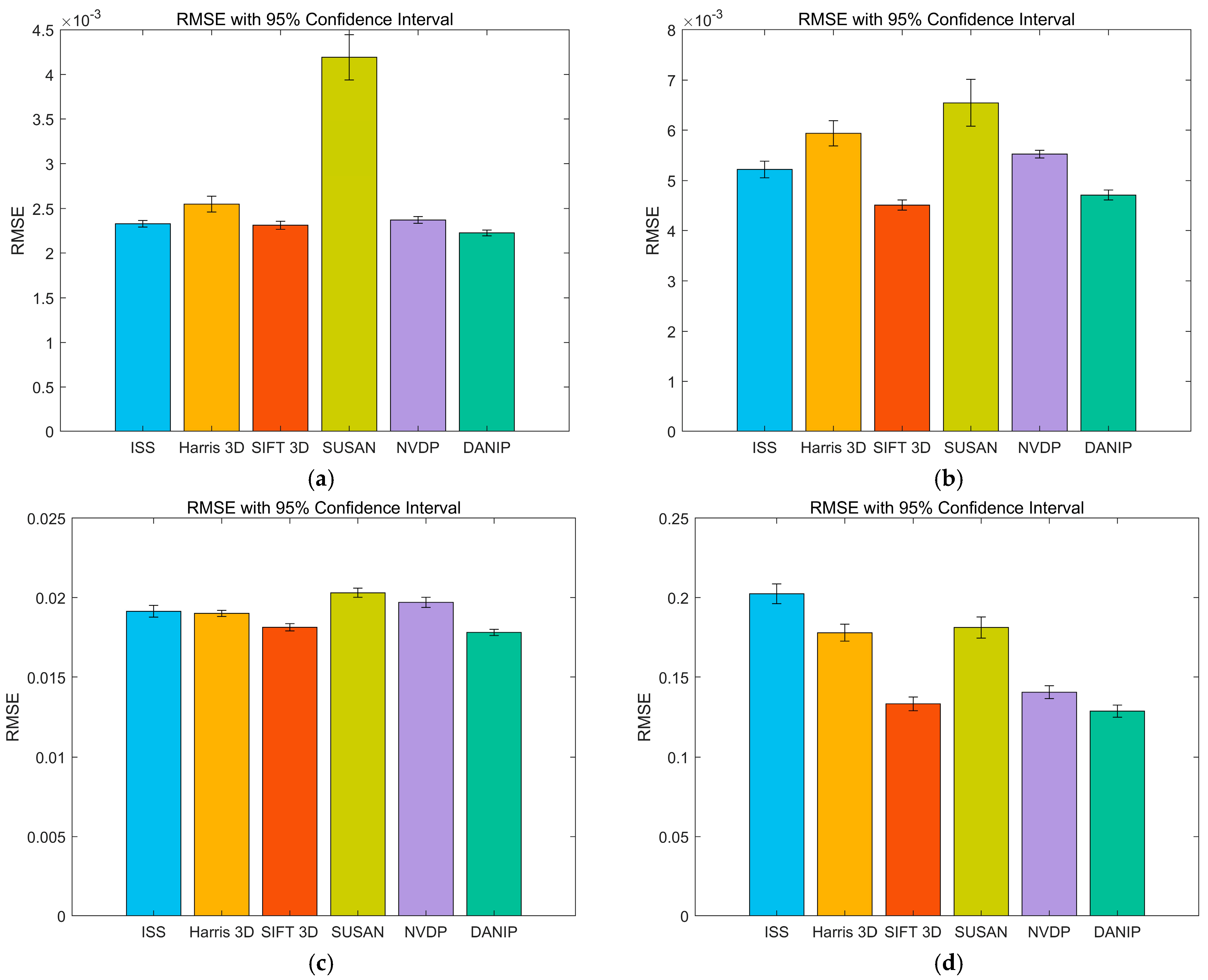
4.2. Coarse Registration Comparison
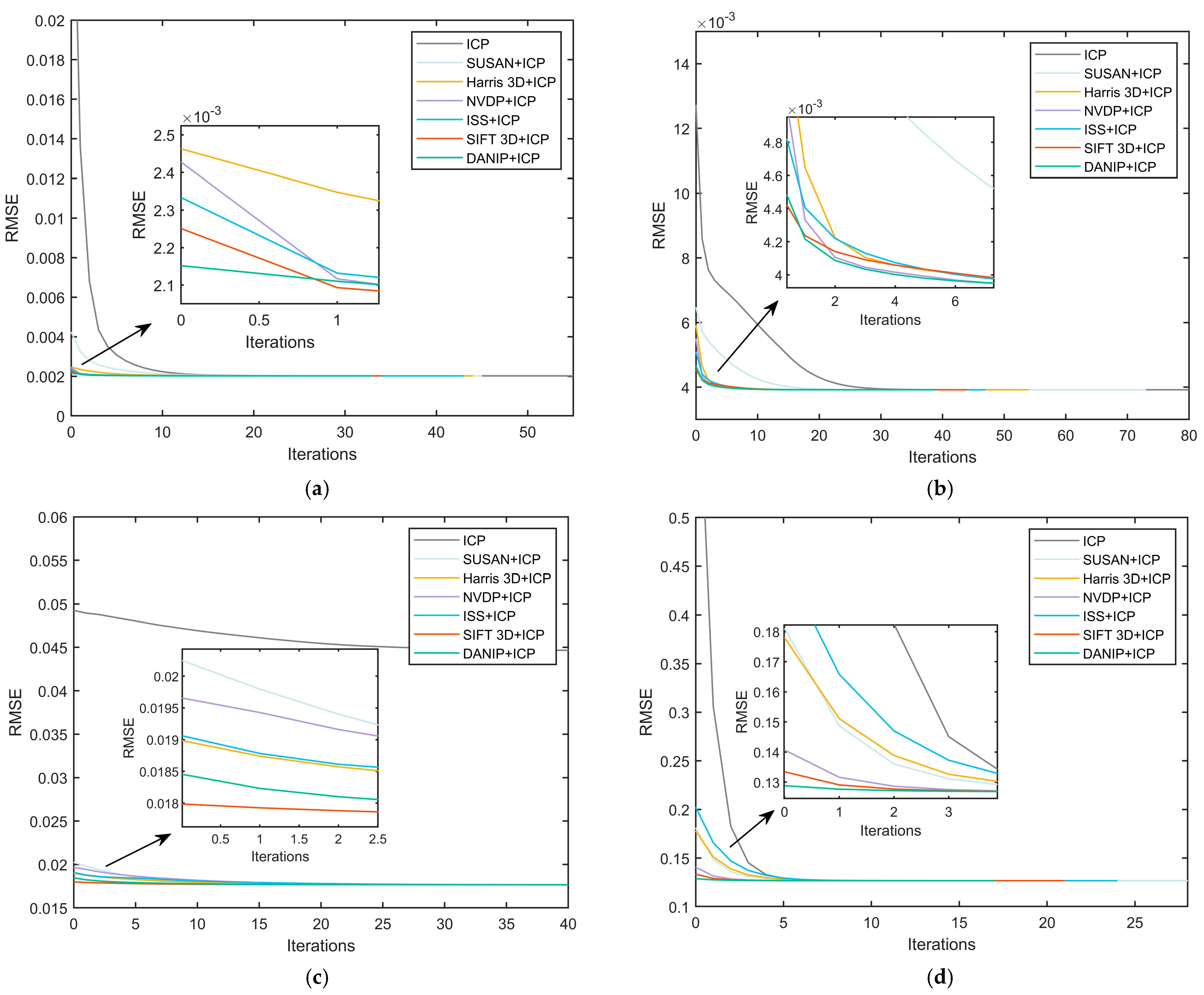
4.3. Coarse-to-Fine Registration Comparison
4.4. Pipe Fitting Registration Performance
5. Conclusions and Future Work
- A novel keypoint detection method, DANIP, is proposed. Experimental results in keypoint detection show that, compared to other classical methods, DANIP achieves higher detection accuracy and computational efficiency on public datasets such as Stanford, Kinect, Queen, and ASL-LRD.
- A coarse-to-fine registration method combining DANIP and ICP is proposed. This method effectively avoids the local minima problem in the ICP algorithm, significantly improving convergence efficiency and computational performance. Under optimal conditions, the runtime is reduced by 66.93%, 78.01%, 75.48%, and 23.69% on the Stanford, Kinect, Queen, and ASL-LRD datasets, respectively.
- Compared to other classical registration algorithms, the coarse-to-fine point cloud registration based on DANIP and ICP achieves higher accuracy even in the presence of severe data loss in multi-view industrial pipe datasets. These findings validate the robustness of the proposed method against data loss caused by reflectivity and highlight its potential in engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Guan, Y.; Wang, X.; Zhou, C.; Xun, Y.; Gui, L. Experimental and numerical studies on heat transfer characteristics of vertical deep-buried U-bend pipe in intermittent heating mode. Geothermics 2019, 79, 14–25. [Google Scholar] [CrossRef]
- Hong, S.-P.; Yoon, S.-J.; Kim, D.-J.; Kim, Y.-J.; Huh, N.-S. Enhanced elastic stress solutions for junctions in various pipe bends under internal pressure and combined loading (90° pipe bend, U-bend, double-bend pipe). Int. J. Press. Vessel. Pip. 2024, 212, 105343. [Google Scholar] [CrossRef]
- Cao, R.; Ma, D.; Chen, W.; Li, M.; Dai, H.; Wang, L. Multistable dynamic behaviors of cantilevered curved pipes conveying fluid. J. Fluids Struct. 2024, 130, 104196. [Google Scholar] [CrossRef]
- Feigang, T.; Kaiyuan, L.; Lifeng, L.; Yang, W. An Intelligent Detection System for Full Crew of Elevator Car. In Proceedings of the 2018 11th International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 22–23 September 2018; pp. 183–185. [Google Scholar] [CrossRef]
- Tan, F.; Zhai, M.; Zhai, C. Foreign object detection in urban rail transit based on deep differentiation segmentation neural network. Heliyon 2024, 10, e37072. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.-S.; Lin, J.-J.; Chen, B.-R. A novel 3D scanning technique for reflective metal surface based on HDR-like image from pseudo exposure image fusion method. Opt. Lasers Eng. 2023, 168, 107688. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-ICP. In Robotics: Science and Systems V; University of Washington: Seattle, DC, USA, 2009. [Google Scholar] [CrossRef]
- Serafin, J.; Grisetti, G. NICP: Dense normal based point cloud registration. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 742–749. [Google Scholar] [CrossRef]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A Globally Optimal Solution to 3D ICP Point-Set Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2241–2254. [Google Scholar] [CrossRef]
- Lei, J.; Song, J.; Peng, B.; Li, W.; Pan, Z.; Huang, Q. C2FNet: A Coarse-to-Fine Network for Multi-View 3D Point Cloud Generation. IEEE Trans. Image Process. 2022, 31, 6707–6718. [Google Scholar] [CrossRef]
- Yue, X.; Liu, Z.; Zhu, J.; Gao, X.; Yang, B.; Tian, Y. Coarse-fine point cloud registration based on local point-pair features and the iterative closest point algorithm. Appl. Intell. 2022, 52, 12569–12583. [Google Scholar] [CrossRef]
- Li, Q.; Yan, Y.; Li, W. Coarse-to-fine segmentation of individual street trees from side-view point clouds. Urban For. Urban Green. 2023, 89, 128097. [Google Scholar] [CrossRef]
- Liu, Z.; Yue, X.; Zhu, J. SPROSAC: Streamlined progressive sample consensus for coarse–fine point cloud registration. Appl. Intell. 2024, 54, 5117–5135. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Zhao, H.; Tang, M.; Ding, H. HoPPF: A novel local surface descriptor for 3D object recognition. Pattern Recognit. 2020, 103, 107272. [Google Scholar] [CrossRef]
- Yuan, C.; Lin, J.; Liu, Z.; Wei, H.; Hong, X.; Zhang, F. BTC: A Binary and Triangle Combined Descriptor for 3-D Place Recognition. IEEE Trans. Robot. 2024, 40, 1580–1599. [Google Scholar] [CrossRef]
- Barath, D.; Matas, J. Graph-Cut RANSAC. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6733–6741. [Google Scholar] [CrossRef]
- Ivashechkin, M.; Barath, D.; Matas, J. VSAC: Efficient and Accurate Estimator for H and F. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 15223–15232. [Google Scholar] [CrossRef]
- Li, J.; Shi, P.; Hu, Q.; Zhang, Y. QGORE: Quadratic-Time Guaranteed Outlier Removal for Point Cloud Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11136–11151. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 689–696. [Google Scholar]
- Zaharescu, A.; Boyer, E.; Varanasi, K.; Horaud, R. Surface feature detection and description with applications to mesh matching. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 373–380. [Google Scholar] [CrossRef]
- Steder, B.; Rusu, R.B.; Konolige, K.; Burgard, W. NARF: 3D Range Image Features for Object Recognition. Available online: http://ais.informatik.uni-freiburg.de/publications/papers/steder10irosws.pdf (accessed on 11 November 2025).
- Sipiran, I.; Bustos, B. Harris 3D: A robust extension of the Harris operator for interest point detection on 3D meshes. Vis. Comput. 2011, 27, 963–976. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3d is here: Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Suwajanakorn, S.; Snavely, N.; Tompson, J.; Norouzi, M. Discovery of latent 3d keypoints via end-to-end geometric reasoning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS’18), Red Hook, NY, USA, 3 December 2018; pp. 2063–2074. [Google Scholar]
- Li, J.; Lee, G.H. USIP: Unsupervised Stable Interest Point Detection From 3D Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 361–370. [Google Scholar] [CrossRef]
- Bai, X.; Luo, Z.; Zhou, L.; Fu, H.; Quan, L.; Tai, C.-L. D3Feat: Joint Learning of Dense Detection and Description of 3D Local Features. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6358–6366. [Google Scholar] [CrossRef]
- Luo, Z.; Xue, W.; Chae, J.; Fu, G. SKP: Semantic 3D Keypoint Detection for Category-Level Robotic Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 5437–5444. [Google Scholar] [CrossRef]
- Tordoff, B.; Murray, D. Guided-MLESAC: Faster image transform estimation by using matching priors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1523–1535. [Google Scholar] [CrossRef]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1 August 1996; pp. 303–312. [Google Scholar]
- Tombari, F.; Salti, S.; Stefano, L.D. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 356–369. [Google Scholar] [CrossRef]
- Kiforenko, L.; Drost, B.; Tombari, F.; Krüger, N.; Buch, A.G. A performance evaluation of point pair features. Comput. Vis. Image Underst. 2018, 166, 66–80. [Google Scholar] [CrossRef]
- Pomerleau, F.; Liu, M.; Colas, F.; Siegwart, R. Challenging data sets for point cloud registration algorithms. Int. J. Robot. Res. 2012, 31, 1705–1711. [Google Scholar] [CrossRef]
- Smith, S.M.; Brady, J.M. SUSAN—A New Approach to Low Level Image Processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar] [CrossRef]
- Biber, P. The Normal Distributions Transform: A New Approach to Laser Scan Matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar]
- Fitzgibbon, A.W. Robust registration of 2D and 3D point sets. Image Vis. Comput. 2003, 21, 1145–1153. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar] [CrossRef]





| No. | Datasets | Acquisition Method | Characteristic | Quality | Degree of Data Loss | Model Number |
|---|---|---|---|---|---|---|
| 1 | Stanford | Cyberware 3030 MS | Diversity | High | Low | 6 |
| 2 | Kinect | Microsoft Kinect | Low density | Low | Medium | 7 |
| 3 | Queen | Minolta vivid | Scanning error | Medium | Medium | 5 |
| 4 | ASL-LRD | Hokuyo UTM-30LX | Large size and noise | Medium | High | 8 |
| Parameter | Datasets | ISS | Harris 3D | NVDP | SIFT 3D | DANIP |
|---|---|---|---|---|---|---|
| F1 | Stanford | 0.9326 | 0.7415 | 0.8939 | 0.9645 | 0.9512 |
| Kinect | 0.7729 | 0.8162 | 0.9162 | 0.9443 | 0.9302 | |
| Queen | 0.9821 | 0.9503 | 0.9240 | 1.0000 | 1.0000 | |
| ASL-LRD | 0.7468 | 0.8416 | 0.9771 | 0.9677 | 0.9891 | |
| Time(s) | Stanford | 0.7471 | 1.0388 | 0.8571 | 2.8569 | 0.8879 |
| Kinect | 0.2384 | 0.2201 | 0.1676 | 2.0467 | 0.3374 | |
| Queen | 0.2073 | 0.0941 | 0.1399 | 1.7302 | 0.2001 | |
| ASL-LRD | 0.4775 | 0.3389 | 0.5979 | 3.1702 | 1.0059 |
| Parameter | Datasets | ISS | Harris 3D | SIFT 3D | SUSAN | NVDP | DANIP |
|---|---|---|---|---|---|---|---|
| RMSE | Stanford | 0.0023 | 0.0025 | 0.0023 | 0.0042 | 0.0024 | 0.0022 |
| Kinect | 0.0052 | 0.0059 | 0.0045 | 0.0065 | 0.0055 | 0.0047 | |
| Queen | 0.0191 | 0.0190 | 0.0181 | 0.0203 | 0.0197 | 0.0181 | |
| ASL-LRD | 0.2024 | 0.1780 | 0.1334 | 0.1812 | 0.1407 | 0.1288 | |
| MRE | Stanford | 0.000947 | 0.001312 | 0.000896 | 0.002344 | 0.001065 | 0.000855 |
| Kinect | 0.003975 | 0.004772 | 0.002948 | 0.005016 | 0.004028 | 0.003406 | |
| Queen | 0.011691 | 0.010521 | 0.009631 | 0.012468 | 0.012118 | 0.009432 | |
| ASL-LRD | 0.137210 | 0.112940 | 0.072324 | 0.113120 | 0.093307 | 0.065782 | |
| BIC | Stanford | 71.1403 | 71.2232 | 71.1121 | 71.4602 | 71.1886 | 71.0851 |
| Kinect | 64.2029 | 64.3675 | 64.1186 | 64.3946 | 64.3104 | 64.1285 | |
| Queen | 64.0053 | 64.0011 | 63.9651 | 64.1606 | 64.0278 | 63.9607 | |
| ASL-LRD | 79.9788 | 78.0622 | 76.4428 | 78.4243 | 76.6458 | 76.2269 | |
| Time(s) | Stanford | 2.92 | 4.32 | 4.79 | 4.33 | 2.93 | 2.44 |
| Kinect | 2.49 | 2.10 | 4.26 | 3.07 | 1.75 | 1.26 | |
| Queen | 1.44 | 2.35 | 4.10 | 2.24 | 2.09 | 1.21 | |
| ASL-LRD | 3.52 | 4.27 | 5.90 | 3.09 | 3.42 | 3.32 |
| Parameter | Datasets | ISS | Harris 3D | SIFT 3D | SUSAN | NVDP | DANIP |
|---|---|---|---|---|---|---|---|
| Medians | Stanford | 0.00237 | 0.00251 | 0.00228 | 0.00441 | 0.00243 | 0.00224 |
| Kinect | 0.00518 | 0.00587 | 0.00453 | 0.00663 | 0.00554 | 0.00472 | |
| Queen | 0.01917 | 0.01902 | 0.01816 | 0.02026 | 0.01975 | 0.01798 | |
| ASL-LRD | 0.19853 | 0.17973 | 0.14412 | 0.19213 | 0.14572 | 0.12919 | |
| IQR | Stanford | 0.00008 | 0.00028 | 0.00012 | 0.00052 | 0.00007 | 0.00003 |
| Kinect | 0.000212 | 0.000336 | 0.000164 | 0.000735 | 0.000107 | 0.000131 | |
| Queen | 0.001475 | 0.000821 | 0.000902 | 0.001015 | 0.001242 | 0.000901 | |
| ASL-LRD | 0.002019 | 0.001826 | 0.001263 | 0.001938 | 0.001312 | 0.000553 |
| Algorithm | Metric | Stanford bun000&045 | Kinect PeterRabbit000&001 | Queen im0&2 | ASL-LRD Hokuyo 0&1 |
|---|---|---|---|---|---|
| ICP | Runtime(s) | 14.3966 | 12.6766 | 9.7429 | 7.1939 |
| SUSAN + ICP | Runtime(s) | 7.9865 | 5.2159 | 3.1650 | 6.1760 |
| Rate of decline | 44.53% | 58.85% | 67.51% | 14.15% | |
| Harris 3D + ICP | Runtime(s) | 7.3926 | 3.7220 | 3.6199 | 6.6802 |
| Rate of decline | 48.65% | 70.64% | 62.85% | 7.14% | |
| NVDP + ICP | Runtime(s) | 5.3924 | 3.1112 | 3.1004 | 5.7802 |
| Rate of decline | 62.54% | 75.46% | 68.18% | 19.65% | |
| ISS + ICP | Runtime(s) | 6.5340 | 4.0449 | 2.7233 | 6.0138 |
| Rate of decline | 54.61% | 68.09% | 72.05% | 16.40% | |
| SIFT 3D + ICP | Runtime(s) | 7.5215 | 5.7851 | 5.3045 | 8.3011 |
| Rate of decline | 47.76% | 54.36% | 45.56% | N/A | |
| DANIP + ICP | Runtime(s) | 4.7604 | 2.7873 | 2.3889 | 5.4896 |
| Rate of decline | 66.93% | 78.01% | 75.48% | 23.69% |
| Point Cloud | Number of Point | ICP | LM-ICP | P-ICP | G-ICP | NDT | DANIP-ICP |
|---|---|---|---|---|---|---|---|
| elbow01&02 | 131,071&139,978 | 0.5011 | 0.4951 | 0.5085 | 0.5082 | 0.7039 | 0.4935 |
| elbow03&04 | 127,826&122,986 | 0.3937 | 0.3793 | 0.4996 | 0.5201 | 1.2531 | 0.3778 |
| elbow07&08 | 123,277&115,856 | 0.7988 | 0.7983 | 0.5057 | 0.5118 | 1.3206 | 0.4327 |
| elbow15&16 | 121,585&122,655 | 0.7716 | 0.7719 | 0.8615 | 0.8948 | 2.3735 | 0.7712 |
| reducer01&02 | 84,686&85,298 | 0.2289 | 0.2191 | 0.2409 | 0.3386 | 0.2278 | 0.2151 |
| reducer03&04 | 83,436&89,881 | 0.4864 | 0.4890 | 0.6087 | 0.6603 | 0.4129 | 0.4063 |
| tee01&02 | 153,909&149,825 | 1.3562 | 1.3533 | 1.3998 | 1.4392 | 2.8303 | 1.3433 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Yue, X. Enhancing Point Cloud Registration for Pipe Fittings: A Coarse-to-Fine Approach with DANIP Keypoint Detection and ICP Optimization. Sensors 2025, 25, 7012. https://doi.org/10.3390/s25227012
Liu Z, Yue X. Enhancing Point Cloud Registration for Pipe Fittings: A Coarse-to-Fine Approach with DANIP Keypoint Detection and ICP Optimization. Sensors. 2025; 25(22):7012. https://doi.org/10.3390/s25227012
Chicago/Turabian StyleLiu, Zeyuan, and Xiaofeng Yue. 2025. "Enhancing Point Cloud Registration for Pipe Fittings: A Coarse-to-Fine Approach with DANIP Keypoint Detection and ICP Optimization" Sensors 25, no. 22: 7012. https://doi.org/10.3390/s25227012
APA StyleLiu, Z., & Yue, X. (2025). Enhancing Point Cloud Registration for Pipe Fittings: A Coarse-to-Fine Approach with DANIP Keypoint Detection and ICP Optimization. Sensors, 25(22), 7012. https://doi.org/10.3390/s25227012





