An Upper-Probability-Based Softmax Ensemble Model for Multi-Sensor Bearing Fault Diagnosis
Abstract
1. Introduction
- Uncertainty-Aware Predictive Augmentation: Rather than relying solely on the most probable class, the proposed approach incorporates the top two high-confidence predictions from each sensor-specific model. This mechanism facilitates more stable and reliable decisions, particularly under noisy or ambiguous input conditions.
- Sensor Reliability-Aware Decision Weighting: The influence of each sensor’s prediction in the final ensemble decision is adaptively adjusted based on its individual classification performance, enabling the system to place greater trust in more reliable sensors.
- Adaptive Boosting-Based Integration: Through an iterative AdaBoost-based process, the ensemble framework progressively corrects sensor-specific misclassifications, achieving enhanced diagnostic robustness without relying on complex feature extraction or fusion pipelines.
- Architectural Simplicity and Computational Efficiency: By operating directly on the prediction-level outputs of individual models, the framework eliminates the need for deep or fused intermediate representations. This design significantly reduces computational overhead while maintaining high diagnostic accuracy, rendering the approach suitable for real-time industrial applications.
2. Methods
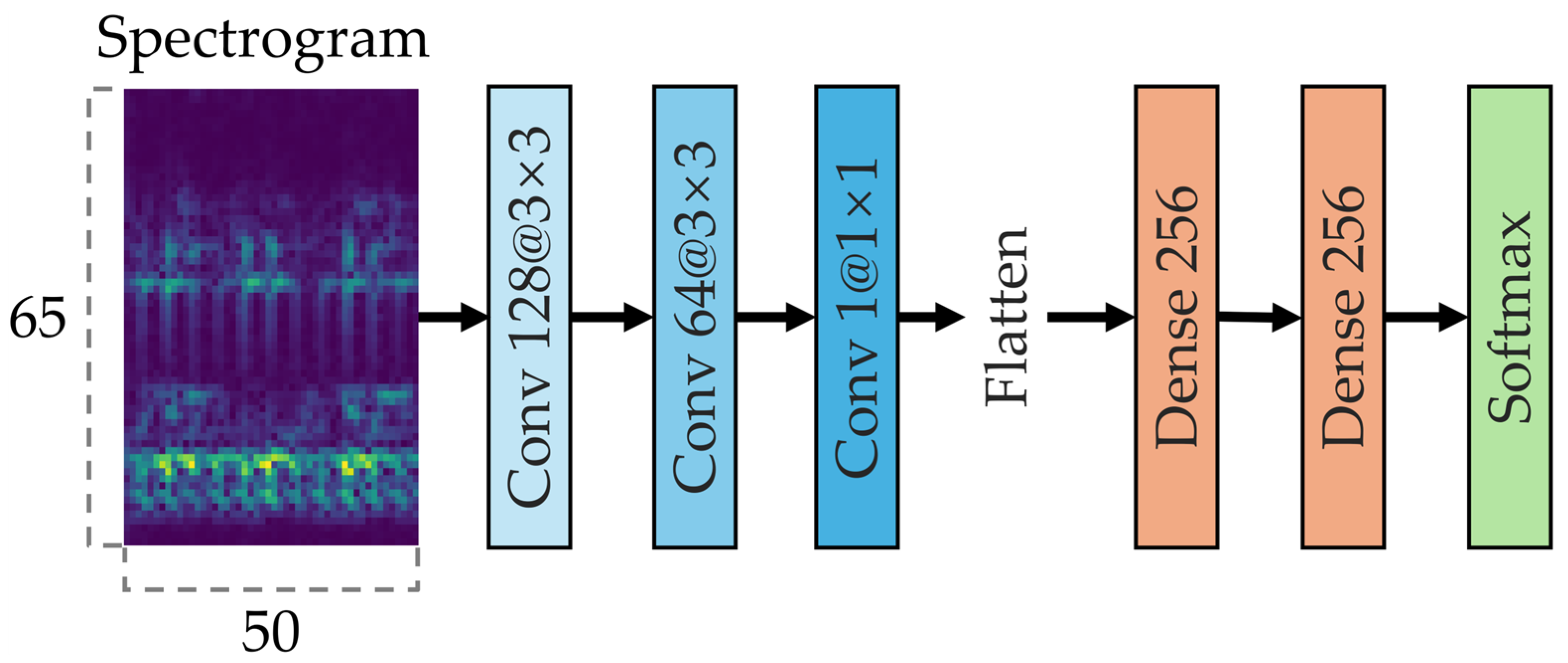
2.1. Architecture of Individual CNN Models
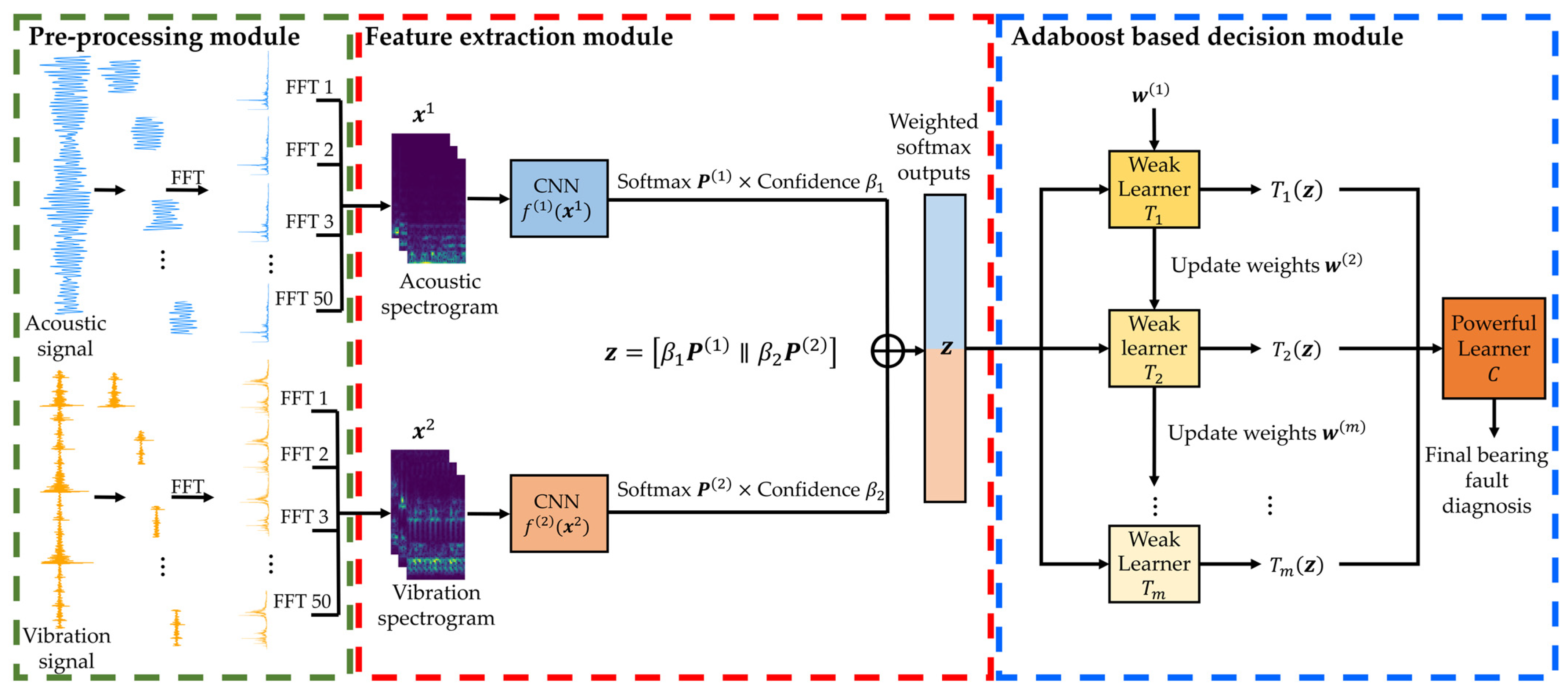
2.2. Softmax-Based Ensemble Modeling
- (1)
- Sensor-Wise softmax prediction
- (2)
- Classifier weighting based on accuracy
- (3)
- Concatenated ensemble inputs
- (4)
- AdaBoost training process
- (5)
- Final Ensemble prediction
3. Experiments
3.1. Metrics
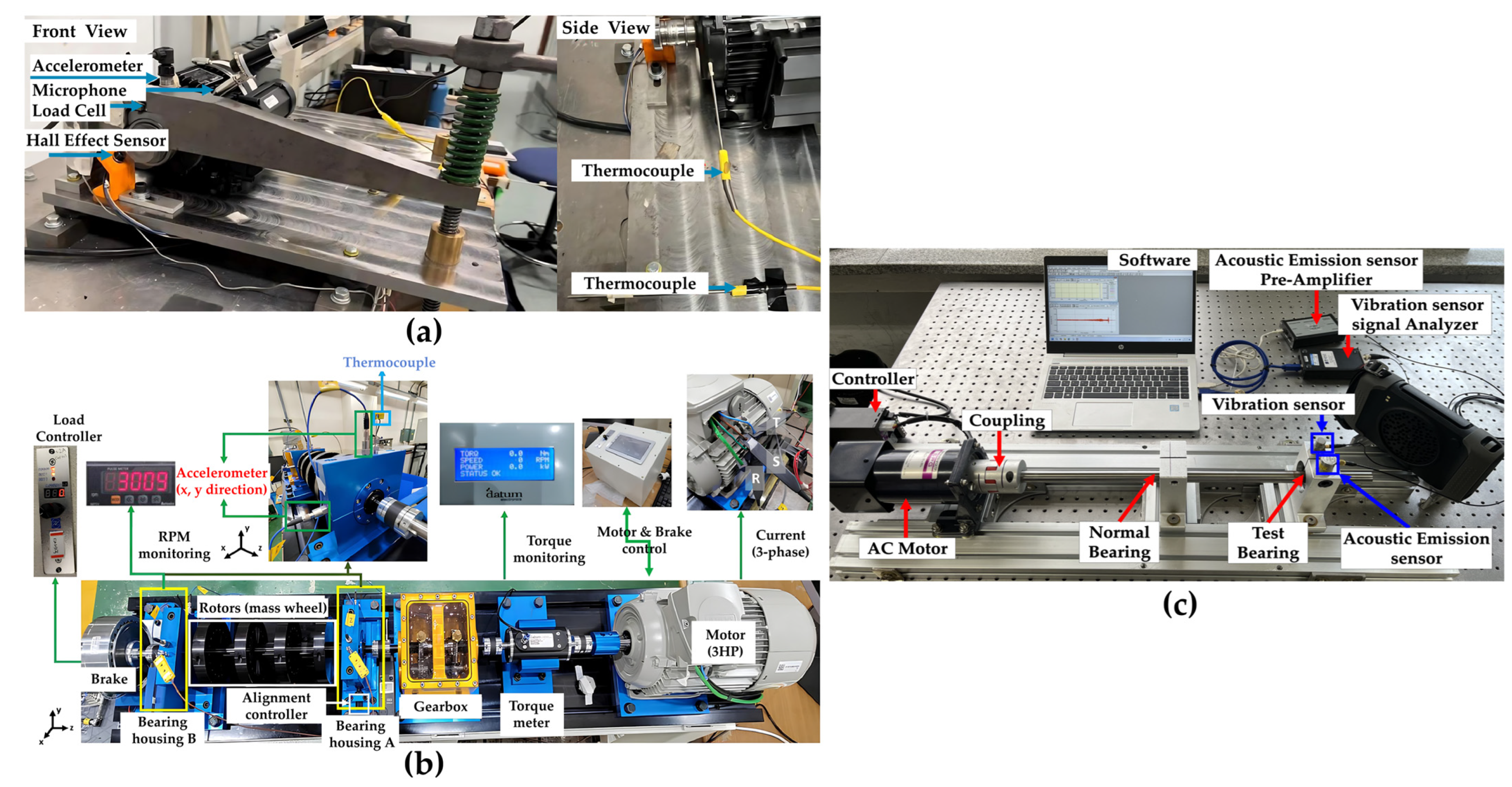
3.2. Dataset Description
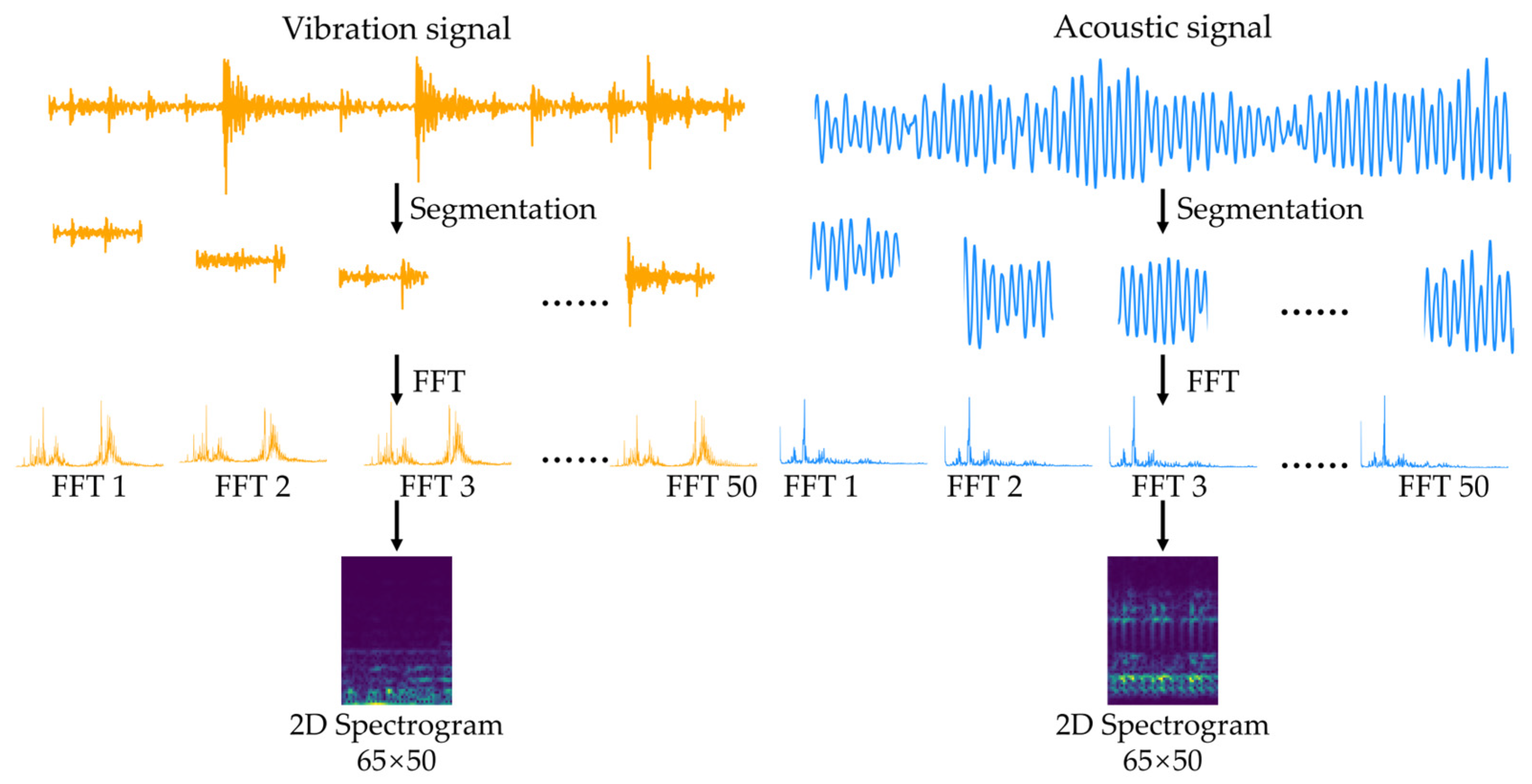
3.3. Pre-Processing
3.4. Softmax Output Analysis and Evaluation
3.5. Comparative Performance Results
3.6. Missing-Data Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guang, R.; Li, X.; Lei, Y.; Li, N.; Yang, B. Non-contact machine vibration sensing and fault diagnosis method based on event camera. In Proceedings of the 2023 CAA Symposium on Fault Detection, Supervision and Safety for Technical Processes (SAFEPROCESS), Yibin, China, 22–24 September 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Wang, R.; Qian, J. A novel fault diagnosis method based on multi-level information fusion and hierarchical adaptive convolutional neural networks for centrifugal blowers. Measurement 2021, 185, 109970. [Google Scholar] [CrossRef]
- Qiao, Z.; Liu, Y.; Liao, Y. An improved method of EWT and its application in rolling bearings fault diagnosis. Shock Vib. 2020, 2020, 4973941. [Google Scholar] [CrossRef]
- Ghazali, M.H.; Wan, W.R. Vibration analysis for machine monitoring and diagnosis: A systematic review. Shock Vib. 2021, 2021, 9469318. [Google Scholar] [CrossRef]
- Keshun, Y.; Zengwei, L.; Yingkui, G. A performance-interpretable intelligent fusion of sound and vibration signals for bearing fault diagnosis via dynamic CAME. Nonlinear Dyn. 2024, 112, 20903–20940. [Google Scholar] [CrossRef]
- Yoo, Y.; Jo, H.; Ban, S.-W. Lite and efficient deep learning model for bearing fault diagnosis using the CWRU dataset. Sensors 2023, 23, 3157. [Google Scholar] [CrossRef]
- Gao, H.; Ma, J.; Zhang, Z.; Cai, C. Bearing fault diagnosis method based on attention mechanism and multi-channel feature fusion. IEEE Access 2024, 12, 45011–45025. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, B.; Lin, Y. Machine learning based bearing fault diagnosis using the Case Western Reserve University data: A review. IEEE Access 2021, 9, 155598–155608. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing fault detection and diagnosis using Case Western Reserve University dataset with deep learning approaches: A review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Xu, M.; Guan, P.; Shi, X.; Jiang, R.; Tian, J.; Geng, J.; Xiong, G. Research on bearing fault diagnosis methods based on various convolutional neural network architectures. IEEE Access 2025, 13, 44445–44465. [Google Scholar] [CrossRef]
- Xu, Z.; Mei, X.; Wang, X.; Yue, M.; Jin, J.; Yang, Y.; Li, C. Fault diagnosis of wind turbine bearing using a multi-scale convolutional neural network with bidirectional long short term memory and weighted majority voting for multi-sensors. Renew. Energy 2022, 182, 615–626. [Google Scholar] [CrossRef]
- Song, R.; Bai, X.; Zhang, R.; Jia, Y.; Pan, L.; Dong, Z. Bearing fault diagnosis method based on multidomain heterogeneous information entropy fusion and model self-optimisation. Shock Vib. 2022, 2022, 7214822. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Li, X.; Tang, C. An investigation of vibrations of a flexible rotor system with the unbalanced force and time-varying bearing force. Chin. J. Mech. Eng. 2025, 38, 25. [Google Scholar] [CrossRef]
- Chen, J.; Li, T.; He, J.; Liu, T. An interpretable wavelet Kolmogorov–Arnold convolutional LSTM for spatial-temporal feature extraction and intelligent fault diagnosis. J. Dyn. Monit. Diagn. 2025, 4, 183–193. [Google Scholar] [CrossRef]
- Spirto, M.; Nicolella, A.; Melluso, F.; Malfi, P.; Cosenza, C.; Savino, S.; Niola, V. Enhancing SDP-CNN for gear fault detection under variable working conditions via multi-order tracking filtering. J. Dyn. Monit. Diagn. 2025. [Google Scholar] [CrossRef]
- Niola, V.; Savino, S.; Quaremba, G.; Cosenza, C.; Nicolella, A.; Spirto, M. Discriminant Analysis of the Vibrational Behavior of a Gas Micro-Turbine as a Function of Fuel. Machines 2022, 10, 925. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, K.; Zheng, Q.; Ding, G.; Hao, W.; Zhang, H.; Zhang, W. Unsupervised fault detection with multi-source anomaly sensitivity enhancing convolutional autoencoder for high-speed train bogie bearings. Expert Syst. Appl. 2025, 281, 127570. [Google Scholar] [CrossRef]
- Yan, X.; Jiang, D.; Xiang, L.; Xu, Y.; Wang, Y. CDTFAFN: A novel coarse-to-fine dual-scale time-frequency attention fusion network for machinery vibro-acoustic fault diagnosis. Inf. Fusion 2024, 112, 102554. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Elasha, F.; Greaves, M.; Mba, D.; Fang, D. A comparative study of the effectiveness of vibration and acoustic emission in diagnosing a defective bearing in a planetary gearbox. Appl. Acoust. 2017, 115, 181–195. [Google Scholar] [CrossRef]
- Dai, M.; Jo, H.; Kim, M.; Ban, S.-W. MSFF-Net: Multi-sensor frequency-domain feature fusion network with lightweight 1D CNN for bearing fault diagnosis. Sensors 2025, 25, 4348. [Google Scholar] [CrossRef]
- Kibrete, F.; Woldemichael, D.E.; Gebremedhen, H.S. Multi-sensor data fusion in intelligent fault diagnosis of rotating ma-chines: A comprehensive review. Measurement 2024, 232, 114658. [Google Scholar] [CrossRef]
- Guo, J.; He, Q.; Zhen, D.; Gu, F.; Ball, A.D. Multi-sensor data fusion for rotating machinery fault detection using improved cyclic spectral covariance matrix and motor current signal analysis. Rel. Eng. Syst. Saf. 2023, 230, 108969. [Google Scholar] [CrossRef]
- Chaleshtori, A.E.; Aghaie, A. Data fusion techniques for fault diagnosis of industrial machines: A survey. arXiv 2022, arXiv:2211.09551. Available online: https://arxiv.org/abs/2211.09551 (accessed on 25 June 2025). [CrossRef]
- Wang, J.; Wang, D.; Wang, S.; Li, W.; Song, K. Fault diagnosis of bearings based on multi-sensor information fusion and 2D convolutional neural network. IEEE Access 2021, 9, 23717–23725. [Google Scholar] [CrossRef]
- Tao, J.; Liu, Y.; Yang, D. Bearing fault diagnosis based on deep belief network and multisensor information fusion. Shock Vib. 2016, 2016, 9306205. [Google Scholar] [CrossRef]
- Wang, S.; Feng, Z. Multi-sensor fusion rolling bearing intelligent fault diagnosis based on VMD and ultra-lightweight GoogLeNet in industrial environments. Digit. Signal Process. 2024, 145, 104306. [Google Scholar] [CrossRef]
- Shao, H.; Lin, J.; Zhang, L.; Galar, D.; Kumar, U. A novel approach of multisensory fusion to collaborative fault diagnosis in maintenance. Inf. Fusion 2021, 74, 65–76. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, M.; Liu, F.; Zhang, B. Multidimensional feature fusion and ensemble learning-based fault diagnosis for the braking system of heavy-haul train. IEEE Trans. Ind. Inform. 2021, 17, 41–51. [Google Scholar] [CrossRef]
- Xu, X.; Song, D.; Wang, Z.; Zheng, Z. A Novel Collaborative Bearing Fault Diagnosis Method Based on Multisignal Decision-Level Dynamically Enhanced Fusion. IEEE Sens. J. 2024, 24, 34766–34776. [Google Scholar] [CrossRef]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the 13th International Conference on Machine Learning (ICML), San Francisco, CA, USA, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Song, L.; Tan, J. Rotation Error Prediction of CNC Spindle Based on Short-Time Fourier Transform of Vibration Sensor Signals and Improved Weighted Residual Network. Sensors 2024, 24, 4244. [Google Scholar] [CrossRef] [PubMed]
- Luo, T.; Qiu, M.; Wu, Z.; Zhao, Z.; Zhang, D. Bearing fault diagnosis based on multi-scale spectral images and convolutional neural network. J. Vibroeng. 2025, 27, 1012–1027. [Google Scholar] [CrossRef]
- Biswas, S.; Al Mamun, A.; Islam, M.S.; Bappy, M.M. Interpretable CNN models for computationally efficient bearing fault diagnosis using learnable Gaussian/Sinc filters. Manuf. Lett. 2025, 44, 110–120. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, M.; Huang, X. Bearing fault diagnosis based on speed signal and CNN model. Energy Rep. 2022, 8, 904–913. [Google Scholar] [CrossRef]
- Jia, H.-X.; Zhang, Y.-J. Fast AdaBoost training algorithm by dynamic weight trimming. Chin. J. Comput. 2009, 32, 336. [Google Scholar] [CrossRef]
- Wang, G.; Li, P. Dynamic Adaboost ensemble extreme learning machine. In Proceedings of the 2010 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), Chengdu, China, 20–22 August 2010; pp. V3-54–V3-58. [Google Scholar] [CrossRef]
- Sehri, M.; Dumond, P.; Bouchard, M. University of Ottawa constant load and speed rolling-element bearing vibration and acoustic fault signature datasets. Data Brief 2023, 49, 109327. [Google Scholar] [CrossRef]
- Jung, W.; Kim, S.-H.; Yun, S.-H.; Bae, J.; Park, Y.-H. Vibration, acoustic, temperature, and motor current dataset of rotating machine under varying operating conditions for fault diagnosis. Data Brief 2023, 48, 109049. [Google Scholar] [CrossRef]
- ISO 10816-1:1995; Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts—Part 1: General Guidelines. International Organization for Standardization: Geneva, Switzerland, 1995. Available online: https://www.iso.org/standard/18866.html (accessed on 30 June 2025).
- ISO 8528-10:2022; Reciprocating Internal Combustion Engine Driven Alternating Current Generating Sets—Part 10: Measurement of Airborne Noise. International Organization for Standardization: Geneva, Switzerland, 2022. Available online: https://www.iso.org/standard/74983.html (accessed on 30 May 2025).
- Zhang, J.; Kong, Y.; Han, Q.; Wang, T.; Dong, M.; Liu, H.; Chu, F. Multimodal data imputation and fusion for trustworthy fault diagnosis of mechanical systems. Eng. Appl. Artif. Intell. 2025, 150, 110663. [Google Scholar] [CrossRef]
- Kwak, S.K.; Kim, J.H. Statistical data preparation: Management of missing values and outliers. Korean J. Anesthesiol. 2017, 70, 407. [Google Scholar] [CrossRef]
| Approach | Inputs | Main Contribution | |
|---|---|---|---|
| Number of Sensors | Sensor Type | ||
| Data fusion (Wang, X et al. [19]) | 2 | Accelerometer/Microphone | The diagnostic performance was enhanced through sensor data fusion based on 1D-CNN, resulting in an increase in computational load due to signal-level integration. |
| Data fusion (Wang, J et al. [25]) | 3 | Acceleration | By integrating raw signals from multiple locations using a 2D-CNN, information loss was reduced, while the computational cost remained high. |
| Data fusion (Tao, J et al. [26]) | 3 | Magnet acceleration | Feature representations from multiple sensors were fused using a deep belief network (DBN), leading to improved diagnostic accuracy accompanied by increased structural complexity. |
| Data fusion (Wang, S et al. [27]) | 2 | Acceleration | Multi-sensor signals decomposed by variational mode decomposition (VMD) were analyzed using an ultra-lightweight GoogLeNet (UL-GoogLeNet), achieving high accuracy but not reflecting sensor-specific reliability. |
| Feature fusion (Song, R et al. [12]) | 2 | Accelerometer | Spatiotemporal fusion with entropy-based weighting enhanced representational capability, while multiple stages of feature extraction resulted in an increased number of preprocessing steps. |
| Feature fusion (Yan, X et al. [18]) | 2 | Accelerometer/Microphone | Spatial, temporal, and frequency features were fused using dual-scale attention, resulting in improved feature integration but increased complexity due to high-dimensional combination and intermediate fusion stages. |
| Feature fusion (Dai, M et al. [21]) | 2 | Accelerometer/Microphone | Two frequency-domain signals were fused via FFT and diagnosed using a lightweight 1D-CNN, achieving high accuracy and low computational cost, though the simple fusion method may cause information redundancy. |
| Decision fusion (Shao, H et al. [28]) | 7 | Vibration | Diagnostic accuracy was improved through predictive fusion based on a stacked wavelet auto-encoder, while the weight configuration remained empirical. |
| Decision fusion (Liu, Z et al. [29]) | 2≤ Sensors | Air pressure | Multidimensional features from multiple sensors were fused and used in ensemble learning to diagnose braking system faults, resulting in effective fault identification but increased model complexity and computational cost. |
| Decision fusion (Xu, X et al. [30]) | 4 | Vibration/Acoustic | Dynamic decision-level fusion adaptively calibrated multi-signal classification results using statistical features from a variational autoencoder, improving diagnostic accuracy and reliability but increasing real-time computational load and model complexity. |
| Bearing Type | Pitch Diameter | Ball Diameter | Number of Balls |
|---|---|---|---|
| KBC 6204 | 9.52 mm | 36 mm | 7 |
| Vib | AE | |
|---|---|---|
| Sampling frequency | 12,000 Hz | 7168 Hz |
| Frequency range | 0.5~10,000 Hz | 15,000~40,000 Hz |
| Resonant Frequency | - | 28,000 Hz |
| Dataset | Sensor Type | Decision Level | Mean Accuracy (%) | Min. Accuracy (%) | Max. Accuracy (%) |
|---|---|---|---|---|---|
| Case 1 | Acoustic | Top-1 | 99.54 | 99.10 | 99.80 |
| Top-2 | 99.92 | 99.80 | 100 | ||
| Vibration | Top-1 | 99.52 | 99.20 | 99.80 | |
| Top-2 | 99.94 | 99.90 | 100 | ||
| Case 2 | Acoustic | Top-1 | 99.93 | 99.88 | 99.97 |
| Top-2 | 100 | 100 | 100 | ||
| Vibration | Top-1 | 99.98 | 99.96 | 99.99 | |
| Top-2 | 100 | 100 | 100 | ||
| Case 3 | Acoustic emission | Top-1 | 99.80 | 98.68 | 99.85 |
| Top-2 | 100 | 100 | 100 | ||
| Vibration | Top-1 | 99.94 | 99.90 | 99.97 | |
| Top-2 | 100 | 100 | 100 |
| Dataset | Acoustic | Vibration | Proposed Model |
|---|---|---|---|
| Case1 | 99.52 ± 0.0022% | 99.52 ± 0.0019% | 99.93 ± 0.0003% |
| Case2 | 99.93 ± 0.0003% | 99.98 ± 0.0002% | 99.99 ± 0.0001% |
| Case3 | 99.80 ± 0.0006% | 99.94 ± 0.0002% | 99.95 ± 0.0003% |
| Dataset | Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|---|
| Case 1 | MFF-GBDT | 81.75 ± 0.0420 | 82.05 ± 0.0420 | 81.04 ± 0.0420 | 81.17 ± 0.0420 |
| CDTFAFN | 99.90 ± 0.0060 | 99.90 ± 0.0060 | 99.90 ± 0.0060 | 99.90 ± 0.0060 | |
| MSFF-Net | 99.91 ± 0.0003 | 99.91 ± 0.0003 | 99.91 ± 0.0003 | 99.91 ± 0.0003 | |
| Proposed model | 99.90 ± 0.0004 | 99.93 ± 0.0004 | 99.93 ± 0.0004 | 99.93 ± 0.0004 | |
| Case 2 | MFF-GBDT | 98.38 ± 0.0035 | 98.41 ± 0.0036 | 93.36 ± 0.0035 | 98.38 ± 0.0038 |
| CDTFAFN | 99.95 ± 0.0008 | 99.95 ± 0.0007 | 99.95 ± 0.0008 | 99.95 ± 0.0008 | |
| MSFF-Net | 99.25 ± 0.0188 | 99.40 ± 0.0142 | 99.25 ± 0.0187 | 99.23 ± 0.0192 | |
| Proposed model | 99.98 ± 0.0004 | 99.99 ± 0.0003 | 99.99 ± 0.0003 | 99.99 ± 0.0003 | |
| Case 3 | MFF-GBDT | 78.00 ± 0.0710 | 79.15 ± 0.0710 | 78.00 ± 0.0710 | 87.20 ± 0.0710 |
| CDTFAFN | 99.99 ± 0.0006 | 99.99 ± 0.0006 | 99.99 ± 0.0006 | 99.99 ± 0.0006 | |
| MSFF-Net | 99.91 ± 0.0002 | 99.91 ± 0.0002 | 99.9 ± 0.0002 | 99.91 ± 0.0030 | |
| Proposed model | 99.99 ± 0.0003 | 99.99 ± 0.0003 | 99.99 ± 0.0003 | 99.99 ± 0.0004 |
| Multi-Sensory Fusion Methods | FLOPs (M) | Model Size (MB) | Inference Time (s) | ||
|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |||
| MFF-GBDT | 0.0015 | 0.757 | 0.00006 | 0.00004 | 0.00006 |
| CDTFAFN | 34.5781 | 200.000 | 0.01680 | 0.01670 | 0.01670 |
| MSFF-Net | 236.4972 | 27.500 | 0.00175 | 0.00200 | 0.00190 |
| Proposed model | 0.0003 | 0.068 | 0.00002 | 0.00002 | 0.00003 |
| Method | Missing Rate (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 10 | 20 | 30 | |||||||
| Acou-Miss | Ens | Acou-Miss | Ens | Acou-Miss | Ens | Vib-Miss | Ens | Vib-Miss | Ens | Vib-Miss | Ens | |
| Case1 | 90.29 | 98.26 | 82.47 | 98.98 | 74.29 | 98.52 | 88.15 | 96.20 | 80.77 | 98.20 | 74.41 | 98.18 |
| Case2 | 91.76 | 99.64 | 83.36 | 99.75 | 75.72 | 99.95 | 90.71 | 99.69 | 82.49 | 99.85 | 75.93 | 99.85 |
| Case3 | 91.60 | 97.14 | 82.99 | 98.57 | 74.37 | 99.98 | 91.53 | 95.71 | 82.69 | 98.57 | 74.14 | 99.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, H.; Yoo, Y.; Dai, M.; Ban, S.-W. An Upper-Probability-Based Softmax Ensemble Model for Multi-Sensor Bearing Fault Diagnosis. Sensors 2025, 25, 6887. https://doi.org/10.3390/s25226887
Jo H, Yoo Y, Dai M, Ban S-W. An Upper-Probability-Based Softmax Ensemble Model for Multi-Sensor Bearing Fault Diagnosis. Sensors. 2025; 25(22):6887. https://doi.org/10.3390/s25226887
Chicago/Turabian StyleJo, Hangyeol, Yubin Yoo, Miao Dai, and Sang-Woo Ban. 2025. "An Upper-Probability-Based Softmax Ensemble Model for Multi-Sensor Bearing Fault Diagnosis" Sensors 25, no. 22: 6887. https://doi.org/10.3390/s25226887
APA StyleJo, H., Yoo, Y., Dai, M., & Ban, S.-W. (2025). An Upper-Probability-Based Softmax Ensemble Model for Multi-Sensor Bearing Fault Diagnosis. Sensors, 25(22), 6887. https://doi.org/10.3390/s25226887