Abstract
Cavitation phenomenon in piston pumps not only causes vibration and noise but also leads to component damage. Conventional diagnostic methods suffer from low accuracy, while deep learning approaches lack interpretability. To address these limitations, this paper proposes an intelligent fault diagnosis method based on the rough set Attribute Weighted Convolutional Neural Network (RSAW-CNN). First, based on cavitation mechanisms and the mathematical model, the computational fluid dynamics model of the piston pump is established to simulate the failure condition. Subsequently, employing rough set theory, an original fault decision table is constructed, discretized, and subjected to attribute reduction. A weight matrix is generated according to the importance of each data channel in the classification decision and embedded into the input layer of the Convolutional Neural Network (CNN) to enhance the influence of key features. Decision rules are also extracted to provide interpretable decision support for fault diagnosis. Experimental results demonstrate that the proposed RSAW-CNN method achieves an average diagnostic accuracy of over 99.2%. Compared to the backpropagation neural network, residual neural network, CNN, and the CNN with squeeze-and-excitation networks, its average accuracy has improved by 15.87%, 10.83%, 7.48%, and 5.40%. The proposed method not only exhibits high diagnostic accuracy but also offers strong interpretability and reliability.
1. Introduction
Axial piston pumps serve as the power source of high-end equipment hydraulic systems, delivering continuous and stable hydraulic power to actuators [1]. Once a malfunction in a piston pump can compromise the entire hydraulic system, leading to degraded equipment performance, reduced operational efficiency, and even complete system failure [2]. Among these failures, cavitation represents a particularly common and detrimental type of failure. Prolonged cavitation significantly shortens the service life of piston pump components, potentially causing critical failures such as damage to the valve plate or cracking of the cylinder block [3,4]. Such failures not only incur substantial repair costs but also result in production delays or safety incidents due to unexpected equipment downtime [5,6]. This underscores the significant value of cavitation fault diagnosis research.
Since cavitation occurs internally within the pump, technicians cannot directly observe and make precise judgments about its occurrence based on visual inspection alone [7]. Furthermore, cavitation faults often manifest as weak characteristic signals with low distinguishability, presenting considerable challenges for accurate diagnosis [8]. Traditional diagnostic approaches, including visual observation, pressure/flow signal analysis, and vibration signal analysis, have inherent limitations [9,10]. High-speed camera visualization allows direct observation of cavitation phenomena [11] but lacks sensitivity in capturing micro-cavitation and intermittent cavitation [12]. Quantitative assessment of cavitation through pressure and flow signal analysis is possible, yet it frequently misdiagnoses early subtle changes [13,14]. In contrast, vibration signal analysis is highly sensitive to the high-frequency shock responses induced by cavitation [15]. Nevertheless, the complexity of vibration sources necessitates specialized signal processing techniques to effectively distinguish cavitation from other mechanical faults [16,17]. Therefore, integrating multiple diagnostic methods is a promising approach to enhance both accuracy and reliability.
The advancement of artificial intelligence has spurred the adoption of intelligent diagnostic methods [18]. Machine learning techniques (e.g., decision trees, support vector machines, neural networks) [19] and multi-channel CNN models [20] have shown promise but suffer from data redundancy and poor interpretability [21]. Composite approaches integrating data preprocessing have addressed these issues to some extent: wavelet analysis combined with rough set rule generation and fuzzy classification [22], improved CNN variants [23,24], and transient flow measurement with enhanced transfer learning [25] have optimized feature extraction and reduced redundancy [26]. Collectively, these composite methods reduce data redundancy through preprocessing, and optimize feature extraction, leading to improved model performance and generalization capabilities [27,28].
In summary, composite fault diagnosis methods not only leverage the synergistic advantages of multiple techniques to improve diagnostic accuracy but also provide more intuitive insights, thereby strengthening operators trust and understanding of equipment condition [29,30]. Although deep learning models such as convolutional neural network (CNN) have demonstrated great potential in the field of fault diagnosis for axial piston pumps, they still face challenges, including low diagnostic efficiency, poor interpretability, and insufficient credibility. Deep learning models fail to identify the key input features causing faults, leading to a lack of targeting in subsequent maintenance work. Their “black-box” nature prevents users from directly participating in the decision-making process, greatly reducing user trust and severely limiting their practical application value. To address these issues, there is an urgent practical demand for an intelligent diagnostic model with both high accuracy and strong interpretability. This paper proposes an intelligent fault diagnosis method based on a rough set attribute-weighted convolutional neural network (RSAW-CNN), enhancing the accuracy and interpretability of fault diagnosis. It provides a novel approach to improving the intelligence and reliability of axial piston pumps. Our contributions are as follows:
- (1)
- Proposal of a novel Rough Set-based Attribute Weighted Convolutional Neural Network (RSAW-CNN) model for fault diagnosis. This model achieves a deep integration of the knowledge discovery capability inherent in rough set theory and the deep learning power of a one-dimensional convolutional neural network (1DCNN). Guided by the feature importance derived from rough set theory, the CNN learning process is enhanced, effectively improving both model convergence speed and diagnostic accuracy. Furthermore, the decision rules obtained through rough set theory augment the model’s fault diagnosis efficiency and interpretability.
- (2)
- Introduction of an innovative weighting mechanism for the 1DCNN. Based on rough set theory, an attribute weight matrix is generated to quantify the importance of each input channel. This matrix is embedded into the input layer of the CNN, thereby incorporating derived prior knowledge at the initial stage of model learning. Guiding the CNN learning based on input feature importance directs the network focus towards identified critical attributes, enhancing the efficiency and targeted nature of feature learning.
- (3)
- Achievement of dual interpretability concerning both the diagnostic process and the underlying fault mechanism. Based on the physical mechanism and mathematical model of cavitation, an original fault decision table for cavitation faults is constructed. Following rough set-based discretization and attribute reduction, rules for cavitation faults are derived to serve as the decision basis. When physical parameters, such as piston pump outlet pressure and outlet flow rate, fall within specific threshold ranges, concrete cavitation fault states are deduced. This provides engineers with valuable, interpretable analysis concerning the fault mechanism, thereby enhancing the reliability and trustworthiness of the diagnostic system.
The remainder of this paper is structured as follows: Section 2 introduces the cavitation failure mechanisms and mathematical models. Section 3 describes the computational fluid dynamics simulation analysis of the piston pump. Section 4 details the proposed methodology, incorporating rough set theory and convolutional neural networks. Section 5 presents the RSAW-CNN fault diagnosis model and discusses the diagnostic results. Finally, Section 6 provides the conclusion of the study.
2. Cavitation Failure Mechanisms and Mathematical Models
2.1. Cavitation Failure Mechanisms
This study focuses on the swash plate type axial piston pump. The schematic diagram of the piston pump structure is shown in Figure 1. The key components include the drive shaft, bearings, valve plate, cylinder block, pistons, slippers, and swashplate. The piston pump acts as a power unit that converts mechanical energy into hydraulic energy. Mechanical power is transmitted to the cylinder block via shafts. The cylinder block, combined with the piston and sliding shoe assembly, converts oscillating motion into linear reciprocating motion. The reciprocating movement of each piston causes periodic volume changes in its respective piston chamber. This cycle draws in low-pressure fluid through the inlet port and expels high-pressure fluid through the outlet port. Each piston chamber communicates with ports on the valve plate, which are connected to the pump inlet and outlet, facilitating fluid intake and discharge.
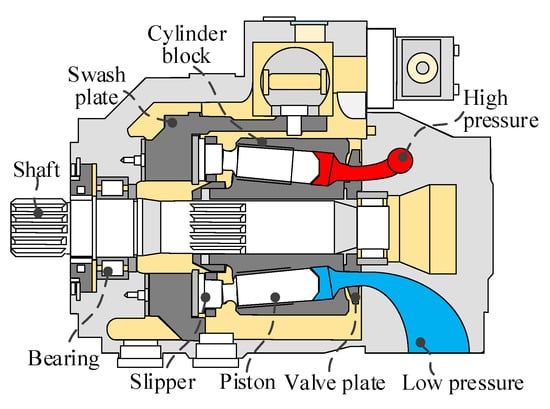
Figure 1.
Schematic diagram of the piston pump structure.
Figure 2 illustrates the complete process of cavitation inception, development, and collapse. During the suction process of the piston pump, the piston moves outward within its cylinder bore. As a result, the sealed volume of the suction chamber increases, creating a localized low-pressure region. If the pressure in this region drops below the saturated vapor pressure of the hydraulic oil, dissolved gases are released, forming bubbles. Simultaneously, partial vaporization of the oil may occur, producing vapor bubbles and initiating cavitation. As the piston moves back inward, the suction chamber volume decreases and the pressure increases. Under this high pressure, the bubbles implode violently, generating localized high-temperature, high-pressure micro-jets that impinge on critical components such as the piston, cylinder bore, and valve plate. This repeated impingement leads to material fatigue and erosion, directly impairing pump performance and service life.
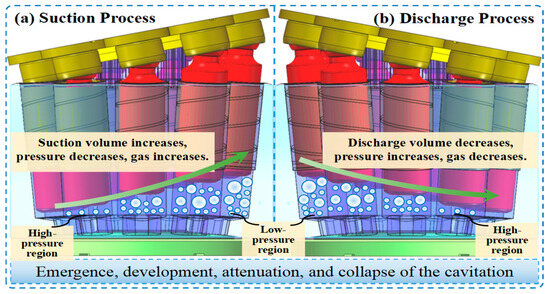
Figure 2.
Process of cavitation formation, development, and collapse.
Furthermore, cavitation induces pressure fluctuations in the hydraulic oil, resulting in noise and vibration. These effects accelerate component wear, compromise sealing integrity, and reduce the volumetric efficiency of the pump.
2.2. Mathematical Models
The hydraulic oil within the piston pump is a mixture composed of gas and liquid phases, and its behavior is governed by the following equilibrium equation.
where is the average density of the gas–liquid two-phase flow, is the average velocity of the gas–liquid two-phase flow.
During operation, the oil in the gas–liquid two-phase flow experiences varying pressures at different locations. The pressure coefficient is used to represent the pressure variation at a specific point in the oil.
where is the pressure at a point in the fluid, is the reference pressure of the fluid, is the density of the oil within the piston pump, is the flow velocity of the oil.
When in the oil fluid, gas will separate out to form cavitation. Defining as the cavitation initiation state, the cavitation initiation coefficient is expressed as
where is the cavitation initiation coefficient, is the saturated vapor pressure.
Simultaneously, from a microscopic perspective of cavitation, the kinetic equation for bubble formation is introduced to model cavitation. The bubble radius can be described as
where is the radius of the cavitation bubble.
Considering the surface tension coefficient of bubbles, the bubble generation rate and compression ratio can be expressed as
where is the bubble generation rate, is the bubble compression ratio, is the gas mass fraction, is the gas surface tension coefficient, is the transfer coefficient, and are constants.
3. Simulation Analysis
3.1. Simulation Model
This study employs the computational fluid dynamics (CFD) method and utilizes the PumpLinx v4.6.0 simulation software to conduct simulation analysis on the system characteristics of piston pumps under different cavitation levels. Figure 3 presents a schematic diagram of the simulation analysis, which primarily consists of three steps. Firstly, the three-dimensional geometric model of the piston pump fluid domain is constructed using SolidWorks 2012 software, imported into the PumpLinx simulation platform, with interfaces constructed to ensure geometric feature integrity, and the fluid domain is discretized using high-precision Cartesian hexahedral meshes to enhance subsequent simulation accuracy. Subsequently, the necessary parameters for the simulation model are set, including the cavitation model, boundary conditions, parameters of the research object, and operating conditions. Finally, different cavitation levels are simulated by adjusting the inlet pressure. Meanwhile, the necessary data from the simulation analysis is collected and analyzed. Table 1 lists the key structural parameters of the piston pump under investigation, which mainly include displacement, rated pressure, peak pressure, maximum speed, number of pistons, and swash plate inclination angle.
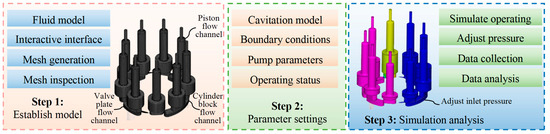
Figure 3.
Schematic diagram of simulation analysis.

Table 1.
Main parameters of the piston pump.
3.2. Simulation Result
A significant negative correlation exists between the cavitation severity of the piston pump and its inlet pressure. When the hydraulic oil flows from the oil tank into the piston pump through the suction line, the pressure is highly prone to dropping below the vapor pressure of the oil. Conversely, if the inlet pressure of the piston pump is maintained at a relatively high level and consistently exceeds the oil vapor pressure, the release of dissolved gases from the oil is effectively inhibited, and cavitation can thus be suppressed significantly. Figure 4 illustrates the four cavitation levels corresponding to different inlet pressures of the piston pump. Specifically, by setting the piston pump inlet pressure to 0.4 MPa, 0.3 MPa, 0.2 MPa, and 0.1 MPa, respectively, the corresponding cavitation levels are defined as four states: normal operation, mild cavitation, moderate cavitation, and severe cavitation.
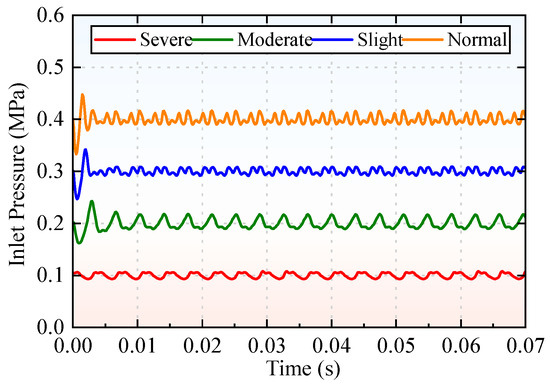
Figure 4.
Different cavitation levels corresponding to different inlet pressures.
Based on the four cavitation states corresponding to different inlet pressures, the pressure and flow characteristics at the key positions of the piston pump are analyzed. Figure 5 presents the characteristic curves of the piston pump under various cavitation levels, including inlet flow rate, outlet pressure, outlet flow rate, and piston chamber pressure. As an axial piston pump is a positive-displacement hydraulic pump, all curves exhibit an overall periodic variation throughout its continuous oil suction and discharge cycles.
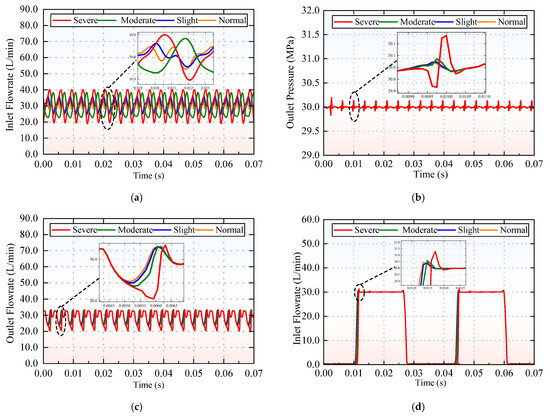
Figure 5.
Characteristic curves of the different cavitation levels: (a) inlet flow rate; (b) outlet pressure; (c) outlet flow rate; and (d) piston chamber pressure.
In the normal cavitation state, only a small quantity of cavitation bubbles is generated, and these bubbles dissolve in the surrounding hydraulic fluid. With the gradual deterioration of cavitation severity, the number of cavitation bubbles increases progressively—this is accompanied by increasingly significant fluctuations in pressure and flow rate at the key positions of the piston pump. Figure 5a illustrates the inlet flow rate. As shown in Figure 5a,c, the flow fluctuations become more pronounced with intensifying cavitation. Figure 5b shows the outlet pressure. Since the research object is a nine-piston axial piston pump, the pressure presents nine distinct peaks during one full rotation of the cylinder block. Notably, both the pressure and flow rate of the pistons display increasingly large fluctuations with worsening cavitation. Figure 5c depicts the outlet flow rate. Consistent with the structural characteristics of the nine-piston pump, the flow rate also forms nine peaks per complete rotation of the cylinder block. Figure 5d presents the dynamic pressure of the piston chamber. When the piston pump operates in the oil discharge zone, the piston chamber pressure rises to the rated pressure of 30 MPa with a certain degree of fluctuation. When it operates in the oil suction zone, the pressure in the piston chamber drops to near atmospheric pressure. The variation trend of this curve clearly indicates that the piston pump alternates between the oil discharge and suction phases during operation.
4. Rough Set Attribute Weighted Convolutional Neural Network
4.1. Rough Set Theory
The rough set theory, proposed by Polish mathematician Zdzisław Pawlak, is a mathematical framework for handling incomplete, imprecise, and vague data. Its core idea lies in describing unknown and ambiguous concepts using known and observable information. Without relying on prior knowledge external to the data, it excavates hidden patterns solely through the indiscernibility of data. The fundamental theories of rough sets are defined and described as follows [31,32].
The first definition is the knowledge representation system. knowledge representation system is composed of universe of discourse U, attribute set A, value domain V, and factor mapping relationship f. The mapping assigns values to all attributes within the system. For any and , then . If the A satisfies the conditions that and where denotes the conditional attribute set C and denotes the decision attribute set D then the system constituted by and is defined as a decision table [33].
The second definition is the indiscernibility relation. For , the indistinguishable relationship IND(B) is described as follows:
The IND(B) is an equivalence relation, satisfying .
The decision table are and . The breakpoints in the domain are denoted as (a, c). Selecting a set of breakpoints for within the domain defines the classification .
Arbitrary classification constitutes a new decision-making system.
Divide the values of a conditional attribute into equidistant intervals based on specified parameters, disregarding the number of values within each interval. If the maximum and minimum values of a given attribute are and , respectively, and a parameter k is specified such that the distance between intervals is , this can be expressed as .
Attribute reduction: Ensures diagnostic capability remains unchanged while retaining critical knowledge and eliminating irrelevant information.
Relative reduction: If , the H is a K-reduction in J, and only if the H is a K-independent subfamily of J and . The K-reductions in J are relative reductions.
In the , the importance of each attribute can be computed without relying on prior knowledge based on rough set theory. represents the degree of dependence of attribute C on category D. When removing a specific attribute from the overall attribute set C, the change in can be used to evaluate the attribute importance. The attribute importance is defined as follows:
where represents the dependency level of attribute C on category D, represents the dependency level of category D after removing attribute C, a smaller value indicates that the attribute has a lesser impact on the entire system and a smaller influence on fault diagnosis, making it an unimportant attribute. Conversely, a larger value indicates an important attribute.
The steps for calculating attribute weights primarily consist of the following four parts.
- (1)
- Determine the cavitation failure decision attribute D and the conditional attribute set C.
- (2)
- Establish a discretized decision table.
- (3)
- Calculate the values of and , respectively, using the following expressions:
- (4)
- Finally, calculate the weight for each conditional attribute as described below:
4.2. Convolutional Neural Network
A convolutional neural network (CNN), a typical feedforward neural network, features sparse connectivity and weight sharing. Sparse connectivity, through spatial topological structures, creates a non-fully connected relationship between adjacent layers, reducing the number of parameters for model training. Weight sharing mainly serves to prevent algorithmic overfitting. The CNNs have been widely applied in fields such as image recognition and fault diagnosis [34].
Depending on the type of input data, the CNN architectures can be categorized into 1D (one-dimensional), 2D (two-dimensional), and 3D (three-dimensional) models. Since the signals collected in this study, such as pressure and flow rate signals of the piston pump, are data-type signals, the 1D CNN is selected for fault diagnosis, with its network structure illustrated in Figure 6. The 1D CNN architecture comprises an input layer, convolutional layers, pooling layers, fully connected layers, and an output layer. During the early feature extraction phase of the CNN, convolutional layers and pooling layers are alternately utilized to extract features from the input data. Near the output layer, a conventional multi-layer neural network structure is employed.
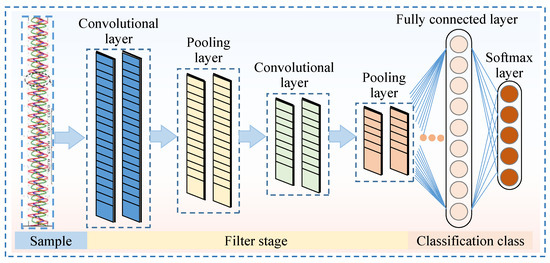
Figure 6.
Schematic diagram of the 1D CNN architecture.
In the convolutional layer, the convolution kernel performs a convolution operation on the feature vectors output by the previous layer. A nonlinear activation function is then used to construct the output feature vectors. The output of each convolutional layer corresponds to the convolution results of multiple input features, and its mathematical model can be described as follows:
where l denotes the number of network layers, j represents the number of channels, f is the activation function, is the dth vector in the jth convolution kernel, and is the network bias term.
The pooling layer maps data from the convolutional layer, typically employing a max pooling operator. This operator extracts local maxima from data features, thereby reducing the number of training parameters while enhancing feature robustness. The max pooling function can be described as
where is the jth feature vector in the lth pooling layer, t ranges over , W is the pooling width, is the value of the l + 1th layer neuron.
The output of the 1D CNN employs the Softmax classifier to address the fault classification problem. The function can be expressed as
where and represent the bias vector and weight matrix, respectively, and denotes the feature vector.
5. Fault Diagnosis Process and Results
5.1. Fault Diagnosis Model
This paper puts forward an intelligent fault diagnosis method based on the rough set attribute weighted convolutional neural network (RSAW-CNN). As shown in Figure 7, the workflow and architecture of this state recognition method are presented. The core architecture consists of the following components: data input layer, rough-set (RS)-based attribute weight assignment layer, convolutional layers, pooling layers, fully connected layers, result output layer, and RS-rule-based auxiliary decision-making layer.
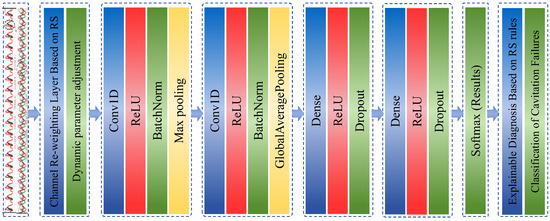
Figure 7.
Flowchart of the RSAW-CNN-based cavitation fault diagnosis model.
- (1)
- Data input layer.
A transient computational fluid dynamics (CFD) model of the axial piston pump is established. This CFD model is used to generate signals (e.g., flow rate and pressure) for the healthy axial piston pump; meanwhile, based on the cavitation mechanism of the piston pump, it simulates flow rate, pressure, and other signals under different cavitation levels. Both the healthy and cavitation fault signals are collected as the original dataset for subsequent processing.
- (2)
- Rough set attribute weighted layer.
The input channel signals are preprocessed to identify condition attributes and decision attributes for plunger pump cavitation faults based on rough set theory, thereby establishing the original fault decision table. The table is then discretized to obtain a discretized decision table. Attribute dependencies are calculated to determine channel weights, which are dynamically adjusted to highlight key channel information most relevant to cavitation faults. This process not only optimizes feature extraction but also significantly enhances the interpretability of the network model.
- (3)
- Convolutional layers.
The convolutional layer module consists of two one-dimensional convolutional layers designed to extract local features from the input signal. The ReLU activation function is then applied to provide nonlinear transformation capabilities, enabling the model to learn more complex feature relationships. Concurrently, data normalization is employed to accelerate training convergence and improve the model’s overall stability.
- (4)
- Pooling layers.
Max pooling and global average pooling are implemented. These operations reduce the number of parameters while preserving the most significant features, thereby enhancing the model’s anti-interference ability.
- (5)
- Fully connected layers.
Two fully connected layers are employed. The first layer integrates the extracted local features into a global representation, while the second layer functions as the classifier for cavitation faults. A Dropout layer is also incorporated to further prevent overfitting.
- (6)
- Result output layer and RS rule-based auxiliary decision-making layer.
This layer outputs the classification results for cavitation faults. Based on rough set theory, we first construct the initial decision table for piston pump cavitation faults. Then, through data discretization, we obtain a discrete decision table. Next, we apply genetic algorithms for attribute reduction, extracting the minimal reduced attribute set and its corresponding decision rules. These rules are used to assist in cavitation fault diagnosis, effectively enhancing the stability, interpretability, and credibility of the RSAW-CNN model. This approach meets the industrial demand for trustworthy artificial intelligence models.
Table 2 presents the parameters of the fault diagnosis model. The configured model parameters primarily include input shape, rough set attribute weighted layer, convolution layer, pooling layer, dense layer, Softmax layer, and optimizer.

Table 2.
Parameters of the RSAW-CNN-based cavitation fault diagnosis model.
5.2. Fault Diagnosis Process
The piston pump operates at an outlet pressure of 30 MPa and a rotational speed of 1800 r/min. Cavitation of varying degrees is induced by adjusting the inlet pressure of the piston pump. Specifically, inlet pressures of 0.4 MPa, 0.3 MPa, 0.2 MPa, and 0.1 MPa are set, which represent four cavitation levels: normal, no cavitation, mild cavitation, and severe cavitation. A total of 4800 datasets are collected across the four cavitation levels (one set corresponding to a 5 s continuous operation cycle of the piston pump), with 1200 sets per level to ensure balanced sample distribution. Among these, training samples constitute 80% of the total (3840 sets) for model training and parameter optimization, while test samples comprise the remaining 20% (960 sets) for independent validation of diagnostic performance, as shown in Table 3.

Table 3.
Four cavitation levels and fault data.
This paper applies wavelet transform noise filtering to the acquired signals. The dbN wavelet family is selected for signal decomposition and reconstruction. The signal undergoes five-level decomposition and reconstruction using wavelet basis functions. The noise-reduced signals achieve a signal-to-noise ratio exceeding 30 dB, demonstrating effective noise reduction.
Computing attribute weights and extracting rules based on rough set theory. Features are extracted based on the rough set theory. The domain U represents 4800 sample datasets. The conditional attributes C1–C5 are outlet pressure, outlet flow rate, inlet flow rate, piston chamber pressure, and piston chamber volume. The decision attribute D is categorized as normal, slight cavitation, moderate cavitation, and severe cavitation, labeled as classes 0, 1, 2, and 3, respectively. This constructs the decision table for cavitation faults, as shown in Table 4.

Table 4.
Decision table for cavitation failures.
The core of rough set theory lies in indistinguishable relations and equivalence classes, requiring the discretization of continuous attributes. Signals such as the outlet pressure of the piston pump are continuous and must be discretized. After equidistant discretization of the decision table for piston pump cavitation faults, the resulting discrete cavitation table is shown in Table 5.

Table 5.
Discrete cavitation table for piston pump.
The attribute importance and weights for the five input channels (conditional attributes) are calculated according to Equation (16), as shown in Table 6.

Table 6.
Rough set attribute weight table.
Compared to classical attribute reduction algorithms, the genetic algorithm is more suitable for handling large-scale and high-dimensional data, and it is less prone to becoming trapped in local optima, thereby having a higher probability of finding the global optimal reduction subset. Using attribute reduction based on the genetic algorithm, five reduced conditional attributes are obtained: outlet pressure, outlet flow rate, inlet flow rate, piston chamber pressure, and piston chamber volume. We have explicitly set the key parameters of the genetic algorithm. The population size is 335; the maximum number of iterations is 200; the crossover method adopts single-point crossover with a crossover probability of 0.8; the mutation method uses bit-flipping mutation with a mutation probability of 0.01. Meanwhile, we have clarified the core mechanism of the algorithm: each individual is encoded as a binary string, whose length is equal to the number of original conditional attributes. A bit value of 1 indicates that the corresponding attribute is selected into the reduced subset, while 0 indicates elimination. The fitness function is defined as Fitness = 0.9 × classification accuracy + 0.1 × (1 − reduction rate). This function aims to balance classification accuracy and the parsimony of the attribute set, where classification accuracy refers to the accuracy of the decision table composed of the subset obtained through rough set classification, and reduction rate is the ratio of the size of the reduced subset to the size of the original attribute set. The weight coefficient of 0.9 implies that we prioritize maintaining high classification performance. Retaining the reduced attributes and removing duplicate rows yields the minimal decision table presented in Table 7.

Table 7.
Minimal decision table.
The decision rules derived from rough sets are shown in Table 8. Each rule consists of conditional attributes (different monitoring features) and a decision attribute (cavitation fault type or severity), forming a conditional logic. For example, Rule 1 can be interpreted as follows: If the outlet pressure is in the range of 29.9701 MPa to 30.0237 MPa, the outlet flow rate is in 30.4636 mL/r to 34.3511 mL/r, the inlet flow rate is in 24.2675 mL/r to 29.7890 mL/r, the piston chamber pressure is in 0.0576 MPa to 7.7585 MPa, and the piston chamber volume is in 0.0019 L to 0.0024 L, then the decision result is normal. The Right-Hand Side Coverage is 0.016667, and the RHS Accuracy is 0.454545. These rules transform the implicit features of piston pump cavitation faults into interpretable quantitative interval logic. In practical decision-making support, they not only provide a method to quickly determine fault types based on parameter intervals but also quantify the reliability of each rule through coverage and accuracy indicators.

Table 8.
Decision rules.
To mitigate the effects of random variations, ten trials are conducted to improve the reliability and accuracy of the results. The loss rate and accuracy of the RSAW-CNN diagnostic method are presented in Figure 8.
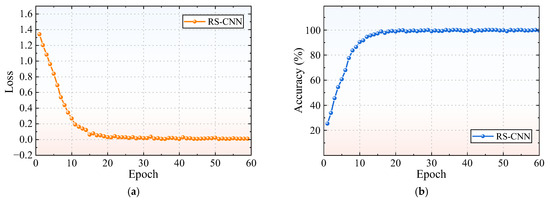
Figure 8.
Experimental results of the RSAW-CNN: (a) Loss; (b) Accuracy.
In Figure 8a, as the number of epochs increases, the loss rate gradually decreases and tends to be stable and finally stabilizes close to 0. This indicates that the prediction error of the model for the fault diagnosis task is continuously reduced, and the learning effect is good. From Figure 8b, it can be seen that the accuracy of the RSAW-CNN model rises rapidly with the increase in epochs. After the number of epochs reaches a certain value (about 22), the accuracy gradually becomes stable and finally stabilizes at a high level close to 100%. This shows that the model can perform fault diagnosis very accurately and has high classification performance.
5.3. Comparative Analysis
To validate the effectiveness of the proposed RSAW-CNN model, a comparative analysis has been carried out with five diagnostic approaches: Backpropagation Neural Network (BPNN), Residual Neural Network (ResNet), conventional Convolutional Neural Network (CNN), CNN-SENet (a CNN incorporating a squeeze-and-excitation attention mechanism) [35], and the proposed RSAW-CNN model. To maintain consistency, the CNN architecture and input data remain identical for all models. The input data comprises five-channel cavitation fault signals collected from a piston pump, with 3840 samples used for training and 960 for testing. Each experiment has been repeated ten times, and the average of the results is considered as the final outcome.
Figure 9 illustrates the loss and accuracy curves of the five diagnostic methods. The loss values of all methods eventually approach zero, which indicates no overfitting occurs. Among them, the RSAW-CNN model demonstrates the best performance, showing higher stability and superior diagnostic accuracy compared to the other four methods. In the later training stages, the loss of the proposed RSAW-CNN model converges to a value close to zero (0.006). The accuracy reaches 100% by the 22nd epoch and remains stable afterwards. The CNN-SENet model exhibits the second-best performance, while the baseline CNN outperforms ResNet. The BPNN model displays the lowest performance among all the methods compared.
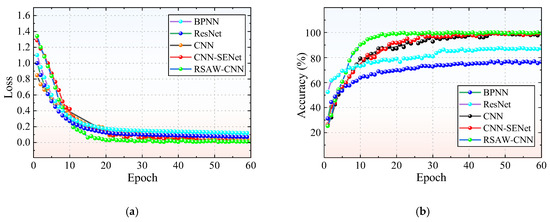
Figure 9.
Comparison of test results for different diagnostic methods: (a) Loss; (b) Accuracy.
As shown in Figure 10, Figure 10a–e illustrate the diagnostic performance of five methods (BPNN, ResNet, CNN, CNN-SENet, and RSAW-CNN) for cavitation faults via confusion matrices. The vertical axis displays the model’s diagnostic results, while the horizontal axis shows the actual fault labels. The labels NM, SC, MC, and LC denote the following: NM for Normal Condition, SC for Slight Cavitation, MC for Moderate Cavitation, and LC for Severe Cavitation. The BPNN model struggles to accurately distinguish between Normal Condition and Slight Cavitation, as well as between Slight Cavitation and Moderate Cavitation. The ResNet and CNN models also fail to accurately differentiate between Normal Condition and Slight Cavitation, while CNN-SENet cannot precisely identify Moderate and Severe Cavitation. The primary reasons are as follows: the BPNN model is prone to local optimization issues; the ResNet model suffers from low computational efficiency due to its complex parameters; and the pure CNN treats the importance of each channel as equivalent, failing to capture subtle differences in weak faults, thereby generating diagnostic errors and resulting in inconsistent fault identification capabilities. As shown in Figure 10e, compared to the other four methods, RSAW-CNN can accurately identify cavitation faults across all categories. The model demonstrates robust performance and high diagnostic accuracy, making it well-suited for piston pump cavitation fault diagnosis.
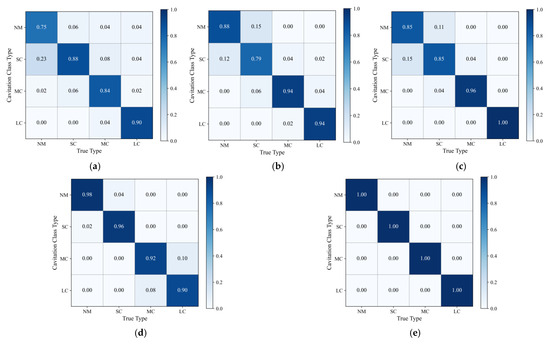
Figure 10.
Confusion matrix for five fault diagnosis methods: (a) BPNN; (b) ResNet; (c) CNN; (d) CNN-SENet; (e) RSAW-CNN.
The proposed RSAW-CNN method employs a rough set theory-weighted convolutional neural network diagnostic approach. It focuses more on critical information across multiple channels, allocates weights rationally, and utilizes rough set decision rules to assist diagnosis. This enables accurate identification of cavitation faults across various categories, enhancing the interpretability and reliability of fault diagnosis. Figure 11 shows the average accuracy across ten trials on the dataset. The BPNN method achieves an average accuracy of 83.33%, the ResNet method reaches 88.37%, the CNN method attains 91.72%, and the CNN-SENet method achieves 93.80%. Comparative analysis with other methods demonstrates that the RSAW-CNN method exhibits significant advantages in performance metrics such as accuracy and training speed, with an average accuracy of 99.2%. Compared to the BPNN, ResNet, CNN, and CNN-SENet methods, its average accuracy has improved by 15.87%, 10.83%, 7.48%, and 5.40%, respectively. This validates the proposed method’s significant advantages in diagnosing cavitation faults in piston pumps.
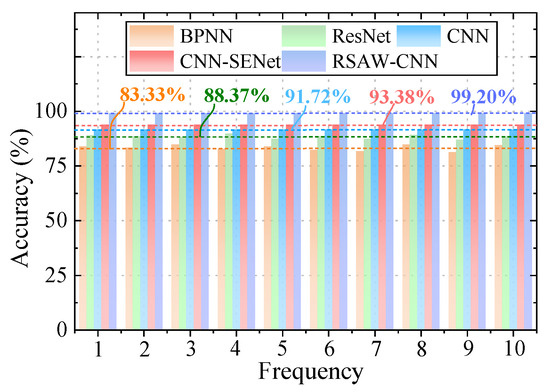
Figure 11.
Average accuracy of three methods.
6. Conclusions
The proposed rough set attribute weighted convolutional neural network (RSAW-CNN) model does not rely on prior knowledge. It assigns weights to each channel sensor based on conditional attribute weights, enabling the model to focus on important conditional attributes and enhance classification performance. The model learns classification rules from data, embodying them as weights, thereby improving model interpretability and credibility. Through multiple experiments, the RSAW-CNN fault diagnosis model demonstrated high accuracy for piston pump cavitation diagnosis, achieving an average accuracy of 99.2% with stable convergence. Compared to the BPNN, ResNet, CNN, and CNN-SENet, its average accuracy has improved by 15.87%, 10.83%, 7.48%, and 5.40%, exhibiting higher accuracy and greater stability.
The RSAW-CNN fault diagnosis method employs rough set theory to extract rules for auxiliary diagnosis. While ensuring high accuracy, it significantly enhances the reliability and credibility of the diagnostic process, aligning with industry demands for trustworthy AI. This fully demonstrates the method’s application value in future industrial equipment health management, driving axial piston pump fault diagnosis toward smarter, more reliable, and more efficient solutions.
Author Contributions
Conceptualization, M.L. and Z.L.; methodology, M.L.; software, J.C.; validation, M.L., Z.L. and W.J.; formal analysis, Z.M.; investigation, L.M.; resources, Z.L.; data curation, M.L.; writing—original draft preparation, M.L.; writing—review and editing, Z.L.; visualization, J.C.; supervision, Z.M.; project administration, Y.K.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanxi Province Major Science and Technology Special Projects Program: Open Bidding for Talents (202401150102004), Shanxi Provincial Key R&D Program Project (202202100401021), Provincial Graduate Education Innovation Program Project (2024KY630) and Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (2023L444).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational Fluid Dynamics |
| CNN | Convolutional Neural Networks |
| 1D CNN | One-dimensional Convolutional Neural Networks |
| CNN-SENet | Convolutional Neural Networks Squeeze-and-Excitation Networks |
| LC | Severe Cavitation |
| MC | Moderate Cavitation |
| NM | Normal State |
| RSAW-CNN | Rough Set Attribute Weighted Convolutional Neural Network |
| SC | Slight Cavitation |
References
- Ye, S.; Sun, Y.; Zhang, J.; Chen, J.; Xu, B.; Zhao, S.; Liu, H. A new coupled dynamic model to study the vibration and lubrication characteristics of slipper/swash-plate interface in an axial piston pump. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2025, 239, 13506501241308942. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, L.; Xiao, J.; Fang, G.; Li, J. Current status and applications for hydraulic pump fault diagnosis: A Review. Sensors 2022, 22, 9714. [Google Scholar] [CrossRef]
- Dong, C.; Tao, J.; Sun, H.; Chao, Q.; Liu, C. Inverse transient analysis based calibration of surrogate pipeline model for fault simulation of axial piston pumps. Mech. Syst. Signal Process. 2023, 205, 110829. [Google Scholar] [CrossRef]
- Wang, H.; Lin, N.; Yuan, S.; Liu, Z.; Yu, Y.; Zeng, Q.; Fan, J.; Li, D.; Wu, Y. Structural improvement, material selection and surface treatment for improved tribological performance of friction pairs in axial piston pumps: A review. Tribol. Int. 2024, 198, 109838. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Lu, Y.; Wang, Y.; Dong, H. Hydraulic piston pump in civil aircraft: Current status, future directions and critical technologies. Chin. J. Aeronaut. 2020, 33, 16–30. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, P.; Li, M.; Zhang, S. Axial piston pump fault diagnosis method based on symmetrical polar coordinate image and fuzzy c-means clustering algorithm. Shock Vib. 2021, 1, 6681751. [Google Scholar] [CrossRef]
- Hallaji, S.; Fang, Y.; Brandon, K. Predictive maintenance of pumps in civil infrastructure: State-of-the-art, challenges and future directions. Autom. Constr. 2022, 134, 104049. [Google Scholar] [CrossRef]
- Pang, H.; Wu, D.; Deng, Y.; Cheng, Q.; Liu, Y. Effect of working medium on the noise and vibration characteristics of water hydraulic axial piston pump. Appl. Acoust. 2021, 183, 108277. [Google Scholar] [CrossRef]
- Tang, H.; Wang, Z.; Wu, Y. A multi-fault diagnosis method for piston pump in construction machinery based on information fusion and PSO-SVM. J. Vibroeng. 2019, 21, 1904–1916. [Google Scholar] [CrossRef]
- Ebada, Y.; Elshennawy, A.; Elbrashy, A.; Rashad, M. Performance optimization of centrifugal pumps: Experimental analysis of flow enhancement and cavitation mitigation under variable operating conditions. Flow Meas. Instrum. 2025, 106, 103043. [Google Scholar] [CrossRef]
- Shang, B.; Tong, Z.; Liu, H. A lightweight vision transformer framework integrated with flow visualization for incipient cavitation diagnosis in centrifugal pumps. Flow Meas. Instrum. 2025, 106, 103016. [Google Scholar] [CrossRef]
- Lan, Y.; Li, Z.; Liu, S.; Huang, J.; Niu, L.; Xiong, X.; Niu, C.; Wu, B.; Zhou, X.; Yan, J.; et al. Experimental investigation on cavitation and cavitation detection of axial piston pump based on MLP-Mixer. Measurement 2022, 200, 111582. [Google Scholar] [CrossRef]
- Chao, Q.; Xu, Z.; Tao, J.; Liu, C.; Zhai, J. Cavitation in a high-speed aviation axial piston pump over a wide range of fluid temperatures. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022, 236, 727–737. [Google Scholar] [CrossRef]
- Yin, F.; Kong, X.; Ji, H.; Nie, S.; Lu, W. Research on the pressure and flow characteristics of seawater axial piston pump considering cavitation for reverse osmosis desalination system. Desalination 2022, 540, 115998. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, H.; Cao, X.; Westerdahld, D.; Jin, X. Cavitation diagnosis for water distribution pumps: An early-stage approach combing vibration signal-based neural network with high-speed photography. Sustain. Energy Technol. Assess. 2023, 55, 102919. [Google Scholar] [CrossRef]
- Wang, T.; Liu, S.; Fu, Y.; Ma, J. Health state evaluation index system for aviation piston pumps based on asynchronous multi-source information fusion. Results Eng. 2025, 27, 107076. [Google Scholar] [CrossRef]
- Wang, W.; Chao, Q.; Shi, J.; Liu, C. Condition monitoring of axial piston pumps based on machine learning-driven real-time CFD simulation. Eng. Appl. Comput. Fluid Mech. 2025, 19, 2474676. [Google Scholar] [CrossRef]
- Lei, Y.; Jiang, W.; Niu, H.; Shi, X.; Yang, X. Fault diagnosis of axial piston pump based on extreme-point symmetric mode decomposition and random forests. Shock Vib. 2021, 1, 6649603. [Google Scholar]
- Stephen, C.; Basu, B.; McNabola, A. Evaluation of supervised machine learning techniques for cavitation detection and diagnosis in a pump-as-turbine system. Expert Syst. Appl. 2025, 296, 129167. [Google Scholar] [CrossRef]
- Chao, Q.; Tao, J.; Wei, X.; Wang, Y.; Meng, L.; Liu, C. Cavitation intensity recognition for high-speed axial piston pumps using 1-D convolutional neural networks with multi-channel inputs of vibration signals. Alex. Eng. J. 2020, 07, 052. [Google Scholar] [CrossRef]
- Dai, C.; Hu, S.; Zhang, Y.; Chen, Z.; Dong, L. Cavitation state identification of centrifugal pump based on CEEMD-DRSN. Nucl. Eng. Technol. 2023, 55, 1507–1517. [Google Scholar] [CrossRef]
- Muralidharan, V.; Sugumaran, V. Rough set based rule learning and fuzzy classification of wavelet features for fault diagnosis of monoblock centrifugal pump. Measurement 2013, 46, 3057–3063. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. An improved convolutional neural network with an adaptable learning rate towards multi-signal fault diagnosis of hydraulic piston pump. Adv. Eng. Inf. 2021, 50, 101406. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault identification of hydraulic pump using deep adaptive normalized CNN and synchrosqueezed wavelet transform. Reliab. Eng. Syst. Saf. 2022, 224, 108560. [Google Scholar] [CrossRef]
- Wang, R.; Xu, Y.; Mu, W.; Chen, Y.; Jiao, Z. Cavitation intensity recognition for axial piston pump based on transient flow rate measurement and improved transfer learning method. Mech. Syst. Signal Process. 2025, 232, 112667. [Google Scholar] [CrossRef]
- Zhou, Z.; Ming, Z.; Wang, J.; Tang, S.; Cao, Y.; Han, X.; Xiang, G. A Novel Belief Rule-Based Fault Diagnosis Method with Interpretability. Comp. Model. Eng. Sci. 2023, 136, 025399. [Google Scholar] [CrossRef]
- Barraza, J.; Droguett, E.; Martins, M. FS-SCF network: Neural network interpretability based on counterfactual generation and feature selection for fault diagnosis. Expert Syst. Appl. 2024, 237, 121670. [Google Scholar] [CrossRef]
- Zhu, Y.; Su, H.; Tang, S.; Zhang, S.; Zhou, T.; Wang, J. A novel fault diagnosis method based on SWT and VGG-LSTM model for hydraulic axial piston pump. J. Mar. Sci. Eng. 2023, 11, 594. [Google Scholar] [CrossRef]
- Liu, J.; Meng, S.; Zhou, X.; Gu, L. A hydraulic axial piston pump fault diagnosis based on instantaneous angular speed under non-stationary conditions. Lubricants 2023, 11, 406. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Zhong, Y.; Tang, H. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Sig. Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, D.; Wang, H. Optimal granularity selection based on algorithm stability with application to attribute reduction in rough set theory. Inf. Sci. 2024, 654, 119845. [Google Scholar] [CrossRef]
- Nosheen, F.; Qamar, U.; Raza, M. A parallel rule-based approach to compute rough approximations of dominance based rough set theory. Eng. Appl. Artif. Intell. 2022, 115, 105285. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Z.; Cui, J.; Kong, Y. A fault diagnosis method of the shearer hydraulic heightening system based on a rough set and RBF neural network. Energies 2023, 16, 956. [Google Scholar] [CrossRef]
- Zhou, T.; Yu, X.; Zhang, J.; Shi, L.; Xu, H. Pressure pulsations intelligent prediction model for load rejection of pumped storage power station based on data augmentation and one-dimensional convolutional neural network. Energy 2025, 330, 136915. [Google Scholar] [CrossRef]
- Xu, F.; Sui, Z.; Ye, J.; Xu, J. Ternary Precursor Centrifuge Rolling Bearing Fault Diagnosis Based on Adaptive Sample Length Adjustment of 1DCNN-SeNet. Processes 2024, 12, 702. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).