Improved Robust Model Predictive Trajectory Tracking Control for Intelligent Vehicles Based on Multi-Cell Hyperbody Vertex Modeling and Double-Layer Optimization
Abstract
1. Introduction
2. Modeling
2.1. Vehicle Dynamic Model
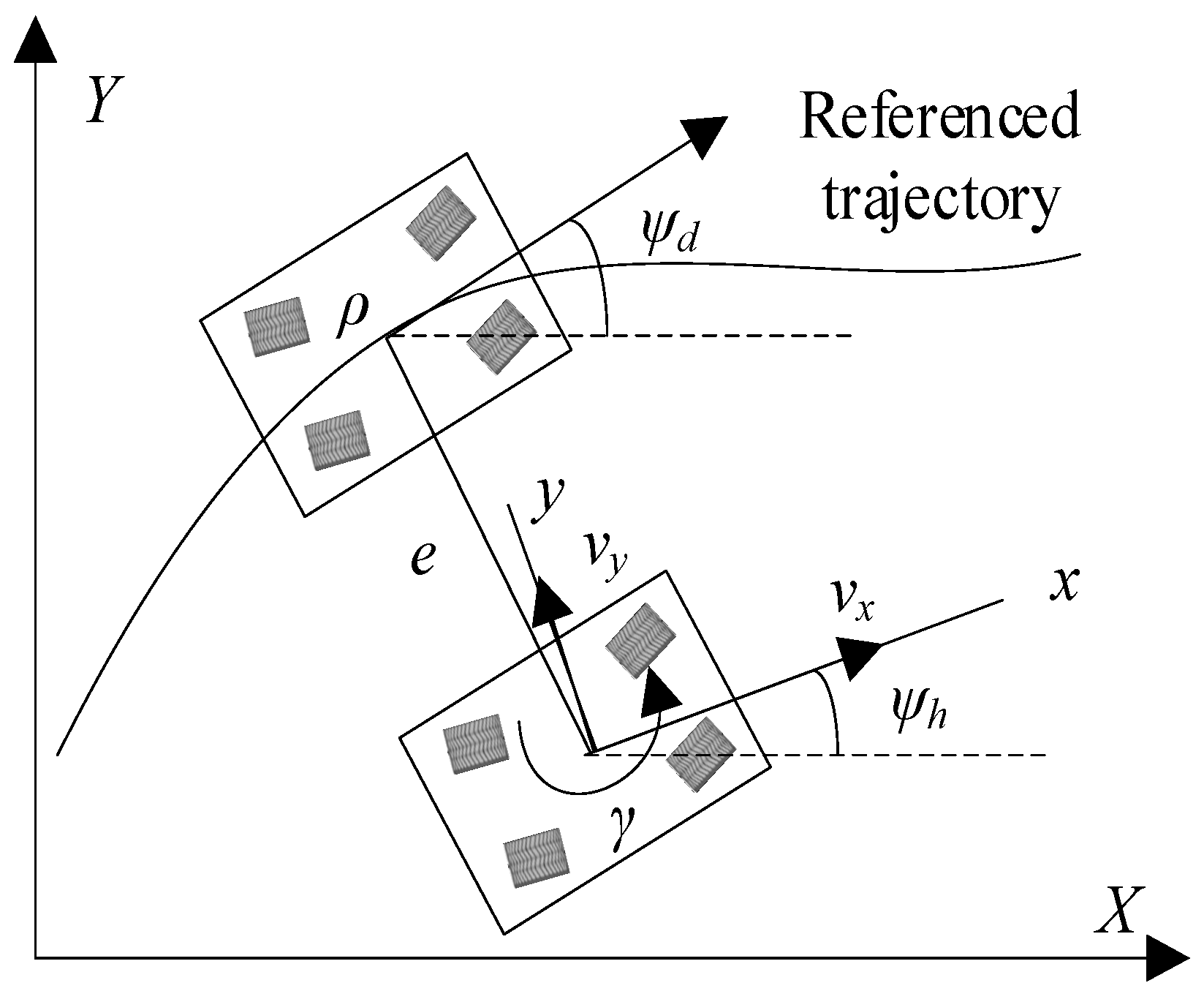
2.2. Trajectory Tracking Control Error Model
2.3. Vehicle Multicellular Uncertainty Model Considering Parameter Perturbation
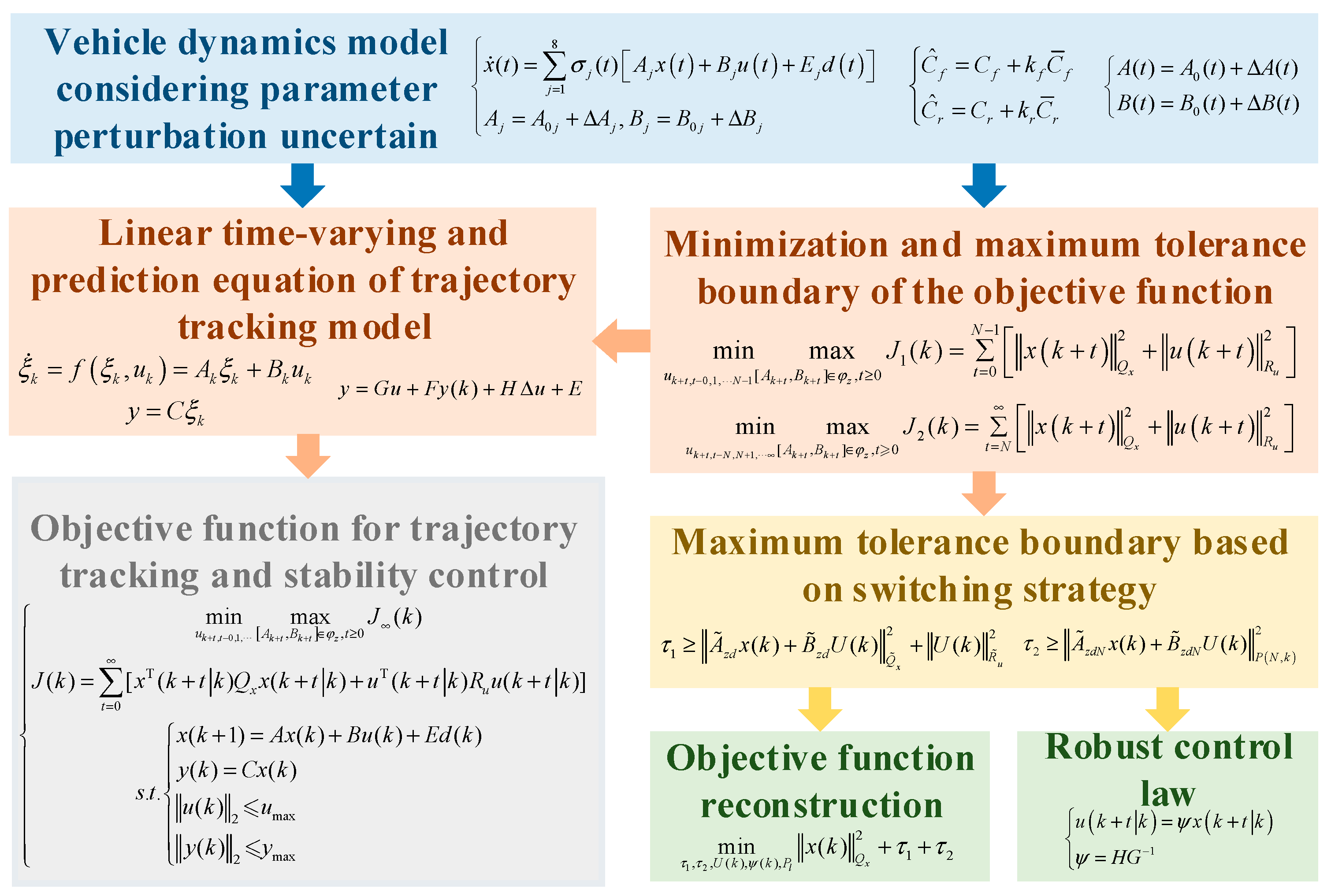
3. Robust Control Method for Trajectory Tracking with Parameter Uncertainty
3.1. Predictive Control of Min-Max Robust Model Based on LMI
3.2. Predictive Control of Min-Max Robust Model Based on Improved LMI
4. Simulation Results
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.; Xiao, Y.; Liang, Z.; Wong, P.K.; Xie, Z.; Ma, X. Adaptive event-triggered interval type-2 T-S fuzzy control for lateral dynamic stabilization of AEVs with intermittent measurements and actuator failure. IEEE Trans. Transp. Electrif. 2023, 9, 254–265. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Li, M.; Shang, Z. Dynamic measurement method for steering wheel angle of autonomous agricultural vehicles. Agriculture 2024, 14, 1602. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.K.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2024, 113, 9373–9398. [Google Scholar] [CrossRef]
- Li, H.; Li, B.; Yang, H.; Mu, C. Nonlinear Model Predictive Control for Time-Optimal Turning Around of an Autonomous Vehicle Under Steering Lag. IEEE/ASME Trans. Mechatron. 2025, 30, 577–586. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Y.; Xiao, F.; Lin, Z.; Deng, C. Coordinated Control of Active Suspension and DYC for Four-Wheel Independent Drive Electric Vehicles Based on Stability. Appl. Sci. 2022, 12, 11768. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Liu, W.; Sun, D.; Jiang, Y.; Ding, R. A Review of Recent Advances in Roll Stability Control in On-Road and Off-Road Vehicles. Appl. Sci. 2025, 15, 5491. [Google Scholar] [CrossRef]
- Zhu, Z.; Chai, X.; Xu, L.; Quan, L.; Yuan, C.; Tian, S. Design and Performance of a Distributed Electric Drive System for a Series Hybrid Electric Combine Harvester. Biosyst. Eng. 2023, 236, 160–174. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X. Sideslip angle fusion estimation method of three-axis autonomous vehicle based on composite model and adaptive cubature Kalman filter. IEEE Trans. Transp. Electrif. 2024, 10, 316–330. [Google Scholar] [CrossRef]
- Park, J.Y.; Na, S.; Cha, H.; Yi, K. Direct yaw moment control with 4WD torque-vectoring for vehicle handling stability and agility. Int. J. Automot. Technol. 2022, 23, 555–565. [Google Scholar] [CrossRef]
- Cui, K.; He, J.; Yao, X.; Gu, X. Adaptive Model Predictive Control Based on Stability Index for Path Tracking of Autonomous Vehicles Considering Model Error. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 9372–9396. [Google Scholar] [CrossRef]
- Zhao, W.Q. Real-Time Model Predictive Control of Path-Following for Autonomous Vehicles Towards Model Mismatch and Uncertainty. Control Eng. Pract. 2024, 142, 105678. [Google Scholar] [CrossRef]
- Feng, H.; Tao, Y.; Feng, J.; Zhang, Y.; Xue, H.; Wang, T.; Xu, X.; Chen, P. Fault-tolerant collaborative control of four-wheel-drive electric vehicle for one or more in-wheel motors’ faults. Sensors 2025, 25, 1540. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Dong, J.; Wong, P.K.; Liu, J.; Pang, T.H.; Yang, Z.; Ma, X.; Xie, Z. Random multiphysics measurement for electro-hydraulic system with hysteresis diagnosis. IEEE Trans. Instrum. Meas. 2025, 74, 1002214. [Google Scholar] [CrossRef]
- Luo, Y.S.; Wei, L.L.; Xu, L.Z.; Zhang, Q.; Liu, J.Y.; Cai, Q.B.; Zhang, W.B. Stereo-vision-based multi-crop harvesting edge detection for precise automatic steering of combine harvester. Biosyst. Eng. 2022, 215, 115–128. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X. Trajectory and velocity planning method of emergency rescue vehicle based on segmented three-dimensional quartic Bezier curve. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3461–3475. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, H. Stability, scalability, speedability, and string stability of connected vehicle systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2819–2832. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive Disturbance Observer-Based Fixed Time Nonsingular Terminal Sliding Mode Control for Path-Tracking of Unmanned Agricultural Tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Lee, J.E.; Kim, B.W. A Novel Adaptive Non-Singular Fast Terminal Sliding Mode Control for Direct Yaw Moment Control in 4WID Electric Vehicles. Sensors 2025, 25, 941. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, K.; Ding, R.; Jiang, Y.; Jiang, Y. A Novel Hydraulic Interconnection Design and Sliding Mode Synchronization Control of Leveling System for Crawler Work Machine. Agriculture 2025, 15, 137. [Google Scholar] [CrossRef]
- Meng, D.; Chu, H.; Tian, M.; Gao, B.; Chen, H. Real-Time High-Precision Nonlinear Tracking Control of Autonomous Vehicles Using Fast Iterative Model Predictive Control. IEEE Trans. Intell. Veh. 2024, 9, 3644–3657. [Google Scholar] [CrossRef]
- Liang, J.; Tian, Q.; Feng, J.; Pi, D.; Yin, G. A Polytopic Model-Based Robust Predictive Control Scheme for Path Tracking of Autonomous Vehicles. IEEE Trans. Intell. Veh. 2024, 9, 3928–3939. [Google Scholar] [CrossRef]
- Zhao, J.; Li, R.; Liang, Z.; Yang, Z.; Ding, Z.; Wong, P.K. Discrete Constrained Switched Robust Control for Path Following of Autonomous Ground Vehicles with Interval Uncertainties. IEEE Trans. Consum. Electron. 2025. [Google Scholar] [CrossRef]
- Huang, K.; Wei, K.; Li, F.; Yang, C.; Gui, W. LSTM-MPC: A Deep Learning Based Predictive Control Method for Multimode Process Control. IEEE Trans. Ind. Electron. 2022, 70, 11544–11554. [Google Scholar] [CrossRef]
- Zhao, J.; Li, R.; Zhang, G.; Huang, C.; Liang, Z.; Ding, Z. Supervisor-Based Hierarchical Adaptive MPC for Yaw Stabilization of FWID-EVs Under Extreme Conditions. IEEE Trans. Intell. Transp. Syst. 2025, 6, 1852–1863. [Google Scholar] [CrossRef]
- Hua, X.; Xiang, K.; Cheng, X.; Ning, X. An Adaptive Compound Control Strategy of Electric Vehicles for Coordinating Lateral Stability and Energy Efficiency. Appl. Sci. 2025, 15, 3347. [Google Scholar] [CrossRef]
- Tao, Y.; Ge, C.; Feng, H.; Xue, H.; Yao, M.; Tang, H.; Liao, Z.; Chen, P. A novel approach for adaptively separating and extracting compound fault features of the in-wheel motor bearing. ISA Trans. 2025, 159, 337–351. [Google Scholar] [CrossRef]
- Micheli, F.; Bersani, M.; Arrigoni, S.; Braghin, F.; Cheli, F. NMPC Trajectory Planner for Urban Autonomous Driving. Veh. Syst. Dyn. 2023, 61, 1387–1409. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Z.; Xu, X.; Cai, Y.; Chen, L.; Dou, G. Modularized and hierarchical state estimation strategy of 4WIDEV based on global-local dynamics model decoupling. ISA Trans. 2025, 166, 309–324. [Google Scholar] [CrossRef]
- Pinho, J.; Costa, G.; Lima, P.U.; Ayala Botto, M. Learning-Based Model Predictive Control for Autonomous Racing. World Electr. Veh. J. 2023, 14, 163. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Cai, Y.; Chen, L.; Li, K. QPSOMPC-based chassis coordination control of 6WIDAGV for vehicle stability and trajectory tracking. J. Frankl. Inst. 2025, 362, 107458. [Google Scholar] [CrossRef]
- Manzano, J.M.; Limon, D.; de la Peña, D.M.; Calliess, J.P. Robust learning-based MPC for nonlinear constrained systems. Automatica 2020, 117, 108948. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, H.; Guo, K.; Zhang, N. A Hierarchical Control Strategy for FWID-EVs Based on Multi-Agent with Consideration of Safety and Economy. Energies 2022, 15, 9112. [Google Scholar] [CrossRef]
- Wang, B.; Du, X.X.; Wang, Y.N.; Mao, H.P. Multi-machine collaboration realization conditions and precise and efficient production mode of intelligent agricultural machinery. Int. J. Agric. Biol. Eng. 2024, 17, 27–36. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhou, X.Y.; Wang, J.M. Extremum-Seeking-Based Adaptive Model-Free Control and Its Application to Automated Vehicle Path Tracking. IEEE-ASME Trans. Mechatron. 2022, 27, 3874–3884. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Zhao, J.; Li, R.; Zheng, X.; Li, W.; Hu, C.; Liang, Z. Constrained fractional-order model predictive control for robust path following of FWID-AGVs with asymptotic prescribed performance. IEEE Trans. Veh. Technol. 2025, 74, 2692–2705. [Google Scholar] [CrossRef]
- ISO 26262:2018; Road Vehicles—Functional Safety. International Organization for Standardization: Geneva, Switzerland, 2018.


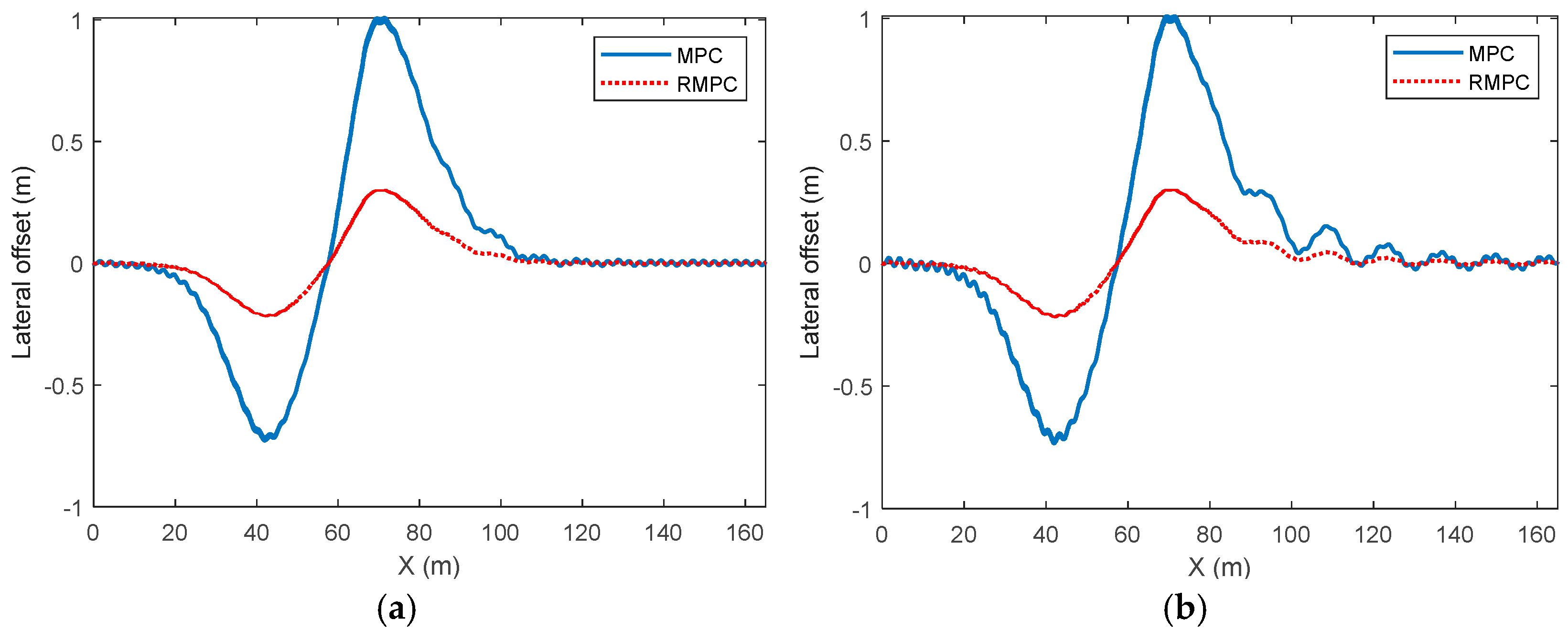
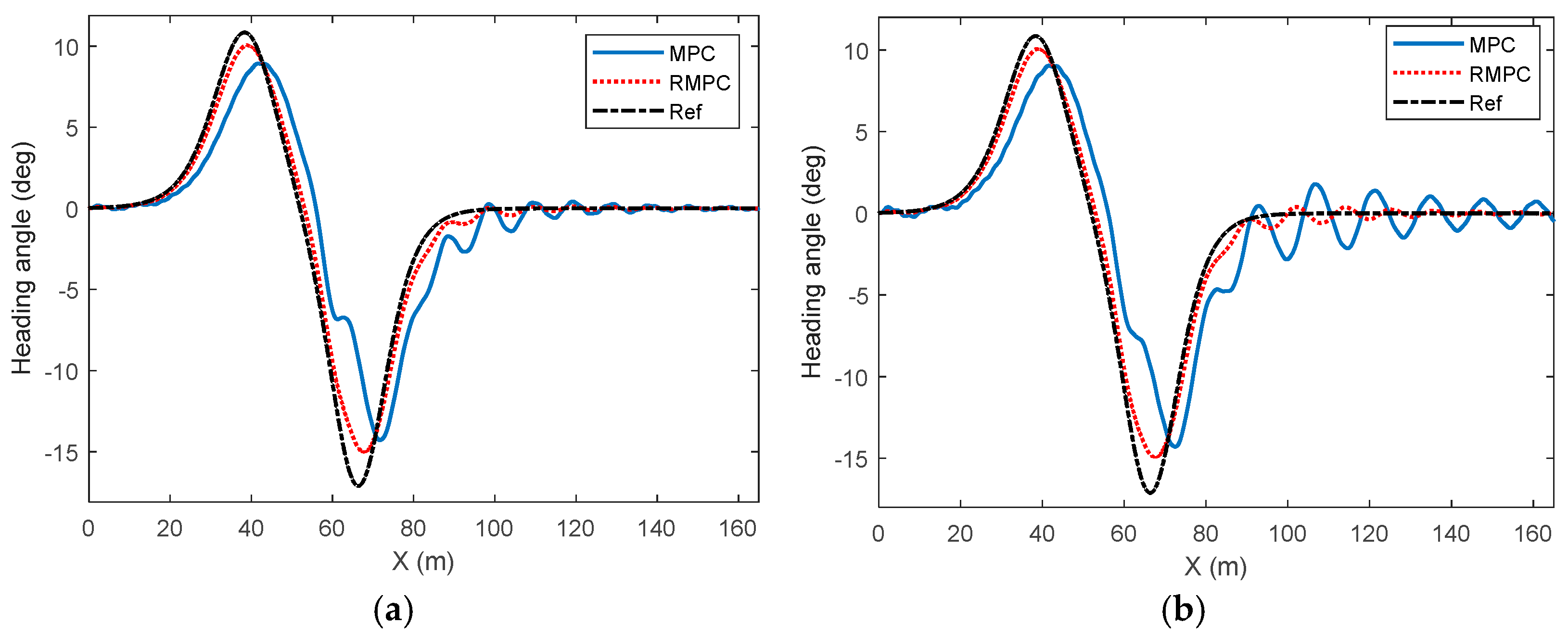
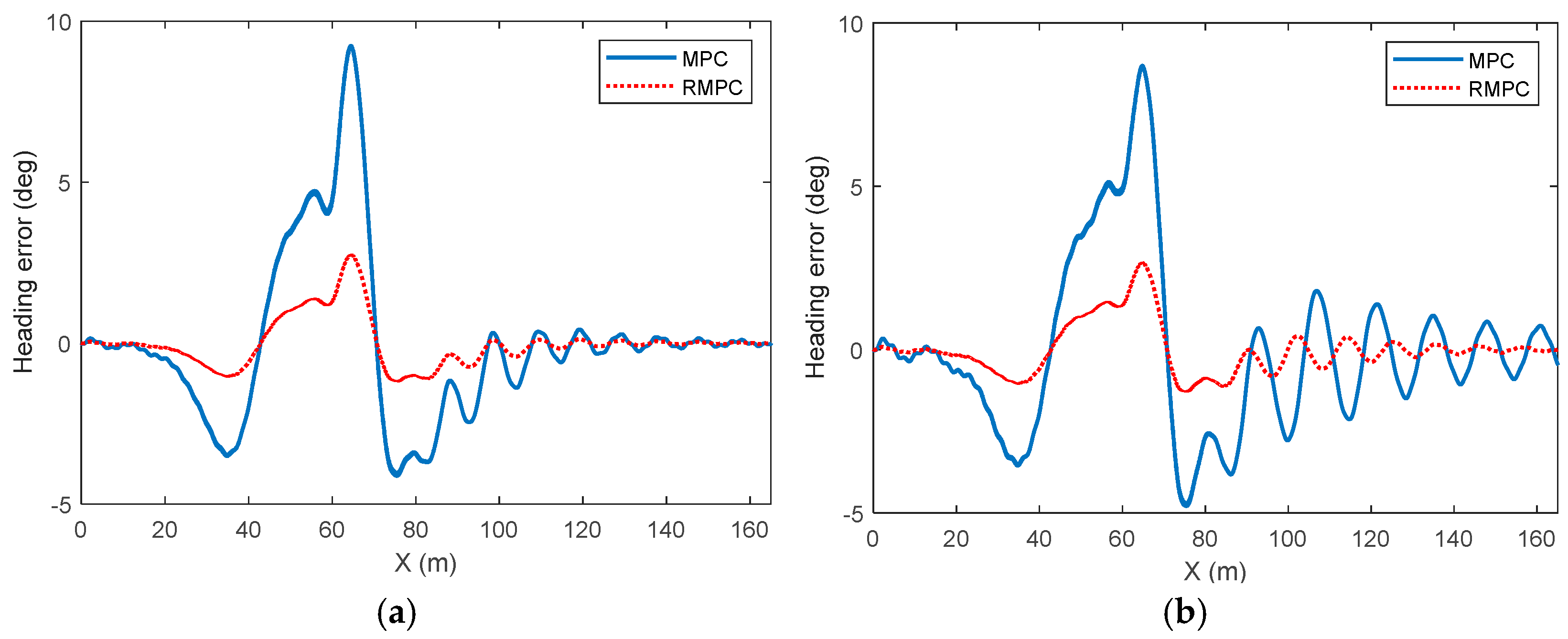
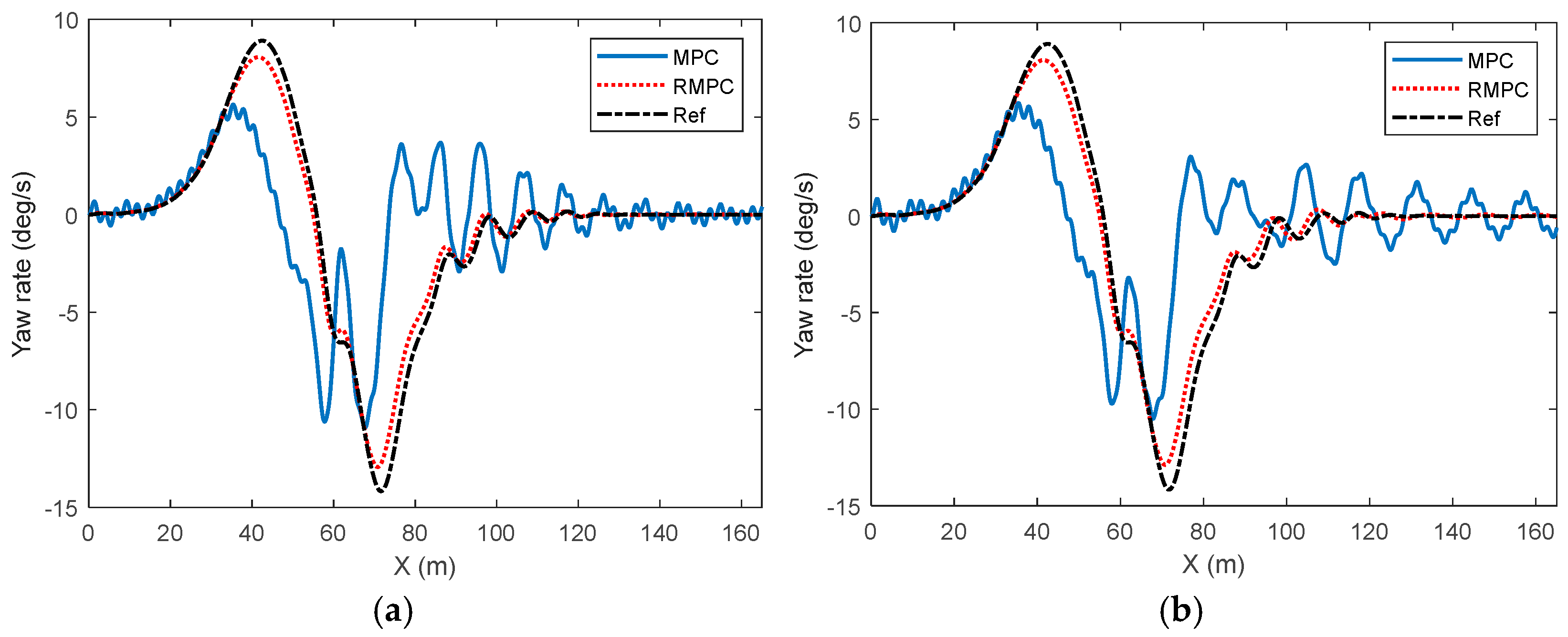

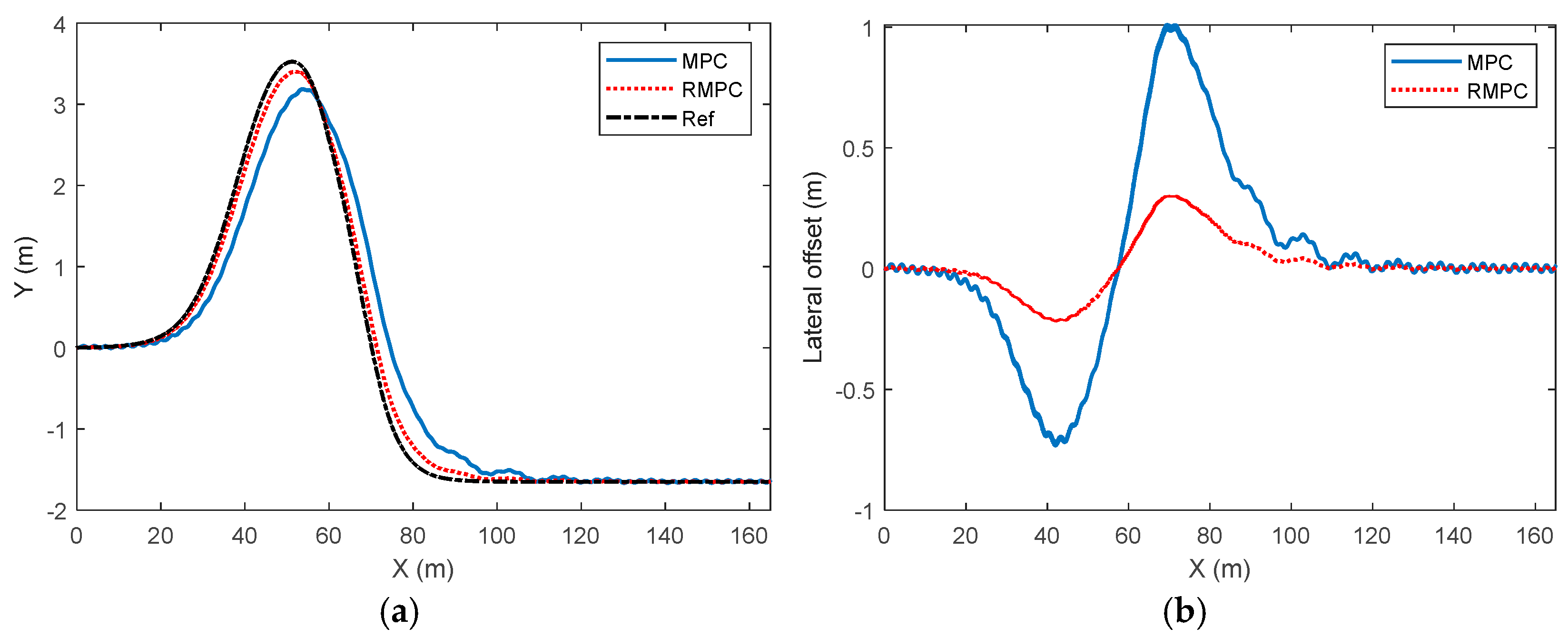
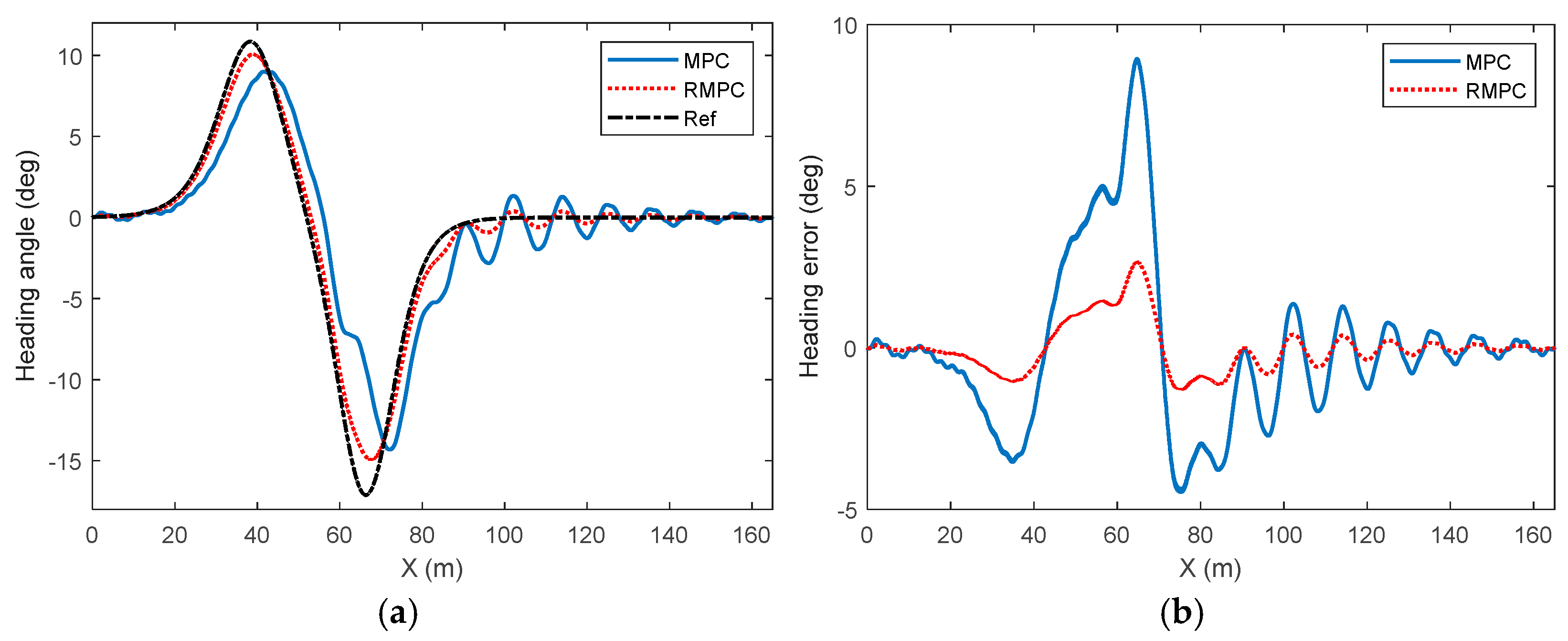

| Error | Control Method | PRE | AVE | RMSE |
|---|---|---|---|---|
| Lateral offset | MPC | 3.0685 | 0.1419 | 0.2111 |
| RMPC | 0.9273 | 0.0498 | 0.0722 | |
| Heading error | MPC | 12.8862 | 2.6808 | 0.9838 |
| RMPC | 7.6397 | 0.0769 | 0.0948 | |
| Tracking error of yaw rate | MPC | 8.3736 | 1.7961 | 1.6440 |
| RMPC | 0.8216 | 0.1319 | 0.1799 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Dou, G.; Chen, T.; Lu, J. Improved Robust Model Predictive Trajectory Tracking Control for Intelligent Vehicles Based on Multi-Cell Hyperbody Vertex Modeling and Double-Layer Optimization. Sensors 2025, 25, 6537. https://doi.org/10.3390/s25216537
Wang X, Dou G, Chen T, Lu J. Improved Robust Model Predictive Trajectory Tracking Control for Intelligent Vehicles Based on Multi-Cell Hyperbody Vertex Modeling and Double-Layer Optimization. Sensors. 2025; 25(21):6537. https://doi.org/10.3390/s25216537
Chicago/Turabian StyleWang, Xiaoyu, Guowei Dou, Te Chen, and Jiankang Lu. 2025. "Improved Robust Model Predictive Trajectory Tracking Control for Intelligent Vehicles Based on Multi-Cell Hyperbody Vertex Modeling and Double-Layer Optimization" Sensors 25, no. 21: 6537. https://doi.org/10.3390/s25216537
APA StyleWang, X., Dou, G., Chen, T., & Lu, J. (2025). Improved Robust Model Predictive Trajectory Tracking Control for Intelligent Vehicles Based on Multi-Cell Hyperbody Vertex Modeling and Double-Layer Optimization. Sensors, 25(21), 6537. https://doi.org/10.3390/s25216537





