AttenResNet18: A Novel Cross-Domain Fault Diagnosis Model for Rolling Bearings
Abstract
1. Introduction
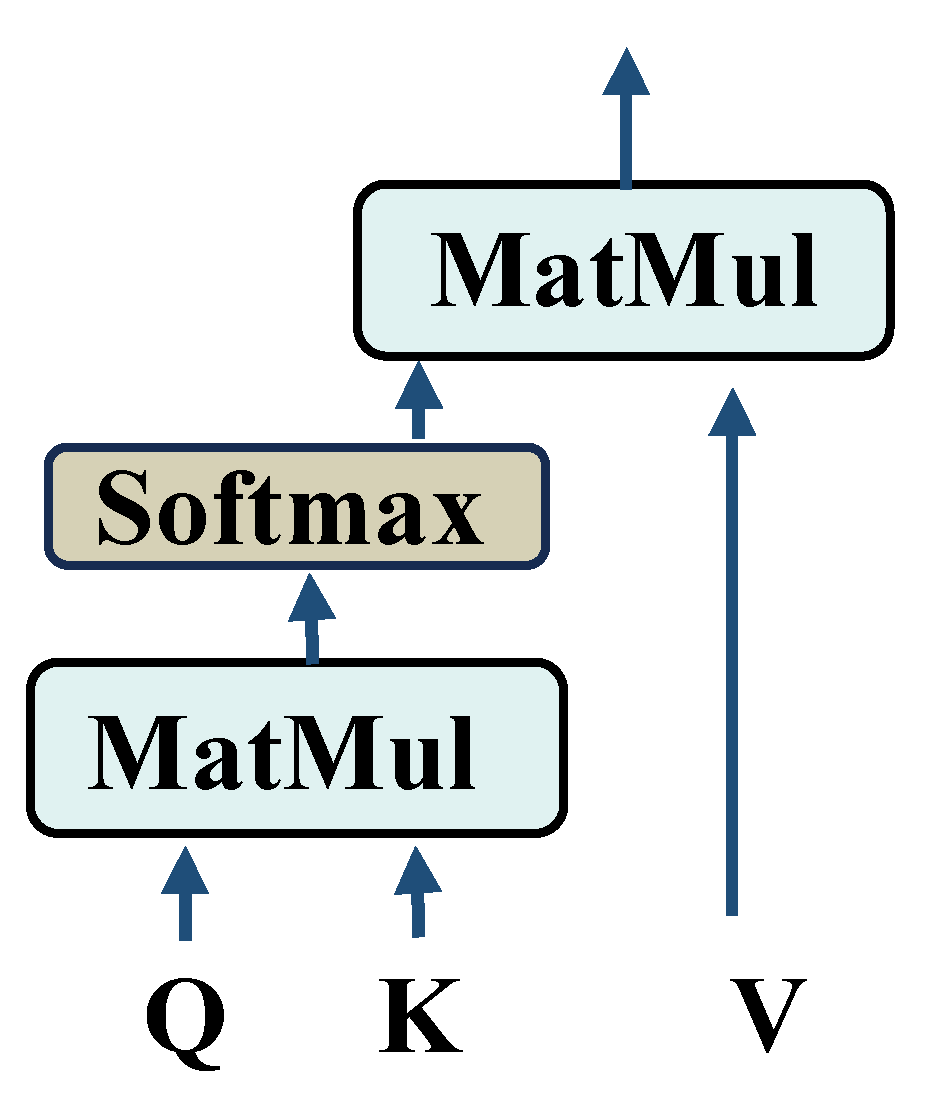
- A one-dimensional self-attention mechanism is integrated into the AttenResNet18 structure, effectively tackling the issue of noise obscuring fault-related features.
- A Dynamic Balance Distribution Adaptation (DBDA) mechanism is proposed, which constructs the MCFM by fusing the MMD and CORAL to reduce distribution discrepancies. Furthermore, an adaptive factor is introduced to automatically assign weights to the marginal and conditional distributions based on their relative importance, eliminating the need for additional cross-validation and thus enabling more efficient adaptation to different tasks.
2. Proposed Method
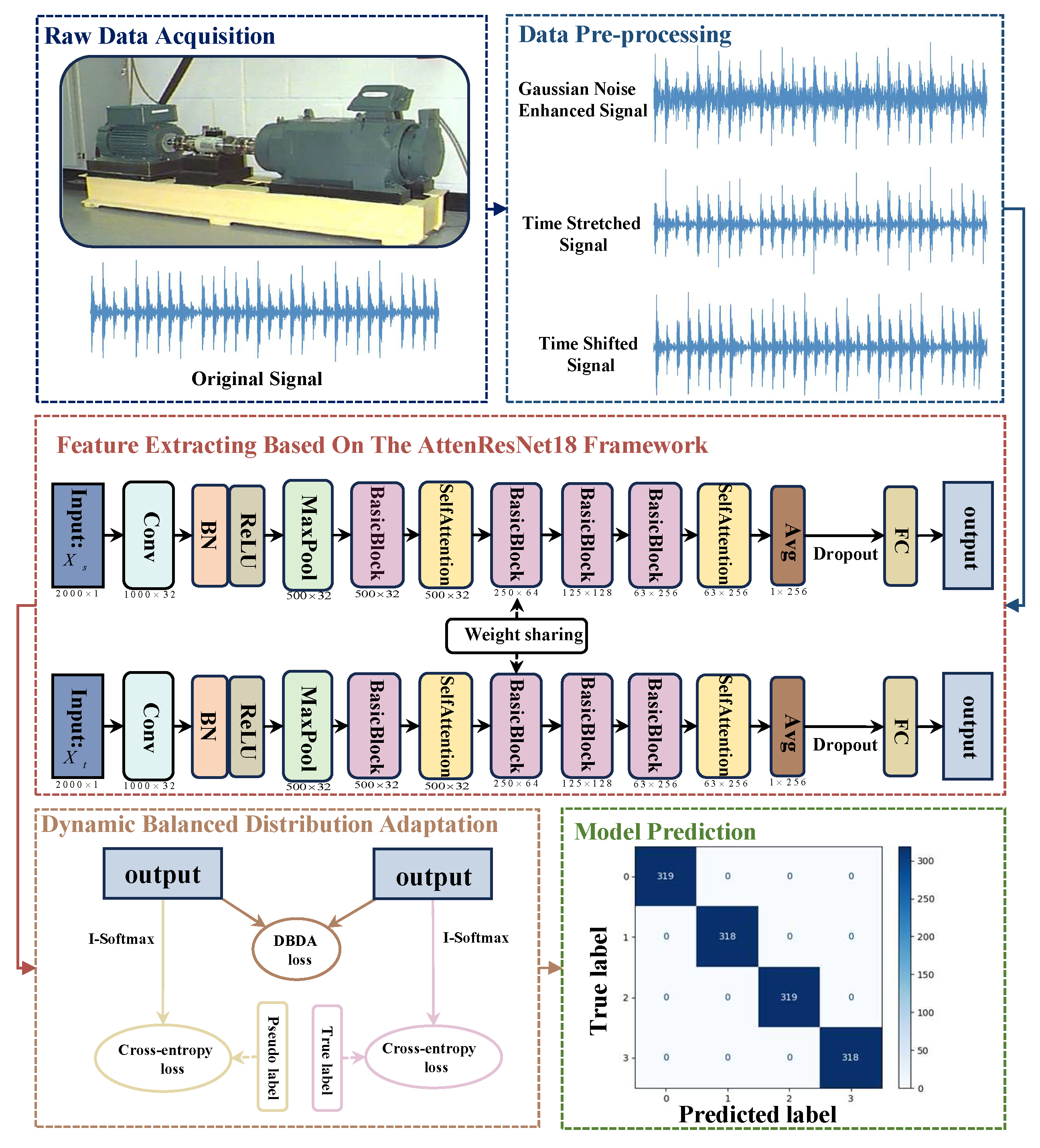
2.1. Process of the Proposed Method
2.2. Assumptions
- Distribution Shift: Both the marginal distributions and conditional distributions exhibit domain mismatch.
- Shared Label Space: .
2.3. Data Preprocessing
- Sliding Window Sampling: A sliding window strategy is adopted to mitigate sample scarcity, generating continuous subsequences that preserve temporal characteristics and improve data utilization.
- Dataset Splitting: To prevent data leakage, stratified sampling is directly applied to the original target domain dataset, dividing it into training and testing subsets with a 7:3 ratio. Although this strategy may introduce class imbalance in the test set, it better reflects the actual data distribution.
- Data Balancing: Resampling techniques ensure a balanced class distribution in the training set.
- Data Augmentation and Standardization: To enhance the model’s resilience against environmental disturbances and fluctuating operational states, specific data augmentation techniques are applied, followed by standardization. Table 1 details the augmentation methods.
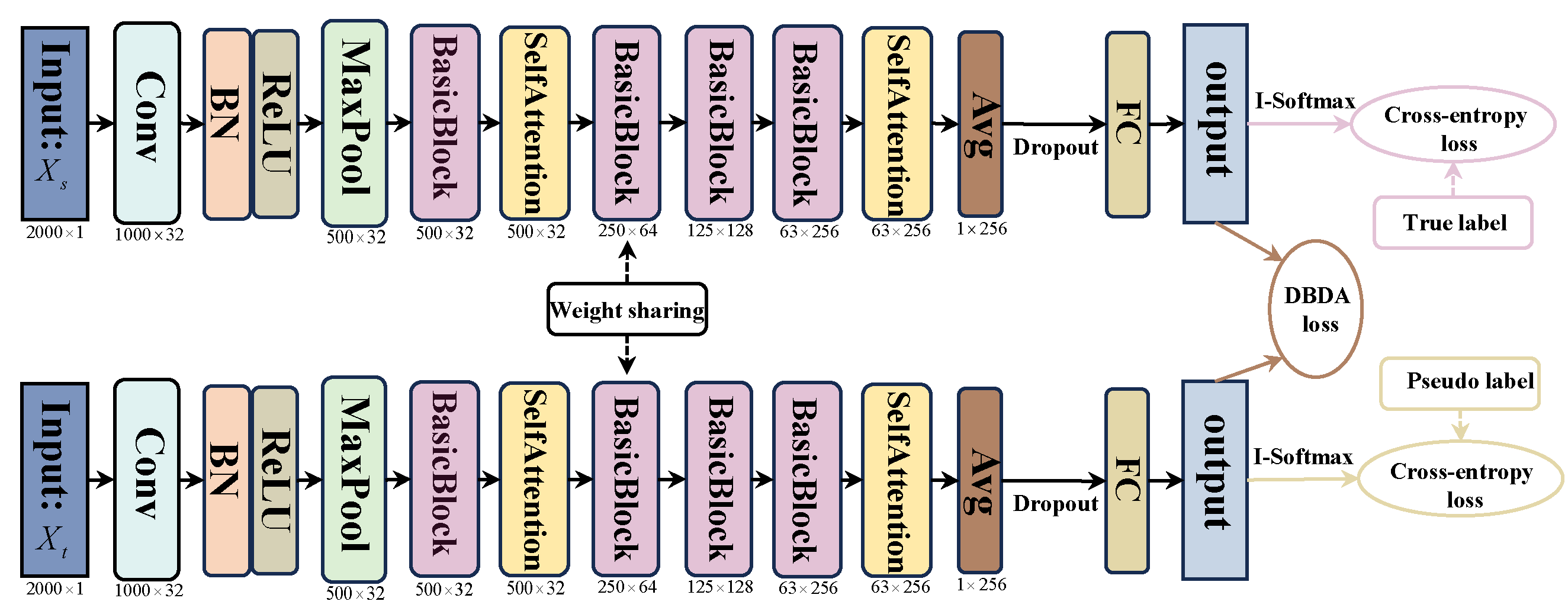
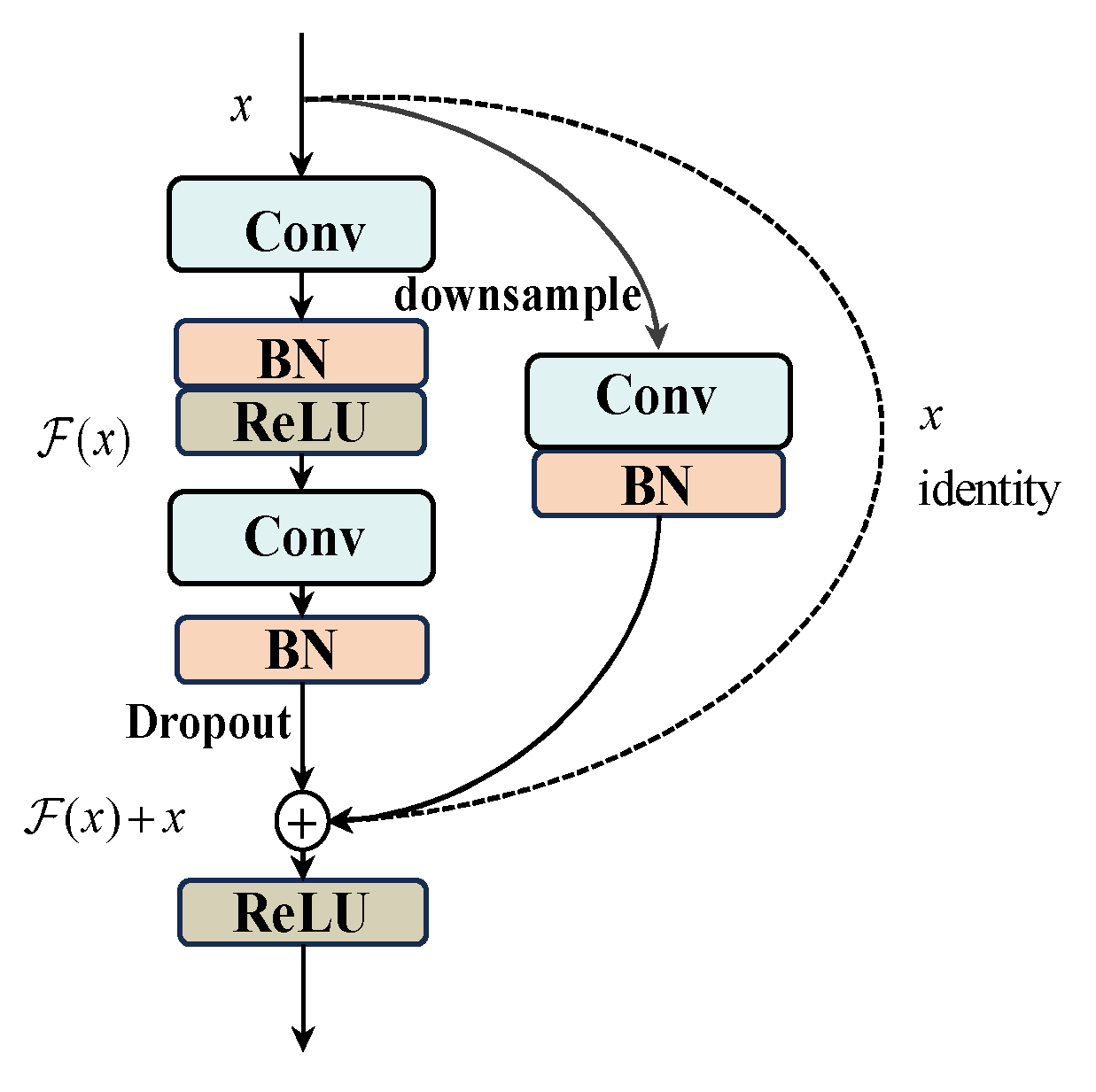
2.4. Feature Extraction Based on the AttenResNet18 Framework
2.5. Dynamic Balanced Distribution Adaptation
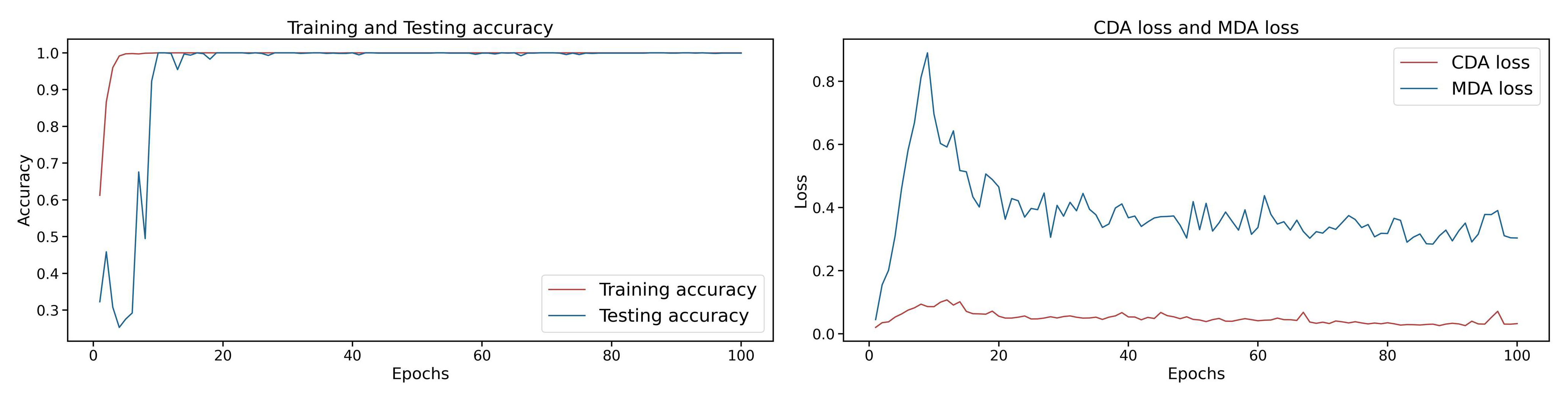
2.6. Loss Function of the AttenResNet18
3. Experimental Validation
3.1. Dataset Description
3.1.1. CWRU
3.1.2. The BJTU-RAO Bogie Dataset
3.2. Fault Diagnosis
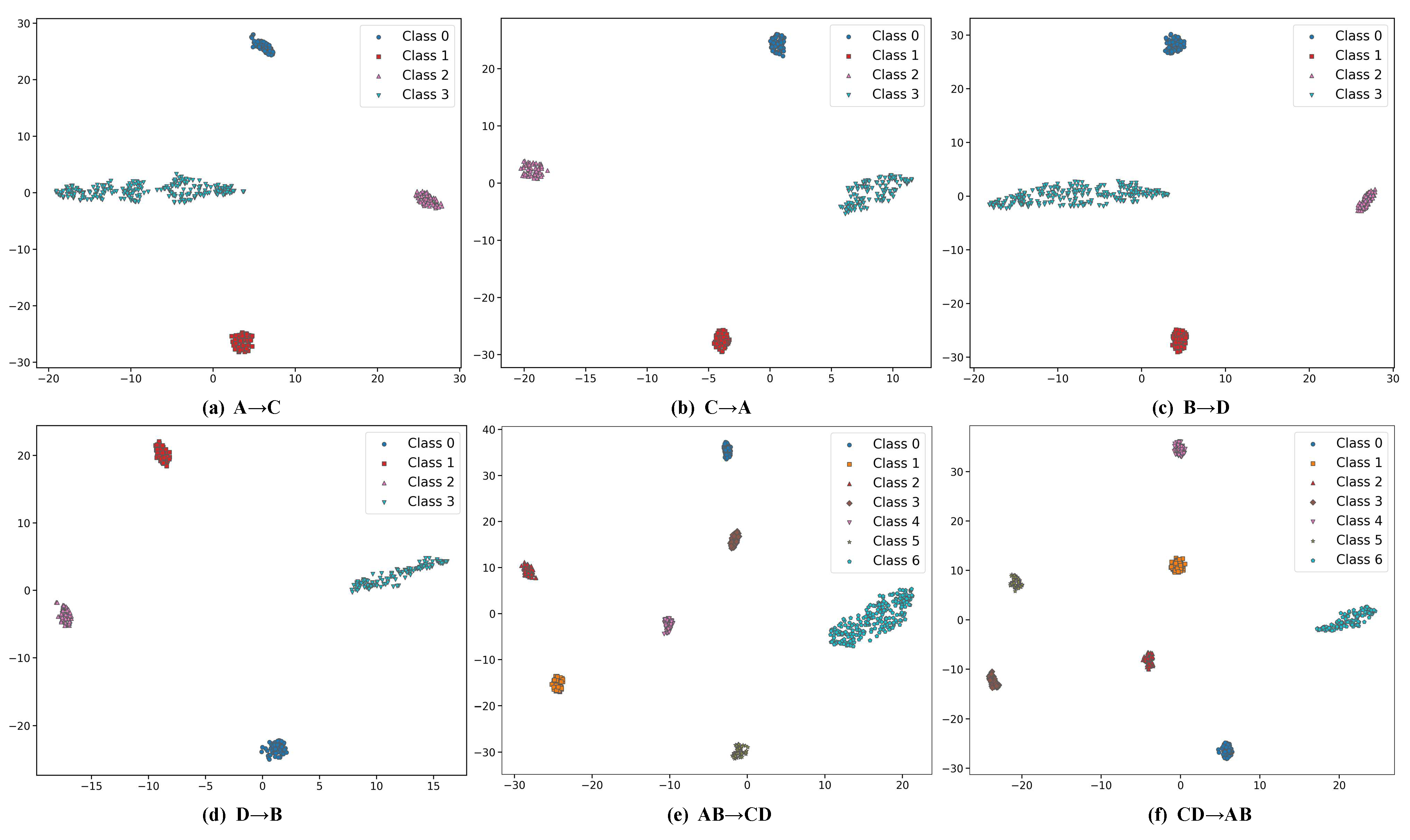
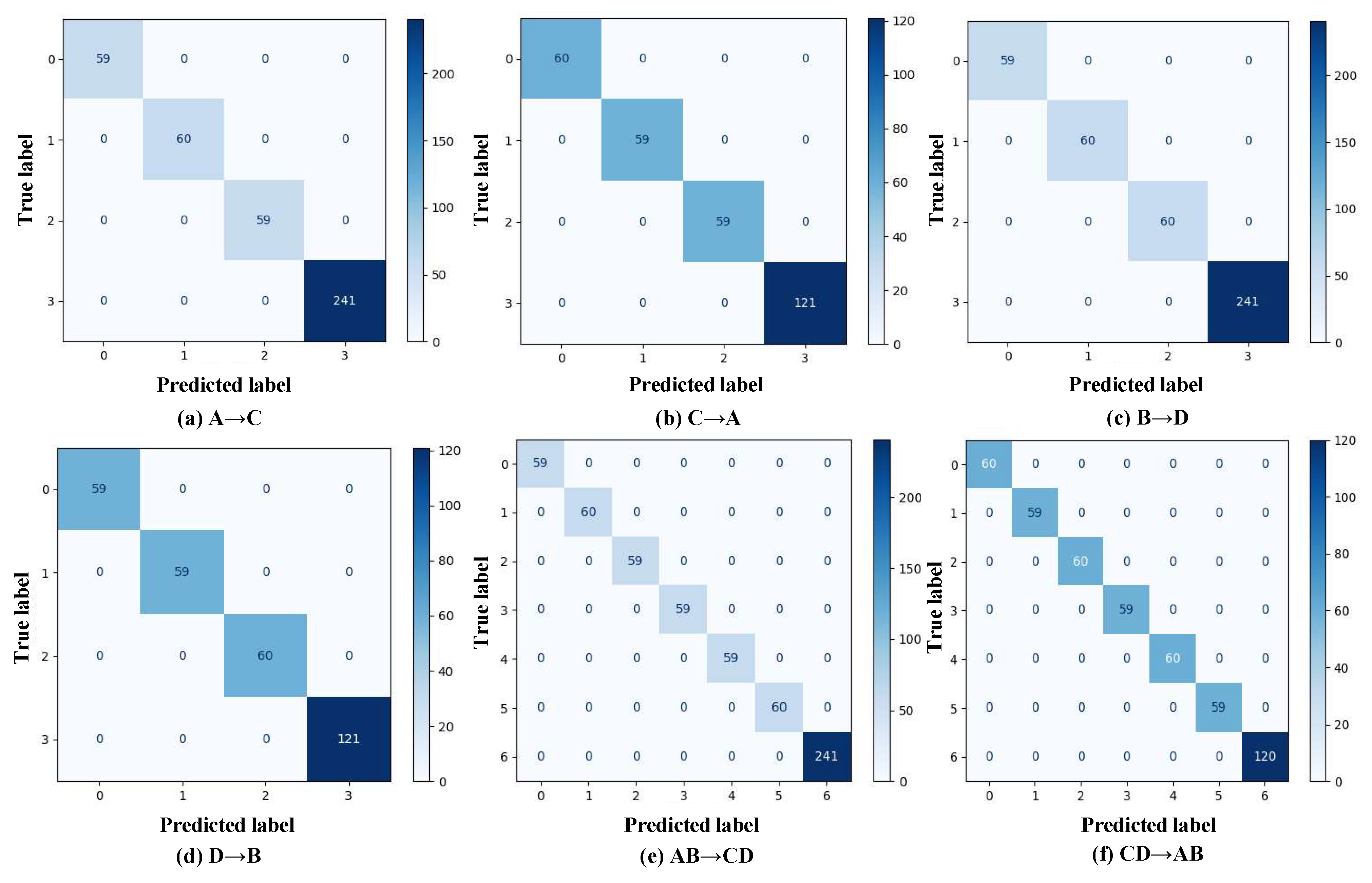
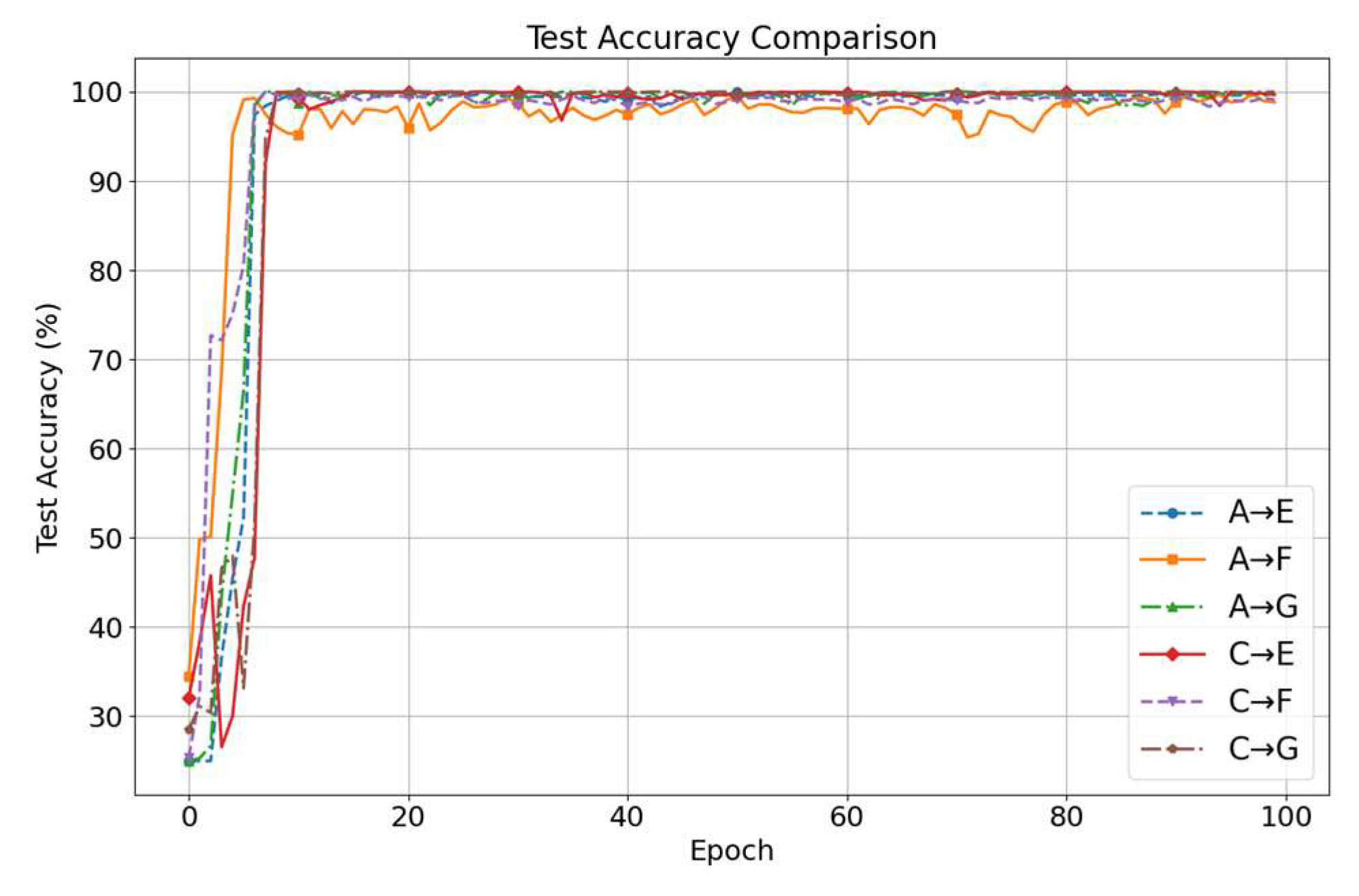
3.2.1. Case 1: Fault Transfer Diagnosis Across Different Working Conditions on the Same Machine
- Implementation details
- 2.
- Experimental results and discussion
3.2.2. Case 2: Cross-Machine Diagnosis
- Implementation details
- 2.
- Experimental results and discussion
3.3. Ablation Study
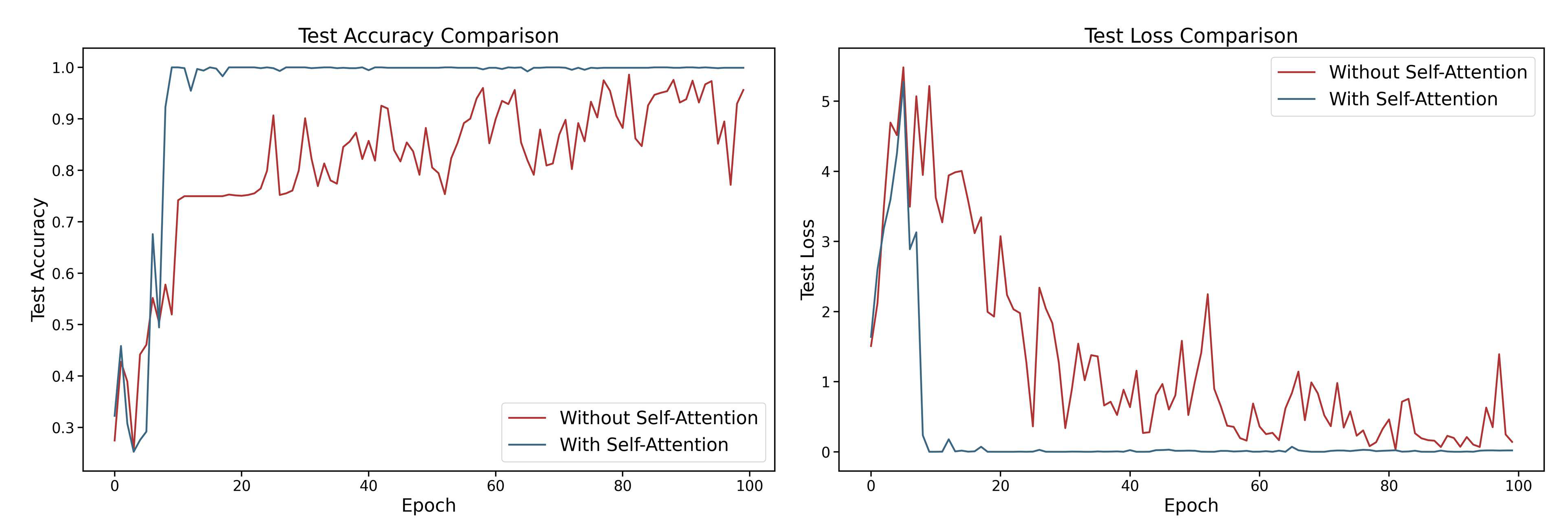
3.3.1. Architectural Ablation: One-Dimensional Self-Attention
3.3.2. Effectiveness Analysis of DBDA
3.3.3. Impact of the Adaptive Factor
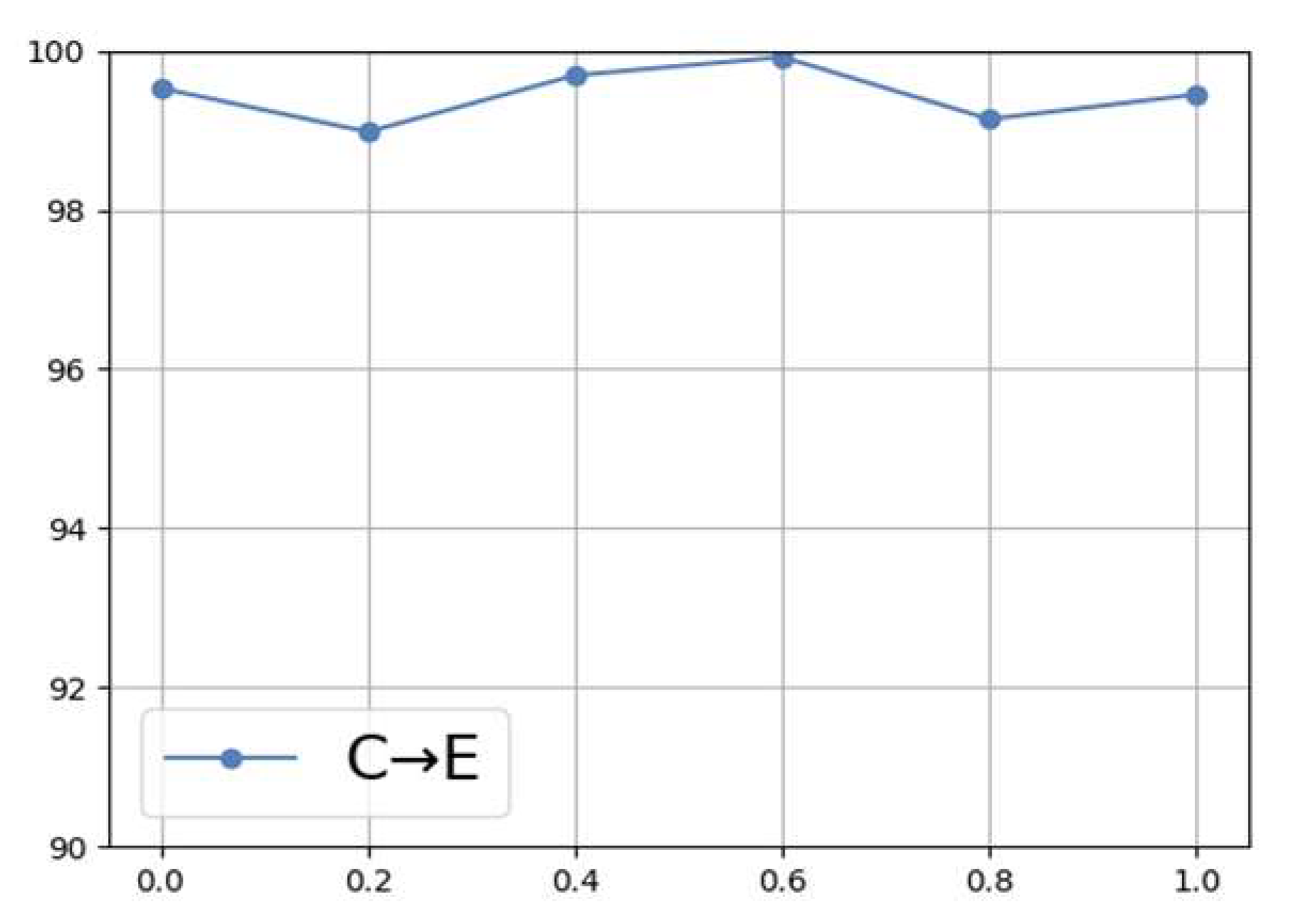
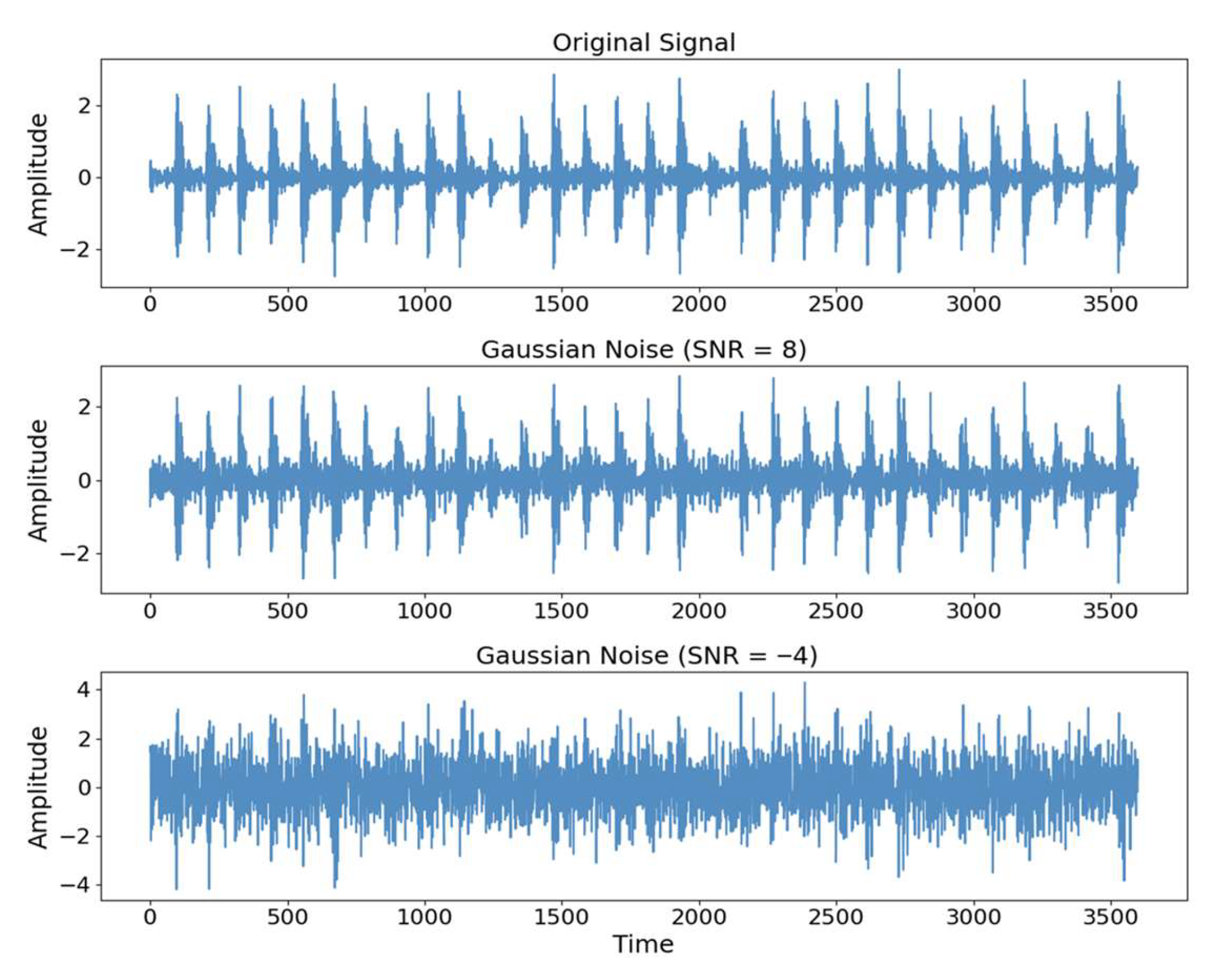
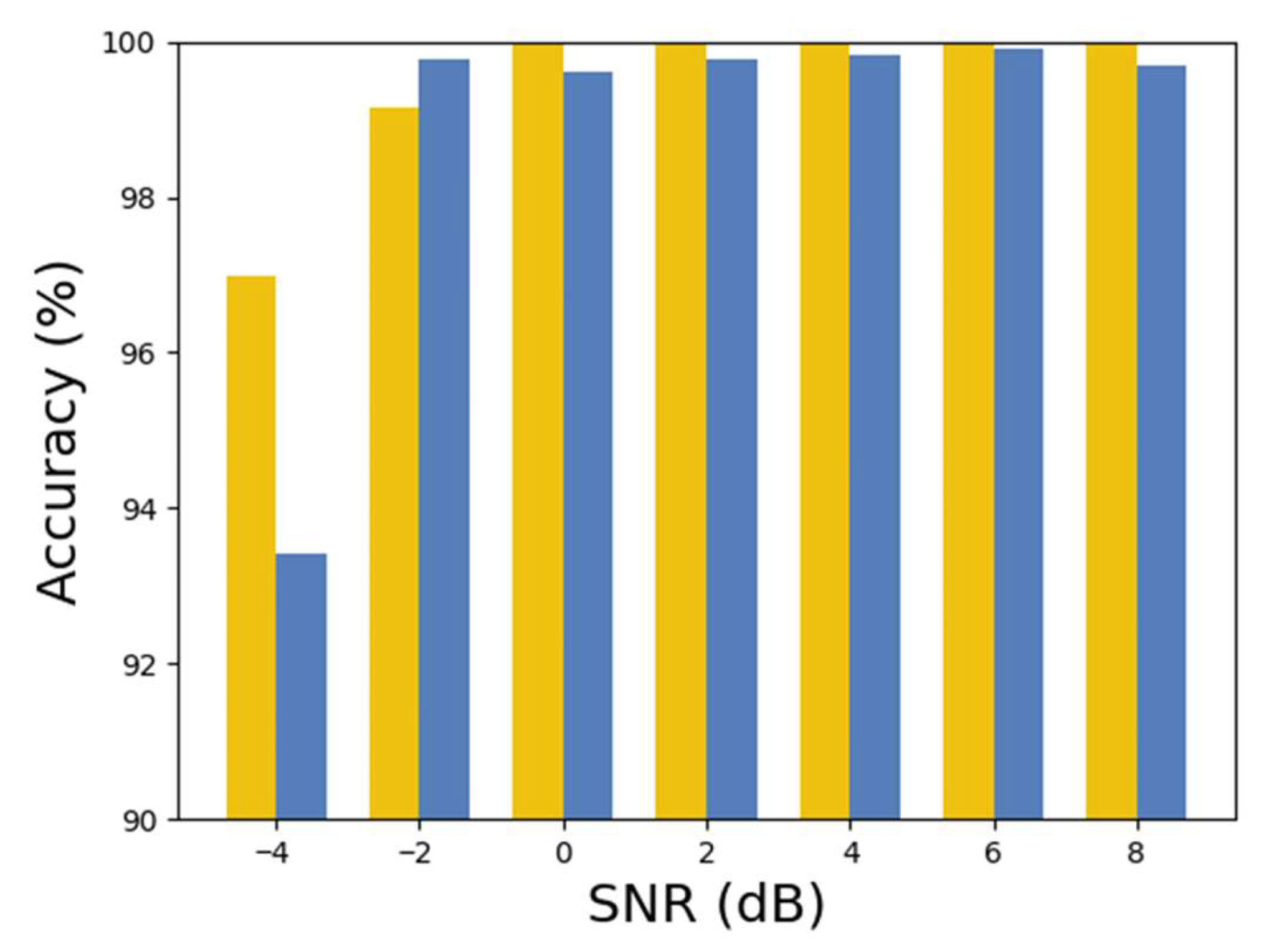
3.4. Noise Resistance Experiment
3.5. Comparative Experiments
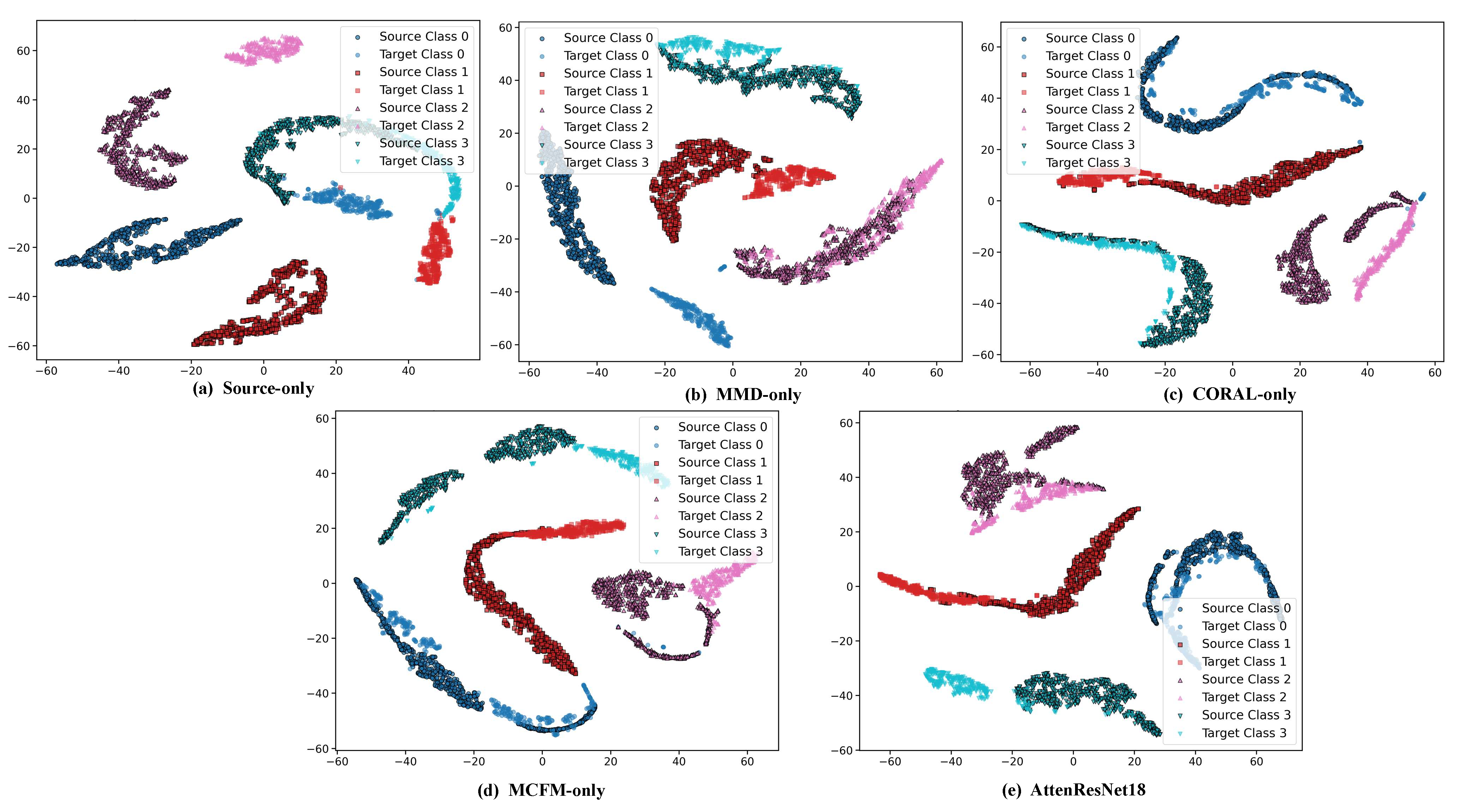
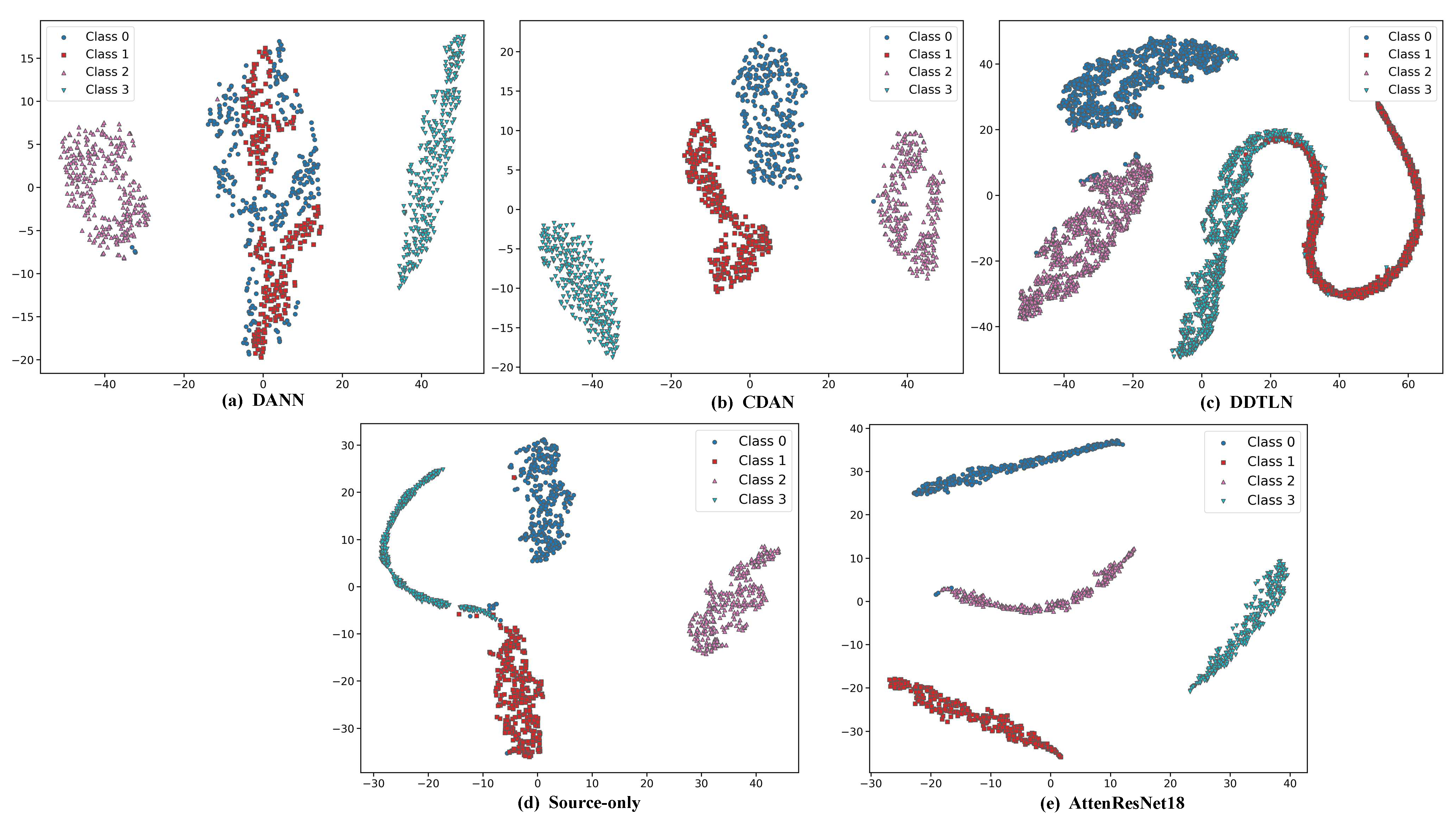
3.6. Model Interpretability Analysis Combined with t-SNE
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| Abbreviation | Full Term |
| AF | Adaptive Filtering |
| AttenResNet18 | Attention-Enhanced Residual Network |
| BDA | Balanced Distribution Adaptation |
| CDA | Conditional Distribution Alignment |
| CDAN | Conditional Domain Adversarial Network |
| CNNs | Convolutional Neural Networks |
| CORAL | CORrelation ALignment |
| CWRU | Case Western Reserve University |
| DA | Domain Adaptation |
| DANN | Domain-Adversarial Neural Network |
| DBDA | Dynamic Balance Distribution Adaptation |
| DBN | Deep Belief Network |
| DDTLN | Deep Discriminative Transfer Learning Network |
| DRSN | Deep Residual Shrinkage Network |
| ECA | Efficient Channel Attention |
| FD-SAE | Feature Distance Stacked Autoencoder |
| GAN | Generative Adversarial Networks |
| I-Softmax | Improved Softmax |
| IJDA | Improved Joint Distribution Adaptation |
| JAADA | Joint Attention Adversarial Domain Adaptation |
| JDA | Joint Distribution Adaptation |
| LMMD | Local Maximum Mean Discrepancy |
| LSTM | Long Short-Term Memory |
| MCFM | MMD-CORAL Fusion Metric |
| MDA | Marginal Distribution Alignment |
| MMCLE | Multi-Channel and Multi-Scale CNN-LSTM-ECA |
| MMD | Maximum Mean Discrepancy |
| RKHS | Reproducing Kernel Hilbert Space |
| RQA-Bayes-SVM | Recurrence Quantification Analysis–Bayesian Optimization–Support Vector Machine |
| SNR | Signal-to-Noise Ratio |
| SSA | Salp Swarm Algorithm |
| SVM | Support Vector Machine |
| t-SNE | t-distributed Stochastic Neighbor Embedding |
| UDA | Unsupervised Domain Adaptation |
| VMD | Variational Mode Decomposition |
References
- Wu, G.; Yan, T.; Yang, G.; Chai, H.; Cao, C. A Review on Rolling Bearing Fault Signal Detection Methods Based on Different Sensors. Sensors 2022, 22, 8330. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, X.; Li, T.; She, L.; Guo, X.; Yang, F. Intelligent Fault Diagnosis for Rotating Machinery via Transfer Learning and Attention Mechanisms: A Lightweight and Adaptive Approach. Actuators 2025, 14, 415. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y.; Choi, H.-J.; Ji, B. Uncertainty-Aware Fault Diagnosis of Rotating Compressors Using Dual-Graph Attention Networks. Machines 2025, 13, 673. [Google Scholar] [CrossRef]
- Li, S.; Gong, Z.; Wang, S.; Meng, W.; Jiang, W. Fault Diagnosis Method for Rolling Bearings Based on a Digital Twin and WSET-CNN Feature Extraction with IPOA-LSSVM. Processes 2025, 13, 2779. [Google Scholar] [CrossRef]
- Deng, X.; Sun, Y.; Li, L.; Peng, X. A Multi-Level Fusion Framework for Bearing Fault Diagnosis Using Multi-Source Information. Processes 2025, 13, 2657. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.; Liu, T.; Li, S.; Zhang, B.; Zhou, G.; Huang, T. Composite Fault Diagnosis for Rolling Bearing Based on Parameter-Optimized VMD. Measurement 2022, 201, 111637. [Google Scholar] [CrossRef]
- Wang, B.; Qiu, W.; Hu, X.; Wang, W. A Rolling Bearing Fault Diagnosis Technique Based on Recurrence Quantification Analysis and Bayesian Optimization SVM. Appl. Soft Comput. 2024, 156, 111506. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Dai, M.; Jo, H.; Kim, M.; Ban, S.-W. MSFF-Net: Multi-Sensor Frequency-Domain Feature Fusion Network with Lightweight 1D CNN for Bearing Fault Diagnosis. Sensors 2025, 25, 4348. [Google Scholar] [CrossRef]
- Gao, S.; Xu, L.; Zhang, Y.; Pei, Z. Rolling Bearing Fault Diagnosis Based on SSA Optimized Self-Adaptive DBN. ISA Trans. 2022, 128, 485–502. [Google Scholar] [CrossRef]
- Cui, M.; Wang, Y.; Lin, X.; Zhong, M. Fault Diagnosis of Rolling Bearings Based on an Improved Stack Autoencoder and Support Vector Machine. IEEE Sens. J. 2021, 21, 4927–4937. [Google Scholar] [CrossRef]
- Hakim, M.; Omran, A.; Ahmed, A.; Al-Waily, M.; Abdellatif, A. A Systematic Review of Rolling Bearing Fault Diagnoses Based on Deep Learning and Transfer Learning: Taxonomy, Overview, Application, Open Challenges, Weaknesses and Recommendations. Ain Shams Eng. J. 2023, 14, 101945. [Google Scholar] [CrossRef]
- Bhuiyan, M.R.; Uddin, J. Deep Transfer Learning Models for Industrial Fault Diagnosis Using Vibration and Acoustic Sensors Data: A Review. Vibration 2023, 6, 218–238. [Google Scholar] [CrossRef]
- Chen, X.; Yang, R.; Xue, Y.; Huang, M.; Ferrero, R.; Wang, Z. Deep Transfer Learning for Bearing Fault Diagnosis: A Systematic Review Since 2016. IEEE Trans. Instrum. Meas. 2023, 72, 1–21. [Google Scholar] [CrossRef]
- Sobie, C.; Freitas, C.; Nicolai, M. Simulation-Driven Machine Learning: Bearing Fault Classification. Mech. Syst. Signal Process. 2018, 99, 403–419. [Google Scholar] [CrossRef]
- Matania, O.; Cohen, R.; Bechhoefer, E.; Bortman, J. Zero-Fault-Shot Learning for Bearing Spall Type Classification by Hybrid Approach. Mech. Syst. Signal Process. 2025, 224, 112117. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Han, B.; Wang, J.; Zhang, Z.; Bao, H. Dynamic Simulation Model-Driven Fault Diagnosis Method for Bearing under Missing Fault-Type Samples. Appl. Sci. 2023, 13, 2857. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the 28th International Conference RPEon Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Jin, Y.; Song, X.; Yang, Y.; Hei, X.; Feng, N.; Yang, X. An Improved Multi-Channel and Multi-Scale Domain Adversarial Neural Network for Fault Diagnosis of the Rolling Bearing. Control Eng. Pract. 2025, 154, 106120. [Google Scholar] [CrossRef]
- Long, M.; Cao, Z.; Wang, J.; Jordan, M.I. Conditional Adversarial Domain Adaptation. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Liang, J.; Wei, J.; Jiang, Z. Generative Adversarial Networks GAN Overview. J. Front. Comput. Sci. Technol. 2020, 14, 1–17. [Google Scholar] [CrossRef]
- Fang, L.; Liu, Y.; Li, X.; Chang, J. Intelligent Fault Diagnosis of Rolling Bearing Based on Deep Transfer Learning. In Proceedings of the 2024 6th International Conference on Natural Language Processing (ICNLP), Xi’an, China, 22–24 March 2024. [Google Scholar] [CrossRef]
- Wang, Z.; Ming, X. A Domain Adaptation Method Based on Deep Coral for Rolling Bearing Fault Diagnosis. In Proceedings of the 2023 IEEE 14th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Chania, Greece, 28–31 August 2023. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, D.; Sun, G.; Wang, Y. A Fault Diagnosis Method Based on Improved Adaptive Filtering and Joint Distribution Adaptation. IEEE Access 2020, 8, 159683–159695. [Google Scholar] [CrossRef]
- Qian, Q.; Qin, Y.; Luo, J.; Wang, Y.; Wu, F. Deep Discriminative Transfer Learning Network for Cross-Machine Fault Diagnosis. Mech. Syst. Signal Process. 2023, 186, 109884. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, R.; He, T.; Wei, K.; Yuan, J. A Novel Bearing Fault Diagnosis Method Based Joint Attention Adversarial Domain Adaptation. Reliab. Eng. Syst. Saf. 2023, 237, 109345. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Feng, W.; Shen, Z. Balanced Distribution Adaptation for Transfer Learning. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Y. A Cross Domain Feature Extraction Method for Bearing Fault Diagnosis Based on Balanced Distribution Adaptation. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- He, D.; Zhang, Z.; Jin, Z.; Zhang, F.; Yi, C.; Liao, S. RTSMFFDE-HKRR: A Fault Diagnosis Method for Train Bearing in Noise Environment. Measurement 2025, 239, 115417. [Google Scholar] [CrossRef]
- Kim, D.-Y.; Kareem, A.B.; Domingo, D.; Shin, B.-C.; Hur, J.-W. Advanced Data Augmentation Techniques for Enhanced Fault Diagnosis in Industrial Centrifugal Pumps. J. Sens. Actuator Netw. 2024, 13, 60. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.-Q. Intelligent Rotating Machinery Fault Diagnosis Based on Deep Learning Using Data Augmentation. J. Intell. Manuf. 2020, 31, 433–452. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer Feature Learning with Joint Distribution Adaptation. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013. [Google Scholar] [CrossRef]
- Yu, S.; Wang, F.; Yu, C.; Tian, H. An Unsupervised Domain Adaptation Method with Coral-Maximum Mean Discrepancy for Subway Train Transmission System Fault Diagnosis. Smart Resilient Transp. 2025. [Google Scholar] [CrossRef]
- Zhong, J.; Lin, C.; Gao, Y.; Zhong, J.; Zhong, S. Fault Diagnosis of Rolling Bearings Under Variable Conditions Based on Unsupervised Domain Adaptation Method. Mech. Syst. Signal Process. 2024, 215, 111430. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Ding, A.; Qin, Y.; Wang, B.; Guo, L.; Jia, L.; Cheng, X. Evolvable Graph Neural Network for System-Level Incremental Fault Diagnosis of Train Transmission Systems. Mech. Syst. Signal Process. 2024, 210, 111175. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing Data Using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Babak, V.; Zaporozhets, A.; Kuts, Y.; Fryz, M.; Scherbak, L. Identification of Vibration Noise Signals of Electric Power Facilities. In Noise Signals: Modelling and Analyses; Springer Nature Switzerland: Cham, Switzerland, 2025; Volume 567, pp. 143–170. [Google Scholar] [CrossRef]





| Technique | Parameter Range | Scope | Implementation |
|---|---|---|---|
| Gaussian noise [31] | Source and target domain training sets | Addition of Gaussian white noise controlled by a specified signal-to-noise ratio (SNR) | |
| Time stretching [32] | Source domain training set | Adjust length based on a random factor , then interpolate to the original length (: rotational speed decrease; : rotational speed increase) | |
| Time shifting [33] | Source domain training set | Circularly shift the signal to simulate phase changes |
| Layer Name | Input Size | Output Size | ||
|---|---|---|---|---|
| Conv1d_1 | Convolution BN Relu | |||
| Pooling | MaxPool1d | |||
| BasicBlock_1 | Dropout = 0.35 | |||
| Attention1 | SelfAttention1D | / | ||
| BasicBlock_2 | Dropout = 0.35 | |||
| BasicBlock_3 | Dropout = 0.35 | |||
| BasicBlock_4 | Dropout = 0.35 | |||
| Attention2 | SelfAttention1D | / | ||
| Classification | AdaptiveAvgPool1d Dropout = 0.5 FC | / | 4 |
| Task | Fault Type | Label |
|---|---|---|
| Four-class | Ball | 0 |
| Inner | 1 | |
| Outer | 2 | |
| Normal | 3 | |
| Seven-class | Ball_007 | 0 |
| Inner_007 | 1 | |
| Outer_007 | 2 | |
| Ball_014 | 3 | |
| Inner_014 | 4 | |
| Outer_014 | 5 | |
| Normal | 6 |
| Name | Datasets | Load | Speed | Fault Diameters |
|---|---|---|---|---|
| A | CWRU | 0 hp | 1797 rpm | 0.007 in |
| B | CWRU | 0 hp | 1797 rpm | 0.014 in |
| C | CWRU | 2 hp | 1750 rpm | 0.007 in |
| D | CWRU | 2 hp | 1750 rpm | 0.014 in |
| E | BJTU-RAO | 0 kN | 2400 rpm | / |
| F | BJTU-RAO | +10 kN | 2400 rpm | / |
| G | BJTU-RAO | 0 kN | 3600 rpm | / |
| Model | Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Avg (%) |
|---|---|---|---|---|---|---|
| Source-only | 52.98 | 47.57 | 63.03 | 54.63 | 61.85 | 56.01 |
| MMD-only | 98.59 | 99.22 | 98.67 | 98.27 | 98.27 | 98.60 |
| CORAL-only | 99.14 | 99.06 | 98.98 | 98.74 | 98.74 | 98.93 |
| MCFM-only | 98.51 | 99.06 | 99.14 | 97.80 | 99.14 | 98.73 |
| AttenResNet18 | 99.69 | 100 | 99.84 | 99.92 | 100 | 99.89 |
| SNR (dB) | −4 | −2 | 0 | 2 | 4 | 6 | 8 |
|---|---|---|---|---|---|---|---|
| A + B → C + D | 96.98 | 99.16 | 100 | 100 | 100 | 100 | 100 |
| C → E | 93.41 | 99.76 | 99.61 | 99.76 | 99.84 | 99.92 | 99.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, G.; Wu, S.; Zhang, Y.; Wei, W.; Fu, W.; Zhang, J.; Yang, Y.; Fu, J. AttenResNet18: A Novel Cross-Domain Fault Diagnosis Model for Rolling Bearings. Sensors 2025, 25, 5958. https://doi.org/10.3390/s25195958
Huang G, Wu S, Zhang Y, Wei W, Fu W, Zhang J, Yang Y, Fu J. AttenResNet18: A Novel Cross-Domain Fault Diagnosis Model for Rolling Bearings. Sensors. 2025; 25(19):5958. https://doi.org/10.3390/s25195958
Chicago/Turabian StyleHuang, Gangjin, Shanshan Wu, Yingxiao Zhang, Wuguo Wei, Weigang Fu, Junjie Zhang, Yuxuan Yang, and Junheng Fu. 2025. "AttenResNet18: A Novel Cross-Domain Fault Diagnosis Model for Rolling Bearings" Sensors 25, no. 19: 5958. https://doi.org/10.3390/s25195958
APA StyleHuang, G., Wu, S., Zhang, Y., Wei, W., Fu, W., Zhang, J., Yang, Y., & Fu, J. (2025). AttenResNet18: A Novel Cross-Domain Fault Diagnosis Model for Rolling Bearings. Sensors, 25(19), 5958. https://doi.org/10.3390/s25195958





