SAC-MS: Joint Slice Resource Allocation, User Association and UAV Trajectory Optimization with No-Fly Zone Constraints
Abstract
1. Introduction
- To meet the customized demands of diverse services under resource-constrained conditions, this paper introduces a dynamic radio access network slicing mechanism within the architecture of a SAGIN, subject to NFZ constraints. This design aims to enable on-demand allocation and efficient management of communication resources.
- We formulate a joint optimization problem that integrates user association, slice resource allocation, and UAV trajectory optimization, aiming to maximize the system utility, defined as the difference between the total system gains and the system costs. It is then decomposed into three subproblems: user association, UAV trajectory optimization and slice resource allocation.
- We propose the SAC-MS algorithm to solve the joint optimization problem. Specifically, a many-to-one matching game is adopted to achieve stable user–base station association, the SCA method is employed to transform the non-convex UAV trajectory optimization problem into convex subproblems, and a deep reinforcement learning-based algorithm is introduced for adaptive slice resource allocation in dynamic networks.
- Simulation results show that the proposed algorithm improves system utility by 10.53%, 13.17%, 31.25%, and 45.38% compared to the benchmark algorithms (TD3-MS, DDPG-MS, DQN-MS, and Hard_slicing), respectively.
2. Related Works
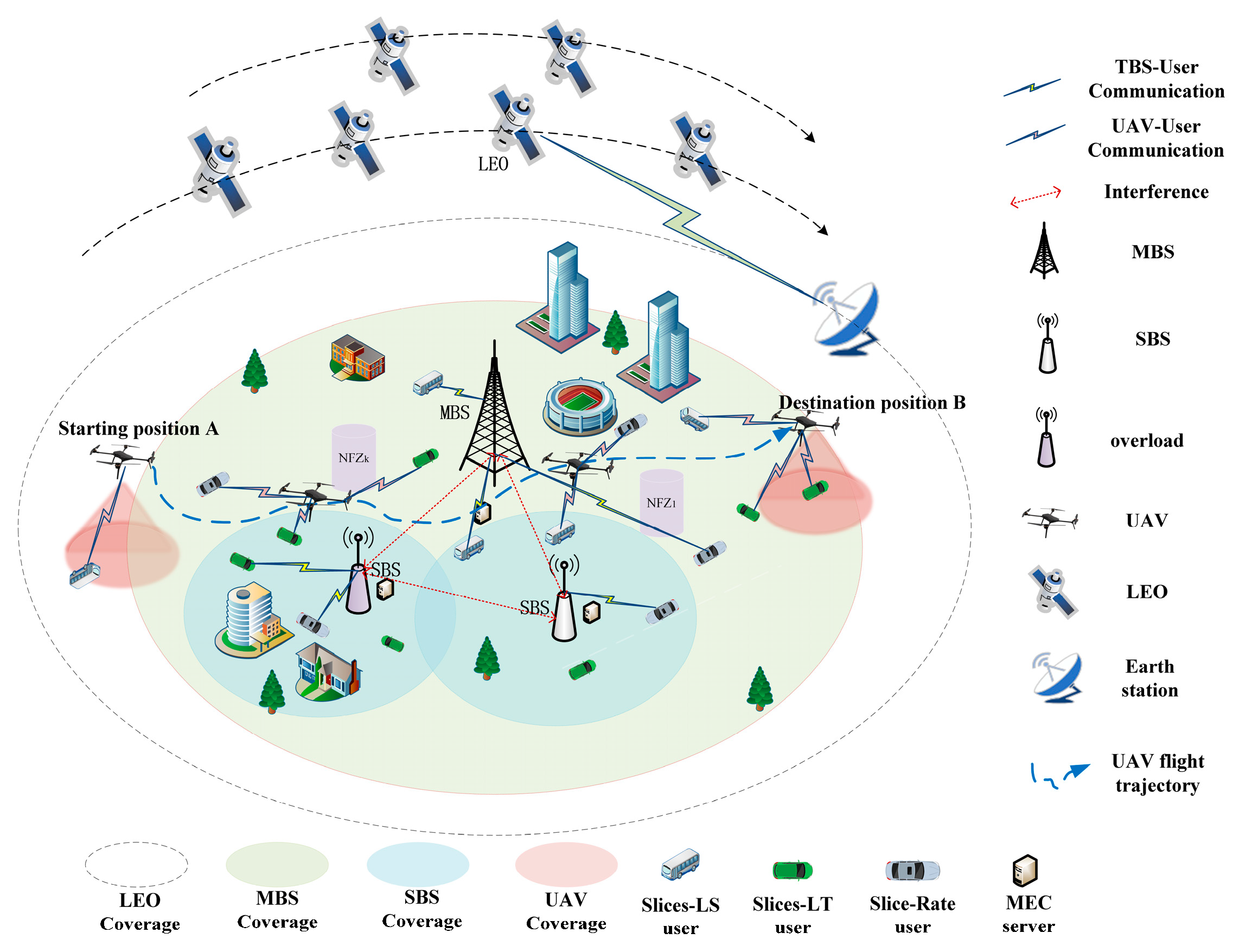
3. System Model
3.1. Network Model
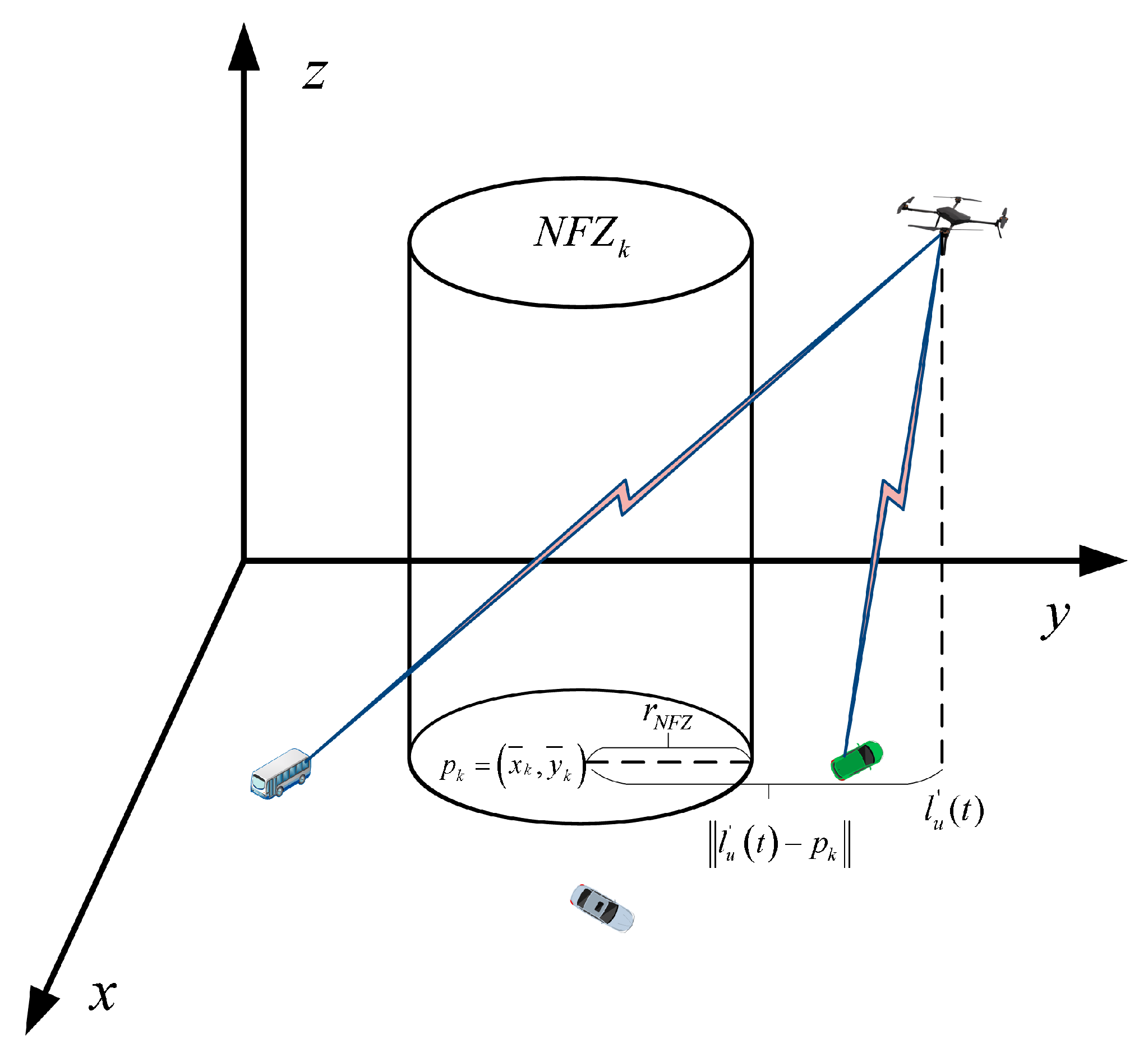
3.2. UAV Mobility Model
3.3. NFZ Model
3.4. Communication Model
3.4.1. LEO-User Communication Model
3.4.2. UAV–User Communication Model
3.4.3. TBS-User Communication Model
3.4.4. Computation Model
4. Problem Formulation
4.1. System Cost
4.1.1. Operational Cost
4.1.2. Reconfiguration Cost
4.2. System Revenue
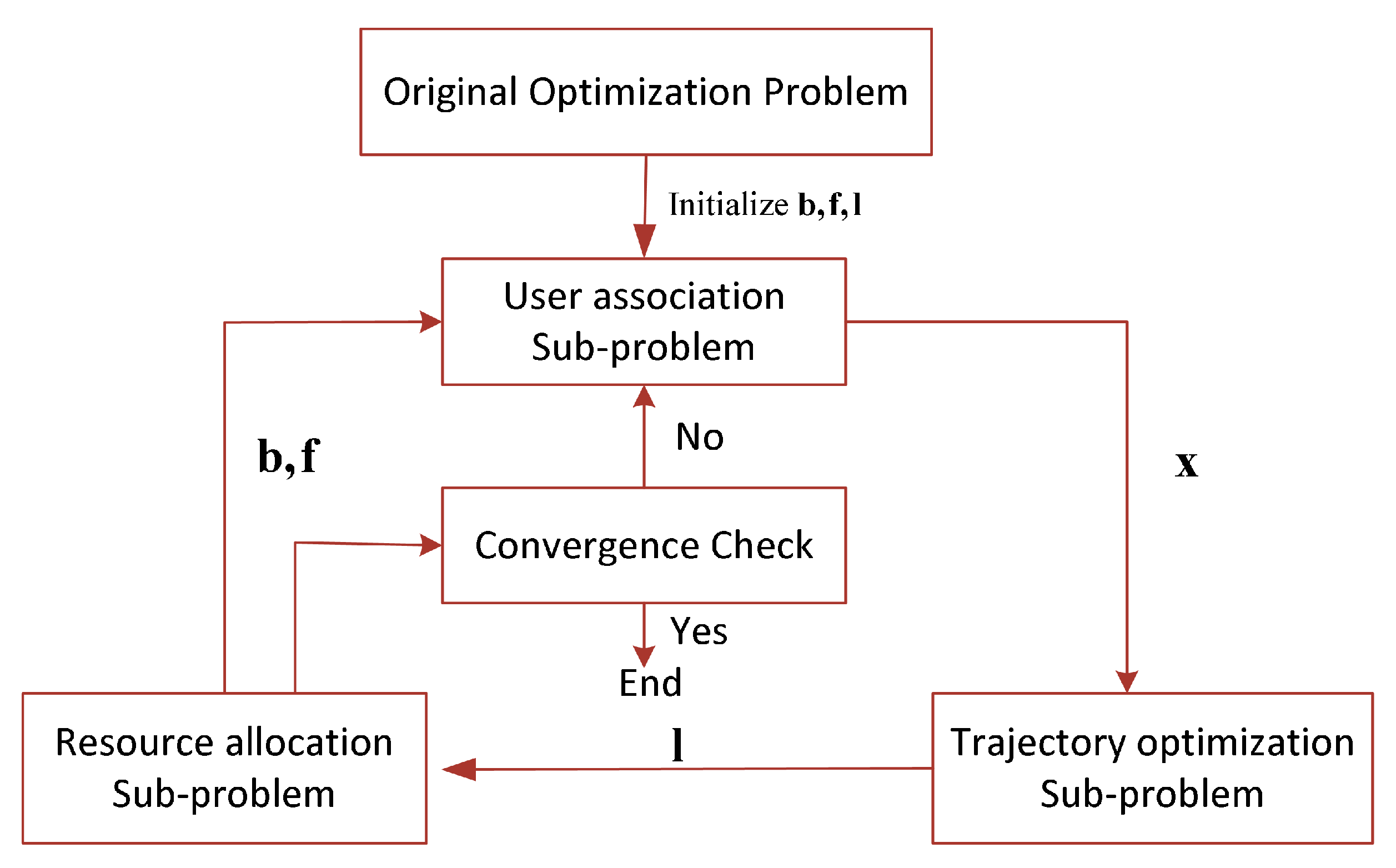
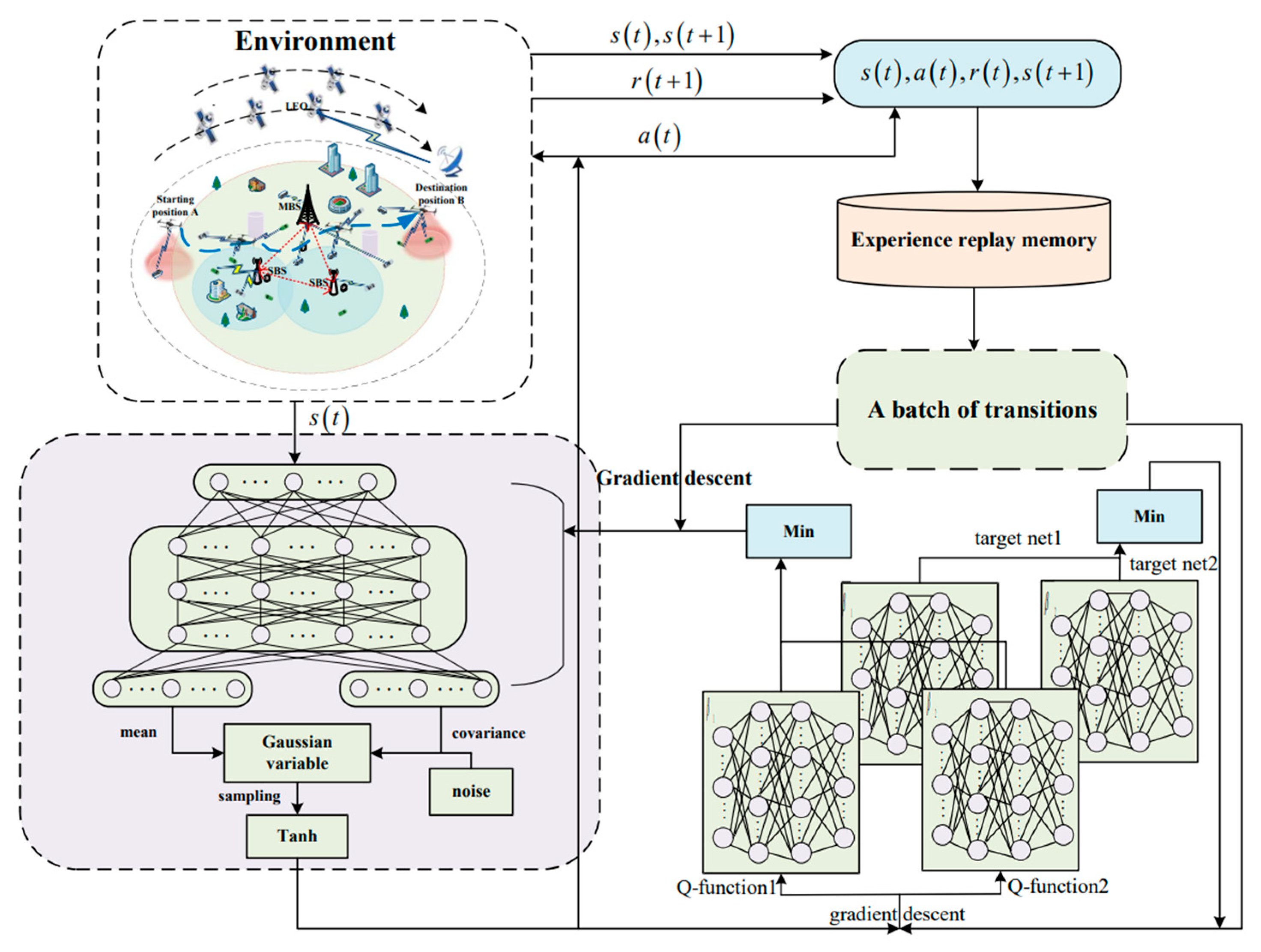
5. Proposed Algorithm
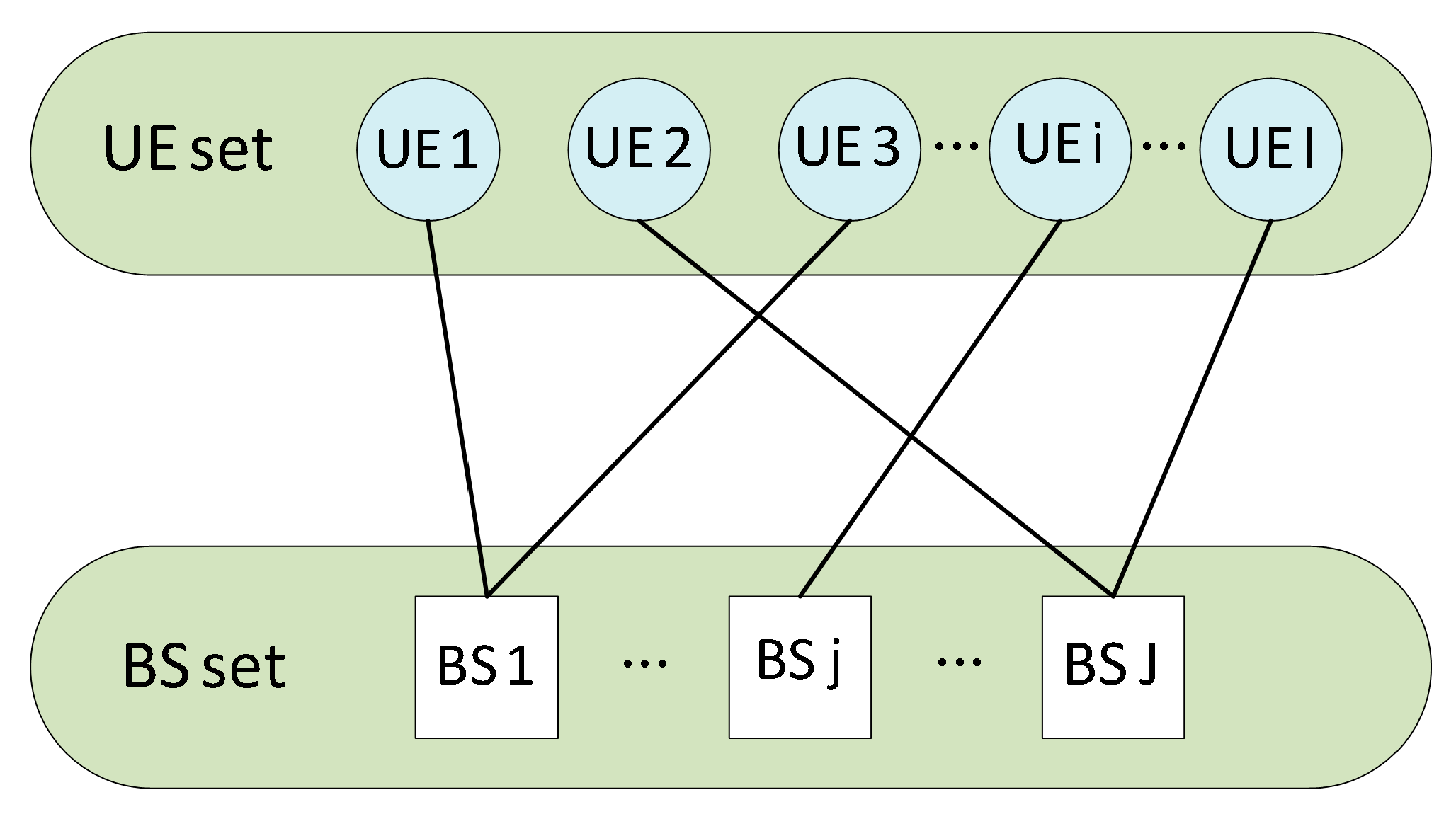
5.1. User Association (UA)
| Algorithm 1: Association Algorithm Based on Stable Matching Game. | |
| 1: | Preference matrices for BSs and users, Utility functions for both BSs and users to calculate preferences |
| 2: | Stable matching results between BSs and users |
| 3: | Initialize: |
| 4: | (a) Set all users as “free” (not yet matched); |
| 5: | (b) Set all BSs with empty connected user lists; |
| 6: | (c) Set BSs’ rejection list; |
| 7: | (d) Set a list of requests for each user; |
| 8: | Composition of preference lists: |
| 9: | (a) BS and user exchange their listing information; |
| 10: | (b) Each user constructs its preference list based on its own Utility Function , and rank BSs in descending order of preference; |
| 11: | (c) Each BS constructs its preference list based on its own Utility Function , and rank users in descending order of preference; |
| 12: | Match Process: |
| 13: | Repeat: |
| 14: | For each user that is free: |
| 15: | applies to the highest-ranked BS in its preference list; |
| 16: | For each BS : |
| 17: | (a) j receives applications from users; |
| 18: | (b) Sort users in the application list according to BS j preference list; |
| 19: | If the number of applicants for j exceeds the quota: |
| 20: | (a) Select the top users based on preference; |
| 21: | (b) Reject the remaining users and add them to rejection list; |
| 22: | else: |
| 23: | (a) Accept all applicants and add them to BS waiting list; |
| 24: | (b) Add accepted UAVs to ’s matched UAVs list; |
| 25: | For each user : |
| 26: | If is rejected by a BS: |
| 27: | (a) re-applies to the next most preferred BS; |
| 28: | (b) Update the application list of and write down the BS that has been applied; |
| 29: | end if |
| 30: | end for |
| 31: | For each BS : |
| 32: | (a) Update the waiting list based on the newly accepted users; |
| 33: | (b) Combine the original waiting list with the newly accepted users; |
| 34: | end for |
5.2. UAV Trajectory Optimization (TO)
| Algorithm 2: UAV Trajectory Optimization Algorithm Based on SCA. | |
| 1: | User Association Strategy , Slice Resource Allocation Ratio ,, Initial trajectory , NFZ’s Information and , Maximum Iterations ; |
| 2: | Optimized UAV trajectory |
| 3: | Initialize iteration index ; |
| 4: | Repeat: |
| 5: | For the -th iteration, given reference trajectory |
| 6: | Solve the convex optimization problem (sub-TO2): |
| 7: | Let be the optimal solution of the above problem; |
| 8: | Update ; |
| 9: | Until |
| 10: | Return |
5.3. Resource Allocation (RA)
| Algorithm 3: SAC-RA Algorithm. | |
| 1: | policy network , Q-functions and , Parameters of target networks , replay buffer , learning rate , discount factor , entropy coefficient . |
| 2: | for each episode do |
| 3: | Initialize state ; |
| 4: | for step t = 1 to do |
| 5: | Selects action according to ; |
| 6: | Execute action , and observe the immediate reward and the state |
| 7: | Store in the experience replay buffer ; |
| 8: | if replay buffer size batch size then |
| 9: | Randomly sample batch from buffer ; |
| 10: | Calculate the target Q-value, i.e., Equation (43); |
| 11: | Update Q Network: |
| 12: | Update policy-function parameter: i.e., Equation (44), ; |
| 13: | Update the target network using soft updates: ; |
| 14: | end if |
| 15: | end for |
| 16: | end for |
6. Simulation Results and Analysis
6.1. Simulation Setup
6.2. Parameter Analysis
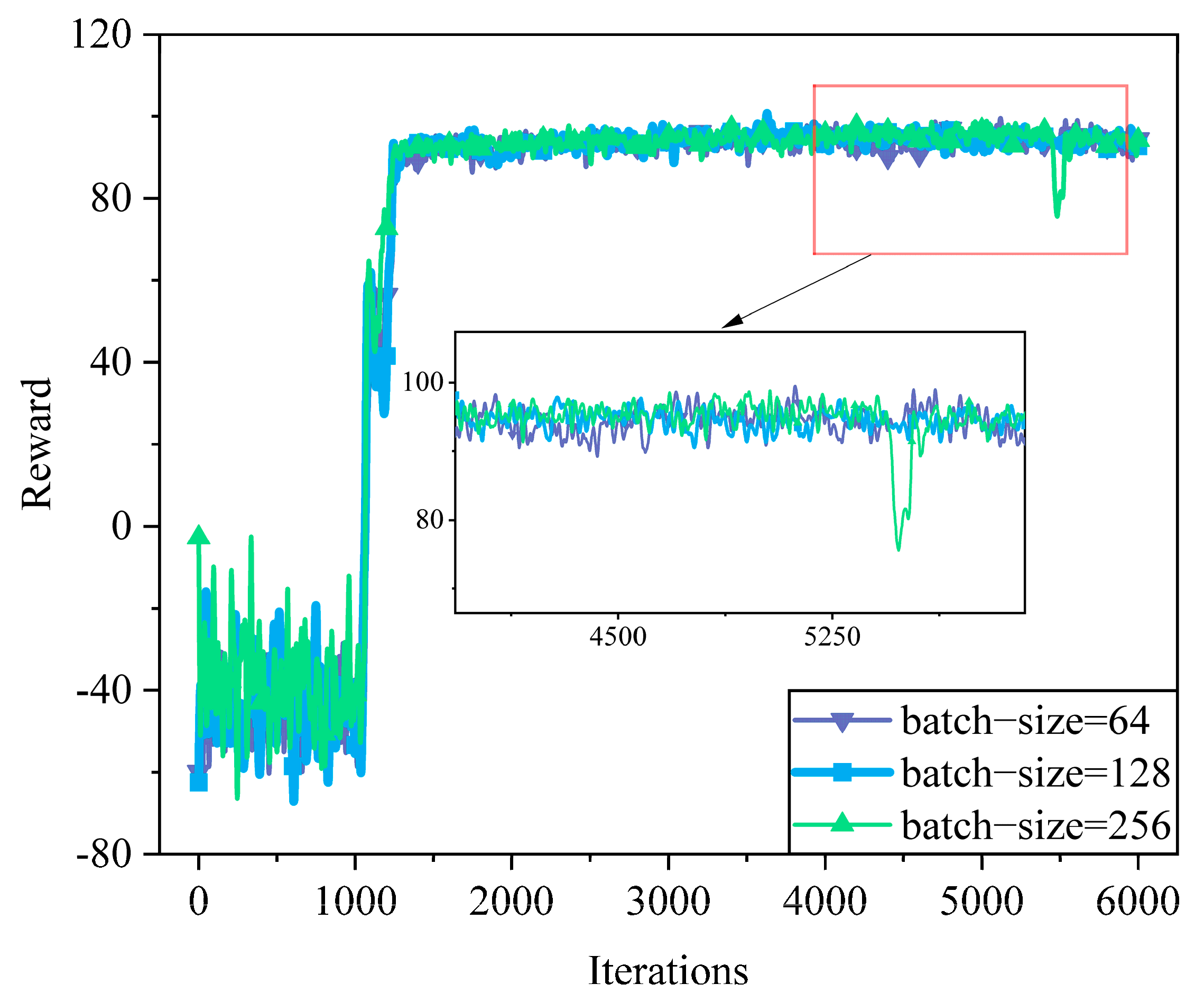
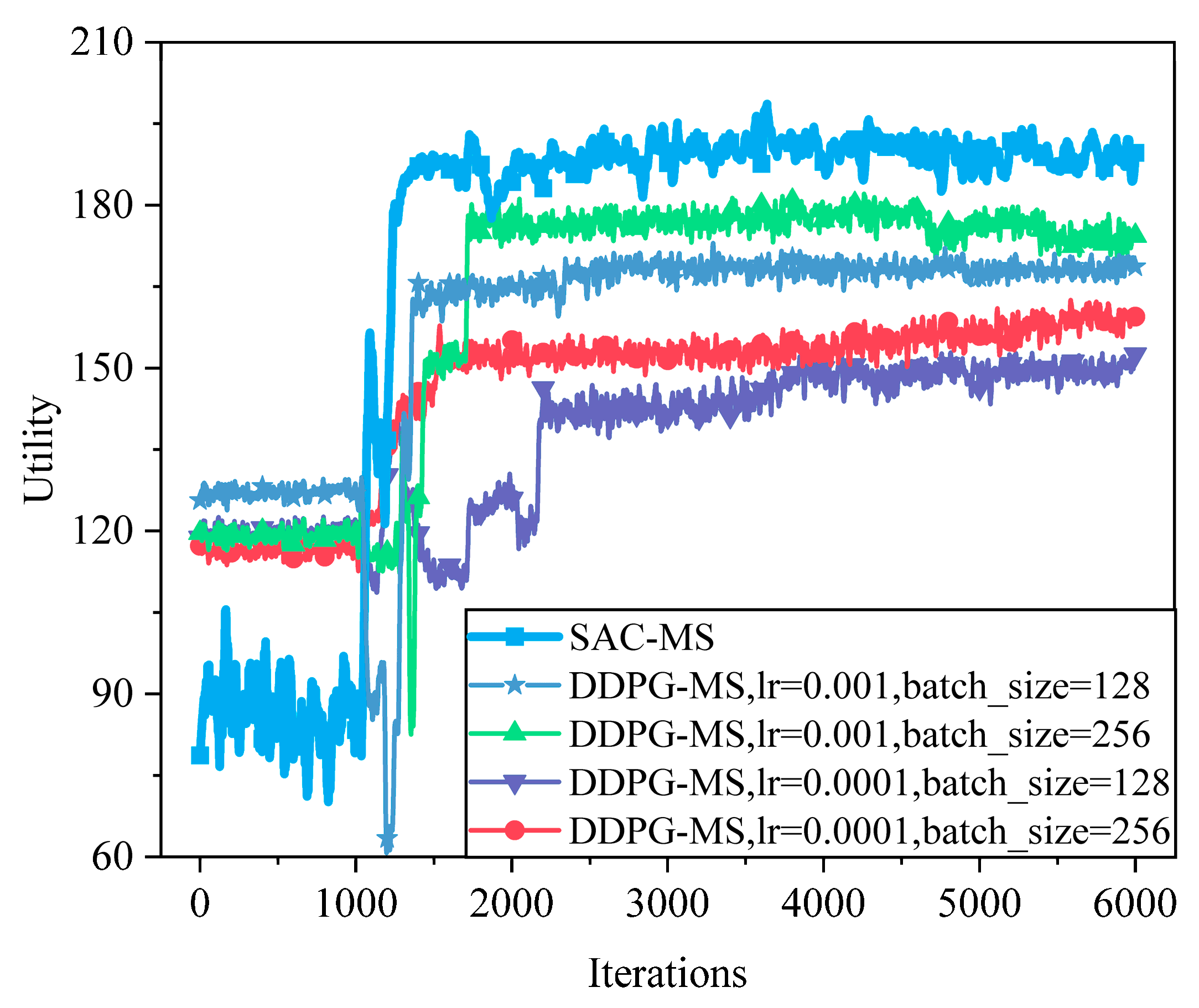
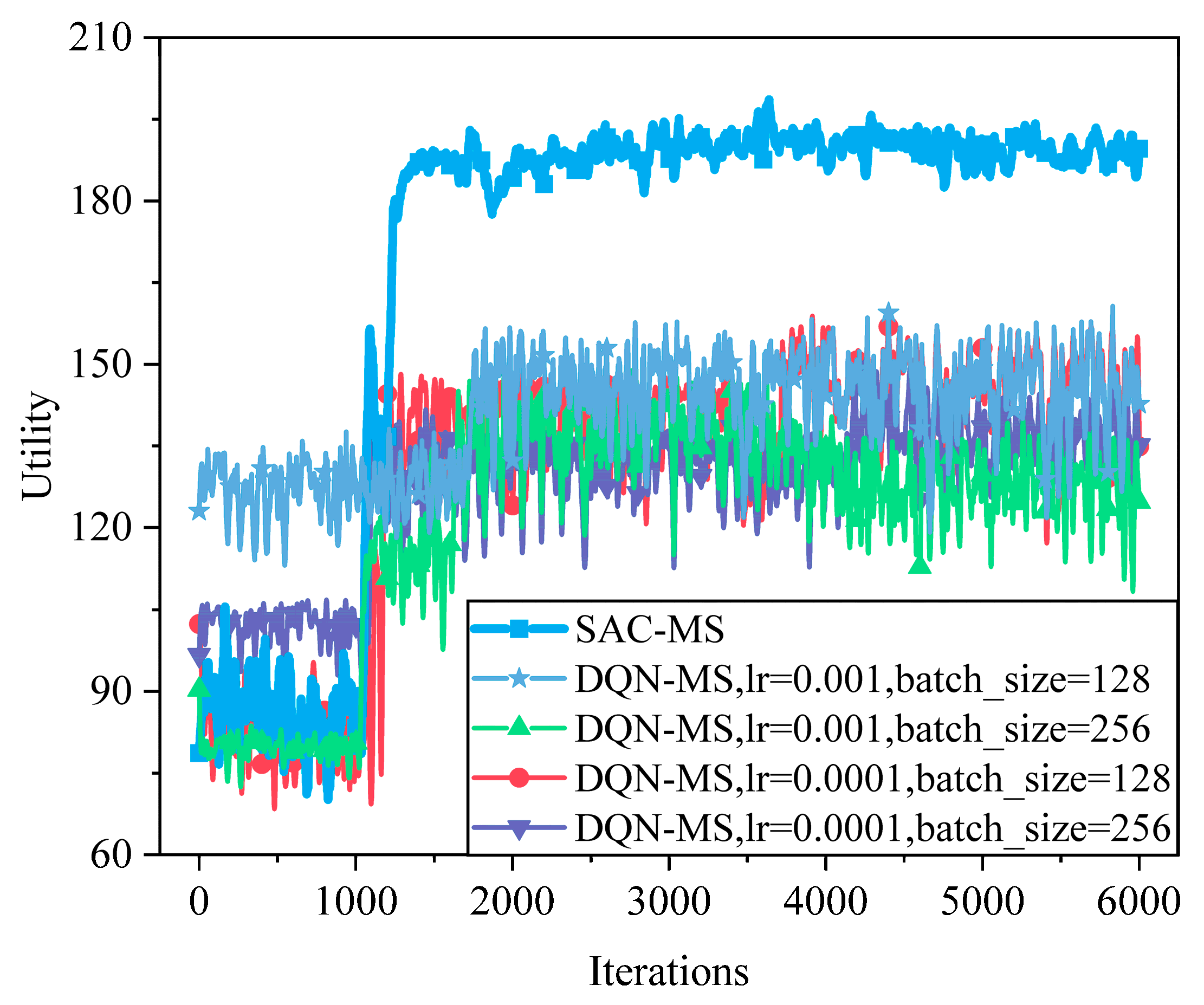
6.2.1. Analysis of Hyperparameters
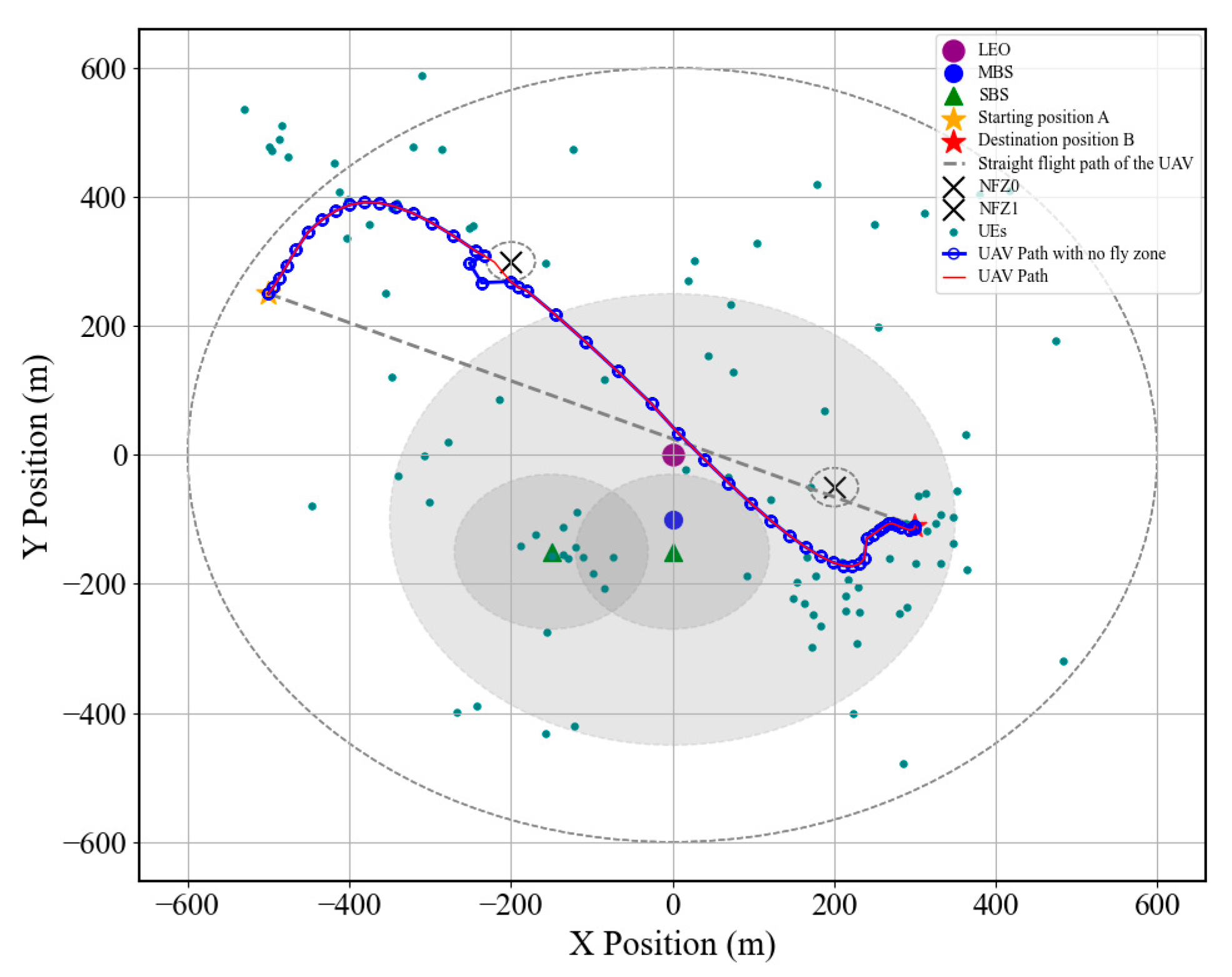
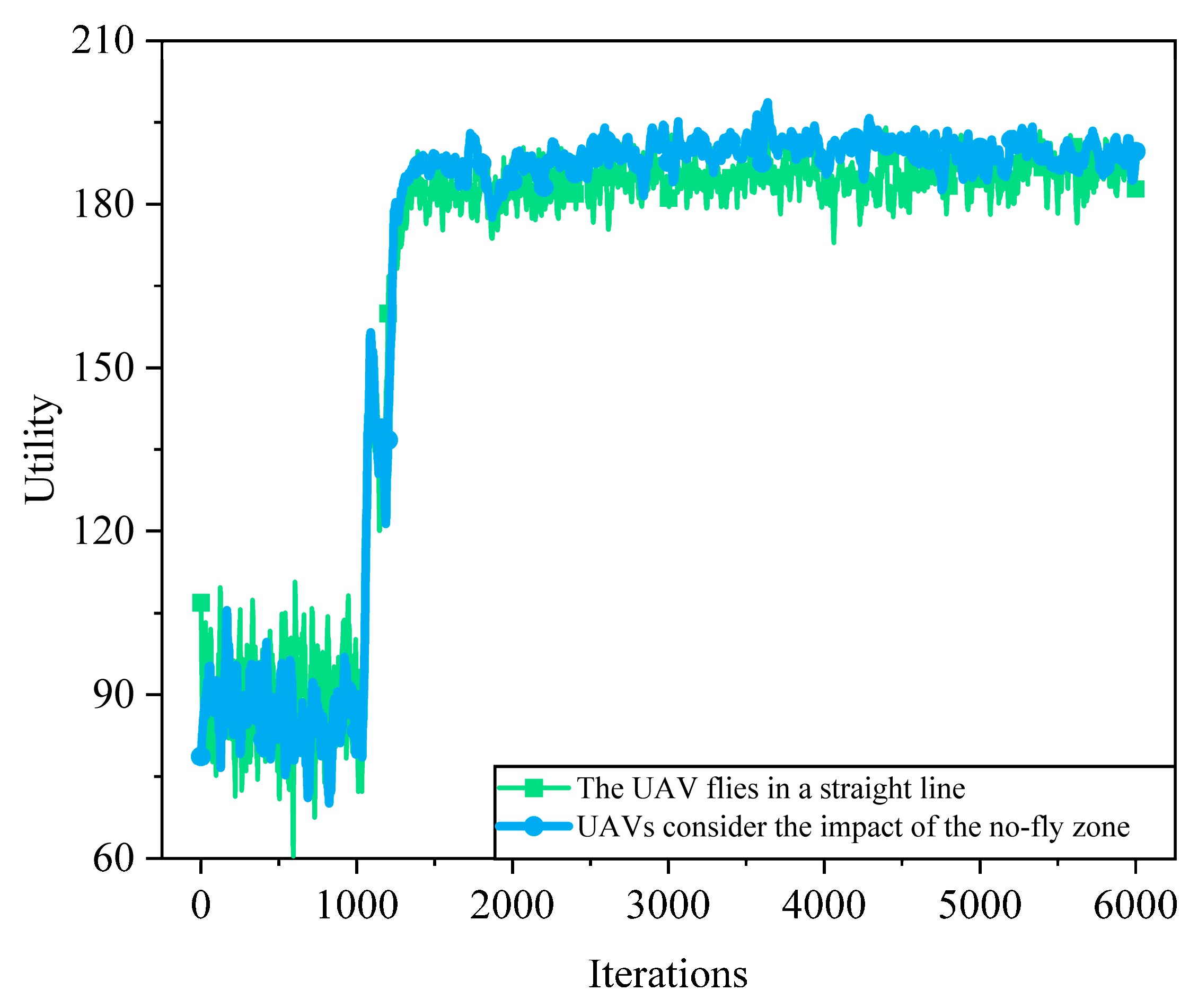
6.2.2. Analysis of Environmental Parameters
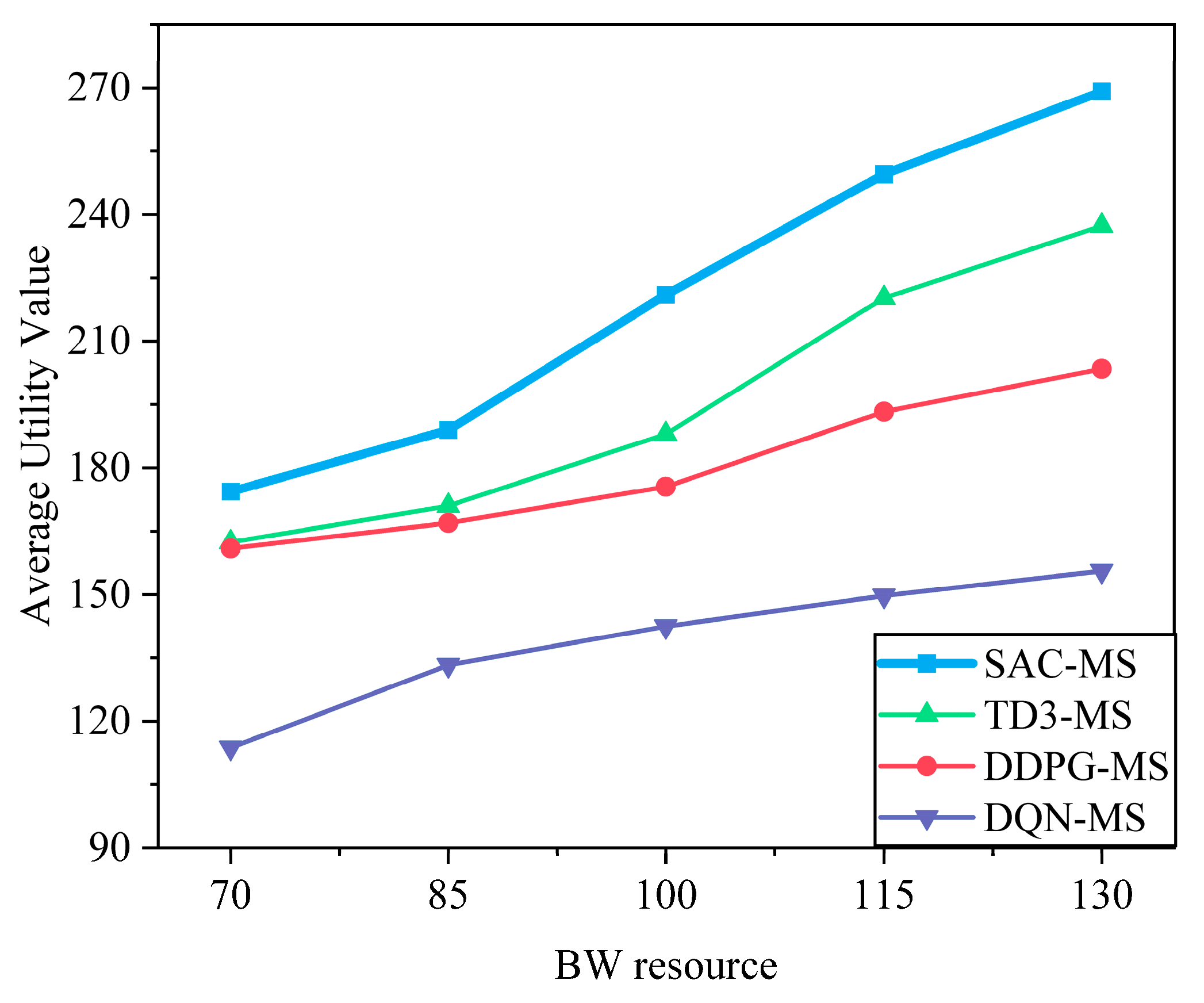
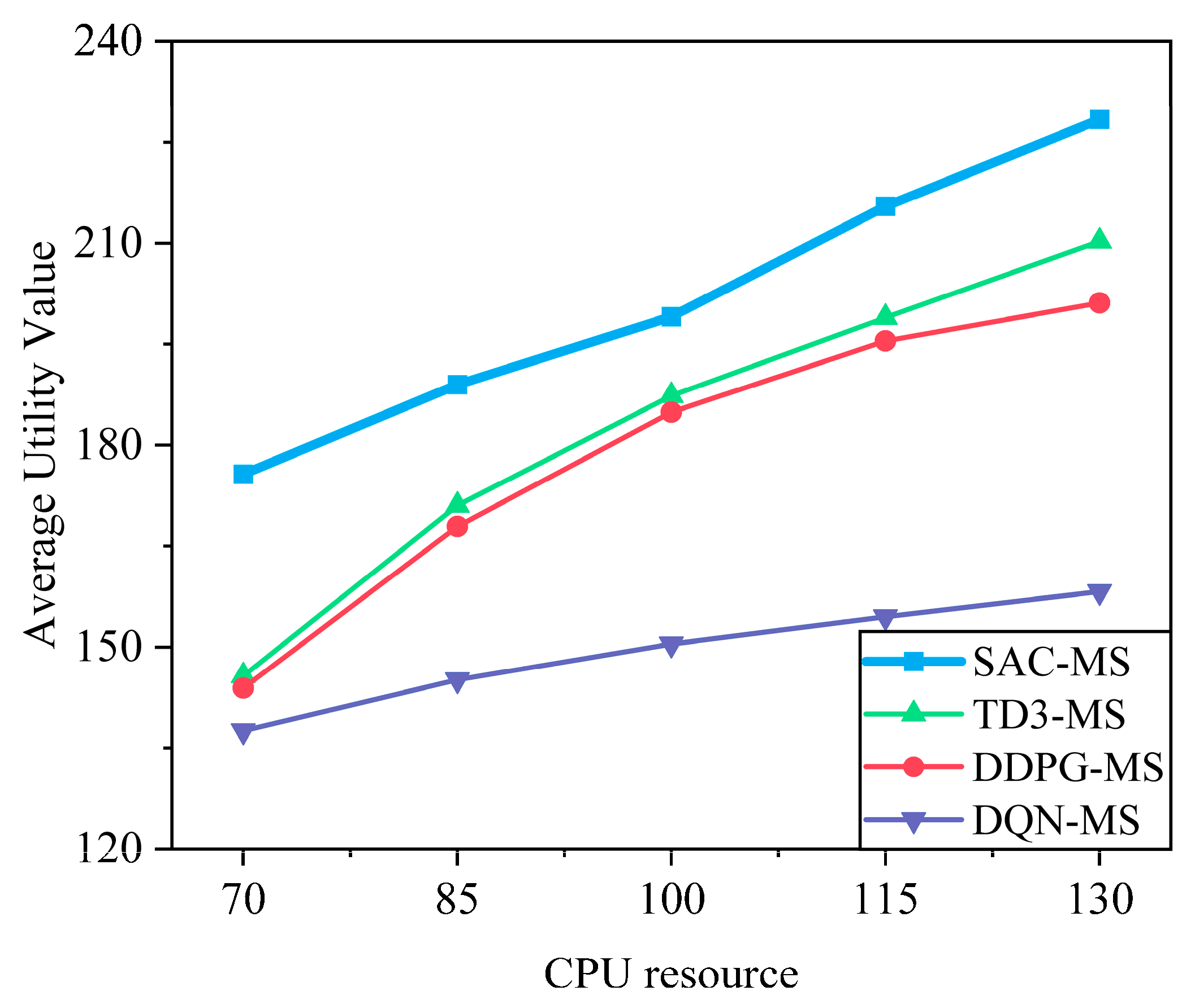
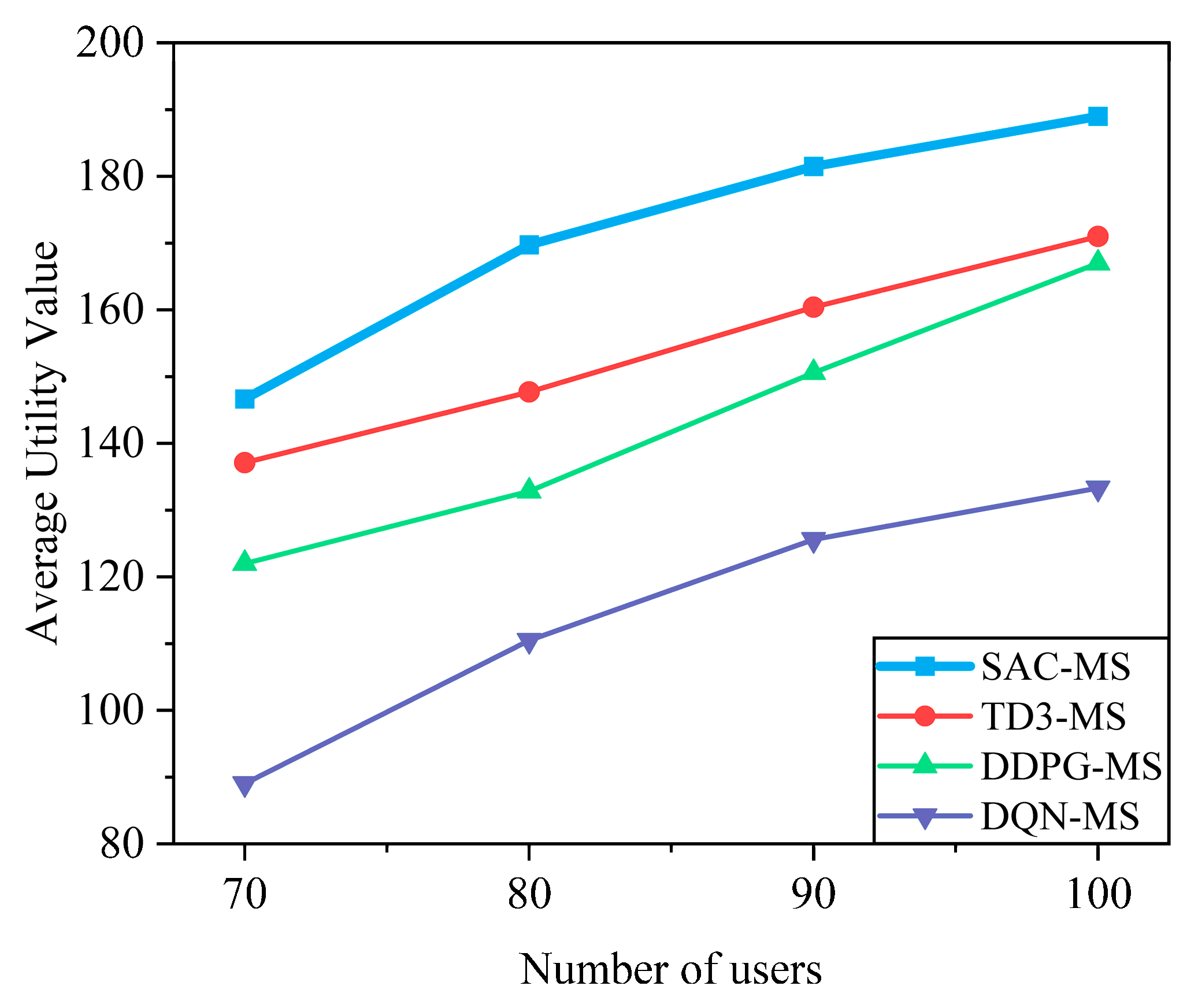
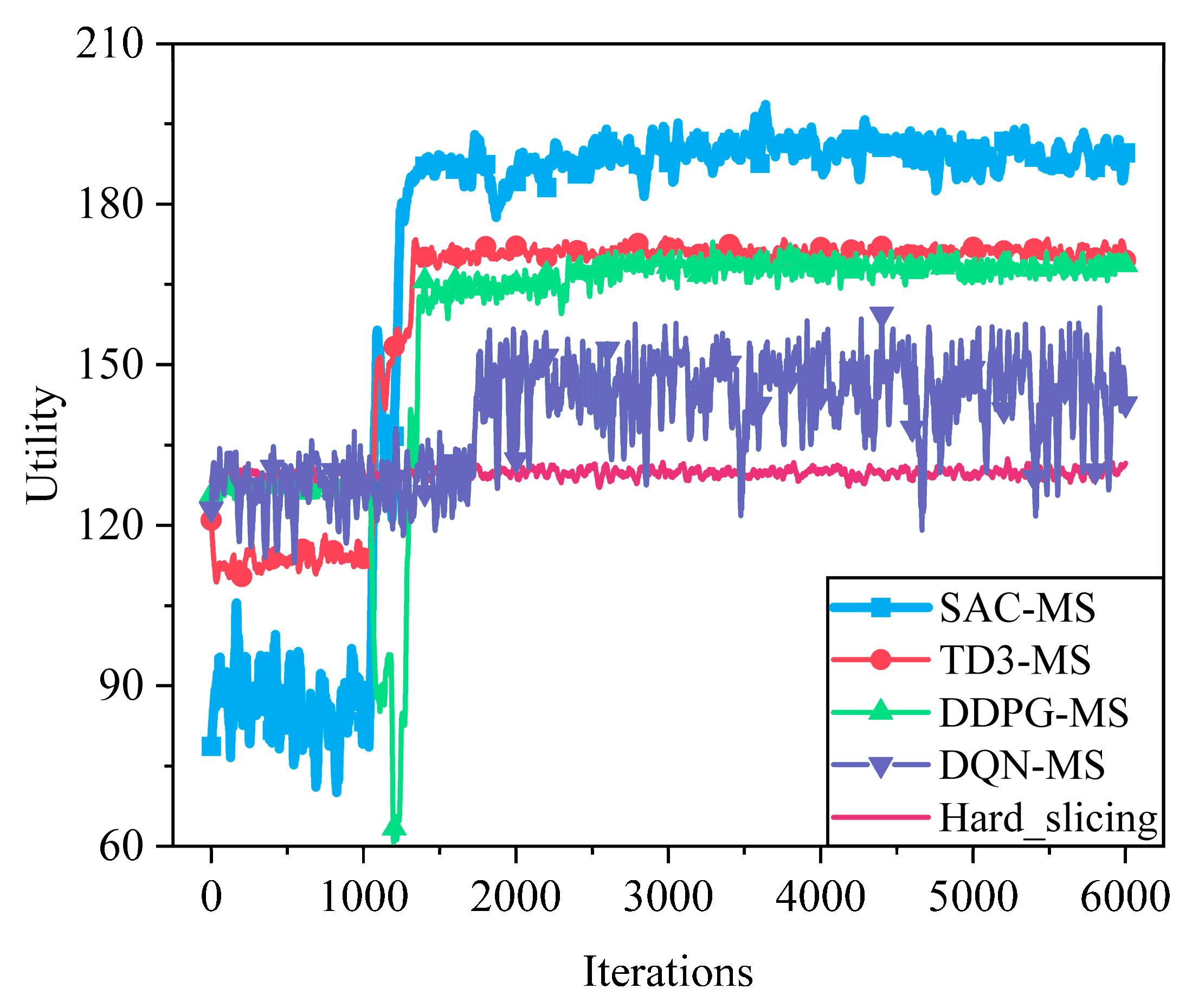
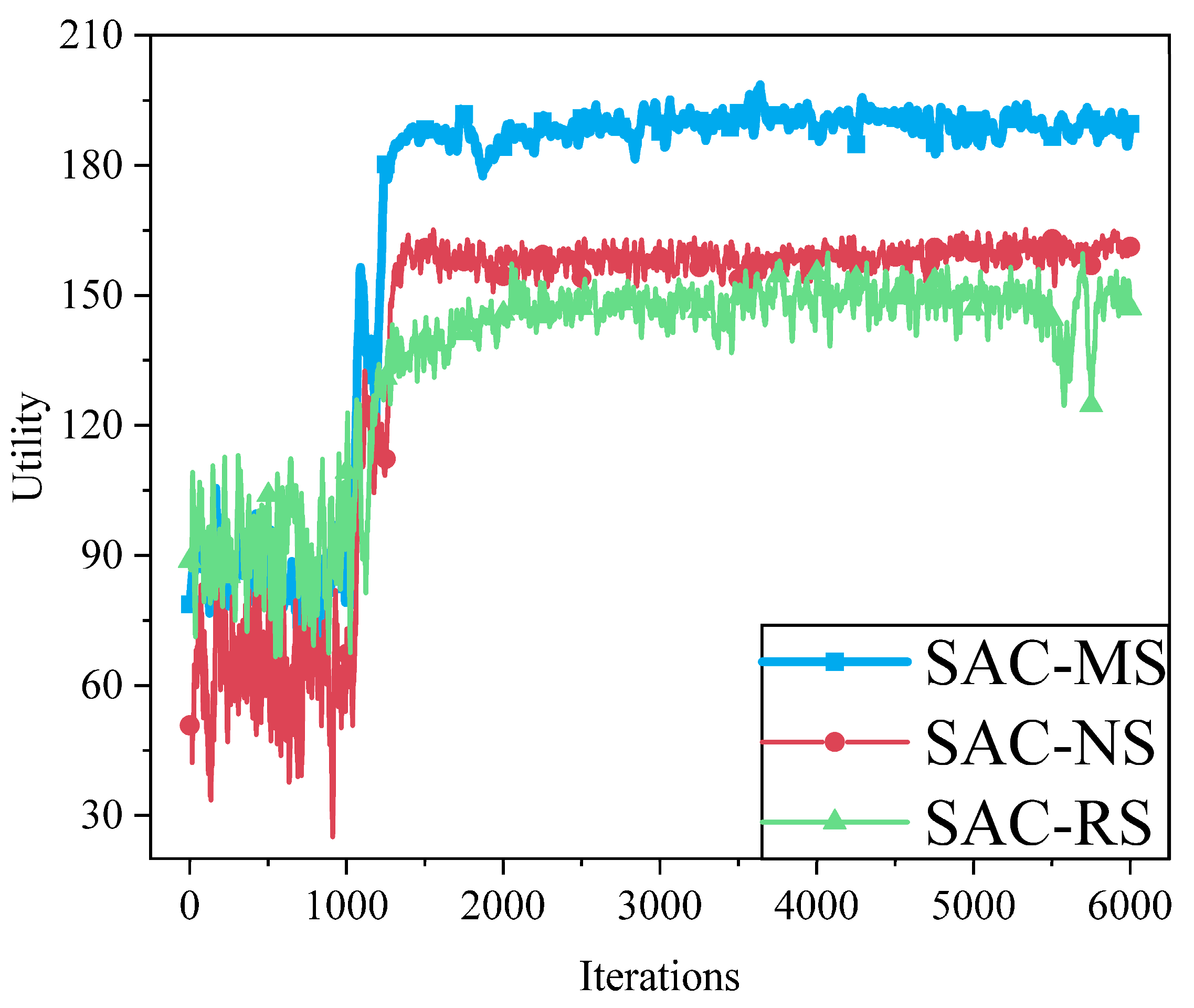
6.2.3. Performance Comparison
7. Discussion and Future Direction
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hossain, A.R.; Ansari, N. Priority-based downlink wireless resource provisioning for radio access network slicing. IEEE Trans. Veh. Technol. 2021, 70, 9273–9281. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6g internet of things: A comprehensive survey. IEEE Internet Things J. 2021, 9, 359–383. [Google Scholar] [CrossRef]
- You, X.; Wang, C.-X.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Huang, Y.; Zhang, C.; Jiang, Y.; Wang, J.; et al. Towards 6g wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, 110301. [Google Scholar] [CrossRef]
- Liu, J.; Du, X.; Cui, J.; Pan, M.; Wei, D. Task-oriented intelligent networking architecture for the space–air–ground–aqua integrated network. IEEE Internet Things J. 2020, 7, 5345–5358. [Google Scholar] [CrossRef]
- Zhou, G.; Zhao, L.; Zheng, G.; Song, S.; Zhang, J.; Hanzo, L. Multi objective optimization of space–air–ground-integrated network slicing relying on a pair of central and distributed learning algorithms. IEEE Internet Things J. 2023, 11, 8327–8344. [Google Scholar] [CrossRef]
- Hu, Z.; Zeng, F.; Xiao, Z.; Fu, B.; Jiang, H.; Xiong, H.; Zhu, Y.; Alazab, M. Joint resources allocation and 3d trajectory optimization for uav-enabled space-air-ground integrated networks. IEEE Trans. Veh. Technol. 2023, 72, 14214–14229. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, Z.; Li, H.; Li, S. Joint power and trajectory design for physical-layer secrecy in the uav-aided mobile relaying system. IEEE Access 2018, 6, 62849–62855. [Google Scholar] [CrossRef]
- Yi, W.; Liu, Y.; Bodanese, E.; Nallanathan, A.; Karagiannidis, G.K. A unified spatial framework for uav-aided mmwave networks. IEEE Trans. Commun. 2019, 67, 8801–8817. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for uav-enabled multiple access. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Sohail, M.F.; Leow, C.Y.; Won, S. Non-orthogonal multiple access for unmanned aerial vehicle assisted communication. IEEE Access 2018, 6, 22716–22727. [Google Scholar] [CrossRef]
- Wang, J.; Liu, M.; Sun, J.; Gui, G.; Gacanin, H.; Sari, H.; Adachi, F. Multiple unmanned-aerial-vehicles deployment and user pairing for nonorthogonal multiple access schemes. IEEE Internet Things J. 2020, 8, 1883–1895. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y.; Hanzo, L. Trajectory design and power control for multi-uav assisted wireless networks: A machine learning approach. IEEE Trans. Veh. Technol. 2019, 68, 7957–7969. [Google Scholar] [CrossRef]
- Zhai, D.; Li, H.; Tang, X.; Zhang, R.; Ding, Z.; Yu, F.R. Height optimization and resource allocation for noma enhanced uav-aided relay networks. IEEE Trans. Commun. 2020, 69, 962–975. [Google Scholar] [CrossRef]
- Wu, P.; Yuan, X.; Hu, Y.; Schmeink, A. Trajectory and user assignment design for uav communication network with no-fly zone. IEEE Trans. Veh. Technol. 2024, 73, 15820–15825. [Google Scholar] [CrossRef]
- Li, R.; Wei, Z.; Yang, L.; Ng, D.W.K.; Yuan, J.; An, J. Resource allocation for secure multi-uav communication systems with multi-eavesdropper. IEEE Trans. Commun. 2020, 68, 4490–4506. [Google Scholar] [CrossRef]
- Gao, Y.; Tang, H.; Li, B.; Yuan, X. Joint trajectory and power design for uav-enabled secure communications with no-fly zone constraints. IEEE Access 2019, 7, 44459–44470. [Google Scholar] [CrossRef]
- Lyu, F.; Yang, P.; Wu, H.; Zhou, C.; Ren, J.; Zhang, Y.; Shen, X. Service-oriented dynamic resource slicing and optimization for space-air-ground integrated vehicular networks. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7469–7483. [Google Scholar] [CrossRef]
- Mao, S.; He, S.; Wu, J. Joint uav position optimization and resource scheduling in space-air-ground integrated networks with mixed cloud-edge computing. IEEE Syst. J. 2020, 15, 3992–4002. [Google Scholar] [CrossRef]
- Cheng, N.; Lyu, F.; Quan, W.; Zhou, C.; He, H.; Shi, W.; Shen, X. Space/aerial-assisted computing offloading for iot applications: A learning-based approach. IEEE J. Sel. Areas Commun. 2019, 37, 1117–1129. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, P.; Kumar, N.; Guizani, M. Space-air-ground integrated network resource allocation based on service function chain. IEEE Trans. Veh. Technol. 2022, 71, 7730–7738. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Y.; Wu, W. Dynamic resource allocation for remote iot data collection in sagin. IEEE Internet Things J. 2024, 11, 20575–20589. [Google Scholar] [CrossRef]
- Gonçalves, D.M.; Bittencourt, L.F.; Madeira, E.R. Overhead and performance of dynamic network slice allocation for mobile users. Future Gener. Comput. Syst. 2024, 160, 739–751. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-uav enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Qin, P.; Wu, X.; Fu, M.; Ding, R.; Fu, Y. Latency minimization resource allocation and trajectory optimization for uav-assisted cache-computing network with energy recharging. IEEE Trans. Commun. 2025, 73, 5715–5728. [Google Scholar] [CrossRef]
- Zhang, Y.; Gang, Y.; Wu, P.; Fan, G.; Xu, W.; Ai, B.; Wu, Q. Integrated sensing, communication, and computation in sagin: Joint beamforming and resource allocation. IEEE Trans. Cogn. Commun. Netw. 2025. [Google Scholar] [CrossRef]
- Qin, P.; Wu, X.; Cai, Z.; Zhao, X.; Fu, Y.; Wang, M.; Geng, S. Joint trajectory plan and resource allocation for uav-enabled c-noma in air-ground integrated 6g heterogeneous network. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3421–3434. [Google Scholar]
- Skouroumounis, C.; Krikidis, I. An evolutionary game for mobile user access mode selection in sub-6 ghz/mmwave cellular networks. IEEE Trans. Wirel. Commun. 2022, 21, 5644–5657. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Liu, Y.; Xu, W.; Nallanathan, A. Cache-enabling uav communications: Network deployment and resource allocation. IEEE Trans. Wirel. Commun. 2020, 19, 7470–7483. [Google Scholar] [CrossRef]
- Zhao, N.; Liang, Y.-C.; Niyato, D.; Pei, Y.; Wu, M.; Jiang, Y. Deep reinforcement learning for user association and resource allocation in heterogeneous cellular networks. IEEE Trans. Wirel. Commun. 2019, 18, 5141–5152. [Google Scholar] [CrossRef]
- Han, Q.; Yang, B.; Miao, G.; Chen, C.; Wang, X.; Guan, X. Backhaul-aware user association and resource allocation for energy-constrained hetnets. IEEE Trans. Veh. Technol. 2016, 66, 580–593. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Le, L.B.; Girard, A. Integrated computation offloading, uav trajectory control, edge-cloud and radio resource allocation in sagin. IEEE Trans. Cloud Comput. 2023, 12, 100–115. [Google Scholar] [CrossRef]
- Wei, Q.; Chen, Y.; Jia, Z.; Bai, W.; Pei, T.; Wu, Q. Energy-efficient caching and user selection for resource-limited sagins in emergency communications. IEEE Trans. Commun. 2024, 73, 4121–4136. [Google Scholar] [CrossRef]
- Chen, G.; Sun, F.; Liang, H.; Zeng, Q.; Zhang, Y.-D. Maddpg-m&l: Uav-assisted joint user association and slicing resource allocation in hetnets. IEEE Trans. Netw. Sci. Eng. 2025, 12, 2878–2894. [Google Scholar]
- Cui, Y.; Shi, H.; Wang, R.; He, P.; Wu, D.; Huang, X. Multi-agent reinforcement learning for slicing resource allocation in vehicular networks. IEEE Trans. Intell. Transp. Syst. 2023, 25, 2005–2016. [Google Scholar] [CrossRef]
- Chen, G.; Qi, S.; Shen, F.; Zeng, Q.; Zhang, Y.-D. Information-aware driven dynamic leo-ran slicing algorithm joint with communication, computing, and caching. IEEE J. Sel. Areas Commun. 2024, 42, 1044–1062. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, Y.; Loo, J.; Yang, D.; Xiao, L. Joint computation and communication design for uav-assisted mobile edge computing in iot. IEEE Trans. Ind. Inform. 2019, 16, 5505–5516. [Google Scholar] [CrossRef]
- Li, R.; Wei, Z.; Yang, L.; Ng, D.W.K.; Yang, N.; Yuan, J.; An, J. Joint trajectory and resource allocation design for uav communication systems. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Lhazmir, S.; Oualhaj, O.A.; Kobbane, A.; Ben-Othman, J. Matching game with no-regret learning for iot energy-efficient associations with uav. IEEE Trans. Green Commun. Netw. 2020, 4, 973–981. [Google Scholar] [CrossRef]
- LeAnh, T.; Tran, N.H.; Saad, W.; Le, L.B.; Niyato, D.; Ho, T.M.; Hong, C.S. Matching theory for distributed user association and resource allocation in cognitive femtocell networks. IEEE Trans. Veh. Technol. 2017, 66, 8413–8428. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.2. March 2014. Available online: http://cvxr.com/cvx (accessed on 15 September 2025).
- Tian, J.; Liu, Q.; Zhang, H.; Wu, D. Multiagent deep-reinforcement-learning-based resource allocation for heterogeneous qos guarantees for vehicular networks. IEEE Internet Things J. 2021, 9, 1683–1695. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, L.; Ye, T.; Sun, W. Computation bits maximization in uav-assisted mec networks with fairness constraint. IEEE Internet Things J. 2022, 9, 20997–21009. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Li, Y.; Sheng, M.; Sun, Y.; Shi, Y. Joint optimization of bs operation, user association, subcarrier assignment, and power allocation for energy-efficient hetnets. IEEE J. Sel. Areas Commun. 2016, 34, 3339–3353. [Google Scholar] [CrossRef]



| Notation | Definition |
|---|---|
| The set of LEO satellite | |
| The set of terrestrial base stations | |
| The set of unmanned aerial vehicle | |
| The set of users associated with slice | |
| The set of all base stations | |
| The set of network slice | |
| The set of No-Fly Zone | |
| The set of bandwidth resources | |
| The set of computing resources | |
| Association variable between user and base station on slice | |
| Bandwidth allocation ratio for slice | |
| Computation resource allocation ratio for slice | |
| Bandwidth allocation ratio from base station to user on slice | |
| Weight coefficients | |
| No-fly zone radius | |
| Path loss exponent | |
| Temperature coefficient | |
| Latency tolerance threshold of slice | |
| Minimum transmission rate threshold |
| Acronyms | Definition |
|---|---|
| SAGIN | Space–Air–Ground Integrated Network |
| UAV | Unmanned Aerial Vehicle |
| LEO | Low Earth Orbit |
| TBS | Terrestrial Base Station |
| MBS | Macro Base Station |
| SBS | Small Base Station |
| NFZ | No-Fly Zone |
| SLS | Latency-Sensitive Slice |
| SLT | Latency-Tolerant Slice |
| SR | High-Data-Rate Slice |
| UA | User Association |
| TO | Trajectory Optimization |
| RA | Resource Allocation |
| SAC | Soft Actor–Critic |
| TD3 | No-fly zone radius |
| DDPG | Deep Deterministic Policy Gradient |
| DQN | Deep Q-Network |
| SAC-MS | Matching game, Sequential Convex Approximation, and Soft Actor–Critic-based Multi-Slice optimization algorithm |
| Related Paper | Objective | UAV | Network Slicing | NFZ | UAV Trajectory Optimization | User Association | Resource Allocation |
|---|---|---|---|---|---|---|---|
| [18] | minimize the maximum computation delay | √ | × | × | √ | × | √ |
| [19] | Minimize the total system cost | √ | × | × | × | × | √ |
| [21] | Maximize the long term network utility | × | × | × | × | × | √ |
| [23] | Maximize the minimum throughput | √ | × | × | √ | √ | × |
| [24] | Minimize the system latency | √ | × | × | √ | × | √ |
| [25] | Maximize the system EE | √ | × | × | √ | × | √ |
| [26] | Minimize the system’s weighted energy consumption | √ | × | × | × | × | √ |
| [27] | SINR, average rate, and mobility-induced time overhead | × | × | × | × | √ | × |
| [28] | Maximizing QoE of users | √ | × | × | √ | √ | √ |
| [29] | Maximum long-term overall network utility | × | × | × | × | √ | √ |
| [30] | Maximize the network utility reflecting proportional fairness | × | × | × | × | √ | √ |
| [31] | Weighting of maximized throughput, SINR and minimized delay | √ | √ | × | × | √ | √ |
| [32] | Minimize the weighted energy consumption | √ | × | × | √ | √ | √ |
| [33] | Maximize the residual energy of the satellite | √ | × | × | × | √ | × |
| Our work | Maximum long-term overall system utility | √ | √ | √ | √ | √ | √ |
| Training Parameters | Value |
|---|---|
| Number of terrestrial base stations | 3 |
| Number of UAV | 1 |
| Number of ground users | 100 |
| UAV flight altitude (m) | 80 |
| Noise Power (dBm) | −174 |
| Learning rate of actor network LR_a | 0.001 |
| Learning rate of critic network LR_c | 0.0015 |
| discount factor | 0.99 |
| entropy coefficient | 0.001 |
| Target network soft update coefficient | 0.005 |
| Replay Buffer Capacity | 100,000 |
| batch size | 128 |
| Max episode | 6000 |
| Convergence threshold | 0.001 |
| Activation function | Tanh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Sun, F.; Jing, G.; Pang, T. SAC-MS: Joint Slice Resource Allocation, User Association and UAV Trajectory Optimization with No-Fly Zone Constraints. Sensors 2025, 25, 5833. https://doi.org/10.3390/s25185833
Chen G, Sun F, Jing G, Pang T. SAC-MS: Joint Slice Resource Allocation, User Association and UAV Trajectory Optimization with No-Fly Zone Constraints. Sensors. 2025; 25(18):5833. https://doi.org/10.3390/s25185833
Chicago/Turabian StyleChen, Geng, Fang Sun, Gang Jing, and Tianyu Pang. 2025. "SAC-MS: Joint Slice Resource Allocation, User Association and UAV Trajectory Optimization with No-Fly Zone Constraints" Sensors 25, no. 18: 5833. https://doi.org/10.3390/s25185833
APA StyleChen, G., Sun, F., Jing, G., & Pang, T. (2025). SAC-MS: Joint Slice Resource Allocation, User Association and UAV Trajectory Optimization with No-Fly Zone Constraints. Sensors, 25(18), 5833. https://doi.org/10.3390/s25185833







