Partitioned RIS-Assisted Vehicular Secure Communication Based on Meta-Learning and Reinforcement Learning
Abstract
1. Introduction
1.1. Background
1.2. Motivation
1.3. Our Method and Main Contributions
- We investigate a partitioned RIS aided wireless VANET, where the source station transmits both confidential messages and AN. The partitioned RIS elements are configured to reflect the legitimate signals toward the intended vehicular receiver and direct the AN toward the eavesdropper. The wireless communication network’s overall secrecy performance is strengthened by this dual-reflection technique, which improves the signal strength for the authorized vehicular user while amplifying the AN’s disruptive effect on eavesdropper.
- We propose a secure communication scheme that integrates a meta-learning based partitioning method with reinforcement learning based optimization of the RIS reflection matrix for dynamic eavesdropping environments. Specifically, when encountering a new eavesdropping scenario, the meta-learning model rapidly determines the optimal RIS partitioning ratio to balance the reflection of legitimate signals and artificial noise. Subsequently, reinforcement learning is utilized to optimize beamforming as well as RIS reflection matrixes, thereby making the wireless communication network as secure as possible.
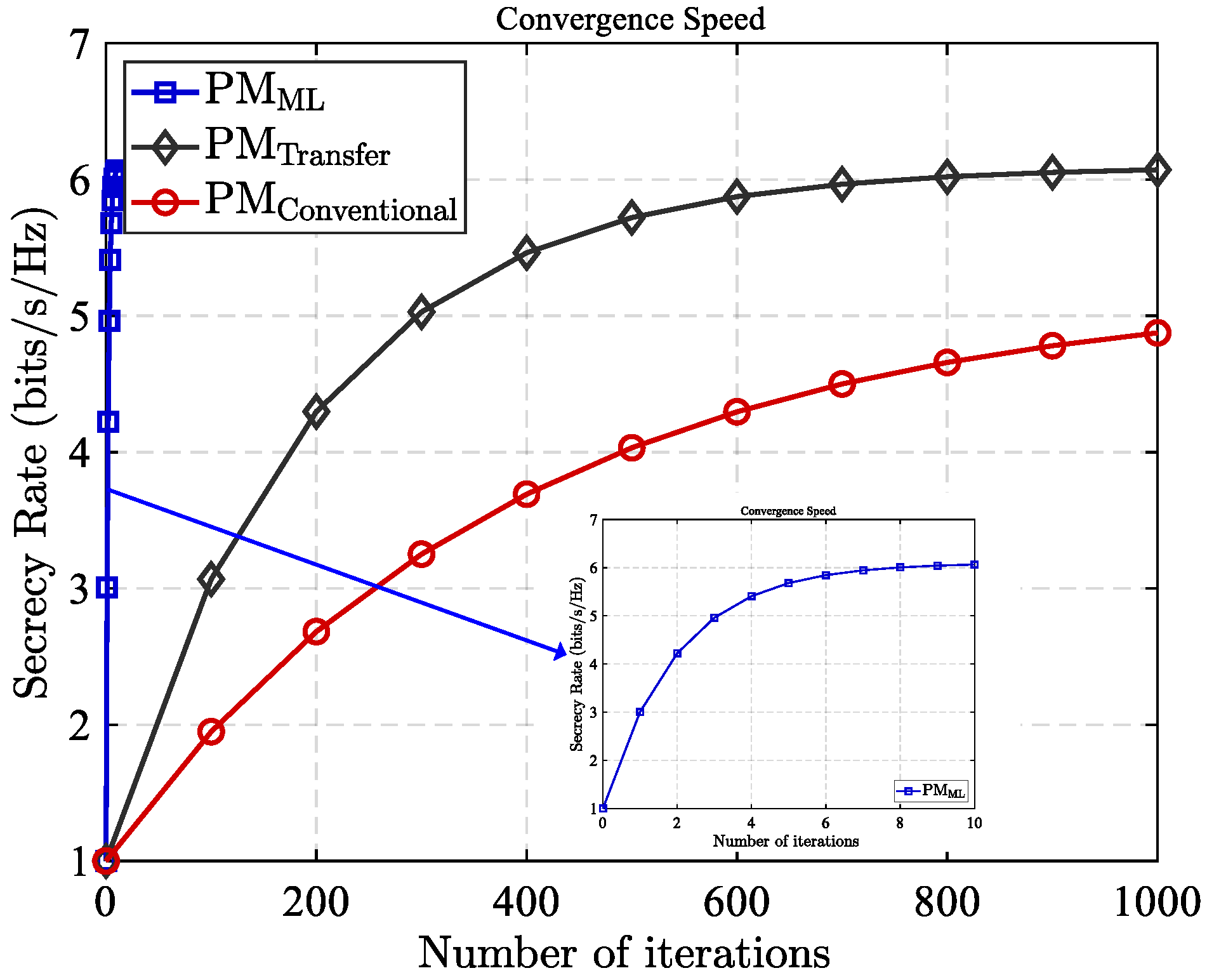
- We conduct comprehensive simulation experiments to confirm the suggested scheme’s efficacy in enhancing communication security under dynamic eavesdropping conditions. Compared to traditional RIS-assisted wireless systems, our approach exhibits significantly improved secure communication performance. Moreover, the meta-learning based partitioning method demonstrates faster convergence than conventional deep learning techniques, enabling better adaptability to rapidly changing eavesdropping environments.
1.4. Related Work
2. System Model
2.1. Signal Transmission Model
2.2. Secrecy Rate Maximization Formulation
2.2.1. Secrecy Rate
2.2.2. Secrecy Rate Maximization
2.2.3. Optimization of Beamforming Vectors via Semidefinite Relaxation
2.3. Beamforming and Partitioned Optimization Based on Meta-Learning and Reinforcement Learning
- Environment Initialization: System parameters, such as CSI, location of possible eavesdroppers, and reconfigurable intelligent surface (RIS) configuration settings are gathered to initialize the state of the communication environment.
- Meta-Learning Inference (MLBPM): a model-agnostic meta-learning (MAML) model, which has been pre-trained, is utilized to infer the optimal RIS partitioning ratio from the observed channel state information (CSI). This enables rapid adaptation to evolving eavesdropping threats.
- State Augmentation: The inferred optimal partitioning ratio is integrated with historical channel state information and the present RIS reflection configuration to form a holistic state representation for the reinforcement learning process.
- MADDPG Optimization: Employing the augmented state representation, MADDPG agents optimize both the beamforming vectors and RIS reflection matrices. Actor networks generate the corresponding actions, whereas critic networks assess their efficacy using the achieved secrecy rate as the reward metric.
- Actor Networks: Decentralized actor networks dynamically adjust beamforming vectors and reflection coefficients, enabling real-time optimization that ensures scalability in large-scale reconfigurable intelligent surface (RIS) implementations.
- Critic Networks: Centralized critic networks assess the collective actions by leveraging global channel state information (CSI) and deliver evaluative feedback to the actor networks, thereby facilitating and directing the overall learning trajectory.
- Execution and Optimization: The optimized parameters including the RIS partitioning ratio, reflection coefficients, and beamforming vectors are deployed to significantly improve communication secrecy.
- Online Update: The environment is persistently monitored for dynamic variations, such as shifts in eavesdropper position. Substantial changes initiate a feedback loop to the meta-learning inference phase, prompting re-optimization to maintain rapid, low-latency adaptive performance.
2.3.1. Meta-Learning
2.3.2. Model-Agnostic Meta-Learning (MAML)
2.3.3. Meta-Learning Based Partitioning Method (MLBPM)
- Support Set: For every task , the support set comprises K paired examples (conforming to a K-shot learning setup), with each pair represented as , where denotes the training CSI feature vector. These examples facilitate the inner-loop adaptation process.
- Query Set: The query set for task consists of distinct instances, denoted as , where represents the test CSI feature vector. These instances are utilized to compute the meta-loss and update the master model, thereby enhancing its generalization capability across tasks.
- Input: A formatted tensor representing the composite CSI (e.g., , etc.).
- Architecture:
- -
- Convolutional Layers: The architecture consists of three successive layers employing 32, 64, and 128 filters. Each layer integrates a convolutional kernel, a ReLU activation function, and is subsequently followed by a max-pooling operation.
- -
- Flattening: The feature maps from the last convolutional layer are flattened into a one-dimensional vector.
- -
- Fully Connected (Dense) Layers: Two fully connected layers subsequently process these features: the first contains 128 units with ReLU activation, followed by a second layer comprising 64 units, also utilizing ReLU activation.
- -
- Output Layer: A concluding dense layer, equipped with a single neuron and a sigmoid activation function, generates the predicted partitioning ratio .
- Loss Function: The mean squared error (MSE) serves as loss function for each task:
2.3.4. Multiobjective Optimization Based on the Markov Game
2.3.5. Beamforming and Reflection Matrix Coefficients Optimization Based on MADDPG
| Algorithm 1 MADDPG algorithm. |
|
| Algorithm 2 Joint meta-learning partitioning and MADDPG optimization pipeline. |
|
2.3.6. Clarification on the Multi-Agent MADDPG Framework
- Agent Definition: The RIS elements are partitioned into G groups. Each agent is assigned to control the reflection coefficients (phase and amplitude) for all elements within its respective group. This strategy significantly reduces the per-agent action space dimensionality, making the learning process tractable and efficient.
- Centralized Training with Decentralized Execution (CTDE):
- -
- Centralized Critic: Throughout the training process, the critic network for each agent utilizes global state, such as complete CSI, along with the actions taken by every other agent. This allows the critic to assess the joint action’s impact on the global reward (the system secrecy rate ).
- -
- Decentralized Actors: Each actor network only requires the local observations of its agent (e.g., the CSI relevant to its group of RIS elements). This enables decentralized execution during operation, which is crucial for real-time implementation.
- Collaborative Goal: All agents share a common, cooperative reward . This aligns their objectives, encouraging collaborative behavior to maximize the global security performance. The beamforming vectors and are included in the joint action space and are optimized concurrently by the agents.
2.4. Complexity and Convergence Analysis
2.4.1. Theoretical Complexity Analysis
- Inner-Loop Adaptation: For a previously unseen eavesdropping scenario (task ), the model executes N gradient steps using a support set containing K examples. Computational complexity for the inner-loop adaptation is . Given that both N and K are generally small (e.g., , ), this adaptation process remains computationally efficient.
- Meta-Updating (Meta-Training): The meta update phase requires calculating gradients through the inner loop adaptation across a batch of tasks, involving second-order derivatives with a complexity of per task. Although more computationally intensive than conventional training, this is a single offline procedure. Subsequent online inference for new tasks solely relies on the efficient inner loop adaptation, ensuring low computational overhead during deployment.
- Centralized Critic Update: The critic network for each agent is updated utilizing global state and action information. The computational complexity for a single gradient update of one critic is . Consequently, for a system with A agents, the total complexity per training step amounts to .
- Actor Update: Each actor network is updated via a policy gradient step guided by its respective critic’s output, with a computational complexity of per agent. The aggregate complexity for updating all actors is .
2.4.2. Empirical Runtime and Scaling Performance
3. Simulation Results
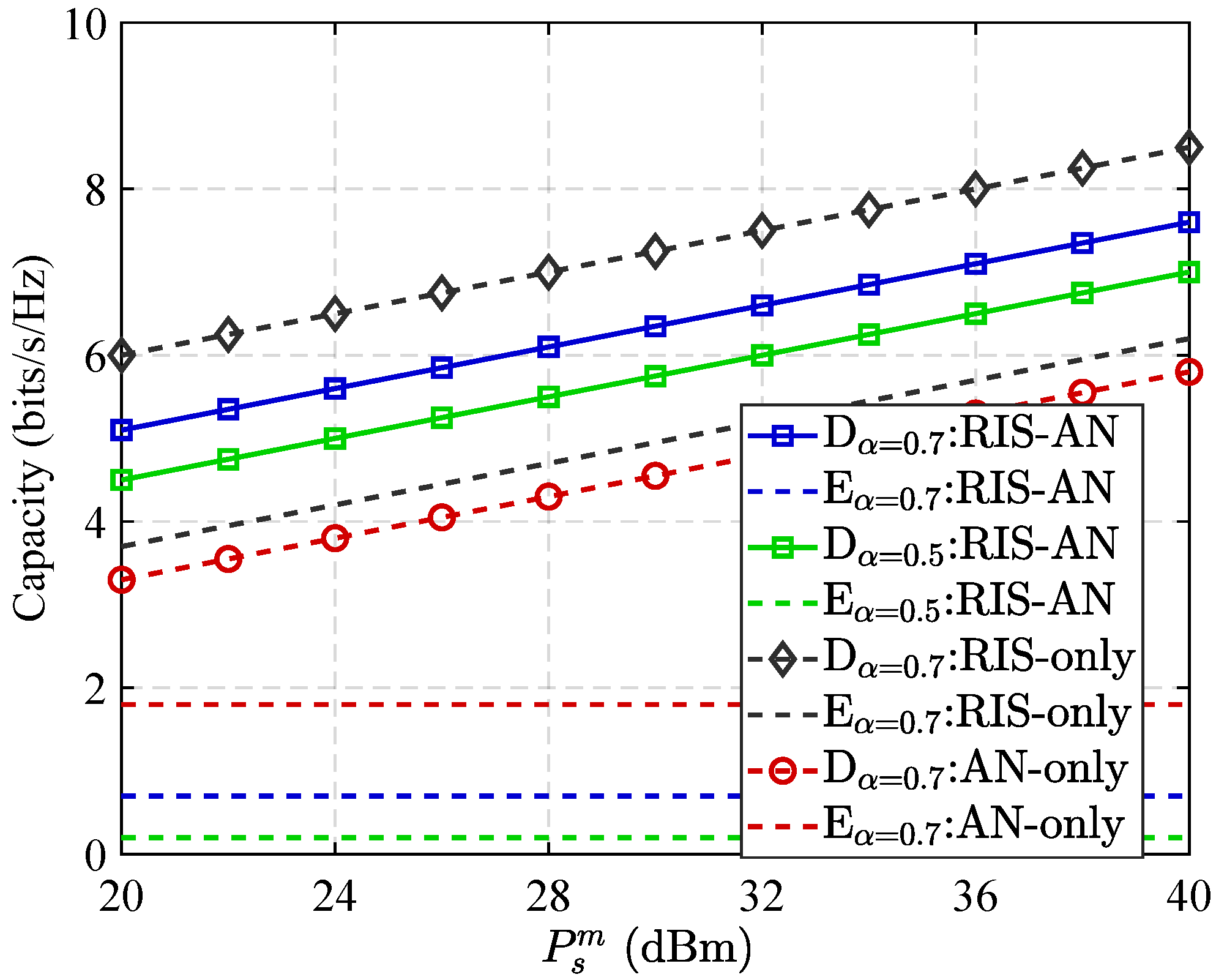
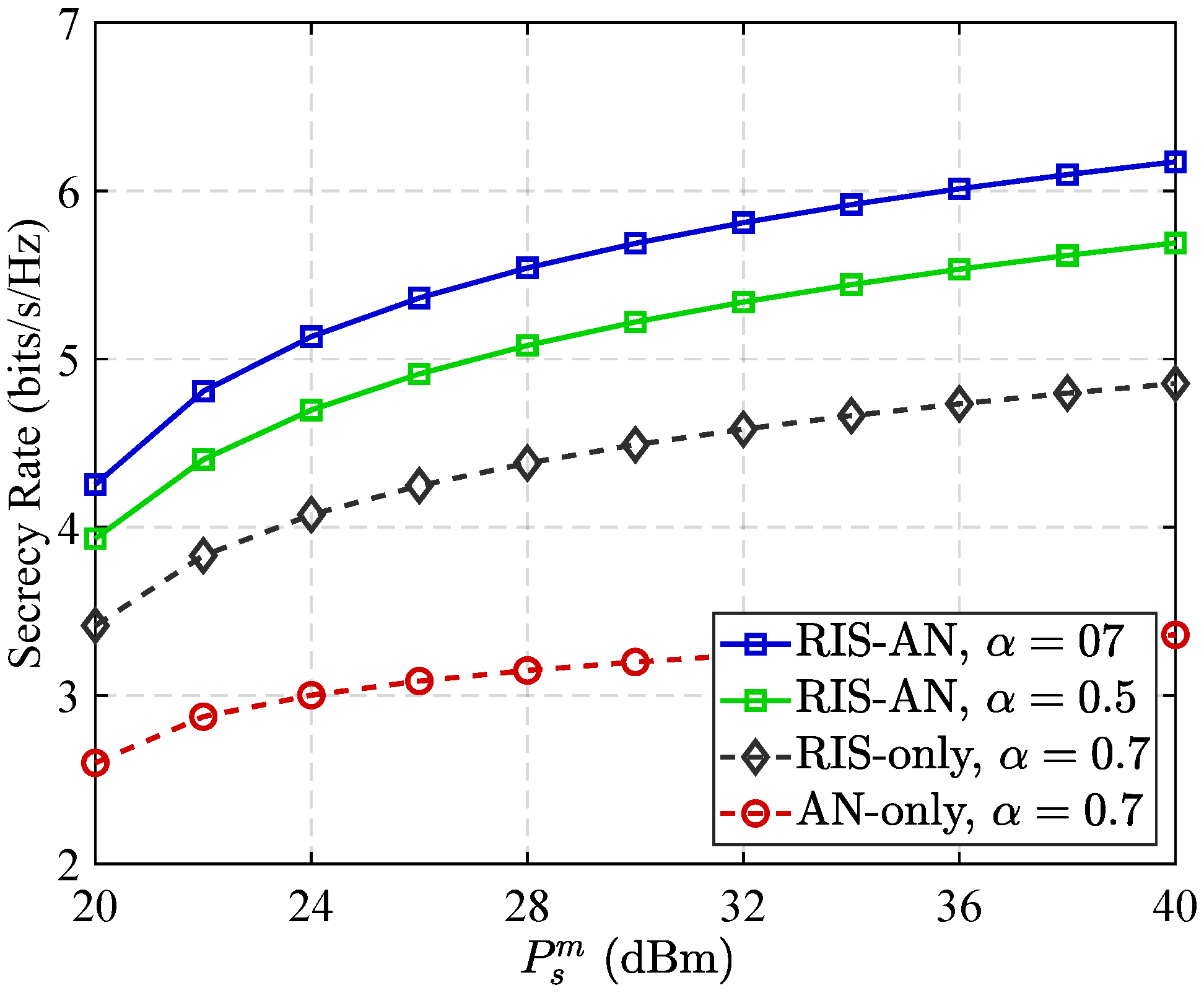
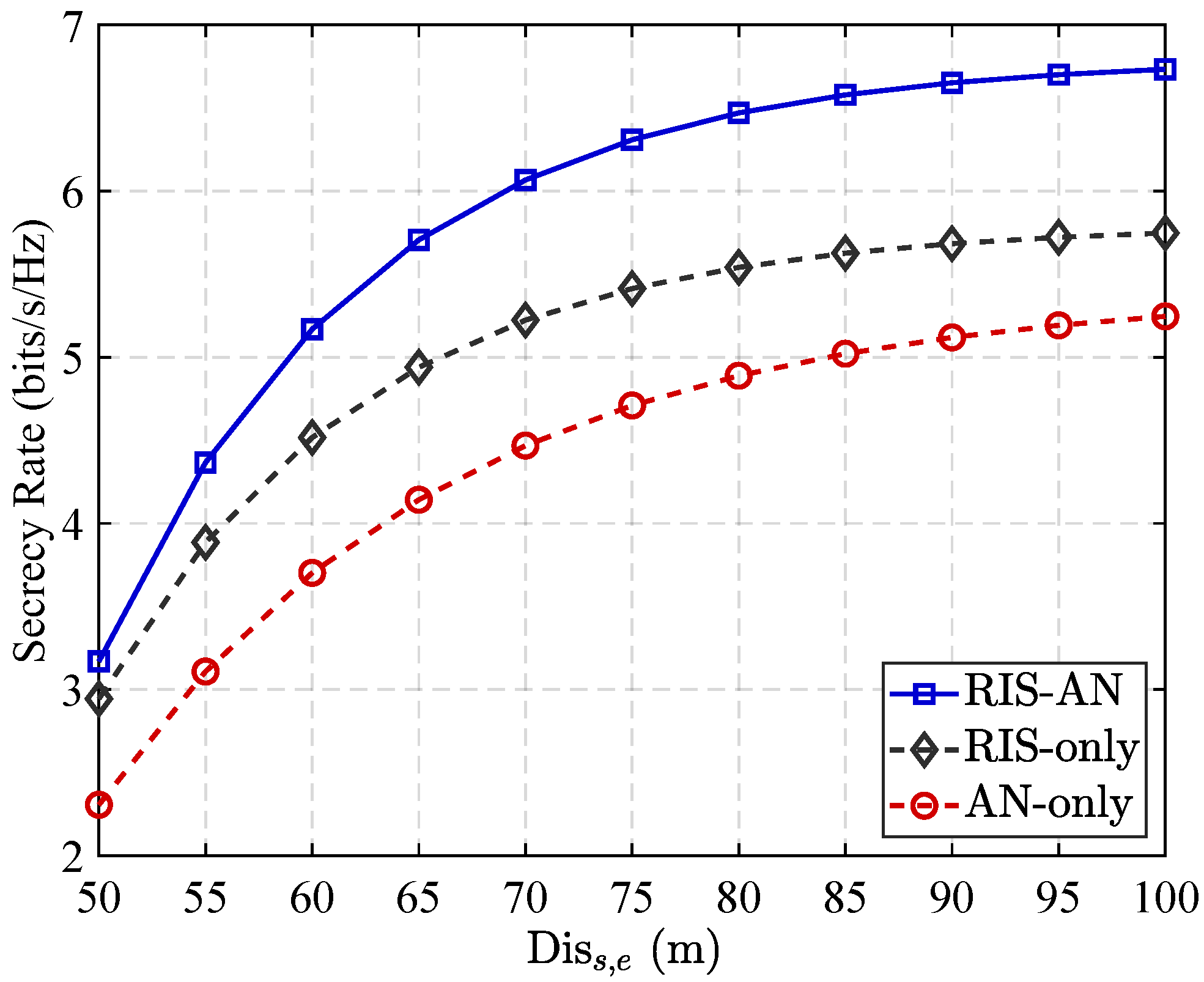
3.1. Capacity and Secrecy Rate Performance in Different Communication Scenarios
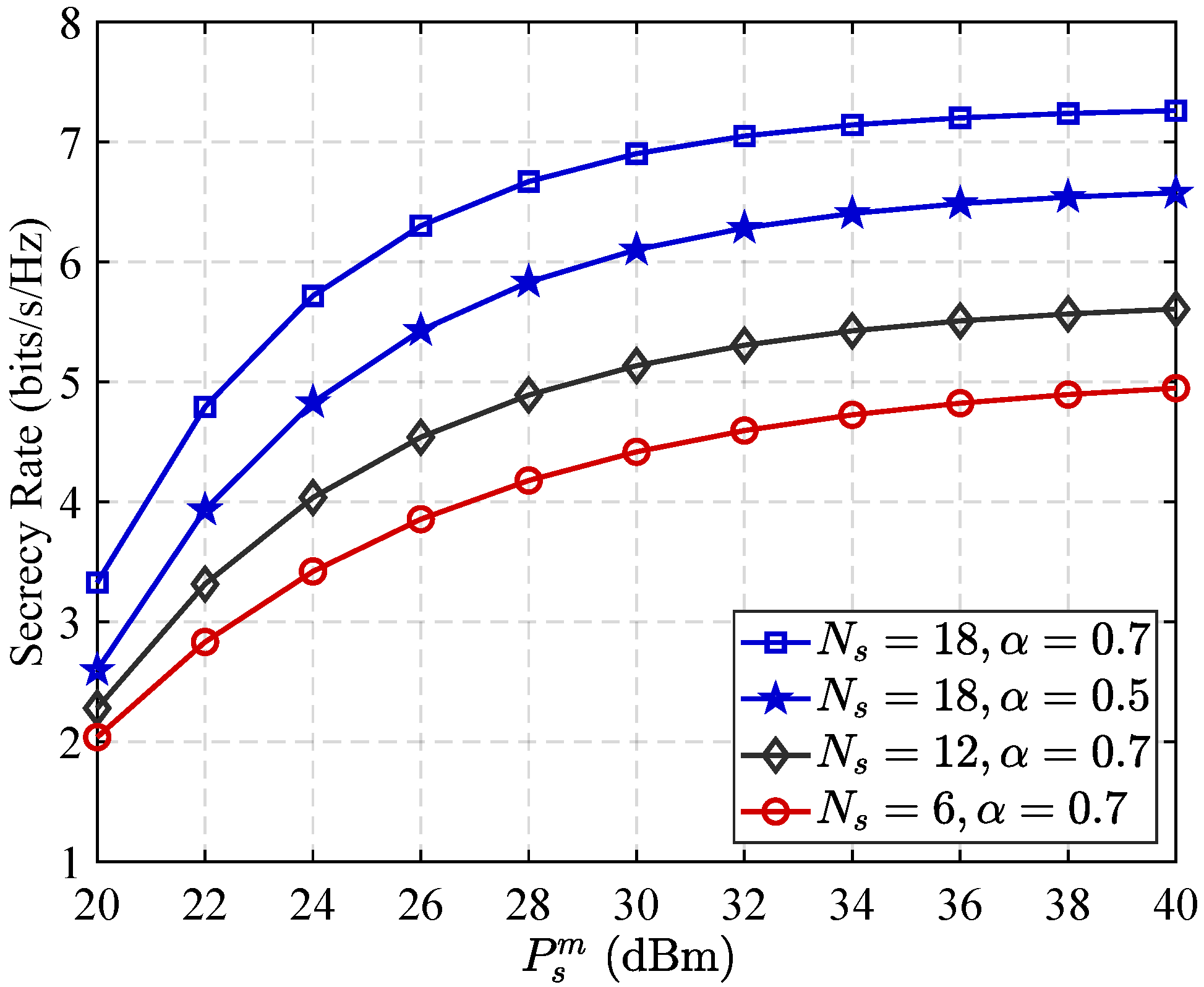
3.2. Scalability Analysis with RIS Size
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Love, D.J.; Krogmeier, J.V.; Anderson, C.R.; Heath, R.W.; Buckmaster, D.R. Challenges and opportunities of future rural wireless communications. IEEE Commun. Mag. 2022, 59, 16–22. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, W.; Zhang, R. Movable antennas for wireless communication: Opportunities and challenges. IEEE Commun. Mag. 2023, 62, 114–120. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, D.; Du, Y.; You, C.; Zhang, J.; Huang, K. Toward an intelligent edge: Wireless communication meets machine learning. IEEE Commun. Mag. 2020, 58, 19–25. [Google Scholar] [CrossRef]
- Wen, Y.; Huo, Y.; Ma, L.; Jing, T.; Gao, Q. Quantitative models for friendly jammer trustworthiness evaluation in IoT networks. Ad Hoc Netw. 2022, 137, 102994. [Google Scholar]
- Akyildiz, I.F.; Kak, A.; Nie, S. 6G and beyond: The future of wireless communications systems. IEEE Access 2020, 8, 133995–134030. [Google Scholar] [CrossRef]
- Mucchi, L.; Jayousi, S.; Caputo, S.; Panayirci, E.; Shahabuddin, S.; Bechtold, J.; Morales, I.; Stoica, R.A.; Abreu, G.; Haas, H. Physical-layer security in 6G networks. IEEE Open J. Commun. Soc. 2021, 2, 1901–1914. [Google Scholar] [CrossRef]
- Xie, N.; Li, Z.; Tan, H. A survey of physical-layer authentication in wireless communications. IEEE Commun. Surv. Tutor. 2020, 23, 282–310. [Google Scholar]
- Wen, Y.; Huo, Y.; Ma, L.; Jing, T.; Gao, Q. A scheme for trustworthy friendly jammer selection in cooperative cognitive radio networks. IEEE Trans. Veh. Technol. 2019, 68, 3500–3512. [Google Scholar] [CrossRef]
- Ye, R.; Peng, Y.; Al-Hazemi, F.; Boutaba, R. A robust cooperative jamming scheme for secure UAV communication via intelligent reflecting surface. IEEE Trans. Commun. 2023, 72, 1005–1019. [Google Scholar] [CrossRef]
- Zheng, T.X.; Yang, Z.; Wang, C.; Li, Z.; Yuan, J.; Guan, X. Wireless covert communications aided by distributed cooperative jamming over slow fading channels. IEEE Trans. Wirel. Commun. 2021, 20, 7026–7039. [Google Scholar] [CrossRef]
- Hong, S.; Pan, C.; Ren, H.; Wang, K.; Nallanathan, A. Artificial-noise-aided secure MIMO wireless communications via intelligent reflecting surface. IEEE Trans. Commun. 2020, 68, 7851–7866. [Google Scholar]
- Wen, Y.; Liu, L.; Li, J.; Li, Y.; Wang, K.; Yu, S.; Guizani, M. Covert communications aided by cooperative jamming in overlay cognitive radio networks. IEEE Trans. Mob. Comput. 2024, 23, 12878–12891. [Google Scholar] [CrossRef]
- Wen, Y.; Jing, T.; Gao, Q. Trustworthy Jammer Selection with Truth-Telling for Wireless Cooperative Systems. Wirel. Commun. Mob. Comput. 2021, 2021, 6626355. [Google Scholar]
- Wen, Y.; Wang, F.; Wang, H.M.; Li, J.; Qian, J.; Wang, K.; Wang, H. Cooperative Jamming Aided Secure Communication for RIS Enabled Symbiotic Radio Systems. IEEE Trans. Commun. 2024, 73, 2936–2949. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J.; Xie, W.; Hasna, M.O.; Tsiftsis, T.; Di Renzo, M. Secrecy performance analysis of RIS-aided wireless communication systems. IEEE Trans. Veh. Technol. 2020, 69, 12296–12300. [Google Scholar] [CrossRef]
- Mu, X.; Liu, Y.; Guo, L.; Lin, J.; Schober, R. Simultaneously transmitting and reflecting (STAR) RIS aided wireless communications. IEEE Trans. Wirel. Commun. 2021, 21, 3083–3098. [Google Scholar] [CrossRef]
- Pogaku, A.C.; Do, D.T.; Lee, B.M.; Nguyen, N.D. UAV-assisted RIS for future wireless communications: A survey on optimization and performance analysis. IEEE Access 2022, 10, 16320–16336. [Google Scholar] [CrossRef]
- Cao, X.; Başar, T. Distributed constrained online convex optimization over multiple access fading channels. IEEE Trans. Signal Process. 2022, 70, 3468–3483. [Google Scholar] [CrossRef]
- Amiriara, H.; Ashtiani, F.; Mirmohseni, M.; Nasiri-Kenari, M. Irs-user association in irs-aided miso wireless networks: Convex optimization and machine learning approaches. IEEE Trans. Veh. Technol. 2023, 72, 14305–14316. [Google Scholar]
- Feng, K.; Wang, Q.; Li, X.; Wen, C.K. Deep reinforcement learning based intelligent reflecting surface optimization for MISO communication systems. IEEE Wirel. Commun. Lett. 2020, 9, 745–749. [Google Scholar] [CrossRef]
- Lu, X.; Xiao, L.; Dai, C.; Dai, H. UAV-aided cellular communications with deep reinforcement learning against jamming. IEEE Wirel. Commun. 2020, 27, 48–53. [Google Scholar] [CrossRef]
- Feriani, A.; Hossain, E. Single and multi-agent deep reinforcement learning for AI-enabled wireless networks: A tutorial. IEEE Commun. Surv. Tutor. 2021, 23, 1226–1252. [Google Scholar] [CrossRef]
- Hu, S.; Chen, X.; Ni, W.; Hossain, E.; Wang, X. Distributed machine learning for wireless communication networks: Techniques, architectures, and applications. IEEE Commun. Surv. Tutor. 2021, 23, 1458–1493. [Google Scholar]
- Huo, Y.; Wu, Y.; Li, R.; Gao, Q.; Luo, X. A learning-aided intermittent cooperative jamming scheme for nonslotted wireless transmission in an IoT system. IEEE Internet Things J. 2021, 9, 9354–9366. [Google Scholar] [CrossRef]
- Tusha, A.; Arslan, H. Interference burden in wireless communications: A comprehensive survey from PHY layer perspective. IEEE Commun. Surv. Tutor. 2024, 27, 2204–2246. [Google Scholar] [CrossRef]
- Dai, L.; Huang, H.; Zhang, C.; Qiu, K. Silent flickering RIS aided covert attacks via intermittent cooperative jamming. IEEE Wirel. Commun. Lett. 2023, 12, 1027–1031. [Google Scholar] [CrossRef]
- Arzykulov, S.; Celik, A.; Nauryzbayev, G.; Eltawil, A.M. Artificial noise and RIS-aided physical layer security: Optimal RIS partitioning and power control. IEEE Wirel. Commun. Lett. 2023, 12, 992–996. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, J.; Ma, Y.; Yang, C. Meta-learning for wireless communications: A survey and a comparison to gnns. IEEE Open J. Commun. Soc. 2024, 5, 1987–2015. [Google Scholar] [CrossRef]
- Cai, C.; Yuan, X.; Zhang, Y.J.A. RIS partitioning based scalable beamforming design for large-scale MIMO: Asymptotic analysis and optimization. IEEE Trans. Wirel. Commun. 2023, 22, 6061–6077. [Google Scholar] [CrossRef]
- Chen, P.; Li, X.; Matthaiou, M.; Jin, S. DRL-based RIS phase shift design for OFDM communication systems. IEEE Wirel. Commun. Lett. 2023, 12, 733–737. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, L.; Li, J.; Hou, X.; Zhang, N.; Dong, M.; Atiquzzaman, M.; Wang, K.; Huo, Y. A covert jamming scheme against an intelligent eavesdropper in cooperative cognitive radio networks. IEEE Trans. Veh. Technol. 2023, 72, 13243–13254. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J.; Wang, H.; Han, C.; Chen, G.; Du, J.; Hu, C.; Mumtaz, S. Physical layer security for wireless-powered ambient backscatter cooperative communication networks. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 927–939. [Google Scholar] [CrossRef]
- Su, N.; Liu, F.; Masouros, C. Sensing-assisted eavesdropper estimation: An ISAC breakthrough in physical layer security. IEEE Trans. Wirel. Commun. 2023, 23, 3162–3174. [Google Scholar] [CrossRef]
- Saggese, F.; Croisfelt, V.; Kotaba, R.; Stylianopoulos, K.; Alexandropoulos, G.C.; Popovski, P. On the impact of control signaling in RIS-empowered wireless communications. IEEE Open J. Commun. Soc. 2024, 5, 4383–4399. [Google Scholar] [CrossRef]
- Chapala, V.K.; Zafaruddin, S.M. Intelligent connectivity through RIS-assisted wireless communication: Exact performance analysis with phase errors and mobility. IEEE Trans. Intell. Veh. 2023, 8, 4445–4459. [Google Scholar] [CrossRef]
- Liang, J.C.; Zhang, L.; Luo, Z.; Jiang, R.Z.; Cheng, Z.W.; Wang, S.R.; Sun, M.K.; Jin, S.; Cheng, Q.; Cui, T.J. A filtering reconfigurable intelligent surface for interference-free wireless communications. Nat. Commun. 2024, 15, 3838. [Google Scholar] [CrossRef]
- Aung, P.S.; Park, Y.M.; Tun, Y.K.; Han, Z.; Hong, C.S. Energy-efficient communication networks via multiple aerial reconfigurable intelligent surfaces: DRL and optimization approach. IEEE Trans. Veh. Technol. 2023, 73, 4277–4292. [Google Scholar] [CrossRef]
- Zhang, S.; Bao, S.; Chi, K.; Yu, K.; Mumtaz, S. DRL-based computation rate maximization for wireless powered multi-AP edge computing. IEEE Trans. Commun. 2023, 72, 1105–1118. [Google Scholar] [CrossRef]
- Luo, Z.-Q.; Ma, W.-K.; So, A.M.-C.; Ye, Y.; Zhang, S. Semidefinite relaxation of quadratic optimization problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Ahmed, M.; Raza, S.; Soofi, A.A.; Khan, F.; Khan, W.U.; Abideen, S.Z.U.; Xu, F.; Han, Z. Active reconfigurable intelligent surfaces: Expanding the frontiers of wireless communication-a survey. IEEE Commun. Surv. Tutor. 2024, 27, 839–869. [Google Scholar] [CrossRef]





| Method | Mean Runtime (s) | Std Dev (s) |
|---|---|---|
| Proposed (MLBPM-MADDPG) | 0.95 | 0.07 |
| Standalone MADDPG (Transfer) | 1.82 | 0.13 |
| SDR-MADDPG | 4.31 | 0.25 |
| Simulation Parameter | Value |
|---|---|
| The maximum power of S (dBm) | 30 |
| The number of antennas of S | 8 |
| The number of elements of the partitioned RIS | 18 |
| The distances between S to D (m) | 100 |
| The distances between S to E (m) | 90 |
| Noise power spectral density (dBm/Hz) | −127 |
| Transmission bandwidth B (MHz) | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, F.; Qian, J.; Zhu, P.; Zhou, A. Partitioned RIS-Assisted Vehicular Secure Communication Based on Meta-Learning and Reinforcement Learning. Sensors 2025, 25, 5874. https://doi.org/10.3390/s25185874
Li H, Wang F, Qian J, Zhu P, Zhou A. Partitioned RIS-Assisted Vehicular Secure Communication Based on Meta-Learning and Reinforcement Learning. Sensors. 2025; 25(18):5874. https://doi.org/10.3390/s25185874
Chicago/Turabian StyleLi, Hui, Fengshuan Wang, Jin Qian, Pengcheng Zhu, and Aiping Zhou. 2025. "Partitioned RIS-Assisted Vehicular Secure Communication Based on Meta-Learning and Reinforcement Learning" Sensors 25, no. 18: 5874. https://doi.org/10.3390/s25185874
APA StyleLi, H., Wang, F., Qian, J., Zhu, P., & Zhou, A. (2025). Partitioned RIS-Assisted Vehicular Secure Communication Based on Meta-Learning and Reinforcement Learning. Sensors, 25(18), 5874. https://doi.org/10.3390/s25185874







