MultivariateSystem Identification of Differential Drive Robot: Comparison Between State-Space and LSTM-Based Models
Abstract
1. Introduction
2. Review of the State-of-the-Art
3. Methodology
3.1. Mobile Robotic Platform
3.2. Experimental Data Collection
3.3. Evaluation Metrics
3.4. State-Space Model (SSM)
- Order 2. This is the minimum reasonable order for this modeling approach, which can capture the relationships between the input velocity (, ) and the actual velocities (v, ). It can also include some effect of inertia and delay in response.
- Order 3. This is a more detailed model that may capture accelerations and decelerations of the robot. It could be useful if the robot has a slower dynamic or if there are mechanical delays in its response.
- Order 4. This can capture additional effects such as friction, sliding, or external disturbances, but could be more accurate. However, the model becomes more complex and less interpretable.
- Order 5. This is a highly detailed model that could capture more complex nonlinear dynamics. This is rarely used unless the robot has complicated dynamics, as it can over-fit the data.
3.5. Recurrent Neural Network Model (LSTM)
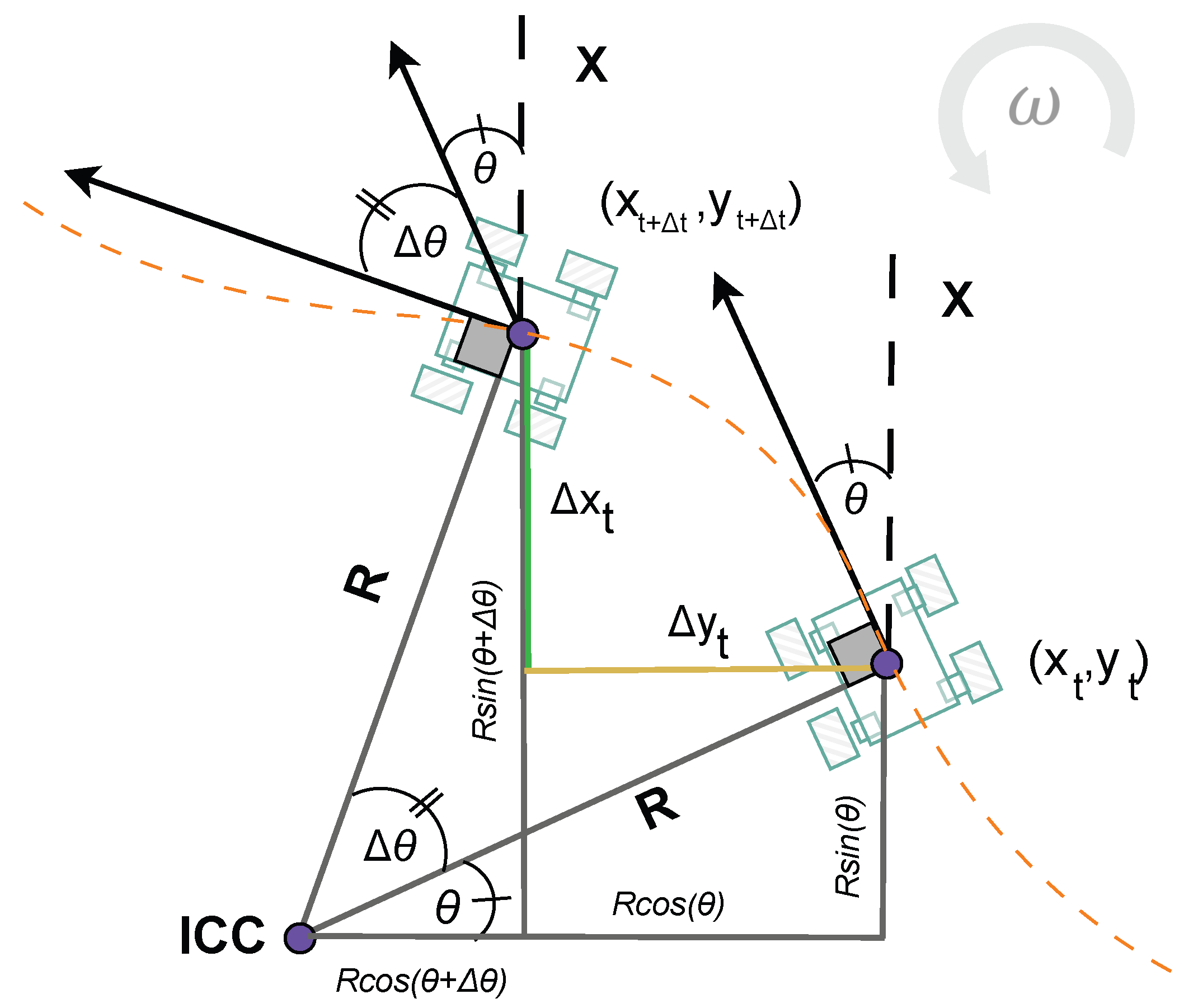
3.6. Odometry Calculation from Predictions of SSM and LSTM Models
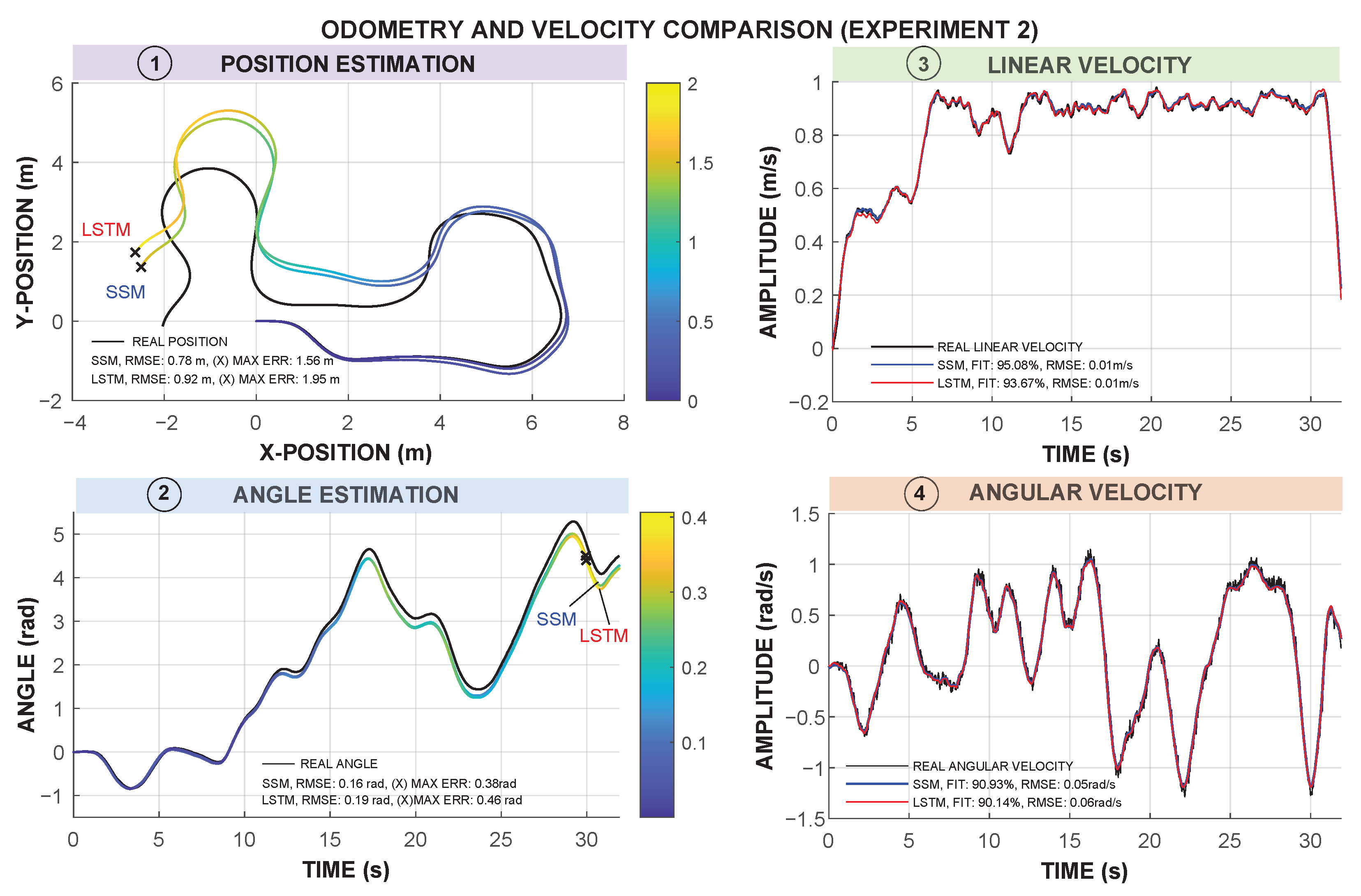
4. Results
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siwek, M.; Panasiuk, J.; Baranowski, L.; Kaczmarek, W.; Prusaczyk, P.; Borys, S.; Kowalczuk, A.; Kaczmarek, P.; Mazur, P.; Siwek, M.; et al. Identification of Differential Drive Robot Dynamic Model Parameters. Materials 2023, 16, 683. [Google Scholar] [CrossRef] [PubMed]
- Kok, M.; Hol, J.D.; Schön, T.B. Using Inertial Sensors for Position and Orientation Estimation. Found. Trends Signal Process. 2017, 11, 1–153. [Google Scholar] [CrossRef]
- Tran, A.M.D.; Vu, T.V.; Nguyen, Q.D. A Study on General State Model of Differential Drive Wheeled Mobile Robots. J. Adv. Eng. Comput. 2023, 7, 174–186. [Google Scholar] [CrossRef]
- Juarez-Lora, A.; Rodriguez-Angeles, A. Bio-Inspired Autonomous Navigation and Formation Controller for Differential Mobile Robots. Entropy 2023, 25, 582. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, B.; Warnell, G.; Stone, P. Motion planning and control for mobile robot navigation using machine learning: A survey. Auton. Robot. 2022, 46, 569–597. [Google Scholar] [CrossRef]
- Zarzycki, K.; Ławryńczuk, M. Long Short-Term Memory Neural Networks for Modeling Dynamical Processes and Predictive Control: A Hybrid Physics-Informed Approach. Sensors 2023, 23, 8898. [Google Scholar] [CrossRef] [PubMed]
- Vagale, A.; Šteina, L.; Vēciņš, V. Time Series Forecasting of Mobile Robot Motion Sensors Using LSTM Networks. Appl. Comput. Syst. 2021, 26, 150–157. [Google Scholar] [CrossRef]
- Cherubini, A.; Chaumette, F.; Oriolo, G.; Djelal, N.; Ouanane, A.; Bouriachi, F. LSTM-Based Visual Control for Complex Robot Interactions. J. Eur. Syst. Autom. 2023, 56, 863–870. [Google Scholar] [CrossRef]
- Yin, H.; Mahbub, A.; Win, M.Z. Deep Learning-Based Autonomous Robot Navigation with Sensor Fusion. Robot. Auton. Syst. 2021, 145, 103865. [Google Scholar] [CrossRef]
- Carreón Díaz de León, C.L.; Vergara-Limon, S.; Gonzalez-Calleros, J.M.; Vargas-Treviño, M.A.D. Red neuronal artificial para la extracción de parámetros dinámicos de robots a partir de información incompleta de su movimiento. Rev. Colomb. Comput. 2021, 22, 37–47. [Google Scholar] [CrossRef]
- Khalil, W.; Dombre, E. Modeling, Identification and Control of Robots; Taylor & Francis: Boca Raton, FL, USA, 2003. [Google Scholar]
- Yeom, K. Design of Deep Neural Network Based Model Predictive Controller for a Car-like Mobile Robot. Int. J. Mech. Eng. Robot. Res. 2022, 11, 606–613. [Google Scholar] [CrossRef]
- Li, C.; Hu, Z.; Zhang, D.; Wang, X. System Identification and Navigation of an Underactuated Underwater Vehicle Based on LSTM. J. Mar. Sci. Eng. 2025, 2, 276. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, Y.; Yang, M.; Jiang, C.; Han, X.; Li, Q. Time series clustering adaptive enhanced method for time-dependent reliability analysis and design optimization. Comput. Methods Appl. Mech. Eng. 2025, 443, 118099. [Google Scholar] [CrossRef]
- Alcayaga, J.M.; Menéndez, O.A.; Torres-Torriti, M.A.; Vásconez, J.P.; Arévalo-Ramirez, T.; Romo, A.J.P. LSTM-Enhanced Deep Reinforcement Learning for Robust Trajectory Tracking Control of Skid-Steer Mobile Robots Under Terra-Mechanical Constraints. Robotics 2025, 6, 74. [Google Scholar] [CrossRef]
- Reginald, N. Visual–Inertial–Wheel Odometry with Slip Compensation Based on Deep Kernel GPR and LSTM. Sensors 2025, 25, 1537. [Google Scholar] [CrossRef]
- Zheng, L. Predictive Control of the Mobile Robot under the Deep Long-Short Term Memory Neural Network Model. Comput. Intell. Neurosci. 2022, 2022, 1835798. [Google Scholar] [CrossRef]
- Fariña, B.; Acosta, D.; Toledo, J.; Acosta, L. Improving Odometric Model Performance Based on LSTM Networks. Sensors 2023, 23, 961. [Google Scholar] [CrossRef]
- Guffanti, D.; Mora Murillo, M.F.; Hinojosa, M.A.; Bustamante Sanchez, S.; Obregón Gutiérrez, J.O.; Gutiérrez, N.; Sánchez, M. Comparison of Two System Identification Approaches for a Four-Wheel Differential Robot Based on Velocity Command Execution. Sensors 2025, 25, 3553. [Google Scholar] [CrossRef]
- Čerkala, J.; Klein, T.; Jadlovska, A. Modeling and Control of Mobile Robot with Differential Chassis; Technical University of Košice: Košice, Slovakia, 2015; pp. 20–25. [Google Scholar]
- Teji, M.D.; Zou, T.; Zeleke, D.S. A Survey of Off-Road Mobile Robots: Slippage Estimation, Robot Control, and Sensing Technology. J. Intell. Robot. Syst. 2023, 109, 38. [Google Scholar] [CrossRef]
- Nourizadeh, P.; Stevens McFadden, F.J.; Browne, W.N. In situ slip estimation for mobile robots in outdoor environments. J. Field Robot. 2023, 40, 467–482. [Google Scholar] [CrossRef]
- Nourizadeh, P.; McFadden, F.J.S.; Browne, W.N. In situ skid estimation for mobile robots in outdoor environments. J. Field Robot. 2024, 41, 179–194. [Google Scholar] [CrossRef]
- Botta, A.; Botta, G.; Corti, M.; Pisu, L.; Tani, L. An Estimator for the Kinematic Behaviour of a Mobile Robot. Appl. Sci. 2021, 11, 1594. [Google Scholar] [CrossRef]

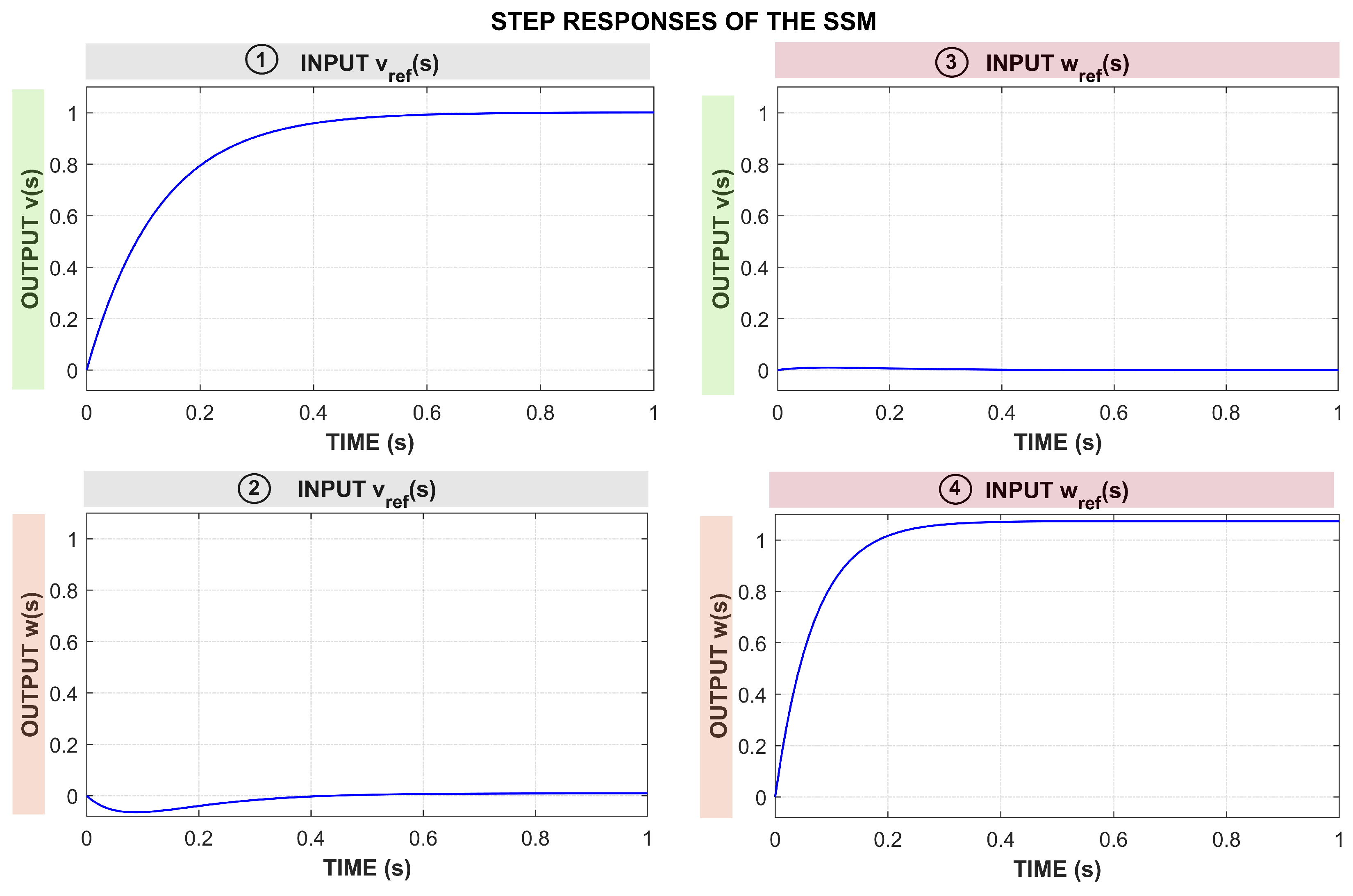

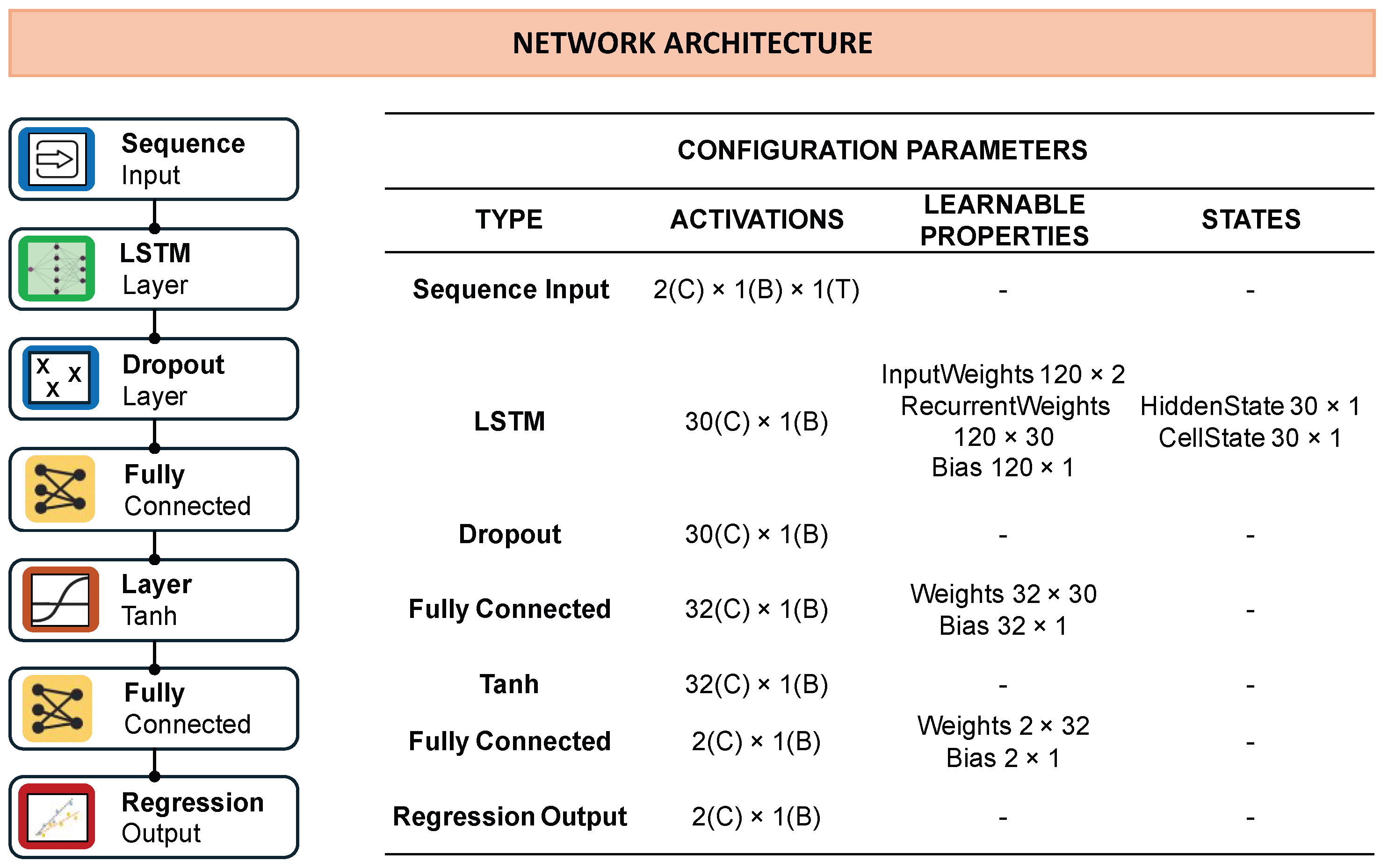

| Order | TEST | |||
|---|---|---|---|---|
| FIT | RMSE | |||
| v (%) | (%) | v (m/s) | (rad/s) | |
| 2 | 97.25 | 87.72 | 0.03 | 0.07 |
| 3 | 97.43 | 87.79 | 0.03 | 0.07 |
| 4 | 97.42 | 88.04 | 0.03 | 0.07 |
| 5 | 97.41 | 85.23 | 0.03 | 0.09 |
| ID | ARCH | N | ACT | OPT | WS | BS | VF | VP | Validation | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FIT | RMSE | FIT | RMSE | |||||||||||||
| v (%) | (%) | v (m/s) | (rad/s) | v (%) | (%) | v (m/s) | (rad/s) | |||||||||
| 1 | LSTM (1) | 20 | tanh | Adam | 10 | 16 | 20 | 20 | 92.53 | 89.59 | 0.06 | 0.08 | 92.39 | 90.09 | 0.06 | 0.08 |
| 2 | LSTM (1) | 30 | tanh | Adam | 20 | 16 | 20 | 20 | 95.49 | 90.25 | 0.04 | 0.07 | 95.40 | 90.36 | 0.04 | 0.08 |
| 3 | LSTM (1) | 50 | tanh | Adam | 50 | 16 | 20 | 20 | 90.92 | 91.54 | 0.08 | 0.06 | 90.72 | 91.75 | 0.08 | 0.07 |
| 4 | LSTM (1) | 100 | tanh | Adam | 100 | 16 | 20 | 20 | 93.16 | 89.54 | 0.06 | 0.08 | 93.19 | 90.03 | 0.06 | 0.08 |
| 5 | LSTM (1) | 30 | tanh | Adam | 70 | 32 | 10 | 10 | 95.35 | 90.82 | 0.04 | 0.07 | 94.99 | 91.25 | 0.04 | 0.07 |
| 6 | LSTM (1) | 100 | tanh | Adam | 30 | 32 | 10 | 20 | 95.20 | 90.47 | 0.04 | 0.07 | 94.94 | 90.13 | 0.04 | 0.08 |
| 7 | LSTM (2) | 30 | tanh | Adam | 20 | 16 | 20 | 30 | 95.28 | 90.12 | 0.04 | 0.08 | 95.33 | 89.51 | 0.04 | 0.08 |
| 8 | LSTM (1) | 30 | ReLU | Adam | 20 | 16 | 20 | 20 | 94.36 | 90.73 | 0.05 | 0.07 | 94.39 | 90.79 | 0.05 | 0.07 |
| 9 | LSTM (1) | 30 | tanh | RMSProp | 20 | 16 | 20 | 20 | 93.62 | 88.98 | 0.05 | 0.09 | 93.68 | 90.32 | 0.06 | 0.08 |
| Linear Velocity | Angular Velocity | ||||
|---|---|---|---|---|---|
| (m/s) | (rad/s) | ||||
| SSM | LSTM | SSM | LSTM | ||
| Experiment 1 | FIT (%) | 94.31 | 92.53 | 92.49 | 91.75 |
| RMSE | 0.01 | 0.02 | 0.05 | 0.06 | |
| Experiment 2 | FIT (%) | 95.08 | 93.67 | 90.93 | 90.14 |
| RMSE | 0.01 | 0.01 | 0.05 | 0.06 | |
| Average | FIT (%) | 94.70 | 93.10 | 91.71 | 90.95 |
| RMSE | 0.01 | 0.01 | 0.05 | 0.06 | |
| Position Estimation | Angle Estimation | ||||
|---|---|---|---|---|---|
| (m) | (rad/s) | ||||
| SSM | LSTM | SSM | LSTM | ||
| Experiment 1 | RMSE | 0.92 | 1.26 | 0.17 | 0.27 |
| Mean | 0.74 | 0.95 | 0.15 | 0.23 | |
| STD | 0.55 | 0.83 | 0.08 | 0.15 | |
| Max. Error | 1.74 | 2.63 | 0.29 | 0.48 | |
| Experiment 2 | RMSE | 0.78 | 0.92 | 0.16 | 0.19 |
| Mean | 0.59 | 0.66 | 0.13 | 0.14 | |
| STD | 0.51 | 0.65 | 0.10 | 0.12 | |
| Max. Error | 1.56 | 1.95 | 0.38 | 0.46 | |
| Average | RMSE | 0.85 | 1.09 | 0.17 | 0.23 |
| Mean | 0.67 | 0.80 | 0.14 | 0.19 | |
| STD | 0.53 | 0.74 | 0.09 | 0.13 | |
| Max. Error | 1.65 | 2.29 | 0.33 | 0.47 | |
| Metric | SSM | LSTM | Difference (LSTM-SSM) |
|---|---|---|---|
| Sim Time Mean (ms) | 4.05 | 53.89 | 49.84 |
| Sim Time Std (ms) | 11.58 | 67.28 | 55.70 |
| Avg Time/Step Mean (ms) | 0.00257 | 0.0342 | 0.03163 |
| Avg Time/Step Std (ms) | 0.00734 | 0.0427 | 0.03536 |
| Mem Usage Mean (MB) | 0.00155 | 0.03082 | 0.02927 |
| Mem Usage Std (MB) | 0.00802 | 0.29999 | 0.29197 |
| Mem Usage per Step (bytes) | 1.03 | 20.49 | 19.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guffanti, D.; Pavon, W. MultivariateSystem Identification of Differential Drive Robot: Comparison Between State-Space and LSTM-Based Models. Sensors 2025, 25, 5821. https://doi.org/10.3390/s25185821
Guffanti D, Pavon W. MultivariateSystem Identification of Differential Drive Robot: Comparison Between State-Space and LSTM-Based Models. Sensors. 2025; 25(18):5821. https://doi.org/10.3390/s25185821
Chicago/Turabian StyleGuffanti, Diego, and Wilson Pavon. 2025. "MultivariateSystem Identification of Differential Drive Robot: Comparison Between State-Space and LSTM-Based Models" Sensors 25, no. 18: 5821. https://doi.org/10.3390/s25185821
APA StyleGuffanti, D., & Pavon, W. (2025). MultivariateSystem Identification of Differential Drive Robot: Comparison Between State-Space and LSTM-Based Models. Sensors, 25(18), 5821. https://doi.org/10.3390/s25185821







