Radar-Based Road Surface Classification Using Range-Fast Fourier Transform Learning Models
Abstract
1. Introduction
- Comprehensive surface condition analysis: Six representative road surface states (dry, wet, thin-ice, ice, snow, and sludge) were systematically implemented on both asphalt and concrete specimens using a controlled temperature and humidity chamber, enabling thorough analysis of hazardous conditions.
- Temporal signal behavior investigation: Radar data were collected at fixed time intervals to quantitatively observe transitions in surface conditions, providing insights into the dynamic behavior of reflected signals during state changes.
- Dual-approach feature extraction: The collected data were processed using Range-FFT to generate range-based spectra, from which both statistical features and image representations were extracted, enabling comprehensive classification strategies.
- Comprehensive model evaluation: These features were applied to conventional machine learning algorithms (XGBoost, LightGBM, Random Forest, SVM), CNN-based deep learning models, and Vision Transformer (ViT) to comprehensively evaluate classification performance across different surface conditions and material types.
- Advanced deep learning comparison: The study provides detailed performance analysis and comparison between CNN and ViT models, demonstrating their distinct characteristics and capabilities in road surface condition classification.
- Robustness evaluation framework: Comprehensive robustness testing under various noise and blur conditions was conducted for both CNN and ViT models, providing insights into their degradation patterns and practical applicability in challenging environments.
2. Materials and Methods
2.1. Millimeter-Wave Radar Background
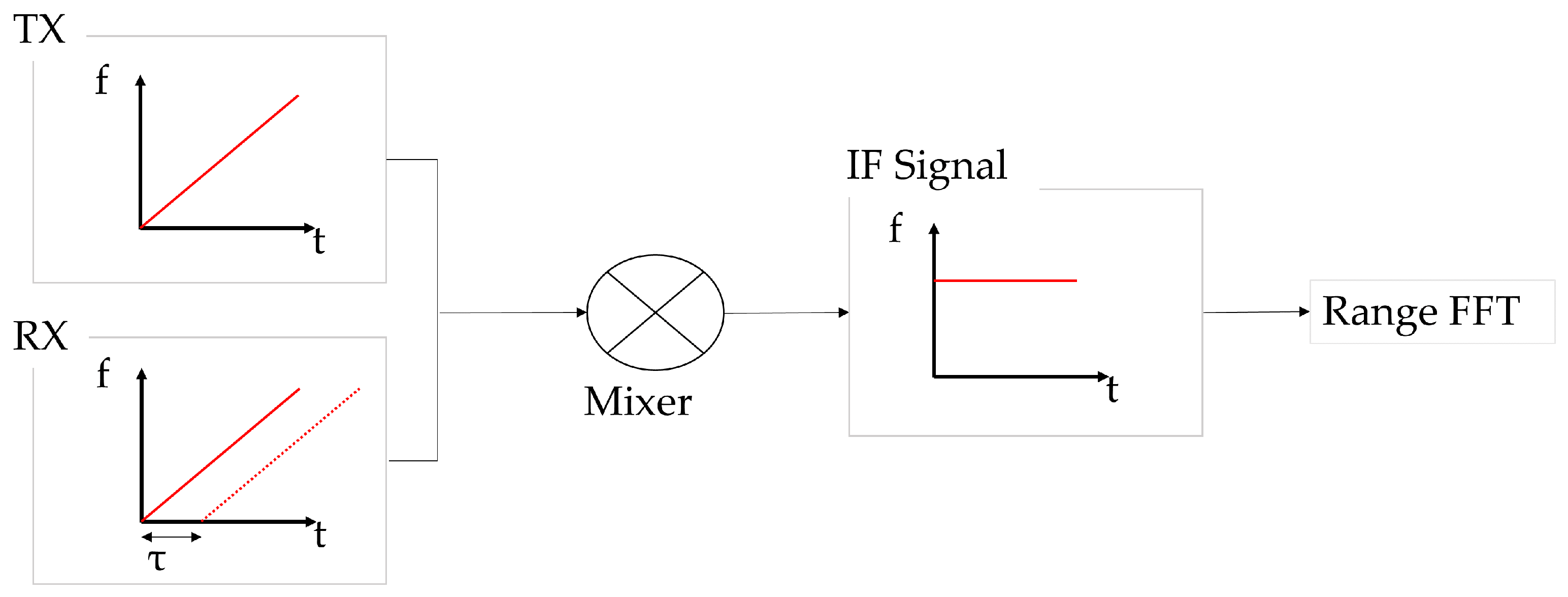
2.1.1. FMCW (Frequency-Modulated Continuous Wave)
2.1.2. Raw Data Processing
- : number of frames,
- : number of chirps per frame,
- : number of transmit antennas,
- : number of receive antennas,
- : number of ADC samples per chirp.
2.2. Learning Background
2.2.1. Random Forest (RF)
2.2.2. Support Vector Machine (SVM)
2.2.3. XGBoost
2.2.4. Light Gradient Boosting Machine (LightGBM)
2.2.5. Convolutional Neural Network (CNN)
2.2.6. Vision Transformer
2.3. Experimental Setup
2.3.1. Sensor and System
2.3.2. Experimental Environment
2.4. Data Acquisition
2.5. Data Processing and Feature Extraction
2.6. Classification and Analysis
3. Results
3.1. Example of Data
3.2. Classification Performance
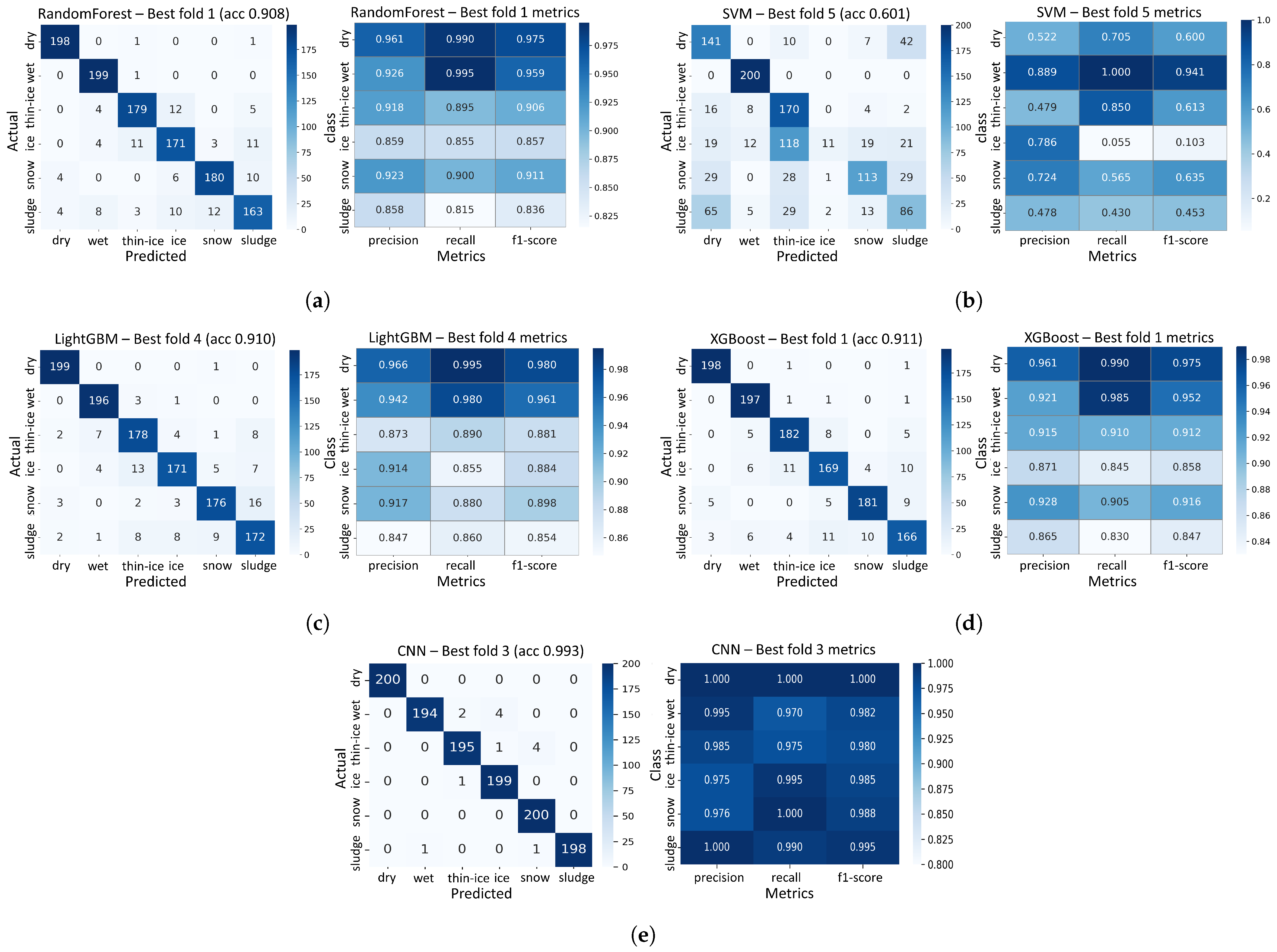
3.2.1. Asphalt Results
- Dry: CNN (1.000), LightGBM (0.980), Random Forest (0.975), and XGBoost (0.975) demonstrated excellent performance;
- Wet: Most models demonstrated excellent performance, with CNN and LightGBM achieving the highest F1-score of 0.982 and 0.961, respectively;
- Thin-Ice: CNN and XGBoost achieved the highest F1-scores of 0.980 and 0.912, respectively;
- Ice: CNN and LightGBM achieved the highest F1-scores of 0.985 and 0.884, respectively;
- Snow: CNN and XGBoost achieved the highest F1-scores of 0.988 and 0.916, respectively;
- Sludge: CNN (0.995), Random Forest (0.836), LightGBM (0.854) and XGBoost (0.847) were recorded.
3.2.2. Concrete Results
- Dry: CNN (0.995), LightGBM (0.959), Random Forest (0.958), XGBoost (0.939);
- Wet: All models demonstrated excellent performance, with CNN, LightGBM, Random Forest and XGBoost each achieving an F1-score of at least 0.97;
- Thin-Ice: Overall performance was lower; however, CNN (0.967) maintained stable results;
- Ice: CNN (0.980) and LightGBM (0.879) achieved the highest F1-scores;
- Snow: CNN (0.985), XGBoost (0.904), and LightGBM (0.903) demonstrated strong performance;
- Sludge: CNN (0.995), LightGBM (0.791), Random Forest (0.832), and XGBoost (0.798).
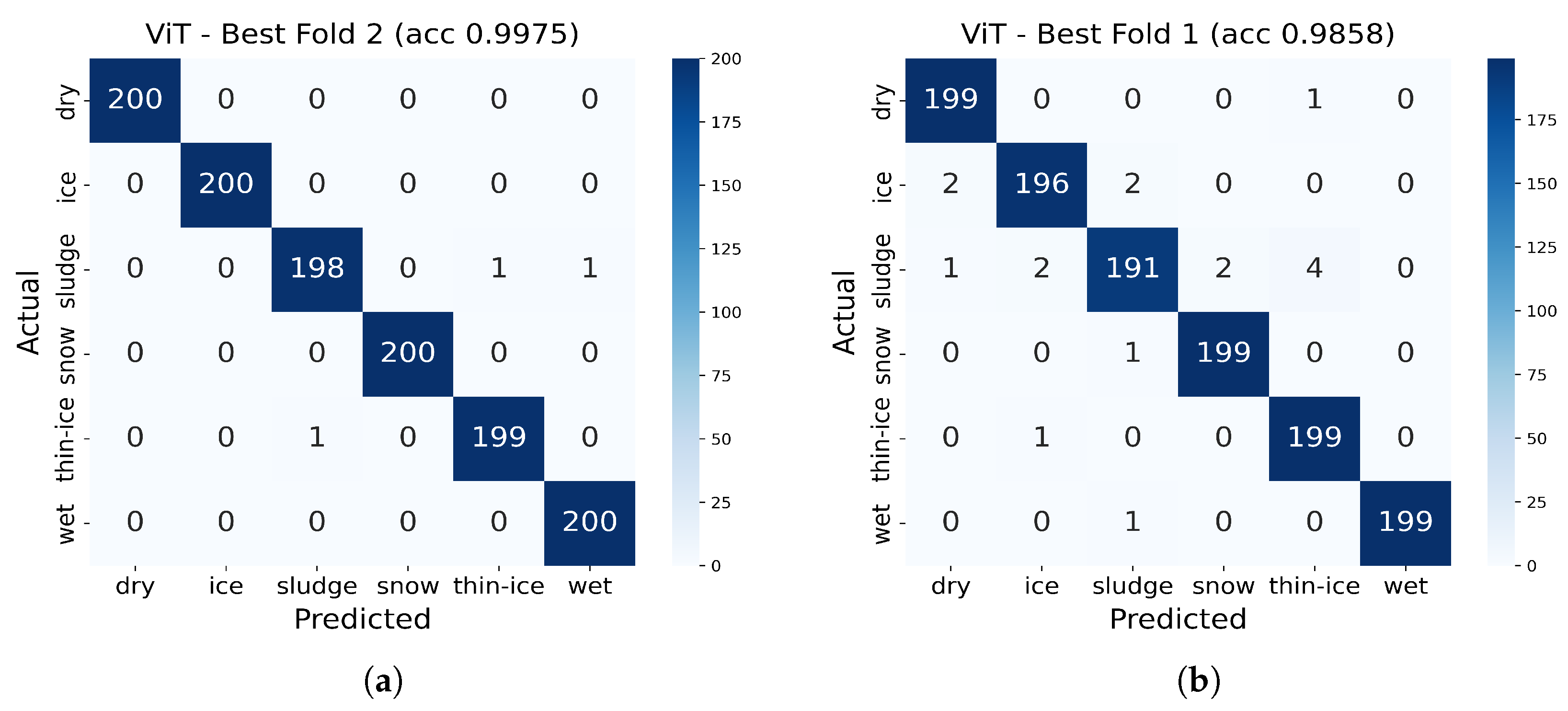
3.2.3. Vision Transformer Performance Analysis
- Dry: Precision 1.000, Recall 1.000, F1-score 1.000
- Wet: Precision 0.995, Recall 1.000, F1-score 0.998
- Thin-Ice: Precision 0.995, Recall 0.995, F1-score 0.995
- Ice: Precision 1.000, Recall 1.000, F1-score 1.000
- Snow: Precision 1.000, Recall 1.000, F1-score 1.000
- Sludge: Precision 0.995, Recall 0.990, F1-score 0.993
- Dry: Precision 0.985, Recall 0.985, F1-score 0.985
- Wet: Precision 0.980, Recall 0.980, F1-score 0.980
- Thin-Ice: Precision 0.975, Recall 0.970, F1-score 0.972
- Ice: Precision 0.970, Recall 0.965, F1-score 0.967
- Snow: Precision 0.965, Recall 0.975, F1-score 0.970
- Sludge: Precision 0.980, Recall 0.975, F1-score 0.977
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korea Road Traffic Authority. Statistical Analysis of Traffic Accidents on Icy Roads. (In Korea). Available online: https://www.koroad.or.kr/main/board/6/301689/board_view.do?&sv=%EA%B2%B0%EB%B9%99&cp=1&listType=list&bdOpenYn=Y&bdNoticeYn=N (accessed on 8 September 2025).
- U.S. Federal Highway Administration (FHWA). Snow and Ice. Available online: https://ops.fhwa.dot.gov/weather/weather_events/snow_ice.htm (accessed on 8 September 2025).
- Sezgin, F.; Vriesman, D.; Steinhauser, D.; Lugner, R.; Brandmeier, T. Safe Autonomous Driving in Adverse Weather: Sensor Evaluation and Performance Monitoring. In Proceedings of the 2023 IEEE Intelligent Vehicles Symposium (IV), Anchorage, AK, USA, 4–7 June 2023. [Google Scholar] [CrossRef]
- Ramos-Romero, C.; Asensio, C.; Moreno, R.; de Arcas, G. Urban Road Surface Discrimination by Tire-Road Noise Analysis and Data Clustering. Sensors 2022, 22, 9686. [Google Scholar] [CrossRef]
- Heo, J.; Im, B.; Shin, S.; Ha, S.; Kang, D.; Song, T.; Gu, Y.; Han, S. Experimental Analysis of Sensor’s Performance Degradation Under Adverse Weather Conditions. Int. J. Precis. Eng. Manuf. 2025, 26, 1655–1672. [Google Scholar] [CrossRef]
- Shanbhag, H.; Madani, S.; Isanaka, A.; Nair, D.; Gupta, S.; Hassanieh, H. Contactless Material Identification with Millimeter Wave Vibrometry. In Proceedings of the 21st Annual International Conference on Mobile Systems, Applications and Services (MobiSys ’23), Helsinki, Finland, 18–22 June 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 475–488. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, M.; Feng, Q.; He, Z.; Tian, M. Current Non-Contact Road Surface Condition Detection Schemes and Technical Challenges. Sensors 2022, 22, 9583. [Google Scholar] [CrossRef]
- Lamane, M.; Tabaa, M.; Klilou, A. New Approach Based on Pix2Pix–YOLOv7 mmWave Radar for Target Detection and Classification. Sensors 2023, 23, 9456. [Google Scholar] [CrossRef] [PubMed]
- Yeo, J.; Lee, J.; Kim, G.; Jang, K. Estimation of Road Surface Condition during Summer Season Using Machine Learning. J. Korea Inst. Intell. Transp. Syst. 2018, 17, 121–132. [Google Scholar] [CrossRef]
- Lee, H.; Kang, M.; Song, J.; Hwang, K. The Detection of Black Ice Accidents for Preventative Automated Vehicles Using Convolutional Neural Networks. Electronics 2020, 9, 2178. [Google Scholar] [CrossRef]
- Soumya, A.; Krishna Mohan, C.; Cenkeramaddi, L.R. Recent Advances in mmWave-Radar-Based Sensing, Its Applications, and Machine Learning Techniques: A Review. Sensors 2023, 23, 8901. [Google Scholar] [CrossRef]
- Hao, S.; Liu, B.; Jiang, B.; Lin, Y.; Xu, B. Material Surface Classification Based on 24GHz FMCW MIMO Radar. In Proceedings of the IEEE MTT-S International Wireless Symposium (IWS), Beijing, China, 16–19 May 2024. [Google Scholar] [CrossRef]
- Southcott, M.; Zhang, L.; Liu, C. Millimeter Wave Radar-Based Road Segmentation. In Radar Sensor Technology XXVII; SPIE: Bellingham, WA, USA, 2023; Volume 12535. [Google Scholar] [CrossRef]
- Cho, J.; Hussen, H.; Yang, S.; Kim, J. Radar-Based Road Surface Classification System for Personal Mobility Devices. IEEE Sens. J. 2023, 23, 16343–16350. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H.; Chen, Y.; Zhou, Y.; Peng, Y. Urban Traffic Imaging Using Millimeter-Wave Radar. Remote Sens. 2022, 14, 5416. [Google Scholar] [CrossRef]
- Kim, J.; Kim, E.; Kim, D. A Black Ice Detection Method Based on 1-Dimensional CNN Using mmWave Sensor Backscattering. Remote Sens. 2022, 14, 5252. [Google Scholar] [CrossRef]
- Bouwmeester, W.; Fioranelli, F.; Yarovoy, A.G. Road Surface Conditions Identification via HαA Decomposition and Its Application to mm-Wave Automotive Radar. IEEE Trans. Radar Syst. 2023, 1, 132–145. [Google Scholar] [CrossRef]
- He, S.; Qian, Y.; Zhang, H.; Zhang, G.; Xu, M.; Fu, L.; Cheng, X.; Wang, H.; Hu, P. Accurate Contact-Free Material Recognition with Millimeter Wave and Machine Learning. In Proceedings of the International Conference on Wireless Algorithms, Systems and Applications, Dalian, China, 24–26 November 2022; pp. 609–620. [Google Scholar] [CrossRef]
- Vassilev, V. Road Surface Recognition at mm-Wavelengths Using a Polarimetric Radar. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6985–6990. [Google Scholar] [CrossRef]
- Qiu, Z.; Shao, J.; Guo, D.; Yin, X.; Zhai, Z.; Duan, Z.; Xu, Y. A Multi-Feature Fusion Approach for Road Surface Recognition Leveraging Millimeter-Wave Radar. Sensors 2025, 25, 3802. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, Y.; Liu, J.; Wang, Z.; Zhang, Z. Automated Recognition of Snow-Covered and Icy Road Surfaces Based on T-Net of Mount Tianshan. Remote Sens. 2024, 16, 3727. [Google Scholar] [CrossRef]
- Jia, F.; Li, C.; Bi, S.; Qian, J.; Wei, L.; Sun, G. TC–Radar: Transformer–CNN Hybrid Network for Millimeter-Wave Radar Object Detection. Remote Sens. 2024, 16, 2881. [Google Scholar] [CrossRef]
- Bhatia, J.; Dayal, A.; Jha, A.; Vishvakarma, S.K.; Joshi, S.; Srinivas, M.B.; Yalavarthy, P.K.; Kumar, A.; Lalitha, V.; Koorapati, S.; et al. Classification of Targets Using Statistical Features from Range FFT of mmWave FMCW Radars. Electronics 2021, 10, 1965. [Google Scholar] [CrossRef]
- Hyun, E.; Jin, Y.-S.; Lee, J.-H. A Pedestrian Detection Scheme Using a Coherent Phase Difference Method Based on 2D Range-Doppler FMCW Radar. Sensors 2016, 16, 124. [Google Scholar] [CrossRef]
- Häkli, J.; Säily, J.; Koivisto, P.; Huhtinen, I.; Dufva, T.; Rautiainen, A. Road Surface Condition Detection Using 24 GHz Automotive Radar Technology. In Proceedings of the 14th International Radar Symposium (IRS), Dresden, Germany, 19–21 June 2013; Available online: https://ieeexplore.ieee.org/document/6581661 (accessed on 8 September 2025).
- Sabery, S.; Bystrov, A.; Gardner, P.; Stroescu, A.; Gashinova, M. Road Surface Classification Based on Radar Imaging Using Convolutional Neural Network. IEEE Sens. J. 2021, 21, 18725–18732. [Google Scholar] [CrossRef]
- Bouwmeester, W.; Fioranelli, F.; Yarovoy, A. Statistical Polarimetric RCS Model of an Asphalt Road Surface for mm-Wave Automotive Radar. In Proceedings of the 20th European Radar Conference (EuRAD), Berlin, Germany, 20–22 September 2023; pp. 18–21. [Google Scholar] [CrossRef]
- Tavanti, E.; Rizik, A.; Fedeli, A.; Caviglia, D.; Randazzo, A. A Short-Range FMCW Radar-Based Approach for Multi-Target Human–Vehicle Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2003816. [Google Scholar] [CrossRef]
- Paek, D.; Kong, S.; Wijaya, K.T.K. K-radar: 4D Radar Object Detection for Autonomous Driving in Various Weather Conditions. Adv. Neural Inf. Process. Syst. 2022, 35, 3819–3829. Available online: https://proceedings.neurips.cc/paper_files/paper/2022/hash/185fdf627eaae2abab36205dcd19b817-Abstract-Datasets_and_Benchmarks.html (accessed on 8 September 2025).
- Gupta, S.; Rai, P.K.; Kumar, A.; Yalavarthy, P.K.; Cenkeramaddi, L.R. Target Classification by mmWave FMCW Radars Using Machine Learning on Range-Angle Images. IEEE Sens. J. 2021, 21, 19993–20001. [Google Scholar] [CrossRef]
- Liang, X.; Chu, L.; Hua, B.; Shi, Q.; Shi, J.; Meng, C.; Braun, R. Road Target Recognition Based on Radar Range-Doppler Spectrum with GS–ResNet. Int. J. Remote Sens. 2024, 45, 8290–8312. [Google Scholar] [CrossRef]
- Winkler, V. Range Doppler Detection for Automotive FMCW Radar. In Proceedings of the European Microwave Conference, Munich, Germany, 8–12 October 2007; pp. 166–169. [Google Scholar] [CrossRef]
- Moroto, Y.; Maeda, K.; Togo, R.; Ogawa, T.; Haseyama, M. Multimodal Transformer Model Using Time-Series Data to Classify Winter Road Surface Conditions. Sensors 2024, 24, 3440. [Google Scholar] [CrossRef] [PubMed]
- Bouwmeester, W.; Fioranelli, F.; Yarovoy, A. Dynamic Road Surface Signatures in Automotive Scenarios. In Proceedings of the 18th European Radar Conference (EuRAD), London, UK, 5–7 April 2022; pp. 285–288. [Google Scholar] [CrossRef]
- Wang, Z.; Wen, T.; Chen, N.; Tang, R. Assessment of Landslide Susceptibility Based on the Two-Layer Stacking Model—A Case Study of Jiacha County, China. Remote Sens. 2025, 17, 1177. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Y.; Jin, D.; Su, L.; Vasilakos, A.V. A Survey of Millimeter Wave Communications (mmWave) for 5G: Opportunities and Challenges. Wirel. Netw. 2015, 21, 2657–2676. [Google Scholar] [CrossRef]
- Dokhanchi, S.H.; Mysore, B.S.; Mishra, K.V.; Ottersten, B. A mmWave Automotive Joint Radar-Communications System. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1241–1260. [Google Scholar] [CrossRef]
- Zhou, T.; Yang, M.; Jiang, K.; Wong, H.; Yang, D. MMW Radar-Based Technologies in Autonomous Driving: A Review. Sensors 2020, 20, 7283. [Google Scholar] [CrossRef]
- Kong, H.; Huang, C.; Yu, J.; Shen, X. A Survey of mmWave Radar-Based Sensing in Autonomous Vehicles, Smart Homes and Industry. IEEE Commun. Surv. Tutor. 2025, 27, 463–508. [Google Scholar] [CrossRef]
- Zhang, J.; Xi, R.; He, Y.; Sun, Y.; Guo, X.; Wang, W.; Na, X.; Liu, Y.; Shi, Z.; Gu, T. A Survey of mmWave-Based Human Sensing: Technology, Platforms and Applications. IEEE Commun. Surv. Tutor. 2023, 25, 2052–2087. [Google Scholar] [CrossRef]
- Weiß, J.; Santra, A. One-Shot Learning for Robust Material Classification Using Millimeter-Wave Radar System. IEEE Sens. Lett. 2018, 2, 7001504. [Google Scholar] [CrossRef]
- van Delden, M.; Westerdick, S.; Musch, T. Investigations on Foam Detection Utilizing Ultra-Broadband Millimeter Wave FMCW Radar. In Proceedings of the 2019 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Bochum, Germany, 16–18 July 2019; pp. 103–105. [Google Scholar] [CrossRef]
- Ciattaglia, G.; Iadarola, G.; Battista, G.; Senigagliesi, L.; Gambi, E.; Castellini, P.; Spinsante, S. Displacement Evaluation by mmWave FMCW Radars: Method and Performance Metrics. IEEE Trans. Instrum. Meas. 2024, 73, 8505313. [Google Scholar] [CrossRef]
- Jardak, S.; Alouini, M.S.; Kiuru, T.; Metso, M.; Ahmed, S. Compact mmWave FMCW Radar: Implementation and Performance Analysis. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 36–44. [Google Scholar] [CrossRef]
- Iovescu, C.; Rao, S. The Fundamentals of Millimeter Wave Radar Sensors; Texas Instruments: Dallas, TX, USA, 2020; pp. 1–7. Available online: https://www.ti.com/lit/wp/spyy005a/spyy005a.pdf (accessed on 8 September 2025).
- Li, X.; Wang, X.; Yang, Q.; Fu, S. Signal Processing for TDM MIMO FMCW Millimeter-Wave Radar Sensors. IEEE Access 2021, 9, 167959–167971. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30, 52. Available online: https://proceedings.neurips.cc/paper/2017/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html (accessed on 8 September 2025).
- Ghaderpour, E.; Pagiatakis, S.D.; Mugnozza, G.S.; Mazzanti, P. On the Stochastic Significance of Peaks in the Least-Squares Wavelet Spectrogram and an Application in GNSS Time Series Analysis. Signal Process. 2024, 223, 109581. [Google Scholar] [CrossRef]
- Boateng, E.Y.; Otoo, J.; Abaye, D.A. Basic Tenets of Classification Algorithms: K-Nearest-Neighbor, Support Vector Machine, Random Forest and Neural Network—A Review. J. Data Anal. Inf. Process. 2020, 8, 341–357. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting Hard Rock Pillar Stability Using GBDT, XGBoost, and LightGBM Algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine Learning Models for Predicting the Residual Value of Heavy Construction Equipment: An Evaluation of Modified Decision Tree, LightGBM, and XGBoost Regression. Autom. Constr. 2021, 129, 103827. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time Series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995; p. 3361. Available online: https://hal.science/hal-05083427/document (accessed on 8 September 2025).
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent Advances in Convolutional Neural Networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Tabian, I.; Fu, H.; Sharif Khodaei, Z. A Convolutional Neural Network for Impact Detection and Characterization of Complex Composite Structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. Available online: https://arxiv.org/pdf/2010.11929/1000 (accessed on 8 September 2025). [CrossRef]
- Texas Instruments. IWR1843 Single-Chip 76- to 81-GHz FMCW mmWave Sensor Datasheet; Texas Instruments: Dallas, TX, USA, 2022; Available online: https://www.ti.com/lit/pdf/SWRS228 (accessed on 8 September 2025).
- Browne, M.W. Cross-Validation Methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. Available online: https://proceedings.neurips.cc/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html (accessed on 8 September 2025). [CrossRef]
- Morgan, N.; Bourlard, H. Generalization and Parameter Estimation in Feedforward Nets: Some Experiments. Adv. Neural Inf. Process. Syst. 1989, 2, 630–637. Available online: https://proceedings.neurips.cc/paper_files/paper/1989/hash/63923f49e5241343aa7acb6a06a751e7-Abstract.html (accessed on 8 September 2025).
- Krogh, A.; Hertz, J. A Simple Weight Decay Can Improve Generalization. Adv. Neural Inf. Process. Syst. 1991, 4, 950–957. Available online: https://proceedings.neurips.cc/paper_files/paper/1991/file/8eefcfdf5990e441f0fb6f3fad709e21-Paper.pdf (accessed on 8 September 2025).
- Chen, Y.; Gu, X.; Liu, Z.; Liang, J. A Fast Inference Vision Transformer for Automatic Pavement Image Classification and Its Visual Interpretation Method. Remote Sens. 2022, 14, 1877. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Wen, T.; Wang, L. Step-Like Displacement Prediction of Reservoir Landslides Based on a Metaheuristic-Optimized KELM: A Comparative Study. Bull. Eng. Geol. Environ. 2024, 83, 322. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, F.; Chang, S.; Liu, Y.; Wu, H.; Feng, Z. Mmwave Radar and Vision Fusion for Object Detection in Autonomous Driving: A Review. Sensors 2022, 22, 2542. [Google Scholar] [CrossRef]
- Bijelic, M.; Gruber, T.; Mannan, F.; Kraus, F.; Ritter, W.; Dietmayer, K.; Heide, F. Seeing Through Fog Without Seeing Fog: Deep Multimodal Sensor Fusion in Unseen Adverse Weather. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11682–11692. Available online: https://openaccess.thecvf.com/content_CVPR_2020/html/Bijelic_Seeing_Through_Fog_Without_Seeing_Fog_Deep_Multimodal_Sensor_Fusion_CVPR_2020_paper.html (accessed on 8 September 2025).
- Nabati, R.; Qi, H. CenterFusion: Center-Based Radar and Camera Fusion for 3D Object Detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 5–9 January 2021; pp. 1527–1536. Available online: https://openaccess.thecvf.com/content/WACV2021/html/Nabati_CenterFusion_Center-Based_Radar_and_Camera_Fusion_for_3D_Object_Detection_WACV_2021_paper.html (accessed on 8 September 2025).
- Nobis, F.; Shafiei, E.; Karle, P.; Betz, J.; Lienkamp, M. Radar Voxel Fusion for 3D Object Detection. Appl. Sci. 2021, 11, 5598. [Google Scholar] [CrossRef]







| Model | Summary of Features | Strengths | Limitations | Recommended Use Cases |
|---|---|---|---|---|
| Random Forest | Ensemble of multiple decision trees using random sampling |
|
|
|
| SVM | Learns decision boundaries by maximizing the margin in high-dimensional space |
|
|
|
| XGBoost | Boosted tree model with enhanced performance and efficiency over traditional gradient boosting |
|
|
|
| LightGBM | Faster and more memory-efficient boosting model optimized for large datasets |
|
|
|
| CNN | Automatically extracts spatial features from 2D images |
|
|
|
| ViT | Transformer-based architecture that processes images as sequences of patches |
|
|
|
| Model | Parameter | Setting Value |
|---|---|---|
| Random Forest | n_estimators | 100 |
| max_depth | None | |
| min_samples_split | 2 | |
| SVM | kernel | rbf |
| XGBoost | n_estimators | 100 |
| max_depth | 6 | |
| learning_rate | 0.3 | |
| LightGBM | n_estimators | 100 |
| num_leaves | 31 | |
| learning_rate | 0.1 |
| Parameter | Setting Value |
|---|---|
| Learning rate | |
| Weight decay | |
| Batch size | 16 |
| Max epochs | 50 |
| Early stopping | 10 |
| Optimizer | Adam |
| Loss Function | Cross Entropy Loss |
| Parameter | Setting Value |
|---|---|
| Model Architecture | google/vit-base-patch16-224 |
| Learning rate | |
| Weight decay | 0.01 |
| Batch size | 8 |
| Max epochs | 50 |
| Early stopping | 15 |
| Optimizer | AdamW |
| Loss Function | Cross Entropy Loss |
| Layers | 12 |
| Attention Heads | 12 |
| Specimen | Range (m) | Feature Set | # Features | Cross-Validation Accuracy |
|---|---|---|---|---|
| Asphalt/Concrete | 0.10–0.24 | Range-FFT | 5 | 0.904/0.888 |
| Range-FFT + ST-LSSA | 16 | 0.898/0.886 | ||
| ST-LSSA | 11 | 0.350/0.359 | ||
| 0.07–0.27 | Range-FFT | 5 | 0.895/0.875 | |
| Range-FFT + ST-LSSA | 16 | 0.887/0.880 | ||
| ST-LSSA | 11 | 0.350/0.359 | ||
| 0.04–0.30 | Range-FFT | 5 | 0.901/0.881 | |
| Range-FFT + ST-LSSA | 16 | 0.896/0.878 | ||
| ST-LSSA | 11 | 0.350/0.359 |
| Mean (dB) | Max (dB) | Std (dB) | Median (dB) | Mode (dB) | File_Name | Label |
|---|---|---|---|---|---|---|
| 74.50 | 82.04 | 6.139 | 73.95 | 64.98 | radar_0_20250701_112732.pcap | Dry |
| 78.46 | 92.57 | 10.88 | 77.38 | 59.97 | radar_0_20250702_165220.pcap | Dry |
| 78.50 | 93.41 | 11.04 | 76.19 | 60.89 | radar_0_20250702_165948.pcap | Dry |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Specimen | Range (m) | Model | Accuracy (%) |
|---|---|---|---|
| Asphalt/Concrete | 0.10–0.24 | RF | 90.38/88.83 |
| SVM | 59.37/52.17 | ||
| XGBoost | 91.48/88.73 | ||
| LightGBM | 91.22/89.35 | ||
| CNN | 98.67/97.42 | ||
| 0.07–0.27 | RF | 89.53/87.95 | |
| SVM | 57.32/44.12 | ||
| XGBoost | 90.18/88.70 | ||
| LightGBM | 90.33/89.18 | ||
| CNN | 99.00/98.50 | ||
| 0.04–0.30 | RF | 90.08/88.08 | |
| SVM | 58.50/51.60 | ||
| XGBoost | 90.40/88.12 | ||
| LightGBM | 90.53/88.45 | ||
| CNN | 99.25/98.75 |
| Specimen | Model | Clean (%) | Gaussian Noise (SNR dB) | Motion Blur (k) | ||
|---|---|---|---|---|---|---|
| 20 dB | 15 dB | k = 3 | k = 5 | |||
| Asphalt | CNN | 99.83 | 99.17 () | 95.75 () | 95.92 () | 95.08 () |
| ViT | 99.75 | 99.70 () | 91.15 () | 96.20 () | 90.02 () | |
| Concrete | CNN | 98.92 | 98.75 () | 95.25 () | 95.58 () | 94.17 () |
| ViT | 98.58 | 98.47 () | 88.97 () | 91.36 () | 85.89 () | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kim, J.; Ko, K.; Han, H.; Youm, M. Radar-Based Road Surface Classification Using Range-Fast Fourier Transform Learning Models. Sensors 2025, 25, 5697. https://doi.org/10.3390/s25185697
Lee H, Kim J, Ko K, Han H, Youm M. Radar-Based Road Surface Classification Using Range-Fast Fourier Transform Learning Models. Sensors. 2025; 25(18):5697. https://doi.org/10.3390/s25185697
Chicago/Turabian StyleLee, Hyunji, Jiyun Kim, Kwangin Ko, Hak Han, and Minkyo Youm. 2025. "Radar-Based Road Surface Classification Using Range-Fast Fourier Transform Learning Models" Sensors 25, no. 18: 5697. https://doi.org/10.3390/s25185697
APA StyleLee, H., Kim, J., Ko, K., Han, H., & Youm, M. (2025). Radar-Based Road Surface Classification Using Range-Fast Fourier Transform Learning Models. Sensors, 25(18), 5697. https://doi.org/10.3390/s25185697






