A Performance Study of Deep Neural Network Representations of Interpretable ML on Edge Devices with AI Accelerators
Abstract
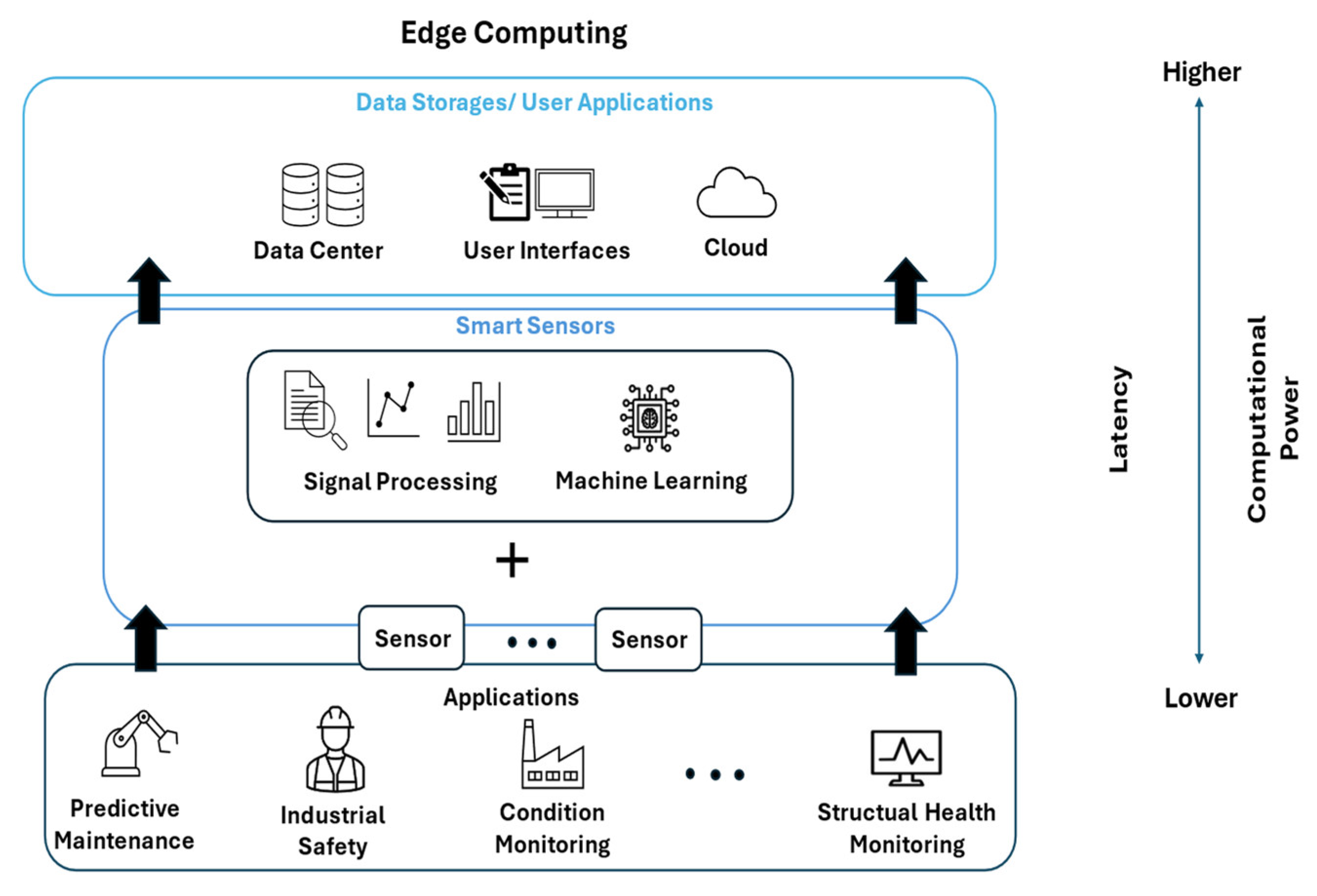
1. Introduction
- We introduced a novel method to run interpretable ML on DNN-specific AI accelerators.
- The proposed method outperforms conventional implementations in terms of the inference time and energy efficiency.
- The proposed method was evaluated using implementations at different quantization levels on two hardware platforms.
2. Materials and Methods
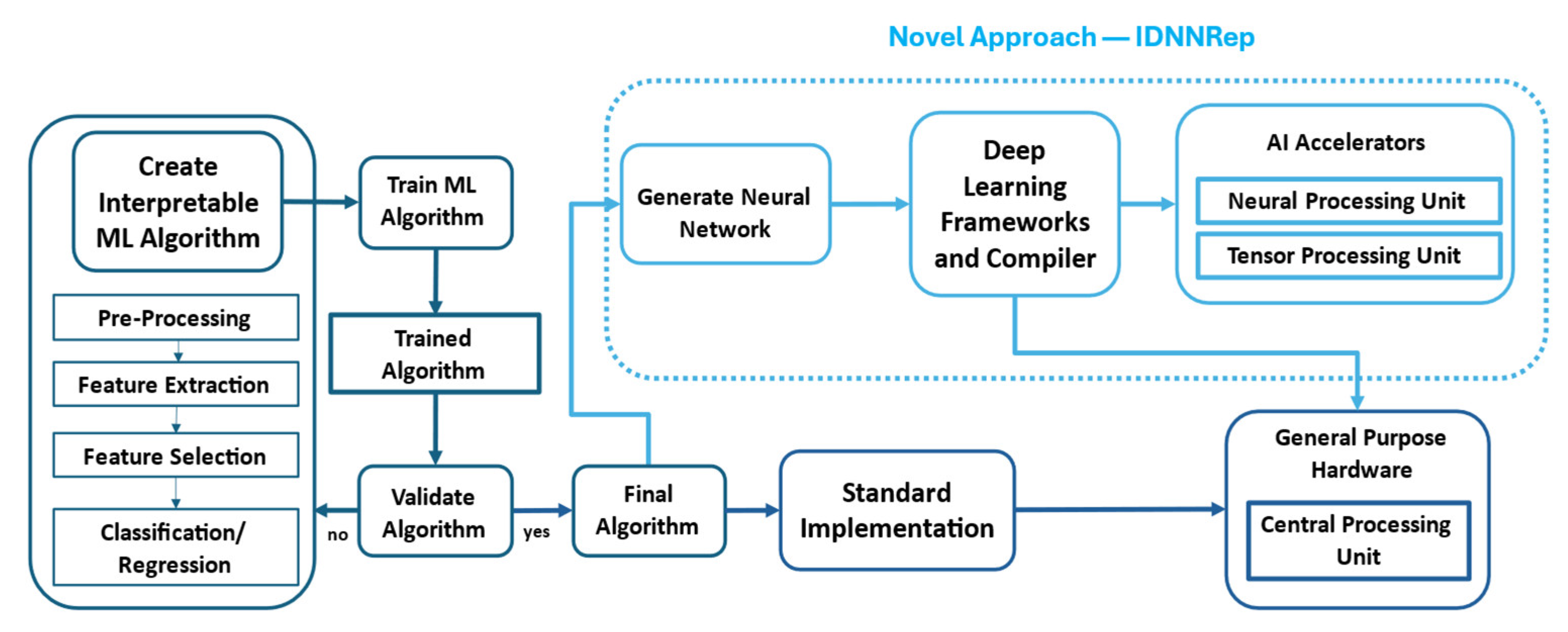
2.1. Interpretable Machine Learning Approach and ML Toolbox
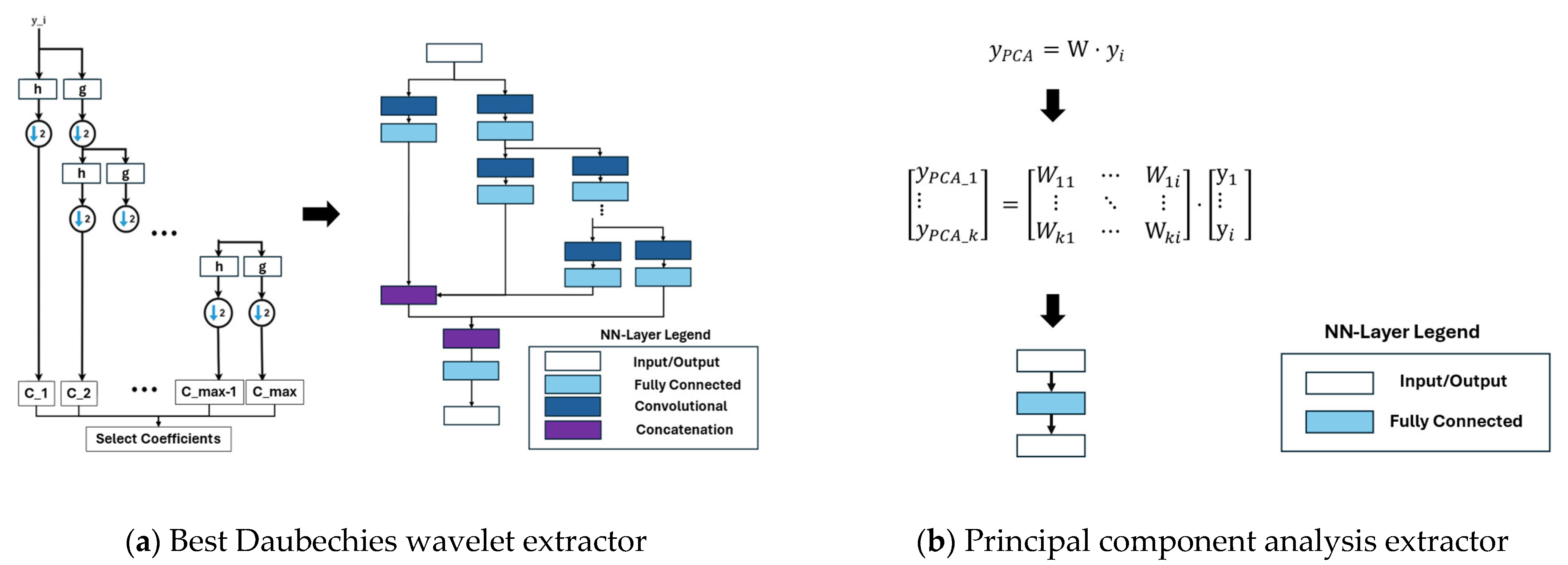
2.1.1. Feature Extraction
2.1.2. Feature Selection
2.1.3. Classification/Regression
2.2. Interpretable Deep Neural Network Representation
2.3. Deep Learning Frameworks
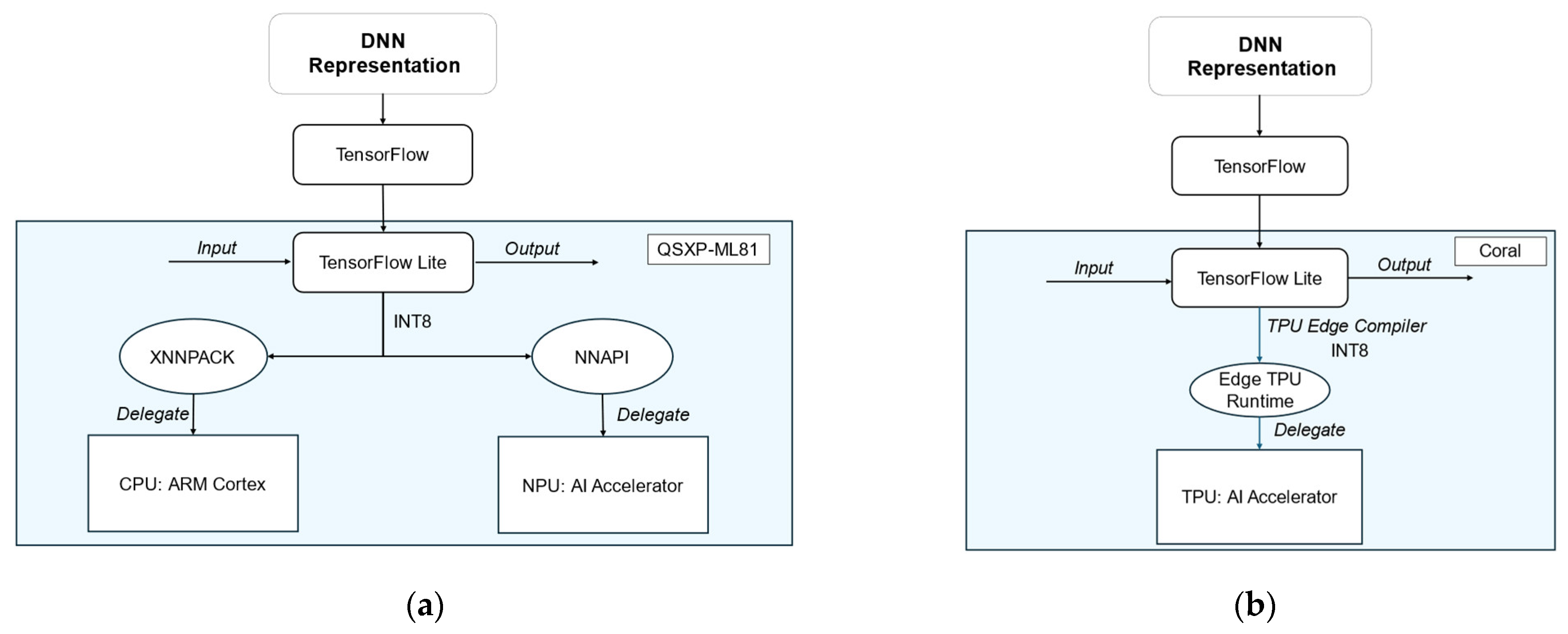
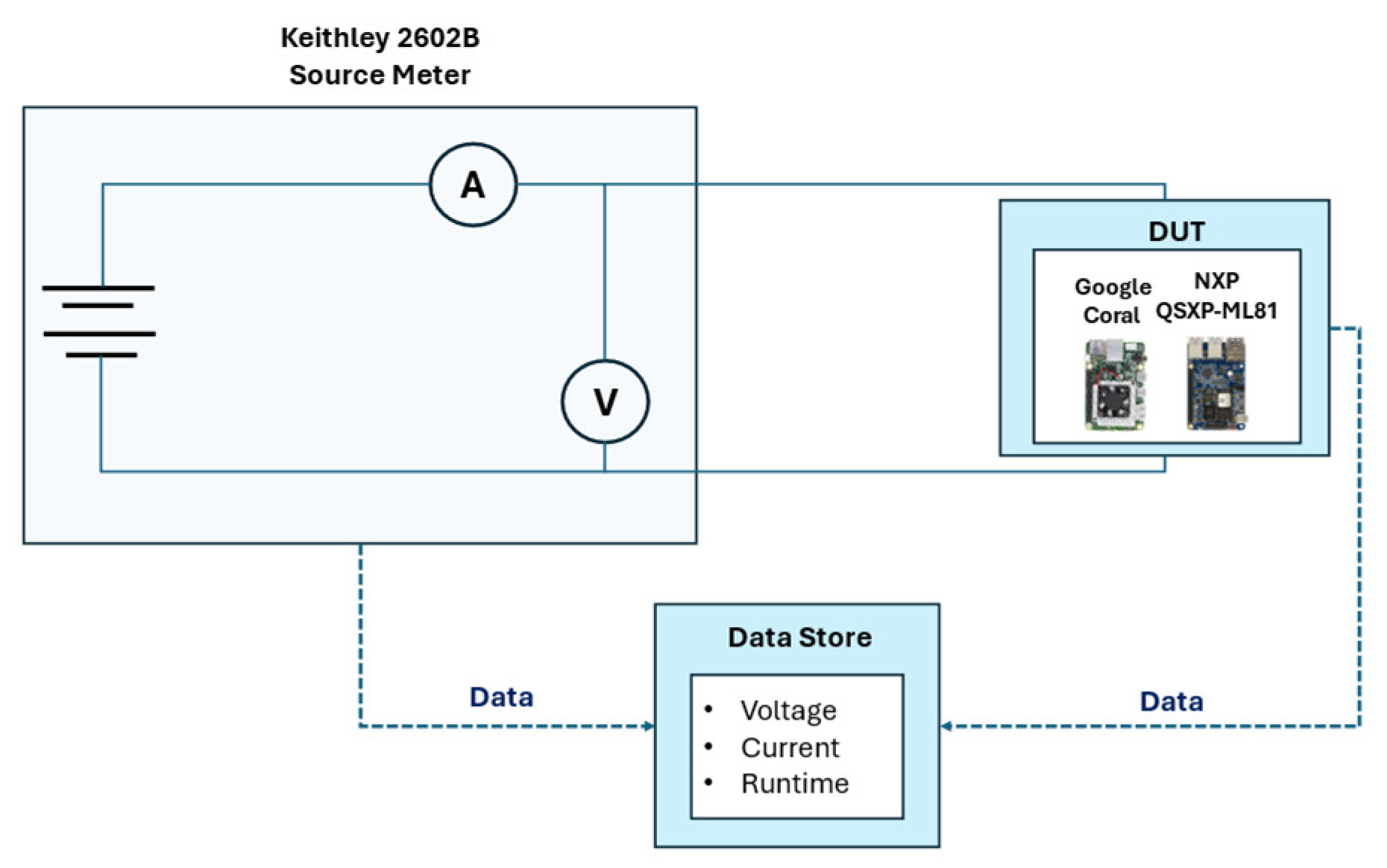
2.4. Hardware
2.4.1. NXP Neural Processing Unit
2.4.2. Google Tensor Processing Unit
2.5. Data
2.6. Evaluation
2.6.1. Accuracy
2.6.2. Inference Time
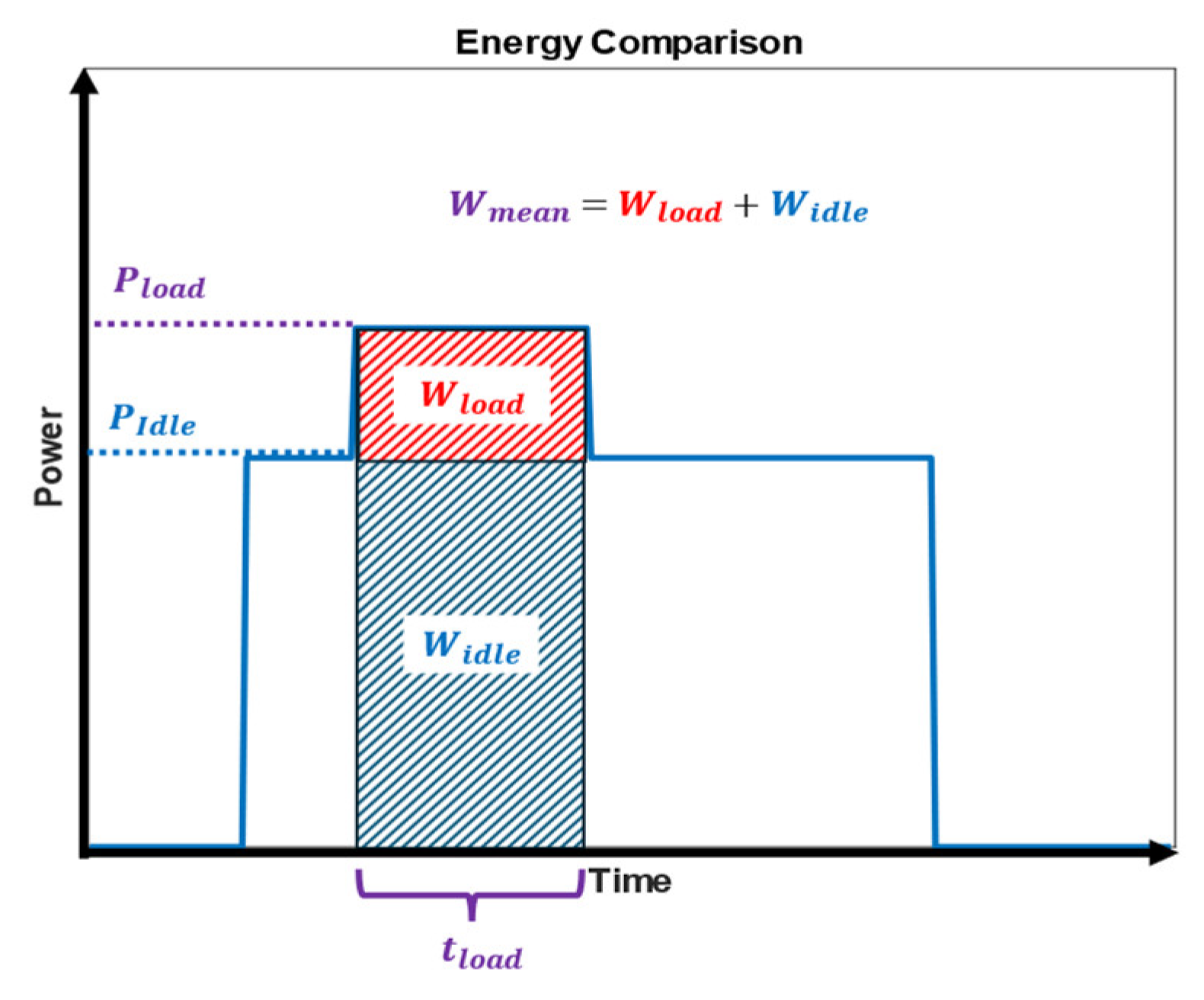
2.6.3. Energy Consumption
3. Results
3.1. Interpretable ML Algorithm
3.2. IDNNRep
3.2.1. Regression Dataset HS (Acm)
3.2.2. Classification Dataset HS (Valve)
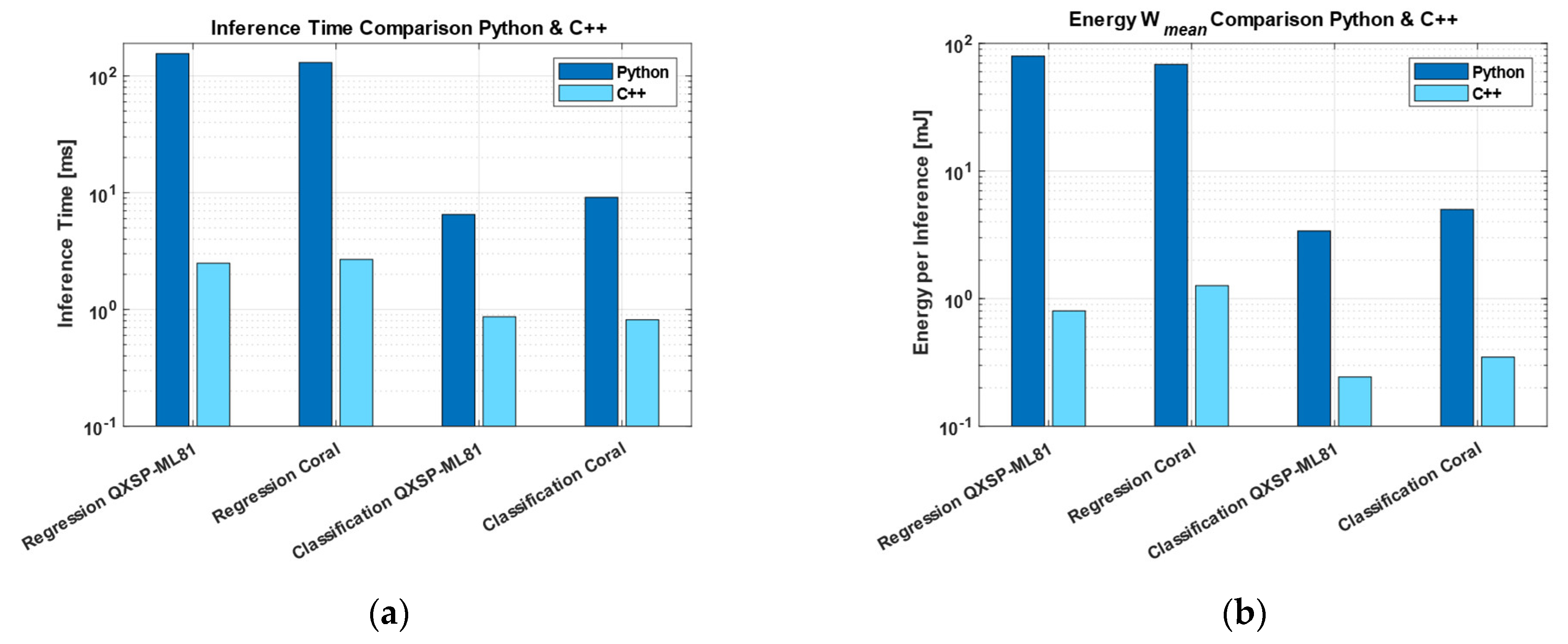
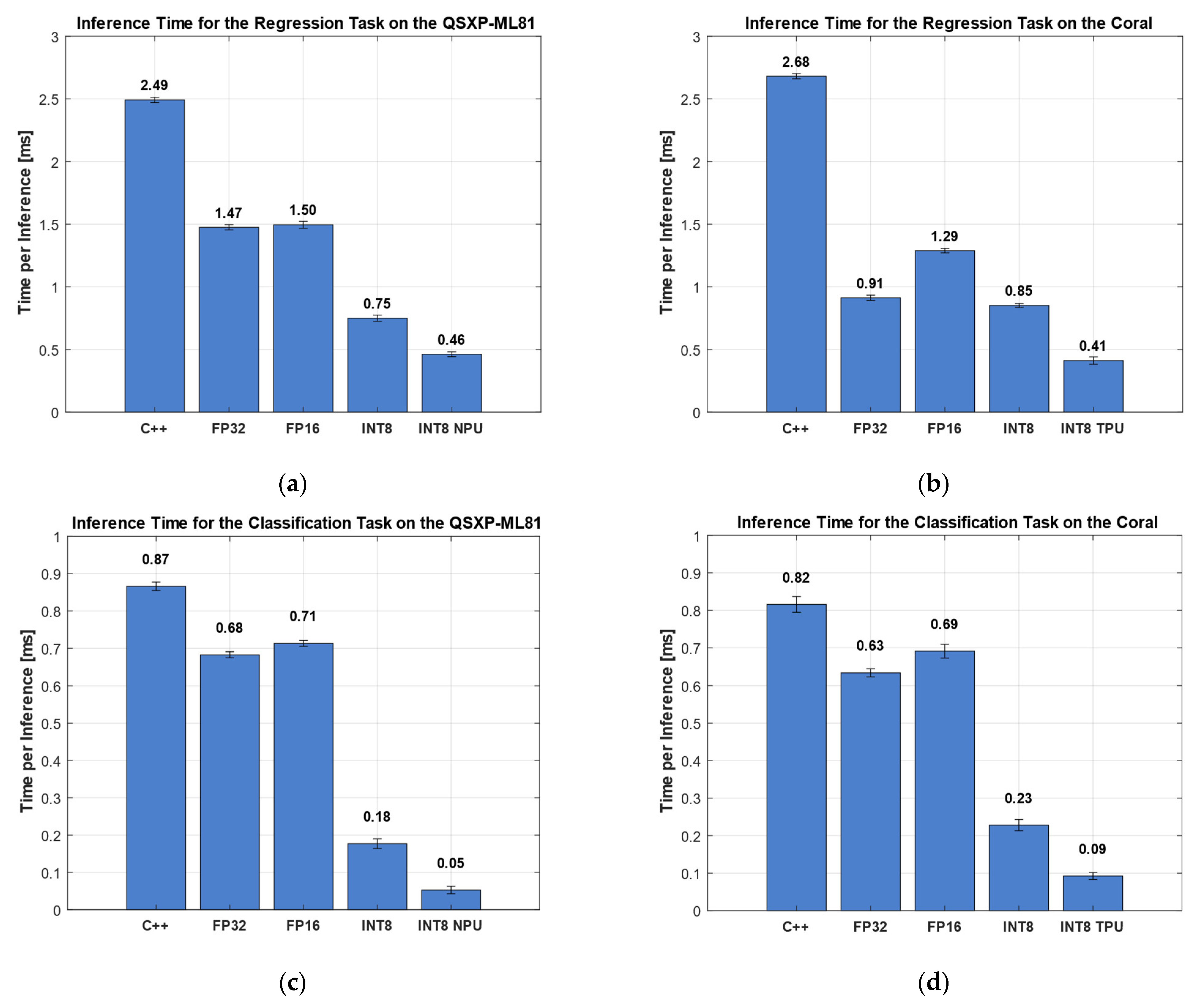
3.3. Inference Time
3.3.1. Regression Dataset HS (Acm)
3.3.2. Classification Dataset HS (Valve)
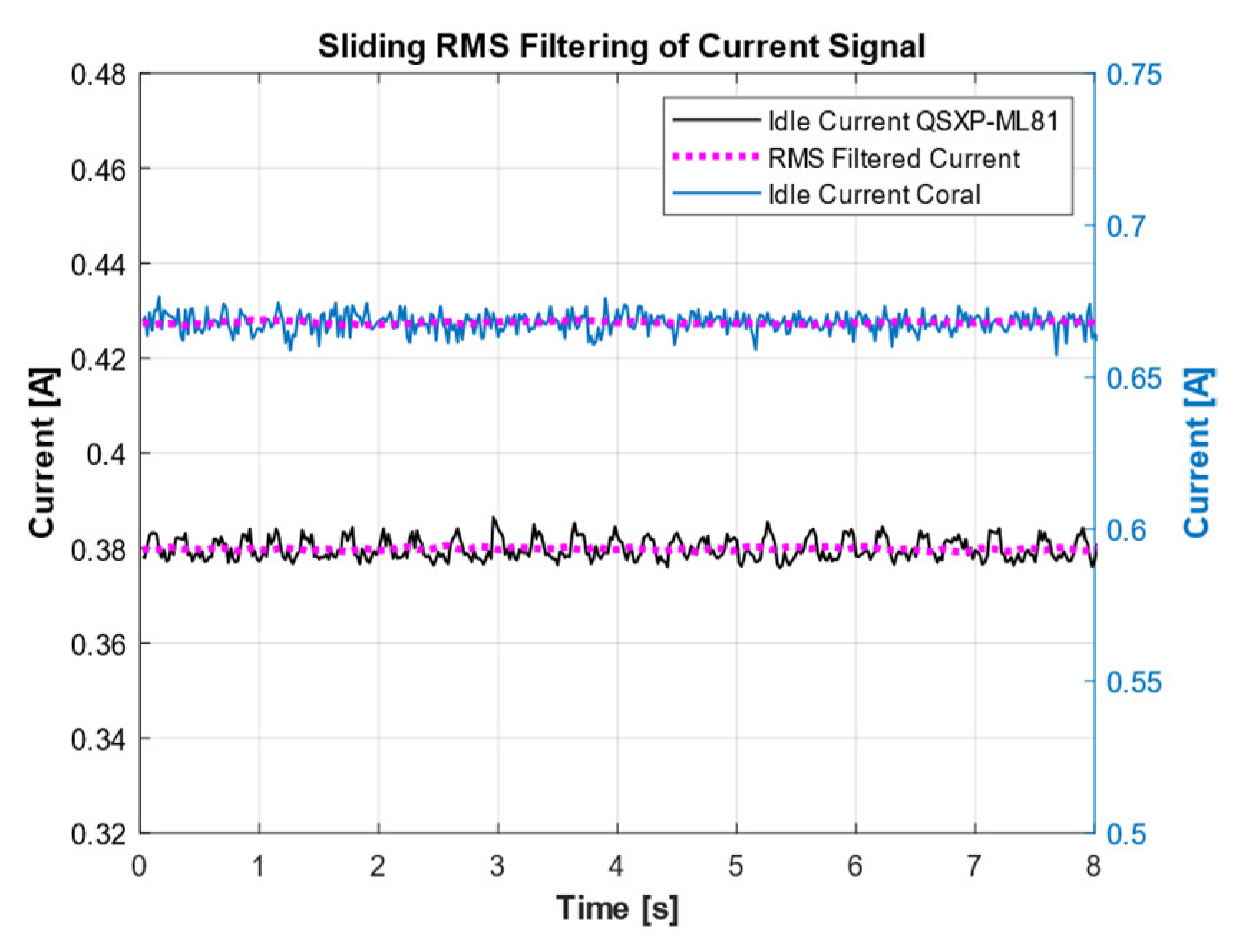
3.4. Current
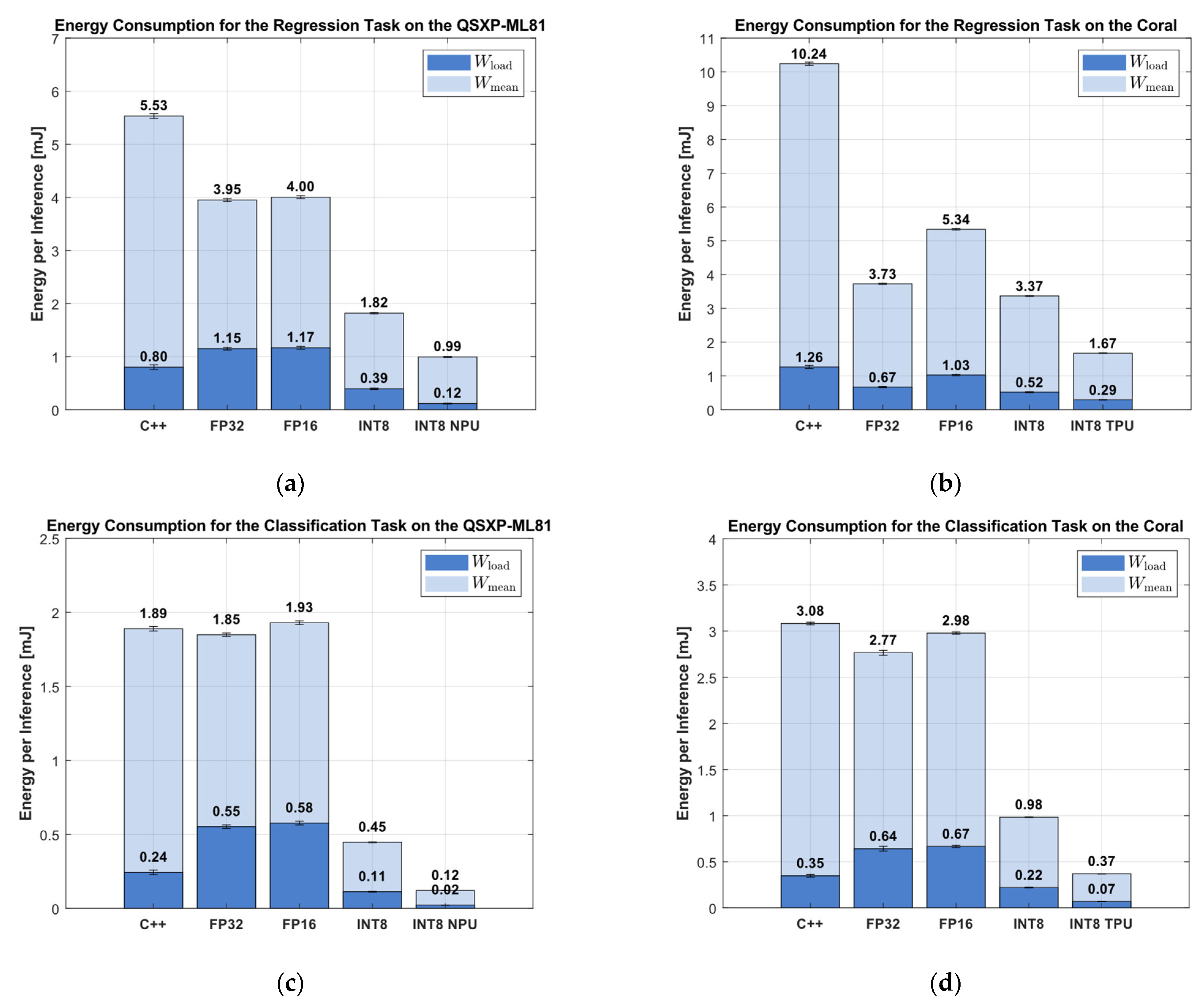
3.5. Energy Consumption
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ALA | Adaptive Linear Approximation |
| Acm | Accumulator (Hydraulic) |
| ASIC | Application-Specific Integrated Circuit |
| BDW | Best Daubechies Wavelet |
| C/R | Classification and Regression |
| CPU | Central Processing Unit |
| DLF | Deep Learning Framework |
| DNN | Deep Neural Network |
| DUT | Device under Test |
| FE | Feature Extraction |
| FESC/R | Feature Extraction, Feature Selection, and Regression or Classification |
| FP16 | Floating Point 16 |
| FP32 | Floating Point 32 |
| FPGA | Field-Programmable Gate Array |
| FS | Feature Selection |
| GM | Gas Measurement |
| GPU | Graphical Processing Unit |
| HS | Hydraulic System |
| IDNNRep | Interpretable Deep Neural Network Representation |
| INT8 | Integer 8 |
| LDA-MD | Linear Discriminant Analysis with Mahalanobis Distance Classification |
| ML | Machine Learning |
| NPU | Neural Processing Unit |
| ONNX | Open Neural Network Exchange |
| PCA | Principal Component Analysis |
| Pearson | Pearson Correlation Coefficient |
| PLSR | Partial Least Squares Regression |
| PM | Predictive Maintenance |
| PTQ | Post-Training Quantization |
| RFESVM | Recursive Feature Elimination Support Vector Machine |
| RMSE | Root Mean Square Error |
| SHM | Structural Health Monitoring |
| SM | Source Meter |
| SMU | Source Measure Unit |
| SoC | System-on-Chip |
| Spearman | Spearman Correlation Coefficient |
| StatMom | Statistical Moment |
| TL | Transfer Learning |
| TPU | Tensor Processing Unit |
References
- Mobley, R.K. An Introduction to Predictive Maintenance; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 978-0-7506-7531-4. [Google Scholar]
- Plevris, V.; Papazafeiropoulos, G. AI in Structural Health Monitoring for Infrastructure Maintenance and Safety. Infrastructures 2024, 9, 225. [Google Scholar] [CrossRef]
- Rao, B.k.n. Handbook of Condition Monitoring; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Z.; Zhang, X.; Wang, Z. Energy Aware Edge Computing: A Survey. Comput. Commun. 2020, 151, 556–580. [Google Scholar] [CrossRef]
- Kirianaki, N.V.; Yurish, S.Y.; Shpak, N.O.; Deynega, V.P. Data Acquisition and Signal Processing for Smart Sensors; Wiley: New York, NY, USA, 2002; ISBN 978-0-470-84610-0. [Google Scholar]
- Schütze, A.; Helwig, N.; Schneider, T. Sensors 4.0—Smart Sensors and Measurement Technology Enable Industry 4.0. J. Sens. Sens. Syst. 2018, 7, 359–371. [Google Scholar] [CrossRef]
- Singh, R.; Gill, S.S. Edge AI: A Survey. Internet Things Cyber-Phys. Syst. 2023, 3, 71–92. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Bavikadi, S.; Dhavlle, A.; Ganguly, A.; Haridass, A.; Hendy, H.; Merkel, C.; Reddi, V.J.; Sutradhar, P.R.; Joseph, A.; Dinakarrao, S.M.P. A Survey on Machine Learning Accelerators and Evolutionary Hardware Platforms. IEEE Des. Test 2022, 39, 91–116. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Zhou, X.; Chen, H. A Survey of FPGA-Based Deep Learning Accelerators: Challenges and Opportunities. IEEE Access 2018, 6, 12345–12356. [Google Scholar] [CrossRef]
- Park, E.; Kim, D.; Yoo, S. Energy-Efficient Neural Network Accelerator Based on Outlier-Aware Low-Precision Computation. In Proceedings of the 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 1–6 June 2018; pp. 688–698. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Zhang, Y.; Wang, Y.; Yang, Y. A Comparative Study of Open Source Deep Learning Frameworks. In Proceedings of the 2018 IEEE International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 26–28 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Carvalho, C.; Almeida, L.; Lima, J.; Santos, J.; Pinto, F. An Evaluation of Modern Accelerator-Based Edge Devices for Object Detection Applications. Mathematics 2021, 10, 4299. [Google Scholar] [CrossRef]
- Ajani, T.S.; Imoize, A.L.; Atayero, A.A. An Overview of Machine Learning within Embedded and Mobile Devices–Optimizations and Applications. Sensors 2021, 21, 4412. [Google Scholar] [CrossRef]
- Cheng, B.; Li, X.; Zhang, Y.; Chen, Z.; Xie, L. Deep Learning on Mobile Devices With Neural Processing Units. IEEE Comput. 2023, 56, 22–31. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Y.; Song, L.; Chen, F.; Tang, T. A Survey of Accelerator Architectures for Deep Neural Networks. Engineering 2020, 6, 264–274. [Google Scholar] [CrossRef]
- Silvano, C.; Ielmini, D.; Ferrandi, F.; Fiorin, L.; Curzel, S.; Benini, L.; Conti, F.; Garofalo, A.; Zambelli, C.; Calore, E.; et al. Survey on Deep Learning Hardware Accelerators for Heterogeneous HPC Platforms. ACM Comput. Surv. 2025, 57, 1–39. [Google Scholar] [CrossRef]
- Juracy, L.R.; Garibotti, R.; Moraes, F.G. From CNN to DNN Hardware Accelerators: A Survey on Design, Exploration, Simulation, and Frameworks. Found. Trends® Electron. Des. Autom. 2023, 13, 270–344. [Google Scholar] [CrossRef]
- Buhrmester, V.; Münch, D.; Arens, M. Analysis of Explainers of Black Box Deep Neural Networks for Computer Vision: A Survey. Mach. Learn. Knowl. Extr. 2021, 3, 966–989. [Google Scholar] [CrossRef]
- Dorst, T.; Robin, Y.; Schneider, T.; Schütze, A. Automated ML Toolbox for Cyclic Sensor Data. In Proceedings of the Mathematical and Statistical Methods for Metrology MSMM, Virtual, 31 May–1 June 2021. [Google Scholar]
- Schneider, T.; Helwig, N.; Schütze, A. Automatic Feature Extraction and Selection for Classification of Cyclical Time Series Data. Tm-Tech. Mess. 2017, 84, 198–206. [Google Scholar] [CrossRef]
- Schneider, T.; Helwig, N.; Schütze, A. Industrial Condition Monitoring with Smart Sensors Using Automated Feature Extraction and Selection. Meas. Sci. Technol. 2018, 29, 094002. [Google Scholar] [CrossRef]
- Goodarzi, P.; Schütze, A.; Schneider, T. Domain Shifts in Industrial Condition Monitoring: A Comparative Analysis of Automated Machine Learning Models. J. Sens. Sens. Syst. 2025, 14, 119–132. [Google Scholar] [CrossRef]
- Zaniolo, L.; Garbin, C.; Marques, O. Deep Learning for Edge Devices. IEEE Potentials 2023, 42, 39–45. [Google Scholar] [CrossRef]
- Voghoei, S.; Tonekaboni, N.H.; Wallace, J.G.; Arabnia, H.R. Deep Learning at the Edge. In Proceedings of the 2018 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 12–14 December 2018; pp. 895–901. [Google Scholar] [CrossRef]
- Hsu, K.-C.; Tseng, H.-W. Accelerating Applications Using Edge Tensor Processing Units. In Proceedings of the International Conference for High Performance Computing, New York, NY, USA, 14–19 November 2021; Networking, Storage and Analysis; Association for Computing Machinery: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Pan, Z.; Mishra, P. Hardware Acceleration of Explainable Machine Learning. In Proceedings of the 2022 Design, Automation & Test in Europe Conference & Exhibition, Antwerp, Belgium, 14–23 March 2022; pp. 1127–1130. [Google Scholar] [CrossRef]
- Schauer, J.; Goodarzi, P.; Schütze, A.; Schneider, T. Deep Neural Network Representation for Explainable Machine Learning Algorithms: A Method for Hardware Acceleration. In Proceedings of the 2024 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, Scotland, 20–23 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Schauer, J.; Goodarzi, P.; Schütze, A.; Schneider, T. Efficient hardware implementation of interpretable machine learning based on deep neural network representations for sensor data processing. J. Sens. Sens. Syst. 2025, 14, 169–185. [Google Scholar] [CrossRef]
- Schauer, J.; Goodarzi, P.; Schütze, A.; Schneider, T. Energy-Efficient Implementation of Explainable Feature Extraction Algorithms for Smart Sensor Data Processing. In Proceedings of the 2024 IEEE SENSORS, Kobe, Japan, 20–23 October 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Choukroun, Y.; Kravchik, E.; Yang, F.; Kisilev, P. Low-Bit Quantization of Neural Networks for Efficient Inference. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3009–3018. [Google Scholar] [CrossRef]
- ZeMA-gGmbh LMT-ML-Toolbox. GitHub Repository. 2017. Available online: https://github.com/ZeMA-gGmbH/LMT-ML-Toolbox (accessed on 19 December 2024).
- Matlab Matlab, Version R2023b; The MathWorks: Natick, MA, USA, 2012.
- Olszewski, R.T. Generalized Feature Extraction for Structural Pattern Recognition in Time-Series Data; Carnegie Mellon University: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Rowe, A.C.; Abbott, P.C. Daubechies Wavelets and Mathematica. Comput. Phys. 1995, 9, 635–648. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Yong, M.; Daoying, P.; Yuming, L.; Youxian, S. Accelerated Recursive Feature Elimination Based on Support Vector Machine for Key Variable Identification. Chin. J. Chem. Eng. 2006, 14, 65–72. [Google Scholar] [CrossRef]
- Wissler, C. The Spearman Correlation Formula. Science 1905, 22, 309–311. [Google Scholar] [CrossRef] [PubMed]
- Riffenburgh, R.H. Linear Discriminant Analysis. Ph.D. Thesis, Virginia Polytechnic Institute, Blacksburg, VA, USA, 1957. [Google Scholar] [CrossRef]
- McLachlan, G.J. Mahalanobis Distance. Resonance 1999, 4, 20–26. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial Least-Squares Regression: A Tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- ONNX Contributors. Open Neural Network Exchange (ONNX). 2023. Available online: https://onnx.ai (accessed on 23 November 2024).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283, ISBN 978-1-931971-33-1. [Google Scholar]
- TensorFlow Authors. TensorFlow Lite Post-Training Quantization. 2022. Available online: https://www.tensorflow.org/lite/performance/post_training_quantization (accessed on 8 September 2025).
- Nahshan, Y.; Chmiel, B.; Baskin, C. Loss Aware Post-Training Quantization. Mach. Learn. 2021, 110, 3245–3262. [Google Scholar] [CrossRef]
- Semiconductors, NXP. eIQ Toolkit: End-to-End Model Development and Deployment. 2025. Available online: https://www.nxp.com/assets/block-diagram/en/EIQ-TOOLKIT.pdf (accessed on 1 October 2024).
- Karo electronics. QXSP Documentation. Available online: https://karo-electronics.github.io/docs/getting-started/qsbase3/quickstart-qsbase3.html (accessed on 8 September 2025).
- Google. Coral Dev Board Documentation. 2023. Available online: https://coral.ai/products/dev-board/#documentation (accessed on 20 January 2025).
- Schneider, T.; Klein, S.; Manuel, B. Condition Monitoring of Hydraulic Systems Data Set at ZeMA. Zenodo. 2018. Available online: https://doi.org/10.5281/zenodo.1323610 (accessed on 20 September 2024).
- Tektronix. Series 2600B System Source Meter Instrument Reference Manual. 2016. Available online: https://download.tek.com/manual/2600BS-901-01_C_Aug_2016_2.pdf (accessed on 8 September 2025).
- Tu, X.; Mallik, A.; Chen, D.; Han, K.; Altintas, O.; Wang, H.; Xie, J. Unveiling Energy Efficiency in Deep Learning: Measurement, Prediction, and Scoring across Edge Devices. In Proceedings of the Eighth ACM/IEEE Symposium on Edge Computing, Wilmington, DE, USA, 6–9 December 2023; pp. 80–93. [Google Scholar] [CrossRef]
- Zoni, D.; Galimberti, A.; Fornaciari, W. A Survey on Run-Time Power Monitors at the Edge. ACM Comput. Surv. 2023, 55, 1–33. [Google Scholar] [CrossRef]
- TensorFlow. TensorFlow Lite. 2020. Available online: https://www.tensorflow.org/lite/guide (accessed on 20 January 2025).
- Cpp. Date and Time Library. 2024. Available online: https://en.cppreference.com/w/cpp/chrono/steady_clock.html (accessed on 20 January 2025).
- Python. Time Access and Conversions. 2024. Available online: https://docs.python.org/3/library/time.html (accessed on 20 January 2025).
- Ahn, H.; Chen, T.; Alnaasan, N.; Shafi, A.; Abduljabbar, M.; Subramoni, H.; Panda, D.K. Performance Characterization of Using Quantization for DNN Inference on Edge Devices. In Proceedings of the 2023 IEEE 7th International Conference on Fog and Edge Computing (ICFEC), Bangalore, India, 1–4 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Robin, Y.; Amann, J.; Schneider, T.; Schütze, A.; Bur, C. Comparison of Transfer Learning and Established Calibration Transfer Methods for Metal Oxide Semiconductor Gas Sensors. Atmosphere 2023, 14, 1123. [Google Scholar] [CrossRef]



| Processing Step | Methods |
|---|---|
| Feature Extraction | Adaptive linear approximation (ALA) [34] |
| Best Daubechies wavelet (BDW) [35] | |
| Principal component analysis (PCA) [36] | |
| Statistical moment (StatMom) [22] | |
| Feature Selection | Pearson correlation coefficient (Pearson) [37] |
| RELIEFF [38] | |
| Recursive feature elimination support vector machine (RFESVM) [39] | |
| Spearman correlation coefficient (Spearman) [40] | |
| Classification | Linear discriminant analysis with Mahalanobis distance classification (LDA-MD) [41,42] |
| Regression | Partial least squares regression (PLSR) [43] |
| Dataset | Observations | Signal Size | Task |
|---|---|---|---|
| HS (Valve) | 1449 | 6000 | Classification |
| HS (Acm) | 1449 | 6000 | Regression |
| Range | Accuracy | |
|---|---|---|
| Voltage Source Specification | 0 ... 6 V | |
| Current Measurement Specification | 0 ... 3 A |
| Task | Accuracy: FP32 Python, C++, DNN | Accuracy: FP16 | Accuracy: INT8 |
|---|---|---|---|
| Regression | 91.8% (RMSE: 10.6 bar) | 90.4% (RMSE: 12.5 bar) | 85.9% (RMSE: 18.3 bar) |
| Classification | 99.9% | 99.8% | 99.4% |
| Regression [%] | Classification [%] | |||
|---|---|---|---|---|
| QXSP-ML81 | Coral | QXSP-ML81 | Coral | |
| FP32 | −40.8 | −65.9 | −22.9 | −22.3 |
| FP16 | −40.0 | −51.9 | −19.5 | −15.3 |
| INT8 | −69.9 | −68.3 | −80.0 | −72.1 |
| INT8 AI ACC | −81.5 | −84.6 | −94.0 | −88.7 |
| Regression [%] | Classification [%] | |||||||
|---|---|---|---|---|---|---|---|---|
| QXSP-ML81 | Coral | QXSP-ML81 | Coral | |||||
| FP32 | −28.6 | +43.6 | −63.6 | −47.0 | −2.2 | +127.2 | −10.3 | +84.2 |
| FP16 | −27.6 | +45.4 | −47.9 | −18.8 | −2.1 | +137.0 | −3.4 | +91.4 |
| INT8 | −67.1 | −50.8 | −67.1 | −58.9 | −76.3 | −53.5 | −68.1 | −36.8 |
| INT8 AI ACC | −82.0 | −85.6 | −83.7 | −76.8 | −93.6 | −90.9 | −88.0 | −80.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schauer, J.; Goodarzi, P.; Morsch, J.; Schütze, A. A Performance Study of Deep Neural Network Representations of Interpretable ML on Edge Devices with AI Accelerators. Sensors 2025, 25, 5681. https://doi.org/10.3390/s25185681
Schauer J, Goodarzi P, Morsch J, Schütze A. A Performance Study of Deep Neural Network Representations of Interpretable ML on Edge Devices with AI Accelerators. Sensors. 2025; 25(18):5681. https://doi.org/10.3390/s25185681
Chicago/Turabian StyleSchauer, Julian, Payman Goodarzi, Jannis Morsch, and Andreas Schütze. 2025. "A Performance Study of Deep Neural Network Representations of Interpretable ML on Edge Devices with AI Accelerators" Sensors 25, no. 18: 5681. https://doi.org/10.3390/s25185681
APA StyleSchauer, J., Goodarzi, P., Morsch, J., & Schütze, A. (2025). A Performance Study of Deep Neural Network Representations of Interpretable ML on Edge Devices with AI Accelerators. Sensors, 25(18), 5681. https://doi.org/10.3390/s25185681







