A Hybrid Model Based on a Dual-Attention Mechanism for the Prediction of Remaining Useful Life of Aircraft Engines
Abstract
1. Introduction
- (1)
- To overcome the limitations of traditional models in feature extraction, the proposed approach introduces distinct attention mechanisms to separately capture temporal and sensor-specific features, thereby enhancing the richness of the learned representations.
- (2)
- For temporal feature extraction, a multi-head full attention mechanism is employed. Specifically, an inverted module from the iTransformer architecture is adopted to allow the model to focus on the temporal behavior of individual sensor sequences while disregarding inter-sensor interference.
- (3)
- For sensor feature extraction, a channel attention mechanism is utilized to learn sensor-specific weights. This study is, to our knowledge, the earliest to implement a channel attention strategy tailored for sensor-wise feature learning in the context of RUL estimation.
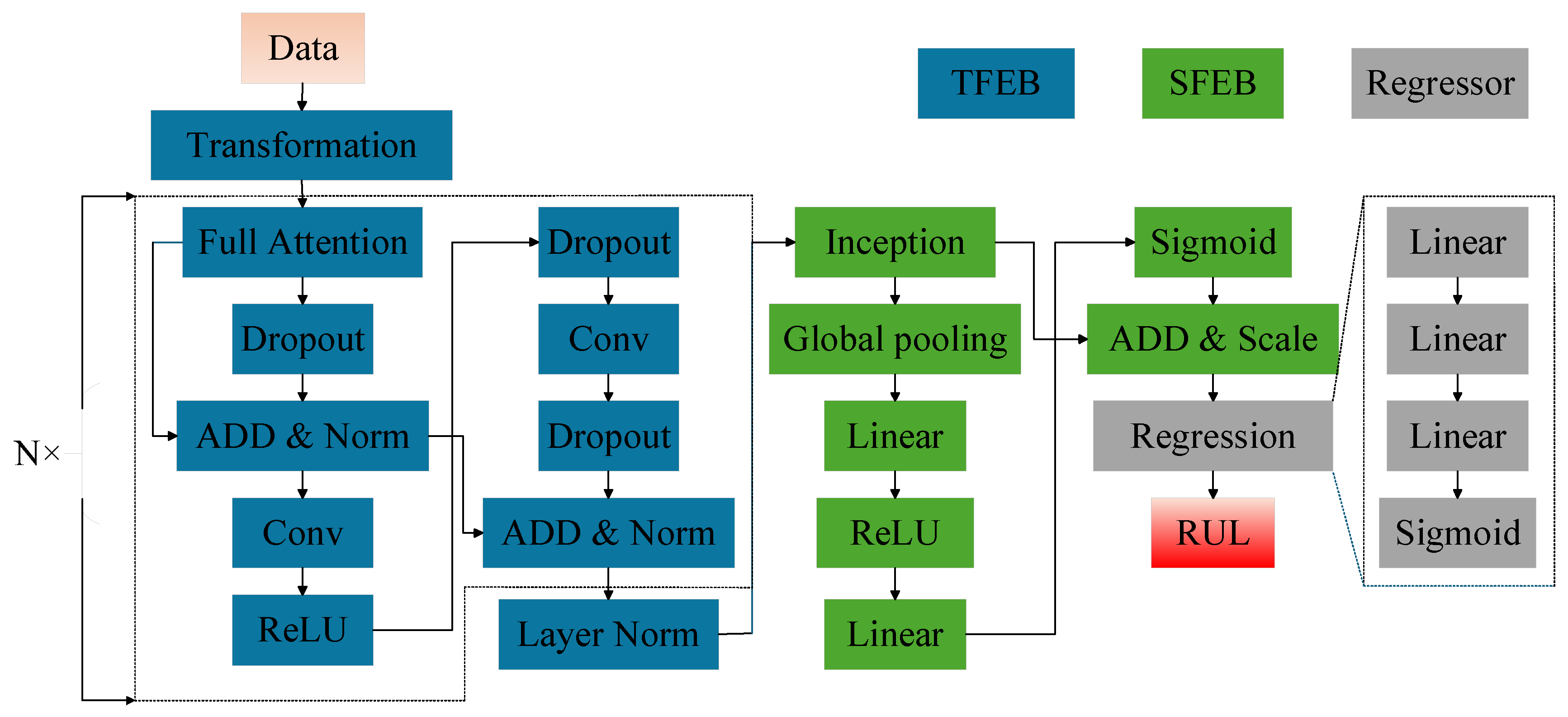
2. Proposed Methodology
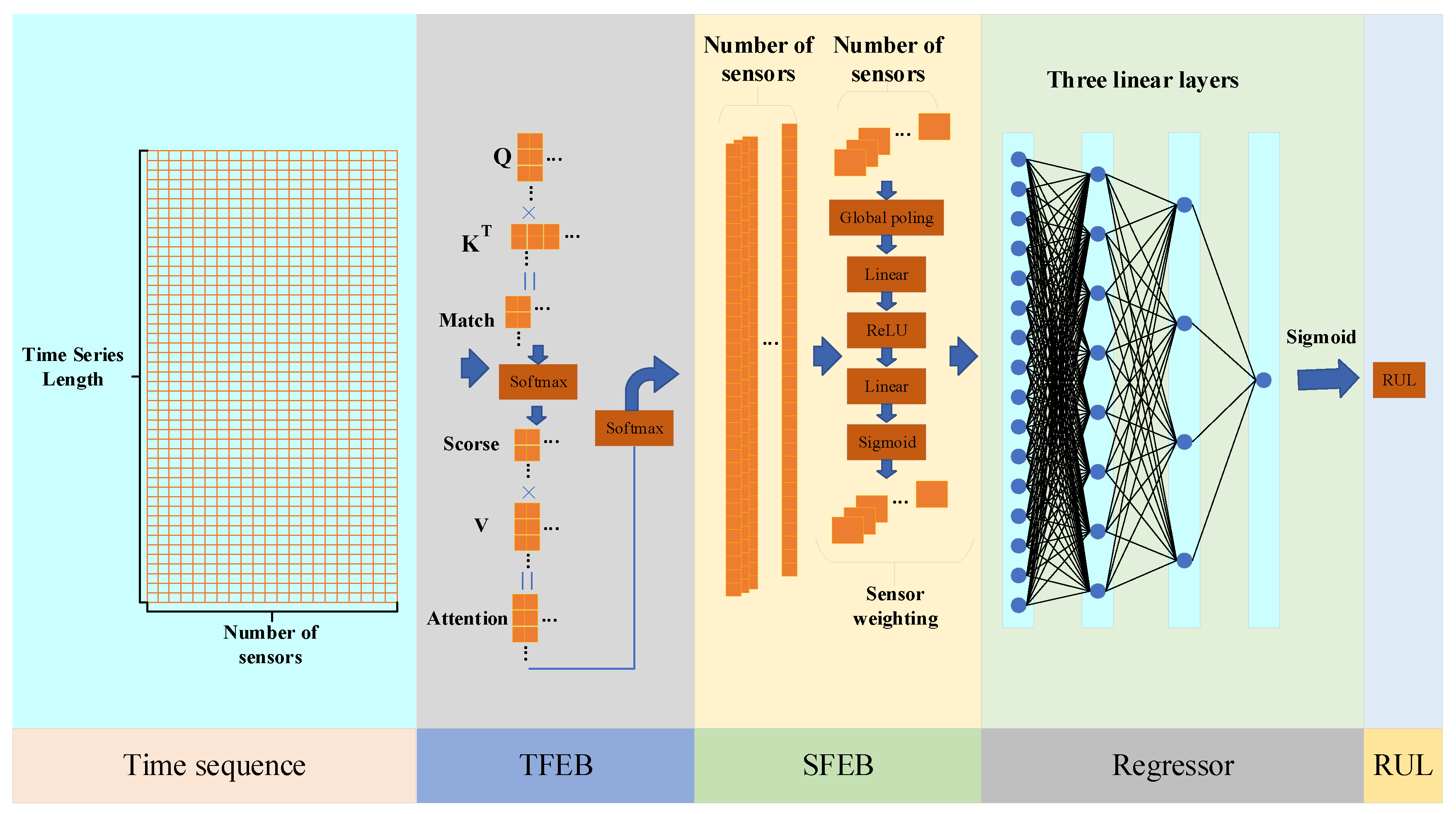
2.1. Time Feature Extraction Block
2.1.1. Embedding Layer
2.1.2. Temporal Attention Mechanism
2.1.3. Projection Layer
2.2. Sensor Feature Extraction Block
- (1)
- Squeeze: The temporal data in each sensor channel is compressed into a global feature vector, summarizing the overall temporal behavior of each sensor.
- (2)
- Excitation: A nonlinear transformation is applied to the global feature vector, and attention weights are generated using a sigmoid activation function. These weights are then applied to adjust the original input, thereby enhancing the contribution of important sensor features and suppressing less informative ones.
2.3. Regressor
3. Experimental Study
3.1. Dataset
3.2. Experimental Setting
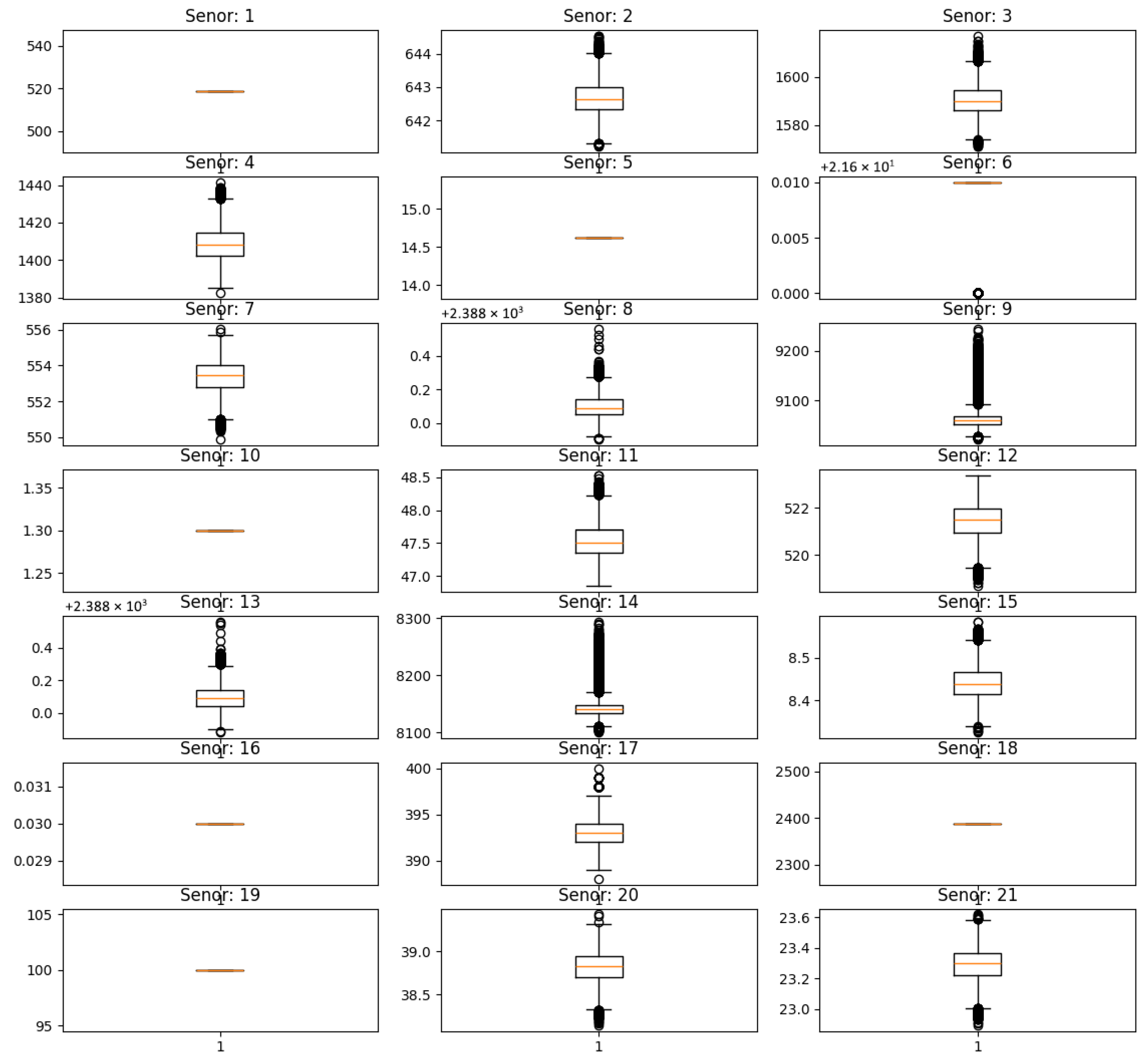
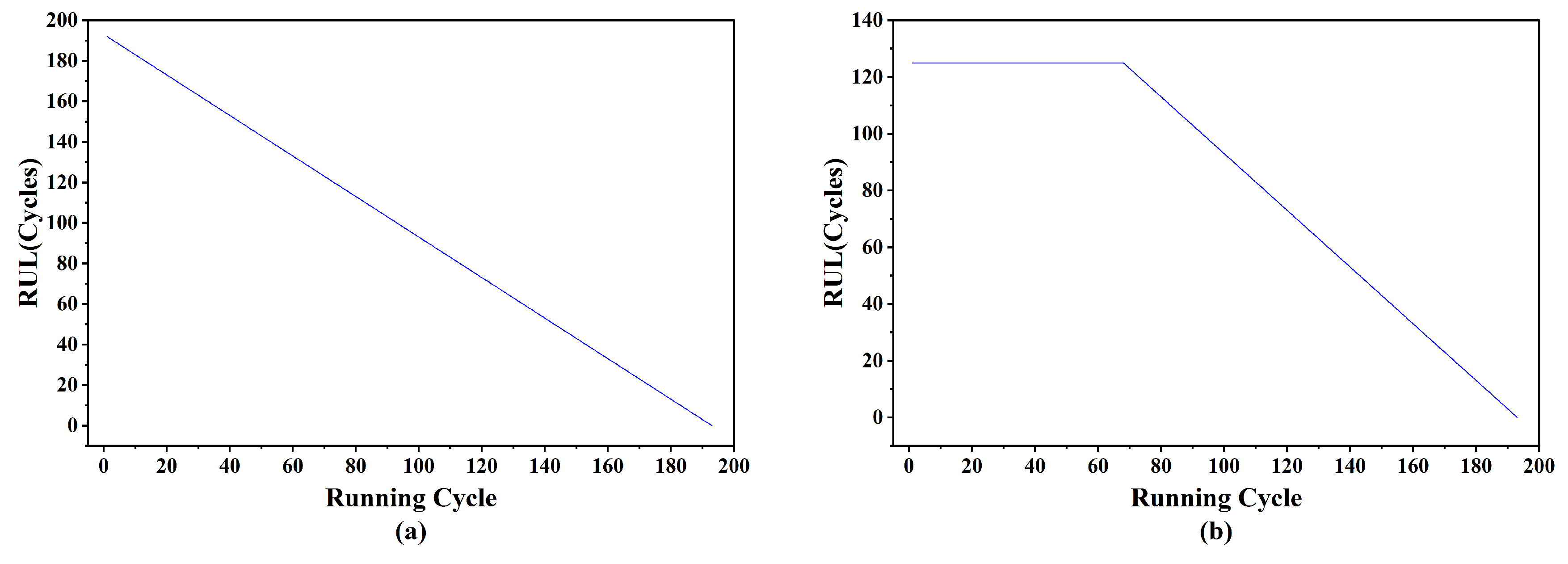
3.2.1. Data Preprocessing
- (1)
- Data filtering
- (2)
- Data normalization
- (3)
- Sliding window settings
- (4)
- Training set and label creation
3.2.2. Evaluation Metrics
3.2.3. Training Parameter Settings
3.3. Analysis of HMDAM
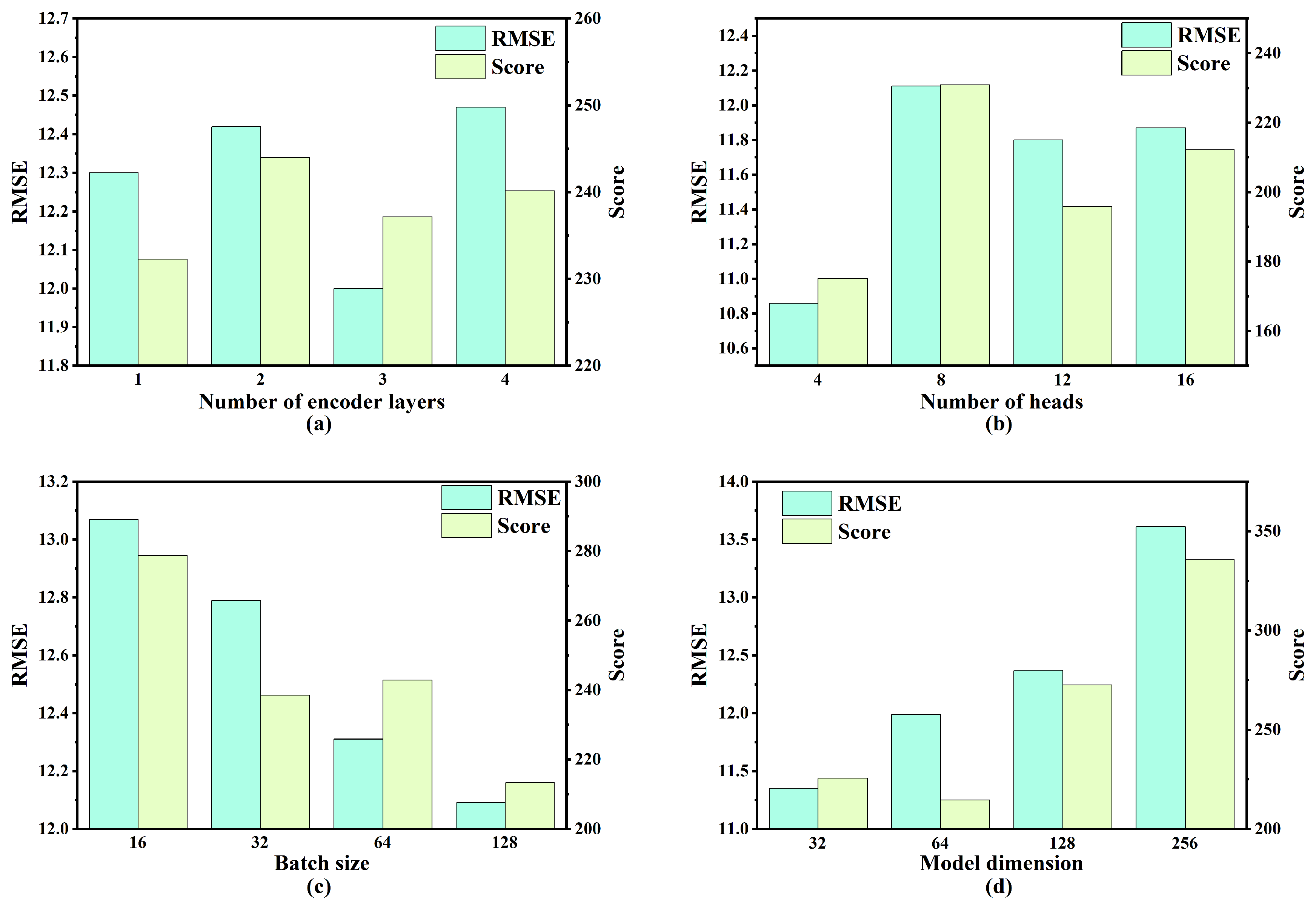
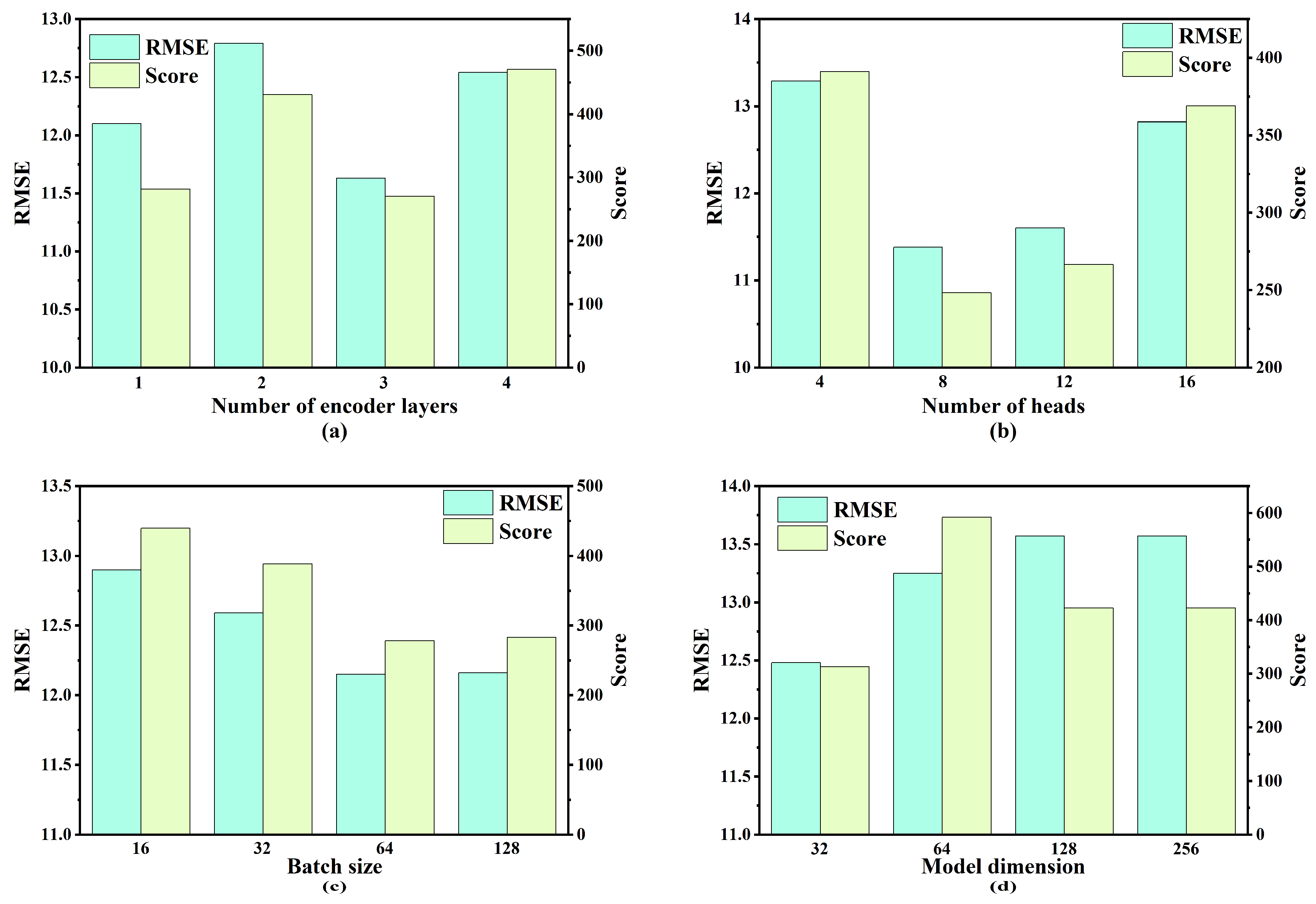
3.3.1. Setting of Sliding Window Size
3.3.2. Model Parameter Settings
3.3.3. HMDAM Ablation Experiment
- (1)
- The baseline Transformer model without any enhancements;
- (2)
- The Transformer model equipped with only the TFEB, referred to as iTransformer;
- (3)
- The Transformer model integrated solely with the SFEB, referred to as ST.
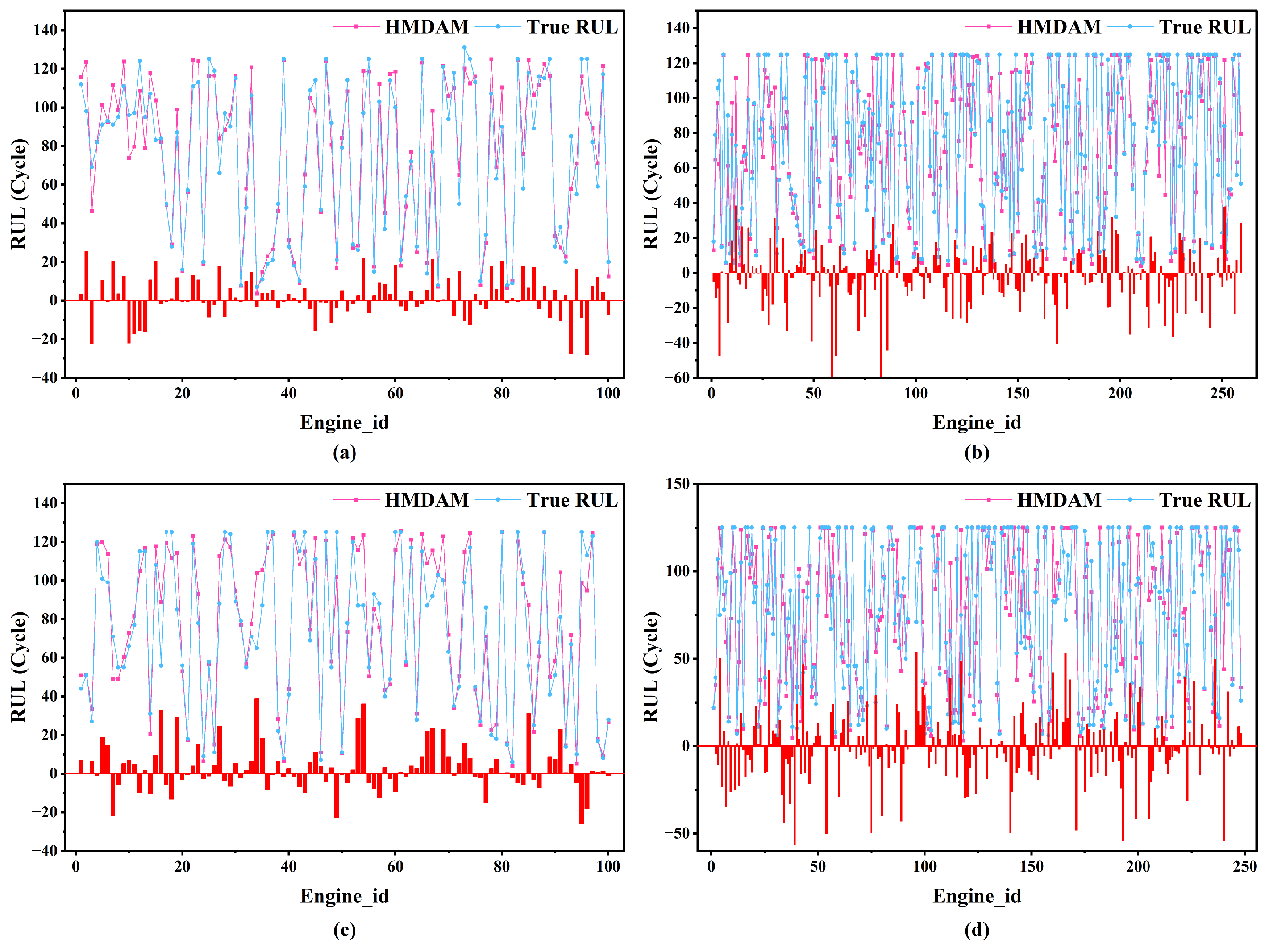
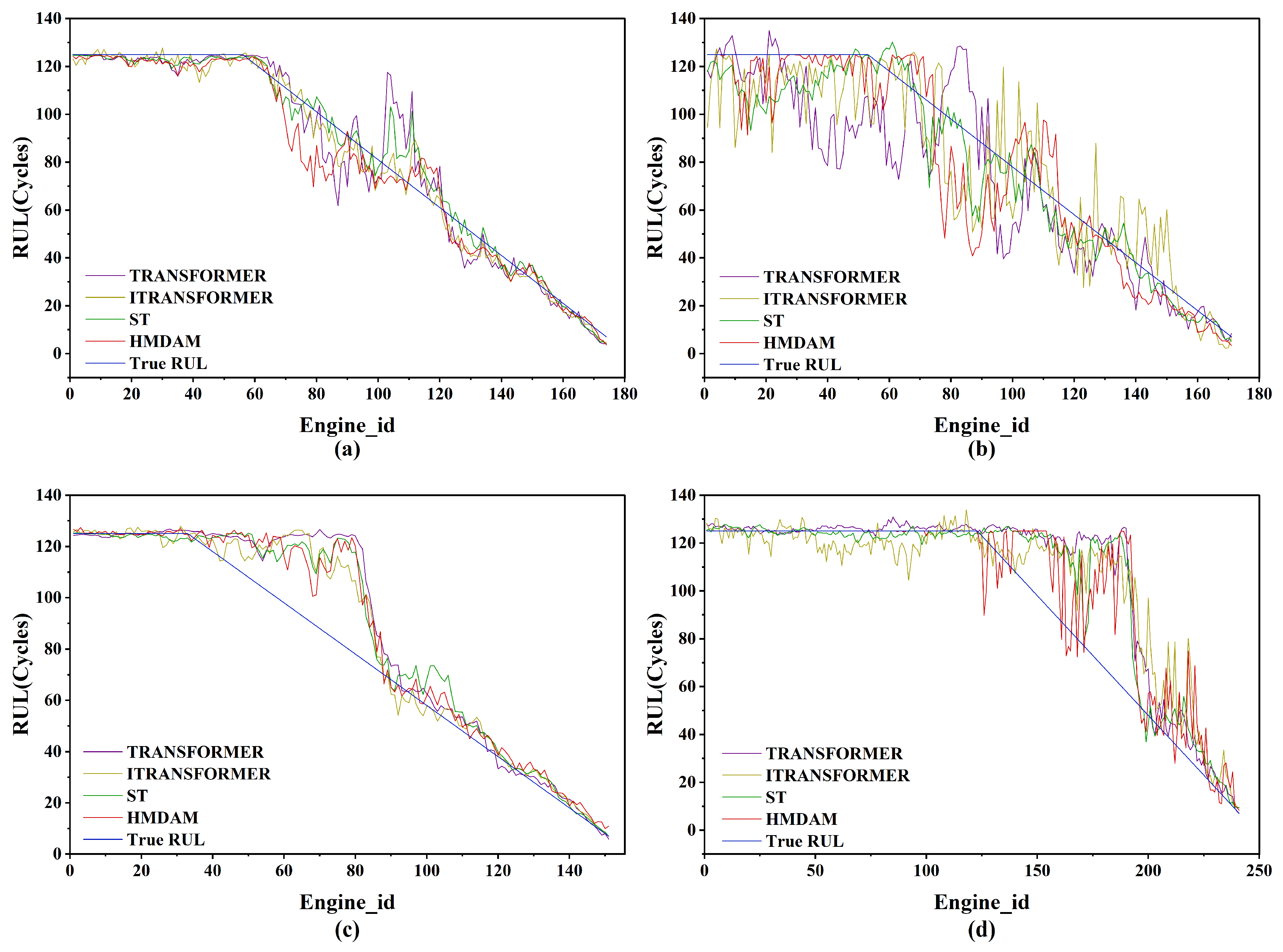
3.3.4. Analysis of Model Results
3.3.5. Model Efficiency Analysis
3.3.6. Comparison with Other Methods
| Method | FD001 | FD002 | FD003 | FD004 | Average |
|---|---|---|---|---|---|
| BiLSTM ([45]) | 13.65 | 23.18 | 13.74 | 24.86 | 18.86 |
| DCNN ([46]) | 12.61 | 22.36 | 12.64 | 23.31 | 17.73 |
| CatBoos ([47]) | 15.8 | 21.4 | 16.0 | 22.4 | 18.90 |
| CDLSTM ([48]) | 13.99 | 17.53 | 12.15 | 20.91 | 16.15 |
| HMC ([49]) | 13.84 | 20.74 | 14.41 | 22.73 | 17.93 |
| BiGRU-AS ([50]) | 13.68 | 20.81 | 15.53 | 27.31 | 19.33 |
| DSAN ([30]) | 13.4 | 22.06 | 15.12 | 21.03 | 17.90 |
| DAA ([51]) | 12.25 | 17.08 | 13.39 | 19.86 | 15.65 |
| IMDSSN ([52]) | 12.14 | 17.40 | 12.35 | 19.78 | 15.42 |
| BGT ([44]) | 12.09 | 11.46 | 10.16 | 13.89 | 11.9 |
| CTNet ([43]) | 11.64 | 13.67 | 11.28 | 14.62 | 12.80 |
| HMDAM | 10.82 | 15.33 | 11.21 | 17.48 | 13.71 |
| Method | FD001 | FD002 | FD003 | FD004 | Average |
|---|---|---|---|---|---|
| BiLSTM ([45]) | 295 | 4130 | 317 | 5430 | 2543 |
| DCNN ([46]) | 273.7 | 1041.2 | 284.1 | 12,466 | 5858.9 |
| CatBoos ([47]) | 398.7 | 3493.2 | 584.2 | 3203.4 | 1919.9 |
| CDLSTM ([48]) | 320 | 1758 | 221 | 2633 | 1233 |
| HMC ([49]) | 427 | 19,400 | 2977 | 10,374 | 8295 |
| BiGRU-AS ([50]) | 284 | 2454 | 428 | 4708 | 1968.5 |
| DSAN ([30] | 336 | 1946 | 251 | 3671 | 1571.3 |
| DAA ([51]) | 198 | 1575 | 290 | 1741 | 951 |
| IMDSSN ([52]) | 206.11 | 1775.15 | 229.54 | 2852.81 | 1265.9 |
| BGT ([44]) | 262.67 | 550.52 | 196.94 | 963.36 | 493.37 |
| CTNet ([43]) | 187 | 809 | 187 | 844 | 506.75 |
| HMDAM | 170.07 | 1030.42 | 239.47 | 1738.19 | 794.53 |
4. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.G.; Li, N.P.; Guo, L.; Li, N.B.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Proc. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Hu, Y.; Miao, X.W.; Si, Y.; Pan, E.S.; Zio, E. Prognostics and health management: A review from the perspectives of design, development and decision. Reliab. Eng. Syst. Saf. 2022, 217, 108063. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Shu, T.X.; Wan, J.F.; de Silva, C.W.; Wang, Z.R. A Two-Stage Approach for the Remaining Useful Life Prediction of Bearings Using Deep Neural Networks. IEEE Trans. Ind. Inform. 2019, 15, 3703–3711. [Google Scholar] [CrossRef]
- She, D.M.; Jia, M.P. A BiGRU method for remaining useful life prediction of machinery. Measurement 2021, 167, 108277. [Google Scholar] [CrossRef]
- Zhou, J.H.; Qin, Y.; Luo, J.; Wang, S.L.; Zhu, T. Dual-Thread Gated Recurrent Unit for Gear Remaining Useful Life Prediction. IEEE Trans. Ind. Inform. 2023, 19, 8307–8318. [Google Scholar] [CrossRef]
- Pan, Y.; Kang, S.J.; Kong, L.G.; Wu, J.J.; Yang, Y.H.; Zuo, H.F. Remaining useful life prediction methods of equipment components based on deep learning for sustainable manufacturing: A literature review. AI EDAM-Artif. Intell. Eng. Des. Anal. Manuf. 2025, 39, e4. [Google Scholar] [CrossRef]
- Song, L.Y.; Lin, T.J.; Jin, Y.; Zhao, S.K.; Li, Y.; Wang, H.Q. Advancements in bearing remaining useful life prediction methods: A comprehensive review. Meas. Sci. Technol. 2024, 35, 092003. [Google Scholar] [CrossRef]
- Ge, M.F.; Liu, Y.B.; Jiang, X.X.; Liu, J. A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 2021, 174, 109057. [Google Scholar] [CrossRef]
- Ferreira, C.; Goncalves, G. Remaining Useful Life prediction and challenges: A literature review on the use of Machine Learning Methods. J. Manuf. Syst. 2022, 63, 550–562. [Google Scholar] [CrossRef]
- Kong, Z.M.; Cui, Y.; Xia, Z.; Lv, H. Convolution and Long Short-Term Memory Hybrid Deep Neural Networks for Remaining Useful Life Prognostics. Appl. Sci. 2019, 9, 4156. [Google Scholar] [CrossRef]
- Long, W.; Yan, D.; Liang, G. A new ensemble residual convolutional neural network for remaining useful life estimation. Math. Biosci. Eng. 2019, 16, 862–880. [Google Scholar] [CrossRef]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN Variants for Computer Vision: History, Architecture, Application, Challenges and Future Scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.P.; Jia, F.; Lei, Y.G.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Wu, S.W.; Sun, F.; Zhang, W.T.; Xie, X.; Cui, B. Graph Neural Networks in Recommender Systems: A Survey. ACM Comput. Surv. 2023, 55, 1–37. [Google Scholar] [CrossRef]
- Yang, X.Y.; Zheng, Y.; Zhang, Y.; Wong, D.S.H.; Yang, W.D. Bearing Remaining Useful Life Prediction Based on Regression Shapalet and Graph Neural Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.H.; Chen, H.T.; Chen, X.H.; Guo, J.Y.; Liu, Z.H.; Tang, Y.H.; Xiao, A.; Xu, C.J.; Xu, Y.X.; et al. A Survey on Vision Transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.F.; Jia, M.P.; Miao, Q.H.; Cao, Y.D. A novel time-frequency Transformer based on self-attention mechanism and its application in fault diagnosis of rolling bearings. Mech. Syst. Signal Proc. 2022, 168, 108616. [Google Scholar] [CrossRef]
- Wang, L.; Cao, H.R.; Xu, H.; Liu, H.C. A gated graph convolutional network with multi-sensor signals for remaining useful life prediction. Knowl.-Based Syst. 2022, 252, 109340. [Google Scholar] [CrossRef]
- Huang, C.G.; Huang, H.Z.; Li, Y.F.; Peng, W.W. A novel deep convolutional neural network-bootstrap integrated method for RUL prediction of rolling bearing. J. Manuf. Syst. 2021, 61, 757–772. [Google Scholar] [CrossRef]
- Liu, Y.W.; Sun, J.; Shang, Y.L.; Zhang, X.D.; Ren, S.; Wang, D.T. A novel remaining useful life prediction method for lithium-ion battery based on long short-term memory network optimized by improved sparrow search algorithm. J. Energy Storage 2023, 61, 106645. [Google Scholar] [CrossRef]
- Ma, P.; Li, G.F.; Zhang, H.L.; Wang, C.; Li, X.K. Prediction of Remaining Useful Life of Rolling Bearings Based on Multiscale Efficient Channel Attention CNN and Bidirectional GRU. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, P.H.; Yang, X.; Hu, A.J.; Su, H. Fault detection of wind turbine based on SCADA data analysis using CNN and LSTM with attention mechanism. Measurement 2021, 175, 109094. [Google Scholar] [CrossRef]
- Li, M.W.; Xu, D.Y.; Geng, J.; Hong, W.C. A hybrid approach for forecasting ship motion using CNN-GRU-AM and GCWOA. Appl. Soft Comput. 2022, 114, 108084. [Google Scholar] [CrossRef]
- Chen, D.Q.; Hong, W.C.; Zhou, X.Z. Transformer Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Access 2022, 10, 19621–19628. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Song, W.; Li, Q.Q. Dual-Aspect Self-Attention Based on Transformer for Remaining Useful Life Prediction. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Brauwers, G.; Frasincar, F. A General Survey on Attention Mechanisms in Deep Learning. IEEE Trans. Knowl. Data Eng. 2023, 35, 3279–3298. [Google Scholar] [CrossRef]
- Chen, Z.H.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.Q.; Li, X.L. Machine Remaining Useful Life Prediction via an Attention-Based Deep Learning Approach. IEEE Trans. Ind. Electron. 2021, 68, 2521–2531. [Google Scholar] [CrossRef]
- Xia, J.; Feng, Y.W.; Teng, D.; Chen, J.Y.; Song, Z.C. Distance self-attention network method for remaining useful life estimation of aeroengine with parallel computing. Reliab. Eng. Syst. Saf. 2022, 225, 108636. [Google Scholar] [CrossRef]
- Niu, Z.Y.; Zhong, G.Q.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Zhang, Q.; Ye, Z.J.; Shao, S.Y.; Niu, T.L.; Zhao, Y.W. Remaining useful life prediction of rolling bearings based on convolutional recurrent attention network. Assem. Autom. 2022, 42, 372–387. [Google Scholar] [CrossRef]
- Fan, Z.Y.; Li, W.R.; Chang, K.C. A Two-Stage Attention-Based Hierarchical Transformer for Turbofan Engine Remaining Useful Life Prediction. Sensors 2024, 24, 824. [Google Scholar] [CrossRef] [PubMed]
- Xiang, S.; Li, P.H.; Huang, Y.; Luo, J.; Qin, Y. Single gated RNN with differential weighted information storage mechanism and its application to machine RUL prediction. Reliab. Eng. Syst. Saf. 2024, 242, 109741. [Google Scholar] [CrossRef]
- Xiang, S.; Zheng, X.Y.; Miao, J.G.; Qin, Y.; Li, P.H.; Hou, J.; Ilolov, M. Dynamic Self-Learning Neural Network and Its Application for Rotating Equipment RUL Prediction. IEEE Internet Things J. 2025, 12, 12257–12266. [Google Scholar] [CrossRef]
- Li, P.H.; Zheng, X.Y.; Xiang, S.; Hou, J.; Qin, Y.; Kurboniyon, M.S.; Ren, W. Channel Independence Bidirectional Gated Mamba With Interactive Recurrent Mechanism for Time Series Forecasting. In Proceedings of the IEEE Transactions on Industrial Electronics, Piscataway, NJ, USA, 10 July 2025. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2024, arXiv:2310.06625. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Zheng, S.; Ristovski, K.; Farahat, A.; Gupta, C. Long Short-Term Memory Network for Remaining Useful Life Estimation. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 88–95. [Google Scholar]
- Zhang, Y.; Xin, Y.; Liu, Z.-W.; Chi, M.; Ma, G. Health status assessment and remaining useful life prediction of aero-engine based on BiGRU and MMoE. Reliab. Eng. Syst. Saf. 2022, 220, 108263. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, H.; Sun, Y.C.; Wang, H.; Zhang, H.Y. CTNet: Improving the non-stationary predictive ability of remaining useful life of aero-engine under multiple time-varying operating conditions. Measurement 2025, 243, 116345. [Google Scholar] [CrossRef]
- Xiang, F.F.; Zhang, Y.M.; Zhang, S.Y.; Wang, Z.L.; Qiu, L.M.; Choi, J.H. Bayesian gated-transformer model for risk-aware prediction of aero-engine remaining useful life. Expert Syst. Appl. 2024, 238, 121859. [Google Scholar] [CrossRef]
- Wang, J.; Wen, G.; Yang, S.; Liu, Y. Remaining Useful Life Estimation in Prognostics Using Deep Bidirectional LSTM Neural Network. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 1037–1042. [Google Scholar]
- Li, H.; Zhao, W.; Zhang, Y.; Zio, E. Remaining useful life prediction using multi-scale deep convolutional neural network. Appl. Soft Comput. 2020, 89, 106113. [Google Scholar] [CrossRef]
- Deng, K.; Zhang, X.; Cheng, Y.; Zheng, Z.; Jiang, F.; Liu, W.; Peng, J. A remaining useful life prediction method with long-short term feature processing for aircraft engines. Appl. Soft Comput. 2020, 93, 106344. [Google Scholar] [CrossRef]
- Sayah, M.; Guebli, D.; Zerhouni, N.; Masry, Z.A. Towards Distribution Clustering-Based Deep LSTM Models for RUL Prediction. In Proceedings of the 2020 Prognostics and Health Management Conference (PHM-Besançon), Besançon, France, 4–7 May 2020; pp. 253–256. [Google Scholar]
- Benker, M.; Furtner, L.; Semm, T.; Zaeh, M.F. Utilizing uncertainty information in remaining useful life estimation via Bayesian neural networks and Hamiltonian Monte Carlo. J. Manuf. Syst. 2021, 61, 799–807. [Google Scholar] [CrossRef]
- Duan, Y.; Li, H.; He, M.; Zhao, D. A BiGRU Autoencoder Remaining Useful Life Prediction Scheme with Attention Mechanism and Skip Connection. IEEE Sens. J. 2021, 21, 10905–10914. [Google Scholar] [CrossRef]
- Liu, L.; Song, X.; Zhou, Z. Aircraft engine remaining useful life estimation via a double attention-based data-driven architecture. Reliab. Eng. Syst. Saf. 2022, 221, 108330. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Tian, J.; Luo, H.; Yin, S. An integrated multi-head dual sparse self-attention network for remaining useful life prediction. Reliab. Eng. Syst. Saf. 2023, 233, 109096. [Google Scholar] [CrossRef]




| Dataset | C-MAPSS | |||
|---|---|---|---|---|
| FD001 | FD002 | FD003 | FD004 | |
| Training engines | 100 | 260 | 100 | 249 |
| Test engines | 100 | 256 | 100 | 248 |
| Operating Conditions | 1 | 6 | 1 | 6 |
| Fault modes | 1 | 1 | 2 | 2 |
| Training set size | 20,631 | 53,759 | 24,720 | 45,918 |
| Test set size | 100 | 259 | 100 | 218 |
| Hyperparameter | Description | Option |
|---|---|---|
| Batch size | The number of samples for each backpropagation | 32 |
| Optimizer | Algorithm for minimizing loss | Adam |
| Training epochs | The number of backpropagations for each sample | 100 |
| Learning rate (lr) | Initial learning rate of training | 0.001–0.0001 |
| Dropout rate | Proportion of samples discarded | 0.2 |
| Components | Layers | Parameters | Option |
|---|---|---|---|
| TFEB | Encoder layer | Number of Conv1d layers | 2 |
| Kernel size of Conv1d layer | 1 | ||
| Number of norm layers | 2 | ||
| Number of hidden dimensions | 32 | ||
| Number of extended dimensions | 128 | ||
| Number of heads | 12 | ||
| Activation | ReLU | ||
| Number of encoder layers | 2 | ||
| SFEB | Linear network layer | Number of hidden dimensions | 32 |
| Reduction | 4 | ||
| Activation | ReLU | ||
| Number of linear network layers | 2 | ||
| Projection layer | Activation | Sigmoid | |
| Regressor | Linear network layer | Activation | ReLU |
| Number of linear network layers | 3 | ||
| Prediction layer | Activation | Sigmoid |
| Parameter | A | B | C | D |
|---|---|---|---|---|
| Number of encoder layers | 1 | 2 | 3 | 4 |
| Number of heads | 4 | 8 | 12 | 16 |
| Batch size | 16 | 32 | 64 | 128 |
| Model dimension | 32 | 64 | 128 | 256 |
| Parameter | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Number of encoder layers | 3 | 3 | 3 | 4 |
| Number of heads | 4 | 16 | 8 | 16 |
| Batch size | 128 | 32 | 64 | 32 |
| Model dimension | 32 | 32 | 32 | 32 |
| Methods | FD001 | FD002 | FD003 | FD004 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | S-Score | MAE | RMSE | S-Score | MAE | RMSE | S-Score | MAE | RMSE | S-Score | MAE | |
| Transformer | 14.23 | 379.56 | 10.32 | 18.62 | 3751.61 | 12.74 | 12.86 | 326.55 | 10.26 | 22.87 | 9862.59 | 15.87 |
| iTransformer | 11.47 | 190.37 | 9.10 | 15.9 | 2499 | 14.08 | 12.32 | 298.08 | 8.97 | 20.09 | 2469 | 15.6 |
| ST | 12.58 | 273.66 | 9.51 | 17.35 | 2587.55 | 11.93 | 12.53 | 291.17 | 10.1 | 22.82 | 5936.06 | 15.89 |
| HMDAM | 10.82 | 170.07 | 9.02 | 15.33 | 1130.42 | 10.72 | 11.21 | 239.47 | 8.96 | 17.48 | 1738.19 | 11.88 |
| Method | Number of FLOPs | Number of Parameters |
|---|---|---|
| Transformer | 810.82 K | 87.39 K |
| iTransformer | 441.92 K | 89.66 K |
| ST | 1.185 M | 100.50 K |
| HMDAM | 821.25 K | 89.02 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Li, Z.; Zheng, C.; Zhang, Z.; Zhang, L. A Hybrid Model Based on a Dual-Attention Mechanism for the Prediction of Remaining Useful Life of Aircraft Engines. Sensors 2025, 25, 5682. https://doi.org/10.3390/s25185682
He C, Li Z, Zheng C, Zhang Z, Zhang L. A Hybrid Model Based on a Dual-Attention Mechanism for the Prediction of Remaining Useful Life of Aircraft Engines. Sensors. 2025; 25(18):5682. https://doi.org/10.3390/s25185682
Chicago/Turabian StyleHe, Chenwen, Zixiang Li, Chenyu Zheng, Zikai Zhang, and Liping Zhang. 2025. "A Hybrid Model Based on a Dual-Attention Mechanism for the Prediction of Remaining Useful Life of Aircraft Engines" Sensors 25, no. 18: 5682. https://doi.org/10.3390/s25185682
APA StyleHe, C., Li, Z., Zheng, C., Zhang, Z., & Zhang, L. (2025). A Hybrid Model Based on a Dual-Attention Mechanism for the Prediction of Remaining Useful Life of Aircraft Engines. Sensors, 25(18), 5682. https://doi.org/10.3390/s25185682






