1. Introduction
Visual impairment is a prevalent global health issue. According to the data from The Lancet Global Health Commission [
1], as of 2020, there were 596 million visually impaired people (VIPs) globally, including 43 million who were blind. By 2050, these figures are expected to rise to 895 million and 61 million, respectively. Given that visual information accounts for approximately 80% of human perception, the large population of VIPs faces significant challenges in their daily lives and mobility.
With the rapid advancement of smartphone technology and wireless communication, Remote Sighted Assistance (RSA) systems have emerged to support VIPs in navigation and other daily tasks [
2]. A typical RSA system includes four core components: visual information acquisition, data transmission, remote assistance, and user feedback. In such systems, users can request help via a mobile platform, and remote sighted agents provide guidance based on real-time visual data captured from wearable or mobile cameras. RSA applications have been developed for mobility assistance [
3], text recognition [
3,
4,
5], and object identification [
3,
4,
5]. Notable commercial platforms include BeMyEyes [
3], TapTapSee [
4], and Aira [
5], while research prototypes include VizWiz [
6], BeSpecular [
7], and CrowdViz [
8]. Despite recent progress, RSA systems still face several critical challenges, including reliable real-time communication, precise localization in GNSS-degraded areas, environmental understanding, and intuitive user feedback design.
Recent studies have identified two key challenges in RSA systems: (1) remote sighted agents experience stress and encounter difficulties in making accurate judgments when navigating unfamiliar environments, and (2) visually impaired users often feel anxious and uneasy when navigating unknown areas [
2,
9]. Research has also shown that incorporating 3D maps can help remote sighted agents better understand the environment [
10]. Therefore, enabling both remote sighted agents and visually impaired users to preview route information in advance has the potential to significantly enhance RSA effectiveness and user experience. Although commercial mapping services such as Google Maps [
11] and OpenStreetMap (OSM) [
12] provide extensive road network and satellite imagery data, they are not well-aligned with real-world first-person perspectives, thereby limiting their effectiveness for pedestrian navigation. In this study, we use the term “real-world first-person perspectives” to describe video content captured from the viewpoint of a pedestrian walking along the route, closely replicating what a VIP would perceive during navigation. Unlike Google Maps or similar services, which primarily provide top-down maps or static street-view images, this approach aligns with a VIP’s forward-facing, step-by-step experience. Furthermore, publicly available imagery such as Google Street View is often outdated, lacks comprehensive coverage, and may not accurately reflect temporary environmental changes, such as construction or obstacles. Moreover, existing map data primarily focuses on the vehicular road network, resulting in sparse or incomplete coverage of pedestrian pathways. To address this limitation and support the need for prior environmental awareness in RSA services, this study proposes a video-based map, as presented in
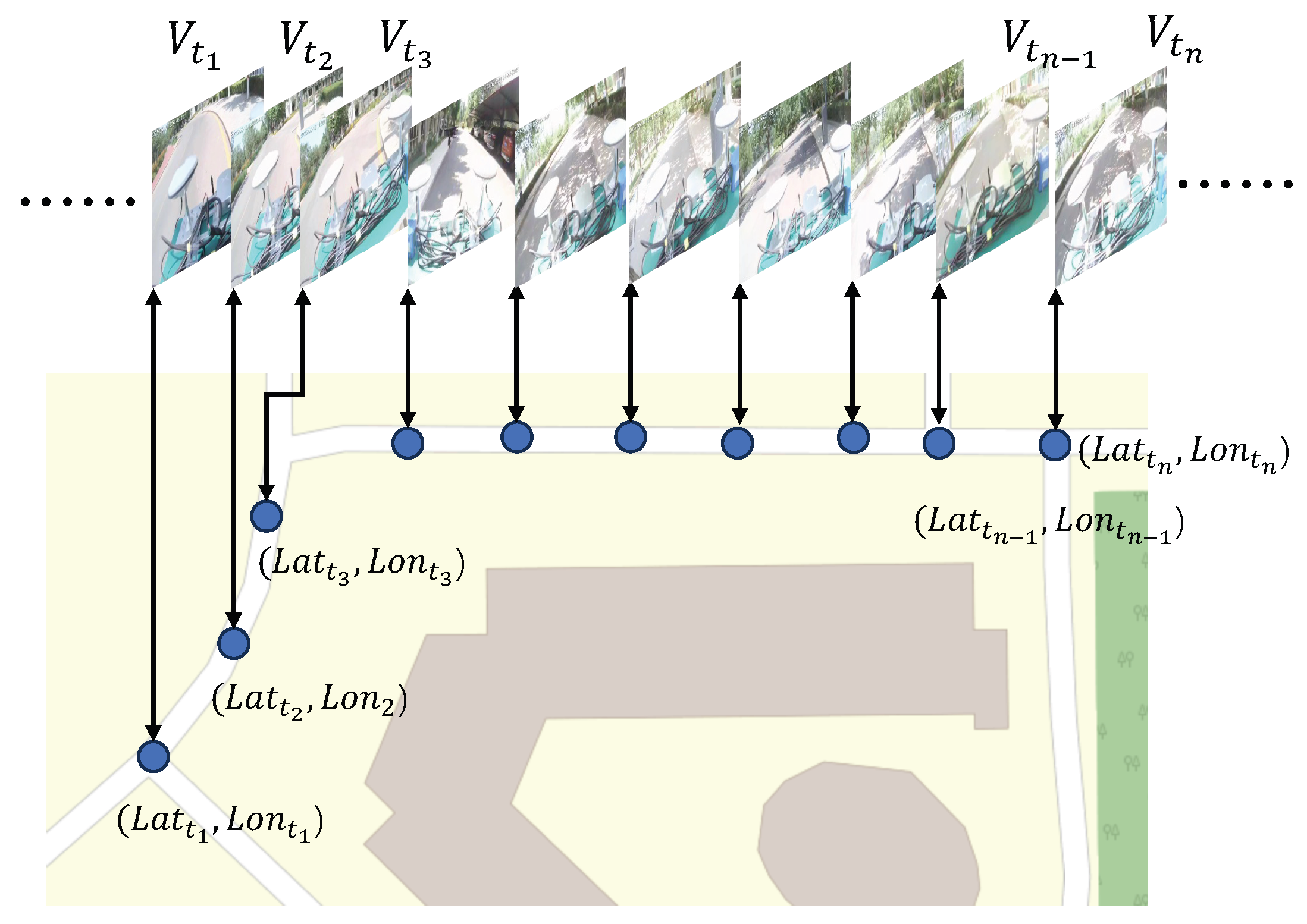
Figure 1. The system captures pedestrian environments through pre-recorded videos and establishes precise spatiotemporal correspondences to enhance mobility assistance in RSA scenarios. Remote sighted agents can preview the video-based map prior to the assistance session and summarize key information—such as route layout, landmarks, and potential obstacles—to visually impaired users via voice instructions. Compared with costly 3D mapping technologies, our video-based map offers a lightweight, low-cost, and perceptually aligned alternative that is well suited for outdoor remote vision assistance in real-world urban environments.
To precisely associate video frames with geographic locations, spatial positions are represented using latitude and longitude coordinates. While video acquisition is relatively straightforward, the primary challenge lies in establishing an accurate mapping between time and space. Numerous studies have investigated smartphone-based pedestrian localization methods [
13,
14,
15,
16,
17]. Smartphones equipped with Global Navigation Satellite System (GNSS) modules estimate absolute positions by measuring pseudoranges and applying trilateration techniques [
18,
19]. However, common urban environments with buildings and trees often cause multipath propagation and Non-Line-of-Sight (NLOS) effects, leading to significant GNSS positioning errors or even failures [
20,
21]. To improve GNSS accuracy, researchers have developed algorithms based on weighted least squares [
22,
23], Kalman filtering (KF) [
24,
25], extended Kalman filtering (EKF) [
26], and factor graph optimization (FGO) [
27,
28]. Among these, FGO is particularly effective, as it leverages a sequence of historical measurements to produce more accurate estimates [
29]. However, a study from the Hong Kong Polytechnic University indicates that even FGO based solely on GNSS can result in errors exceeding 20 m in urban settings [
30].
In contrast to GNSS, Inertial Measurement Unit (IMU)-based localization provides continuous relative positioning without relying on external signals [
31,
32,
33]. Most modern smartphones are equipped with MEMS-based IMUs, which enable pedestrian dead reckoning (PDR) using accelerometer, gyroscope, and magnetometer data [
13,
34]. PDR typically involves three key components: step detection, step length estimation, and heading estimation. It provides relative motion estimates between consecutive steps, which are then accumulated to reconstruct the pedestrian trajectory. However, due to sensor noise and drift, PDR is susceptible to cumulative errors that can reach tens of meters [
13,
34].
To overcome the limitations of individual systems, GNSS/PDR fusion algorithms integrate the absolute positioning accuracy of GNSS with the continuous tracking capability of PDR, enabling robust localization in urban environments [
14,
15,
16,
17,
35,
36,
37,
38]. Recent efforts have increasingly focused on smartphone-based fusion methods [
14,
15,
16,
17,
39,
40,
41]. Angrisano et al. [
39] and Basso et al. [
41] proposed loosely coupled fusion architectures based on EKF frameworks to integrate GNSS and PDR, thereby improving system reliability. Meng et al. [
15] introduced a KF-based GNSS/PDR fusion method with adaptive measurement adjustments. Zhang et al. [
40] applied an adaptive EKF (AEKF) to enhance robustness and mitigate cumulative errors. Jiang et al. [
14] pioneered the use of FGO for smartphone-based GNSS/PDR fusion, proposing both position and step-length constraint factors. Zhong et al. [
16] introduced PDR displacement factors derived from accelerometer data, which were jointly optimized with GNSS pseudorange and Doppler observations, achieving an average positioning accuracy of 18.51 m. Building on this work, Jiang et al. [
17] developed an adaptive FGO (A-FGO) framework that dynamically adjusts observation covariances to suppress outliers, achieving sub 4 m accuracy in certain test scenarios. Overall, FGO-based GNSS/PDR fusion methods have demonstrated superior localization accuracy compared to EKF-based approaches [
14,
17,
29,
42].
This study proposes a smartphone-based method for video-based map collection, motivated by the low cost and the widespread adoption of smartphones in RSA systems. In addition, we develop a high-precision pedestrian localization algorithm that builds upon existing solutions. For data acquisition, we employ a custom-designed multi-camera module and a mobile application to capture forward-facing video with a 180° field of view. For localization, we adopt an FGO framework that fuses GNSS and PDR data. To enhance performance, we introduce novel road anchor factors, an anchor-matching algorithm, and a coarse-to-fine optimization strategy [
43]. In this framework, GNSS factors provide global position constraints to correct accumulated PDR drift; PDR factors enhance robustness by mitigating GNSS outliers; and anchor factors leverage road features to correct residual localization errors. The FGO-based fusion framework further refines trajectories by integrating multi-source historical data. The main contributions of this work are summarized as follows:
We propose a method for constructing a video-based map by associating video frames with corresponding spatial locations to enhance the RSA service. This map serves as a preview tool for RSA agents and provides prior environmental knowledge for visually impaired users, which helps to reduce anxiety in unfamiliar environments. It also provides valuable assistance under low-light or poor network connectivity conditions, thereby enhancing the overall safety and reliability of RSA services.
To establish accurate spatiotemporal correspondence, we propose a novel FGO-based GNSS/PDR fusion framework. This framework integrates road-anchor constraints, a turning-point-based anchor-matching method, and a coarse-to-fine optimization strategy to improve positioning accuracy. The incorporation of anchor factors further refines the localization results.
We conducted extensive real-world experiments and collected datasets from three representative urban routes to evaluate the proposed localization algorithm. The results demonstrate that our anchor-aided FGO-based GNSS/PDR fusion method achieves high localization accuracy that is sufficient for video-based map construction.
The remainder of this paper is organized as follows.
Section 2 presents the proposed method for constructing the video-based map, with a focus on the localization framework, including the PDR algorithm, the PDR factor, the anchor factor, the GNSS factor, and the FGO-based data fusion strategy.
Section 3 presents the experimental results obtained from two real-world test scenarios and provides a detailed performance analysis.
Section 4 discusses the proposed PDR algorithm, the role of anchor factors, system robustness, and potential directions for future research. Finally,
Section 5 concludes the paper.
2. Materials and Methods
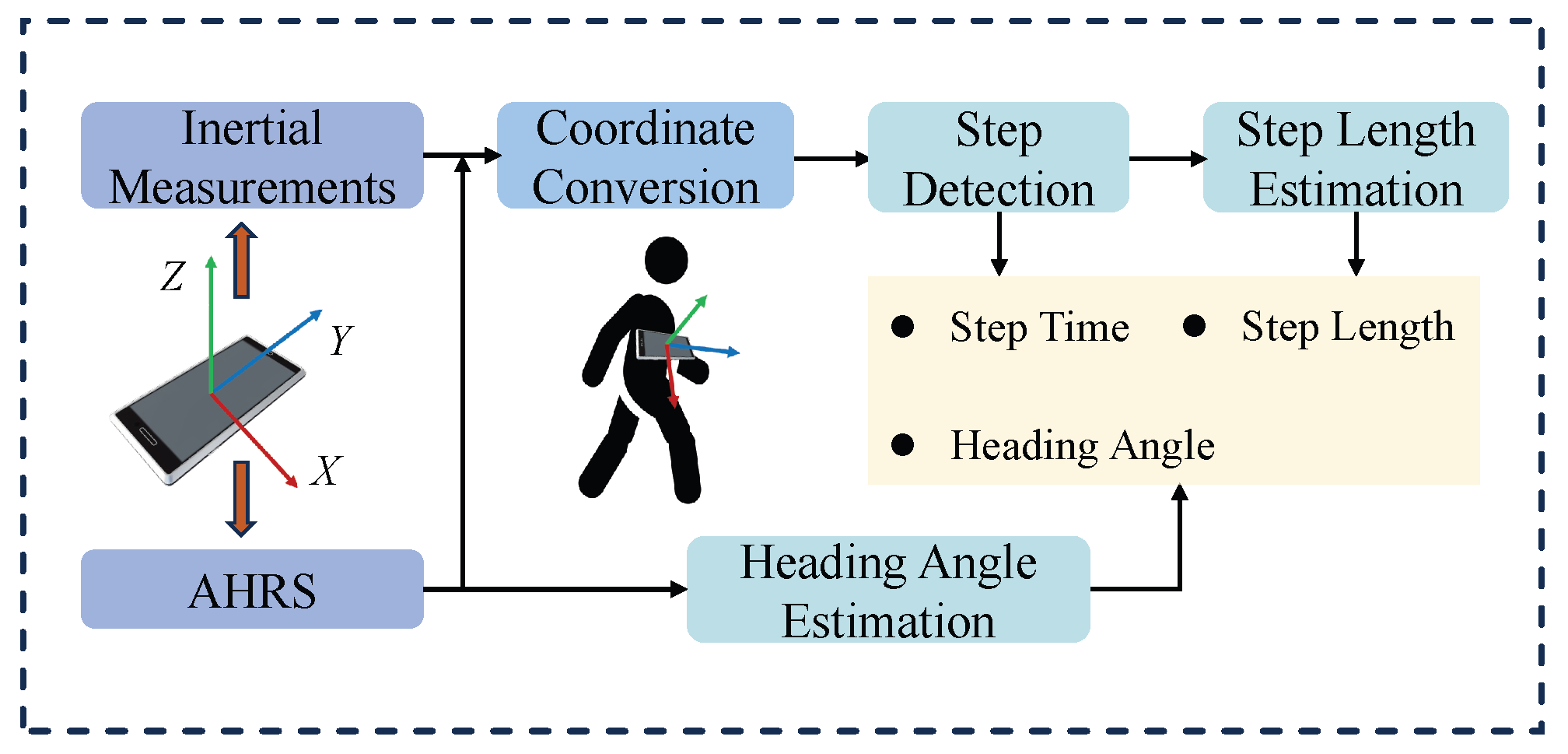
The construction of the proposed video-based map involves two primary stages: data acquisition and post-processing. In the data acquisition phase, participants are equipped with a smartphone and a multi-camera module to capture video data, GNSS positioning measurements, and sensor readings from the IMU and the attitude and heading reference system (AHRS). A major challenge in this system lies in accurately associating the captured video stream with corresponding spatial coordinates, which is the core focus of the present study. During the post-processing stage, the data are used to estimate pedestrian positions and to establish a correspondence between video timestamps and spatial locations.
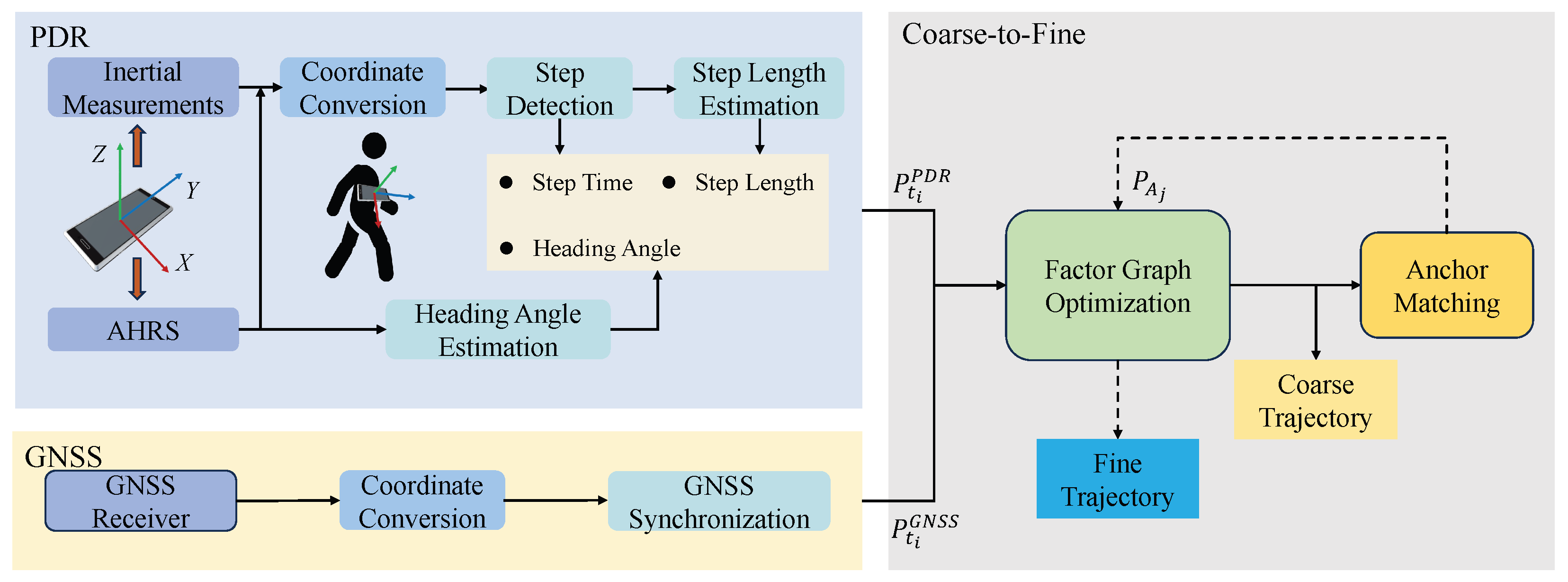
The overview of the proposed anchor-aided FGO-GNSS/PDR localization algorithm is illustrated in
Figure 2. The framework adopts a coarse-to-fine optimization strategy inspired by techniques commonly used in computer vision. Initially, pedestrian motion is estimated using a PDR algorithm driven by inertial and AHRS data from the smartphone. The PDR process includes coordinate transformation from the device frame to the East–North–Up (ENU) frame, step detection, step length estimation, and heading estimation. Next, smartphone GNSS positioning measurements are combined with the PDR results to construct an initial factor graph, producing a coarse localization estimate along the pedestrian trajectory. This preliminary trajectory is then automatically matched to predefined road anchors. The resulting anchor constraints are incorporated into the graph for fine-grained optimization, yielding the final localization result. Notably, all optimization is conducted in the ENU coordinate frame.
2.1. PDR Mechanism
In the PDR process, the algorithm estimates the pedestrian’s relative displacement by detecting step events, estimating the step length and heading direction at each step. By accumulating these step-wise displacements, the complete pedestrian trajectory can be reconstructed.
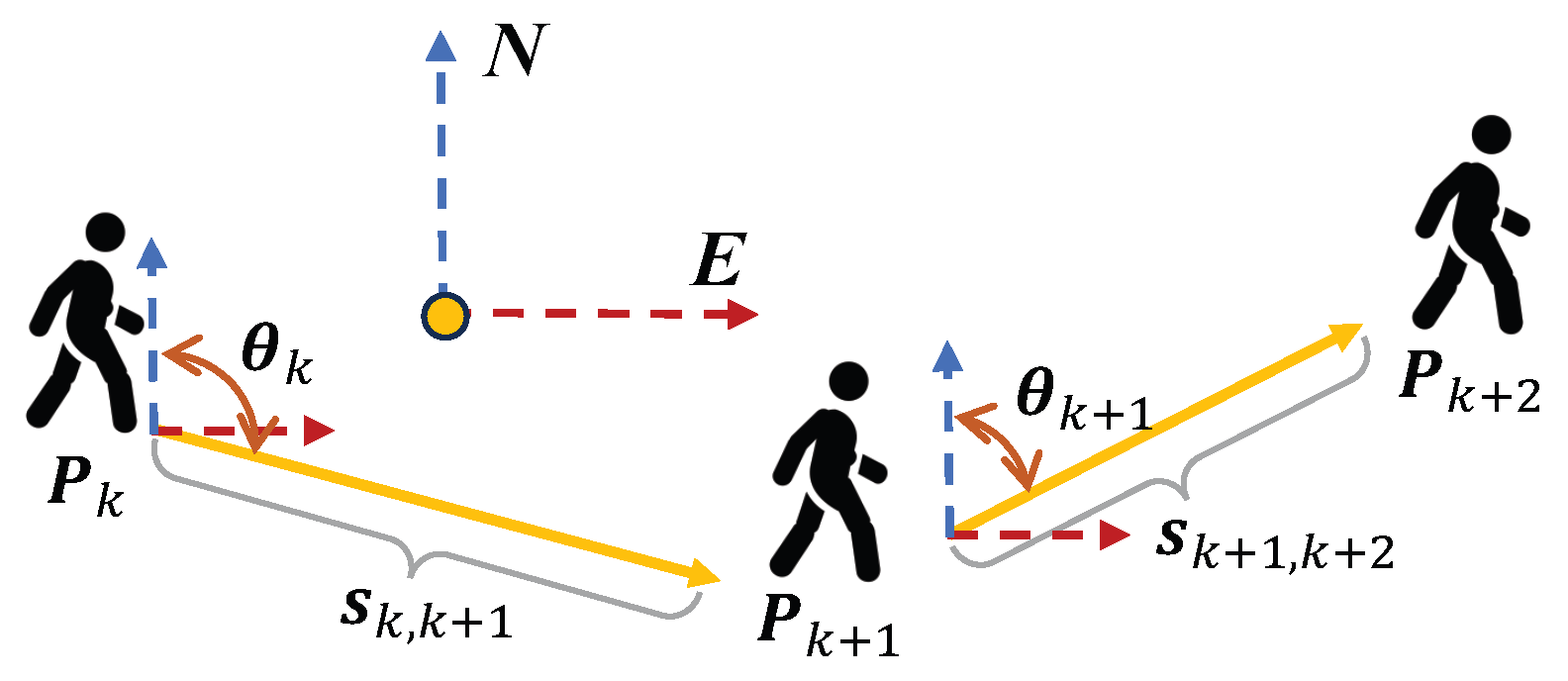
Figure 3 illustrates the mechanism of position updates. In the ENU coordinate frame, this process can be mathematically expressed as follows:
Assuming the initial position is
,
The position update at step
can then be expressed as
where
denotes the pedestrian position at the beginning of step
and
represents the updated position after the step.
and
correspond to the East and North components in the ENU coordinate frame.
is the estimated step length, and
is the heading angle of the current step with respect to the north direction.
2.1.1. PDR Modeling
In this study, the smartphone is placed on the user’s chest, with the Y-axis aligned vertically in the walking direction. Compared to the waist, the chest offers a more stable and centrally aligned mounting position, reducing the influence of lateral sway. Although this setup may slightly compromise step-frequency sensitivity, it enhances heading stability and is more practical for real-world deployment in remote assistance scenarios. The overall PDR framework is illustrated in
Figure 4. We use the smartphone’s accelerometer and AHRS outputs as inputs.
The accelerometer output
a is transformed to the ENU coordinate frame using the rotation matrix
R from the AHRS system. The transformation from the smartphone’s device frame to the ENU frame is defined as follows:
Here, denotes the rotation matrix that transforms vectors from the smartphone coordinate frame to the ENU coordinate frame. , , and are rotation matrices derived from the Euler angles provided by the AHRS system, and the symbol @ indicates matrix multiplication.
The PDR algorithm consists of three main steps: step detection, step length estimation, and heading estimation, which are described below:
- (a)
Step Detection: The algorithm detects steps by identifying valleys in the vertical acceleration signal. A fixed threshold is set to filter out noise and avoid false detections.
- (b)
Step Length Estimation: Step length is estimated using the Weinberg method [
44] based on the peak and valley values of the vertical acceleration during a step. The empirical formula is given as
where
l denotes the estimated step length,
is a step length coefficient, and
and
represent the maximum and minimum vertical acceleration values within a step.
- (c)
Heading Estimation: The heading angle is estimated using the yaw output from the smartphone’s AHRS, corrected by an offset angle of −90° in our placement scenario. To mitigate fluctuations caused by body sway, a moving average filter is applied to smooth the yaw signal. Since direct angle averaging may lead to errors near the boundary, we project the yaw angles onto the unit circle, average the projected values, and then convert the result back to an angle.
2.1.2. PDR Factor
The PDR model described above produces horizontal displacements in the ENU coordinate frame at each step. Given an initial position, the full pedestrian trajectory can be obtained. In our factor graph optimization framework, the PDR factor imposes a relative motion constraint between two consecutive positions.
The horizontal displacement between two consecutive steps is defined as
where
and
denote the pedestrian positions at timestamps
and
, respectively, in the ENU coordinate frame. Thus,
represents the relative displacement between two consecutive time steps.
The formulation of the PDR factor is then given by
Here,
denotes the relative displacement estimated by the PDR algorithm at time
, and
is the actual displacement between two adjacent positions as described above.
is the residual of the PDR factor at timestamp
, and
is the covariance matrix of the PDR output at time
. In our FGO framework, each PDR factor models the 2D relative displacement on the horizontal plane (E and N). To simplify the modeling, we assume that the noise in the E and N directions is uncorrelated and identically distributed. Accordingly, we adopt an isotropic noise model, represented by a fixed diagonal covariance matrix:
The value of is empirically determined based on the observed noise characteristics of the PDR output in our datasets. While more complex noise models could be applied, this simplified isotropic formulation enables efficient optimization while maintaining robust performance.
2.2. Anchor-Matching Method
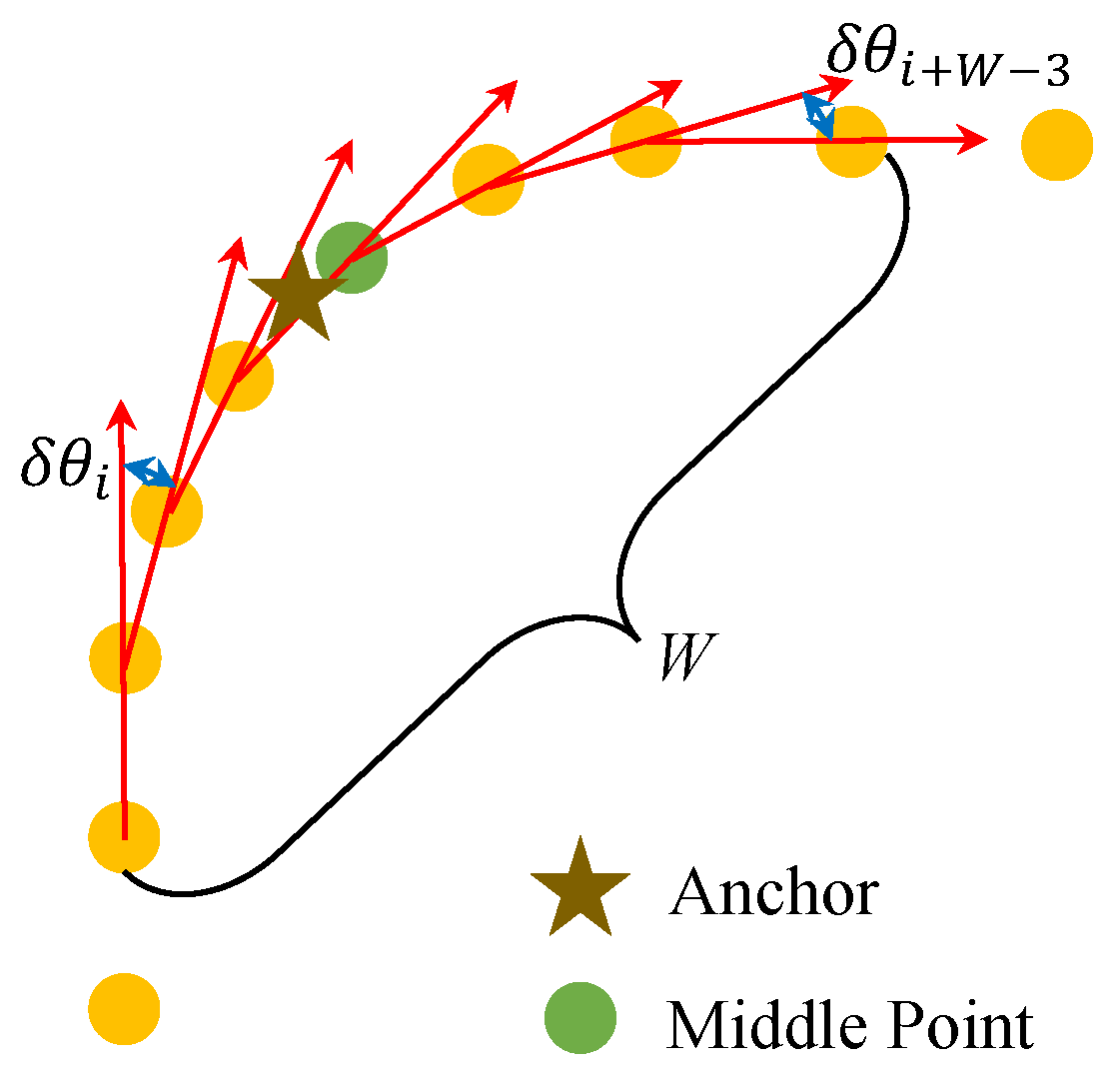
To improve the localization accuracy, the proposed method incorporates anchor constraints derived from the available road geometry, specifically at turning points. These anchors serve as auxiliary constraints to correct the fused trajectory during optimization. Each anchor is placed at the geometric center of a turning region, with its true geographic coordinates (latitude and longitude) obtained through prior measurement. When the pedestrian trajectory passes through such a region, the corresponding anchor is automatically matched based on the local trajectory geometry.
To match each predefined anchor point with the corresponding pedestrian location along the trajectory, the method first selects a set of candidate points from the coarse localization result. Specifically, all trajectory points between the first and last points that lie within a 10 m radius of the anchor are selected, ensuring spatial continuity along the path.
Assume that
N candidate points are obtained for a given anchor. From these
N points, the method computes
forward-direction vectors
representing the pedestrian’s heading between consecutive points:
Then, the angular differences (turning angles) between adjacent heading vectors are calculated to produce
direction change values
:
A fixed-length sliding window of size W is applied to the turning angle sequence. For each window, the cumulative turning angle is computed as
As illustrated in
Figure 5, the window with the maximum cumulative turning angle is identified, and its center point is selected as the matched location for the current anchor. Formally, the index of the matched point
is determined as
This method ensures that anchor points are matched to the portions of the trajectory exhibiting the most significant local turning behavior, improving the robustness and accuracy of anchor alignment in complex environments.
2.3. Anchor Factor
To further improve localization accuracy, we introduce an anchor factor that leverages known geometric landmarks, specifically road turning points, as additional spatial constraints in the factor graph. These anchors serve as reference points to mitigate accumulated drift from GNSS and PDR estimates.
The anchor factor is defined as a residual between the estimated pedestrian position and the known ENU position of the corresponding anchor point:
Here,
denotes the true ENU coordinate of the anchor
, and
is the estimated pedestrian position at time
when matched to this anchor. The residual
quantifies the positional deviation between the estimated and ground-truth anchor location. The covariance matrix
models the uncertainty associated with anchor matching. Similar to the PDR factor, the anchor factor also adopts an isotropic noise model. Specifically, for a matched anchor
, the anchor factor models the 2D positional deviation between the estimated pedestrian position
and the ground-truth anchor position
on the horizontal plane (E and N). We assume that the uncertainties in the E and N directions are uncorrelated and identically distributed, allowing the covariance matrix
to be represented as a fixed diagonal matrix:
The parameter is empirically determined based on the variability observed in anchor-matching performance in our datasets.
This anchor factor enhances the robustness of trajectory optimization by introducing strong spatial constraints in turning regions, where PDR performance tends to deteriorate. In our current implementation, the start and end positions are assumed to be approximately known, based on external information such as commercial maps or fixed landmarks (e.g., building entrances). This simplifying assumption reflects common RSA scenarios, where the origin and destination are often predefined. While this improves the stability of FGO by providing fixed anchor constraints, we acknowledge that it may not hold in all real-world cases. In future work, we aim to relax this assumption by integrating visual place recognition techniques, such as OrienterNet [
45], to support autonomous initialization and termination without relying on predefined points. These points are also treated as anchor nodes and incorporated into the factor graph as prior constraints. The formulation of their residuals follows the same structure as that of regular anchors.
2.4. GNSS Factor
GNSS positioning provides absolute spatial references, serving as global constraints in the optimization process. To incorporate this information, we introduce GNSS factors into the factor graph. In our implementation, the GNSS positions are obtained from the Android device solution [
46]. First, the device solution results are transformed from geodetic coordinates (latitude, longitude, height) to the Earth-Centered Earth-Fixed (ECEF) coordinate system. To simplify the transformation, a fixed height is assumed in this work, which is reasonable in flat urban areas but may introduce errors in hilly terrains. Then, given a known reference point, the rotation matrix
is computed to convert the ECEF coordinates into the local ENU frame. The GNSS factor is formulated as
Here, represents the GNSS position at time , and denotes the estimated pedestrian position at the same timestamp. The residual measures the deviation between the GNSS position and the current state estimate. Similar to the PDR and anchor factors, the GNSS factor also adopts an isotropic noise model. Specifically, for a GNSS observation at time , the GNSS factor models the 2D positional deviation between the estimated pedestrian position and the GNSS position on the horizontal plane (E and N). We assume that the errors in the E and N directions are uncorrelated and identically distributed, so the covariance matrix can be represented as a fixed diagonal matrix:
The value of is empirically determined from the observed noise characteristics of GNSS positioning in our datasets.
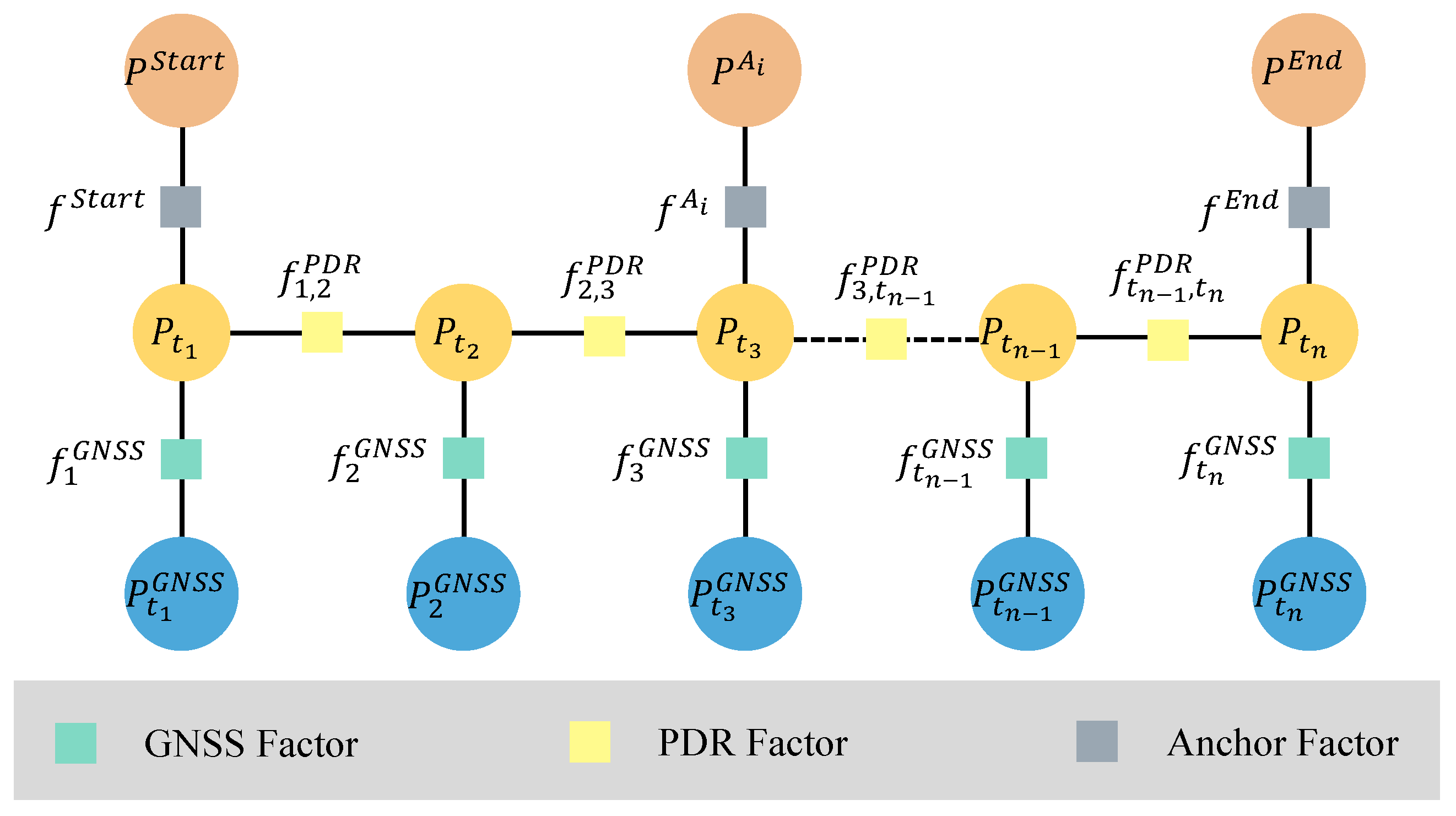
2.5. Factor Graph Integration
In the proposed optimization framework, we adopt a coarse-to-fine strategy. Initially, the GNSS factor, PDR factor, and start&end anchor constraints are used to perform a coarse optimization and obtain an initial trajectory estimate. The corresponding loss function is defined as
The resulting trajectory is then used as input to the anchor-matching algorithm, which determines matched anchor positions. These anchor constraints are subsequently incorporated into the factor graph for fine-grained optimization. The final objective function for the complete factor graph optimization is given by
The optimized trajectory
represents the best estimate of the pedestrian position at each timestamp
based on the fused constraints. The structure of the final factor graph is illustrated in
Figure 6. It consists of three types of factors: PDR, anchor, and GNSS. In our implementation, we use the Georgia Tech Smoothing and Mapping (GTSAM) library [
47], an open-source optimization framework developed by Georgia Institute of Technology, to perform factor graph optimization. The Levenberg–Marquardt algorithm [
48] is applied to solve the entire nonlinear optimization problem.
3. Results
3.1. Experiment Setup
To validate the effectiveness of the proposed method, we collected real-world data in three challenging urban environments. These environments feature dense buildings and vegetation, which induce GNSS positioning errors due to multipath propagation and NLOS conditions. These characteristics pose significant challenges for GNSS localization.
In addition, we intentionally used a consumer-grade smartphone (OPPO PESM10, manufactured by OPPO Guangdong Mobile Telecommunications Corp., Ltd., Dongguan, China) rather than the high-end devices commonly adopted in similar studies [
14,
16,
17]. The device supports multi-constellation GNSS, including GPS, GLONASS, BeiDou, Galileo, QZSS, and A-GPS. GNSS data were recorded at a frequency of 1 Hz using the Android fused location provider. The smartphone is also equipped with a typical suite of inertial sensors: a 3-axis accelerometer, a 3-axis gyroscope, and a 3-axis magnetometer. The smartphone data were collected using the GetSensorData app [
46], which records inertial and AHRS outputs at 50 Hz. The GNSS data were logged at a frequency of 1 Hz.
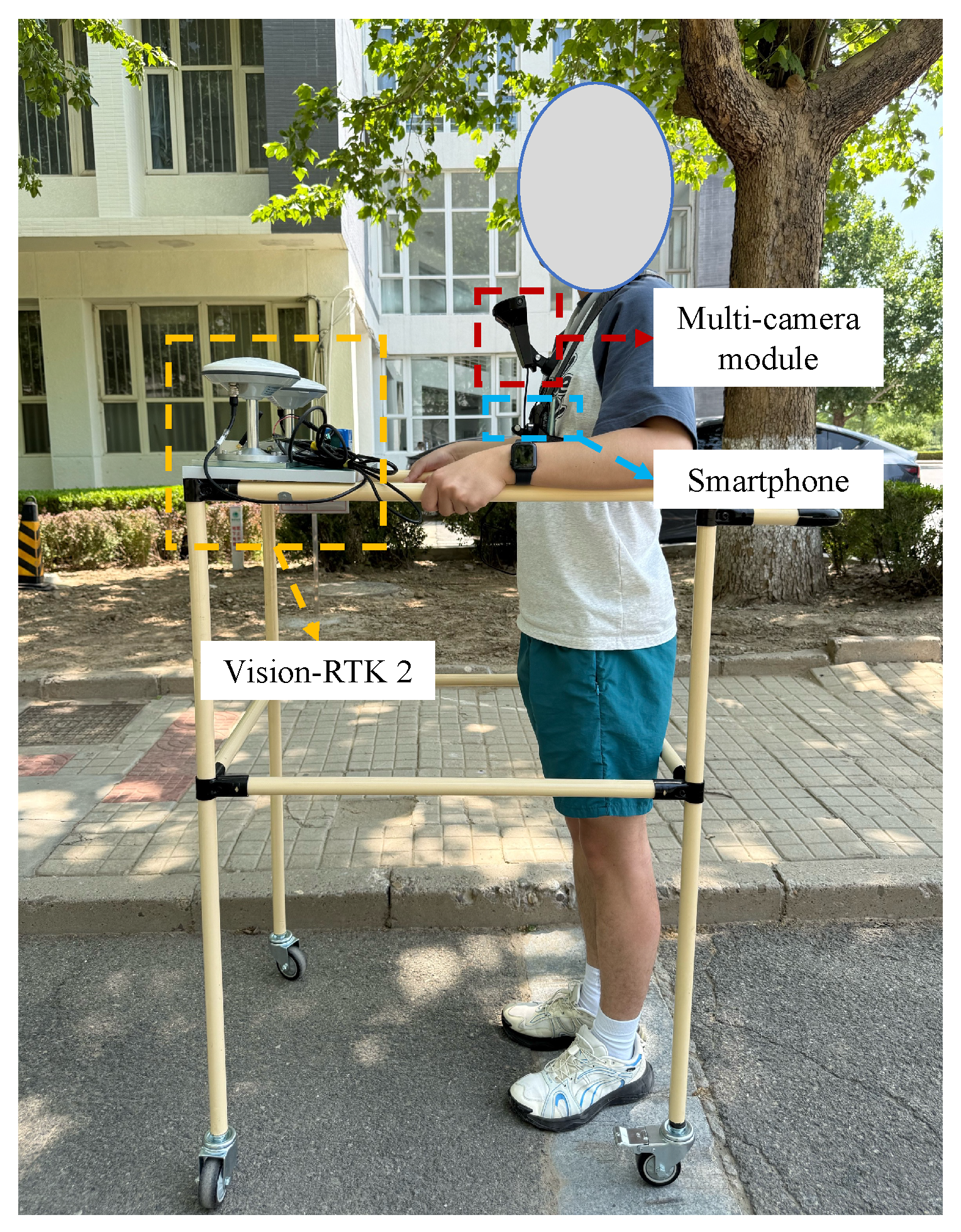
The data acquisition setup is depicted in
Figure 7. The smartphone was chest-mounted on the user, following the configuration described in the methodology section. For ground-truth acquisition, we employed a Vision-RTK 2 system that integrates visual-inertial odometry with RTK corrections to achieve centimeter-level accuracy. As shown in
Figure 7, the RTK receiver was mounted on a wheeled platform moving alongside the user, enabling accurate reference trajectory collection at 10 Hz. All experiments were performed on a desktop computer equipped with an Intel i5-13490F 2.5 GHz CPU and 32 GB of RAM, running Ubuntu 24.04.
3.2. Evaluation Metrics and Methods
We adopt four commonly used evaluation metrics to evaluate the performance of the proposed method: mean error (MEAN), standard deviation (STD), root mean square error (RMSE), and maximum error (MAX). All evaluations are performed in the ENU coordinate frame. To validate the effectiveness of the proposed anchor factor, we compare the localization results of the following three methods:
GNSS: The GNSS positions are obtained from the on-chip fused GNSS location estimates provided by the Android device via the GetSensorData app.
FGO-GNSS/PDR: Localization results obtained from the coarse optimization stage using GNSS, PDR, and start&end anchor constraints.
FGO-GNSS/PDR + Anchor: The final localization results obtained by incorporating the proposed anchor factor into the factor graph and applying the complete coarse-to-fine optimization strategy.
We acknowledge that all experiments in this study were conducted using a single smartphone model (OPPO PESM10), which may limit the generalizability of the results across different devices. Variations in GNSS hardware, antenna quality, and sensor fusion implementations among smartphone models could influence positioning performance. In future work, we plan to investigate the robustness and adaptability of the proposed method across multiple device types to assess cross-device generalization.
3.3. Experiment 1 in Urban Areas
To evaluate the effectiveness of the proposed method, we selected a representative and challenging urban environment. The scene map and corresponding trajectory layout is shown in
Figure 8. The path includes five turning anchors, where PDR performance typically deteriorates due to heading estimation errors and changes in gait dynamics introduced by turning motions. This makes the environment particularly suitable for evaluating the effectiveness of the proposed anchor factor. In this area, we collected three walking datasets with durations of 376 s, 396 s, and 397 s and corresponding step counts of 608, 616, and 629, respectively.
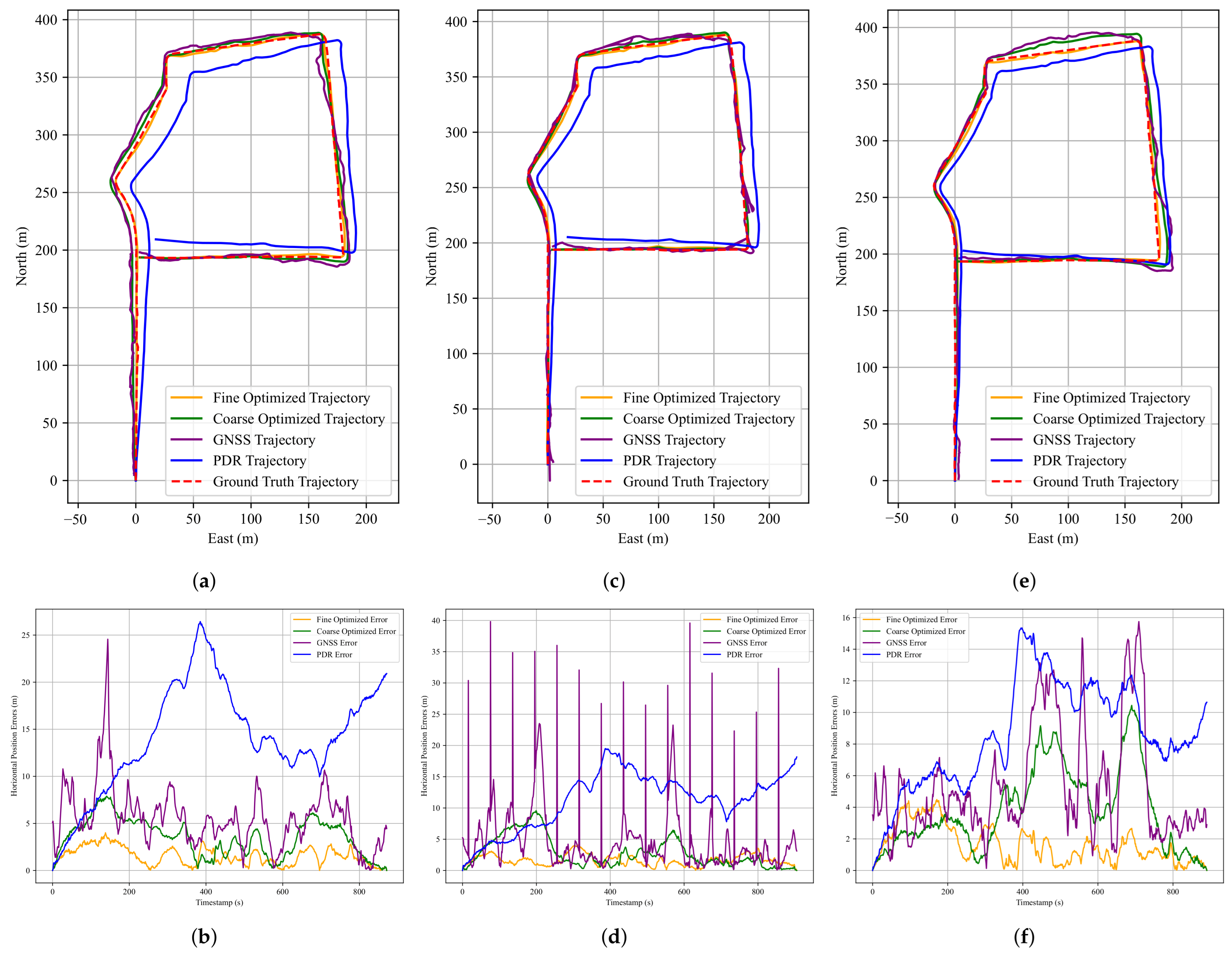
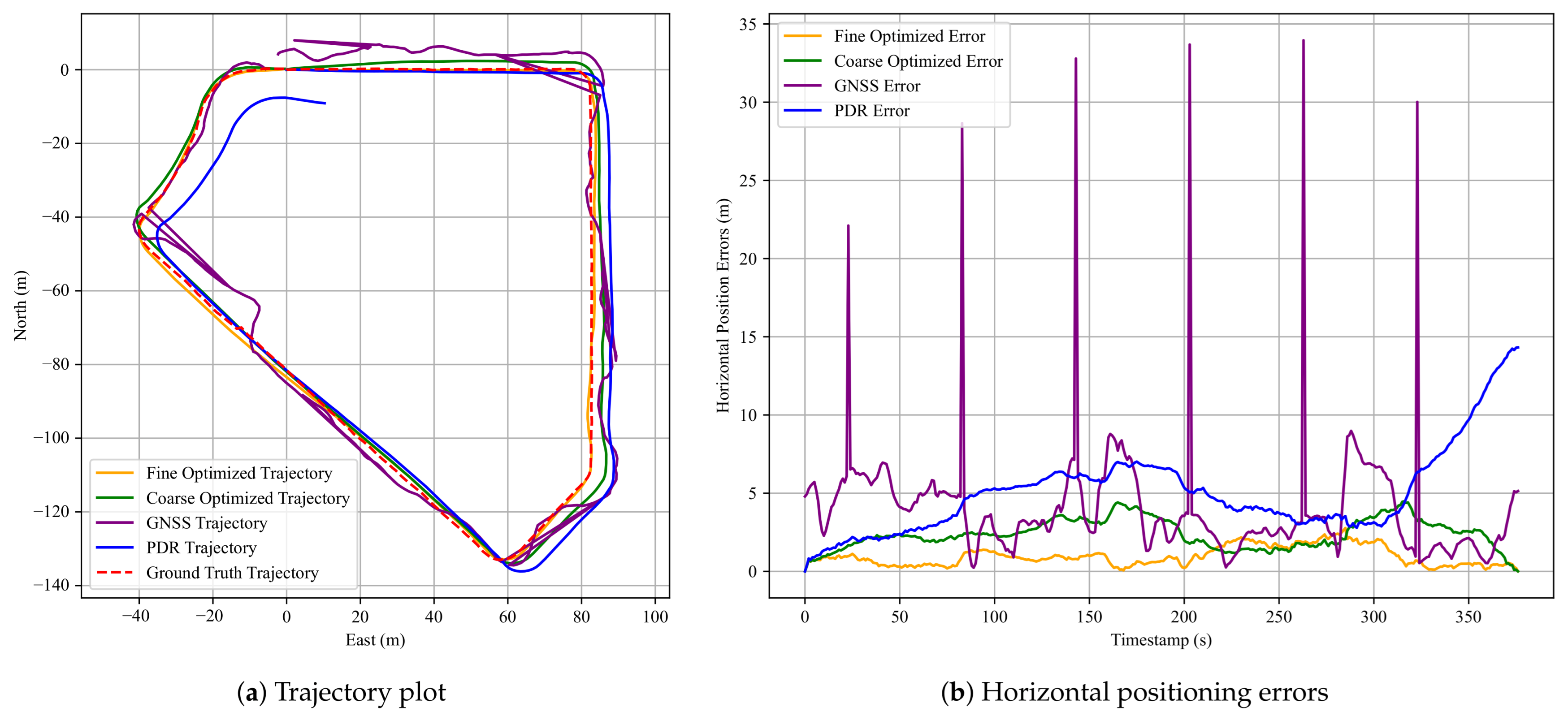
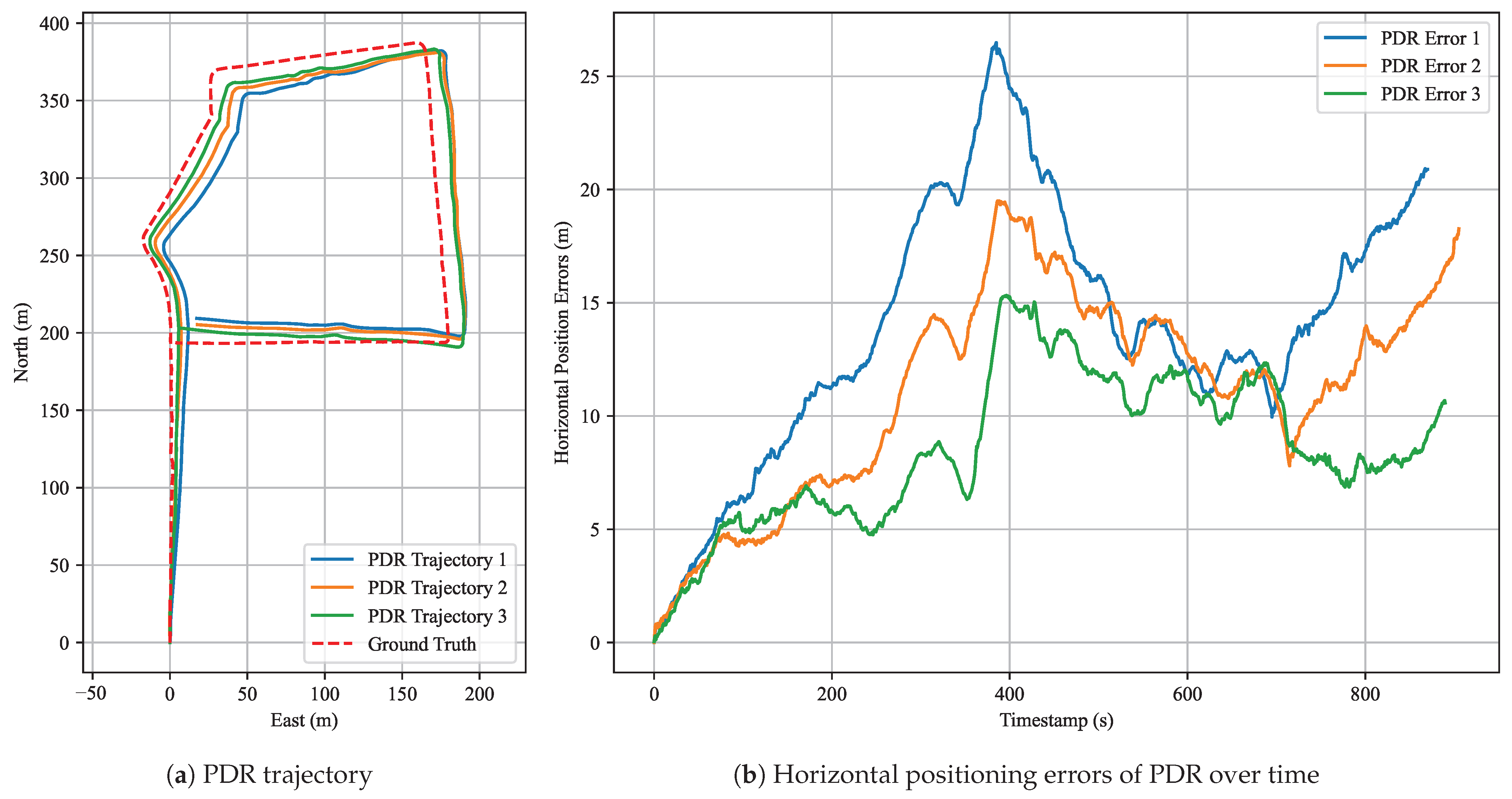
Figure 9 presents the corresponding pedestrian trajectories and the horizontal positioning errors for the first dataset. In the trajectory plot, the red dashed line denotes the ground-truth trajectory, the purple solid line shows the raw GNSS trajectory, the green solid line illustrates the result of FGO-GNSS/PDR, and the orange solid line depicts the final output after incorporating the proposed anchor factor. As observed, the FGO-GNSS/ PDR + Anchor method yields a trajectory that closely aligns with the ground-truth trajectory, while both the raw GNSS and FGO-GNSS/PDR trajectories exhibit noticeable deviations. In particular, the GNSS result shows substantial drift. This observation is further supported by the horizontal error plot, where the raw GNSS solution reaches a peak error of 33.95 m. Additional results are visualized in
Appendix A.1.
Table 1 summarizes the localization errors of the three methods using four standard metrics: RMSE, MEAN, STD, and MAX.
Table 2 presents the performance improvement of the FGO-GNSS/PDR + Anchor method compared to the baseline FGO-GNSS/PDR approach. The performance gap between raw GNSS and the optimized methods highlights the limitations of GNSS localization in urban environments. The raw GNSS trajectories suffer from large deviations, particularly in areas surrounded by tall buildings or vegetation, with maximum errors exceeding 30 m. Although the FGO-GNSS/PDR method effectively suppresses noise by leveraging inertial data, it still experiences drift over time due to the absence of reliable global constraints, as is evident in the third dataset, where the maximum error remains above 11 m.
In contrast, the proposed FGO-GNSS/PDR + Anchor method consistently achieves lower localization errors across all datasets. The maximum errors are reduced to below 3.1 m, and the error distributions are notably tighter. The significantly lower standard deviations indicate not only improved accuracy but also greater stability and robustness. This demonstrates the value of incorporating anchor constraints derived from known road geometry, especially in turning regions where PDR is prone to degradation.
The third dataset exhibits the most substantial improvement, with RMSE reduced by 71%, MEAN by 65%, STD by 82%, and MAX error by 76% compared to the FGO-GNSS/PDR baseline. These results suggest that the proposed anchor factor is particularly beneficial in complex urban scenarios involving multiple turns, where it can provide tighter constraints on trajectory estimation.
Moreover, the consistent improvements observed across all three datasets demonstrate the potential of the proposed method in structured urban environments. The error reduction rates suggest that anchor-aided optimization not only decreases average errors but also effectively suppresses large deviations. Nevertheless, further evaluation across more diverse routes and scenarios is needed to validate its generalization and robustness.
3.4. Experiment 2 in Urban Areas
In Experiment 2, we selected a more challenging long-range test environment featuring curves and an extended walking path. The scene map and corresponding trajectory layout are shown in
Figure 10. This setting allows for a more comprehensive evaluation of the robustness of the proposed anchor-aided localization approach. Three datasets were collected with walking durations of 871 s, 904 s, and 890 s and corresponding step counts of 1274, 1324, and 1317, respectively.
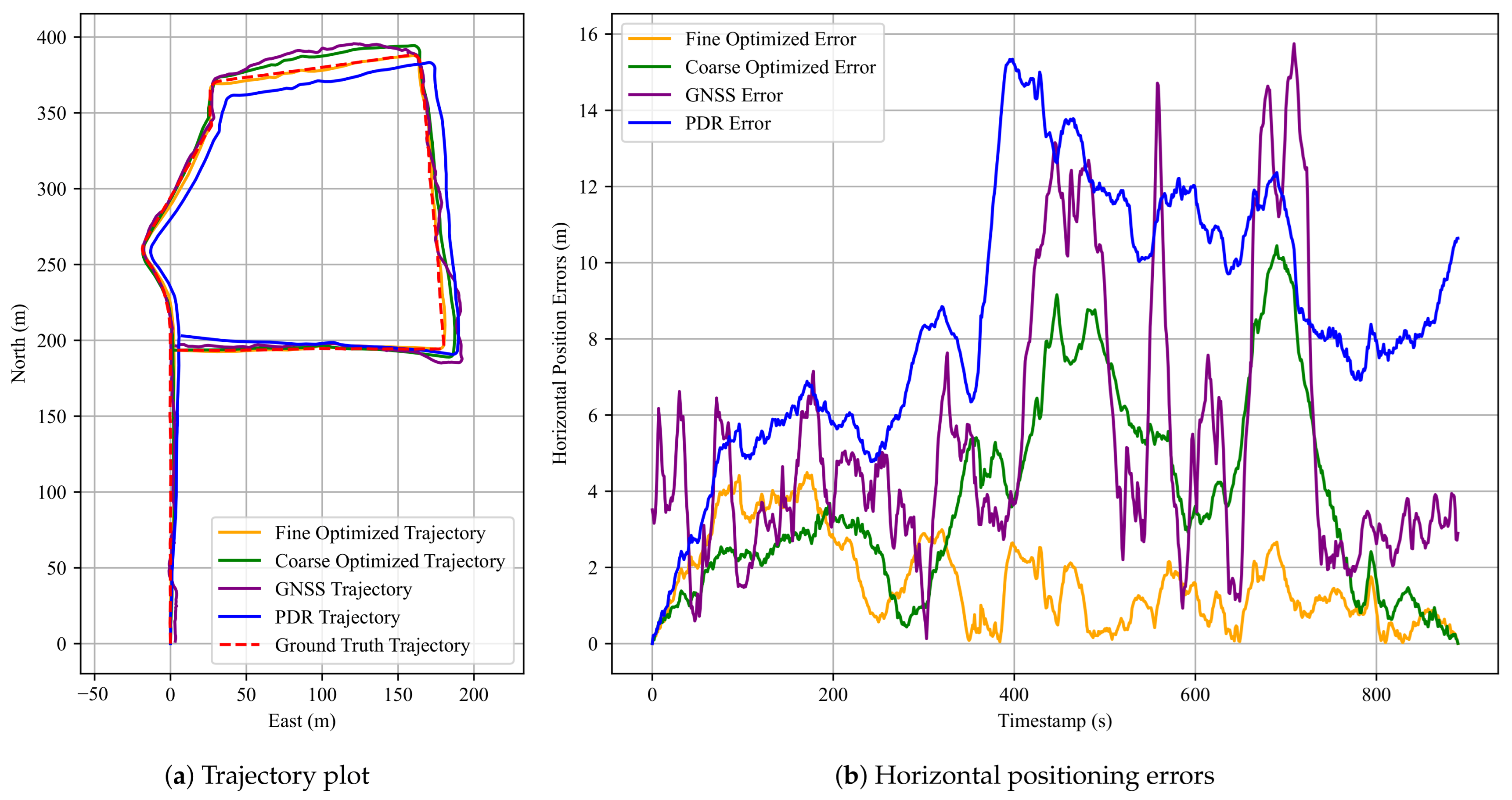
Similar to Experiment 1,
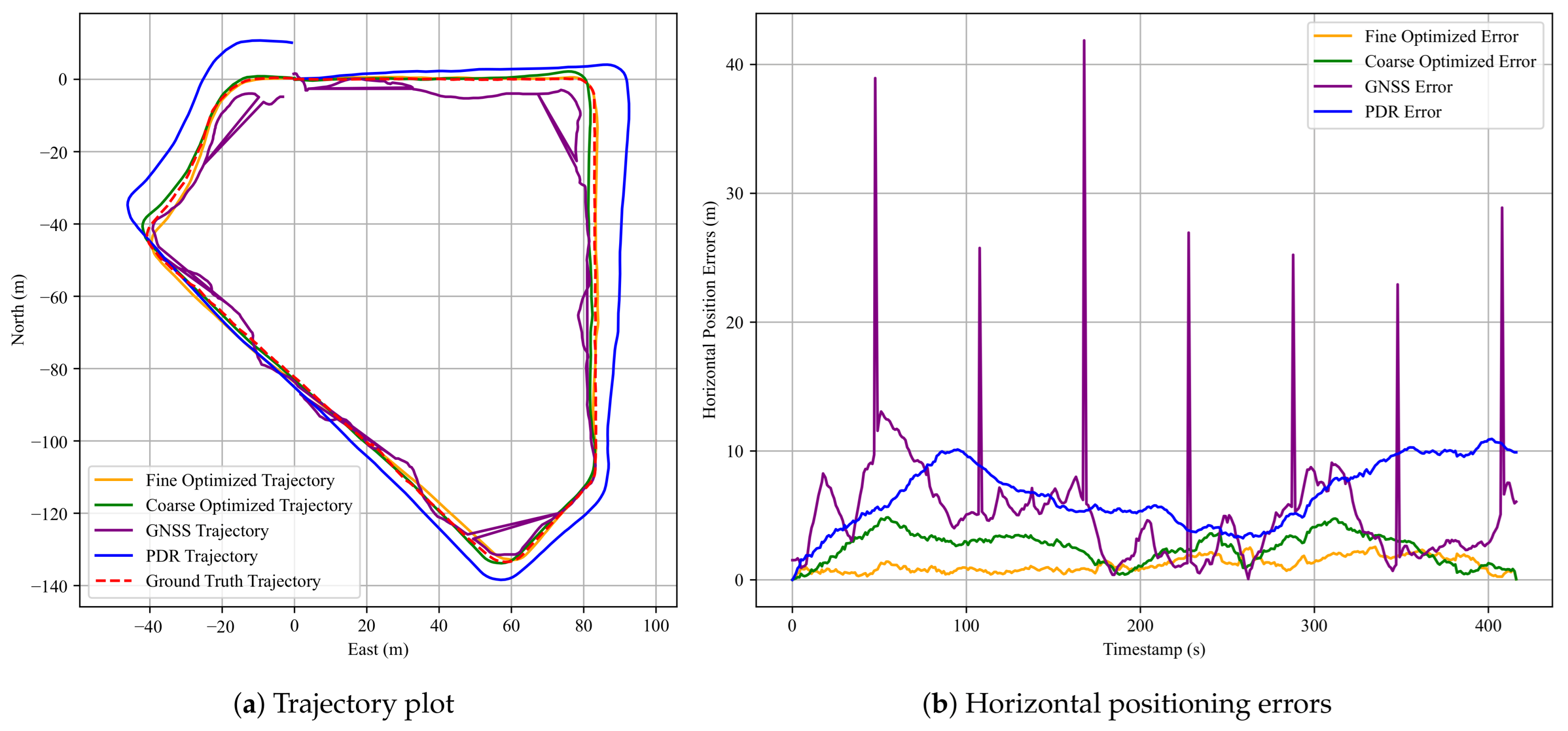
Figure 11 presents the pedestrian trajectories and horizontal positioning errors for the third dataset.
Table 3 summarizes the positioning performance (RMSE, MEAN, STD, MAX) of all three methods, while
Table 4 shows the improvement rates of the FGO-GNSS/PDR + Anchor method compared to the baseline FGO-GNSS/PDR. Consistent with previous results, the proposed FGO-GNSS/PDR + Anchor method achieves the highest accuracy across all datasets. Additional results are provided in
Appendix A.2.
As shown in the horizontal error plot, the FGO-GNSS/PDR method still exhibits considerable deviations from the ground-truth trajectory, particularly in the third dataset, where the maximum error reaches 10.44 m. In contrast, the FGO-GNSS/PDR + Anchor method effectively reduces the maximum error to 4.49 m—a reduction of 57%. Likewise, the mean error decreases from 3.79 m to 1.63 m, representing a 57% improvement. These results confirm the effectiveness of anchor constraints in correcting accumulated drift in complex scenes. In the first dataset, the best mean error achieved is only 1.54 m, and the STD is as low as 0.93 m. These results further confirm the effectiveness of the proposed anchor factor. These findings demonstrate that the proposed anchor factor significantly improves both the accuracy and stability of position estimation.
An interesting observation can be made in
Figure 11b, where the fine-optimized trajectory exhibits a slightly higher positioning error than the coarse-optimized trajectory during the 0–200 s interval of the third dataset. This behavior may be attributed to the redistribution of constraint weights in the factor graph. Specifically, during fine optimization, the relative influence of GNSS constraints decreases due to the incorporation of additional anchor constraints. While this adjustment improves robustness in challenging areas, it reduces the contribution of reliable GNSS data in well-performing segments. Since the GNSS signal quality is relatively high in the initial 0–200 s, the reduced contribution of GNSS data may lead to a marginal degradation in accuracy. This trade-off highlights the importance of appropriately balancing the contributions of anchor and GNSS factors.
Overall, the results of Experiment 2 demonstrate the effectiveness of our approach under similar walking conditions. While the method shows robustness to small path deviations and heading variations, further evaluation on more diverse walking patterns is necessary to fully validate its generalizability. It also shows that the proposed anchor-aided FGO-GNSS/PDR remains effective in extended-range, geometrically complex urban settings, thereby highlighting the method’s suitability for real-world pedestrian localization applications.
3.5. Experiment 3 in Urban Areas
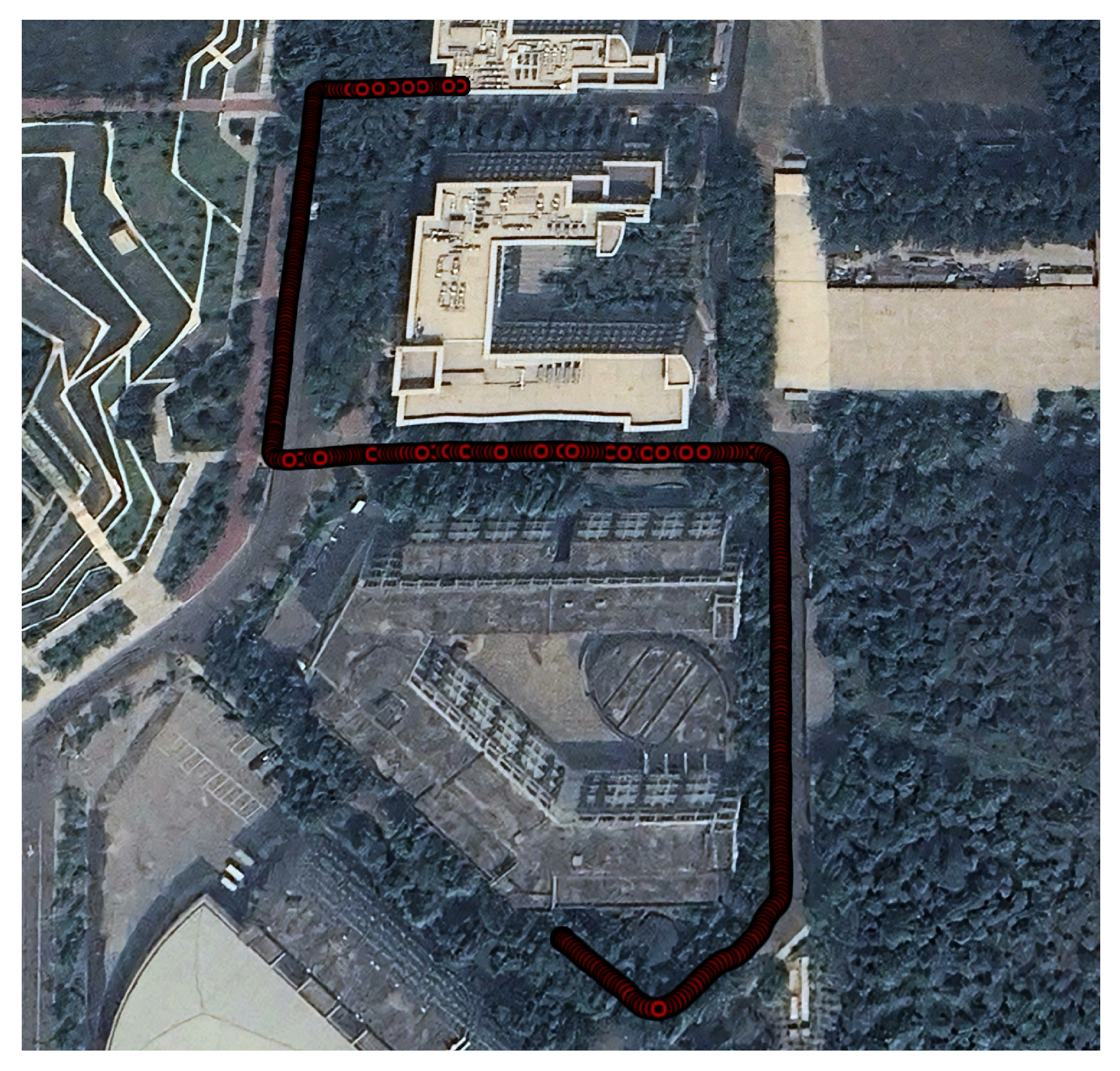
In Experiment 3, we collected a dataset that contains a partial trajectory overlapping with that in Experiment 1. The corresponding scene map and trajectory layout are illustrated in
Figure 12. This trajectory includes three anchor points from Experiment 1 and two additional newly deployed anchors, enabling a denser spatial constraint distribution. The dataset was recorded with a total walking duration of 434 s, covering a step count of 658.
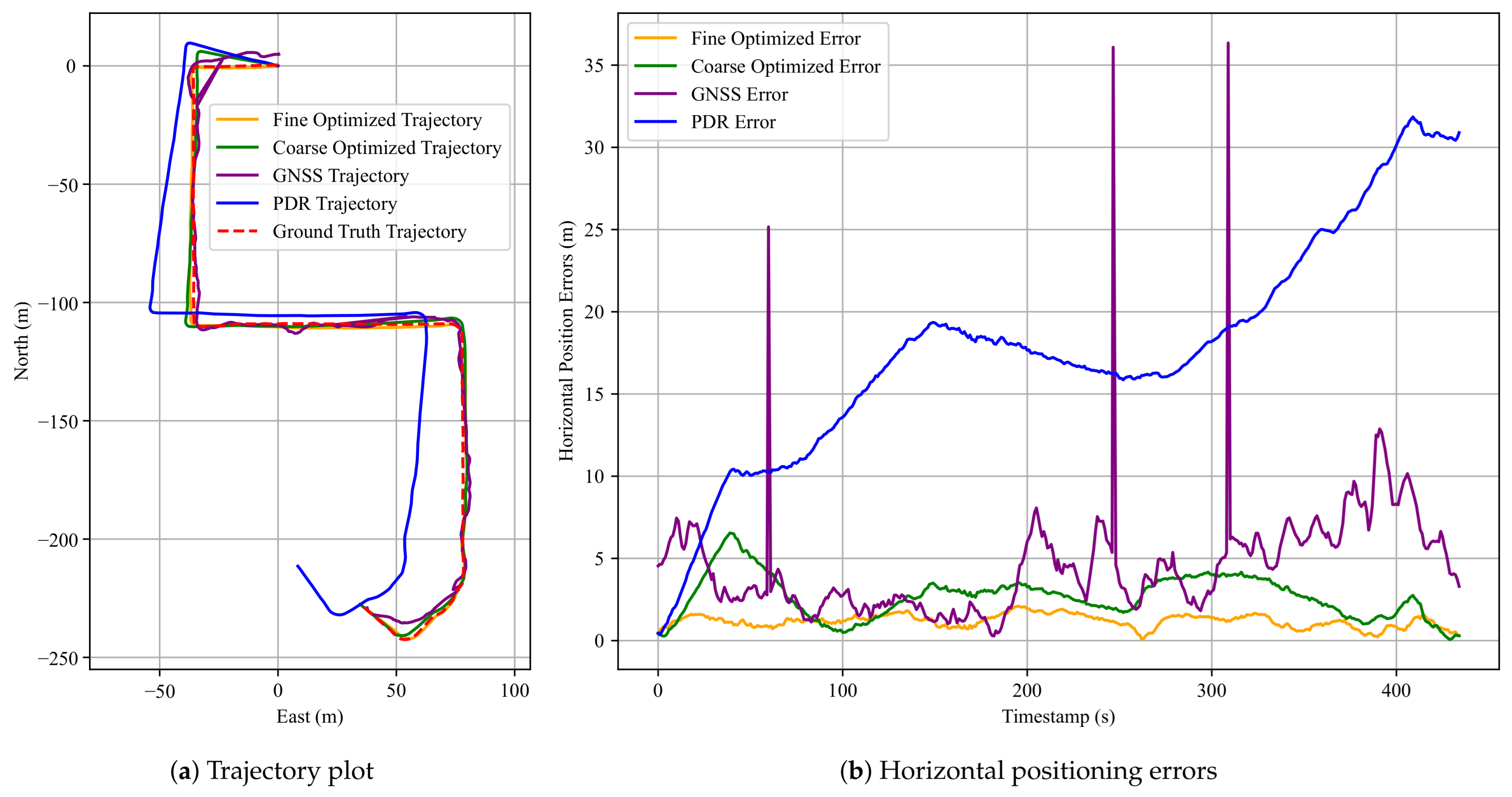
The pedestrian trajectories and horizontal positioning errors for this dataset are presented in
Figure 13, while the quantitative positioning performance is summarized in
Table 5 and
Table 6. As depicted in
Figure 13a, the PDR trajectory exhibits large angular deviations similar to those observed in dataset 3 of Experiment 1, indicating accumulated heading drift. Nevertheless, after fine optimization, the resulting trajectory closely matches the ground truth, highlighting the corrective effect of the anchor constraints.
Figure 13b further shows that the fine optimized solution maintains low error levels throughout most of the trajectory, whereas the GNSS and standalone PDR results suffer from significant fluctuations and drifts.
The RMSE, MEAN, STD, and MAX errors are compared across the three evaluated methods. It can be clearly observed that the proposed FGO-GNSS/PDR + Anchor method yields the most accurate results, with trajectories that are well-aligned with the ground-truth path. Specifically, as shown in
Table 5, the maximum horizontal error achieved by the proposed method is only 2.10 m, while the mean horizontal error is reduced to 1.19 m. Compared with the GNSS-only and FGO-GNSS/PDR methods, the proposed anchor-assisted approach consistently achieves substantial reductions in all error metrics. The RMSE, MEAN, STD, and MAX values are reduced by 58%, 55%, 70%, and 68%, respectively, relative to the FGO-GNSS/PDR baseline. These results verify that incorporating anchor factors not only improves overall accuracy but also enhances the stability of trajectory estimation in challenging urban environments.
5. Conclusions
In this paper, we introduce the concept of a video-based map in the context of RSA and propose a pedestrian localization method based on FGO-GNSS/PDR integrated with anchor constraints. To enable automatic anchor matching, we design a coarse-to-fine optimization strategy: GNSS positions, PDR results, and start&end anchors are first fused using factor graph optimization to yield coarse localization estimates. Then, trajectory turning angle cues are leveraged to match anchor points, and anchor-based constraints are incorporated to obtain refined localization results through second-stage optimization. We collected multiple real-world datasets in three representative urban scenarios and conducted both single-user repeated experiments and another-user trials. The experimental results demonstrate that the proposed anchor factor significantly improves localization accuracy across diverse scenarios. Specifically, the introduction of anchor constraints reduced the mean horizontal positioning error by 42% to 65% and the maximum error by 38% to 76% across all datasets. In this study, the mean horizontal positioning error was 1.36 m. Moreover, in the another-user experiment, the method maintained strong robustness, achieving a 47% to 53% reduction in RMSE, MEAN, STD, and MAX errors. Furthermore, the experiments demonstrate the effectiveness of the proposed PDR method in providing accurate local motion constraints. For anchor matching, the trajectory-turning-angle-based approach shows promising performance in structured urban environments, enabling reasonable anchor correspondence under typical conditions. While the method supports video-based map construction and enhances remote assistance capabilities for visually impaired users, its generalizability and robustness across more diverse users and walking patterns require further validation in future studies.
In future work, we plan to incorporate GNSS raw measurements into our framework to achieve higher positioning accuracy. We will enhance the PDR algorithm through improved step detection and heading estimation, enabling more reliable displacement constraints in the FGO framework. In addition, the anchor positions and types will be more precisely defined, and a more robust anchor-matching algorithm will be developed. Finally, we aim to implement a real-time, sliding window-based FGO framework for GNSS/PDR integration to enable real-time pedestrian localization in RSA applications.