Fault Diagnosis of Rolling Bearings Based on HFMD and Dual-Branch Parallel Network Under Acoustic Signals
Abstract
1. Introduction
2. Methodologies
2.1. Feature Mode Decomposition
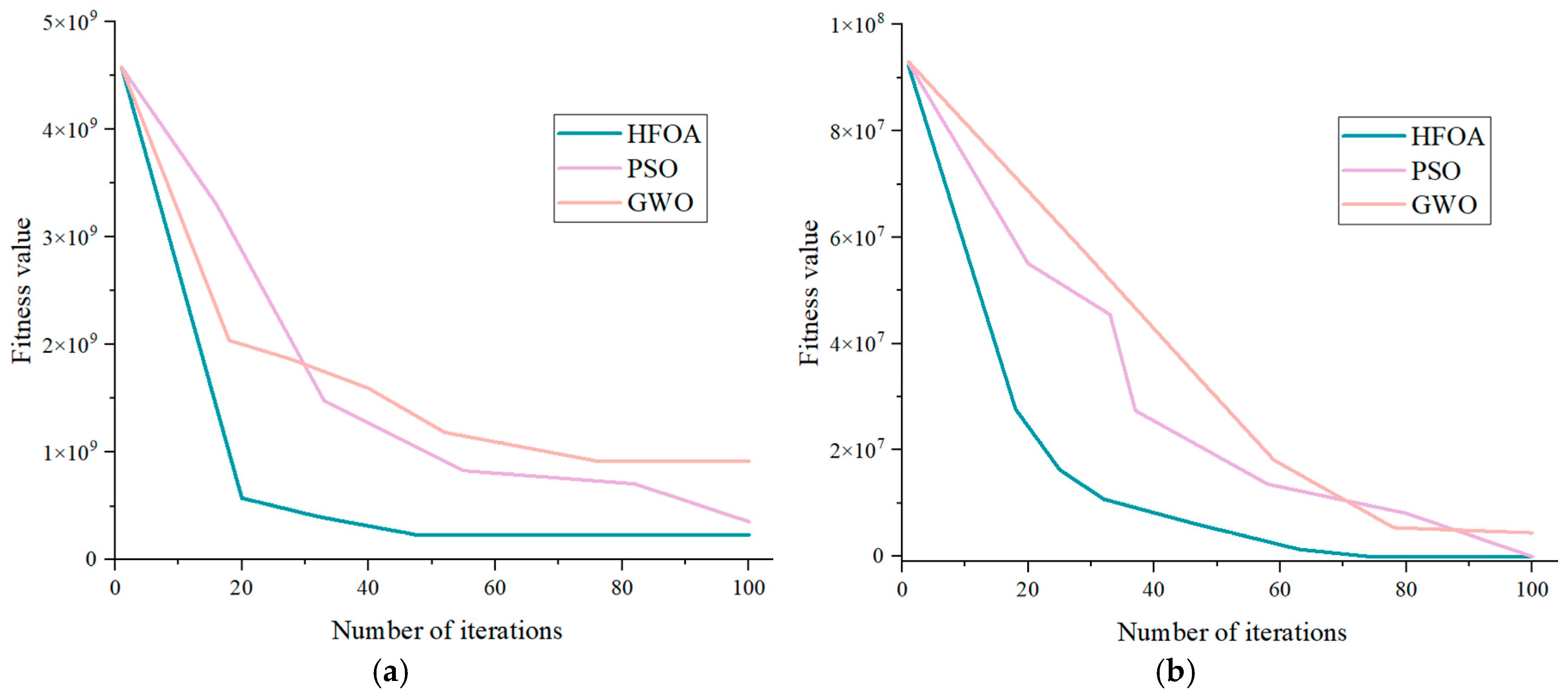
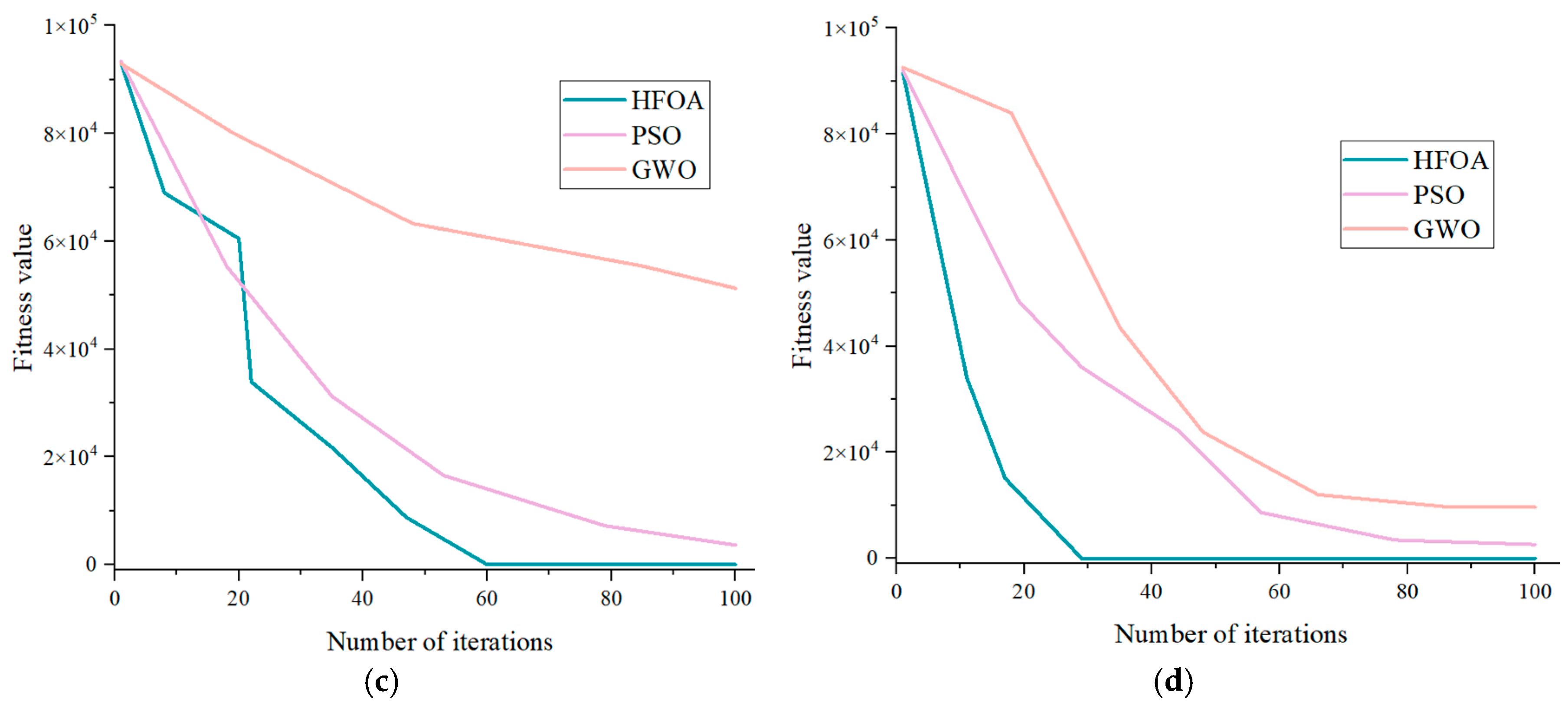
2.2. HawkFish Optimization Algorithm
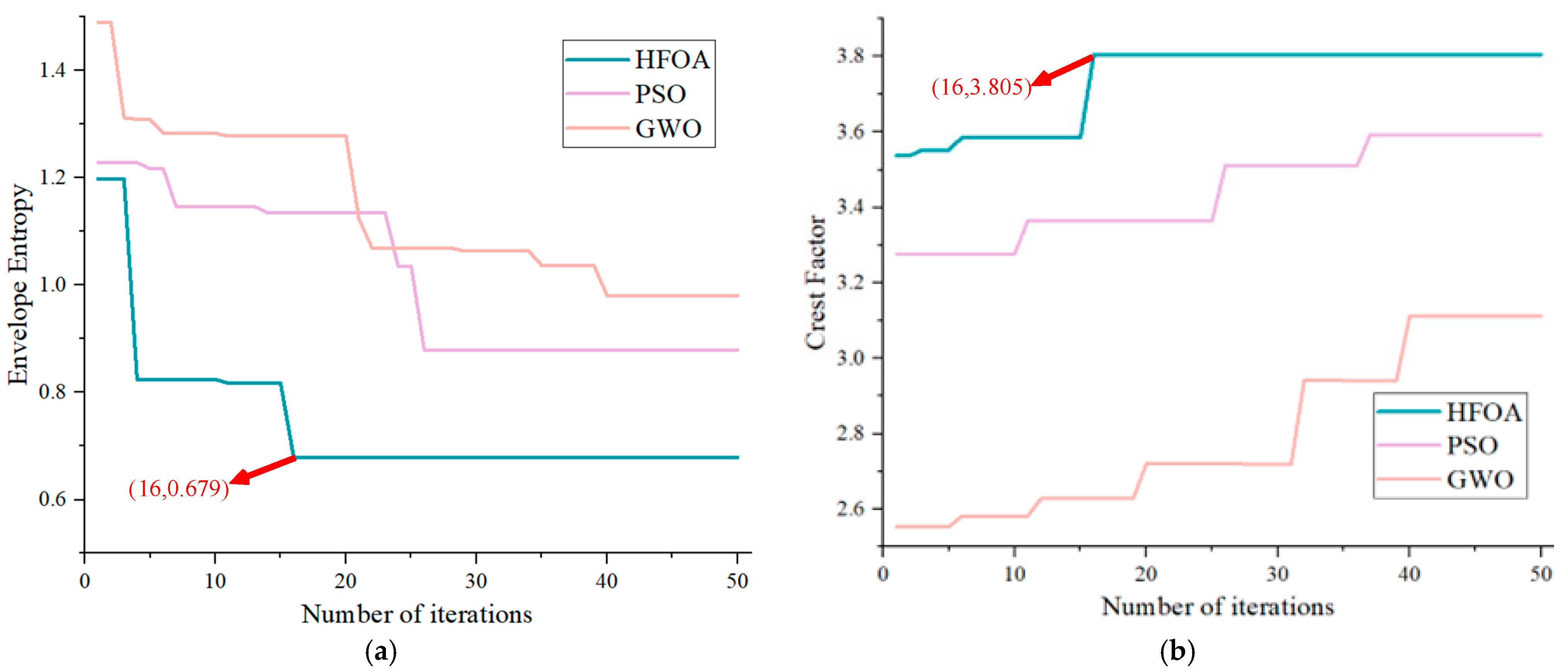
Testing of the HFOA Algorithm
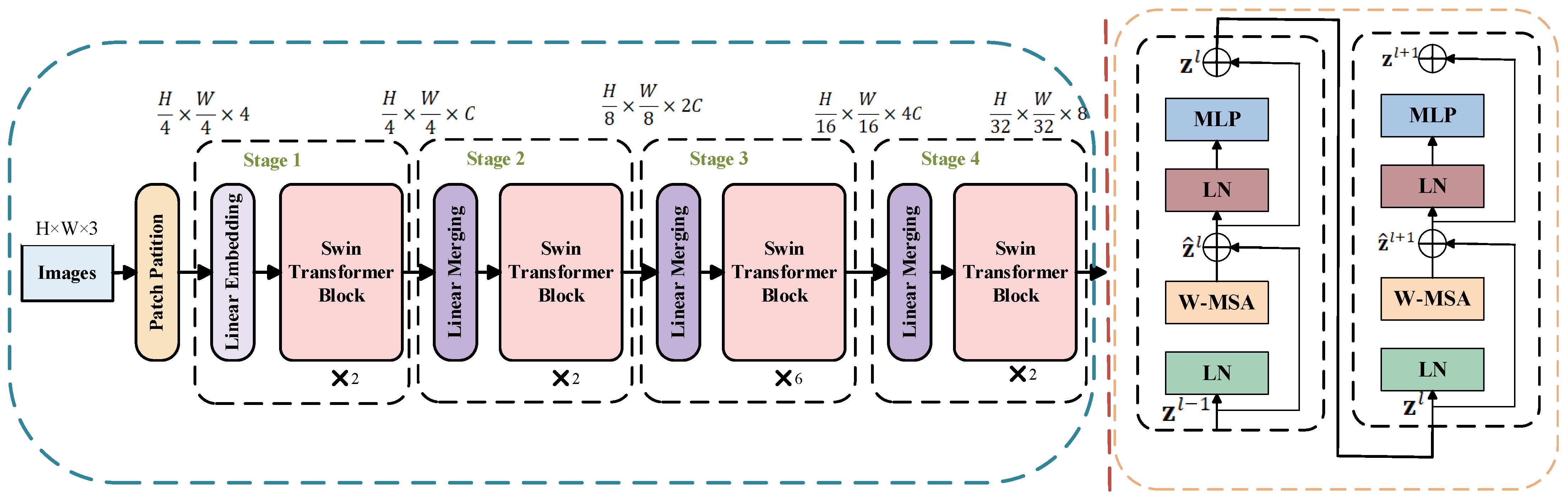
2.3. MSCSA-Swin Transformer
2.3.1. Swin Transformer
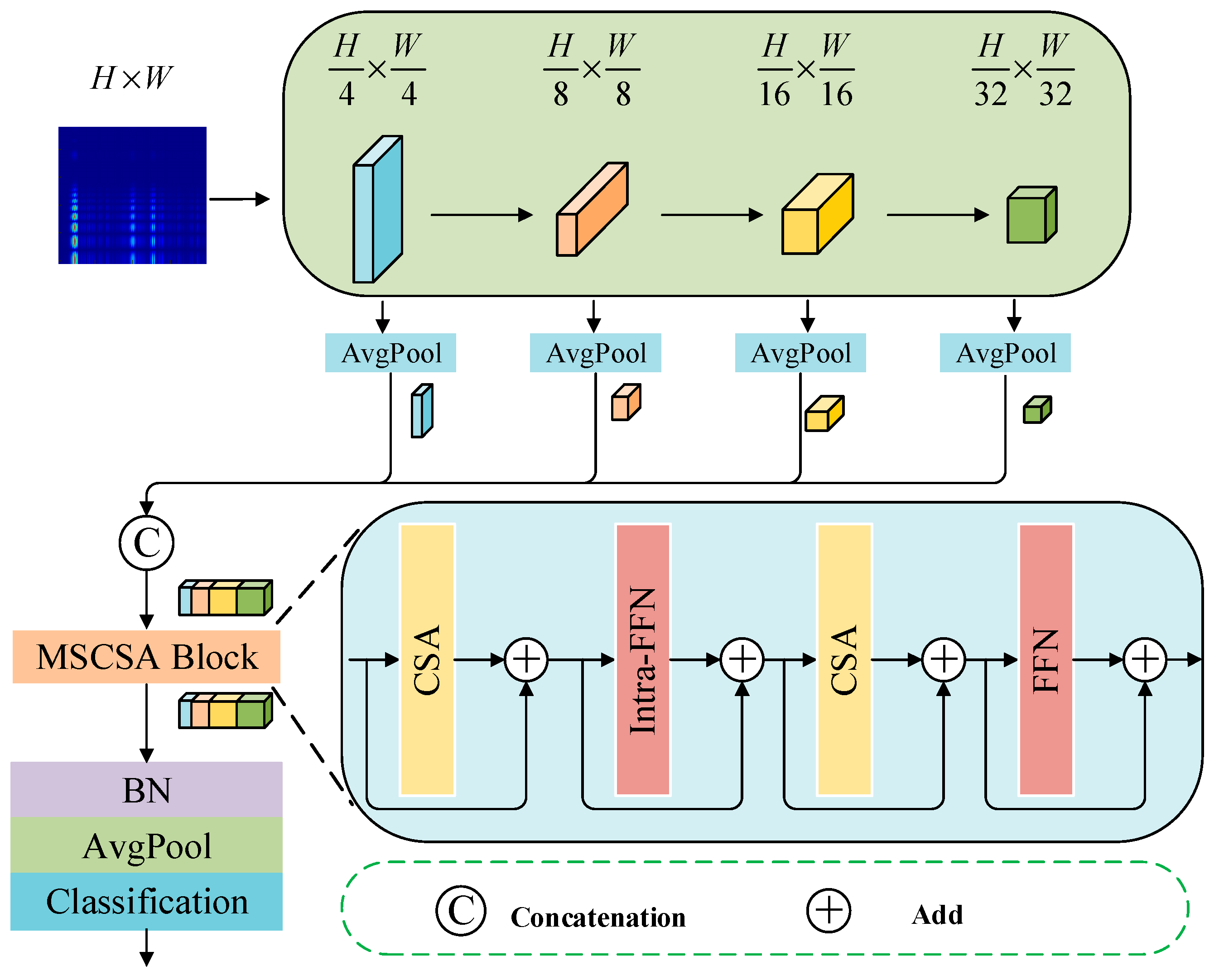
2.3.2. Multi-Stage Cross-Scale Attention Mechanism
2.4. ECA-Res2net
2.4.1. Res2Net
2.4.2. Efficient Channel Attention
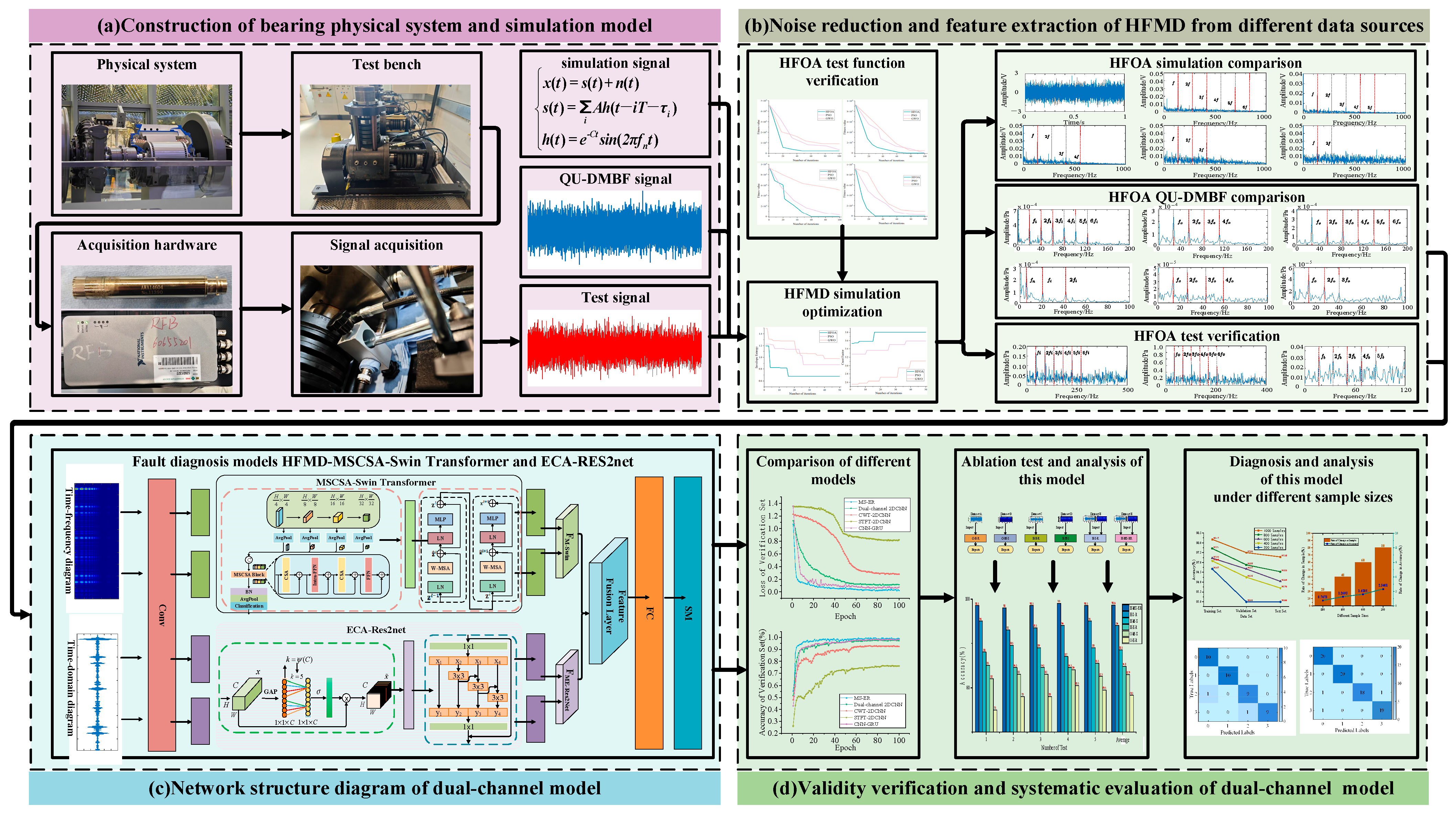
2.5. Introduction to HFMD and the Dual-Branch Parallel Network Model
3. HFMD and Dual-Branch Parallel Network Fault Diagnosis Model
3.1. Validation of HFMD
3.2. Dual-Branch Parallel Network Model
3.3. Research Process of Bearing Fault Diagnosis Based on HFMD and Dual-Branch Parallel Network Under Acoustic Signals
4. Open-Source Data Verification
4.1. QU-DMBF Test Bearing and Test Bench
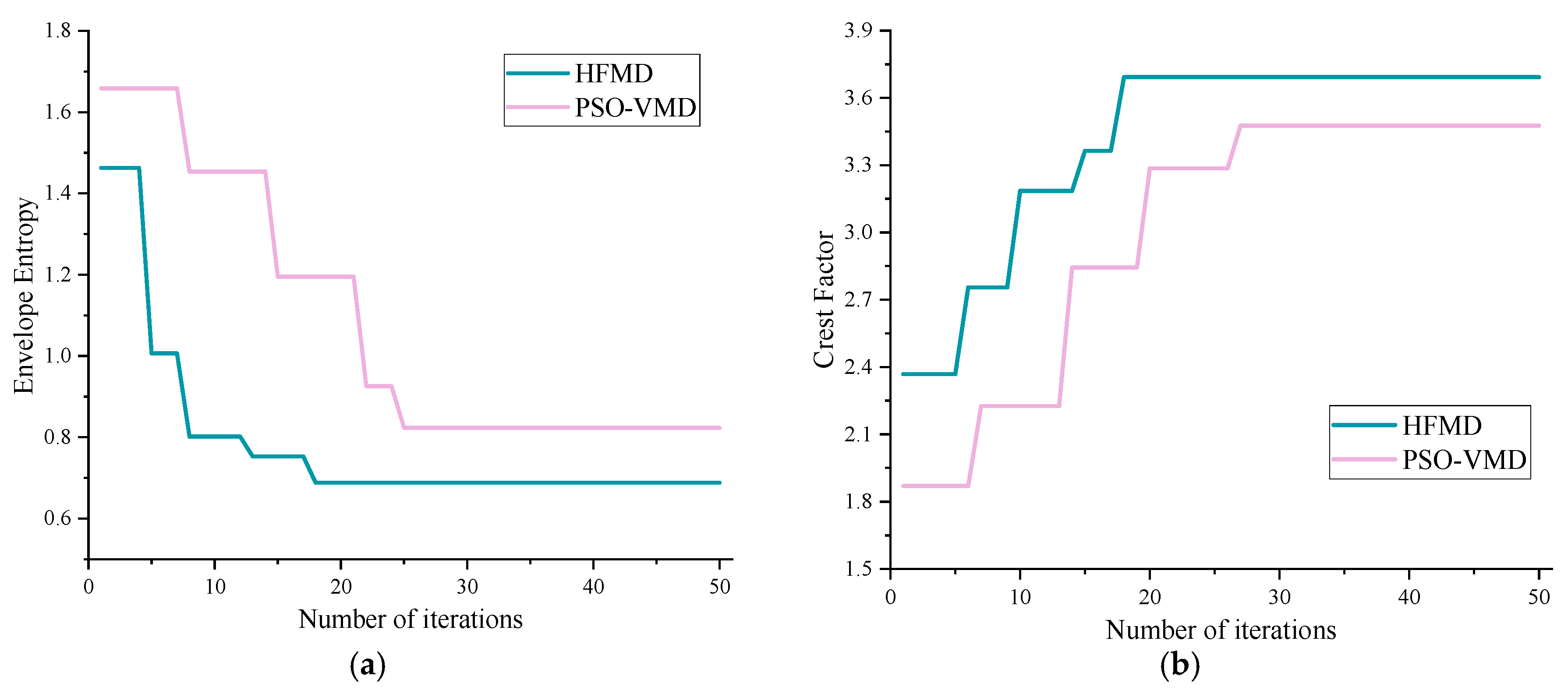
4.2. Verification of HFMD Denoising Effect
4.3. Introduction to the QU-DMBF Dataset
4.4. MSCSA-Swin Transformer and ECA-RES2net Verification and Analysis
4.5. CWRU Data Verification and Analysis
5. Acoustic Signal Test Verification and Analysis
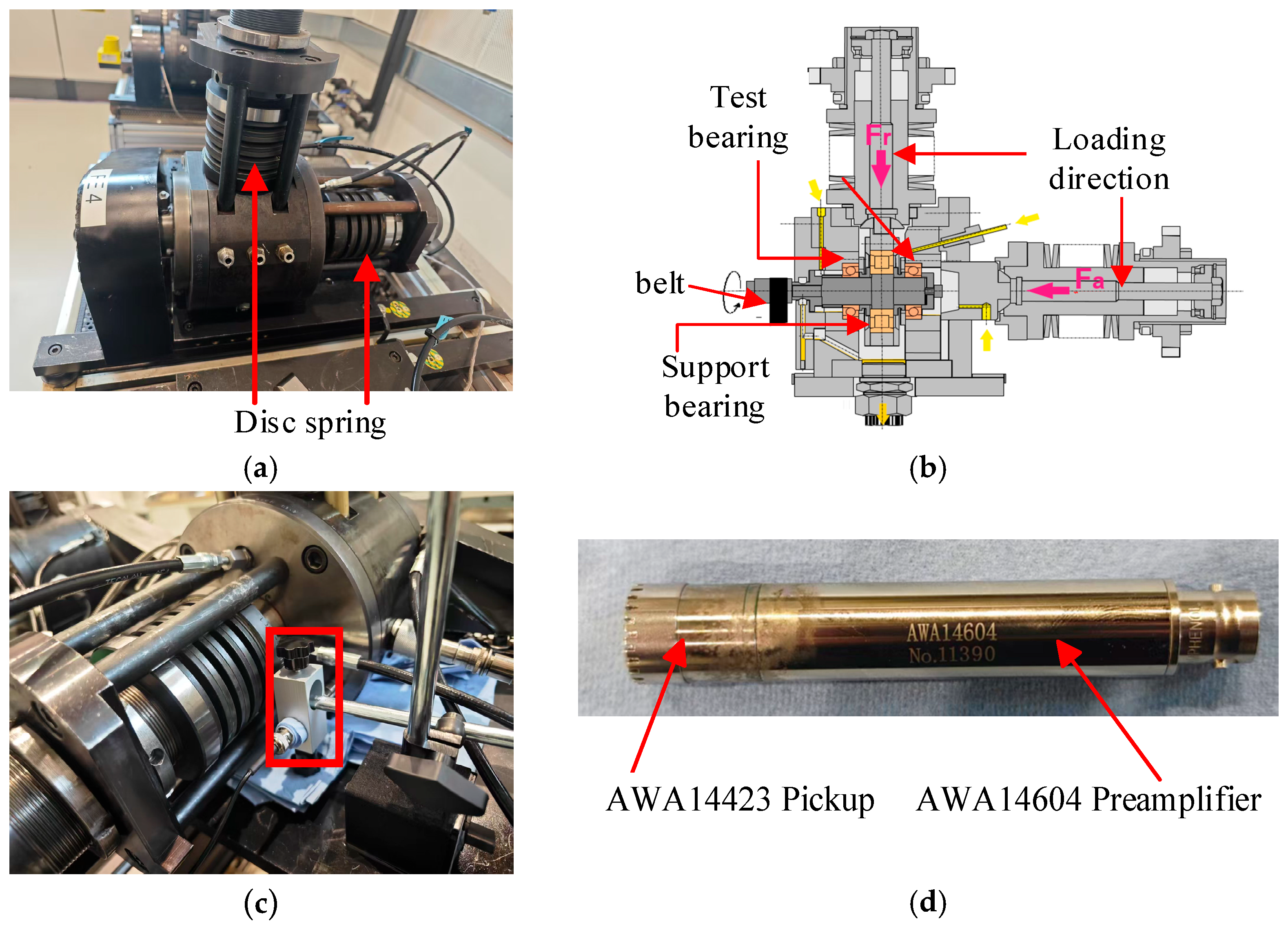
5.1. Test Bench and Bearings
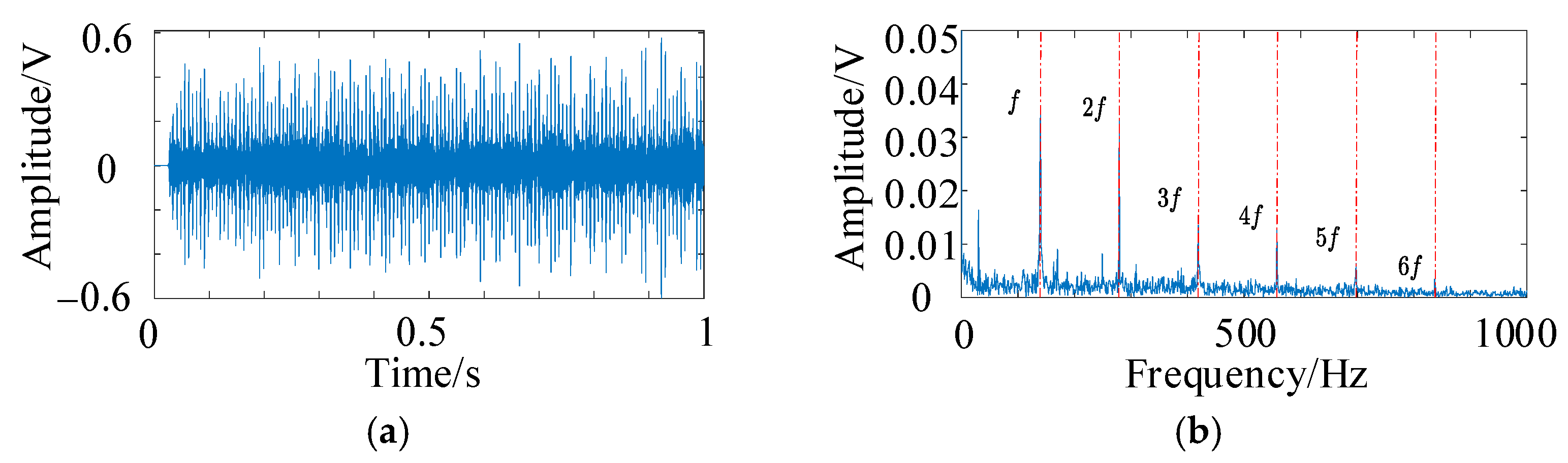
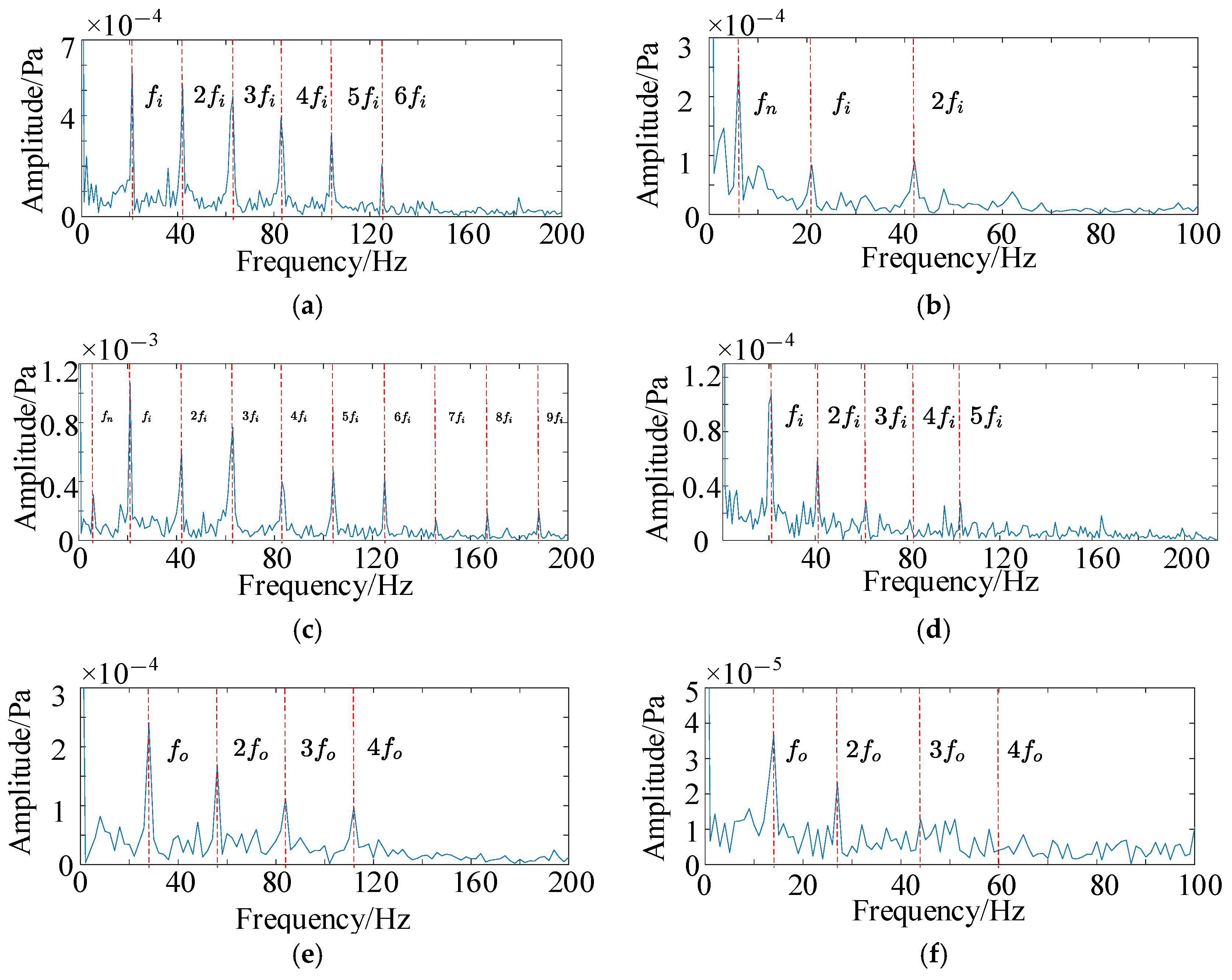
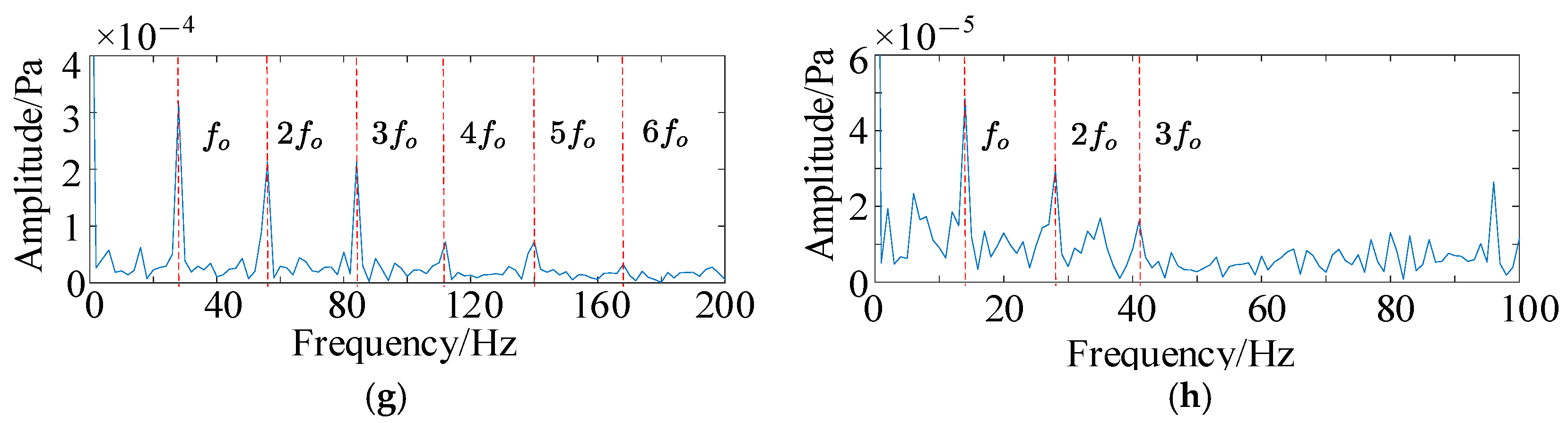
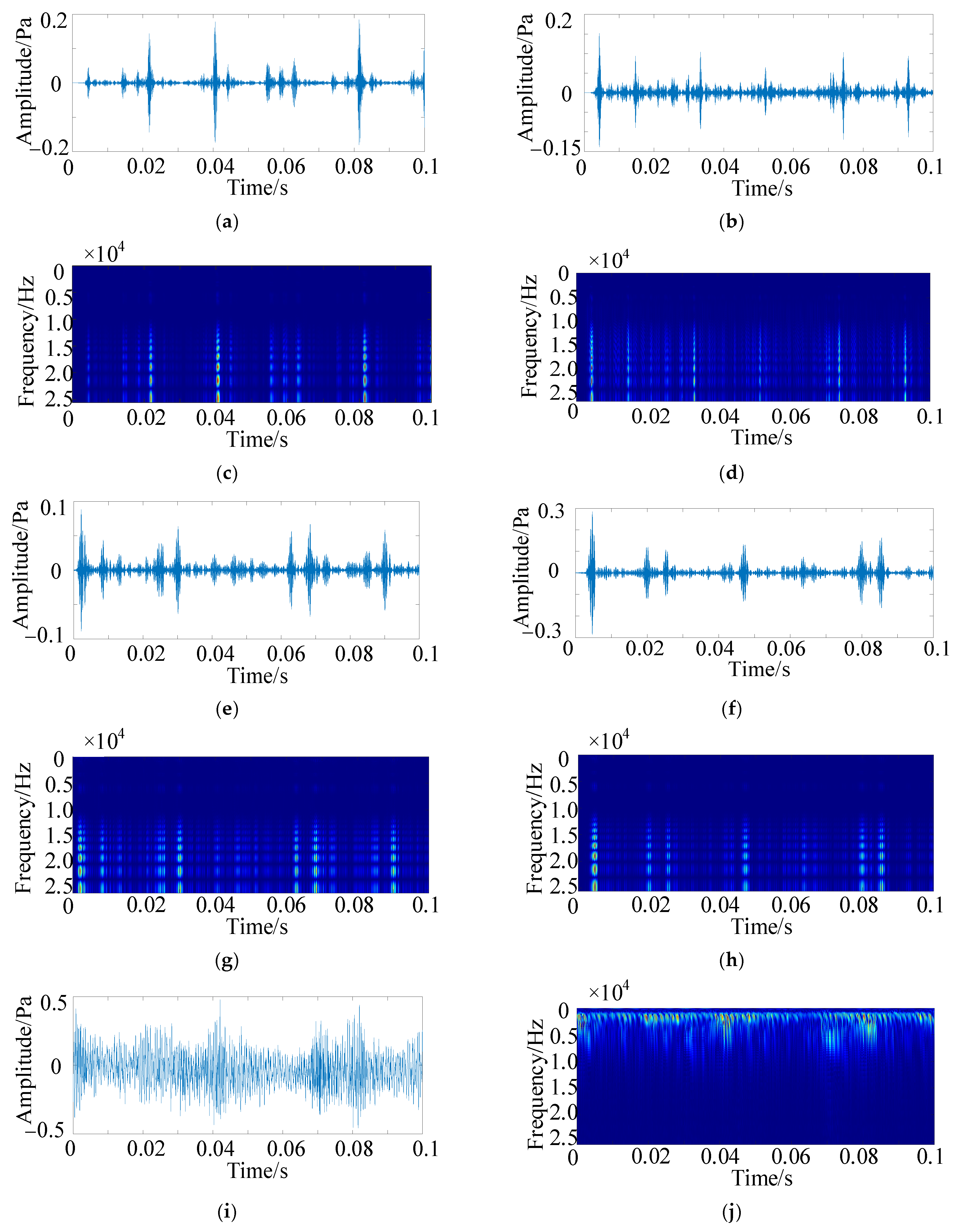
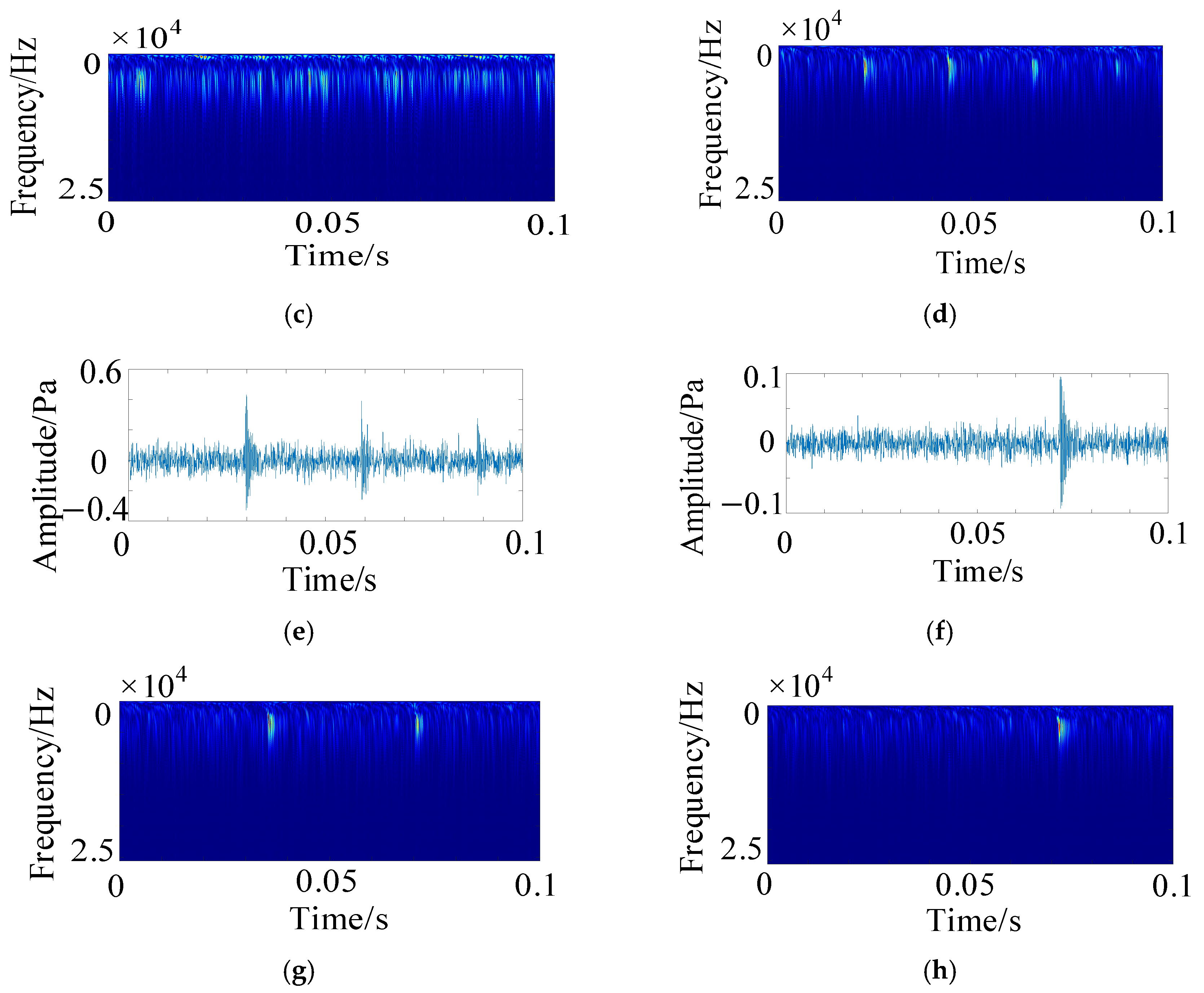
5.2. Verification and Analysis of HFMD Under Test Acoustic Signals
5.3. Validation and Analysis of HFMD-MSCSA-Swin Transformer and ECA-RES2net
5.3.1. Parallel Network Model Data Processing
5.3.2. Introduction to the Test Dataset
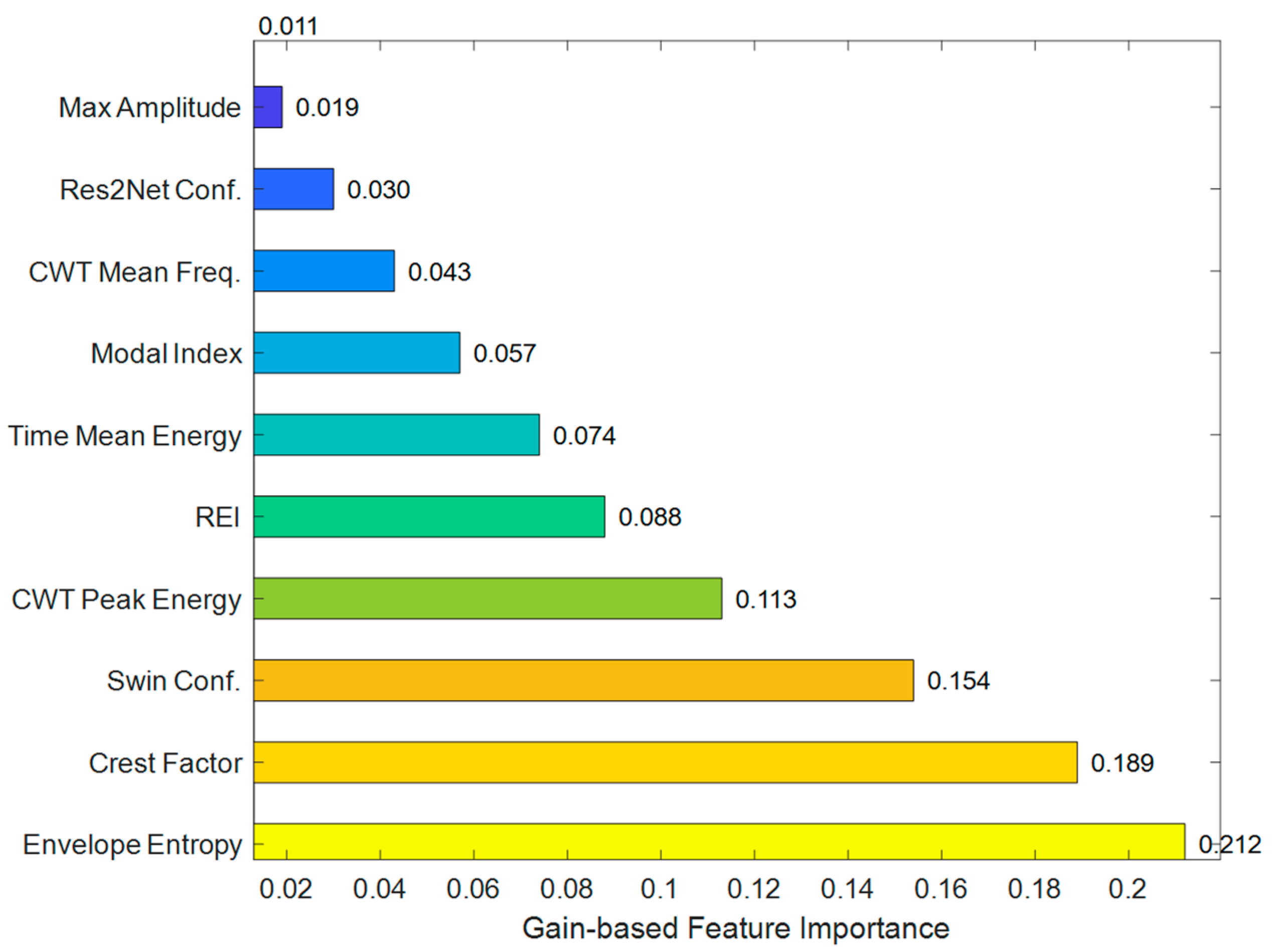
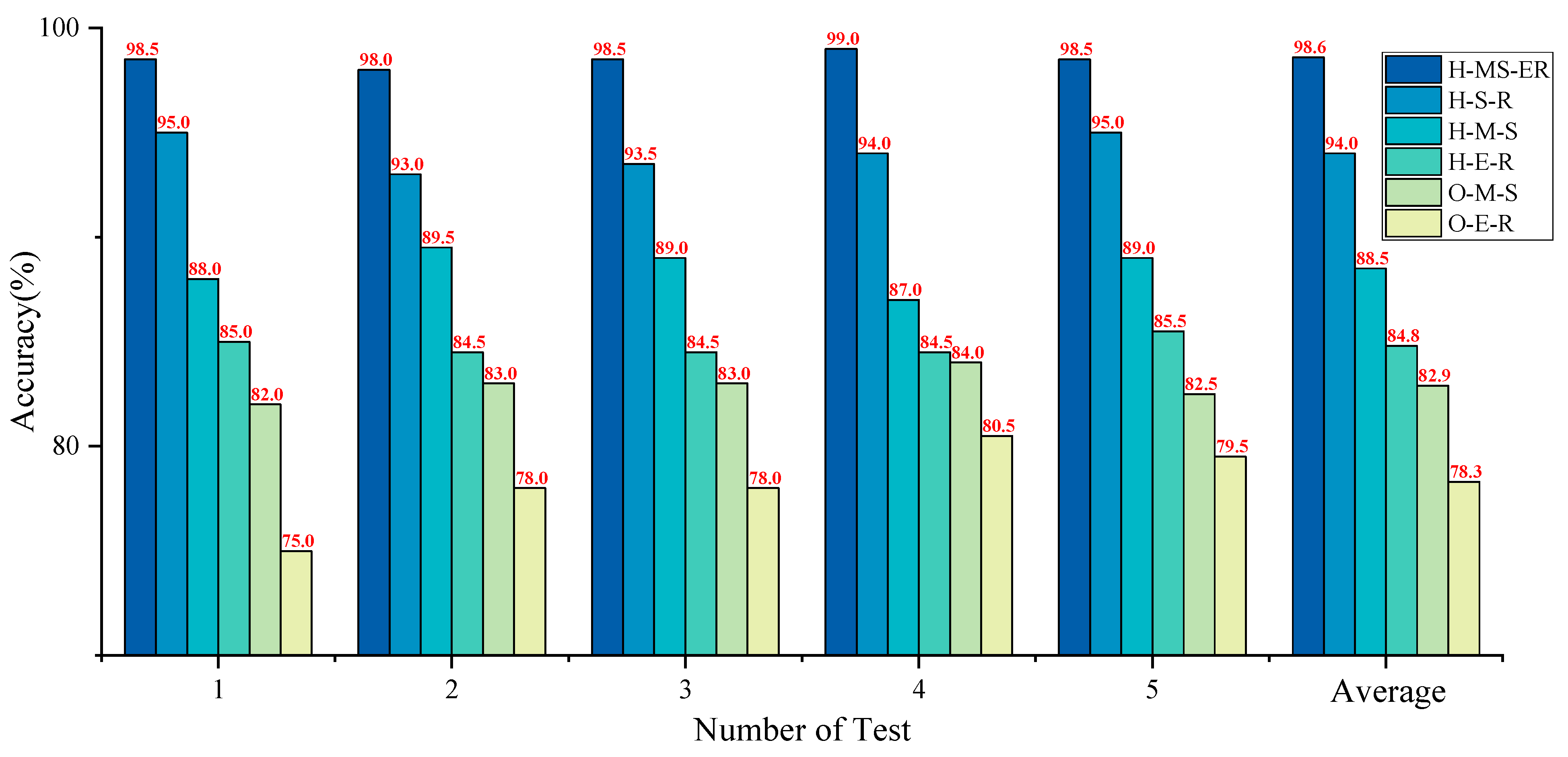
5.3.3. Comparative Analysis of Different Diagnostic Models
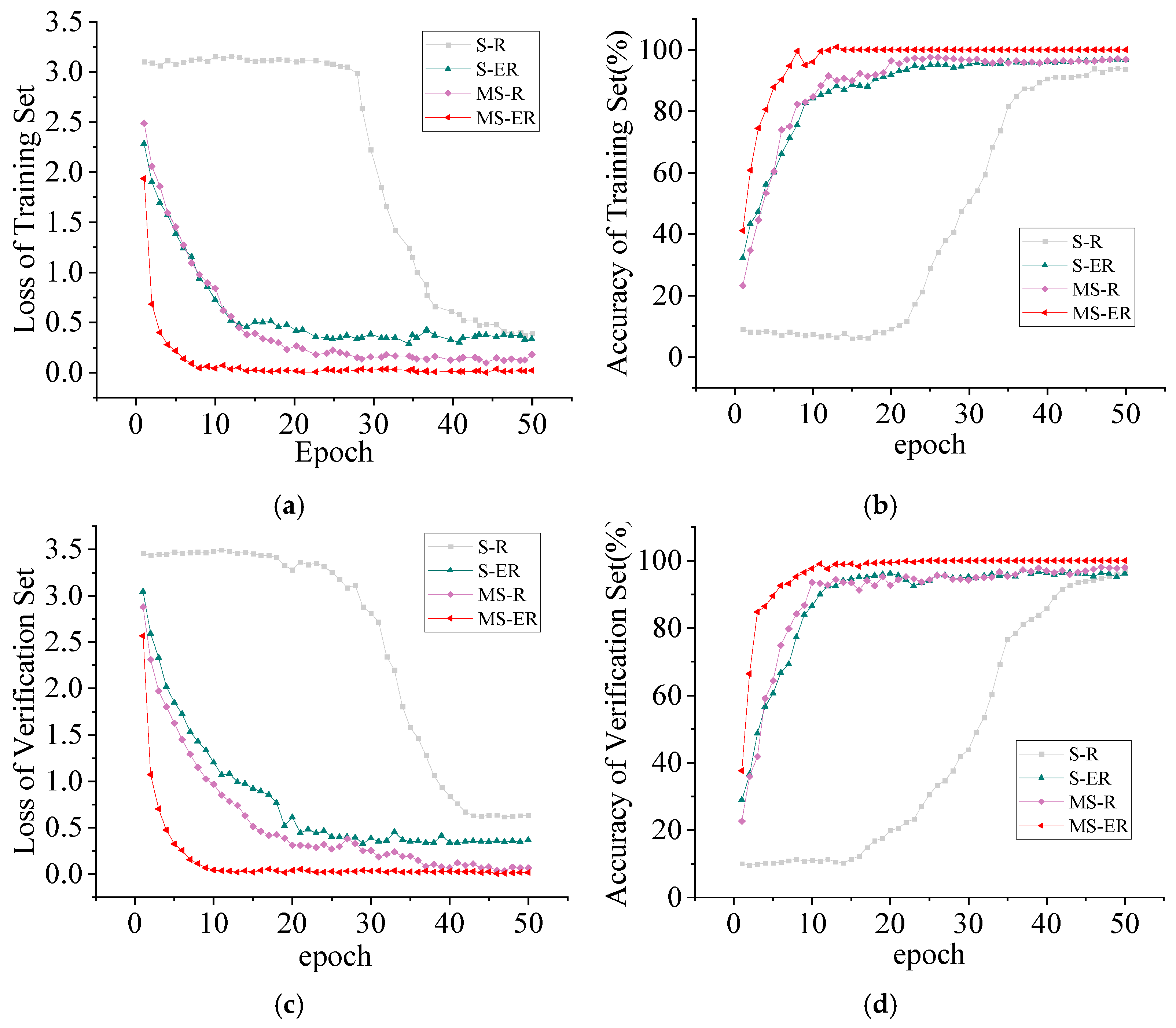
5.3.4. Diagnostic Model Ablation Test
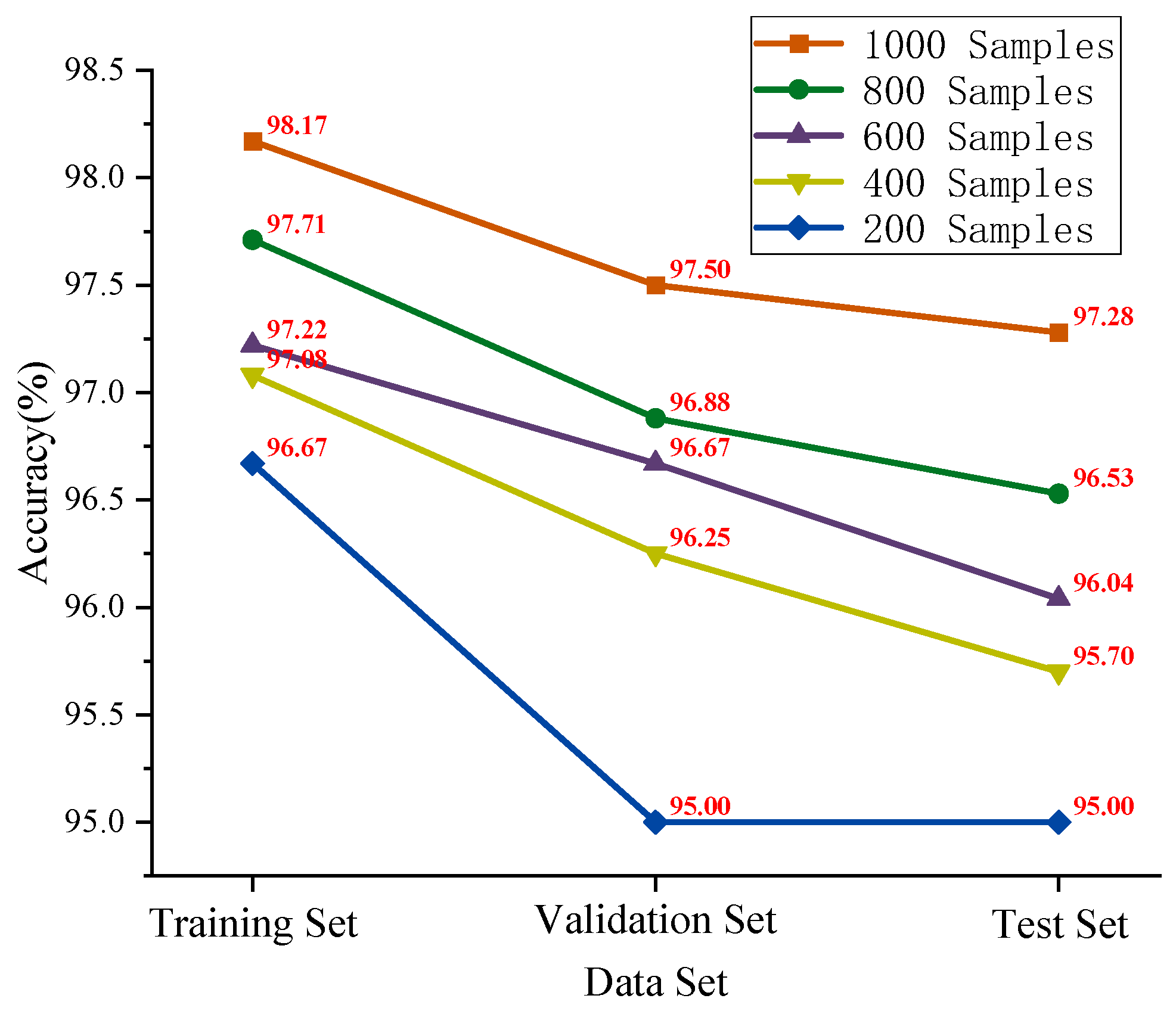
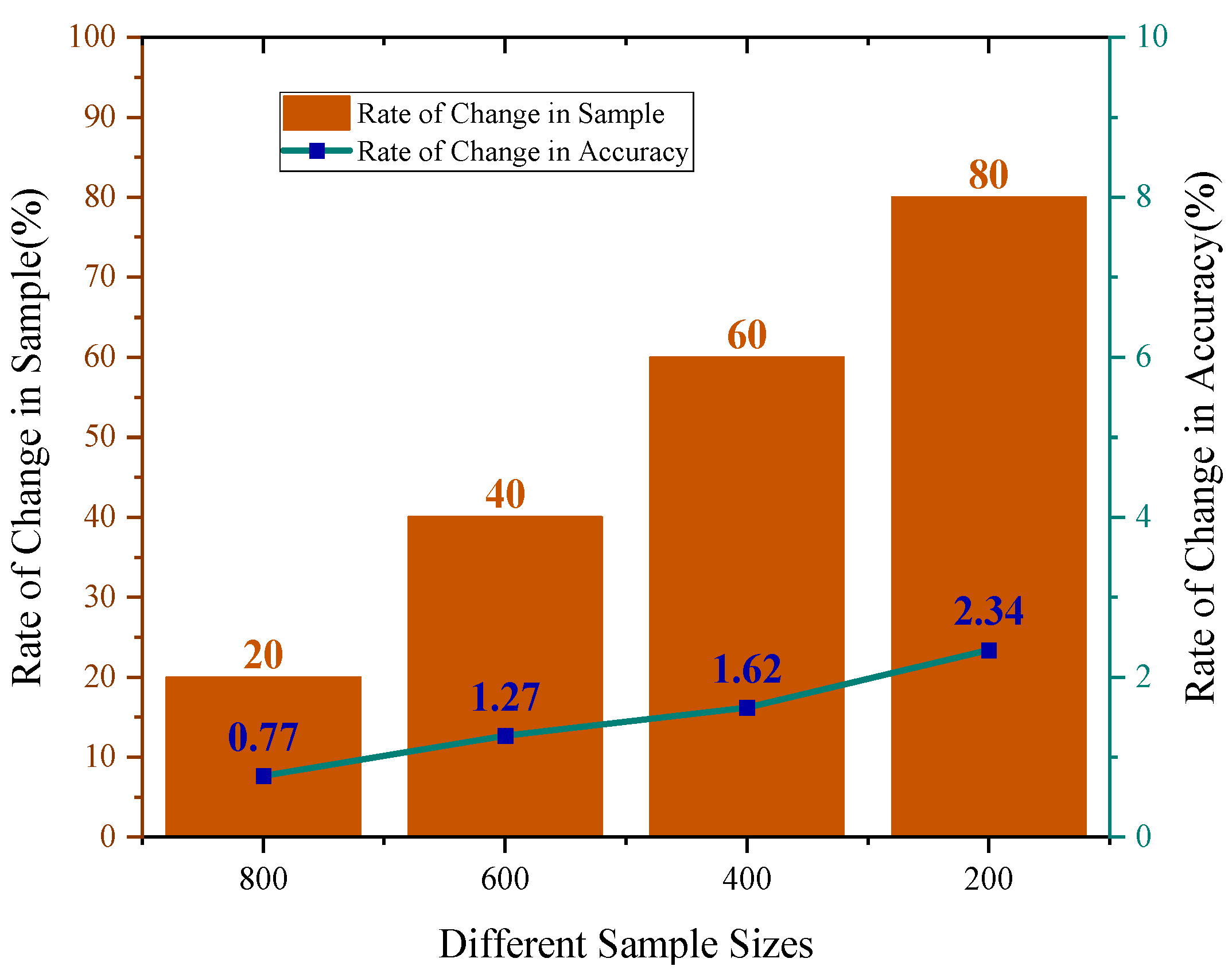
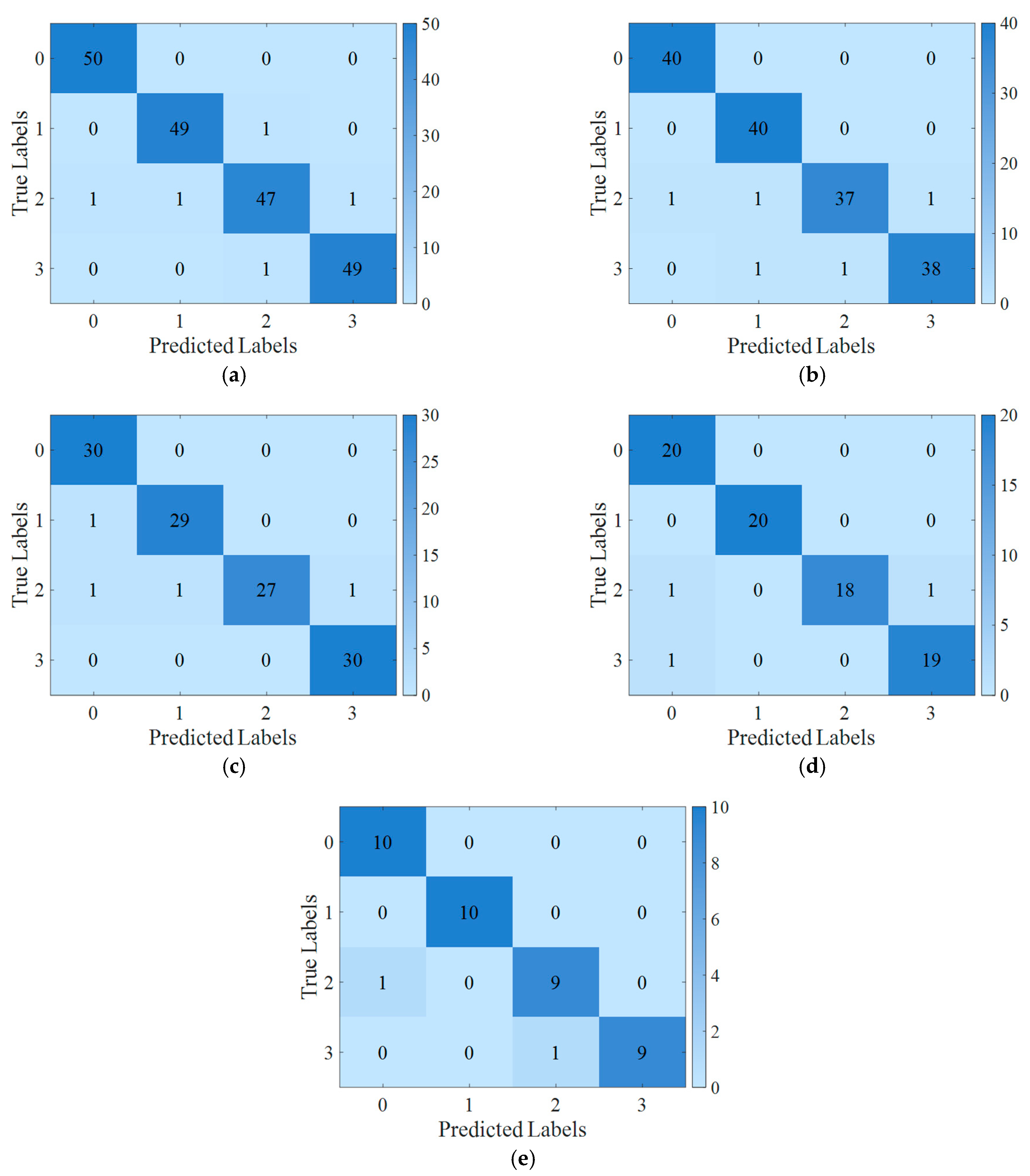
5.3.5. Validation and Analysis of Diagnostic Models Under Different Sample Sizes
6. Conclusions and Prospects
6.1. Conclusions
6.2. Prospects
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Pseudocode (Within 1–5 Lines)
| Algorithm A1: Rolling Bearing Fault Diagnosis via hawkFish Optimization + HFMD + Dual-Branch Network |
| Input: Raw audio signal dataset Output: Predicted fault category label 1. Feature Mode Decomposition and Optimal Mode Extraction (HFMD + hawkFish) For each input signal x: // 1.1 Adaptively optimizing FMD parameters using the hawkFish Optimization Algorithm Initialize population size N and dimension S = 4 Set parameter ranges: n ∈ [3, 10] // Modal number L ∈ [50, 300] // filter length K ∈ [5, 12] // Number of stopbands m ∈ [5, 15] // Periodic parameter Set max iterations: max_iter = 50 Initialize control parameters for hawkFish: w, α, β Randomly initialize N fish positions (candidate parameter sets) For t = 1 to max_iter: For i = 1 to N: Decompose x using FMD with candidate params [ni, Li, Ki, mi] Compute fitnessi = envelope_entropy × peak_factor End For Update fish positions using hawkFish movement rules: Position ← Position + w·(Position − best) + α·rand()·β·(Position − neighbor)·(1 − d) Enforce bounds on Position End For Select optimal parameter group with minimum fitness Perform FMD again using optimal parameters → modes {u1, u2, …, u_K} // 1.2 Select the optimal modality For each mode u_k: Compute REI_k = envelope_entropy(u_k) × peak_factor(u_k) Select u_min with minimum REI // 1.3 Generate input samples Apply Continuous Wavelet Transform (CWT) to u_min → Obtain: time-domain signal x_time time-frequency image x_freq End For 2. Dual-branch deep feature extraction network (dual-branch network) // 2.1 Time-domain branch: Res2Net + ECA attention Input: x_time → Res2Net Block(s) → ECA Attention → Global Average Pooling → Output: time-domain features A ∈ ℝ512 // 2.2 time-frequency branch: Swin Transformer + MSCSA Input: x_freq → Patch Partition and embedding → Swin Transformer + MSCSA multi-scale attention module (×multi-layer) → Patch Merging → Global Average Pooling → Output: frequency-domain features B ∈ ℝ768 3. Multimodal Feature Fusion and Classification Module Concatenate A and B → F ∈ ℝ1280 Apply 1×1 Conv → G ∈ ℝ1024 Feed G into FC layer → Softmax Output: Predicted class label 4. Data preprocessing stage (pre-training data preparation) Set sample length = 2048 Set sliding step = 1500 For each raw signal: Apply sliding window segmentation Normalize each segment (Z-score) End For Split dataset: Training set (60%) Validation set (20%) Test set (20%) 5. Model training process Initialize optimizer (e.g., Adam), learning rate, and loss function For epoch = 1 to MaxEpoch: For each batch (x, y) in training set: For each sample: Apply HFMD + hawkfish → get x_time and x_freq End For Forward pass through dual-branch network Compute loss = cross entropy(prediction, y) Backpropagate gradients and update parameters End For Validate on validation set Save best model based on validation accuracy End For 6. Model Testing and Evaluation For each test sample: Apply HFMD → x_time and x_freq Predict class using trained model Compare with ground truth End For Compute: Accuracy = correct predictions/total samples Optionally: precision, recall, F1-score Return: Final classification result and evaluation metrics End Algorithm |
Appendix A.2. Detailed Explanation of Each Module’s Function (Within 1–5 Lines)
Appendix A.3. Module Integration and Collaboration Mechanism Description (Within 1–5 Lines)
| Module | Function | Support for Subsequent Modules. |
| HFMD (HFOA Optimization) | Noise Reduction + Mode Screening | Delivers High-Quality Signal Input with Clear Structure and Focused Information. |
| ECA-Res2Net | Extract time-domain pulses and multi-scale shocks | Support identification of localized short-term features and enhance noise immunity. |
| MSCSA-Swin | Extract cross-scale frequency domain dependencies | Supports global modeling of frequency bands, enhancing non-stationary signal processing capability. |
| Fusion layer | Integrates time and frequency dimension information | Enhances diagnostic decision accuracy and robustness. |
References
- Gonzalez-Jimenez, D.; Del-Olmo, J.; Poza, J.; Garramiola, F.; Madina, P. Data-driven fault diagnosis for electric drives: A review. J. Sens. 2021, 21, 4024. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Research on bearing fault feature extraction based on singular value decomposition and optimized frequency band entropy. J. Mech. Syst. Signal Process. 2019, 118, 477–502. [Google Scholar] [CrossRef]
- Michalak, A.; Wodecki, J.; Wyłomańska, A.; Zimroz, R. Application of cointegration to vibration signal for local damage detection in gearboxes. J. Appl. Acoust. 2019, 144, 4–10. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. J. Meas. 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Reda, A.; Kgosiemang, I.M.; Ja’e, I.A.; Oyetunji, A.K.; Olukolajo, M.A.; Igwe, I.B. Guidelines on asset management of offshore facilities for monitoring, sustainable maintenance, and safety practices. J. Sens. 2022, 22, 7270. [Google Scholar] [CrossRef]
- Tsao, W.-C.; Li, Y.-F.; Du Le, D.; Pan, M.-C. An insight concept to select appropriate IMFs for envelope analysis of bearing fault diagnosis. J. Meas. 2012, 45, 1489–1498. [Google Scholar] [CrossRef]
- Deng, Q.; Zhao, G.; Jiang, W.; Wu, J.; Dai, T. Multilayer Fused Correntropy Reprsenstation for Fault Diagnosis of Mechanical Equipment. J. Sens. 2024, 24, 6142. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A Survey on Fault Diagnosis of Rolling Bearings. Algorithms 2022, 15, 347. [Google Scholar] [CrossRef]
- Wu, G.; Yan, T.; Yang, G.; Chai, H.; Cao, C. A Review on Rolling Bearing Fault Signal Detection Methods Based on Different Sensors. Sensors 2022, 22, 8330. [Google Scholar] [CrossRef]
- Mao, M.; Jiang, Z.; Tan, Z.; Xiao, W.; Du, G. Tilting Pad Thrust Bearing Fault Diagnosis Based on Acoustic Emission Signal and Modified Multi-Feature Fusion Convolutional Neural Network. J. Sens. 2025, 25, 904. [Google Scholar] [CrossRef]
- Keshun, Y.; Zengwei, L.; Yingkui, G. A performance-interpretable intelligent fusion of sound and vibration signals for bearing fault diagnosis via dynamic CAME. J. Nonlinear Dyn. 2024, 112, 20903–20940. [Google Scholar] [CrossRef]
- Arifin, M.S.; Wang, W.; Uddin, M.N. A Modified EMD Technique for Broken Rotor Bar Fault Detection in Induction Machines. J. Sens. 2024, 24, 5186. [Google Scholar] [CrossRef]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. J. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. J. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An optimized VMD method and its applications in bearing fault diagnosis. J. Meas. 2020, 166, 108185. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Li, C.; Lin, J.; Zhang, D. Feature mode decomposition: New decomposition theory for rotating machinery fault diagnosis. IEEE Trans. Ind. Electron. 2022, 70, 1949–1960. [Google Scholar] [CrossRef]
- Jia, G.; Meng, Y. Study on Fault Feature Extraction of Rolling Bearing Based on Improved WOA-FMD Algorithm. J. Shock Vib. 2023, 2023, 5097144. [Google Scholar] [CrossRef]
- Chauhan, S.; Vashishtha, G.; Kumar, R.; Zimroz, R.; Gupta, M.K.; Kundu, P. An adaptive feature mode decomposition based on a novel health indicator for bearing fault diagnosis. J. Meas. 2024, 226, 114191. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. Bearing fault diagnosis via a parameter-optimized feature mode decomposition. J. Meas. 2022, 203, 112016. [Google Scholar] [CrossRef]
- Feng, F.; Zhu, T.; Yang, B.; Zhang, Z.; Zhou, S.; Xiao, S. Probabilistic fatigue life prediction in additive manufacturing materials with a physics-informed neural network framework. Expert Syst. Appl. 2025, 275, 127098. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Y.; Zhang, F.; Zhou, N.; Wang, H.; Jin, B.; Zhang, W. Multi-modal imitation learning for arc detection in complex railway environments. IEEE Trans. Instrum. Meas. 2025, 74, 3529413. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Y.; Wang, Q.; Liu, L.; Zhang, W.; Jin, B. Transformer and graph convolution-based unsupervised detection of machine anomalous sound under domain shifts. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 2827–2842. [Google Scholar] [CrossRef]
- Bai, Y.; Hu, X.; Zheng, K.; Chen, Y.; Tang, Y. A Target Domain-Specific Classifier Weight Partial Transfer Adversarial Network for Bearing Fault Diagnosis. Mathematics 2025, 13, 248. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Sui, Q.; Zhang, F.; Li, Y.; Jiang, M.; Paitekul, P. Intelligent Fault Diagnosis Method of Rolling Bearings Based on Transfer Residual Swin Transformer with Shifted Windows. Struct. Durab. Health Monit. (SDHM) 2024, 18, 91–110. [Google Scholar] [CrossRef]
- Dai, X.; Yi, K.; Wang, F.; Cai, C.; Tang, W. Bearing fault diagnosis based on POA-VMD with GADF-Swin Transformer transfer learning network. Measurement 2024, 238, 115328. [Google Scholar] [CrossRef]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN parameter design based on fault signal analysis and its application in bearing fault diagnosis. J. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, B.; Deng, L.; Liu, X. A hybrid attention improved ResNet based fault diagnosis method of wind turbines gearbox. J. Meas. 2021, 179, 109491. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, C.; Deng, C. An improved GNN using dynamic graph embedding mechanism: A novel end-to-end framework for rolling bearing fault diagnosis under variable working conditions. J. Mech. Syst. Signal Process. 2023, 200, 110534. [Google Scholar] [CrossRef]
- Yin, S.; Chen, Z. Research on Compound Fault Diagnosis of Bearings Using an Improved DRSN-GRU Dual-Channel Model. IEEE Sens. J. 2024, 24, 35304–35311. [Google Scholar] [CrossRef]
- Hu, B.; Liu, J.; Zhao, R.; Xu, Y.; Huo, T. A new dual-channel convolutional neural network and its application in rolling bearing fault diagnosis. J. Meas. Sci. Technol. 2024, 35, 096130. [Google Scholar] [CrossRef]
- Alkharsan, A.; Ata, O. HawkFish Optimization Algorithm: A Gender-Bending Approach for Solving Complex Optimization Problems. J. Electron. 2025, 14, 611. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Shang, L.; Liu, Y.; Lou, Z.; Quan, S.; Adluru, N.; Guan, B.; Sethares, W.A. Vision Backbone Enhancement via Multi-Stage Cross-Scale Attention. arXiv 2023, arXiv:2308.05872. [Google Scholar]
- Gao, S.-H.; Cheng, M.-M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P. Res2net: A new multi-scale backbone architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 652–662. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Kiranyaz, S.; Devecioglu, O.C.; Alhams, A.; Sassi, S.; Ince, T.; Avci, O.; Gabbouj, M. Exploring Sound vs Vibration for Robust Fault Detection on Rotating Machinery. IEEE Sens. J. 2024, 24, 23255–23264. [Google Scholar] [CrossRef]
- Du, J.; Li, X.; Gao, Y.; Gao, L. Integrated gradient-based continuous wavelet transform for bearing fault diagnosis. J. Sens. 2022, 22, 8760. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, L. An intelligent fault diagnosis method of rolling bearings based on short-time Fourier transform and convolutional neural network. J. Fail. Anal. Prev. 2023, 23, 795–811. [Google Scholar] [CrossRef]
- Wang, X.; Hua, T.; Xu, S.; Zhao, X. A novel rolling bearing fault diagnosis method based on BLS and CNN with attention mechanism. J. Mach. 2023, 11, 279. [Google Scholar] [CrossRef]
- Siddique, M.F.; Saleem, F.; Umar, M.; Kim, C.H.; Kim, J.-M. A Hybrid Deep Learning Approach for Bearing Fault Diagnosis Using Continuous Wavelet Transform and Attention-Enhanced Spatiotemporal Feature Extraction. Sensors 2025, 25, 2712. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; Mao, M. Enhancing Fault Diagnosis: A Hybrid Framework Integrating Improved SABO with VMD and Transformer–TELM. Lubricants 2025, 13, 155. [Google Scholar] [CrossRef]


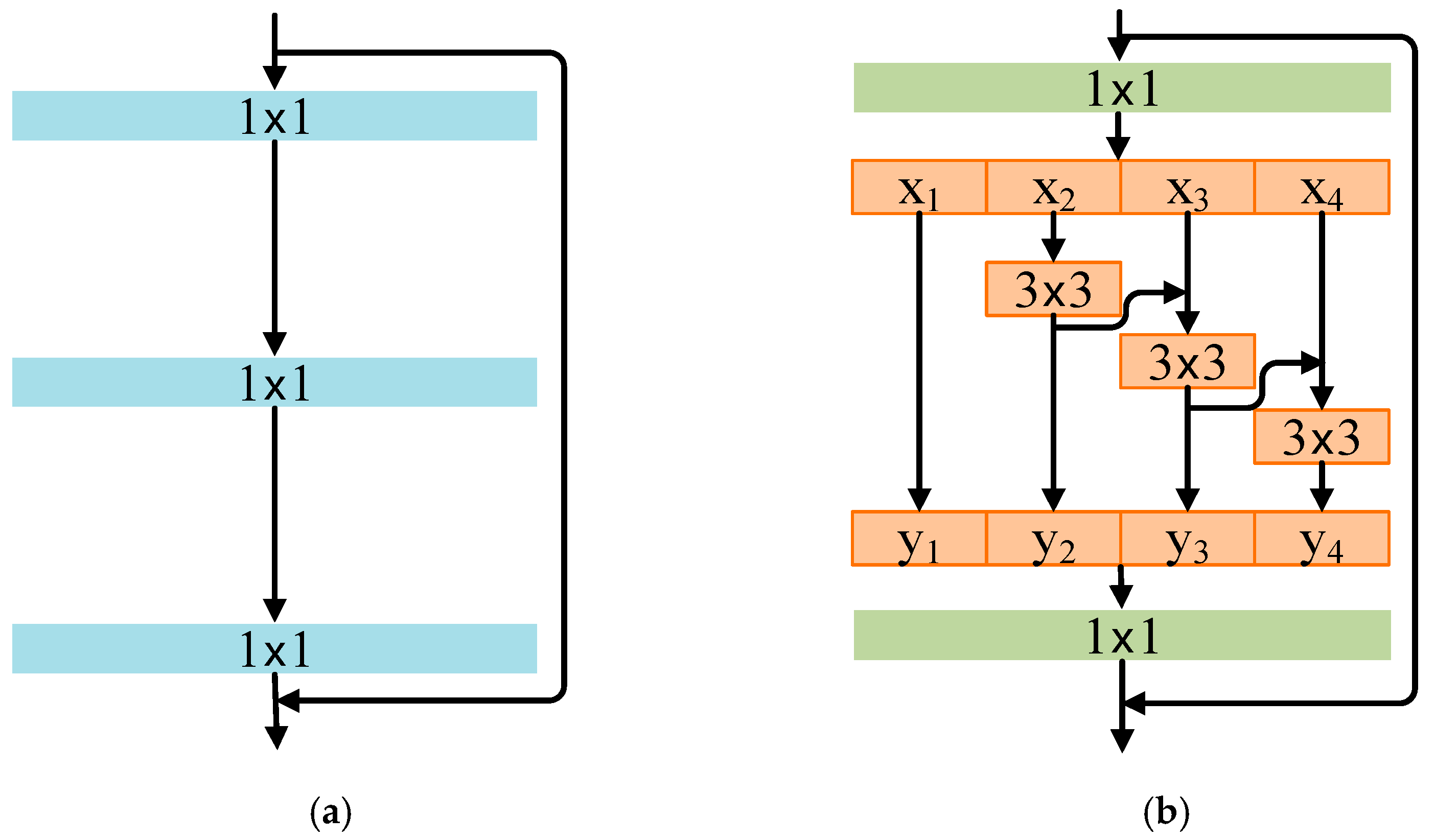








| Layer | Type | Input Dimensions | Output Dimensions | Number of Branches | Convolution Kernel | Parameter Settings |
|---|---|---|---|---|---|---|
| Input1 | Input layer | H × W × 3 | H × W × 3 | 3 | - | Time-frequency domain graph input |
| Patch Embedding | Embedding Layer | H × W × 3 | (H/4) × (W/4) × 96 | 96 | 4 × 4 | Linear embedding, dividing the image into 4 × 4 small patches |
| Swin-T Stage1 | Swin Transformer Block | (H/4) × (W/4) × 96 | (H/4) × (W/4) × 96 | 96 | 7 × 7 | Contains 2 blocks, window size 7, MLP expansion factor 4 |
| Swin-T Stage2 | Swin Transformer Block | (H/4) × (W/4) × 96 | (H/8) × (W/8) × 192 | 192 | 7 × 7 | Containing 2 blocks, window size 7, MLP expansion factor 4, downsampling |
| Swin-T Stage3 | Swin Transformer Block | (H/8) × (W/8) × 192 | (H/16) × (W/16) × 384 | 384 | 7 × 7 | Contains 6 blocks, window size 7, MLP expansion factor 4, downsampling |
| Swin-T Stage4 | Swin Transformer Block | (H/16) × (W/16) × 384 | (H/32) × (W/32) × 768 | 768 | 7 × 7 | Contains 2 blocks, window size 7, MLP expansion factor 4, downsampling |
| MSCSA Module | Attention Module | (H/32) × (W/32) × 768 | (H/32) × (W/32) × 768 | 768 | - | Pool(1,2,4,8) → concat → CSA + Intra-FFN |
| Layer | Type | Input Dimensions | Output Dimensions | Number of Branches | Convolution Kernel | Parameter Settings |
|---|---|---|---|---|---|---|
| Input2 | Input layer | H × W × 1 | H × W × 1 | 1 | - | Time-domain image input |
| Res2Net Stage1 | Res2Net Block | H × W × 1 | H × (W/2) × 64 | 64 | 3 × 3 (stride = 2) | Contains 3 blocks, stride 2, number of branches 64, scale dimension 4 |
| Res2Net Stage2 | Res2Net Block | H × (W/2) × 64 | H×(W/4) × 128 | 128 | 3 × 3 (stride = 2) | Containing 4 blocks, stride 2, number of branches 128, scale dimension 4 |
| Res2Net Stage3 | Res2Net Block | H × (W/4) × 128 | H × (W/8) × 256 | 256 | 3 × 3 (stride = 2) | Consisting of 6 blocks, with a stride of 2, 256 branches, and a scale dimension of 4 |
| Res2Net Stage4 | Res2Net Block | H × (W/8) × 256 | H × (W/16) × 512 | 512 | 3 × 3 (stride = 2) | Containing 3 blocks, stride 2, number of branches 512, scale dimension 4 |
| ECA Module | Attention Module | H × (W/16) × 512 | H × (W/16) × 512 | 512 | 1D-Conv, kernel size = k | GAP → 1D-Conv → Sigmoid → Scale, local cross-branch interaction |
| Layer | Type | Input Dimensions | Output Dimensions | Number of Branches | Convolution Kernel | Parameter Settings |
|---|---|---|---|---|---|---|
| Concatenation | Feature fusion layer | H/32 × W/32 × 768 + H × (W/16) × 512 | H/32 × W/32 × (768 + 512) | 1280 | - | Branch splicing |
| 1 × 1 Convolution | Branch compression | H/32 × W/32 × 1280 | H/32 × W/32 × 1024 | 1024 | 1 × 1 | Adjust the number of branches |
| Global Average Pooling | Pooling layer | H/32 × W/32 × 1024 | 1 × 1 × 1024 | 1024 | - | Global average pooling |
| Fully Connected | Fully connected layer | 1 × 1 × 1024 | 1 × 1 × C (C is the number of categories) | C | - | Categorized output |
| Step | Instructions |
|---|---|
| 1. The original acoustic signal x(t) | The input initial vibration signal. |
| 2. HFMD decomposition (HFOA optimized parameters n, L, K, m) | Optimize HFMD parameters using HFOA to decompose signals into multiple modes. |
| 3. Optimal modal time-domain diagram | Select the optimal time-domain modal signal. |
| 4. CWT transform → optimal modal time-frequency diagram. | Perform CWT on the modal signal to obtain the time-frequency diagram. |
| 5. Res2Net + ECA module | Feature extraction from the optimal modal time-domain diagram. |
| 6. Swin Transformer + MSCSA module | Multi-scale attention feature extraction for optimal modal time-frequency diagrams. |
| 7. Channel concatenation (Concat) | Concatenate the features of the two branches. |
| 8. 1 × 1 convolution for channel dimension reduction | Use 1 × 1 convolution to reduce feature channels and decrease computational complexity. |
| 9. Global Average Pooling (GAP) | Pooling operation to generate global feature vectors. |
| 10. Fully connected layer (classification output) | Perform fault classification output. |
| Fault Type | Fault Diameter | Training Set | Validation Set | Test Set | Tag Value |
|---|---|---|---|---|---|
| Normal state | 0.00 mm | 180 | 60 | 60 | 0 |
| Inner raceway fault | 0.35 mm | 180 | 60 | 60 | 1 |
| Inner raceway fault | 0.40 mm | 180 | 60 | 60 | 2 |
| Outer raceway fault | 0.35 mm | 180 | 60 | 60 | 3 |
| Outer raceway fault | 0.40 mm | 180 | 60 | 60 | 4 |
| Total | -- | 900 | 300 | 300 | -- |
| Model | QU-DMBF Accuracy (%) | Number of Parameters (M) | FLOPs (G) |
|---|---|---|---|
| S-R | 94.83 | 1.45 | 0.98 |
| MS-R | 97.17 | 3.12 | 2.04 |
| S-ER | 96.50 | 2.98 | 1.89 |
| MS-ER | 100.00 | 3.95 | 2.80 |
| Fault Type | Training Set | Validation Set | Test Set | Tag Value |
|---|---|---|---|---|
| Normal state | 150 | 50 | 50 | 0 |
| Inner raceway fault | 150 | 50 | 50 | 1 |
| Inner raceway fault | 150 | 50 | 50 | 2 |
| Outer raceway fault | 150 | 50 | 50 | 3 |
| Total | 600 | 200 | 200 | -- |
| Model | CWRU Accuracy (%) | Number of Parameters (M) | FLOPs (G) |
|---|---|---|---|
| STFT-2DCNN | 81.0 | 1.10 | 0.65 |
| CWT-2DCNN | 83.1 | 1.34 | 0.84 |
| CNN-GRU | 92.9 | 3.22 | 2.85 |
| Dual channel 2DCNN | 93.1 | 3.75 | 2.92 |
| BiLSTM-ResNet | 93.5 | 4.20 | 3.60 |
| Transformer-TELM | 94.8 | 4.90 | 3.95 |
| MS-ER | 98.8 | 3.95 | 2.80 |
| Fault Characteristic Frequency | Value |
|---|---|
| , Hz | 45 |
| , Hz | 34 |
| , Hz | 17 |
| Type | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 |
|---|---|---|---|---|---|---|
| Inner raceway | 0.096 | 0.086 | 0.174 | 0.031 | 0.207 | -- |
| Outer raceway | 0.229 | 0.165 | 0.139 | 0.033 | -- | -- |
| Rolling element | 0.213 | 0.153 | 0.129 | 0.074 | 0.026 | 0.265 |
| Fault Types | Training Set | Validation Set | Test Set | Label Value |
|---|---|---|---|---|
| Normal condition | 150 | 50 | 50 | 0 |
| Inner raceway fault | 150 | 50 | 50 | 1 |
| Outer raceway fault | 150 | 50 | 50 | 2 |
| Rolling element fault | 150 | 50 | 50 | 3 |
| Total | 600 | 200 | 200 | -- |
| Model | CWRU Accuracy (%) | Number of Parameters (M) | FLOPs (G) |
|---|---|---|---|
| STFT-2DCNN | 74.2 | 1.10 | 0.65 |
| CWT-2DCNN | 82.2 | 1.34 | 0.84 |
| CNN-GRU | 93.5 | 3.22 | 2.85 |
| Dual channel 2DCNN | 94.2 | 3.75 | 2.92 |
| MS-ER | 98.4 | 3.95 | 2.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, H.; Xie, J. Fault Diagnosis of Rolling Bearings Based on HFMD and Dual-Branch Parallel Network Under Acoustic Signals. Sensors 2025, 25, 5338. https://doi.org/10.3390/s25175338
Wang H, Wang H, Xie J. Fault Diagnosis of Rolling Bearings Based on HFMD and Dual-Branch Parallel Network Under Acoustic Signals. Sensors. 2025; 25(17):5338. https://doi.org/10.3390/s25175338
Chicago/Turabian StyleWang, Hengdi, Haokui Wang, and Jizhan Xie. 2025. "Fault Diagnosis of Rolling Bearings Based on HFMD and Dual-Branch Parallel Network Under Acoustic Signals" Sensors 25, no. 17: 5338. https://doi.org/10.3390/s25175338
APA StyleWang, H., Wang, H., & Xie, J. (2025). Fault Diagnosis of Rolling Bearings Based on HFMD and Dual-Branch Parallel Network Under Acoustic Signals. Sensors, 25(17), 5338. https://doi.org/10.3390/s25175338





