Development of a Dynamic Path Planning System for Autonomous Mobile Robots Using a Multi-Agent System Approach
Abstract
1. Introduction
2. Related Literature
2.1. Mobile Robot Path Planning
2.2. Mobile Robot Conflict Resolution
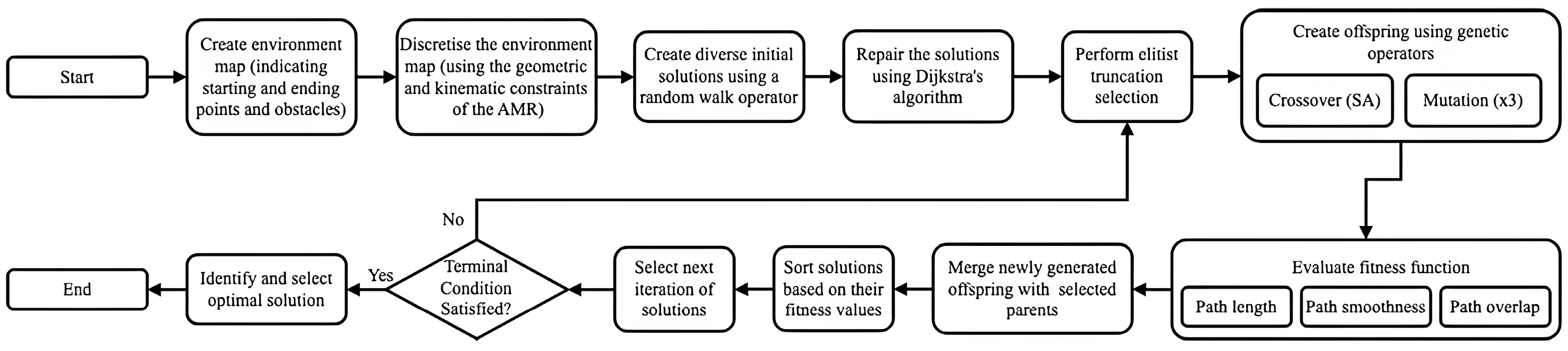
3. Design of the Path Planning System
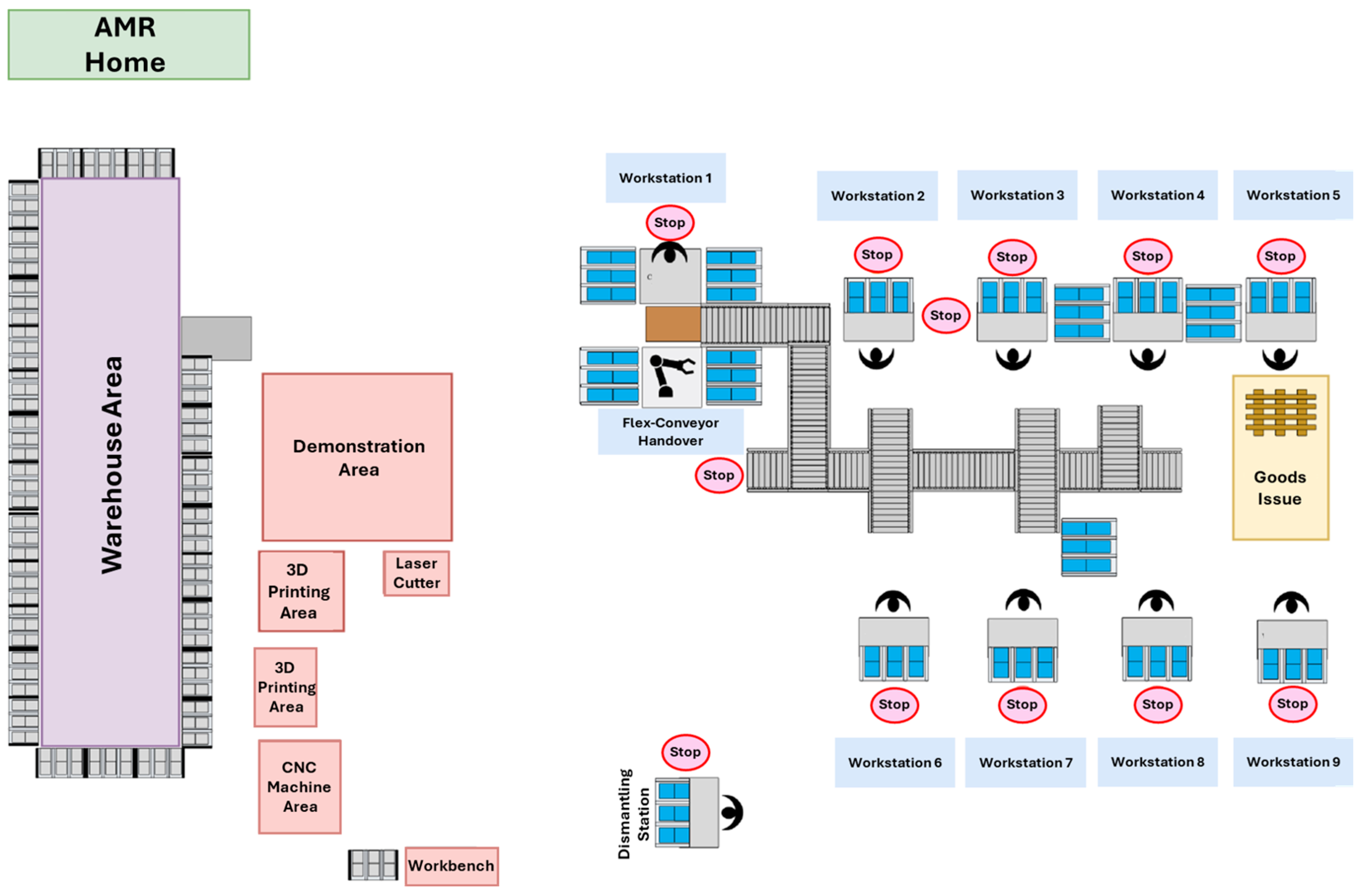
3.1. Environmental Modelling
3.2. Hybrid GA Formulation
3.3. Multi-Agent System Design
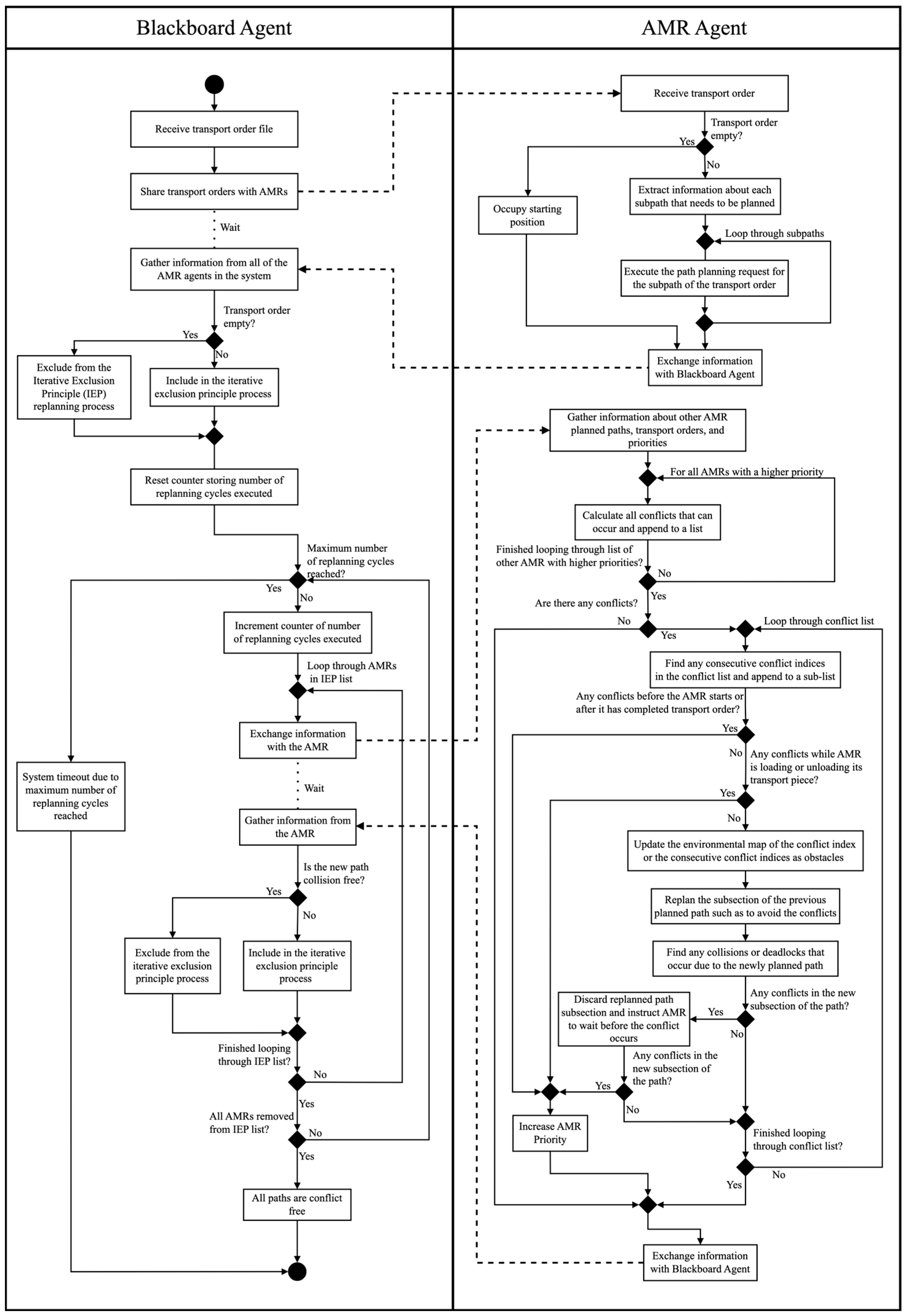
3.4. Multi-Robot Conflict-Resolution Mechanism
3.4.1. Receiving and Assigning Transport Orders
3.4.2. Path Generation and Priority Assignment
3.4.3. Knowledge Sharing of the Joint Paths
3.4.4. Inclusion and Replanning Process
4. Evaluation and Results
4.1. Evaluation Against Other Path Planning Algorithms
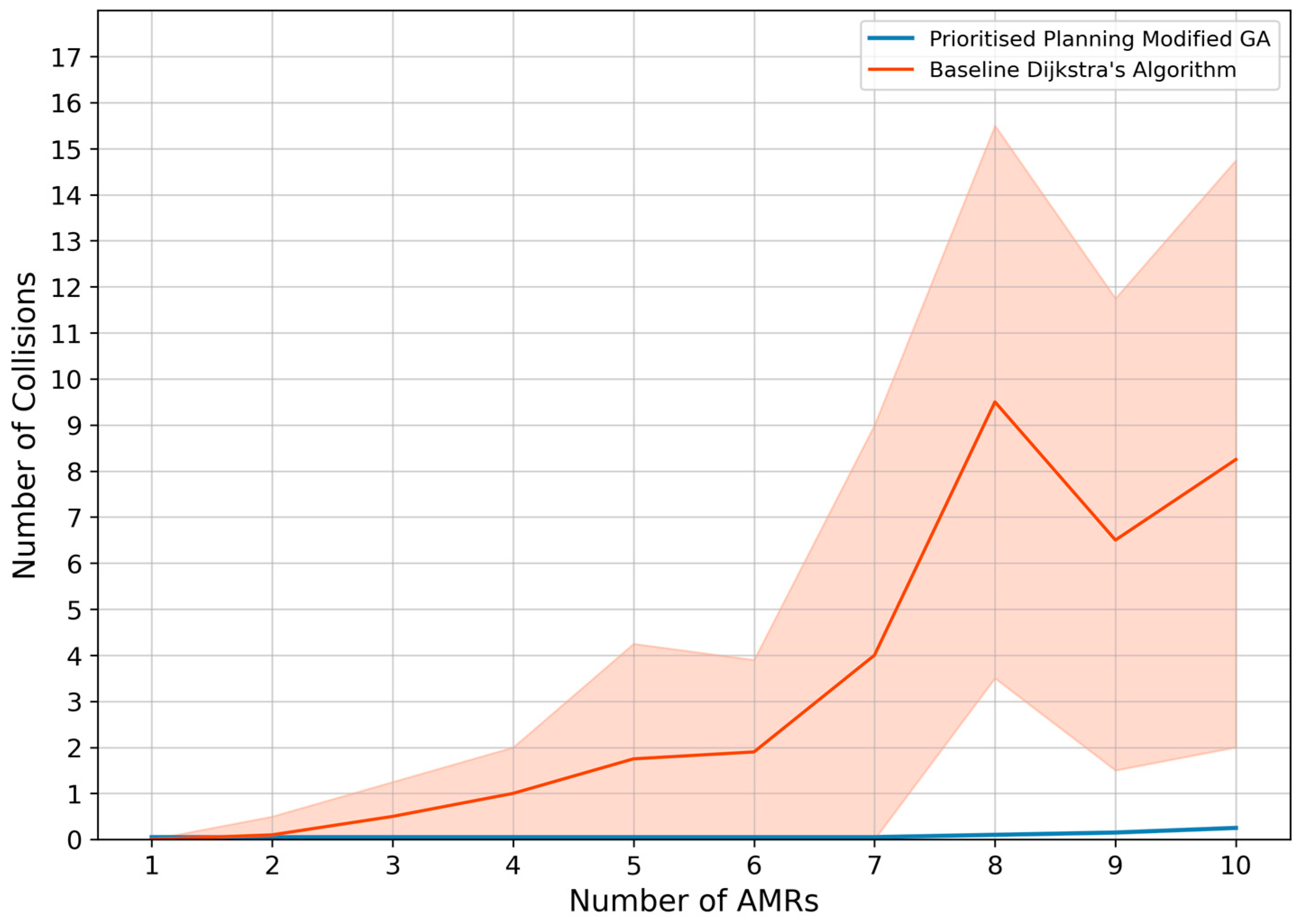
4.2. Evaluation Under Increasing Number of AMRs
4.3. Evaluation Under Various Disturbance Scenarios
- (1)
- Scenario 1: Missing part at workstation;
- (2)
- Scenario 2: Excess supply at workstation;
- (3)
- Scenario 3: Addition of a static obstacle;
- (4)
- Scenario 4: Failure of transport system;
- (5)
- Scenario 5: Addition of a dynamic obstacle;
- (6)
- Scenario 6: Machine breakdown at workstation.
- Scenario 1: Missing part at workstation
- Scenario 2: Excess supply at workstation
- Scenario 3: Addition of a static obstacle
- Scenario 4: Failure of transport system
- Scenario 5: Addition of a dynamic obstacle
- Scenario 6: Machine breakdown at workstation
- Summary
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| ACO | Ant Colony Optimisation |
| AMR | Autonomous Mobile Robot |
| CBD | Cell-Based Decomposition |
| CNN | Convolutional Neural Network |
| DDQN | Double Deep Q-Network |
| FMS | Flexible Manufacturing System |
| FNN | Feedforward Neural Network |
| GA | Genetic Algorithm |
| GRU | Gated Recurrent Units |
| IEP | Iterative Exclusion Principle |
| ISO | International Organisation for Standardisation |
| MAS | Multi-Agent System |
| MPCA | Multi-Party Collision Avoidance |
| RL | Reinforcement Learning |
| PCA | Predictive Collision Avoidance |
| PP | Priority-based Planning |
| PSO | Particle Swarm Optimisation |
References
- Demir, N.; Demircioglu, P.; Bogrekci, I. Advancing Industry 4.0 With ROS: A Case Study On Autonomous Mobile Robot Technological Advancements. Int. J. 3D Print. Technol. Dig. Ind. 2024, 8, 130–142. [Google Scholar] [CrossRef]
- Lackner, T.; Hermann, J.; Kuhn, C.; Palm, D. Review of Autonomous Mobile Robots in Intralogistics: State-of-the-Art, Limitations and Research Gaps. Procedia CIRP 2024, 130, 930–935. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, Z.; Yan, Y.; Yang, C.; Hu, Y. Multi-Agent Policy Learning-Based Path Planning for Autonomous Mobile Robots. Eng. Appl. Artif. Intell. 2024, 129, 107631. [Google Scholar] [CrossRef]
- AbuJabal, N.; Baziyad, M.; Fareh, R.; Brahmi, B.; Rabie, T.; Bettayeb, M. A Comprehensive Study of Recent Path-Planning Techniques in Dynamic Environments for Autonomous Robots. Sensors 2024, 24, 8089. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Zakaria, M.A.; Younas, M. Path Planning Trends for Autonomous Mobile Robot Navigation: A Review. Sensors 2025, 25, 1206. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path Planning Techniques for Mobile Robots: Review and Prospect. Expert. Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Matos, D.M.; Costa, P.; Sobreira, H.; Valente, A.; Lima, J. Efficient Multi-Robot Path Planning in Real Environments: A Centralized Coordination System. Int. J. Intell. Robot. Appl. 2024, 9, 217–244. [Google Scholar] [CrossRef]
- Reda, M.; Onsy, A.; Ghanbari, A.; Haikal, A.Y. Path Planning Algorithms in the Autonomous Driving System: A Comprehensive Review. Rob. Auton. Syst. 2024, 174, 104630. [Google Scholar] [CrossRef]
- Loganathan, A.; Ahmad, N.S. A Systematic Review on Recent Advances in Autonomous Mobile Robot Navigation. Eng. Sci. Technol. Int. J. 2023, 40, 101343. [Google Scholar] [CrossRef]
- Heselden, J.R.; Das, G.P. Heuristics and Rescheduling in Prioritised Multi-Robot Path Planning: A Literature Review. Machines 2023, 11, 1033. [Google Scholar] [CrossRef]
- Abujabal, N.; Fareh, R.; Sinan, S.; Baziyad, M.; Bettayeb, M. A Comprehensive Review of the Latest Path Planning Developments for Multi-Robot Formation Systems. Robotica 2023, 41, 2079–2104. [Google Scholar] [CrossRef]
- Marek, D.; Paszkuta, M.; Szyguła, J.; Biernacki, P.; Domański, A.; Szczygieł, M.; Król, M.; Wojciechowski, K. Swarm of Drones in a Simulation Environment—Efficiency and Adaptation. Appl. Sci. 2024, 14, 3703. [Google Scholar] [CrossRef]
- Kvitko, D.; Rybin, V.; Bayazitov, O.; Karimov, A.; Karimov, T.; Butusov, D. Chaotic Path-Planning Algorithm Based on Courbage–Nekorkin Artificial Neuron Model. Mathematics 2024, 12, 892. [Google Scholar] [CrossRef]
- Rothfuß, S.; Prezdnyakov, R.; Flad, M.; Hohmann, S. Decentralized Path Planning for Cooperating Autonomous Mobile Units. Forsch. Im Ingenieurwesen/Eng. Res. 2019, 83, 137–147. [Google Scholar] [CrossRef]
- Wang, C.; Mao, J. Summary of AGV Path Planning. In Proceedings of the 2019 IEEE 3rd International Conference on Electronic Information Technology and Computer Engineering, Xiamen, China, 18–20 October 2019; pp. 332–335. [Google Scholar]
- De Ryck, M.; Versteyhe, M.; Debrouwere, F. Automated Guided Vehicle Systems, State-of-the-Art Control Algorithms and Techniques. J. Manuf. Syst. 2020, 54, 152–173. [Google Scholar] [CrossRef]
- Fragapane, G.; de Koster, R.; Sgarbossa, F.; Strandhagen, J.O. Planning and Control of Autonomous Mobile Robots for Intralogistics: Literature Review and Research Agenda. Eur. J. Oper. Res. 2021, 294, 405–426. [Google Scholar] [CrossRef]
- Dong, H.; Li, W.; Zhu, J.; Duan, S. The Path Planning for Mobile Robot Based on Voronoi Diagram. In Proceedings of the 3rd International Conference on Intelligent Networks and Intelligent Systems, Shenyang, China, 1–3 November 2010; pp. 446–449. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-Objective Multi-Robot Path Planning in Continuous Environment Using an Enhanced Genetic Algorithm. Expert. Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Patle, B.K.; Babu L, G.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A Review: On Path Planning Strategies for Navigation of Mobile Robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Qiu, L.; Wang, J.; Chen, W.; Wang, H. Heterogeneous AGV Routing Problem Considering Energy Consumption. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics, Zhuhai, China, 6–9 December 2015; pp. 1894–1899. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning. IEEE Trans. Industr Inform. 2013, 9, 132–141. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Dou, S.; Peng, L.; Su, X. Research Summary of Intelligent Optimization Algorithm for Warehouse AGV Path Planning. In LISS 2021: Proceedings of the 11th International Conference on Logistics, Informatics and Service Sciences; Springer Nature: Singapore, 2022; pp. 96–110. [Google Scholar] [CrossRef]
- Stern, R. Multi-Agent Path Finding—An Overview; Springer: Cham, Switzerland, 2019; Volume 11866, ISBN 978-3-030-33274-7. [Google Scholar]
- Van Den Berg, J.P.; Overmars, M.H. Prioritized Motion Planning for Multiple Robots. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 430–435. [Google Scholar] [CrossRef]
- Samek, J.; Šišlák, D.; Volf, P.; Pǐchouček, M. Multi-Party Collision Avoidance among Unmanned Aerial Vehicles. In Proceedings of the IEEE/WIC/ACM International Conference on Intelligent Agent Technology, Fremont, CA, USA, 2–5 November 2007; pp. 403–406. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Shojaeipour, S.; Mohamed Haris, S.; Khairir, M.I. Vision-Based Mobile Robot Navigation Using Image Processing and Cell Decomposition. In Proceedings of the First International Visual Informatics Conference, Kuala Lumpur, Malaysia, 11–13 November 2009; Volume 5857, pp. 90–96. [Google Scholar]
- Sarkar, R.; Barman, D.; Chowdhury, N. Domain Knowledge Based Genetic Algorithms for Mobile Robot Path Planning Having Single and Multiple Targets. J. King Saud. Univ. Comput. Inf. Sci. 2022, 34, 4269–4283. [Google Scholar] [CrossRef]
- Lee, J.; Davari, H.; Singh, J.; Pandhare, V. Industrial Artificial Intelligence for Industry 4.0-Based Manufacturing Systems. Manuf. Lett. 2018, 18, 20–23. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Desing to Implementation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 978-0-470-27858-1. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.W. An Effective Initialization Method for Genetic Algorithm-Based Robot Path Planning Using a Directed Acyclic Graph. Inf. Sci. 2016, 332, 1–18. [Google Scholar] [CrossRef]
- Li, G.; Chou, W. Path Planning for Mobile Robot Using Self-Adaptive Learning Particle Swarm Optimization. Sci. China Inf. Sci. 2018, 61, 052204. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Z.; Xie, Y. Path Planning of Mobile Robot Based on Improved Genetic Algorithm. In Proceedings of the 2020 3rd International Conference on Electron Device and Mechanical Engineering, Suzhou, China, 1–3 May 2020; pp. 691–695. [Google Scholar] [CrossRef]
- Xue, Y. Mobile Robot Path Planning with a Non-Dominated Sorting Genetic Algorithm. Appl. Sci. 2018, 8, 2253. [Google Scholar] [CrossRef]
- Tuncer, A.; Yildirim, M. Dynamic Path Planning of Mobile Robots with Improved Genetic Algorithm. Comput. Electr. Eng. 2012, 38, 1564–1572. [Google Scholar] [CrossRef]
- Wu, M.; Chen, E.; Shi, Q.; Zhou, L.; Chen, Z.; Li, M. Path Planning of Mobile Robot Based on Improved Genetic Algorithm. In Proceedings of the 2017 Chinese Automation Congress, Jinan, China, 20–22 October 2017; pp. 6696–6700. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-Agent Systems: A Survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Sousa, N.; Oliveira, N.; Praça, I. A Multi-Agent System for Autonomous Mobile Robot Coordination. arXiv 2021, arXiv:2109.12386. [Google Scholar] [CrossRef]
- Balaji, P.G.; Srinivasan, D. An Introduction to Multi-Agent Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 310, ISBN 9783642144349. [Google Scholar]
- Rocha, J. (Ed.) Multi-Agent Systems; IntechOpen: London, UK, 2017; ISBN 978-953-51-3536-4. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Li, J.; Chen, Y.; Zhao, X.N.; Huang, J. An Improved DQN Path Planning Algorithm. J. Supercomput. 2022, 78, 616–639. [Google Scholar] [CrossRef]
- Quan, H.; Li, Y.; Zhang, Y. A Novel Mobile Robot Navigation Method Based on Deep Reinforcement Learning. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420921672. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated Feedback Recurrent Neural Networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 3, pp. 2067–2075. [Google Scholar]
- Yuan, J.; Wang, H.; Lin, C.; Liu, D.; Yu, D. A Novel GRU-RNN Network Model for Dynamic Path Planning of Mobile Robot. IEEE Access 2019, 7, 15140–15151. [Google Scholar] [CrossRef]
- Schuhmacher, J.; Hummel, V. Development of an Intelligent Warehouse and Autonomously Controlled Intralogistics Scenario to Investigate the Mastering of Short-Term Turbulences at Werk150. In Proceedings of the Conference on Learning Factories (CLF) 2021, Graz, Austria, 9 June 2021. [Google Scholar] [CrossRef]
- Sonnenberg, M. Comprehensive Configuration- and Rating System for a Cyber—Physical Production System for a Small Batch Production. In Proceedings of the 12th Conference on Learning Factories (CLF 2022), Singapore, 15 April 2022. [Google Scholar] [CrossRef]





| Factor | Weight | Reason for Inclusion | Scoring Scheme |
|---|---|---|---|
| Weighted Path Length | 3 | A shorter path length indicates a more efficient path. | The score is the weighted average path length of the two AMRs, with a 60% weighting assigned to the prioritised AMR and a 40% weighting assigned to the other AMR. A single normalised score is then obtained by dividing the weighted average path length for the AMRs by the path length obtained by Dijkstra’s algorithm. |
| Weighted Path Smoothness | 3 | The path smoothness determines the energy usage, which should be minimised. | The score is the weighted average path smoothness, with a 60% weighting assigned to the prioritised AMR and a 40% weighting assigned to the other AMR. The final path smoothness score is obtained by dividing the weighted average path smoothness of the AMRs by the path smoothness obtained by Dijkstra’s algorithm. |
| Total Path Overlap | 3 | The path overlap score is represented by the total overlap between AMR paths and needs to be minimised to reduce the risk of replanning, which also increases the execution time. | The score is the total path overlap score obtained by dividing the total overlap between the AMR paths by the total path length. The final path overlap score value is obtained by dividing the path overlap score by the total path overlap obtained by Dijkstra’s algorithm. |
| Execution Time | 2 | The system should be reactive and allow for fast planning and replanning for all of the cases. | The execution time value is the number of seconds of execution time required for the dynamic path planning system during implementation. |
| Number of Failures | 5 | The algorithm fails if it not able to plan any sub-path during the path planning task. | The failure score is obtained by using the frequency count of the total failures during the experiment. |
| Number of Collisions | 4 | The system should be robust to various scenarios and the number of collisions should be minimised to avoid failure of the system. | The score is the frequency count of the failures due to collisions during implementation. |
| Number of Deadlocks | 4 | A deadlock is a situation where two AMRs cannot continue following their pre-planned paths without causing a collision with each other. | The score is the frequency count of the failures due to deadlocks during implementation. |
| Criteria | Weight | Dijkstra | RL with DDQN GRU– | Hybrid GA |
|---|---|---|---|---|
| CNN Architecture | ||||
| Number of Failures | 5 | 0 | 9 | 0 |
| Number of Collisions | 4 | 9 | 6 | 0 |
| Number of Deadlocks | 4 | 5 | 2 | 0 |
| Weighted Path Length | 3 | 1 | 1.09 | 1.01 |
| Weighted Path Smoothness | 3 | 1 | 2.64 | 0.95 |
| Total Path Overlap | 3 | 1 | 1.80 | 0.44 |
| Execution Time (s) | 2 | 0 | 1.29 | 0.78 |
| Total | 65.00 | 104.09 | 8.76 |
| Mobile Robot | Travel Distance (m) | Smoothness Score (rad) | Overlap Score (m) |
|---|---|---|---|
| Mobile Robot 1 | 86.5600 ± 3.1309 | 29.1226 ± 5.0598 | 24.4800 ± 4.5146 |
| Mobile Robot 2 | 69.0400 ± 2.5632 | 26.7664 ± 5.4410 | 24.4800 ± 4.5146 |
| Factor | Travel Distance (m) | Smoothness Score (rad) | Overlap Score (m) |
|---|---|---|---|
| Mobile Robot 1 | 68.8600 ± 5.0242 | 24.8186 ± 4.6316 | 15.4000 ± 3.0305 |
| Mobile Robot 2 | 70.8000 ± 2.8284 | 27.2690 ± 5.8106 | 15.4000 ± 3.0305 |
| Factor | Travel Distance (m) | Smoothness Score (rad) | Overlap Score (m) |
|---|---|---|---|
| Mobile Robot 1 | 84.8400 ± 2.2889 | 28.2920 ± 4.3829 | 17.5000 ± 2.6049 |
| Mobile Robot 2 | 48.5200 ± 1.7052 | 16.6640 ± 3.1921 | 17.5000 ± 2.6049 |
| Factor | Travel Distance (m) | Smoothness Score (rad) | Overlap Score (m) |
|---|---|---|---|
| Mobile Robot 1 | 22.2400 ± 14.4682 | 6.2489 ± 3.2426 | 10.8400 ± 3.9865 |
| Mobile Robot 2 | 65.0800 ± 6.9424 | 27.7032 ± 7.5232 | 10.8400 ± 3.9865 |
| Factor | Travel Distance (m) | Smoothness Score (rad) | Overlap Score (m) |
|---|---|---|---|
| Mobile Robot 1 | 75.8000 ± 19.3116 | 24.5004 ± 10.2933 | 14.5800 ± 5.1554 |
| Mobile Robot 2 | 67.7000 ± 19.1857 | 28.2682 ± 9.4582 | 14.5800 ± 5.1554 |
| Factor | Travel Distance (m) | Smoothness Score (rad) | Overlap Score (m) |
|---|---|---|---|
| Mobile Robot 1 | 99.4800 ± 13.9023 | 44.7806 ± 7.4470 | 18.6200 ± 4.1151 |
| Mobile Robot 2 | 69.8000 ± 3.6197 | 23.5491 ± 5.4803 | 18.6200 ± 4.1151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fourie, B.; Louw, L.; Bitsch, G. Development of a Dynamic Path Planning System for Autonomous Mobile Robots Using a Multi-Agent System Approach. Sensors 2025, 25, 5317. https://doi.org/10.3390/s25175317
Fourie B, Louw L, Bitsch G. Development of a Dynamic Path Planning System for Autonomous Mobile Robots Using a Multi-Agent System Approach. Sensors. 2025; 25(17):5317. https://doi.org/10.3390/s25175317
Chicago/Turabian StyleFourie, Bradley, Louis Louw, and Günter Bitsch. 2025. "Development of a Dynamic Path Planning System for Autonomous Mobile Robots Using a Multi-Agent System Approach" Sensors 25, no. 17: 5317. https://doi.org/10.3390/s25175317
APA StyleFourie, B., Louw, L., & Bitsch, G. (2025). Development of a Dynamic Path Planning System for Autonomous Mobile Robots Using a Multi-Agent System Approach. Sensors, 25(17), 5317. https://doi.org/10.3390/s25175317






